2011.12 第十二届五年级中环杯初赛试题
12届初赛解析
杯赛速递——三年级中环杯初赛在短短三年内，三年级中环杯的考点变了又变，让人有种琢磨不透的感觉，但不管考点发生了什么变化，对于杯赛考试总有些东西是不变的。
第一个不变的就是我们大多数家长让孩子参加杯赛的原因——小升初。
小升初是一条漫漫长路，三年级的杯赛只是一个开始，只有积累了经验、获得了认可和鼓励，在四年级的冲刺中才会充满信心，所以不论成绩如何，都请您和孩子一起进行反思，鼓励孩子继续努力。
其次，学习依旧是一个持续反复的过程，不会因为你是三年级的孩子就不考察二年级的知识点了，所以有空的时候就让孩子们回顾一下之前所学吧。
我们一直在努力的往前学，但之前所学的我们还记得多少呢？最后，孩子们需要全面的发展，中环杯的考题已经不仅仅是在考察孩子们的数学水平了，竞赛试题要求孩子们有着良好的阅读理解能力，来弄清题意，适当的把孩子们的精力分一些到语文上去吧。
好啦，说了那么多，让我们一起来看看今年三年级中环杯的解析吧~第十二届“中环杯”小学生思维能力训练活动三年级选拔赛试题解析一、填空题1、计算：100-96+92-88+……+12-8+4=（）【解析】考点：速算与巧算（分组法），等差数列求和公式易错点：等差数列求和公式算出项数后需要除以2，求出组数。
100-96+92-88+……+12-8+4 =（100-96）+（92-88）+……+（12-8）+4求出项数：（100-8）÷4+1=24，24÷2=12，12+1=13100-96+92-88+……+12-8+4 =（100-96）+（92-88）+……+（12-8）+4=4×13=52【答案】522、在下列各数字间的适当位置填入恰当的运算符号或括号，使等式成立。
若数字间不填任何符号或括号，则视为一个数。
例如“2 0+1+1”视为“20+1+1”。
2 0 1 1 1 1 0 2 =2011【解析】考点：巧填算符本题的关键是找到2011，然后利用加减乘除和括号进行运算。
第12届中环杯四年级初赛详解
四年级 第十二届中环杯初赛解析第十二届“中环杯”小学生思维能力训练活动 四年级选拔赛试卷全方位解析一、填空题（每题 7 分，共 56 分） ： 1．计算：20112012÷10001＋30363033÷30003＝( 【解析】计算:除法的性质 原式＝20112012÷10001＋10121011÷10001 ＝(20112012＋10121011)÷10001 ＝30233023÷10001 ＝3023 【答案】3023 )2．从 1，3，5，7，……，47，49 这 25 个奇数中，不重复地取数字，至少取出( 中有两个数的和是 46。
【解析】抽屉原理，最不利原则。
先列出和为 46 的两数分组： （1，45） ， （3，43）……（21，25） ，共 11 组； 剩余其他数字为 23，47，49，共 3 个。
)个数，才能保证取出的数考虑最不利原则，先从 11 组中每组取 1 个，将剩下 3 个数全取完，最后再取无论哪个数，都可完成这 件事，即至少取出 11＋3＋1＝15（个） 。
【答案】153．一根绳子围着大树绕 9 圈剩 4 米，如果围着大树绕 10 圈又缺 1 米，那么绕 8 圈还剩( 【解析】盈亏问题。
)米。
由绕 9 圈多 4 米，可将绕 10 圈先绕 9 圈，此时多 4 米，且需再绕一圈，而再绕一圈时缺 1 米，可知 1 圈的长度为 5 米。
算式： （4+1）÷（10-9）=5（米） 由此可知绳长为 9×5＋4＝49（米） ，则绕 8 圈还剩 49－8×5＝9（米） 。
【答案】94． 今年是中国共产党建党 90 周年。
据考证， 伟大的中国共产党的确切成立日期是 1921 年 7 月 23 日。
今年 （2011 年）的 7 月 23 日是星期六，那么 90 年前的这一天是星期( 【解析】余数与周期。
11届中环杯决赛五年级
袜子曰也有可能是掉了的 3 只袜子颜色两两
不同袁于是他只剩 2 双袜子了遥 那么后者的可能性是前者的渊
冤倍遥
2援 A尧B尧C 三辆汽车以相同的速度同时从甲地开往乙地遥 出发后 1 小时袁A 车出
了留半小时后袁以原速度的
5 6
继续前进遥
B尧
C 两车行至距离甲地 240 千米处时袁B 车出了故障袁 于是 C 车继续前进袁B 车停了半
287袁求这两个数的和是多少钥
第十一届野中环杯冶小学生思维能力训练活动 五年级决赛
题型 一尧填空题 二尧动手动脑题
共计
得分
一尧填空题院渊每题 7 分袁共 缘6 分遥 冤
1. 计算院20112011伊1949原19501950伊2009越渊
冤遥
2援 将一堆练习本平均分给班上的同学袁每人可得到 12 本遥如果只分给男生袁则
每个男生可比原来多分到 9 本遥 那么该班男生人数与女生人数的比是渊
冤个盒子里的乒乓球数量相同遥
A
7援 如图袁两个等腰直角三角形重叠在一
E
起袁阴影部分为重合部分袁阴影部分的面积
G
为渊
冤平方厘米遥
7 厘米 H
I
8援 小明有 5 双袜子袁 颜色分别是白色尧 黑色尧红色尧蓝色尧灰色遥 有一天袁他发现掉了
B
D 10 厘米
C 2厘米
F
其中的 3 只袜子遥 情况可能是院掉了的 3 只 袜子其中有 2 只颜色一样袁于是他还有 3 双
小时后袁也以原速度的
5 6
继续前进遥
结果袁C
车比
B 车早 1 小时到达乙地袁B 车比 A
车早 1 小时到达乙地遥 求甲尧乙两地的距离遥
3援 有一种自行车轮胎袁安装在自行车前轮上最多行驶 6000 千米后报废袁安装在 后轮上最多行驶 3600 千米后就报废遥 为了行驶尽可能多的路袁如果采用行驶一段路 程后交换前后轮胎的方法袁 那么安装在自行车上的一对轮胎最多可以行驶多少千 米钥 最好在累积行驶多少千米时交换前后轮胎钥
12届中环杯选拔赛五年级答案
8. 答：951。 观察这个数列后发现，从第 4 个数开始，每个数都是前 3 个数的和。所以所 求的数为 153+281+517＝951。 二、动手动脑题： 1. 答：275 米，450 米或 550 米。 因为两人始终保持匀速，所以从出发开始，甲第二次追上乙所用的总时间是 第一次追上乙所用时间的 2 倍，两人各自所走的路程也是第一次的 2 倍。因 此，甲第二次追上乙时，可以认为乙离开出发点 250×2＝500（米） 。接下来 要分类讨论： 如果这 500 米是不到一圈，那么跑道长 500 50 550 （米） 。 如果这 500 米是超过一圈，那么跑道长 500 50 450 （米） 。 如果这 500 米是不到两圈，那么跑道长（550+50）÷2＝275（米） 如果这 500 米是超过两圈，那么跑道长 500 50 2 225 （米） 。因为甲第 一次追上乙时，乙离开出发点 250 米>225 米，所以舍去。 所以，跑道长 275 米，450 米或 550 米。 2. 答：30 平方厘米。 因为 SBDE SDEC ，所以 D 为 BC 边上的中点，所以 S ADB 方 厘 米 ) 。 又 因 为 SBDE SDEC SACE ， 所 以 SB D E S
4. 答：如图
①
②
③
④
3/3
1 S ABC 90 (平 2
DEC
2 S
ACE
，即
所以 E 为 AB 边上的三等分点， 所以 SADE SADB 3 30（平 SBCE 2SACE ， 方厘米） 3. 答：此题答案不唯一，下图是一种路线。
2/3
第十二届“中环杯”中小学生思维能力训练活动五年级选拔赛答案
2011中环五年级初赛试题
2、如图所示，△ABC的面积是180平方厘米，且△BDE、 △ DEC和△ ACE的面积都相等，求△ ADE面积。
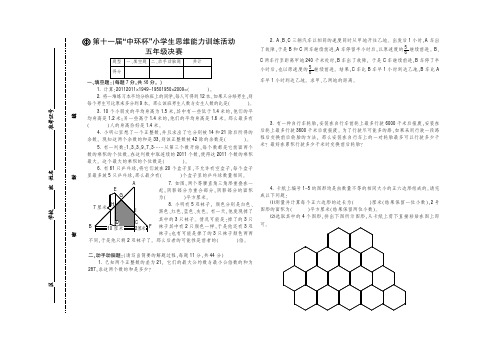
3、某展览馆是一个拥有15间房间的大厅，下图为大厅的平面 图。每天展览馆关门后，都会有一个警卫从大厅的入口进 去，一间房一间房地逐次巡视，最后来到画有 标记的管理 室休息。现在，规定每间房间警卫只能进去一次，且所有 房间都要巡视到。你认为这个警卫应该怎样进行巡视才好 呢？请在图中画出他的巡视路线。
4、如图是一个立方体魔方，我们可以从图中看到它的右侧、上侧和前侧。
如果顺时针转动魔方右侧第一层90度，我们记作进行了一次 R 操作； ' 如果逆时针转动魔方右侧第一层90度，记作 R 。对于上侧和前侧分别进 ' 行相同的旋转操作，分别记为U 、 U '、 F 、 F。现在对魔方进行4次转动： Ｆ Ｒ U ' Ｆ，请你在图中依次画出每完成一次转动后，阴影面 所在的位置。
第十二届“中环杯”小学生意的自然数Ｘ和Ｙ，定义新运算＠：Ｘ＠Ｙ＝
6 XY m X 2Y
，其 中ｍ是一个确定的自然数。如果１＠２＝１，则２＠８＝（ ）。
2、一个各位数字互不相同的五位数，能被3、5、7、11整除， 那么当这个五位数取到最大值的时候，各位数字之和是 （ ）。
6、一支运输小分队奉命把一些物资从驻地送到很远的地方。 每辆运输车装满油最多能行180千米，且途中没有加油站。 由于一辆运输车无法完成任务，队长决定派两辆车执行任 务，其中一辆运输车负责运送物资，另一辆则在中途供给 油料后安全返回驻地。那么，最远可以把物资运到距离驻 地（ ）千米远的地方。
7、现在是上午10点，到（ ）点（ ）分时，时针和分针第 一次重合。
3、从1、2、3、4⋯⋯2000共2000个正整数中，最多能取出 （ ）个数，使得对于取出来的数中的任意三个数a 、b 、 c（ a b c ），都有 ab c 。
五年级数学培优：数阵图、数字谜(含解析)
五年级数学培优：数阵图、数字谜（含解析）将1~11填入图中的○内，使得每条线段上的三个圆圈内数字之和等于22.知识概述1.数阵图的一般解题思路：由于数阵图中没有填充之前各个数的位置无法确定，从每一个单个数上无法进行判断，所以我们采用的是整体与个体相结合考虑的方法，即利用所有相关数和全部相加进行分析.2.数字谜：①数字谜介绍：数字谜从形式上可以分成为横式数字谜与竖式数字谜，从内容上可以分为加减乘除4种数字谜，横式数字谜一般可以转化为竖式数字谜.②数字谜常用的分析法介绍解决数字谜问题最重要的就是找到突破口，突破口你的寻找是需要一定得技巧性，一般来说，首先是观察题目中给出数字的位置，同时找出涉及这些已知数字的所有相关计算，然后根据各种分析法进行突破，突破的顺序一般是三位分析法（个位分析，高位分析和进位借位分析）另外加入三大技巧（估算技巧——结合数位，奇偶分析技巧和分解素因数技巧）等、而且一般应该先从涉及乘法的地方入手，然后在考虑加法后减法的分析（并不完全都是这样）.例1数阵图与数字谜这类问题在历届杯赛中经常出现，属于各大杯赛的高频考点，因为这类题是正确率很高的题目，所以要想取得好成绩，必须掌握这类题型的解题方法. 名师点题【解析】首先求出数阵图中关键位置的数，在数阵图的中间位置，是：（22×5-66）÷4=11，剩下的数从下到大排列，首尾配对即可：1配10，2配9,，3配8，4配7，5配6.在下图中填9个数，使每行、每列、对角线上的三个数的和都相等.那么b处应该填入的数是（）.【解析】这是一个三阶幻方，每行、每列、每条对角线上三个数的和相等，我们称这个相等的和是幻和，幻和是中央的数的3倍，幻和=3b=1.9+b+0.9= 2.8+b，进而得到2b=2.8，b=1.4.在右边的算式中，相同的符号代表相同的数字，不同的符号代表不同的数字，根据这个算式，可以推算出：△□□〇+〇□□△□□☆☆那么：口+○+△+☆=_________.【解析】比较竖式中百位与十位的加法，十位上“□+□”肯定进位，（否则由百位可知□=0），且有“□+□+1＝10+□”，从而□=9，☆=8.例3例2再由个位加法，推知○+△=8.从而口+○+△+☆=9+8+8=25.【巩固拓展】1.将从8开始的11个连续自然数填入下图中的圆圈内，要使每边上的三个数的和都相等，a共有（）种填法.【解析】由于每边上的三个数字和都相等，设每边和为S，从整体考虑将其全部相加和为5S，从个体考虑，除中间数加了5次外，其他数均加了1次，可看作8至18均加了1次，中间数a多加了四次，表示为（8+9+......+18）+4a，列出等式为5S=（8+9+ (18)+4a，化简为5S=143+4a，要使等式成立，4a的末位必须为2，得出三种答案，8，13，18.2.将1-12这十二个自然数分别填入下图的12个圆圈内，使得每条直线上的四个数之和都相等，这个相等的和为__________.【解析】由于每条直线上的四个数之和都相等，设这个相等的和为S，把所有6条直线上的四个数之和相加，得到总和为6S；另一方面，在这样相加中，由于每个数都恰好在两条直线上，所以每个数都被计算了两遍.所以，6(12312)2S=++++⨯，得到S=26，即所求的相等的和为26.3.在右边的竖式中，相同字母代表相同数字，不同字母代表不同数字，则四位数tavs=______.s t v av t s tt t v t t+【解析】首先可以判断t=1，所以s+v=11，v=t+t+1=3，可解得s=11-3=8，又因为a+t=t，所以a=0，1038tavs=.将自然数1、10、19、28、37、46、55分别填人右图中的七个方框中，使每条直线上的三数之和与每个圆周上的三数之和都相等．那么圆心上的那个数应该填多少？【解析】圆心上的数属于三条直线，其余数都属于一条直线一个圆周，所以除中心的数被计算3遍外.其余数都被计算2遍.由()11019283746552392++++++⨯+=+中心数中心数，应是5的倍数，推知中心数为28.【巩固拓展】将3、5、7、11、13、17、19、23、29这9个数分别填人右图的9个○中，使3条边上的○中的数之和都相等.请分别求出满足上述条件的最大的和与最小的和.例1【解析】设三个顶点○内所填的数为a、b、c，每条边上的和为K，三个顶点上的数在求和时各用了2次，所以条边上的三数之和相加得()()3571113171923291273a b c a b c K+++++++++++=+++=；由于所得的和必须能被3整除，而1273421÷=，所以()a b c++的和应被3除余2，a b c++的最小值是571123++=，最大值是29231971++=，所以K的最小值是()12723350+÷=，最大值是()12771366+÷=.请将1～9这9个数填入右图3×3表格中，使得第1,2行三数的乘积分别是70，24，第l、2列三数的乘积分别是21、72.【解析】因为70=2×5×7，21=1×3×7，所以A=7，D等于2或5，因为D×E×F=72，72不能被5整除，所以D为2，72=2×4×9，即E为4或9，且B×E×H=24.24不能被9整除，所以E为4，24=1×4×6，也就是B=1，H=6，剩下的数易得.最后结果为：F IHGEDCBA986542317【巩固拓展】能否在8行8列的方格表的每个空格中（如图），分别填入1、2、3这三个数字中的任一个，使得每行每列及对角线AC、BD上的数字和互不相同？对你的结论加以说明.例2【解析】不可能.这里一共有8行、8列、2条对角线，每行每列及对角线AC、BD上的数字和互不相同，所以数字和一共有8+8+2=18（个）；又根据题目要求，每行、每列及对角线的8个数的和最小取值是8×1=8，最大为8×3=24，8到24一共有17个数.17＜18，所以不可能实现每行每列及对角线AC、BD上的数字和互不相同.将1、2、3、4、5填入5×5的正方形表格的小方格中，使每个数字在每行、每列、每条对角线上都只出现一次，其中部分数字已经填出，请按照以上要求填写其他小方格.【解析】①根据唯一解法，可以快速得到第四行第一列填5；②观察第5列，可知第5行第5列方格中不能填4、5（根据列摒除法）；再观察从左上至右下的对角线，可知第5行第5列方格中不能填1、3（根据对角线摒除法）.那么根据唯一解法，可以确定第5行第5列方格中填2；③对两条对角线进行分析，可以确定第3行第3列方格中只能填4；④再根据唯一解法确定第2行第2列方格中填5；⑤接着可确定第2行第4列方格中填2，第5行第1列方格中填3；至此我们已经填出第1行、第4行、两条对角线上的所有方格中的数字，根据以上解题思路，可以顺势得出其他方格中的数字，最终的问题答案如下：例3【巩固拓展】如右下图，9个3×3的小方格表合并成一个9×9的大方格表，每个格子中填入1-9中的一个数，每个数在每一行、每一列中都只出现一次，并且在原来的每个3 3的小方格表中也只出现一次，10个“☆”处所填数的总和是.【解析】①先确定第6列4个☆的和：（1+2+3+…+8+9）-（1+9+8+4+2）=21；②确定第2层第3宫（9宫格）4个☆的和：（1+2+3+…+8+9）-（3+4+5+6+9）=18；③确定第1行第8列☆：观察所在行、所在列、所在宫，可以确定是5；④确定第3行第1列☆：观察所在行、所在列、所在宫，可以确定是2；所以10个“☆”处所填数的总和是：21+18+5+2=46.将1、3、5、7、9填入等号左边的5个方框中，2、4、6、8填入等号右边的4个方框中，使等式成立，且等号两边的计算结果都是自然数，这个结果最大为.□÷□+□+□□＝□÷□+□□例4【解析】 因为左边必是奇数，所以右边最大值为87.（否则为88），经过尝试，得3÷1+5+79=6÷2+84【巩固拓展】请在算式1111⨯=⨯中填入不同的四个数字，使等号成立.【解析】 在10-19这10个数中，剔除质数后只剩下6数，通过尝试可得到10×18=12×15.在右边的乘法算式中，字母A 、B 和C 分别代表一个不同的数字，每个空格代表一个非零数字.求A 、B 和C 分别代表什么数字.941A B CA B C⨯【解析】 第一个部分积中的9是C×C 的个位数字，所以C 要么是3，要么是7，假设C =3，第二个部分积中的4是积3×B 的个位数字，所以B =8.同理，第三个部分积中的1是积3×B 的个位数字，因此A =7.如果C =7，类似地可知B =2，A =3，但这时第二个部分积不是四位数，因此C ≠7.【巩固拓展】在下图中的除法竖式中，相同的字母代表相同的数字，不同的字母代表不同的数字，那么被除数DEFGF 是多少？例5【解析】显然的D=1，由AB×A=IF可知，A不会超过3，否则得到的乘积应该是3位数，如果A=3，那么B也不能超过3，所以B只能是2，这样的AB×B=32×3=96与AAH矛盾，所以A≠3，所以A=2，根据AB×B=AAH，可以尝试出B=8时，等式成立，得到这些条件既可依次求得：I=5，F=6，E=0，G=9，所以被除数DEFGF是10696.（第十一届中环杯初赛试题及答案）从1至13中选出12个自然数填入3×4的方格中，使每横行四数之和相等，每竖列三数之和也相等（横行的和没有必要与竖列的和相等）.【解析】因为1+2+…+13=91，从中去掉一个数后应该能够被3以及4整除，即能被12整除.由于91÷12=7…7，应该去掉7，所有数的和为84.这样，每个横行的数字之和为84÷3=28，每个竖列的数字之和为84÷4=21.进一步分析可知，六个奇数必须有三个在一列，另外三个在另外一列.三个奇数和为21的，只有1+9+11和3+5+13两组，填好奇数，剩下的数就好填料.典型的两组答案（其余的答案均由这两个答案交换行列得到）如下：1 13 4 10 3 112 12例1如图大、中、小三个正方形组成了8个三角形，现在把2、4、6、8四个数分别填在大正方形的四个顶点；再把2、4、6、8分别填在中正方形的四个顶点上；最后把2、4、6、8分别填在小正方形四个顶点上：（1）能不能使8个三角形顶点上数字之和都相等？ （2）能不能使8个三角形顶点上数字之和各不相同？ 如果能，请画图填上满足要求的数；如果不能，请说明理由.【解析】 （1）不能．如果这8个三角形顶点上数字之和都相等，设它们都等于S.考察外面的4个三角形，每个三角形顶点上的数的和是S ，在它们的和4S 中，大正方形的2、4、6、8各出现一次，中正方形的2、4、6、8各出现二次.即()42468360S =+++⨯=.所以S=60÷4=15.但是三角形每个顶点上的数都是偶数，和不可能是奇数15，因此这8个三角形顶点上数字之和不可能相等.（2）能，下图是一种填法.8个三角形顶点数字之和分别是：8、10、12、14、16、18、20、22.248668862244（第十二届中环杯试题）如图，纸片盖住了乘法算式的所有数字，但是已知每一个被盖住的数都是质数，那么积的个位数是（）【解析】积的个位数等于两个因数的个位数积的个位数；一位质数有2、3、5、7；2×3=6，2×5=10，2×7=14，3×5=15，3×7=21，5×7=35；其中符合积的个位数也是质数的只有3×5=15或5×7=35，故积的个位数是5.在下面的乘法算式中，“数”、“字”、“谜”各代表一个互不相同的数字，求这个算式.⨯数字谜数字谜谜谜谜谜谜【解析】这是集数字谜和填空格于一体的数字问题，从题面上看，提供的信息较少，“谜”所在的位置较多，紧紧抓住“谜”所在的位置特点，逐一突破.由“⨯=数字谜谜谜”可知“谜”≠1，因此“谜”=5或6.例4例3（1）若“谜”=5，“⨯=数字谜数”的乘数的百位数字必须大于3且小于等于5，所以“数”=2，由于“⨯=数字谜字谜”，可知“255⨯=字字”，“字”是单数且小于5，故“字”=1或3，当“字”=1时，21521546225⨯=，不符合条件，当“字”=3时，23523555225⨯=，符合题意.（2）若“谜”=6，同理，“⨯=数字谜数”的乘积的百位数字必须大于4且小于等于6，所以“数”=2，由266⨯=字字，可知“字”=1，但21621646656⨯=，不符合条件.所以满足条件的算式是：23523555225⨯=.下面两个算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字.⨯=美妙数学数数妙，美+妙数学=妙数数.=美妙数学___________【解析】由⨯=美妙数学数数妙知，“美”不为1，且“美”ד妙”＜10，所以“美”≥2，“秒”≤4，“美”+“学”=“数”；1）当“秒”=1，根据“美”ד学”的个位数为“妙”，可知，“美”、“学”为3和7，此时“美”+“学”=10，但题目中“美”+“学”=“数”＜10，所以“妙”不等于1；2）当“妙”=2，根据“美”ד学”的个位数为“妙”，可知，“美”、“学”为3和4，或者4和8，但4+8=12＞10，所以“美”、“学”为3和4，“数”=3+4=7，但274×3=822，积出现重复数字2，不合要求，273×4＞1000也不合要求.3）当“妙”=3，根据“美”ד学”的个位数为“妙”，可知“美”、“学”为7和9，“美”+“学”＞10，不合要求.4）当“妙”=4，根据“美”ד学”的个位数为“妙”，可知“美”、“学”为7和2，或者6和9，又“美”+“学”＜10，所以“美”、“学”为7和2，“数”=7+2=9.497×2=994，合乎要求.因此，2497=美妙数学【练习1】在5×5方格表的空白处填入1-5中的数，使得每行、每列、每条对角线上的数各例5不相同？【解析】先确定右下角的方格，只能填“2”；左下角只能填3，最下一行只能是3、4、5、1、2.其他方格不难填成，结果如下图.【练习2】下图中有五个正方形和12个圆圈，将1-12填入圆圈中，使得每个正方形四角上圆圈中的数字之和都相等.那么这个和是多少？【解析】设每个正方形四角上圆圈中的数字之和为x，则由5个正方形四角的数字之和，相当于将1-12相加，再将中间四个圆圈中的数加两遍，可得()++++=，x x121225 x=，具体填法如：26758649112310121【练习3】下图中有三个正三角形，其中有三条通过四点的线段.请你把1~9这九个自然数分别填在九个黑点的旁边，使每个正三角形顶点上三个数的和相等，每条线段上四个数的和也相等.【解析】每个正三角形顶点上三个数的和：（1+9）×9÷2÷3=15每条线段上四个数的和：[（1+9）×9÷2+15]÷3=20根据以上结论可以得到如下填法（答案不唯一）：【练习4】如下图所示，A B C D E F G H I J、、、、、、、、、表示0-9这10个各不相同的数字.表中的数为所在行与列的对应字母的和，例如“G+C=14”.请将表中其它的数全部填好.A B C D E F G H I J+56771414【解析】 由于A+F=5，B+F=14，所以B-A=14-5=9，所以A 和B 只能是0和9.因此可以推出：A=0，B=9，C=6，D=3，E=2，F=5，G=8，H=1，I=4，J=7.可得下图.1013101041731694113107711881114147765+JI H G FE D C B A【练习5】 电子数字0-9如图所示，右图是由电子数字组成的乘法算式，但有一些模糊不清，请将右图的电子数字恢复，并将它写成横式形式：______________________.【解析】（1）显然乘积的百位只能是2；（2）被乘数的十位和乘数只能是0、2、6、8，才有可能形如，0首先排除；（3）如果被乘数十位是6或8，那么乘数无论是2、6或8，都不可能乘出百位是2的三位数.所以被乘数十位是2，相应得乘数是.（4）被乘数大于25，通过尝试得到符合条件的答案：28×8=224.【练习6】 下面式中不同的汉字代表不同的数字，问：“数学好玩”表示的四位数是多少?【解析】由积的千位数知“数”=1，由积的十位数知“学”=0，由积的百位数知“玩”=9.竖式化简为下式.由于“1真”×9= “10好”，所以“真”=2，“好”=8，“啊”=6.所以，“数学好玩”=1089.【练习7】在□中填入恰当的数字使算式能够成立.2【解析】①这个除法算式从相除的过程可以看出，商数的十位和千位均为0；②除数的2倍是一个三位数，而除数与商的万位相乘，积为两位数，可知商的万位数字为1，同样可知商的个位数字也为1，即商为10201；③又一个两位数的两倍必小于200，故第一次剩余（即被除数的前三位与除数之差）为1.而一个三位数与一个两位数之差为1，只能是100-99=1，故被除数前三位为“100”，而除数为99，由此可知，被除数为99×10201=1009899.。
11届中环杯初赛解析五年级奥数竞赛培训班
第十一届“中环杯”小学生思维能力训练活动(初赛)一、填空题：1．计算：3.6 42.3 3.75 12.5 0.423 28 （）。
【考点】速算与巧算。
【分析】3.6 42.3 3.75 12.5 0.423 283.6 42.3 1.25 3 12.5 0.423 281.25 4.23 108 281.25 4.23 804232．3支铅笔和5支圆珠笔的价格一共是A元，6支铅笔和3支圆珠笔的价格一共是B元，那么一支铅笔和一支圆珠笔的价格一共是（）元。
（用含有A、B的式子表示）【考点】方程解法，消去法。
【分析】设一支铅笔的价格是x元，一支圆珠笔的价格是y元：3x 5y A6x3y B ，解得1x5B3A21，所以1y2A B7111x y 5B 3A 2A B 3A 2B217213．将自然数按从小到大的顺序无间隔地排成一列：123456789101112，则左起第2010位上的数字是（）。
【考点】页码问题。
【分析】一位数共有9个数码，两位数共有180个数码，三位数共有2700个数码。
2010 9 180 3 607，所以第2010位上的数字是第607个三位数的个位，即为706的个位6。
4．一个长42厘米、宽24厘米、高36厘米的长方体木块，表面涂上红漆，再把它锯成若干个相同大小的小正方形体且没有废料。
则表面没有涂上红漆的小正方体至少有（40）块。
【考点】立体图形表面染色。
【分析】要求把长方体木块锯成若干个相同大小的小正方形体且没有废料，那么小正方形体的边长肯定是42、24、36的公约数，又要求表面没有涂上红漆的小正方体尽可能少，那么小正方形体的边长为 42,24,36 6厘米，长方体木块被分割成7 4 6，此时表面没有涂上红漆的小正方体有 7 2 4 2 6 2 40块。
上海学而思教材研发中心5．如图，小正方形的35被阴影部分覆盖，大正方形的7 8被阴影部分覆盖，大正方形的阴影部分面积比小正方形的阴影部分面积大 11 平方米，那么小正方形的面积是（）平方米。
五年级中环杯历届试题
五年级中环杯历届试题五年级中环杯历届试题导语：在所有好的，不好的情绪里，毫无预兆地想念你，是我不可告人的隐疾。
以下小编为大家介绍五年级中环杯历届试题文章，欢迎大家阅读参考!五年级中环杯历届试题一、单项选择题（在下列每题的四个选项中，只有一个选项是符合试题要求的。
请把答案填入答题框中相应的题号下。
每小题1分，共23分）1. 健康牛的体温为( )。
A. 38～39.5°CB. 37～39°CC. 39～41°CD. 37.5～39.5°C2. 动物充血性疾病时，可视黏膜呈现( )。
A. 黄染B. 潮红C. 苍白D. 发绀3. 心肌细胞脂肪变性是指( )。
A. 心肌间质脂肪浸润B. 心肌脂肪组织变性C. 心外膜脂肪细胞堆积D. 心肌细胞胞质中出现脂滴4. 化脓菌入血、生长繁殖、产生毒素、形成多发性脓肿，该病是( )。
A. 脓毒血症B. 毒血症C. 败血症D. 菌血症5. 细胞坏死过程中，核变小、染色质浓聚，被称之为( )。
A. 核溶解B. 核分裂C. 核固缩D. 核碎裂6. 在慢性炎症组织中，最多见的炎症细胞是( )。
A．中性粒细胞 B．嗜酸性粒细胞C．淋巴细胞 D．肥大细胞7. 商品蛋鸡中暑时的胸肌颜色( )。
A．暗红色 B．鲜红色 C．浅白色 D．基本正常8. 甲硝唑主要用于下列哪种情况( )。
A. 大肠杆菌病B. 抗滴虫和厌氧菌C. 需氧菌感染D. 真菌感染9. 下列动物专用抗菌药是( )。
A．环丙沙星 B．氧氟沙星 C．强力霉素 D．泰乐菌素10.被病毒污染的场地，进行消毒时，首选的消毒药是( )。
A．烧碱 B．双氧水 C．来苏儿 D．新洁尔灭11.解救弱酸性药物中毒时加用NaHCO3的目的是( )。
A. 加快药物排泄B. 加快药物代谢C. 中和药物作用D. 减少药物吸收12.国家强制免疫的动物疫病不含( )。
A．禽流感 B．蓝耳病 C．猪瘟 D．新城疫13.鸭传染性浆膜炎的病原为( )。
2012 第十二届 5年级 “中环杯”决赛(详解)
分析：积的个位数等于两个因数的个位数乘积的个位数； 一位质数有 2、3 、5、 7； 2×3=6 ，2 ×5=10，2× 7=14 ，3× 5=15，7× 5=35，其中符合条件 积的个数也是质数的只有 3×5=15， 7×5=35，故积的个位数是 5。 775 33 2325 23 2 5 25575
20
13
分析：如图 1 所示，从上网下看，上面四个的棱长为 12 厘米的正方体的重叠部分是边长为 12+12-20=4 厘米的正方形； 如图 2 所示， 从上网下看，下面四个的棱长为 13 厘米的正方体的重叠部分是边长为 13+13-20=6 厘米的正方形； 如图 3 所示， 从侧面看， 上面四个的棱长为 12 厘米的正方体和下面四个的棱长为 13 厘米的 重叠部分高为 12+13-20=5 厘米； 所有这八个小正方体公共部分的体积是 4× 4×5=80 立方厘米
n个0
以 800 01 9 88 89 能 够 被 3 整 除 但 不 能 被 9 整 除 ； 所 以 88 89 的 数 字 之 和
n个 0 n个8 n个 8
8 8 8 9 8n 9 能够被 3 整除但不能被 9 整除；所以 n 能够被 3 整除但不能被 9 整
n个8
除；n 第二小为 6；故从小到大排列起来，其中第二个是 80000001 8 一个大长方体的尺寸是 n× 11× 10， 它是由一些 1× 1×1 的单位立方体和一个 2× 1×1 的 长方体构成。 2×1 ×1 的长方体在大长方体中有 2671 个位置可以放置。 那么， n=__________ 分析： 当 2× 1×1 的长方体中长度为 2 的棱与 n× 11×10 大长方体中长度为 n 的棱方向一致 时，有（ n-1）×11× 10=110n-110 个位置可以放置；当 2×1 ×1 的长方体中长度为 2 的棱与 n×11× 10 大长方体中长度为 11 的棱方向一致时，有 n×（ 11-1）× 10=100n 个位置可以放 置；当 2× 1×1 的长方体中长度为 2 的棱与 n ×11× 10 大长方体中长度为 10 的棱方向一致 时， 有 n× 11× （ 10-1） =99n 个位置可以放置； 则 2× 1× 1 的长方体在大长方体中有 （110n-110 ） +100n+99n=2671 个位置可以放置；故 n=9 9 如图，有一个长 5 宽 3 的长方形，一个小球从某一个顶点处以 45°的角度向长方形内发 射，碰到长方形壁后会反弹 。那么当小球再一次回到长方形某个顶点的时候，它经历了 __________次碰撞。
十二届五年级中环杯决赛答案
4/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
年 新 好 好 新
年
年
新 年 好 新 好
（2）18 (2 5) 2 4 18
5/5
1/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
有 8889,8888889, 其中不能被 9 整除的最小数是 8889 ，其次为 8888889 。所以能够被 27 整除但不能被 81 整除的第二小数是 80000001 。 8. 答：9 分成三种情况，得 n 1 10 11 n 9 11 n 10 10 2671 ，所以
2/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
2011÷4＝502„„3，所以木块从左向右翻转 2011 次，“13”在右面(如下图)。此时左面 是“3”，后面是“11”，下面是“9”。
木块从前向后翻转 1 次，“9”在正面；翻转 2 次，“11”在正面；翻转 3 次，“7”在正 面；翻转 4 次，“5”在正面。所以木块从前向后翻转 4 次，又回到初始状态。 2012÷4＝503„„0，所以最后木块正面的数字是 5。 2. 答：9 平方厘米 我们知道，4 个同样的等腰直角三角形可以拼成一个正方形。如图，以斜边 AB 为正方形 的边长。
因为正方形的面积是＝AB2＝122＝144(平方厘米)，所以，三角形 ABC 的面积＝144÷4＝ 36(平方厘米)。 1 3 1 又因为在等腰直角三角形 ABC 中，MN＝ BC，PC＝(1－ )AC＝ AC，所以三角形 PMN 的 4 3 4 1 1 1 3 1 1 1 面积是： ×MN×PC＝ × × ×BC×AC＝ ×BC×AC＝ S△ABC＝ ×36＝9(平方厘 2 2 3 4 8 4 4 米)。 3. 答：80 立方厘米 如图，上面四个棱长为 12 厘米的小正方体在大正方体的上底面内交出一个边长为 12＋12 －20＝4(厘米)的正方形，由此可知它们的公共部分是一个长方体，底面为 4×4＝16(平 方厘米)的正方形，高 12 厘米。
中环杯5年级试题
级决赛得分院注意院每小题前的野阴冶由阅卷人员填写袁考生请勿填写遥一尧填空题A院渊每题6 分袁共48 分冤31+6 1 +4 3数列袁比如S3 为3尧12尧21尧噎遥如果306 是S k 中的一项袁所有满足条件的k 之和为遥7. 如图所示的点阵图中袁有条直线能正好经过其中的两个点遥8.如图袁直角吟A B C 中袁AB=3袁AC=4袁点D尧E尧F尧G尧第7 题JI1. 计算院9伊11+31 伊 5 7 = 遥DH尧I 都在长方形K LMJ 上袁且A B ED尧A C HI尧BCGF 都是正 A H20151+ 1 + 1 EM5 7方形遥则KLMJ 的面积为遥 B C2.老师布置了一些数学回家作业遥由于小明基础不好袁所以小明收到的题目数量比小王收到的题目数量多20 道遥若两人收到的题目数量之比为4:3袁则小明回家需要完成道题目遥3.如图袁正八边形的边长为1袁将其进行切割袁切割后灰色部分面K 二尧填空题B院渊每题8 分袁共32 分冤9. 计算院渊104-94+84-74+噎+24-14冤+渊102+92+5伊82+5伊72+9伊62+9伊52+13伊42+13伊32冤= 遥F GL第8 题积与斜线部分面积之差渊大减小冤为遥4.在一组英文字母串中袁第一个字母串a1=A 袁第二个字母串a2=B袁之后每个字母串a n渊n逸3冤都是由a n-1 后面跟着a n-2 的反转构成的遥比如第3 题C A E FD B BE G FC AD G 10. 甲尧乙两人分别从 A 尧B 两地同时出发渊甲从 A 出发冤袁相向而行袁在两地之间不停地往返行走袁甲的速度是乙的 4 倍遥 已知 A 尧B 之间相距 S 千米袁其中 S 为正整数袁并且 S 有 8 个因数遥 第一次袁两人在 C 处碰头渊注意院这里的碰头可以指迎面相遇袁也可以指背后追到冤袁ACa 3=a 2a 1 =BA 渊我们用a i 表示 a i 的反转袁 就是从右往左读这个字母串得到的结果袁 比如A BB = BBA 尧A A BA =A B AA 冤袁a 4=a 3a 2 =BA B 袁a 5=a 4a 3 =BA B A B 袁a 6=a 5a 4 =BA B A B BA B 遥 那么袁这组字母串的前 1000 个中袁有 个是回文字母串渊所谓的回文字母串袁就是指从左往右读与 从右往左读相同袁比如 A BA 尧A A BAA 冤遥5. 如图 a 袁七个字母放置在圆中袁每次将包含中心圆的三个圆渊这三个圆的圆心构成等边三角形冤顺时针旋转 120毅袁这样称为一次操作遥 比如可以将 A 尧B 尧D 进行旋转袁从而 B 出现在原D 的位置渊用 B 邛D 表示这个旋转冤袁D 邛A 袁A 邛B 遥 也可以将 D 尧E 尧F 进行旋转渊D 邛E 袁E 邛F 袁F 邛D 冤袁但是不能将 A 尧D 尧G 或者 C 尧B 尧E 进行旋转遥经过若干次操作后袁 得到图 b 遥 那么袁最少需要操作 次遥 a b的长度是一个整数遥第二次袁两人在D 处碰头袁AD 的长度还是一个整数遥第二次碰头后袁乙感觉自己速度太慢袁所以在D 处附近的村子问老乡借摩托车遥等他借到摩托车回到D 处时袁甲已经到达E 处渊甲还没有到过A 地冤袁AE 的长度又是一个整数遥最后袁乙骑着摩托车去追甲袁摩托车的速度是甲速度的14 倍袁两人同时达到A 地遥那么袁A 尧B 两地相距千米遥11.对任意正整数m尧n袁定义r渊m袁n冤为m衣n 的余数渊比如r渊8袁3冤表示8衣3 的余数袁所以r渊8袁3冤=2冤遥那么满足方程r渊m袁1冤+r渊m袁2冤+r渊m袁3冤+噎+r渊m袁10冤=4 的最小正整数解为遥12. 6 个正整数a尧b尧c尧d尧e尧f 按字母顺序排成一排袁构成一个数列袁其中a=1遥如果某个正整数大于1袁那么比这个正整数小1 的数肯定出现在它的左边遥比如d>1 袁则a尧b尧c 中必有一个值为d-1 遥举例院1袁1袁2袁1袁3袁2 满足要求曰1袁2袁3袁1袁4袁1 满足要求曰1袁2袁2袁4袁3袁2 不满足要求遥6. 我们用S k 表示一个首项为k袁公差为k2 的等差第 5 题W 1 W 2 W 3 D 满足要求的不同排列有 个遥 五年级第 1 页 五年级第 2 页 三尧 动手动脑题院渊每题 10 分袁共 20 分冤 13. 用 1尧2尧3尧4尧5尧6尧7尧9 这 8 个数码组成 4 个两位质数渊每一个数码必须且只能用一次冤袁这 4 个质数有多少种不同的可能钥14. 如图袁吟A BC 中袁BD=DC 遥 在 AC 边上有一块奶酪袁其位置在最靠近点 C 的四等分点上遥 在 AD边上有三个透视镜 W 1尧W 2尧W 3袁这三个透视镜将 AD 四等分遥 有一只疑心病很重的老鼠在 AB 边上爬行渊从 A 爬往 B 冤袁A B=400 米遥 当老鼠尧某个透镜尧奶酪在一条直线上时袁老鼠能观察到奶酪遥 由于老鼠的疑心病很重袁它希望多次看到这块奶酪袁这样就可以保证在它还没有爬到前袁这块奶酪没有被别的老鼠吃掉遥所以它第 1 分钟往前爬 80 米袁第 2 分钟往回退 20 米袁第 3 分钟往前爬 80 米袁第 4 分钟往回退 20 米噎噎依次类推遥 当这只老鼠爬到点 B 后袁它直接沿着 BC 边冲过去吃奶酪遥 问院老鼠在 AB 段上一共可以看到多少次奶酪钥 A奶酪B C。
第十二届中环杯小学生思维能力活动五年级决赛清晰版试题
第十二届中环杯小学生思维能力活动五年级决赛一、填空题1.计算20112010×20122013－20112011×20122012+10002=（）2.在1-2012这2012个自然数中，是平方数但不是立方数的数一共有（）个。
3.某商品按每个10元的利润卖出5个所得的总钱数，与按每个25元利润卖出4的所得的总钱数相等，这种商品每个进价是（）元。
4.如图，半圆连同直径上共有10个点，以这些点为顶点，可以构成（）个三角形？5.如图，纸片盖住了减法算式的所有数字，但是已知每一个被盖住的数都是质数，那么积的个位数是（）6.有一中比赛赛制叫做双败复活赛。
即每两队进行比赛，胜者进入胜者组，负者进入白这组，胜者组的每轮负者降入败者组，败者组中再败则被淘汰，如此直到胜者和败者队的冠军进入决赛，决赛三局两胜。
某次比赛有2012队参赛，不考虑平局，那么要进行（）场能产生最后冠军。
（某轮次如果遇到组内队伍为奇数，抽签绝代让一支队伍本轮轮空。
）7.在8001,800001……这样的最高位上的数字为8，最低位上的数字为1，中间全是0的整数中，将其中能够被27整除但不能被81整除的数从小到大排列起来，其中第二个是（）。
8.一个大长方体的尺寸为n×11×10，它由一些1×1×1的单位立方体和一个2×1×1的长方体构成。
2×1×1的长方体在大长方体中有2671个位置可以放置，那么N=（）9.如图有一个长5宽3的长方形，一个小球从某一个顶点处以45°的角度向长方形内发射，碰到长方形避后会反弹，那么当小球再一次回到某个顶点的时候，它经历了（）次碰撞。
10.1102到2011所有数各数数位上的数字之和是（）二动手动脑1. 如图，一个正方体的木块，六个面非别歇着数，相对面上的两个数的和等于16，按照下图的位置摆好（上面是3，正面是5，右面是7）,先顺时针方向从左向右翻转2011次，再由前向后翻转2012次，这时，这个木块正面的数是多少？2. 如图，三角形ABC 是等腰三角形，斜边AB=12厘米，MN 是BC 的三分之一，AP 是AC 的四分之一，求三角形PMN 的面积。
第十二届中环杯五年级初赛详解
5 ，所 以 abc 98 的 末 位 数 字 为 2 或 7 ，所 以 abc 98 462 或 77 或 847 ，所 ， 以 abc 560
或 175 或 945 ， 由 于 这 个 数 能 被 3 整 除 ， 所 以 其 各 位 数 字 和 能 被 3 整 除 ，经 验 证 ， 只 有 98175 符 合 要 求 ， 所 以 这 个 五 位 数 为 98175 ， 其 各 位 数 字 和 30 。 3. 从 1, 2, 3, 4 , 2000 共 2000 个正整数中，最多能取出 （
Hale Waihona Puke 共有（ ）种不同的入座方式 种不同的入座方式。 【考点】 2012 年第十二届中环杯初赛（五年级） 年第十二届中环杯初赛 ；排列组合，插空法； 【解析】如下图，座位选择共有 座位选择共有 ACEG , ACEH , ACFH , ADFH , BDFH ，共 5 种（或者可以这
上海学而思教材研发中心
5、、 7 11 的整除判断； 【考点】 2012 年第十二届中环杯初赛（五年级） 年第十二届中环杯初赛 ；数论， 3、 的整除判断 【解析】方 法 一 ：能 被 3 、 5、 7 、 11 整 除，既 能 被 [3,5,7,11] 1155 整 除 ，五 位 数 中 最
大 的 为 99330 ， 但 有 相 同 的 数 字， 字 比 99330 小 一 些 的 是 98175 ，各 各 位 数 字 不 同 ，其 数 字 和 为 30 。 方 法 二 ：考 虑 最 大 ， 则 设 这 个 五 位 数 为 98abc ， 由 于 这 个 数 能 被 7 、 11 整 除， 故 这 个 数 能 被 77 整 除， 即 能 abc 98 被 77 整 除， 由 于 这 个 数 能 被 5 整 除 ，所 以 c 0或
初中奥数：中环杯竞赛试题
初中奥数：中环杯竞赛试题【1】1.四个球，编号为1，2，3，4，将他们分放到编号为1，2，3，4的四只箱子里，每箱一个，则至少有一箱恰使球号与箱号相同的放法有几种?2.用数码1，2，3，4.....9各恰好两次，构成不同的质数，使它们的和尽可能小，则该和最小是几?【2】一班,二班,三班各有二人作为数学竞赛优胜者,6人站一排照相,要求同班同学不站在一起,有()种不同的站法?【3】一版邮票有20行20列,共400张邮票,称由3张同一行或同一列相连的邮票组成的纸块为"三联".小亮想剪出尽可能多的三联,他最多能得到几块三联?(五年级）【4】第一次在1，2两数之间写上3；第二次在1，3之间和3，2之间分别写上4，5；以后每一次都在已写上的两个相邻数之间，再写上这两个相邻数之和。
这样的过程共重复8次，那么所以数的和是多少？【5】一次测验共有5道试题，测试后统计如下：有81%的同学做对第1题，有85%的同学做对第2题，有91%的同学做对第3题，有74%的同学做对第4题，有79%的同学做对第5题。
如果做对3道或3道以上试题的同学为考试合格。
请问：这次考试的合格率最多达百分之几？最少达百分之几？【6】把156支铅笔分成n堆（n>等于2)，要求每堆一样多且为偶数支。
有（）种分法。
【7】七个相同的羽毛球,放在四个不同的盒子里,每个盒子里至少放一个,不同的放法有()种.【8】由甲城开往乙城的汽车每隔1小时一班逢整点出发，由乙城开往甲城的汽车每隔1小时一班但逢半点（30分）出发。
从一个城市到另一个城市需要6小时，假定汽车行驶在同一高速公路上，那么一辆开往乙城的汽车最多能遇到（）辆开往甲城的汽车。
【9】一群公猴、母猴和小猴共38只，每天共摘桃子266个。
已知每只公猴每天摘桃10个，每只母猴每天摘桃8个，每只小猴每天摘桃5个，并且公猴比母猴少4只，那么，这群猴子中小猴有多少只？这道题目除了设X做以外还有别的方法吗？。
2010奥数中环杯五年级初赛试题答案11
2021/4/14 星期三
1144
第十四页，共17页。
8个数的和最小是8，最大是24，和的 个数有：24-8+1=17
即有17个抽屉。而8行8列2个对角线共有18个和， 根据抽屉原理至少有两个和是相同，
所以是不能的。
8.红星小学组织学生划船。若乘坐大船，除1条船坐6人外，其余每船 均坐17人。若乘坐小船，则除1船坐2人外，其余每船均坐10人。如果学 生的人数超过100人，不到200人，那么学生共有（ ）人。
解法一：
“若乘坐大船，除1条船坐6人外，其余每船均坐17人 。”说明学生人数÷17余6
“除1船坐2人外，其余每船均坐10人。” 说明学生 人数÷10余2
只有142符合这两个要求。 （142-2）÷10=14 （142-6）÷17=8
2021/4/14 星期三
9
第九页，共17页。
8.红星小学组织学生划船。若乘坐大船，除1条船坐6人外，其余每船均 坐17人。若乘坐小船，则除1船坐2人外，其余每船均坐10人。如果学生 的人数超过100人，不到200人，那么学生共有（ ）人。
6
第六页，共17页。
3600÷180=20 这个人走了一个正二十边形，16×20=320 这要通过画图就能发现。
2021/4/14 星期三
7
第七页，共17页。
7.一只船被发现漏水，已经进了一些水，水均速进入船内。如果10 人淘水，3小时淘完；如果5人淘水，8小时淘完。如果要求2小时淘完
，需要安排（ ）人淘水。
AB两地全长：（70+50）×10=1200（米）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.
从 1, 2,3, 4, 2000 共 2000 个正整数中，最多能取出（ 中的任意三个数 a、b、c a b c ,都有 ab c 。
）个数,使得对于取出来的数
4.
A、B、C、D 四人被安排坐入排成一排的 8 个座位中，若任何两个人都不相邻而坐， 共有（ ）种不同的入座方式。
上海学而思五年级学科部
么，最远可以把物资运到距离驻地（
）千米远的地方。
7.
现在是上午 10 点，到（
）点（
）分时，时针和分针第一次重合。
8.
The number come next in this sequence is (
1,5, 7,13, 25, 45,83,153, 281,517，（ ）
上海学而思五年级学科部
3.
某展览馆是一个拥有 15 间房间的大厅，下图为大厅的平面图。每天展览馆关门后，都 会有一个警卫从大厅的入口进去，一间房一间房地逐次巡视，最后来到画有○标记的 管理室休息。现在，规定每间房间警卫只能进去一次，且所有房间都要巡视到。你认 为这个警卫应该怎样进行巡视才好呢？请在图中画出他的巡视路线。 （本题 10 分）
)。
二、动手动脑题（共 44 分） 1. 甲、乙两人在一条圆形跑道上同时同地同向出发，绕圆形跑道跑步。已知两人在跑步 过程中速度均保持不变， 且甲跑得比乙快。 甲第一次追上乙时，乙离开出发点 250 米。 当甲第二次追上乙时，乙离开出发点 50 米。求跑道长。 （本题 11 分）
2.
如图所示，三角形 ABC 的面积是 180 平方厘米，且三角形 BDE、三角形 DEC 和三角 形 ACE 的面积都相等，求三角形 ADE 面积。 （本题 11 分）
4.
如图是一个立方体魔方，我们可以从图中看到它的右侧、上侧和前侧。如果顺时针转 动魔方右侧第一层 90 度，我们记作进行了一次 R 操作；如果逆时针转动魔方右侧第一 层 90 度，则记作 R’。对于上侧和前侧分别进行相同的旋转操作，分别记为 U、U’、 F、F’。现在对魔方进行 4 次转动：⑴F，⑵R，⑶U’，⑷F。请你在图中依次画出每 完成一次转动后，阴影面所在的位置。 （本题 12 分）
5.
如图，把正方体用一个与它的一面平行的平面切开，分成 A、B 两个长方体。当 A、B 的表面积比是 1: 2 时，用最简单的整数比表示 A 和 B 的体积比是（ ） 。
6.
一支运输小分队奉命把一些物资从驻地送到很远的地方。每辆运输车装满油最多能行 180 千米，且途中没有加油站。由于一辆运输车无法完成任务，队长决定派两辆车执行 任务，其中一辆运输车负责运送物资，另一辆则在中途供给油料后安全返回驻地。那
第十二届“中环杯”小学生思维能力训练活动
一、填空题（每题 7 分，共 56 分） 1. 对于任意的自然数 X 和 Y，定义新运算@： X @ Y 自然数。如果 1@ 2 1 ,则 2@8 （ ） 。
6 XY ，其中 m 是一个确定的 mX 2Y
2.
5、 7、 11 整除，那么当这个五位数取到最大值的 一个各位数字互不相同的五位数，能被 3、 时候