24.1.2《垂直于弦的直径》ppt课件
合集下载
24.垂径定理的应用PPT课件(人教版)

经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根
据垂径定理,D是AB的中点,C是 由题设得
AB 7.2,CD
AB 的中点,CD就是拱高.
2.4, HN 1 MN 1.5.
AD
1
AB
1 7.2
2 3.6,
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
①④ ②③⑤ 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的 ①⑤ ②③④ 另一条弧.
②③ ①④⑤ 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
②④ ②⑤ ③④ ③⑤
①③⑤ 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且
①③④ 平分弦和所对的另一条弧.
①②⑤ 平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于 ①②④ 弦,并且平分弦所对的另一条弧.
O
A
B
P
2、如图,⊙O的直径AB和弦CD相交于点E,
AE=1厘米,EB=5厘米,∠BED=30°,
求CD的长。
D
No 在Rt△OEF中,OE=3-1=2,
∠BED=30°则OF=1
B
Image 又在Rt△DOF中
F OE
A C
DF= OD2 OF2 32 12 2 2
∴CD=2DF= 4 2
2、通过作出弦心距后,可构造直角三角形,然 后用直角三角形的边角关系或勾股定理来求解.
B
AD AB 37.4 18.7,
2
2
R
R-7.2
OD OC DC R 7.2.
在Rt⊿AOD中,由勾股定理,得
O
OA2 AD2 OD 2 ,
即R2 18.72 (R 7.2)2.
24.垂直于弦的直径PPT课件(人教版)

(√ ) (√ ) (×)
轴
经过圆心
中心
圆心
垂直于弦的 直径平分弦,并且平分弦所对的两条弧
垂直
弦所对的两条弧
问题:你知道赵州桥吗?它是1300多年前我国隋代建 造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主 桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主 桥拱的半径吗?
∵AB∥CD,∴ON⊥CD于N
在RtAOM中,AM 5cm,OM OA2 AM2 12cm. 在RtOCN中,CN 12cm,ON OC2 CN 2 5cm.
∵MN=OM-ON,∴MN=7cm. (2)当AB、CD在O点异侧时,如图②所示,
由(1)可知OM=12cm,ON=5cm,MN=OM+ON,
(并2且)平A分M=A(BBM及,AA(DCB=.BC,AD=BD,即直径CD平分弦AB,
这样,我们就得到下面的定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧。进一步,我们还可以得到结论:平 分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 。
知识点一 垂径定理及其推论
C
知识点一 垂径定理及其推论
通过本节课的学习,我们就会很容易解决这一问题.
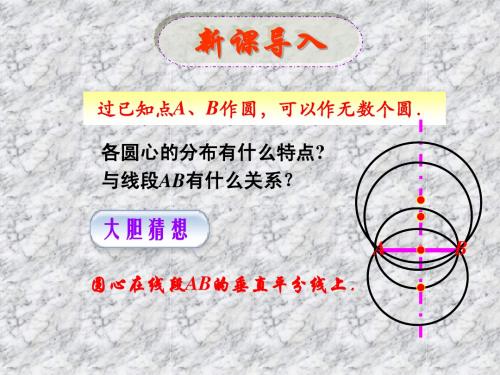
探究:1.圆是轴对称图形吗?如果是,它的对称轴是什 么?你能找到多少条对称轴?
分析讨论:圆是轴对称图形,它的对称轴是直径,我能找到 无数多条直径.
探究: 2.你是用什么方法解决上述问题的?与同伴进行 交流.
分析讨论我:是利用沿着圆的任意一条直径折叠的方法解决 圆的对称轴问题的.
.2垂直于弦的直径
判断:
(1)直径是弦.( √ )
(2)弦是直径. ( × )
垂直于弦的直径课件(共21张PPT)

C E A
O
D
B
三 垂径定理的有关计算 例2 如图,⊙ O的弦AB=8cm ,直径CE⊥AB于
D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D, ∴
1 1 AD AB 8 4 (cm) 2 2
E
方程思想
A
D C
Hale Waihona Puke O ·设OC=xcm,则OD=x-2,根据 勾股定理,得 x2=42+(x-2)2, 解得 x=5, 即半径OC的长为5cm.
试一试:根据刚刚所学,你能利用垂径定理求出引入 中赵州桥主桥拱半径的问题吗?
7.23米
37米
解:如图,用AB表示主桥拱,设 AB所在圆的圆心为O,半径为R. 经过圆心O作弦AB的垂线OC 垂足为D,与弧AB交于点C, 则D是AB的中点,C是弧AB的 中点,CD就是拱高. ∴ AB=37m,CD=7.23m.
C B O A
D
定理及推论,总结: 一条直线只需满足: (1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧 上述条件中的任意两个条件,就能推 出其它三个.
五 学以致用
例2 赵州桥(图24.1-7)是我国隋代建造白石拱桥,距今 约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它 的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高 (弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果 保留小数点后一位).
一 三 垂径定理的有关计算 例1 如图,OE⊥AB于E,若⊙O的 半径 AB 为10cm, 16 61 cm. OE=6cm,则 半径为 AB=
A
E
B
解析:连接OA, ∵ OE⊥AB, ∴∠AEO=90°,AB=2AE
人教版数学《垂直于弦的直径》_上课课件

24.1.2 垂直于弦的直径
———(垂径定理)
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
赵州石拱桥
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧 形,它的跨度(弧所对是弦的长)为37m,拱高(弧的中点到弦的距 离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.1m).
OA2 AD2 OD2
即 解R得2分: 1R析8.:722 7O.A9(2Rm=A)D72.2+O2D2
其中OD=OC-CD
因此,赵州桥的主拱桥的半径约为27.9m。
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
E
B
{(3)平分弦
D
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
① CD是直径 可推得 ② CD⊥AB
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
③AE=BE,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
平分弦(不是直径)的直径垂直于弦,并且
D 平分弦所对的两条弧.(垂径定理推论)
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
判断下列图形,能否使用垂径定理?
———(垂径定理)
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
赵州石拱桥
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧 形,它的跨度(弧所对是弦的长)为37m,拱高(弧的中点到弦的距 离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.1m).
OA2 AD2 OD2
即 解R得2分: 1R析8.:722 7O.A9(2Rm=A)D72.2+O2D2
其中OD=OC-CD
因此,赵州桥的主拱桥的半径约为27.9m。
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
E
B
{(3)平分弦
D
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
① CD是直径 可推得 ② CD⊥AB
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
③AE=BE,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
平分弦(不是直径)的直径垂直于弦,并且
D 平分弦所对的两条弧.(垂径定理推论)
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
【 获 奖 课 件 ppt】人 教版数 学《垂 直于弦 的直径 》_上 课课件 1-课件 分析下 载
判断下列图形,能否使用垂径定理?
九年级上数学《24.1.2 垂直于弦的直径》课件
M
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
人教版九年级数学上册课件:24.1.2垂径定理(共15张PPT)

船能过拱桥吗
AB 7.2,CD 2.4, HN 1 MN 1.5.
AD 1 AB 1 7.2 3.6,
2
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
OA2 AD2 OD 2 ,
即R2 3.62 (R 2.4)2.
A
D
E C
O
B
自学指导(二)
认真阅读课本8 2页赵州桥问题,并思考:
1、解决赵州桥求半径问题做了什么辅助过线圆?心作弦的垂线 2、由图24.1-8知主桥拱是__A_B____, 跨度是__弦_A_B__,拱 高是__C_D__,弦心距是__O_D___,半径是__O_A_,_O_B___ , AD= _B_D___.
任意知道两个量,可根据垂径定理求出第三个量:
必做题:课本P83练习1、2题。 选做题:课本P89第2题。 思考题:课本P89第8题。
判断下列说法的正误
①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥弦的垂直平分线一定经过圆心
2、如图,直径为10cm的圆中,圆心到弦 AB的距离OM为4cm,求弦AB的长。
O
A
M
B
相信自己,我能行
破镜重圆
自学指导(一)
认真阅读课本81页—82页“赵州桥问 题” 上面的内容: 1、圆是______图形, __________都是它 的对称轴,对称轴有____条.
2、垂径定理的内容是_________________.
3、对照24.1-6用符号语言表示垂径定理 ? 4、垂径定理的推论是什么?
24.1.2垂径定理_课件ppt(新人教版九年级上)

E
E
O
O
B
A
A
D
D
B
C
C
• 例2.如图是一条排水管的截面。已知排 水管的半径10cm,水面宽AB=12cm。 求水的最大深度.
O
E
A
D
B
求圆中有关线段的长度时,常借助垂径定 理转化为直角三角形,从而利用勾股定理 来解决问题.
提高练习: 1. 已知⊙O的半径为10,弦AB∥CD, AB=12,CD=16,则AB和CD的距离 为 2或14 .
练习反馈
• 1、判断:
驶向胜利 的彼岸
• ⑴垂直于弦的直线平分这条弦,并且平分弦所对的两 条弧. ( ) • ⑵平分弦所对的一条弧的直径一定平分这条弦所对的 另一条弧. (√ )
• ⑶经过弦的中点的直径一定垂直于弦.(
)
• ⑷圆的两条弦所夹的弧相等,则这两条弦平行 . ( )
• ⑸弦的垂直平分线一定平分这条弦所对的弧. ( √ )
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的 货船要经过拱桥,此货船能否顺利通过这座拱桥?
C M H A E D F B O N
说出你这节课的收获和体验,让大家 与你一起分享!!!
2 2 2 2
O
A
E
B
答:⊙O的半径为5cm.
a r d 2
2 2 2
若下面的弓形高为h, 则r、d、h之间有怎 样的关系?
2.如图,在⊙O中,AB、AC为互相垂直且相等的 两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形 ADOE是正方形.
E
O
O
B
A
A
D
D
B
C
C
• 例2.如图是一条排水管的截面。已知排 水管的半径10cm,水面宽AB=12cm。 求水的最大深度.
O
E
A
D
B
求圆中有关线段的长度时,常借助垂径定 理转化为直角三角形,从而利用勾股定理 来解决问题.
提高练习: 1. 已知⊙O的半径为10,弦AB∥CD, AB=12,CD=16,则AB和CD的距离 为 2或14 .
练习反馈
• 1、判断:
驶向胜利 的彼岸
• ⑴垂直于弦的直线平分这条弦,并且平分弦所对的两 条弧. ( ) • ⑵平分弦所对的一条弧的直径一定平分这条弦所对的 另一条弧. (√ )
• ⑶经过弦的中点的直径一定垂直于弦.(
)
• ⑷圆的两条弦所夹的弧相等,则这两条弦平行 . ( )
• ⑸弦的垂直平分线一定平分这条弦所对的弧. ( √ )
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的 货船要经过拱桥,此货船能否顺利通过这座拱桥?
C M H A E D F B O N
说出你这节课的收获和体验,让大家 与你一起分享!!!
2 2 2 2
O
A
E
B
答:⊙O的半径为5cm.
a r d 2
2 2 2
若下面的弓形高为h, 则r、d、h之间有怎 样的关系?
2.如图,在⊙O中,AB、AC为互相垂直且相等的 两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形 ADOE是正方形.
垂直于弦的直径ppt课件

∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形 .
感悟新知
知2-练
3-1. [模拟·鼓楼区] 如图,AB是⊙O的弦,半径OD⊥AB,
垂足为H,BC⊥AB, 交AD延长线于点C.
感悟新知
(1)求证:D是AC的中点;
⌒
⌒
⌒
⌒
直于 AB,并且AC = CB, AD = DB .
可用几何语言表述为:
⊥ ,
是直径
=⌒,
= ⇒ ⌒
⌒
=⌒ .
不是直径
感悟新知
拓宽视野
对于圆中的一条直线,如果具备下列五个条件
中的任意两个,那么一定具备其他三个:
(1)过圆心;
(2)垂直于弦;
么可用几何语言表述为:
= ,
是直径, ⇒ ⌒
=⌒,
⊥ ,
⌒
=⌒ .
感悟新知
知2-练
例2 如图24.1-9,弦CD垂直于⊙ O的直径AB,垂足
为点H,且 CD=2 , BD= ,则 AB 的长为
(
A. 2
)
B. 3
C. 4
D. 5
思路导引:
感悟新知
1.垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧 .
感悟新知
知1-讲
特别提醒
1. “垂直于弦的直径”中 的“直径”,其实质是:
过圆心且垂直于弦的线段、直线均可.
2. “两条弧”是指弦所对 的劣弧和优弧或两个半圆.
感悟新知
知1-讲
2.示例
如图 24.1-8, CD ⊥ AB 于点 E, CD 是⊙ O 的直径,那
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,∴ OC=OD.
∴△ OCD 为等腰三角形 .
感悟新知
知2-练
3-1. [模拟·鼓楼区] 如图,AB是⊙O的弦,半径OD⊥AB,
垂足为H,BC⊥AB, 交AD延长线于点C.
感悟新知
(1)求证:D是AC的中点;
⌒
⌒
⌒
⌒
直于 AB,并且AC = CB, AD = DB .
可用几何语言表述为:
⊥ ,
是直径
=⌒,
= ⇒ ⌒
⌒
=⌒ .
不是直径
感悟新知
拓宽视野
对于圆中的一条直线,如果具备下列五个条件
中的任意两个,那么一定具备其他三个:
(1)过圆心;
(2)垂直于弦;
么可用几何语言表述为:
= ,
是直径, ⇒ ⌒
=⌒,
⊥ ,
⌒
=⌒ .
感悟新知
知2-练
例2 如图24.1-9,弦CD垂直于⊙ O的直径AB,垂足
为点H,且 CD=2 , BD= ,则 AB 的长为
(
A. 2
)
B. 3
C. 4
D. 5
思路导引:
感悟新知
1.垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧 .
感悟新知
知1-讲
特别提醒
1. “垂直于弦的直径”中 的“直径”,其实质是:
过圆心且垂直于弦的线段、直线均可.
2. “两条弧”是指弦所对 的劣弧和优弧或两个半圆.
感悟新知
知1-讲
2.示例
如图 24.1-8, CD ⊥ AB 于点 E, CD 是⊙ O 的直径,那
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•
3、越是没有本领的就越加自命不凡。 20.12.1 518:55: 1018:5 5Dec-20 15-Dec-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 18:55:1 018:55: 1018:5 5Tuesday, December 15, 2020
•
5、知人者智,自知者明。胜人者有力 ,自胜 者强。 20.12.1 520.12. 1518:5 5:1018: 55:10D ecembe r 15, 2020
E
圆重合,点A与点B重合,线段AE与BE重合,A
B
弧AC与弧BC重合,弧AD与弧BD重合。
D
结论:AE=BE,A⌒D=B⌒D,A⌒C=B⌒C
即直径CD平分弦 AB,
并且平分A⌒B和A⌒CB.
A
C
·OE BD垂径定理:垂直于弦的直径平分 弦,并且平分弦所对的两条弧.
如图1,当直径CD平分弦AB时,CD与AB垂直 吗? ⌒AC=B⌒C,A⌒D=B⌒D吗?如果弦AB也是直径,上述
•
8、业余生活要有意义,不要越轨。20 20年12 月15日 星期二 6时55 分10秒1 8:55:10 15 December 2020
•
9、一个人即使已登上顶峰,也仍要自 强不息 。下午 6时55 分10秒 下午6时 55分18 :55:102 0.12.15
• 10、你要做多大的事情,就该承受多大的压力。12/15/
•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月15 日星期 二下午 6时55 分10秒1 8:55:10 20.12.1 5
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月下午 6时55 分20.12. 1518:5 5December 15, 2020
• 13、无论才能知识多么卓著,如果缺乏热情,则无异 纸上画饼充饥,无补于事。Tuesday, December 15, 2020
15-Dec-2020.12.15
今日作业 教材89页 习题24.1 1、2题
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1520. 12.15Tuesday, December 15, 2020
•
2、阅读一切好书如同和过去最杰出的 人谈话 。18:5 5:1018: 55:1018 :5512/ 15/2020 6:55:10 PM
结论是否成立?
C
推论:平分弦(不是直径)的直径垂
O
直于弦,并且平分弦所对的两条弧. A E
B
D
图1
注意
根据垂径定理与推论可知对于一个 圆和一条直线来说。如果具备
(1)过圆心 (2)垂直于弦 (3)平分弦(4) 平分弦所对的优弧 (5)平分弦所对的劣弧
上述五个条件中的任何两个条件都 可以推出其他三个结论。
解: OE AB
A
E
B
AE 1 AB 1 8 4
2
2
在 Rt △AOE中
·
O
AO2 OE2 AE2
AO OE2 AE2 = 32 +42 =5cm
答:⊙O的半径为5cm.
2.如图,在⊙O中,AB、AC为互相垂直且相等的 两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形 ADOE是正方形.
证明: OE AC OD AB AB AC
OEA 90 EAD 90 ODA 90
∴四边形ADOE为矩形, AE 1 AC,AD 1 AB
2
2
又 ∵AC=AB
C
∴ AE=AD
E
·O
∴ 四边形ADOE为正方形.
A
D
B
判断下列说法的正误
①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
赵州桥主桥拱的半径是多少?
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石 拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧 形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦 的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
实践探究
把一个圆沿着它的任意一条直径对折, 重复几次,你发现了什么?由此你能得到 什么结论?
必平分此弦所对的弧
1
1.在直径是20cm的⊙O中,A⌒B的度数是
60°,那么弦AB的弦心距是 5 3cm 。
O
D
A
B
2.弓形的弦长为6cm,弓形的高为2cm,
则这弓形所在的圆的半径为
13 cm 4
.
C
A
D
B
O
小结:
通过本节课的学习,你掌握了哪些 知识?
本节课学习的数学知识是圆的轴对 称性和垂径定理及其推论。
可以发现: 圆是轴对称图形,任何一条直径所在直线都是 它的对称轴.
活动二
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E. 因为圆是轴对称图形,以直径CD为对称轴把⊙O折叠,你能
发现图中有那些相等的线段和弧?为什么?
C
相等线段: AE=BE
弧:A⌒C=B⌒C,
⌒⌒ AD=BD
·O
把圆沿着直径CD折叠时,CD两侧的两个半
解决求赵州桥拱半径的问题 如图,用A⌒B表示主桥拱AB ,设A⌒B 所在圆的圆心为O,
半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,
O点C,与CA是BA⌒相B交的于中点点D,,C根D 据就前是面拱的高结.论,D 是AB 的中
在图中 AB=37.4,CD=7.2,
AD 1 AB 1 37.4 18.7,
2
2
OD=OC-CD=R-7.2
在Rt△OAD中,由勾股定理,得 A
C
D
B
OA2=AD2+OD2
R
即
R2=18.72+(R-7.2)2
O
AB=37.4m CD=7.2m
解得:R≈27.9(m)
∴赵州桥的主桥拱半径约为27.9m.
活 动 三 练习
1.如图,在⊙O中,弦AB的长为8cm,圆心O 到AB的距离为3cm,求⊙O的半径.
2020 6:55:10 PM18:55:102020/12/15
• 11、自己要先看得起自己,别人才会看得起你。12/15/
谢 谢 大 家 2020 6:55 PM12/15/2020 6:55 PM20.12.1520.12.15
• 12、这一秒不放弃,下一秒就会有希望。15-Dec-2015 December 202020.12.15
