天津南开中学高二上数学周练10
2021年高二数学上学期周练试题(文科零班,12.27)

2021年高二数学上学期周练试题(文科零班,12.27)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.“”是“方程”表示椭圆”的()A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D.既不充分也不必要条件2.若,则等于()A.-1 B.-2 C.1 D.3.若点(1,a)到直线x-y+1=0的距离是,则实数a为()A.-1 B.-1或5 C.5 D.-3或34.设、是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误..的是()A.若,则 B.若,则C.若,则 D.若,则5.已知某几何体的三视图如右图所示,则该几何体的体积是()A. B.C. D.6.设点是曲线上的任意一点,点处的切线的倾斜角为,则角的取值范围是()A. B. C. D.7.已知函数,则这个函数在点处的切线方程是()A. B. C.D.8.已知三棱柱的6个顶点都在球的球面,则球的半径为()A. B. C. D.9.曲线在点(1,2)处的切线为,则直线上的任意点P与圆上的任意点Q之间的最近距离是()A. B. C. D.210.已知椭圆的左、右焦点分别为,点在椭圆上,若是一个直角三角形的三个顶点,则点到轴的距离为()A. B. C.或 D.11.已知双曲线与抛物线有一个共同的焦点F,两曲线的一个交点为P,若,则点F到双曲线的渐近线的距离为()A. B. C. D.12.已知点是圆C: 上的点,过点A且与圆C相交的直线AM、AN的倾斜角互补,则直线MNA B C A 1 B 1C 1 D的斜率为( )A .B .C .D .不为定值二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中的横线上)13.曲线在点(1,2)处切线的斜率为____________.14.经过点且与曲线相切的直线的方程是____________.15.过双曲线的左焦点作圆的切线,切点为E ,延长FE 交抛物线于点P ,O 为坐标原点,若,则双曲线的离心率为____________.16.下列四个命题:①命题“若,则”的否命题是“若,则”;②若命题,则;③若命题“”与命题“或”都是真命题,则命题一定是真命题;④命题“若,则”是真命题.其中正确命题的序号是____________.(把所有正确的命题序号都填上)三、解答题(本大题共6小题,第17小题10分,其余每小题12分,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)设曲线上有点,与曲线切于点的切线为,若直线过且与垂直,则称为曲线在点处的法线,设交轴于点,又作轴于,求的长.18.(本小题满分12分)设命题:函数的定义域为;命题:不等式对一切均成立.(1)如果是真命题,求实数的取值范围;(2)如果命题“或”为真命题,且“且”为假命题,求实数的取值范围.19.(本小题满分12分)在斜三棱柱中,侧面平面,,为中点.(1)求证:;(2)求证:平面;(3)若,,求三棱锥的体积.20.(本小题满分12分)已知直线l:kx-y+1+2k=0(k ∈R)(1)证明:直线l 过定点; (2)若直线l 不经过第四象限,求k 的取值范围; (3)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B ,O 为坐标原点,设△AOB 的面积为S ,求S 的最小值及此时直线l 的方程.21.(本小题满分12分)己知椭圆C:=1(a>b>0)的离心率为,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+=0相切,过点P(4,0)且不垂直于x轴直线,与椭圆C相交于A、B两点.(1)求椭圆C的方程:(2)求的取值范围;(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.22.(本小题满分12分)已知抛物线与双曲线有公共焦点.点是曲线C1,C2在第一象限的交点,且.(1)求双曲线交点及另一交点的坐标和点的坐标;(2)求双曲线的方程;(3)以为圆心的圆M与直线相切,圆N:,过点P(1,)作互相垂直且分别与圆M、圆N相交的直线和,设被圆M截得的弦长为s,被圆N截得的弦长为t,问:是否为定值?如果是,请求出这个定值;如果不是,请说明理由.丰城中学xx学年度上学期高二数学(文)周考试卷答案1—6 BABBAB 7—12 CCCCAA13. 14.或 15. 16.②③17. 解:依题意,,∵与垂直,∴的斜率为,∴直线的方程为:,令,则,∴,容易知道:,于是,.18. 解:(1)若命题为真命题,则恒成立;(2)若命题为真命题,则;“或”为真命题且“且”为假命题,即,一真一假,故. 19.解: (1)证明:因为,所以,又侧面平面,且平面平面,平面,所以平面,又平面,所以 .(2)证明:设与的交点为,连接,在中,分别为,的中点,所以,又平面,平面,所以平面 .(3)解:由(1)知,平面,所以三棱锥的体积为.又 ,,所以 , 所以 . 三棱锥的体积等于. 20. 解: (1)因为直线l:kx-y+1+2k=0(K ∈R) y-1=k(x+2),所以直线l 过定点(-2,1);(2) 由于直线l 恒过定点(-2,1),画出图形,知要使直线l 不经过第四象限必须且只需,故k ∈[0, );(3)由直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B 知:k>0,由直线l:kx-y+1+2k=0中,令则,再令,则,所以有:()2212k 11441111(44)842222k k s k k k k +++=⋅=⋅=++≥⨯=((当且仅当时,取等号),所以,S 的最小值为4,此时l 方程为:x-2y+4=0.21.(1)由题意知,,即.又,,.故椭圆的方程为(2)解:由题意知直线的斜率存在,设直线的方程为由得,由()()()22223244364120k k k ∆=--+->得,设,,则, ①()()()2221212121244416y y k x k x k x x k x x k =--=-++ ()22222121222264123287141625434343k k x x y y k k k k k k -OA⋅OB =+=+⋅-⋅+=-+++ ,,的取值范围是.(3)证:、两点关于轴对称,直线的方程为,令得:又,,由将①代入得:,直线与轴交于定点.22. 解: (1)因为的焦点为,所以双曲线的焦点为、.设,由点在抛物线上,且,由抛物线的定义得,,即,所以,即,所以点A 的坐标为或.(2)由题意知,又因为点在双曲线上,由双曲线定义得:,即,所以,故双曲线的方程为:.(3)为定值.说明如下:设圆M 的方程为:,因为圆M 与直线相切,所以圆M 的半径为.故圆M: .显然,当直线的斜率不存在时不符合题意,所以直线的斜率存在,设的方程为,即.设的方程为,即.所以点到直线的距离为,点到直线的距离为,所以直线被圆M 截得的弦长22221636213332k k k k k s +-=⎪⎪⎪⎭⎫ ⎝⎛+--=,直线被圆M 截得的弦长,所以3)3(2)3(62326362222=--=--=k k k k k k k ts .28587 6FAB 澫$28225 6E41 湁H34476 86AC 蚬226439 6747 杇a25015 61B7 憷30989 790D 礍a29034 716A 煪~28141 6DED 淭22867 5953 奓。
2021年高二上学期周练(10.9)数学试题 含答案

2021年高二上学期周练(10.9)数学试题含答案一、选择题1.用给个零件编号,并用系统抽样的方法从中抽取件作为样本进行质量检测,若第一段中编号为的零件被取出,则第二段中被取出的零件编号为()A. B. C. D.2.用给个零件编号,并用系统抽样的方法从中抽取件作为样本进行质量检测,若第一段中编号为的零件被取出,则第二段中被取出的零件编号为()A. B. C. D.3.现要完成下列3项抽样调查:①从15件产品中抽取3件进行检查;②某公司共有160名员工,其中管理人员16名,技术人员120名,后勤人员24名,为了了解员工对公司的意见,拟抽取一个容量为20的样本;③电影院有28排,每排有32个座位,某天放映电影《英雄》时恰好坐满了观众,电影放完后,为了听取意见,需要请28名观众进行座谈。
较为合理的抽样方法是A.①简单随机抽样,②系统抽样,③分层抽样B.①分层抽样,②系统抽样,③简单随机抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①简单随机抽样,②分层抽样,③系统抽样4.某公司现有职员160人,中级管理人员30人,高级管理人员10人,要从其中抽取20个人进行身体健康检查,如果采用分层抽样的方法,则职员、中级管理人员和高级管理人员各应该抽取多少人A.8,15,7 B.16,2,2 C.16,3,1 D.12,3,55.某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是()A.简单随机抽样法 B.抽签法 C.随机数表法 D.分层抽样法6.某学校有男学生400名,女学生600名,为了解男女学生在学校兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取男学生40名,女学生60名进行调查,则这种抽样方法是()A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法7.为了解凯里地区的中小学生视力情况,拟从凯里地区的中小学生中抽取部分学生进行调查,事先已了解到凯里地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样 B.按性别分层抽样错误!未找到引用源。
南开中学高2010届高三数学文周练

南开中学高2021届高三数学周练(文)一、选择题(此题6个小题,每题10分,共60分)1、{}n a 是等比数列,2512,4a a ==,那么12231n n a a a a a a ++++=…( ) A 、16(14)n --B 、16(12)n --C 、32(14)3n --D 、32(12)3n -- 2、如果1238,,,,a a a a …为各项都大于零的等差数列,公差0,d ≠那么( )A 、1845a a a a >B 、1845a a a a <C 、1845a a a a +>+D 、1845a a a a =3、等差数列{}n a 中,349141510,a a a a a ++++= 那么17S 等于( )A 、34B 、68C 、17D 、514、设数列{}n a 的前n 项和2*32()n S n n n N =-∈,那么当2n ≥时有( )A 、1n n S na na >>B 、1n n S na na <<C 、1n n na S na <<D 、1n n na S na <<5、设有公差不为零的等差数列{}n a 与等比数列{}n b ,两数列有关系;1133,,a b a b ==75a b =,那么( )A 、1113b a =B 、1131b a =C 、1163b a =D 、6311b a = 6、{}n a 是等比数列,且231,a a >=1231231111()()()()0,n n a a a a a a a a -+-+-++->…那么自然数n ( )A 、最大值是4B 、最小值是5C 、最大值是5D 、最小值是6二、填空题(此题4个小题,每题10分,共40分)7、数列{}n a 的前n 项和的公式为2231,n S n n =--那么通项公式为_________。
天津市南开中学高二数学上学期第十五周周练试题 理

南开中学高二上第十五周数学周练本周涉及知识点:1.继续研究双曲线的概念,性质,标准方程2.直线与双曲线的综合考试重点:双曲线的性质,直线与双曲线的综合型试题应知应会:假设双曲线22221x ya b-=的实轴长、虚轴长、焦距成等差数列,那么双曲线的离心率是()()A 2 ()B 3 ()C34()D35若22121x yk k+=---表示核心在y轴上的双曲线,那么它的半焦距的取值范围是()A.()1,+∞B.()0,1C.()1,2D.与k有关设0,4πθ⎛⎫∈ ⎪⎝⎭,那么二次曲线22cot tan1x yθθ-=的离心率的取值范围为().A10,2⎛⎫⎪⎝⎭.B1,22⎛⎝⎭.C2⎛⎝.D)+∞双曲线22221x ya b==(a>0,b>0)的两个核心为F一、F2,假设P为其上一点,且|PF1|=2|PF2|,那么双曲线离心率的取值范围为()A.(1,3)B.(]1,3 C.(3,+∞) D.[)3,+∞假设双曲线12222=-byax的两个核心到一条准线的距离之比为3:2,那么双曲线的离心率是()(A)3 (B)5 (C)3(D)5以下各对曲线中,即有相同的离心率又有相同渐近线的是()()A2213xy-=和22193y x-=()B2213xy-=和2213xy-=()C 2213x y -=和2213y x -= ()D 2213x y -=和22193x y -= 设双曲线以椭圆221259x y +=长轴的两个端点为核心,其准线过椭圆的核心,那么双曲线的渐进线的斜率为( )A .2±B .43±C .12±D .34± 直线1y kx =+与双曲线22:1C x y -=的左支只有一个公共点,那么k 的取值为( ).A (]1,1- .B k = .C []1,1- .D (]1,1-P 是双曲线221916x y -=的右支上一点,,M N 别离是圆()2254x y ++=和()2251x y -+=上的点,那么PM PN -的最大值为( ).A 6 .B 7 .C 8 .D 9 过双曲线222:1y M x b -=的左极点A 作斜率为1的直线l ,假设l 与双曲线M 的两条渐近线别离相交于,B C ,且AB BC =,那么双曲线M 的离心率是 ( ).A .B .C .D设12F F ,别离是双曲线2219y x -=的左、右核心.假设点P 在双曲线上,且120PF PF =,那么12PF PF +=( )A B . C D .过双曲线22196x y -=的左核心,且被双曲线截得线段长为6的直线的条数为_____.已知12F F ,为双曲线22221(00)a b x y a b a b ≠-=>>且,的两个核心,P 为双曲线右支上异于极点的任意一点,O 为坐标原点.下面四个命题( )A.12PF F △的内切圆的圆心必在直线x a =上; B.12PF F △的内切圆的圆心必在直线x b =上;C.12PF F △的内切圆的圆心必在直线OP 上; D.12PF F △的内切圆必通过点0a (),. 其中真命题的代号是(写出所有真命题的代号). 过双曲线22221x y ab -=()0,0a b >>的左核心且垂直于x 轴的直线与双曲线相交于,M N 两点,以MN 为直径的圆恰好于双曲线的右极点,那么双曲线的离心率等于___________. 双曲线2219x y -=有动点P ,12,F F 是曲线的两个核心,那么12PF F ∆的重心M 的轨迹方程为______________. 设双曲线2214x y -=,1F 是它的左核心,直线l 通过它的右核心2F ,且与双曲线右支交于,A B 两点,那么11F A F B ⋅的最小值为________.设点P 是双曲线()222210,0x y a b a b -=>>上任意一点,过点P 的直线与两渐近线别离交于12,P P ,设12P P PP λ=,求证:()12214OP P S abλλ∆+=已知中心在原点的双曲线C 的右核心为()2,0,右极点为)。
2022-2023学年天津市南开中学高二上学期阶段性质量检测(一)数学试卷含详解

高二年级数学阶段性质量检测(一)第I 卷一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.本大题共10小题,每小题4分,共40分.1.已知向量(1,2,3)a = ,(0,1,2)b = ,则2a b -=()A.(2,3,4)B.(2,3,3)C.(2,5,8)D.(2,4,6)2.已知三角形ABC 的三个顶点分别为(1,0)A ,(2,3)B -,(3,3)C ,则AB 边上的中线所在直线的方程为()A.0x y -=B.60x y +-=C .360x y --= D.3120x y +-=3.圆224210x y x y +--+=与圆222210x y x y ++-+=的公切线有()A.1条 B.2条C.3条D.4条4.与直线y =切于点A ,且圆心在x 轴上的圆的方程为()A .22(4)4x y -+= B.22(16x y -+=C.22(36x y ++= D.22(36x y -+=5.若过点(1,1)P -的直线l 与直线23y x =-+的交点位于第一象限,则直线l 斜率的范围是()A.(4,2)-B.(,4][2,)-∞-+∞C.()(),42,-∞-+∞ D.(,2)(2,)-∞-+∞ 6.从点(4,1)A -出发的一条光线l ,经过直线1:30l x y -+=反射,反射光线恰好经过点(3,2)B -,则反射光线所在直线的斜率为()A.2- B.3- C.13-D.35-7.在我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的棱柱称为堑堵.已知三棱柱111ABC A B C -为一堑堵,90ABC ∠=︒,2AB =,BC =12AA =,则直线1CA 与直线1BC 夹角的余弦值为()A.36B.6-C.4D.148.若圆224x y +=上恰有三个点到直线y x b =+的距离为1,则实数b 的值为()A.B. C.1± D.9.已知1F ,2F 分别为椭圆22221(0)x y a b a b+=>>的左、右焦点,点M 为线段2OF 的中点(O 为坐标原点),点P 在椭圆上且满足2PF x ⊥轴,点M 到直线1PF 的距离为12b ,则椭圆的离心率为()A.55或2B.55C.12或15D.1310.已知斜率存在的直线l 与椭圆221164x y +=交于A ,B 两点,且l 与圆22:(1)1C x y -+=切于点P .若P为线段AB 的中点,则直线PC 的斜率为()A. B. C.- D.或第II 卷二.填空题:本大题共6小题,每小题4分,共24分.试题中包含两个空的,答对1个的给2分,全部答对的给4分.11.已知直线1:(1)60l x a y +-+=,直线22:210l ax y a ++-=,当=a ____________时,12l l ⊥.12.圆2220x y x +-=与圆22220x y x y ++-=的公共弦长为____________.13.在空间直角坐标系中,已知三点A (3,2,0),B (2,1,3),C (3,1,0),则点C 到直线AB 的距离为____________.14.已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F ,2F ,点P 为椭圆上一点,线段1F P 与y 轴交于点Q ,若1||2PQ QF =,且12PF F △为等腰三角形,则椭圆的离心率为____________.15.如图,在平行六面体1111ABCD A B C D -中,1160AAD A AB BAD ∠=∠=∠=︒,13AA AB AD ===,点E 为线段1BD 上靠近于点B 的三等分点,设AB a =,AD b =,1AA c = ,则AE = ____________(用含有a ,b,c 的表达式表示);若点G 为棱1CC 上的一个动点,则1EG D G ⋅ 的最小值为____________.16.已知圆222:24120C x y ax y a +--+-=与过点(3,0)P -的直线交于A ,B 两点,若三角形ABC 面积的最大值为8,则实数a 的取值范围是____________.三.解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.17.已知椭圆22:14x y Γ+=,直线l 过点(0,2)-与椭圆Γ交于A ,B 两点,O 为坐标原点.(1)设C 为线段AB 的中点,当直线l 的斜率为32时,求线段OC 的长;(2)当直线l 的斜率为2时,求三角形AOB 的面积.18.为方便师生行动,我校正实施翔宇楼电梯加装工程.我们借此构造了以下模型:已知正四棱柱1111ABCD A B C D -,它抽象自翔宇楼南侧楼心花园所占据的空间,设8AB BC ==,112AA =,O 为底面ABCD 的中心,正四棱柱1111OECF O E C F -与正四棱柱2222OECF O E C F -分别代表电梯井与电梯厢,设22OO =,M 为棱1FF 的中点,N ,K 分别为棱1AA ,1DD 上的点,8AN =,4=DK .(1)求证:OM 平面11A CF ;(2)求直线1AO 与平面11A CF 所成角的正弦值;(3)“你站在桥上看风景,看风景的人在楼上看你.明月装饰了你的窗子,你装饰了别人的梦.”卞之琳诗句中的情景其实正在我们的生活中反复上演,上官琐艾同学站在楼心花园的中心(O 点),她正目送着倚立在电梯厢一角的欧阳南德同学,假定上官同学的目光聚焦于棱OO 2的中点I ,此时,电梯厢中欧阳同学的目光正徘徊在位于N 点的数学办公室与位于K 点的数学实验室,当电梯厢向上启动时,在这时空里便诞生了由点O 与移动着的平面INK 所勾勒的动人风景.现在,请作为“正在看风景的人”的你完成以下问题:当电梯厢自底部(平面OECF 与平面ABCD 重合)运行至顶端(平面2222O E C F 与平面1111D C B A 重合)的过程中,点O 到平面INK 距离的最大值.19.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为22,直线y x =被椭圆C 截得的线段长为833.(1)求椭圆C 的方程;(2)直线l 是圆222:O x y r +=的任意一条不垂直于坐标轴的切线,l 与椭圆C 交于A ,B 两点,若以AB 为直径的圆恒过原点,求:(i )圆O 的方程;(ii )||AB 的最大值.高二年级数学阶段性质量检测(一)第I 卷一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.本大题共10小题,每小题4分,共40分.1.已知向量(1,2,3)a = ,(0,1,2)b = ,则2a b -=()A.(2,3,4)B.(2,3,3)C.(2,5,8)D.(2,4,6)A【分析】由空间向量坐标运算法则可得答案.【详解】因()1,2,3a = ,则()22,4,6a = ,则2a b -=()()20,41,622,3,4---=.故选:A2.已知三角形ABC 的三个顶点分别为(1,0)A ,(2,3)B -,(3,3)C ,则AB 边上的中线所在直线的方程为()A.0x y -=B.60x y +-=C.360x y --=D.3120x y +-=C【分析】先求出AB 的中点,再用两点式求AB 边上的中线所在直线的方程【详解】AB 边的中点为33,22⎛⎫-⎪⎝⎭,∴AB 边上的中线所在直线的方程32333233y x --=---,即360x y --=.故选:C3.圆224210x y x y +--+=与圆222210x y x y ++-+=的公切线有()A.1条 B.2条 C.3条D.4条C【分析】分别求两圆的圆心和半径,进而确定两圆的位置关系,分析判断.【详解】224210x y x y +--+=,即()()22214x y -+-=,则圆心()12,1C ,半径12r =,222210x y x y ++-+=,即()()22111x y ++-=,则圆心()21,1C -,半径21r =,∵123C C ==,即1212C C r r =+,则圆1C 与圆2C 外切,故两圆的公切线有3条.故选:C.4.与直线y =切于点A ,且圆心在x 轴上的圆的方程为()A.22(4)4xy -+= B.22(16xy -+=C.22(36x y++= D.22(36x y -+=D【分析】利用待定系数法,结合点到直线的距离公式进行求解即可.【详解】因为该圆的圆心在x 轴上,所以设该圆的方程为222()(0x a y r r -+=>),于是有:222)36a r a r r ⎧-+=⎧=⎪⇒⎨==⎪⎩即该圆的方程为22(36x y -+=,故选:D5.若过点(1,1)P -的直线l 与直线23y x =-+的交点位于第一象限,则直线l 斜率的范围是()A.(4,2)-B.(,4][2,)-∞-+∞C.()(),42,-∞-+∞ D.(,2)(2,)-∞-+∞ C【分析】用直线l 斜率k 表示出l 方程,再求出直线l 与直线23y x =-+的交点坐标,利用其位于第一象限,可得答案.【详解】由题直线l 斜率存在,则设直线l 斜率为k ,则l 方程为:()11y k x +=-.将其与23y x =-+联立得:()123y kx k y x ⎧-=-+⎨+=⎩,解得4222k x k k y k +⎧=⎪⎪+⎨-⎪=⎪+⎩,故交点坐标为42,22k k k k +-⎛⎫⎪++⎝⎭.因其在第一象限,则402202k k k k +⎧>⎪⎪+⎨-⎪>⎪+⎩,解得()(),42,k ∈-∞-+∞ .故选:C6.从点(4,1)A -出发的一条光线l ,经过直线1:30l x y -+=反射,反射光线恰好经过点(3,2)B -,则反射光线所在直线的斜率为()A.2- B.3- C.13-D.35-B【分析】先求出点(4,1)A -关于直线1:30l x y -+=的对称点(,)D m n ,再结合D 在反射光线上,反射光线恰好通过点(3,2)B -,即可求解.【详解】设点(4,1)A -关于直线1:30l x y -+=的对称点为(,)D m n ,则114413022n m m n -⎧=-⎪⎪+⎨-+⎪-+=⎪⎩,解得21(21)m n D =-=-∴--,,,,由题意可知,D 在反射光线上,又反射光线恰好通过点(3,2)B -,则21332BD k +==--+,即反射光线所在直线的斜率为3-,故选:B﹒7.在我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的棱柱称为堑堵.已知三棱柱111ABC A B C -为一堑堵,90ABC ∠=︒,2AB =,BC =12AA =,则直线1CA 与直线1BC 夹角的余弦值为()A.36B.6-C.4D.14A【分析】平移直线1CA 到其与直线1BC 相交,再解三角形即可.【详解】连接1CB ,交1BC 于点M ,取11A B 中点为N ,连接1,MN C N ,如下所示:显然点M 为1B C 的中点,故在△11A B C 中,点,M N 分别为111,B C A B 的中点,故MN //1AC ,则直线11,A C BC 所成的夹角与直线1,MN MC 所成的夹角相等,则1NMC ∠即为所求角或其补角;在三角形1MNC 中,2211111111242222MN A C A C C C ==+=+=,2211111111843222MC BC B C B B ==+=+=221111183NC NB B C =+=+=,故由余弦定理可得:2221111439cos 2223MN MC NC NMC MN MC +-∠==-⨯⨯⨯36,故直线11,A C BC 所成的夹角的余弦值为36.故选:A 8.若圆224x y +=上恰有三个点到直线y x b =+的距离为1,则实数b 的值为()A.2 B.2- C.1± D.2D【分析】根据圆的性质,结合点到直线的距离公式进行求解即可.【详解】圆224x y +=的圆心坐标为(0,0),半径为2,因为圆224x y +=上恰有三个点到直线y x b =+的距离为1,所以圆心到直线直线y x b =+的距离为1,所以有22121(1)b b =⇒=+-,故选:D9.已知1F ,2F 分别为椭圆22221(0)x y a b a b+=>>的左、右焦点,点M 为线段2OF 的中点(O 为坐标原点),点P 在椭圆上且满足2PF x ⊥轴,点M 到直线1PF 的距离为12b ,则椭圆的离心率为()A.55或22B.55C.12或15D.13A【分析】根据几何关系求出P 和M 的坐标,写出直线1PF 的方程,根据M 到1PF 的距离即可求出离心率.【详解】∵2PF x ⊥轴,∴将x c =代入椭圆可得2by a=±,∴不妨设2,b P c a ⎛⎫ ⎪⎝⎭,∴直线1PF 的斜率为()2202b b a c c ac-=--,则直线1PF 的方程为()22b y x c ac=+,即2220b x acy b c -+=,则,02c M ⎛⎫⎪⎝⎭到直线1PF12b =,整理得()()2222227010a c a c -+=,所以4217010e e +-=,解得212e =或215e =,即22e =或55e =,则椭圆的离心率为22故选:A10.已知斜率存在的直线l 与椭圆221164x y +=交于A ,B 两点,且l 与圆22:(1)1C x y -+=切于点P .若P为线段AB 的中点,则直线PC 的斜率为()A.B.C.-D.或C【分析】利用点差法,结合点P 的坐标满足圆方程,以及CP 与直线AB 垂直,联立方程组求得点P 的坐标,即可求得直线PC 的斜率.【详解】设点,,A B P 的坐标分别为()()()1122,,,,,x y x y m n ,则:222211221,1164164x y x y +=+=,作差后可得:121212121242y y y y x x x x +-⨯=-+-,即:121214y y n m x x -⨯=--;又因为直线CP 与直线AB 垂直,故可得121211y y nm x x -⨯=---,与121214y y n m x x -⨯=--联立后可得:41m m =-,解得43m =,又因为点P 在圆C 上,故可得:()2211m n -+=,解得223n =±,则1nm =±-,即直线CP的斜率为或-.故选:C.第II 卷二.填空题:本大题共6小题,每小题4分,共24分.试题中包含两个空的,答对1个的给2分,全部答对的给4分.11.已知直线1:(1)60l x a y +-+=,直线22:210l ax y a ++-=,当=a ____________时,12l l ⊥.23【分析】确定当1a =时不合题意,则1a ≠时,可求出两直线斜率,根据直线垂直可得斜率之积为1-,即可求得答案.【详解】当1a =时,1:(1)60l x a y +-+=斜率不存在,2:20l x y +=,2l 的斜率为12-,不合题意;故1a ≠时,1l 的斜率为11a --,2l 的斜率为2a-,由于12l l ⊥,故1()112a a -⨯-=--,解得23a =,故答案为:23.12.圆2220x y x +-=与圆22220x y x y ++-=的公共弦长为____________.255【分析】先求出公共弦的方程利用勾股定理即可求得.【详解】由已知圆2220x y x +-=与圆22220x y x y ++-=公共弦所在直线方程为420x y -=因为圆2220x y x +-=圆心为()1,0,半径1r =所以d ==弦长为255=故答案为:513.在空间直角坐标系中,已知三点A (3,2,0),B (2,1,3),C (3,1,0),则点C 到直线AB 的距离为____________.11011【分析】根据空间向量夹角公式,结合同角的三角函数关系式进行求解即可.【详解】由A (3,2,0),B (2,1,3),C (3,1,0),可得:(1,1,3)AB =-- ,(0,1,0)AC =-,所以可得:cos ,AC AB AC AB AC AB ⋅〈〉==⋅因此110sin ,11AC AB 〈〉===,于是点C 到直线AB 的距离为110110sin ,11111AC AC AB ⋅〈〉=⨯=,故答案为:1101114.已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F ,2F ,点P 为椭圆上一点,线段1F P 与y 轴交于点Q ,若1||2PQ QF =,且12PF F△为等腰三角形,则椭圆的离心率为____________.1F P 与y 轴交于点Q ,得P 点横坐标,代入椭圆方程得P 点纵坐标,由12PF F △为等腰三角形,得122F F PF =,用,,a b c 表示此等式转化为离心率e 的方程,解之可得.【详解】1(,0)F c -,线段1F P 与y 轴交于点Q ,1||2PQ QF =,P 在y 右侧,则2P x c =,222241c y ab+=,22224(1)c y b a=-,12PF F △为等腰三角形,则122F F PF =,2c ,2222244b c a c a -=,整理得424810e e -+=,2312e =-,312e -=,15.如图,在平行六面体1111ABCD A B C D -中,1160AAD A AB BAD ∠=∠=∠=︒,13AA AB AD ===,点E 为线段1BD 上靠近于点B 的三等分点,设AB a =,AD b =,1AA c = ,则AE = ____________(用含有a ,b,c 的表达式表示);若点G 为棱1CC 上的一个动点,则1EG D G ⋅ 的最小值为____________.①.211333a b c ++②.114##2.75【分析】第一空,根据空间向量的线性运算,即可求得答案;第二空,设11,01C G C C λλ=≤≤ ,用含有a ,b ,c的表达式表示出1,EG D G ,根据数量积的运算律,将1EG D G ⋅展开化简为关于λ的二次函数,结合二次函数性质,求得答案.【详解】由题意得11111()()333AE AB BE a BD a AD AA AB a b c a =+=+=++-=++-211333a b c =++ ;设11,01C G C C λλ=≤≤ ,则1111D G D C C C a c λλ=+=- ,112122())3333(b c EG ED D G a c a b c a λλ+-+=+=+-=+- ,由题意可知193322a b a c c b ⋅=⋅=⋅=⨯⨯= ,故1122))333[(](EG D G b c a a c λλ=+-⋅+⋅- 22((112222))333333c b a b c c a a c a λλλλλ=-⋅+-⋅+-⋅-⋅- 1929292923()()9323232323λλλλλ=-⨯+⨯-⨯+-⨯--⨯2251191599(),0164λλλλ=-+=-+≤≤,当56λ=时,25119()64λ-+取得最小值114,即则1EG D G ⋅的最小值为114,故答案为:211333a b c ++ ;114.16.已知圆222:24120C x y ax y a +--+-=与过点(3,0)P -的直线交于A ,B 两点,若三角形ABC 面积的最大值为8,则实数a 的取值范围是____________.(,5][1,)-∞-⋃-+∞【分析】根据三角形面积公式,结合圆的性质进行求解即可.【详解】由22222:24120()(2)16C x y ax y a x a y +--+-=⇒-+-=,所以该圆的半径为4,圆心(,2)C a ,11sin 44sin 8sin 22ABC S CA CB ACB ACB ACB =⋅⋅⋅∠=⨯⨯⋅∠=∠ ,所以当π2ACB ∠=时,ABC S 有最大值8,此时三角形ABC 是等腰直角三角形,因此点C 到直线AB 的距离为1122AB ==所以有1PC a ≤⇒≤⇒≥-,或5a ≤-,故答案为:(,5][1,)-∞-⋃-+∞【点睛】关键点睛:利用三角形面积公式,得到三角形ABC 是等腰直角三角形时面积最大是解题的关键.三.解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.17.已知椭圆22:14x y Γ+=,直线l 过点(0,2)-与椭圆Γ交于A ,B 两点,O 为坐标原点.(1)设C 为线段AB 的中点,当直线l 的斜率为32时,求线段OC 的长;(2)当直线l 的斜率为2时,求三角形AOB 的面积.(1)375(2)1【分析】(1)写出直线l 方程,与椭圆方程联立方程组,消去y 得x 的一元二次方程,设()11,A x y ,()22,B x y ,()00,C x y ,应用韦达定理得0x ,从而得中点C 的坐标后可得OC ;(2)同样写出直线l 方程,与椭圆方程联立消元后应用韦达定理求得弦长AB ,再计算出O 到直线AB 的距离后可得三角形面积.【小问1详解】当直线l 的斜率为32时,直线l 的方程为322y x =-.由2232214y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,得251260x x -+=.设()11,A x y ,()22,B x y ,()00,C x y ,则有12125x x +=,由于C 是线段AB 的中点,则有0121625()x x x =+=,0031225y x =-=-.所以||5OC ===.【小问2详解】当直线l的斜率为2时,直线l的方程为22y x =-.由2272214y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,得2230x -+=.设()11,A x y ,()22,B x y,有12x x +=1232x x =.||AB ====2.原点O 到直线l的距离41111112d ==.所以1111411||122211AOB S AB d =⋅=⋅⋅=△.18.为方便师生行动,我校正实施翔宇楼电梯加装工程.我们借此构造了以下模型:已知正四棱柱1111ABCD A B C D -,它抽象自翔宇楼南侧楼心花园所占据的空间,设8AB BC ==,112AA =,O 为底面ABCD 的中心,正四棱柱1111OECF O E C F -与正四棱柱2222OECF O E C F -分别代表电梯井与电梯厢,设22OO =,M 为棱1FF 的中点,N ,K 分别为棱1AA ,1DD 上的点,8AN =,4=DK .(1)求证:OM 平面11A CF ;(2)求直线1AO 与平面11ACF 所成角的正弦值;(3)“你站在桥上看风景,看风景的人在楼上看你.明月装饰了你的窗子,你装饰了别人的梦.”卞之琳诗句中的情景其实正在我们的生活中反复上演,上官琐艾同学站在楼心花园的中心(O 点),她正目送着倚立在电梯厢一角的欧阳南德同学,假定上官同学的目光聚焦于棱OO 2的中点I ,此时,电梯厢中欧阳同学的目光正徘徊在位于N 点的数学办公室与位于K 点的数学实验室,当电梯厢向上启动时,在这时空里便诞生了由点O 与移动着的平面INK 所勾勒的动人风景.现在,请作为“正在看风景的人”的你完成以下问题:当电梯厢自底部(平面OECF 与平面ABCD 重合)运行至顶端(平面2222O E C F 与平面1111D C B A 重合)的过程中,点O 到平面INK 距离的最大值.(1)证明见解析(2)77(3)4705【分析】(1)以O 为坐标原点,OE ,OF,1OO 的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系Oxyz ,求出平面11A CF 的法向量1n ,通过10n OM ⋅=证明OM 平面11A CF ;(2)由(1)知,平面11A CF 的法向量1(6,3,2)n =-,然后利用直线与平面所成角的公式求解;(3)设(0,0,)I λ,[1,11]λ∈,求出平面INK 的法向量26,1,22n λ-⎛⎫=⎪⎝⎭,利用点到平面的距离公式求得点O 到平面INK 的距离d 的表达式,进一步求得d 的最大值.【小问1详解】以O 为坐标原点,OE ,OF,1OO 的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系Oxyz ,则(0,0,0)O ,(0,4,6)M ,1(4,4,12)A --,(4,4,0)C ,1(0,4,12)F .设1(,,)n x y z = 为平面11A CF 的一个法向量,则1111100n A F n CF ⎧⋅=⎪⎨⋅=⎪⎩因为11(4,8,0)A F = ,1(4,0,12)CF =- ,所以4804120x y x z +=⎧⎨-+=⎩取2z =,则1(6,3,2)n =-.因为(0,4,6)OM =,所以10n OM ⋅= ,所以1OM n ⊥ ,因为OM 不在平面11A CF 内,所以OM 平面11A CF .【小问2详解】因为1(4,4,12)A O =- ,所以111111311cos ,77A n A O n O O A n ⋅===-,所以直线1AO 与平面11A CF 所成角的正弦值为77.【小问3详解】设(0,0,)I λ,[1,11]λ∈,又因为(4,4,8)N --,(4,4,4)K -,所以(0,8,4)NK =- ,(4,4,4)IK λ=--.设2(,,)n x y z = 为平面INK 的一个法向量,则2200n NK n IK ⎧⋅=⎪⎨⋅=⎪⎩,即84044(4)0y z x y z λ-=⎧⎨-++-=⎩取1y =,则26,1,22n λ-⎛⎫= ⎪⎝⎭ ,所以点O 到平面INK的距离22OI n d n ⋅====,所以当1328λ=,即283λ=时,d 取得最大值为4705,所以点O 到平面INK的距离的最大值为5.19.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为22,直线y x =被椭圆C 截得的线段长为833.(1)求椭圆C 的方程;(2)直线l 是圆222:O x y r +=的任意一条不垂直于坐标轴的切线,l 与椭圆C 交于A ,B 两点,若以AB 为直径的圆恒过原点,求:(i )圆O 的方程;(ii )||AB 的最大值.(1)22184x y +=(2)(i )2283x y +=;(ii)【分析】(1)根据离心率和椭圆中,,a b c 的关系即可求得方程.(2)(i )问利用直曲联立0OA OB ⋅=可以求得圆的方程,(ii )问中利用弦长公式和基本不等式即可求得最值.【小问1详解】因为22c e a ==,所以222a c =,所以222a b =,所以椭圆222212x y C b b +=:,联立直线y x =,得2223b x =,所以832633b =,所以2b =,所以椭圆22:184x y C +=.【小问2详解】(i )设直线:(0)=+≠l y kx m k ,因为l 与圆O相切,所以r =()2221m kr=+……(1).由22184x y y kx m ⎧+=⎪⎨⎪=+⎩得,()222124280k x kmx m +++-=22648320k m ∆=-+>,所以2284m k <+(*)设()11,A x y ,()22,B x y ,得12221224122812km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩,所以()()()2222121212122812m k y y kx m kx m k x x km x x m k -=++=+++=+由题意得,0OA OB ⋅= ,即22212122288012m m k x x y y k-+-+==+,所以()22813m k =+,符合(*)式.结合(1)式,得283r =,所以圆O 的方程为:2283x y +=.(ii)222||12AB k==+223123123k k ==⋅=++464633=463≤=,等号成立当且仅当212k =所以||AB 的最大值为.。
2021年高二上学期周练(10.16)数学试题 含答案
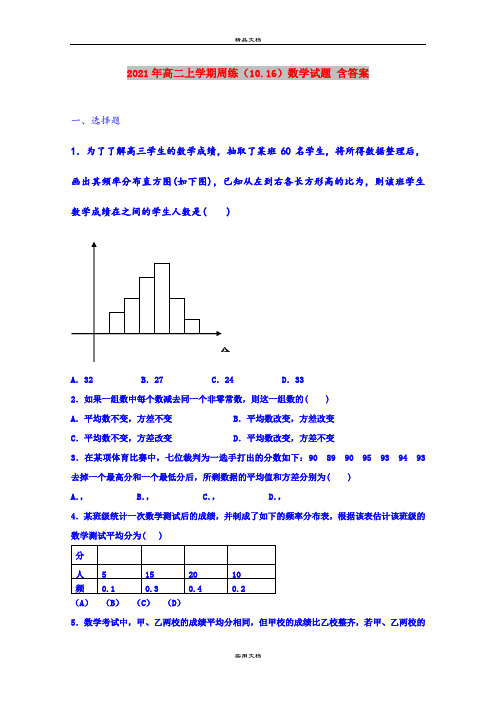
2021年高二上学期周练(10.16)数学试题含答案一、选择题1.为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如下图),已知从左到右各长方形高的比为,则该班学生数学成绩在之间的学生人数是( )A.32 B.27 C.24 D.332.如果一组数中每个数减去同一个非零常数,则这一组数的( )A.平均数不变,方差不变 B.平均数改变,方差改变C.平均数不变,方差改变 D.平均数改变,方差不变3.在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )A., B., C., D.,4.某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )(A)(B)(C)(D)5.数学考试中,甲、乙两校的成绩平均分相同,但甲校的成绩比乙校整齐,若甲、乙两校的成绩方差分别为和,则()A.> B.< C.= D.S1>S26.为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m e,众数为m o,平均值为,则( )(A)m e=m o= (B)m e=m o<(C)m e<m o< (D)m o<m e<7.如图是总体密度曲线,下列说法正确的是( )(A)组距越大,频率分布折线图越接近于它(B)样本容量越小,频率分布折线图越接近于它(C)阴影部分的面积代表总体在(a,b)内取值的百分比(D)阴影部分的平均高度代表总体在(a,b)内取值的百分比8.如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为和,样本标准差分别为s A和s B,则( )(A)>,s A>s B (B)<,s A>s B(C)>,s A<s B (D)<,s A<s B9.为选拔运动员参加比赛,测得7名选手的身高(单位:cm)分布茎叶图为记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数字记为x,那么x的值为( )(A)5 (B)6 (C)7 (D)810.某班有50名学生,该班某次数学测验的平均分为70分,标准差为s,后来发现成绩记录有误:甲生得了80分,却误记为50分;乙生得了70分,却误记为100分.更正后得标准差为s1,则s与s1之间的大小关系为( )(A)s<s1 (B)s>s1(C)s=s1 (D)无法确定11.在演讲比赛决赛中,七位评委给甲、乙两位选手打分的茎叶图如图所示,但其中在处数据丢失.按照规则,甲、乙各去掉一个最高分和一个最低分,用和分别表示甲、乙两位选手获得的平均分,则( )A. B.C. D.和之间的大小关系无法确定12.某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:.若低于60分的人数是15,则该班的学生人数是( )(A)45 (B)50(C)55 (D)60二、填空题13.已知一个样本容量为的样本数据的频率分布直方图如图所示,样本数据落在[40,60)内的频数为 .14.如图是甲,乙两名同学次综合测评成绩的茎叶图,则乙的成绩的中位数是,甲乙两人中成绩较为稳定的是 .15.为了普及环保知识,增强环保意识,某高中随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为,众数为,平均值为,则这三个数的大小关系为_______________.16.对一批产品的长度(单位:毫米)进行抽样检测,右图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)为二等品,在区间[10,15)和[30,35)为三等品.用频率估计概率,现从这批产品中随机抽取1件,则其为二等品的概率是____三、解答题17.某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是,样本数据分组为,,,,.时间频率/组距x0.01250.00650.003102030405060708090100110O(1)求直方图中的值;(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;(3)现有6名上学路上时间小于分钟的新生,其中2人上学路上时间小于分钟. 从这6人中任选2人,设这2人中上学路上时间小于分钟人数为,求的分布列和数学期望.18.在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.(1)求第二小组的频率,并补全这个频率分布直方图;(2)求这两个班参赛的学生人数是多少;(3)这两个班参赛学生的成绩的中位数应落在第几小组内.19.某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:组别频数频率145.5~149.5 8 0.16149.5~153.5 6 0.12153.5~157.5 14 0.28157.5~161.5 10 0.20161.5~165.5 8 0.16165.5~169.5合计(1)求出表中字母所对应的数值;(2)在给出的直角坐标系中画出频率分布直方图;(3)估计该校高一女生身高在149.5~165.5范围内有多少人?20.已知一组数据的频率分布直方图如下.求众数、中位数、平均数.21.如图是总体的一个样本频率分布直方图,且在区间[15,18)内的频数为8.(1)求样本容量;(2)若在[12,15)内的小矩形的面积为0.06,①求样本在[12,15)内的频数;②求样本在[18,33)内的频率。
高二数学上学期第十七周周练试题 理A 试题

南开中学高二第十七周数学周练本周涉及的知识点:1.抛物线的定义、HY方程、几何性质2.直线与抛物线的位置关系3.圆锥曲线综合应知应会:1.抛物线2y x=的准线方程是( ).A.4y+1=0 B.4x+1=0 C.2y+1=0 D.2x+1=02.过抛物线24y x=的焦点作直线交抛物线于11(,)A x y、22(,)B x y两点,假如126x x+=,那么||AB的长是〔〕.A.10 B.8 C.6 D.43.过抛物线22y px=(0)p>的焦点F作弦PQ,那么以PQ为直径的圆与抛物线的准线的位置关系是〔〕.A.相离 B.相切 C.相交 D.不确定4.抛物线()220y px p=>的焦点弦AB的两端点坐标分别为()()1122,,,A x y B x y ,那么1212y y x x 的值一定是( ).A .4B .4-C .2pD . 2p - 5. 过抛物线()20y ax a =>的焦点F 作一直线交抛物线于P 、Q 两点,假设线段PF 与FQ 的长分别为p q 、,那么11p q +等于( ).A .2aB .12aC .4aD .4a6.设双曲线22221(00)x y a b a b -=>>,,且它的一条准线与抛物线24y x =的准线重合,那么此双曲线的方程为〔 〕.A.2211224x y -= B.2214896x y -= C.222133x y -=D.22136x y -=7.点P 是抛物线22y x =上的一个动点,那么点P 到点(0,2)的间隔 与P 到该抛物线准线的间隔 之和的最小值为( ).AB .3 C.928.点P 在抛物线24y x =上,那么点P 到点(21)Q -,的间隔 与点P 到抛物线焦点间隔 之和获得最小值时,点P 的坐标为〔 〕.A .114⎛⎫- ⎪⎝⎭,B .114⎛⎫⎪⎝⎭, C .(12), D .(12)-,9.抛物线2:8C y x =的焦点为F ,准线与x 轴的交点为K ,点A 在C 上且AK =AFK ∆的面积为( ).A.4 B.8 C.16 D.3210.探照灯反射镜的纵断面是抛物线的一局部,光源在抛物线的焦点处,灯口直径60cm ,灯深40cm ,那么光源到反射镜顶点的间隔 是〔 〕. A .11.25cm B .5.625cm C .20cm D .10cm 才能进步:11.抛物线2(0)y ax a =<的焦点坐标是〔 〕.A .)4,0(a B .)41,0(a C .)41,0(a - D .)0,41(a 12.点P 是抛物线221xy =上的动点,P 在直线1-=y 上的射影为M ,定点7(4,)2A ,那么||||PM PA +的最小值为〔 〕. A .92 B .5 C .112 D .613. 椭圆E 的离心率为e,两焦点为12F F 、.抛物线C 以1F 为顶点,2F 为焦点.P 为两曲线的一个交点.假设12PF e PF =,那么e 的值是( ).A .B .C. D 14.定点(1,0)N ,动点A 、B 分别在图中抛物线24y x =及椭圆22143x y += 的实线局部上运动,且AB ∥x 轴,那么NAB 的周长l 的取值范围是〔 〕.A .(2,23)B .(10,43)C .(51,416)D .(2,4)15.双曲线22221(0,0)x y a b a b -=>>,假设它的一条准线与抛物线24y x =的准线重合.设双曲线与抛物线的一个交点为P ,抛物线的焦点为F ,那么||PF = ( ).A .21B .18C .D .416.双曲线22122:1(00)x y C a b a b -=>>,的左准线为l ,左焦点和右焦点分别为1F 和2F ;抛物线2C 的准线为l ,焦点为21F C ;与2C 的一个交点为M ,那么12112F F MF MF MF -等于〔 〕A .1-B .1C .12-D .1217.103k <<,那么关于x 的方程kx的实数解的个数是( ).A .1个B .2个C .3个D .4个18.抛物线将坐标平面分成两局部,我们将焦点所在的局部〔不包括抛物线本身〕称为抛物线的内部.假设点(),N a b 在抛物线()2:20C y px p =>的内部,那么直线:()l by p x a =+与抛物线C 的公一共点的个数为〔 〕.A .0B .1C .2D .不能确定19.抛物线方程为22(0)y px p =>,过焦点F 的直线l 与抛物线交于112211(,)(,),A x y B x y AA BB 、、垂直于准线,垂足分别为11A B 、,AB 的中垂线交x 轴于点R.求证:〔1〕221212,4p x x y y p ==-; 〔2〕通径长为2p ,且通径是最短的焦点弦;〔3〕以AB 为直径的圆与准线相切; 〔4〕1190A FB ︒∠=;〔5〕112AF BF p+=; 〔6〕2AB FR =.(0,3)A -,动点P 在x 轴上挪动,动点Q 在y 轴上,且2APQ π∠=,点R在直线PQ 上且满足12PQ QR=.(1)当点P 在x 轴上挪动时,求动点R 的轨迹C 的方程;〔2〕倾斜角为4π的直线0l 与轨迹C 相切,求切线0l 的方程;〔3〕切线0l与y 轴的交点为B,过点B 的直线l 与轨迹C 交于M 、N 两点,点(0,1)D .假设MDN ∠为钝角,求直线l 的斜率k 的取值范围.。
天津市南开中学2023-2024学年高二上学期第二次学情调查数学试卷

A. -3
B.3
C.
-
2 3
D. 3 2
2.过点 A(1, 2) 的直线在两坐标轴上的截距之和为零,则该直线方程为( )
A. x - y +1 = 0
B. x + y - 1 = 0
C. 2x - y = 0 或 x - y +1 = 0
D. 2x + y = 0 或 x + y +1 = 0
3.方程 x2 + y2 - 2mx - 4y + 2m2 - 4m = 0 所表示的圆的最大面积为( )
.(请写出长度较小的弧与长度较长的弧的长度之比,
三、解答题 15.如图,在四棱锥 P - ABCD 中,底面 ABCD 是边长为 1 的正方形, PC ^ 底面
试卷第31 页,共33 页
ABCD ,且 PC = 1 ,点 E 在线段 PB 上,且 BE = 2EP .
(1)求 BD 与 AE 所成的角的余弦值; (2)求平面 PAC 与平面 ACE 夹角的余弦值; (3)求点 D 到平面 ACE 的距离.
【详解】由直线经过 A(3,5) , B (2, 6) 两点,
则
k
=
6 2
-
5 3
=
-1,
设直线的倾斜角为a ,a Î[0,p ) ,
则 k = tana = -1 ,
则a
=
3p 4
,
故答案为: 3p . 4
答案第51 页,共22 页
10. 5 / 1 33
5
【分析】根据两直线平行求出 a 的值,然后根据平行线间距离公式,求出答案.
y
=
25 5
x
和
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津南开中学高二上数学周练10
一、选择题 (每题4分,共40分)
1. 22530x x --<成立的一个必要不充分条件是 ( )
A .132x -<<
B .102x -<<
C .132
x -<< D .16x -<< 2. 在ABC 中,条件甲:A B <,条件乙:sin sin A B <,则甲是乙的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分又不必要条件
3. >|x ||y |<”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
4. 设0,h >命题甲:实数a b 、满足2a b h -<,命题乙:1,1a h b h -<-<,那么( )
A .甲是乙的充分不必要条件
B .甲是乙的必要不充分条件
C .甲是乙的充要条件
D .甲既不是乙的充分条件,也不是乙的必要条件.
5. 下面各组方程表示同一曲线的是( )
.A 2y x =与y = .B y x =与1y x
=
.C 22log y x =与22log y x = .D 221x y +=与y =6. 已知A ()11,x y ,B ()22,x y 分别是直线l 上和l 外的点,若直线l 的方程为(),0f x y =,则方程
()()11,,f x y f x y =表示( )
.A 直线l .B 过点,A B 的直线
.C 过点B 与l 垂直的直线 .D 过点B 与l 平行的直线
7. 设命题甲为:点P 的坐标适合方程(),0f x y =;命题乙:点P 在曲线C 上;命题丙:点Q 坐标
不适合(),0f x y =;命题丁:点Q 不在曲线C 上.已知甲是乙的必要不充分条件,那么丙是丁的( )条件
.A 充分不必要 .B 必要不充分 .C 充要 .D 既不充分也不必要
8. 如果方程22
2x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ) .A ()0,+∞ .B ()0,2 .C ()1,+∞ .D ()0,1
9. 椭圆的两条准线间的距离是该椭圆的焦距的2倍,则该椭圆的离心率为( )
.A 14 .B 256
.C 92 .D 158 10. 设椭圆的两个焦点分别为12,F F ,过2F 作椭圆长轴的垂线交椭圆于点P ,若12F PF 为等腰直角三
角线,则椭圆的离心率为( )
.A 2 .B 12 .C 2 .D 1
二、填充题(每题4分,共24分)
11. 已知命题:211p x -≥,命题21:045
q x x >+-,则p ⌝是q ⌝的______________条件. 12. 已知命题p :不等式25x x m -++>的解集为R ,命题q :函数()(52)x f x m =--是减函数,
若p 或q 为真,p 且q 为假,则实数m 的取值范围是 _____________.
13. 过()2,4P 作两条互相垂直的直线12,l l ,1l 交x 轴于A 点,2l 交y 轴于B 点,则线段AB 的中点M
的轨迹方程为_______________. ()2501x y x +-=≠
14. 已知k R ∈,则两条动直线()210kx y k -++=与()210x ky k ++-=的交点P 的轨迹方程为
__________________.
15. 椭圆22
55x ky -=的一个焦点为()0,2,则k =__________.
16. 椭圆的中心在原点,以坐标轴为对称轴,且经过两点)1
P ,(2P ,则椭圆方程为______________.
三、解答题(共4大题,共36分)
17. 已知,A B 为两个定点,动点M 到A 与B 的距离比为常数λ,求点M 的轨迹方程,并注明轨迹是
什么曲线.
18. 已知点P 是圆22
4x y +=上的一动点,定点()4,0Q ()1求线段PQ 中点的轨迹方程;
()2设POQ ∠的平分线交PQ 于R ,求点R 的轨迹方程。
19. 已知Q 为椭圆22
298x y +=上一动点,()0,5P 为一定点,求点P 到椭圆的最大和最小距离以及此时Q 的坐标。
20. 设椭圆()22
2210x y a b a b
+=>>的左焦点为F ,上顶点为A ,过点A 与AF 垂直的直线分别交椭圆和x 轴正半轴于,P Q 两点,且P 分向量AQ 所成的比为8:5,
()1求椭圆的离心率;
()
2若过,,A Q F 三点的圆恰好与直线:30l x ++=相切,求椭圆方程。
