原子物理学-习题解答(第一、二章)
原子物理学杨福家1-6章 课后习题答案(2020年7月整理).pdf

原子物理学课后前六章答案(第四版)杨福家著(高等教育出版社)第一章:原子的位形:卢瑟福模型 第二章:原子的量子态:波尔模型 第三章:量子力学导论第四章:原子的精细结构:电子的自旋 第五章:多电子原子:泡利原理 第六章:X 射线第一章 习题1、2解1.1 速度为v 的非相对论的α粒子与一静止的自由电子相碰撞,试证明:α粒子的最大偏离角约为10-4rad.要点分析: 碰撞应考虑入射粒子和电子方向改变.并不是像教材中的入射粒子与靶核的碰撞(靶核不动).注意这里电子要动.证明:设α粒子的质量为Mα,碰撞前速度为V ,沿X 方向入射;碰撞后,速度为V',沿θ方向散射。
电子质量用me 表示,碰撞前静止在坐标原点O 处,碰撞后以速度v 沿φ方向反冲。
α粒子-电子系统在此过程中能量与动量均应守恒,有:222212121v m V M V M e +'=αα (1)ϕθααcos cos v m V M V M e +'= (2)ϕθαsin sin 0v m V M e −'= (3)作运算:(2)×sin θ±(3)×cos θ,(4)(5)再将(4)、(5)二式与(1)式联立,消去V’与v,化简上式,得(6)θϕμϕθμ222sin sin )(sin +=+ (7)视θ为φ的函数θ(φ),对(7)式求θ的极值,有令sin2(θ+φ)-sin2φ=0 即 2cos(θ+2φ)sin θ=0若 sin θ=0, 则 θ=0(极小) (8)(2)若cos(θ+2φ)=0 ,则 θ=90º-2φ (9)将(9)式代入(7)式,有θϕμϕμ2202)(90sin sin sin +=−θ≈10-4弧度(极大)此题得证。
1.2(1)动能为5.00MeV 的α粒子被金核以90°散射时,它的瞄准距离(碰撞参数)为多大? (2)如果金箔厚1.0 μm ,则入射α粒子束以大于90°散射(称为背散射)的粒子数是全部入射粒子的百分之几?要点分析:第二问是90°~180°范围的积分.关键要知道n, 注意推导出n 值.其他值从书中参考列表中找.解:(1)依金的原子序数Z2=79答:散射角为90º所对所对应的瞄准距离为22.8fm.(2)解: 第二问解的要点是注意将大于90°的散射全部积分出来. (问题不知道nA,但可从密度与原子量关系找出)从书后物质密度表和原子量表中查出ZAu=79,AAu=197, ρAu=1.888×104kg/m3依θasin即单位体积内的粒子数为密度除以摩尔质量数乘以阿伏加德罗常数。
原子物理学第二章习题答案

第二章原子得能级与辐射2、1 试计算氢原子得第一玻尔轨道上电子绕核转动得频率、线速度与加速度。
解:电子在第一玻尔轨道上即年n=1。
根据量子化条件,πφ2h nmvr p ==可得:频率21211222ma hma nhavπππν===赫兹151058.6⨯=速度:61110188.2/2⨯===ma h a vνπ米/秒加速度:222122/10046.9//秒米⨯===a v r v w2、2 试由氢原子得里德伯常数计算基态氢原子得电离电势与第一激发电势。
解:电离能为1E E E i -=∞,把氢原子得能级公式2/n Rhc E n -=代入,得:Rhchc R E H i=∞-=)111(2=13、60电子伏特。
电离电势:60.13==eE V ii 伏特第一激发能:20.1060.134343)2111(22=⨯==-=Rhc hc R E H i 电子伏特第一激发电势:20.1011==eE V 伏特2、3 用能量为12、5电子伏特得电子去激发基态氢原子,问受激发得氢原子向低能基跃迁时,会出现那些波长得光谱线?解:把氢原子有基态激发到您n=2,3,4……等能级上去所需要得能量就是:)111(22n hcR E H -=其中6.13=H hcR 电子伏特2.10)211(6.1321=-⨯=E 电子伏特1.12)311(6.1322=-⨯=E 电子伏特8.12)411(6.1323=-⨯=E 电子伏特其中21E E 和小于12、5电子伏特,3E 大于12、5电子伏特。
可见,具有12、5电子伏特能量得电子不足以把基态氢原子激发到4≥n 得能级上去,所以只能出现3≤n 得能级间得跃迁。
跃迁时可能发出得光谱线得波长为:οοολλλλλλAR R ARR A R R H H H H H H 102598)3111(1121543)2111(1656536/5)3121(1322322221221==-===-===-=2、4 试估算一次电离得氦离子+eH 、二次电离得锂离子+iL 得第一玻尔轨道半径、电离电势、第一激发电势与赖曼系第一条谱线波长分别与氢原子得上述物理量之比值。
原子物理学第一章答案

原子物理学第一章答案原子物理学是研究原子及其组成部分的性质和行为的学科。
从原子的结构到原子核的组成,再到原子间的相互作用,原子物理学涵盖了许多重要的概念和理论。
在本文中,我们将讨论原子物理学的一些基本概念和问题,并提供一些答案和解释。
1. 什么是原子?原子是物质的基本单位,是由质子、中子和电子组成的。
质子和中子位于原子的核心,电子则围绕核心旋转。
2. 原子核的组成是什么?原子核由质子和中子组成。
质子带有正电荷,中子没有电荷。
3. 原子中的电子如何围绕核心旋转?电子围绕原子核旋转的轨道被称为电子壳。
每个电子壳可以容纳一定数量的电子,较近核心的壳能容纳更少的电子。
4. 什么是电离能?电离能是将一个原子中的电子从原子中移除所需的能量。
电离能越高,说明移除电子所需的能量越大。
5. 原子的质量是由什么决定的?原子的质量主要由质子和中子的质量决定。
电子的质量相对较小,可以忽略不计。
6. 原子的大小是如何确定的?原子的大小可以通过原子的半径来衡量。
原子的半径是指原子核到最外层电子轨道的距离。
7. 原子间的相互作用是如何发生的?原子间的相互作用主要是通过电磁力来实现的。
相互作用的强度取决于原子之间的距离和电荷。
8. 原子核中的质子和中子如何保持在一起?原子核中的质子和中子通过强相互作用力相互吸引而保持在一起。
这种相互作用力比电磁力要强。
9. 原子的结构如何影响它的性质?原子的结构决定了原子的化学性质和物理性质。
例如,原子的电子结构决定了它的化学反应性,原子核的结构决定了它的放射性。
10. 原子物理学对我们的日常生活有什么实际应用?原子物理学的研究成果广泛应用于许多领域,包括能源、医学、材料科学等。
例如,核能的开发利用了原子核的分裂反应,医学影像学利用放射性同位素来检测和治疗疾病,材料科学利用原子的结构来研究和发展新材料。
总之,原子物理学是一个广泛而重要的学科,它深入研究了原子的组成和性质,对我们的科学和技术发展起着重要的作用。
原子物理学 答案 高教第四版 杨福家

原子物理习题库及解答 第一章 原子的位形1-1)解:α粒子与电子碰撞,能量守恒,动量守恒,故有:⎪⎩⎪⎨⎧+'='+=e e v m v M v M v M mv Mv ρρρ222212121 ⎪⎪⎩⎪⎪⎨⎧='-='-⇒222e e v M m v v v Mm v v ρρρ e v m p ρρ=∆ e p=mv p=mv ∴∆∆,其大小: (1) 222(')(')(')e m v v v v v v v M-≈+-=近似认为:(');'p M v v v v ∆≈-≈22e m v v v M∴⋅∆=有 212e p p Mmv ⋅∆=亦即: (2) (1)2/(2)得22422210e e m v m p Mmv M-∆===p 亦即:()p tg rad pθθ∆≈=-4~101-2) 解:① 22a b ctg Eθπε=228e ;库仑散射因子:a=4)2)(4(420202E Z e E Ze a πεπε==22279()() 1.44()45.545eZ a fmMev fm E Mev πε⨯=== 当901θθ=︒=时,ctg 2122.752b a fm ∴== 亦即:1522.7510b m -=⨯② 解:金的原子量为197A =;密度:731.8910/g m ρ=⨯依公式,λ射α粒子被散射到θ方向,d Ω立体角的内的几率: nt d a dP 2sin16)(42θθΩ=(1)式中,n 为原子核数密度,()AA m n n N ρ∴=⋅=即:A V n Aρ= (2)由(1)式得:在90º→180 º范围内找到α粒子得几率为:(θP 18022490a nt 2sin ()164sin 2d a nt πθθπρθθ︒︒=⋅=⎰将所有数据代入得)(θP 5()9.410ρθ-=⨯这就是α粒子被散射到大于90º范围的粒子数占全部粒子数得百分比。
《原子物理学》部分习题解答(杨福家)

gJ
2
z g J B
氢原子基态 氯原子基态
2
3 2 3
S1/ 2 P3 / 2
1 S ( S 1) L ( L 1) 2 2 J ( J 1)
两束
四束
2
gJ
1 S ( S 1) L ( L 1) 4 2 2 J ( J 1) 3
pc
E k ( E k 2m0c ) E k
2
所以
E k m in p m in c 6 2 M eV
4-2 解: 原子态
2
D3/2
1 2 , J 3 2
可得
gJ 3 2
L 2, S
mJ
1 2
,
3 2
1 S ( S 1) L ( L 1) 4 2 J ( J 1) 5
Ek Ek
3.1keV 0.0094keV
3-3 解:
Ek m0 c 0.511MeV
2
若按非相对论处理
Ek 1 2 m0 v ,有
2
1 2
m0 v m0 c
2
2
v 2c
显然不合理,需要用相对论来处理。
E Ek m0 c 2m0c
2 2
又E mc m0 c
有磁场
m mg
1 2
3
S
1
0
1
0
2
g 2
h 0
3
P0
0
0
m 2 g 2 m1 g 1
2
0
2
相邻谱线的频率差
c
原子物理学 第一章答案
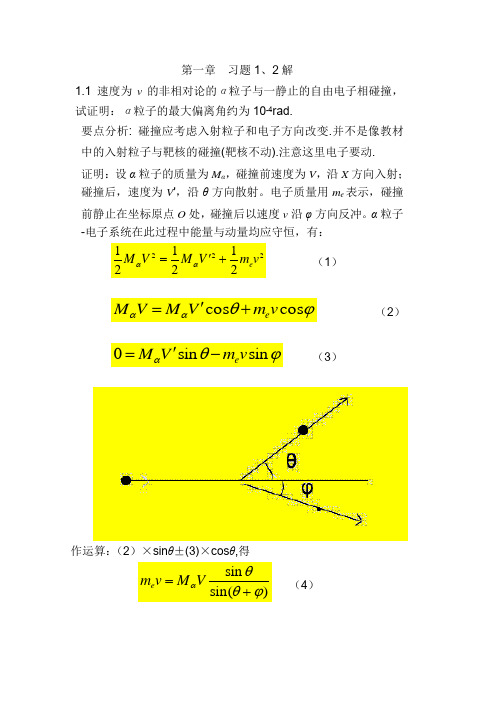
第一章 习题1、2解1.1 速度为v 的非相对论的α粒子与一静止的自由电子相碰撞,试证明:α粒子的最大偏离角约为10-4rad.要点分析: 碰撞应考虑入射粒子和电子方向改变.并不是像教材中的入射粒子与靶核的碰撞(靶核不动).注意这里电子要动. 证明:设α粒子的质量为M α,碰撞前速度为V ,沿X 方向入射;碰撞后,速度为V ',沿θ方向散射。
电子质量用m e 表示,碰撞前静止在坐标原点O 处,碰撞后以速度v 沿φ方向反冲。
α粒子-电子系统在此过程中能量与动量均应守恒,有:222212121v m V M V M e+'=αα (1) ϕθααcos cos v m V M V M e +'= (2)ϕθαsin sin 0v m V M e -'= (3)作运算:(2)×sin θ±(3)×cos θ,得)sin(sin ϕθθα+=VM v m e (4)(5)再将(4)、(5)二式与(1)式联立,消去V’与v,化简上式,得(6)θϕμϕθμ222sin sin )(sin +=+(7)视θ为φ的函数θ(φ),对(7)式求θ的极值,有令sin2(θ+φ)-sin2φ=0 即2cos(θ+2φ)sin θ=0 (1)若 sin θ=0,则 θ=0(极小) (8)(2)若cos(θ+2φ)=0则 θ=90º-2φ (9)将(9)式代入(7)式,有θϕμϕμ2202)(90sin sin sin +=-由此可得θ≈10-4弧度(极大)此题得证。
1.2(1)动能为5.00MeV 的α粒子被金核以90°散射时,它的瞄准距离(碰撞参数)为多大?(2)如果金箔厚1.0 μm ,则入射α粒子束以大于90°散射(称为背散射)的粒子数是全部入射粒子的百分之几?要点分析:第二问是90°~180°范围的积分.关键要知道n , 注意推导出n 值.其他值从书中参考列表中找.解:(1)依金的原子序数Z 2=79答:散射角为90º所对所对应的瞄准距离为22.8fm. (2)解: 第二问解的要点是注意将大于90°的散射全部积分出来. (问题不知道nA,但可从密度与原子量关系找出)从书后物质密度表和原子量表中查出Z Au =79,A Au =197,ρAu =1.888×104kg/m 3 依: θa 2sin即单位体积内的粒子数为密度除以摩尔质量数乘以阿伏加德罗常数。
《原子物理学》第一章习题解答

1第一章习题解答1-1 速度为v 的非相对论α粒子与一静止的自由电子相碰撞,试证明:α粒子的最大偏离角为104- rad 。
证:α粒子在实验系及在质心系下的关系有:粒子在实验系及在质心系下的关系有:a a c c v v v += 由此可得:由此可得:îíì+=+=c c c L cc c L v v v v v v q q q q a aa a cos cos cos cos ①由②解得:由②解得:uC CL +=q qq cos sin tan 其中u=a c c v v ②()c e vm m v m +=aa 00v m m m v ec +=\a a③ ∵ ce c c e v v v v v -=-=a a a ,与坐标系的选择无关,与坐标系的选择无关∴ce c v v v -=a 0 ④又 ∵ 0=+ce e v m v m aa∴0v m m v ece a-= 代入④式,可得:代入④式,可得:0v m m m v e ec aa +=由此可以得到:ec m m v v a a = 代入②式中,可以得到:代入②式中,可以得到:rad m m m m ecec L 410cos sin tan -»£+=aa q q q 证毕。
证毕。
a c vce ve v c va v1-2 (1)(1)动能为动能为5.00Mev 的α粒子被金核以9090°散射时,它的瞄准距离(碰撞参°散射时,它的瞄准距离(碰撞参数)为多大?数)为多大?(2)如果金箔厚1.01.0µµm ,则上述入射α粒子束以大于9090°散射°散射(称为背散射)的粒子数是全部入射例子的百分之几?的粒子数是全部入射例子的百分之几? 解:(1)由库仑散射公式可得(1)由库仑散射公式可得: :b =2a cot 2q =21E e Z Z 02214pe cot 2q =21´E Z Z 21´24pee cot 4p =21´5792´´1.44´1=22.752 fm(2)在大于9090°的情况下,相对粒子数为°的情况下,相对粒子数为°的情况下,相对粒子数为: :òN dN '=nt(E Z Z 421´024pe e )2òW 2sin4q d =t N M A A r (E Z Z 421´024pe e )2q q qp ppdò242sin sin 2 =9.4´105-1-3 试问:4.5Mev 的α粒子与金核对心碰撞的最小距离是多少?若把金核改为7Li 核,则结果如何?核,则结果如何?解:α粒子与金核对心碰撞时金核可看作静止,由此可得到最小距离为:粒子与金核对心碰撞时金核可看作静止,由此可得到最小距离为:r m =a=Ee Z Z 02214pe =EZZ 21´24pe e =1.44´105-´5792´»50.56 fmα粒子与7Li 核对心碰撞时,我们可以在质心系下考虑,我们可以在质心系下考虑,此时此时α粒子与金核相对于质心的和动量为零,质心系能量为各粒子相对于质心的动能之和,因此有:于质心的和动量为零,质心系能量为各粒子相对于质心的动能之和,因此有:221v ECm ==m r e Z Z 02214pe +0=L Li LiE m m m +a 其中L E =21mv 2为入射粒子实验室动能,由此可以得到为入射粒子实验室动能,由此可以得到m r =024pe e LE Z Z 21LiLim mm +a=3.02 fm1-4 (1)假定金核的半径为7.0fm 试问:入射质子需要多少能量,才能在对头碰撞时刚好到达金核的表面?碰撞时刚好到达金核的表面?(2)若金核改为铝核,使质子在对头碰撞时刚好到达铝核表面,那么,入射质子的能量应为多少?设铝核半径为4.0fm. 解:仍然在质心系下考虑粒子的运动,由1仍然在质心系下考虑粒子的运动,由1--3题可知:EC =mr e Z Z 02214pe (1)(1)对金核可视为静止,对金核可视为静止,实验系动能与质心系动能相等,由此得到由此得到 E=E=E=16.25Mev 16.25Mev (2)(2)对铝核,E=对铝核,E=对铝核,E=1.441.44´AlAlp m m m +´413=4.85Mev1-5 动能为动能为1.0Mev 的窄质子束垂直地射在质量厚度为1.5mg/cm 2的金箔上,计数器纪录以6060°角散射的质子,计数器圆形输入孔的面积为°角散射的质子,计数器圆形输入孔的面积为1.5cm 1.5cm²,离金箔散²,离金箔散射区的距离为10cm 10cm,输入孔对着且垂直于射到它上面的质子。
(整理)原子物理学杨福家1-6章 课后习题答案

原子物理学课后前六章答案(第四版)杨福家著(高等教育出版社)第一章:原子的位形:卢瑟福模型 第二章:原子的量子态:波尔模型 第三章:量子力学导论第四章:原子的精细结构:电子的自旋 第五章:多电子原子:泡利原理 第六章:X 射线第一章 习题1、2解1.1 速度为v 的非相对论的α粒子与一静止的自由电子相碰撞,试证明:α粒子的最大偏离角约为10-4rad.要点分析: 碰撞应考虑入射粒子和电子方向改变.并不是像教材中的入射粒子与靶核的碰撞(靶核不动).注意这里电子要动.证明:设α粒子的质量为M α,碰撞前速度为V ,沿X 方向入射;碰撞后,速度为V',沿θ方向散射。
电子质量用me 表示,碰撞前静止在坐标原点O 处,碰撞后以速度v 沿φ方向反冲。
α粒子-电子系统在此过程中能量与动量均应守恒,有:(1)ϕθααcos cos v m V M V M e +'= (2)ϕθαsin sin 0v m V M e -'= (3)作运算:(2)×sin θ±(3)×cos θ,(4)(5)再将(4)、(5)二式与(1)式联立,消去V’与v,化简上式,得(6)θϕμϕθμ222s i n s i n )(s i n +=+ (7)视θ为φ的函数θ(φ),对(7)式求θ的极值,有令sin2(θ+φ)-sin2φ=0 即 2cos(θ+2φ)sin θ=0若 sin θ=0, 则 θ=0(极小) (8)(2)若cos(θ+2φ)=0 ,则 θ=90º-2φ (9)将(9)式代入(7)式,有θϕμϕμ2202)(90si n si n si n +=-θ≈10-4弧度(极大)此题得证。
1.2(1)动能为5.00MeV 的α粒子被金核以90°散射时,它的瞄准距离(碰撞参数)为多大? (2)如果金箔厚1.0 μm ,则入射α粒子束以大于90°散射(称为背散射)的粒子数是全部入射粒子的百分之几?要点分析:第二问是90°~180°范围的积分.关键要知道n, 注意推导出n 值.其他值从书中参考列表中找.解:(1)依金的原子序数Z2=79答:散射角为90º所对所对应的瞄准距离为22.8fm.(2)解: 第二问解的要点是注意将大于90°的散射全部积分出来. (问题不知道nA,但可从密度与原子量关系找出)从书后物质密度表和原子量表中查出ZAu=79,AAu=197, ρAu=1.888×104kg/m3依θa 2sin即单位体积内的粒子数为密度除以摩尔质量数乘以阿伏加德罗常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课
案
v=
网
1+
hν (1 − cos θ ) m p c2
2E = 0.14c M
1350
2.4
0.071 nm
X
∆λ = λ '− λ =
θ = 135o
∆λ = 0.004nm
λ ' = 0.071 + 0.004 = 0.075nm
E=
2.5
1240eV ⋅ nm = 16.5keV 0.075
(3)
λ=
后
hc = 121.6nm ∆E
U = 40.8eV
课
答
hc = 30.4nm λ= ∆E U = 91.8eV hc = 13.5nm λ= ∆E
13.6 eV B++++ n=2 n =1
1.7
B ++++
n=2 1.8 n=1
13.6 × 5 2 = 340eV
255 eV He+ 2741940 2743059m-1
m
1.3 600 10 cm 197 Z 79
100 keV
1.0 mg/cm2 1.0 cm2 Au A
4 3
ρ
1.93×10 kg/m
dn dσ = Nt × × dΩ n dΩ
dσ e 2 2 zZ 2 1 =( ) ( ) 4 dΩ 4πε 0 4 E sin (θ / 2)
= 1.29 × 10 −24 m 2
dσ = dσ dΩ = 1.29 × 10 − 26 m 2 dΩ
1.4
T = 1.2 MeV
ww
dσ = 211b
w.
dσ =
π dσ e 2 2 zZ 2 1 ) ( ) sin θdθ ⋅ dΩ = 2π ∫ ( 4 π / 2 4πε dΩ 4 E sin (θ / 2) 0
网
1.5
后
1.0 MeV 10 min. 0 0 (1) 59 61 0 (2) θ >θ0 = 60 0 (3) θ <θ0 = 10
课
后
H
E0=12.75 eV ER
w.
Z=1 E
E0 = E
+ ER
M
kh
da
r1 = 2a 0 = 1.06 × 10 −10 m = 0.106nm
w.
co
5
m
ER =
2 P2 E2 PR = = 2M 2M 2Mc 2
E0/Mc2
E
12.75 eV/c MV
2 E0
≈ E0 −
2 E0
2 Mc 2
da
485 nm
hc 1240eV ⋅ nm = 2.56eV = λ 485nm 13.6 − 10.19 − 2.56 = 0.85eV
99.2nm
121.5nm
R = 1.097 × 10 7 m −1 ~ ν
R
0.9189, 0.8401, 0.7503 k = 3.5 2.5
R 2
~ = R( 1 − 1 ) ν k2
Z Z=2,
~ = 4 R( 1 − 1 ) ν m2 n2
m =2, n = 4,5,7
w.
π dσ e 2 2 zZ 2 1 dσ = ) ( ) sin θdθ ⋅ dΩ = 2π ∫ ( 4 π / 3 dΩ 4πε 0 4 E sin (θ / 2)
co
4
m
n=3, n=6, 1.12 45 1.13
1.1 (1) (2) (1) V: R
13.6eV. 0.6 µm r 0
v ∞v v R v V (r ) = ∫ E ⋅ dl + ∫ E ⋅ dl
r R
V (r ) = ∫
=
R
r
∞ e⋅r ' e dr '+ ∫ dr ' 3 R 4πε 0 R 4πε 0 r '2
R 0.16 nm (2)
ww
e2 3 8πε 0 R e2 r F= 4πε 0 R 3
13.6eV
网
R = 2.95 ×10−10 m
后
答
案
&& F = me r
w.
&& r e2 2π c 2 = = ω2 = ( ) 3 r 4πε 0 me R λ
θ =π /2
课
1.2
T = 0.87MeV
D=(
zZe 2 1 )( ) 4πε 0 E
R M = R∞
M me + M
~=R ( 1 ) ν M 22
~ me + 4 M P 2741940 ν MP H = ⋅ = ~ ν m M 4 M 2743059 + He e P P
M P : me = 1837.5
1.9 6.0 MeV 1.0×10-4 600
=1.44(eV⋅nm)2(79/4⋅E) (5.9×10 )12π ⋅t =10-4
co
6
m
n=4
υn =
l
e2 1 ⋅ 4πε 0 h n
n =1
2 3 ….
l = meυ n rn = nh
n = 1 2 3 … ..
2.1
632.8 nm
E=
2.2 2.2 eV
1240 = 1.96eV 632.8
kh
938.26 MeV
ν '=
后
答
90o
E ' = hν ' = 90.4 MeV
207 me
ww
(3)
E = 13.6 / 2 = 6.8eV E = 3.4 / 2 = 1.7eV 1 R = R∞ =0.548×107 m-1, 2 1240eV ⋅ nm = 243nm λ= 5.1eV
µ
答
µ
2
207 * 1836 me = 186 me r1 = a0/186 2.85×10- 4 nm 207 + 1836 1 (b) E = − m( αc ) 2 E -2530 eV 2 207 * 1836 * 2 m dµ = me = 196 me 207 + 1836 * 2 E = - 2665 eV 1.16 n=4 n=1 m=
案
答
u 0 ( x) = e
网
−(
mω 2 )x 2h
mω
2
课
mω −( 2h ) x u1 ( x ) = 2 xe h
后
(3) (1)
∆x∆p ≈ h
ww
w.
≈ hω
h2k 2 2m
−
h 2 d 2u + Vu = Eu 2m dx 2
−( mω 2 )x 2h
−
1 h2 ∂2 u( x ) + mω 2 x 2 u( x ) = Eu( x ) 2 2 m ∂x 2
10
n = 3.6 × 10 4 ⋅ 5.8 × 10 −4 × 6 × 10 2 = 1.25 × 10 4
(2)
n = 1.55 × 10 5
(3) 10 180
n = 6.75 × 10 6
答
= 9.83 × 10 −27 m 2
案
α
61o dσ e 2 2 zZ 2 1 ⋅ dΩ = 2π ∫ o ( sin θdθ ) ( ) 4 59 dΩ 4πε 0 4 E sin (θ / 2)
2.16 × 10 7
0 1.6 (1) (2) (3) (1) 10 He+ Li++
1.48 × 10 7
n2 rn = a0 , Z
Z=1: r1 = 0.53 × 10 −10 m ,
vn =
αc Z n
r2 = 2.12 × 10 −10 m
He+
Z=2:
Li++
Z=3: r1 = 0.18 × 10 −10 m ,
(2)
案
T = 13.6eV T = 54.4eV T = 122.4eV
U = ห้องสมุดไป่ตู้0.2eV
ww
v1 = 6.6 × 10 6 m ⋅ s −1 ,
w.
kh
r2 = 0.71 × 10 −10 m
v 2 = 3.3 × 10 6 m ⋅ s −1
E = 13.6eV E = 54.4eV E = 122.4eV
ww
ν
h (1 − cos θ ) me c
w.
2.3 (2)
1
100 MeV
da
900
1240 = 3.54eV 350 3.54 2.2= 1.34 eV E=
w.
co
7
m
350.0 nm
(1) 50 eV (2 50 eV (3) 50 eV 1 50eV
940 MeV
λ=
h 1240 = = 24.8nm 50 p
(2)
u 0 ( x) = e
(3)
E
hω 2 3hω E1 = 2 1 E = mω 2 x 2 2 E0 =
9
kh
h2 ∂2 ; 2m ∂x 2
1.36×10-8 c 4.1 m/s
12.75 eV/c V
E
λ 1.17
≈ E0 −
97.4 nm
2Mc
∆λ
2
= E 0 (1 −
E0 2Mc
2
) = E 0 (1 − 7 × 10 −9 )
6.6×10-7 nm
