专题十三 点、线、面之间的位置关系 听课手册
十三 点、线、面的位置关系及判定与性质(逻辑推理)

点、线、面之间的位置关系及判定与性质(逻辑推理)一、空间的点、直线、平面之间的位置关系1 平面的基本性质公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2:经过不在同一直线上的三点,有且只有一个平面.(三个推论)推理1:经过一条直线和这条直线外的一点有且只有一个平面。
推理2:两条相交直线确定一个平面。
推理3:两条平行直线确定一个平面。
公理3:如果两个平面有一个公共点,那么有且只有一条通过这个点的公共直线.2 平行公理:平行于同一条直线的两条直线互相平行。
等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
3 异面直线(1)定义:不同在任何一个平面内的两条直线。
(2)性质:两条异面直线既不相交也不平行。
(3)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。
(4)异面直线所成的角:例1有下列命题:①若ABC ∆在平面α外,它的三条边所在的直线分别与α交于P 、Q 、R 三点,则P 、Q 、R 三点共线;②若三条直线a 、b 、c 互相平行且分别交直线l 与A 、B 、C 三点,则这四条直线共面;③空间的五个点最多确定10个平面。
其中正确的命题的个数是( )A. 0B. 1C. 2D. 3例2 给出下列命题:①若平面α上的直线a 与平面β上的直线b 为异面直线,直线c 是α与β的交线,那么c 至多与a 、b 中的一条相交;②若直线a 与b 异面,直线b 与c 异面,则直线a 与c 异面;③一定存在平面α同时和异面直线a 、b 都平行。
其中正确的命题为( )A. ①B. ②C. ③D. ① ③例3 在正方体1111D C B A ABCD -中,E 为AB 的中点。
(1)求证:AC ⊥平面BDD 1;(2)求BD 1与CE 所成角的余弦值。
例4 如图所示,E 、F 在AD 上,G 、H 在BC 上,图中8条线段所在的直线,互为异面直线的有 对。
(完整版)点、直线、平面之间的位置关系知识点总结,推荐文档
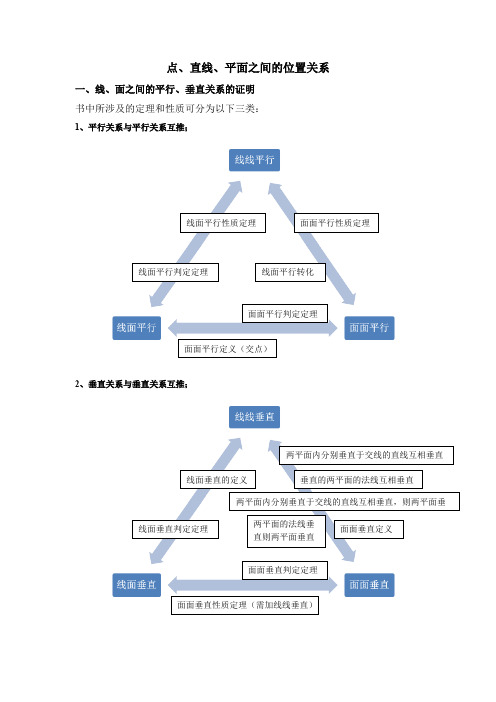
点、直线、平面之间的位置关系一、线、面之间的平行、垂直关系的证明书中所涉及的定理和性质可分为以下三类:1、平行关系与平行关系互推;2、垂直关系与垂直关系互推;线面垂直判定定理线面垂直的定义两平面的法线垂直则两平面垂直面面垂直判定定理线面平行判定定理线面平行性质定理线面平行转化面面平行判定定理面面平行性质定理3、平行关系与垂直关系互推。
以线或面为元素,互推的本质是以某一元素为中介,通过另外两元素与中介元素的垂直或平行关系,推导出该两元素的关系,总共有21种情况,能得出结论的有以下9种情况。
线线平行传递性:;b c c a b a //////⇒⎭⎬⎫面面平行传递性:;γαβγβα//////⇒⎭⎬⎫线面垂直、线面垂直线面平行:;⇒ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥线面垂直线线平行(线面垂直性质定理):;⇒b a b a //⇒⎭⎬⎫⊥⊥αα线面垂直面面平行:;⇒βαβα//⇒⎭⎬⎫⊥⊥a a 线面垂直、面面平行线面垂直:;⇒βαβα⊥⇒⎭⎬⎫⊥a a //线线平行、线面垂直线面垂直:;⇒αα⊥⇒⎭⎬⎫⊥b a b a //线面垂直、线面平行面面垂直:。
⇒βααβ⊥⇒⎭⎬⎫⊥a a //备注:另外证明平行关系时可以从最基本的定义交点入手,证明垂直关系时可以从最基本的定义角度入手。
符号化语言一览表①线面平行;;;ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂αββα////a a ⇒⎭⎬⎫⊂ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥②线线平行:;;;;////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ b a b a //⇒⎭⎬⎫⊥⊥αα////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭b c c a b a //////⇒⎭⎬⎫③面面平行:;;;,////,//a b a b O a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭βαβα//⇒⎭⎬⎫⊥⊥a a γαβγβα//////⇒⎭⎬⎫④线线垂直:;b a b a ⊥⇒⎭⎬⎫⊂⊥αα⑤线面垂直:;;,,a b a b O l l a l b ααα⊂⊂⎫⎪=⇒⊥⎬⎪⊥⊥⎭,l a a a l αβαββα⊥⎫⎪=⇒⊥⎬⎪⊂⊥⎭ ;;βαβα⊥⇒⎭⎬⎫⊥a a //αα⊥⇒⎭⎬⎫⊥b a b a //⑥面面垂直:二面角900; ;;βααβ⊥⇒⎭⎬⎫⊥⊂a a βααβ⊥⇒⎭⎬⎫⊥a a //二、立体几何中的重要方法1、求角:(步骤-------Ⅰ找或作角;Ⅱ求角)⑴异面直线所成角的求法:①平移法:平移直线,构造三角形;②补形法:补成正方体、平行六面体、长方体等,发现两条异面直线间的关系.注:还可用向量法,转化为两直线方向向量的夹角.⑵直线与平面所成的角:①直接法(利用线面角定义);②先求斜线上的点到平面距离h ,与斜线段长度作比,得sin ;③三线三角公式.θ12cos cos cos θθθ=注:还可用向量法,转化为直线的方向向量与平面法向量的夹角.⑶二面角的求法:①定义法:在二面角的棱上取一点(特殊点),作出平面角,再求解;②垂面法:作面与二面角的棱垂直; ③投影法(三垂线定理);④面积摄影法.注:对于没有给出棱的二面角,应先作出棱,然后再选用上述方法;还可用向量法,转化为两个班平面法向量的夹角.2、求距离:(步骤-------Ⅰ找或作垂线段;Ⅱ求距离)⑴两异面直线间的距离:一般先作出公垂线段,再进行计算;或转化为线面距离、点面距离;⑵点到直线的距离:一般用三垂线定理作出垂线段,再求解;⑶点到平面的距离:①垂面法:借助面面垂直的性质作垂线段(确定已知面的垂面是关键),再求解;②等体积法;还可用向量法:.||n d =3、证明平行、垂直的理论途径:①证明直线与直线的平行的思考途径:(1)转化为判定共面二直线无交点(定义);(2)转化为两直线同与第三条直线平行;(3)转化为线面平行;(4)转化为线面垂直;(5)转化为面面平行.②证明直线与平面的平行的思考途径:(1)转化为直线与平面无公共点(定义);(2)转化为线线平行;(3)转化为面面平行.③证明平面与平面平行的思考途径:(1)转化为判定两平面无公共点(定义);(2)转化为线面平行;(3)转化为线面垂直.④证明直线与直线的垂直的思考途径:(1)转化为相交垂直;(2)转化为线面垂直.⑤证明直线与平面垂直的思考途径:(1)转化为该直线与平面内任一直线垂直(定义);(2)转化为该直线与平面内相交的两条直线垂直;(3)转化为该直线与平面的一条垂线平行;(4)转化为该直线垂直于另一个平行平面;(5)转化为该直线与两个垂直平面交线垂直.⑥证明平面与平面的垂直的思考途径:(1)转化为判断二面角是直二面角;(2)转化为线面垂直.。
点线面的位置关系

点线面的位置关系在几何学中,点、线和面是最基本的几何概念。
它们之间存在着一种特殊的位置关系,即点线面的位置关系。
本文将从不同角度来探讨这种位置关系,以加深我们对几何学的理解。
1. 点与线的位置关系在几何学中,点是最基本的元素。
它没有长度、宽度或高度,仅有一个位置。
而线则是由一系列相邻点组成,具有长度但没有宽度。
点与线之间的位置关系主要有以下几种情况:- 点在线上:当一个点的位置恰好与一条线上的点重合时,我们说这个点在这条线上。
- 点在线的延长线上:当一个点的位置在一条线的延长线上时,我们说这个点在这条线的延长线上。
延长线是指无限延伸的线段,即线上的点外面的点。
- 点在线的两侧:当一个点的位置不在一条线上,但在这条线的两侧时,我们说这个点在这条线的两侧。
2. 点与面的位置关系与点与线的位置关系类似,点与面的位置关系也有多种情况:- 点在面上:当一个点的位置恰好与一个面上的点重合时,我们说这个点在这个面上。
- 点在面的内部:当一个点的位置在一个面的内部时,我们说这个点在这个面的内部。
面的内部是指位于面的边界所围成的区域内的点。
- 点在面的外部:当一个点的位置不在一个面上,且在这个面的外部时,我们说这个点在这个面的外部。
即位于面的边界以外的点。
3. 线与线的位置关系线与线之间的位置关系可以分为以下几种情况:- 相交:当两条线交于一点时,我们说这两条线相交。
- 平行:当两条线的方向相同且不相交时,我们说这两条线平行。
平行线永远不会相交。
- 重合:当两条线的位置相同且方向相同时,我们说这两条线重合。
重合的线是完全重合,始终重合。
4. 线与面的位置关系线与面之间的位置关系也有多种情况:- 相交:当一条线与一个面相交于一点时,我们说这条线与这个面相交。
- 平行:当一条线与一个面平行时,我们说这条线与这个面平行。
平行线永远不会与相同平面内的面相交。
- 垂直:当一条线与一个面垂直相交时,我们说这条线与这个面垂直。
点线面间的位置关系知识点总结(含题)(

点线面间的位置关系知识点总结一、三个公理公理1如果一条直线上的两点在一个平面内,那么_________________________________________公理2:过________________________ 的三个点,有且只有一个平面公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________________二、空间两条直线间的位置关系分类为:______________ , ______________ ,_______________ ;其中__________ , _________ 合称为______________三、空间直线与平面间的位置关系分类为:__________________ ,____________ ,__________________ ;其中__________ , _________ 合称为______________四、空间平面与平面间的位置关系分类为:______________ ,当两个平面成90。
时,属于____________ 关系常用证明技巧一、线面平行列1 (2IH1年怀化楓蝌)如图所示*已知几0是单位止方WABCn-A^.C^的面A^BA和面』肮2>的中心*求证:卩总〃平面ncr^n.练习1. 正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q且AP = DQ. 求证:PQ//平面BCE.2・妇匿,四棱链/一乩噸一平面所裁*截面为平厅四边形吕他求证,m/zz面日捌3* (加10年彌考■陕丙雜)如图’在四棱饰P ABCD中.底血ABCD^矩形「只4 丄平SLUJC/h .lP-.Ltf, BP-IiC-1, E, F分别&l f B T PC 的中点.门)证明* EF//平血知";卩)求二棱锥E—.【号「的休枳匚(2)1/3二、线面垂直1、(2006年北京卷)如图,在底面为平行四边形的四棱锥P ABCD中,AB 点E是PD的中点•(I)求证:AC PB ; (n)求证:PB〃平面AEC ;2、( 2006年浙江卷)如图,在四棱锥P-ABCD中,底面为直角梯形BAD=90 ° ,PA丄底面ABCD,且PA= AD=AB=2BC,M、N 分别为PC、PB 求证:PB丄DM;3、(2006年福建卷)如图,四面体ABCD中,0、E分别是BD、BC的中点,CA(I)求证:AO 平面BCD;AC , PA 平面ABCD,且PA AB , CB CD BD 2, AB AD . 2.,AD // BC, /的中点•ADOE4、( 2006年重庆卷)如图,在四棱锥P—ABCD中,PA 底面ABCD, PC、DAB 为直角,AB II CD,AD=CD=24B,E、F 分另U为CD的中点.(I)试证:CD 平面BEF;5、(全国H ?理?9题)如图,在四棱锥SCS-ABCD中,底面ABCD为正方形,侧棱SD丄底面ABCD , E、F分别是AB、的中点。
知识清单点线面之间的位置关系

1 / 3专题五:点、直线与平面的位置关系姓名 班级一、四个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.符号语言: 图形语言:公理1作用:判断直线是否在平面内.(2)公理2:过不在一条直线上的三点,有且只有一个平面.符号语言: 图形语言:公理2作用:确定一个平面的依据.推论:①一条直线和其外一点确定一个平面②两条相交直线确定一个平面 ③两条平行直线确定一个平面(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线符号语言: 图形语言:公理3作用:①判定两个平面相交; ②确定点在直线上(4)公理4:平行于同一条直线的两条直线互相平行符号语言: 图形语言:公理4作用:判断空间两条直线平行的依据二、平行1.直线与平面平行的判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行 简记为:线线平行则线面平行符号语言: 图形语言:2.平面与平面平行的判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行 简记为:线线平行则线面平行符号语言: 图形语言:abca2 / 33.直线与平面平行的性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行 简记为:线面平行则线线平行 符号语言: 图形语言:4.平面与平面平行的性质定理如果两个平行的平面同时与第三个平面相交,那么它们的交线平行 简记为:面面平行则线线平行 符号语言: 图形语言:三、垂直1.直线与平面垂直的判定定理符号语言:2.平面与平面垂直的判定定理一个平面过另一个平面的垂线,则这两个平面垂直符号语言: 图形语言:3.直线与平面垂直的性质定理(1)基本性质:一条直线垂直一个平面,那么 这条直线垂直于这个平面内的任意一条直线符号语言:(2)性质定理:垂直于同一个平面的两条直线平行 符号语言: 图形语言:4.两个平面垂直的性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一 个平面垂直符号语言: 图形语言:四、空间直线、平面的位置关系1.空间的两条直线有三种位置关系:2.直线与平面有三种位置关系:3.平面与平面的位置关系:五、判断平行、垂直的方法1.2.3.3 / 3。
(完整word版)点线面之间的位置关系的知识点总结,推荐文档

高中空间点线面之间位置关系知识点总结第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线 a ∥b 。
2 公理4:平行于 c ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;D CBAα LA ·α C ·B·A · α P· αLβ 共面直线=>a ∥c2⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
专题十三听课手册正文

专题十三化学实验综合考向一合成制备类实验■ 核心透析一、物质制备实验设计的基本思维模式图13-1二、仪器装置的分析1.熟悉易错仪器图13-22.特殊实验装置分析(1)制备在空气中易吸水、潮解以及水解的物质(如Al2S3、AlCl3等),往往在装置的末端再接一个干燥装置,以防止空气中水蒸气的进入。
(2)用液体吸收气体,若气体溶解度较大,要加防倒吸装置。
(3)若制备物易被空气中氧气氧化,应加排空气装置。
三、合成制备综合实验的解题策略1.巧审题,明确实验目的、原理实验原理可从题给的化学情境(或题目所给的实验目的)并结合元素化合物的有关知识获取。
在此基础上,依据可靠性、简捷性、安全性的原则,确定符合实验目的、要求的实验方案。
2.想过程,理清操作先后顺序根据由实验原理所确定的实验方案中的实验过程,确定实验操作的方法和步骤,把握各实验步骤的要点,理清实验操作的先后顺序。
3.看准图,分析各项实验装置的作用有许多综合实验题图文结合,在分析解答过程中,要认真细致地分析图中所示的各项装置,并结合实验目的和原理,确定它们在该实验中的作用。
4.细分析,得出正确的实验结论在分析实验现象(或数据)的过程中,要善于找出影响实验成败的关键以及产生误差的原因,或利用有关数据进行计算所得产品的纯度或产率等。
四、合成制备实验考点拆解分析1.涉及气体的实验装置的连接(1)装置连接顺序图13-32.接口的连接净化装置应:“长”进“短”出量气装置应:“短”进“长”出干燥管应:“粗”进“细”出【示例分析1】三氯化硼(BCl3)的熔点为-107.3 ℃,沸点为12.5 ℃,遇水能够发生水解反应。
某兴趣小组设计如图13-4所示装置,用单质硼与氯气反应制备三氯化硼。
图13-4(1)装置的连接顺序为A、、F。
(2)装置D的作用是,装置F可用一个盛装(填试剂名称)的干燥管代替。
(3)实验过程中,应先点燃A处的酒精灯,当观察到时再点燃B处的酒精灯。
仪器作用A B C D E F制Cl2,Cl2中含有制BCl3,因BCl3遇水发生水解反应,需构造环境干燥冷却,收集低沸点物质除Cl2中、除尾气气体流向由A装置出来的气体,先通过E装置,除去氯化氢,再通过C装置,除去水蒸气,纯净的Cl2进入B装置参与反应,用D装置收集三氯化硼,用F隔水并进行尾气处理五、产物的分离提纯与产率计算1.液体产物的纯化液体产品的提纯往往包括粗分离和精分离两个提纯过程。
点线面的位置关系与平行关系-讲义

点、线、面位置关系以及线面平行关系【知识点梳理】 1、公理及推论公理1:如果一条直线的两点在一个平面,那么这条直线是所有的点都在这个平面.用符号语言表示公理1:,,,A l B l A B l ααα∈∈∈∈⇒⊂. 公理1作用:判断直线是否在平面.公理2:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.符号:平面α和β相交,交线是a ,记作α∩β=a . 符号语言:,P AB A B l P l ∈⇒=∈.公理2作用:①它是判定两个平面相交的方法.②它说明两个平面的交线与两个平面公共点之间的关系:交线必过公共点. ③它可以判断点在直线上,即证若干个点共线的重要依据. 公理3:经过不在同一条直线上的三点,有且只有一个平面.推论:一直线和直线外一点确定一平面;两相交直线确定一平面;两平行直线确定一面. 公理3及其推论作用:①它是空间确定平面的依据;②它是证明平面重合的依据. 公理4:平行于同一条直线的两条直线互相平行. 2、空间直线与直线之间的位置关系(1) 异面直线定义:不同在任何一个平面的两条直线. (2) 异面直线性质:既不平行,又不相交.(3) 异面直线判定:过平面外一点与平面一点的直线与平面不过该店的直线是异面直线.(4) 异面直线所成角:作平行,令两线相交,所得锐角或直角,即所成角.两条异面直线所成角的围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直.(5)求异面直线所成角步骤:A 、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上.B 、证明作出的角即为所求角.C 、利用三角形来求角.(6)异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离.(7)两条异面直线的公垂线有且只有一条.(8)等角定理:如果一个角的两边和另一个角的两边分别平行,那么这两角相等或互补. 3、空间直线与平面之间的位置关系直线在平面——有无数个公共点.三种位置关系的符号表示:a ⊂α;a ∩α=A ;a ∥α. 直线与平面平行、直线与平面相交称为直线在平面外.4、平面与平面之间的位置关系:平行—没有公共点:α∥β;相交—有一条公共直线:α∩β=l .5、直线和平面平行的判定定理:如果平面外一条直线和这个平面一条直线平行,那么这条直线和这个平面平行.(记忆口诀:线线平行线面平行)符号表示为:,,////a b a b a ααα⊄⊂⇒.图形如右图所示.6、面面平行判定定理:如果一个平面有两条相交直线都平行于另一个平面,那么这两个平面平行.用符号表示为:,,////,//a b a b P a b βββααα⊂⊂=⎫⇒⎬⎭. 图形如右图所示.7、直线和平面平行的性质定理:如果一条直线和一个平面平行,经过该直线的平面和这个平面相交,那么这条直线和交线平行.(记忆口诀:线面平行线线平行) 用符号表示为:////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭.图形如右图所示.8、面面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.用符号语言表示为://,,//a b a b αβγαγβ==⇒.其它性质:①//,//l l αβαβ⊂⇒; ②//,l l αβαβ⊥⇒⊥;③夹在平行平面间的平行线段相等. 图形如右图所示.β aαbPabαβ【典型例题】题型一、证明点或线共面、三点共线或三线共点问题例题1:如图,已知空间四边形ABCD 中,E 、F 、G 、H 分别是AB 、AD 、BC 、CD 上的点,且EF 交GH 于P .求证:P 在直线BD 上..变式1:如图,在空间四边形ABCD 中,点E 、H 分别是边AB 、AD 的中点,F 、G 分别是边BC 、CD 上的点,且CF CB =CG CD =23,则( ) (A )EF 与GH 互相平行 (B )EF 与GH 异面(C )EF 与GH 的交点M 可能在直线AC 上,也可能不在直线AC 上 (D )EF 与GH 的交点M 一定在直线AC 上变式2:如图所示,设E ,F ,G ,H 分别是空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且λ==AD AH AB AE ,μ==CDCGCB CF ,求证: (1)E ,F ,G ,H 四点共面;(2)当μλ=时,四边形EFGH 是平行四边形;(3)当μλ≠时,四边形EFGH 是梯形. 题型二、异面直线的判定或求异面直线所成的角例题2: A 是△BCD 平面外的一点,E 、F 分别是BC 、AD 的中点,(1)求证:直线EF 与BD 是异面直线; (2)若AC ⊥BD ,AC =BD ,求EF 与BD 所成的角.变式3:给出下列关于互不相同的直线,,l m n 和平面,,αβγ的三个命题:①若,l m 为异面直线,,l m αβ⊂⊂,则//αβ; ②若//,,l m αβαβ⊂⊂,则//l m ; ③若,,,//l m n l αββγγαγ===,则//m n ,其中真命题的个数为( )A .3B .2C .1D .0题型三、直线与平面、平面与平面平行的判定例题3:如图所示,正方体ABCD —A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E=C 1F .求证:EF∥平面ABCD .变式4:一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.当FG=GD时,在棱AD上确定一点P,使得GP//平面FMC,并给出证明.题型四、证明线面平行与线面平行性质的运用例题4:如下图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE..QPNMFEDCBANMGFEDB变式5:如下图,设a 、b 是异面直线,AB 是a 、b 的公垂线,过AB 的中点O 作平面α与a 、b 分别平行,M 、N 分别是a 、b 上的任意两点,MN 与α交于点P ,求证:P 是MN 的中点.变式6:如图所示,PA 是圆柱的母线,ABCD 为矩形,,,E F G 分别是线段,,PA PD CD 的中点,求证://PB 面EFG .baPQO N BM A变式7:如图,在长方体1111ABCD A B C D 中,,E P 分别是11,BC A D 的中点,,M N 分别是1,AE D C 的中点,求证://MN 面11ADD A .题型五:证明面面平行与面面平行性质的运用例题5:如图,在四棱锥P – ABCD 中,M,N 分别是侧棱PA 和底面BC 边的中点,O 是底面平行四边形ABCD 的对角线AC 的中点.求证:过O 、M 、N 三点的平面与侧面PCD 平行.变式8:正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ;(2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .【方法与技巧总结】 1.位置关系:(1)两条异面直线相互垂直证明方法:①证明两条异面直线所成角为90º;②证明线面垂直,得到线线垂直;(2)直线和平面相互平行证明方法:①证明直线和这个平面的一条直线相互平行;②利用平行四边形.③利用三角形中位线.(3)面与面平行证明方法:主要证明线线平行即可.(4)掌握线性平行,线面平行,面面平行三者之间的相互转化. 2.求角:(1)两条异面直线所成的角求法:①先通过其中一条直线或者两条直线的平移,找出这两条异面直线所成A1的角,然后通过解三角形去求得;②通过两条异面直线的方向量所成的角来求得,但是注意到异面直线所成角得围是]2,0(π;(2)直线和平面所成的角:先找射影,构造成直角三角形.【巩固练习】1.A 、B 、C 表示不同的点,a 、l 表示不同的直线,α、β表示不同的平面,下列推理不正确的是( ) A .ααα⊂⇒∈∈∈∈l B l B A l A ,,,B .βα∈∈A A ,,AB B B =⇒∈∈βαβα ,直线 C .αα∉⇒∈⊄A l A l , D .α∈C B A ,,,β∈C B A ,,且C B A ,,不共线α⇒与β重合 2.对于直线m 、n 和平面α,下面命题中的真命题是( )A .如果m n m ,,αα⊄⊂、n 是异面直线,那么α//nB .如果m n m ,,αα⊄⊂、n 是异面直线,那么α与n 相交C .如果m n m ,//,αα⊂、n 共面,那么n m //D .如果m n m ,//,//αα、n 共面,那么n m // 3.有以下命题,正确命题的序号是.①直线与平面没有公共点,则直线与平面平行;②直线与平面的任何一条直线都不相交,则直线与平面平行; ③直线上有两点,它们到平面的距离相等,则直线与平面平行; ④直线与平面的无数条直线不相交,则直线与平面平行.4.在三棱锥P ABC -中,,O D 分别是,AB PB 的中点.求证://OD 平面PAC .5.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,,E F 分别是,PB PC 的中点,证明://EF 平面PAD .6.如图所示,在三棱柱111ABC A B C -中,D 点为棱AB 的中点,求证:1//AC 平面1CDB .7.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,O 为AC 中点,M 为PD 中点.证明://PB 平面ACM .8.如图,已知DE ∥AB ,2AB=DE ,且F 是CD 的中点,求证:AF ∥平面BCE .9.在棱长为a 的正方体1111ABCD A B C D -中,E 是线段11A C 的中点,底面ABCD 的中心是F ,求证:CE ∥平面1A BD .CAPMO【课后作业】1.已知直线l 1、l 2,平面α,l 1∥l 2,l 1∥α,则l2与α的位置关系是( )A l 2∥αB l 2⊂αC l 2∥α或l 2⊂αD l 2与α相交2.设平面α与平面β交于直线l ,直线α⊂a ,直线β⊂b ,M b a = ,则M_______l .3.直线AB 、AD α⊂,直线CB 、CD β⊂,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线HE 直线FG=M ,则点M 必在直线___________上.4.如图,在棱长为a 的正方体ABCD-A 1B 1C 1D 1中, M 、N 分别为AA 1、C 1D 1的中点,过D 、M 、N 三点 的平面与直线A 1B 1交于点P ,则线段PB 1的长为. 5.如图,正方体ABCD-A 1B 1C 1D 1中,对角线BD 1与过A 1、D 、C 1的平面交于点M ,则BM :MD 1=. (5题) (6题) 6.直线a 、b 不在平面α,a 、b 在平面α的射影是两条平行直线,则a 、b 的位置关系是.7.正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 、H 分别为AA 1、CC 1、C 1D 1、D 1A 1的中点,则四边形EFGH 的形状是. 8.空间四边形ABCD 中, AD=1 , BC=3, BD=213, AC=23, 且BC AD ⊥, 则异面直线AC 和BD 所成的角为.9.在四棱锥P ABCD -中,1//,2AB CD AB DC =,E 为PD 中点,F 为PC 中点.求证://AE 平面PBC .10.如图,矩形ABCD ,AB 为圆O 的直径,点F 在圆O 上,设FC 的中点为M ,求证://OM 平面DAF .DMBFC NDAEEMABHC D AF EG11.M 、N 分别是正方体ABCD-A 1B 1C 1D 1的棱BB 1、B 1C 1的中点,(1)求MN 与AD 所成的角;(2)求MN 与CD 1所成的角.12.如图,已知空间四边形ABCD 的对角线AC=14cm ,BD=14cm ,M 、N 分别是AB ,CD 的中点,MN=37cm ,求异面直线AC 与BD 所成的角.13.已知四面体ABCD 中,M ,N 分别是ABC ∆和ACD ∆的重心,求证:(1)BD//平面CMN ; (2)MN//平面ABD .14.如图,空间四边形ABCD 被一平面所截,截面EFGH 是一个矩形,(1)求证:CD//平面EFGH ; (2)求异面直线AB ,CD 所成的角.15.M ,N ,P 分别为空间四边形ABCD 的边AB ,BC ,CD 上的点,且AM :MB=CN :NB=CP :PD .求证:(1)AC//平面MNP ,BD//平面MNP ;(2)平面MNP 与平面ACD 的交线//AC .【拓展训练】1.(卷)l 1,l 2,l 3是空间三条不同的直线,则下列命题正确的是()A .l 1⊥l 2,l 2⊥l 3⇒l 1∥l 3B .l 1⊥l 2,l 2∥l 3⇒l 1⊥l 3C .l 1∥l 2∥l 3⇒l 1,l 2,l 3共面D .l 1,l 2,l 3共点⇒l 1,l 2,l 3共面 2.(卷)若直线l 不平行于平面α,且l ⊄α,则()A .α的所有直线与l 异面B .α不存在与l 平行的直线C .α存在唯一的直线与l 平行D .α的直线与l 都相交 3.(卷)下列命题正确的是()A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行 5.(卷)如图,在正方体1111ABCD A B C D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成角的大小是____________.6.如图,111111ABCDEF A B C D E F -是底面半径为1的圆柱的接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB 作圆柱的截面交下底面于11C E ,已知113FC =,证明:四边形11FBE C 是平行四边形.7.如图,四棱柱1111ABCD A B C D -的底面ABCD 是平行四边形,,E F 分别在棱11,BB DD 上,且1//EC AF .求证:1//FC AE .N MB 1A 1C 1D 1BD C A【参考答案】 1、巩固练习答案1.【答案】C2.【答案】C3.【答案】①② 4.【答案】 因为,,O D 分别为,AB PB 的中点 所以,//OD PA又因为,PA ⊂平面PAC ,OD ⊄平面PAC 所以,//OD 平面PAC5.【答案】 因为,,E F 分别是,PB PC 的中点 所有,//EF BC由题可得,//AD BC ,即//AD EF 又因为,AD ⊂平面PAD ,EF ⊄平面PAD 所以,//EF 平面PAD6.【答案】连接1C B 交1CB 于点E ,连接ED 在平行四边形11BB CC 中,E 为1C B 中点 又因为D 为AB 中点 所以,1//ED C A又因为,ED ⊂平面1CDB ,1C A ⊄平面1CDB 所以,1//C A 平面1CDB 7.【答案】证明:连接,BD MO在平行四边形ABCD 中,因为O 为AC 的中点,所以O 为BD 的中点, 又M 为PD 的中点,所以//PB MO 因为PB ⊄平面ACM ,MO ⊂平面ACM 所以//PB 平面ACM .8.【答案】取CE 中点P ,连结,FP BP ,∵F 为CD 的中点,∴1//,2PF ED PF ED =又1//,2AB ED AB DE =∴//,AB PF AB PF =∴ABFP 为平行四边形,∴//AF BP .又∵AF ⊄平面BCE ,BP ⊂平面BCE ∴//AF 平面BCE9.【答案】连接1A F因为111111////AA BB CC AA BB CC ==,, 所以11ACC A 为平行四边形,因此1111//,AC A C AC A C = 在正方形ABCD 中,F 为中心,即F 为AC 中点由于E 是线段11A C 的中点,所以11//,FC A E FC A E =, 所以1A EFC 为平行四边形,即1//FA CE 因为1FA ⊂面1A BD ,CE ⊄平面1A BD , 所以CE ∥平面1A BD2、课后作业答案1.【答案】C 2.∈ 3.BD 4.43a5.2:1 6.平行或异面 7.等腰梯形 8.9009.【答案】证明:连接EF ,中点为PD E . F 为PC 中点,则1//,2EF CD EF CD =因为1//,2AB CD AB CD =,所以//,EF AB EF AB =,则四边形ABEF 是平行四边形. 所以//AE BF因为AE 不在平面PBC ,BF 在平面PBC , 所以//AE 平面PBC .10.【答案】设DF 的中点为N ,则MN//12CD ,又AO //12CD ,BAA1B1LMD1C1D CN 则MN//AO,四边形MNAO为平行四边形,∴//OM AN又AN⊂平面DAF,OM⊄平面DAF,∴//OM平面DAF.11.解:(1)在正方体ABCD-A1B1C1D1中,AD//B1C1⇒B1C1与MN所成的锐角(或直角)是AB、CD所成的角.∠⇒B1NM=450⇒MN与AD所成的角为450.(2)连接A1B,过M在面A1B中作A1B的平行线交A1B1于点L,连接LN,LM//D1C∠⇒LMN(或其补角)即为MN与CD1所成的角.∠⇒LMN=600⇒ MN与CD1所成的角为600.12.解:取BC的中点P,连接PM,PN,可证∠MPN(或其补角)是异面直线AC与BD所成的角,在∆PMN中,由MP=NP=7,MN=37,可得cos∠MPN =21-,∠MPN =1200.则异面直线AC与BD所成的角为600.13.连接AM,AN,并延长分别交BC,CD于点E,F,连接EF,由M,N分别是ABC∆和ACD∆的重心,得E,F分别是BC,CD的中点,则EF//BD,易证得BD//平面CMN;由,得MN//EF,可证MN//平面ABD.14.(1)由四边形EFGH是矩形可得,EF//GH,可证得EF//平面BCD,又因CD是过EF的平面ACD与平面BCD的交线,则EF//CD,所以CD//平面EFGH.(2)由CD//平面EFGH,可证得CD//GH;同理可证AB//GF;∠FGH 就是异面直线AB ,CD 所成的角(或补角),因为EFGH 是矩形,所以∠FGH=900,则异面直线AB ,CD 所成的角为900.15.证明:(1)AC//平面MNP ,BD//平面MNP.(2),即平面MNP 与平面ACD 的交线//AC .3、拓展训练答案1.B ,【解析】对于A ,直线l 1与l 3可能异面;对于C ,直线l 1、l 2、l 3可能构成三棱柱三条侧棱所在直线时而不共面;对于D ,直线l 1、l 2、l 3相交于同一个点时不一定共面,所以选B .2.B ,【解析】在α存在直线与l 相交,所以A 不正确;若α存在直线与l 平行,又∵l ⊄α,则有l ∥α,与题设相矛盾,∴B 正确,C 不正确;在α不过l 与α交点的直线与l 异面,D 不正确.3.C ,【解析】若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A 错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B 错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D 错;故选项C 正确. 4.B5.90º6.【答案】证明:因为圆柱的上下底面平行,且11,FB C E 是截面与圆柱上、下底面的交线, 所以11//FB C E依题意得,正六边形ABCDEF 是圆接正六边形, 所以,正六边形的边长等于圆的半径,即1AB AF == 在ABF ∆中,由正六边形的性质可知,120BAF ∠=,所以,2222cos1203BF AB AF AB AF =+-⋅=,即3BF =同理可得113C E =,所以11FB C E =,故四边形11BFC E 是平行四边形.7.【答案】证明:由题可知,在四棱柱1111ABCD A B C D -中,平面11//AA BB 平面11CC DD 因为1//AF EC ,所以,1,,,A F E C 共面1AFECAE ⊂AFEC AFEC CC DD FC =所以,1//AE FC .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点、线、面之间的位置关系1.[2015·广东卷改编] 若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则l与l1,l2中的________相交.2.[2015·江苏卷改编] 如图13-1所示,在直三棱柱ABC - A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E,则DE与平面AA1C1C的位置关系为________.图13-13.[2015·四川卷改编] 如图13-2所示的正方体ABCD -EFGH中,平面BEG与平面ACH的位置关系为________.13-24.[2015·湖南卷改编] 如图13-3所示,直三棱柱ABC - A1B1C1的底面是正三角形,E,F分别是BC,CC1的中点,则平面AEF与平面B1BCC1的位置关系为________.13-35.[2015·湖北卷改编] 如图13-4所示,在四棱锥P - ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,则DE与平面PBC的位置关系为________________.13-46.[2013·湖南卷改编] 如图13-5所示,在直三棱柱ABC - A 1B 1C 1中,∠BAC =90°,AB =AC =2,点E 在棱BB 1上,且EB 1=2,则异面直线AC 与C 1E 所成的角为________.13-57.[2014·新课标全国卷Ⅱ改编] 如图13-6所示,在四棱锥P - ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,设AP =1,AB =32,则点A 到平面PBC 的距离为________.13-6考点一 点、线、面位置关系的判断2015·浙江卷] 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β( )A .若l ⊥β,则α⊥βB .若α⊥β,则l ⊥mC .若l ∥β,则α∥βD .若α∥β,则l ∥m (2)如图13-7所示,在直三棱柱ABC - A 1B 1C 1中,BC =AC ,AC 1⊥A 1B ,M ,N 分别为A 1B 1,AB 的中点.给出下列结论:①C 1M ⊥平面A 1ABB 1;②A 1B ⊥AM ;③平面AMC 1∥平面CNB 1.其中正确结论的个数为( )图13-7A .0B .1C .2D .3[听课笔记][小结] 判断空间点、线、面的位置关系,主要依据四个公理、平行关系和垂直关系的定义及有关定理.解决具体问题时可以构建长方体或三棱锥等模型,把要考查的点、线、面融入模型中,判断会简洁明了.如要否定一个结论,只需找到一个反例即可.(1)如图13-8所示,在正方体ABCD -A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()图13-8A.不存在B.有1条C.有2条D.有无数条(2)已知直线l,m,平面α,β,且满足l⊥α,m⊂β,则“l⊥m”是“α∥β”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件考点二线、面位置关系如图13-9所示,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.(1)设FC的中点为M,求证:OM∥平面DAF;(2)求证:AF⊥平面CBF.图13-9[听课笔记][小结] (1)要证线面平行,主要有两个途径:一是证已知直线与平面内的某直线平行;二是证过已知直线的平面与已知平面平行.转化思想在证明平行关系上起着重要的作用,在寻求平行关系时,利用中位线、平行四边形等是常见的方法.(2)要证线面垂直,关键是在这个平面内能找出两条相交直线和已知直线垂直,即线线垂直⇒线面垂直.结合图形还要注意一些隐含的垂直关系,如等腰三角形的三线合一、菱形的对角线以及经计算得出的垂直关系等.在三棱柱ABC -A1B1C1中,AA1⊥BC,A1B⊥AC,D,E分别是BB1,A1C1的中点.(1)求证:DE∥平面A1BC;(2)若AB⊥BC,求证:A1B⊥平面ABC;(3)在(2)的条件下,若AB=BC=1,BB1=2,求三棱锥A1BCC1的体积.图13-10考点三面面位置关系图13-112015·湖南卷] 如图13-11,直三棱柱ABC - A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.(1)证明:平面AEF⊥平面B1BCC1;(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F - AEC的体积.[听课笔记][小结] 面面存在两种特殊的位置关系:平行与垂直.要证面面垂直,需利用面面垂直的判断定理,转化为证线面垂直;要证面面平行,需在其中一个平面内找到两条相交直线都平行于另一个平面.如图13-12所示,在正四棱台ABCD -A1B1C1D1中,A1B1=a,AB=2a,AA1=2a,E,F分别是AD,AB的中点.(1)求证:平面EFB1D1∥平面BDC1;(2)求证:平面AA1C⊥平面BDC1.图13-12考点四高与距离问题如图13-13所示,在直三棱柱ABC - A1B1C1中,底面ABC为等边三角形,AB=4,AA1=5,M是BB1的中点.图13-13(1)求证:平面A1MC⊥平面AA1C1C;(2)求点A到平面A1MC的距离.[听课笔记][小结] 求点到平面的距离一般有两种方法:一是过此点直接作到平面的垂线;二是利用等面积或等体积法求距离.高考易失分题12 空间中位置关系的证明与体积、距离问题图13-14范例[2015·广东卷] 如图13-14所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.失分分析(1)不能将点C到平面PDA的距离转化为某几何体的高;(2)期望通过直接作出点到面的距离求解;(3)不熟悉等积等价转化方法,将三棱锥C-PDA的体积转化为三棱锥P -ACD的体积;(4)位置关系证明不到位影响点到面距离的计算.高考预测如图13-15所示,在等腰梯形PDCB中,DC∥PB,PB=3DC=3,PD=2,DA⊥PB,垂足为A.将△P AD沿AD折起,使得P A⊥AB,得到四棱锥P -ABCD.(1)证明:平面P AD⊥平面PCD;(2)点M在棱PB上,平面AMC把四棱锥P -ABCD分成两个几何体,当这两个几何体体积的比值V多面体PMACDV三棱锥M -ABC=2时,求点B到平面AMC的距离.图13-15点、线、面之间的位置关系■ 核心知识聚焦1.至少一条 [解析] 若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则l 至少与l 1,l 2中的一条相交.2.平行 [解析] 由题意知,E 为B 1C 的中点, 又D 为AB 1的中点,因此DE ∥AC.又因为DE ⊄平面AA 1C 1C ,AC ⊂平面AA 1C 1C , 所以DE ∥平面AA 1C 1C.3.平行 [解析] 因为ABCD-EFGH 为正方体,所以BC ∥FG ,BC =FG ,又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH ,于是BCHE 为平行四边形,所以BE ∥CH.又CH ⊂平面ACH ,BE ⊄平面ACH , 所以BE ∥平面ACH. 同理BG ∥平面ACH. 又BE ∩BG =B ,所以平面BEG ∥平面ACH.4.垂直 [解析] 因为三棱柱ABC - A 1B 1C 1是直三棱柱,所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC ,因此AE ⊥平面B 1BCC 1,而AE ⊂平面AEF ,所以平面AEF ⊥平面B 1BCC 1.5.垂直 [解析] 因为PD ⊥底面ABCD ,所以PD ⊥BC. 由底面ABCD 为长方形,有BC ⊥CD ,而PD ∩CD =D , 所以BC ⊥平面PCD.又DE ⊂平面PCD ,所以BC ⊥DE. 又因为PD =CD ,点E 是PC 的中点,所以DE ⊥PC , 而PC ∩BC =C ,所以DE ⊥平面PBC. 6.60° [解析] 因为EB 1=2,所以EA 1=22+(2)2=6,所以tan ∠EC 1A 1=EA 1C 1A 1=3,得∠EC 1A 1=60°.因为AC ∥A 1C 1,所以异面直线AC 与C 1E 所成的角就是A 1C 1与C 1E 所成的角,即为60°.7.31313[解析] 作AH ⊥PB 交PB 于点H. 由PA ⊥平面ABCD ,得PA ⊥BC ,又BC ⊥AB , 所以BC ⊥平面PAB ,所以BC ⊥AH. 因为PB ∩BC =B ,所以AH ⊥平面PBC. 又AH =PA·AB PB =31313,所以点A 到平面PBC 的距离为31313.■ 考点考向探究考点一 点、线、面位置关系的判断例1 (1)A (2)D [解析] (1)由两平面垂直的判定定理知,A 正确;对于B ,直线l ,m 相交、平行、异面都有可能,故不正确;对于C ,要求α内两条相交直线都平行于β,才能推出α∥β,故不正确;对于D ,l ,m 平行和异面都有可能,故不正确.(2)因为ABC - A 1B 1C 1为直三棱柱,BC =AC ,M 为A 1B 1的中点,所以C 1M ⊥A 1B 1,所以C 1M ⊥平面A 1ABB 1,所以①正确.因为AC 1⊥A 1B ,且C 1M ⊥平面A 1ABB 1,所以A 1B ⊥平面AMC 1,所以AM ⊥A 1B ,所以②正确.易知AM ∥B 1N ,C 1M ∥CN ,所以平面AMC 1∥平面CNB 1,所以③正确.故选D .变式题 (1)D (2)C [解析] (1)在AA 1上取一点G ,使得AG =14AA 1,连接EG ,D 1G.可证得EG ∥D 1F ,所以E ,G ,D 1,F 四点共面.在平面ADD 1A 1内,平行于D 1G 的直线均平行于平面D 1EF ,故这样的直线有无数条.(2)若l ⊥m ,则α,β可能平行,可能相交,所以充分性不成立; 若α∥β,则l ⊥β,可得l ⊥m ,所以必要性成立.故选C .考点二 线、面位置关系例2 证明:(1)设DF 的中点为N ,连接MN ,AN ,则MN ∥CD ,且MN =12CD.又∵AO ∥CD ,且AO =12CD ,∴MN ∥AO ,且MN =AO ,∴四边形MNAO 为平行四边形,∴OM ∥AN.又∵AN ⊂平面DAF ,OM ⊄平面DAF ,∴OM ∥平面DAF. (2)∵平面ABCD ⊥平面ABEF ,且CB ⊥AB ,∴CB ⊥平面ABEF.∵AF ⊂平面ABEF ,∴AF ⊥CB.又∵AB 为圆O 的直径,∴AF ⊥BF.又∵CB ∩BF =B.∴AF ⊥平面CBF.变式题 解:(1)证明:取A 1C 的中点F ,连接BF ,EF. ∵E 是A 1C 1的中点,∴EF ∥CC 1,且EF =12CC 1.又∵CC 1BB 1,D 是BB 1的中点,∴EF ∥DB ,且EF =DB ,∴四边形BDEF 是平行四边形,∴DE ∥BF ,又DE ⊄平面A 1BC ,BF ⊂平面A 1BC , ∴DE ∥平面A 1BC.(2)证明:∵AA 1⊥BC ,AB ⊥BC ,且AB ∩AA 1=A ,∴BC ⊥平面ABB 1A 1,∴BC ⊥A 1B.又∵A 1B ⊥AC ,AC ∩BC =C ,∴A 1B ⊥平面ABC.(3)由(2)的结论得,A 1B ⊥AB.∵AB ⊥BC ,∴AB ⊥平面A 1BC.∵A 1B 1∥AB ,∴A 1B 1⊥平面A 1BC.由B 1C 1∥BC 可知,B 1C 1∥平面A 1BC. ∵AB =1=A 1B 1,AA 1=BB 1=2,∴A 1B =1, ∴三棱锥A 1 BCC 1的体积V 三棱锥A 1 BCC 1=V 三棱锥C 1 A 1BC =V 三棱锥B 1 A 1BC =13S △A 1BC ·A 1B 1=13×12×1=16. 考点三 面面位置关系例3 解:(1)证明:如图,因为三棱柱ABC - A 1B 1C 1是直三棱柱,所以AE ⊥BB 1. 又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC. 因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF , 所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ,连接A 1D ,CD. 因为△ABC 是正三角形,所以CD ⊥AB. 又三棱柱ABC - A 1B 1C 1是直三棱柱,所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1,于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角. 由题设,∠CA 1D =45°,所以A 1D =CD =32AB = 3. 在Rt △AA 1D 中,AA 1=A 1D 2-AD 2=3-1=2,所以FC =12AA 1=22.故三棱锥F - AEC 的体积V =13S △AEC ·FC =13×32×22=612.变式题 证明:(1)连接A 1C 1,交B 1D 1于点M ,设AC 分别交EF ,BD 于N ,P 两点,连接MN ,C 1P.由题意,BD ∥B 1D 1,因为BD ⊄平面EFB 1D 1,B 1D 1⊂平面EFB 1D 1,所以BD ∥平面EFB 1D 1.因为A 1B 1=a ,AB =2a ,所以MC 1=12A 1C 1=22a.又因为E ,F 分别是AD ,AB 的中点,所以NP =14AC =22a ,所以MC 1=NP.又因为AC ∥A 1C 1,所以MC 1∥NP , 所以四边形MC 1PN 为平行四边形,所以PC 1∥MN.因为PC 1⊄平面EFB 1D 1,MN ⊂平面EFB 1D 1,所以PC 1∥平面EFB 1D 1. 又因为PC 1∩BD =P ,所以平面EFB 1D 1∥平面BDC 1.(2)连接A 1P ,MP.易知A 1C 1∥PC ,A 1C 1=PC , 所以四边形A 1C 1CP 为平行四边形.又易知CC 1=PC =2a ,所以四边形A 1C 1CP 为菱形, 所以A 1C ⊥PC 1.因为MP ⊥平面ABCD ,MP ⊂平面A 1C 1CA , 所以平面A 1C 1CA ⊥平面ABCD.因为BD ⊥AC ,所以BD ⊥平面A 1C 1CA , 又因为A 1C ⊂平面A 1C 1CA ,所以BD ⊥A 1C. 因为PC 1∩BD =P ,所以A 1C ⊥平面BDC 1, 所以平面AA 1C ⊥平面BDC 1. 考点四 高与距离问题例4 解:(1)证明:连接AC 1,交A 1C 于点E ,连接ME ,MC 1,MA. ∵M 是BB 1的中点, ∴MA 1=MA =MC 1=MC =892. 又E 分别是AC 1,A 1C 的中点, ∴ME ⊥AC 1,且ME ⊥A 1C ,∴ME ⊥平面AA 1C 1C.∵ME ⊂平面A 1MC ,∴平面A 1MC ⊥平面AA 1C 1C.(2)过点A 作AH ⊥A 1C 于点H.由(1)知,平面A 1MC ⊥平面AA 1C 1C ,又平面A 1MC ∩平面AA 1C 1C =A 1C ,∴AH ⊥平面A 1MC ,∴AH 即为点A 到平面A 1MC 的距离. 在△A 1AC 中,∠A 1AC =90°,A 1A =5,AC =4,∴A 1C =41,∴AH =5×441=204141,即点A 到平面A 1MC 的距离为204141.高考易失分题12范例 解:(1)证明:因为四边形ABCD 是长方形,所以BC ∥AD.因为BC ⊄平面PDA ,AD ⊂平面PDA ,所以BC ∥平面PDA.(2)证明:因为四边形ABCD 是长方形,所以BC ⊥CD.因为平面PDC ⊥平面ABCD ,平面PDC ∩平面ABCD =CD ,BC ⊂平面ABCD ,所以BC ⊥平面PDC.因为PD ⊂平面PDC ,所以BC ⊥PD.(3)取CD 的中点E ,连接AE 和PE.因为PD =PC ,所以PE ⊥CD ,在Rt △PED 中,PE =PD 2-DE 2=42-32=7.因为平面PDC ⊥平面ABCD ,平面PDC ∩平面ABCD =CD ,PE ⊂平面PDC ,所以PE ⊥平面ABCD.由(2)知,BC ⊥平面PDC ,由(1)知,BC ∥AD ,所以AD ⊥平面PDC.因为PD ⊂平面PDC ,所以AD ⊥PD.设点C 到平面PDA 的距离为h ,因为V 三棱锥C - PDA =V 三棱锥P - ACD ,所以13S △PDA ·h =13S △ACD ·PE ,即h =S △ACD ·PE S △PDA=12×3×6×712×3×4=372,所以点C 到平面PDA 的距离是372.高考预测 解:(1)证明:∵在等腰梯形PDCB 中,DA ⊥PB ,∴在四棱锥P - ABCD 中,DA ⊥AB ,DA ⊥PA.又PA ⊥AB ,DC ∥AB ,∴DC ⊥PA ,DC ⊥DA ,∴DC ⊥平面PAD. ∵DC ⊂平面PCD ,∴平面PAD ⊥平面PCD. (2)∵DA ⊥PA ,且PA ⊥AB ,∴PA ⊥平面ABCD.过M 作MN ⊥AB ,垂足为N ,则MN ∥PA ,∴MN ⊥平面ABCD.依据题意,V 三棱锥M - ABC =13V 四棱锥P - ABCD ,而V 四棱锥P - ABCD =13S 四边形ABCD·PA =12,∴V 三棱锥M - ABC=13S △ABC ·MN =16. 又易知AC =BC =2,AB =2,∴AC 2+BC 2=AB 2,即AC ⊥BC , ∴S △ABC =1,∴MN =12,∴MN =12PA ,∴M 是PB 的中点.由AC ⊥BC ,PA ⊥BC ,得BC ⊥平面PAC ,∴BC ⊥PC.在Rt △PAB ,Rt △PBC 中,CM =AM =12PB =52,又AC =2,故可求得S △MAC =64.设点B 到平面MAC 的距离为d ,则由V 三棱锥M - ABC =V 三棱锥B - MAC=13S △MAC ·d =16,得d =63,故点B 到平面AMC 的距离为63.■教师备用例题[备选理由] 例1是在一个多面体中综合考查线、面平行与垂直的位置关系;例2考查线线垂直及线面平行的位置关系的证明;例3考查线面垂直的判定、面面垂直的性质以及四棱锥体积的计算;例4综合考查线面垂直的位置关系、体积的最值问题以及距离的最值问题.例1(配听课例1使用)在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C,E的动点,则下列说法正确的有()①直线DE与平面ABF平行;②当F为CE的中点时,BF⊥平面CDE;③存在点F使得直线BF与AC平行;④存在点F使得DF⊥BC.A.1个B.2个C.3个D.4个[解析] C因为AB,DE都垂直于平面ACD,所以DE∥AB,所以DE平行于平面ABF,①正确;当F为CE的中点时,取CD的中点G,连接AG,FG,于是FG∥DE,则AB∥FG,且FG=AB=12DE,所以四边形ABFG为平行四边形,则AG∥BF,又AC=AD,所以AG⊥CD,又DE⊥平面ACD,所以AG⊥DE,所以AG⊥平面CDE,则BF⊥平面CDE,②正确;因为AC与平面CBE交于点C,且BF在平面CBE内,所以直线BF与AC不可能平行,③错误;当F为CE的中点时,由②知,BF⊥平面CDE,则DF⊥BF,又CD=DE,所以DF⊥CE,于是DF⊥平面CBE,则DF⊥BC,④正确.例2(配听课例2使用)如图所示,在五面体ABCDEF中,四边形ABCD为正方形,EF ∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,G是EF的中点.(1)证明:AG⊥CD;(2)若点M在线段AC上,且AMMC=13,求证:GM∥平面ABF.证明:(1)因为AE=AF,G是EF的中点,所以AG⊥EF,又因为EF∥AD,所以AG⊥AD.因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,AG⊂平面ADEF,所以AG⊥平面ABCD,又因为CD⊂平面ABCD,所以AG⊥CD.(2)如图,过点M作MN∥BC,交AB于点N,连接NF,GM.因为AM MC =13,所以MN BC =AM AC =14.因为BC =2EF ,G 是EF 的中点,所以BC =4GF. 又因为EF ∥AD ,四边形ABCD 为正方形, 所以GF ∥MN ,且GF =MN ,所以四边形GFNM 是平行四边形, 所以GM ∥FN.又因为GM ⊄平面ABF ,FN ⊂平面ABF ,所以GM ∥平面ABF.例3(配听课例3使用)[2015·陕西卷] 如图(1),在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图(2)中△A 1BE 的位置,得到四棱锥A 1 BCDE.(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1 BCDE 的体积为362,求a 的值.解:(1)证明:在图(1)中,因为AB =BC =12AD =a ,E 是AD 的中点,∠BAD =π2,所以BE ⊥AC ,即在图(2)中,BE ⊥A 1O ,BE ⊥OC , 从而BE ⊥平面A 1OC. 又CD ∥BE ,所以CD ⊥平面A 1OC.(2)由已知,平面A 1BE ⊥平面BCDE , 且平面A 1BE ∩平面BCDE =BE , 又由(1)知,A 1O ⊥BE , 所以A 1O ⊥平面BCDE ,即A 1O 是四棱锥A 1 BCDE 的高. 由图(1)知,A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC·AB =a 2. 从而四棱锥A 1 BCDE 的体积 V =13×S ×A 1O =13×a 2×22a =26a 3.由26a 3=362,得a =6.例4(配听课例4使用)[2015·福建卷] 如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且PO =OB =1.(1)若D 为线段AC 的中点,求证:AC ⊥平面PDO ;(2)求三棱锥P-ABC 体积的最大值;(3)若BC =2,点E 在线段PB 上,求CE +OE 的最小值.解:方法一:(1)证明:在△AOC 中,因为OA =OC ,D 为AC 的中点, 所以AC ⊥DO.又PO 垂直于圆O 所在的平面,所以PO ⊥AC.因为DO ∩PO =O ,DO ⊂平面PDO ,PO ⊂平面PDO , 所以AC ⊥平面PDO. (2)因为点C 在圆O 上,所以当CO ⊥AB 时,C 到AB 的距离最大,且最大值为1. 又AB =2,所以△ABC 面积的最大值为 12×2×1=1. 又因为三棱锥P-ABC 的高PO =1,故三棱锥P-ABC 体积的最大值为13×1×1=13.(3)在△POB 中,PO =OB =1,∠POB =90°, 所以PB =12+12= 2.同理PC =2,所以PB =PC =BC.在三棱锥P-ABC 中,将侧面BCP 绕PB 旋转至平面BC′P, 使之与平面ABP 共面,如图所示.当O ,E ,C ′共线时,CE +OE 取得最小值. 又因为OP =OB ,C ′P =C′B , 所以OC′垂直平分PB ,即E 为PB 中点. 从而OC′=OE +EC′=22+62=2+62, 亦即CE +OE 的最小值为2+62. 方法二:(1)(2)同方法一.(3)在△POB中,PO=OB=1,∠POB=90°,所以∠OPB=45°,PB=12+12= 2.同理PC= 2.所以PB=PC=BC,所以∠CPB=60°.在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示.当O,E,C′共线时,CE+OE取得最小值.所以在△OC′P中,由余弦定理得,OC′2=1+2-2×1×2×cos(45°+60°)=1+2-2 2×(22×12-22×32)=2+3.从而OC′=2+3=2+6 2.所以CE+OE的最小值为22+62.。
