2015年全国高中数学联赛安徽省初赛
2015年全国高中数学联赛安徽赛区获奖情况通知

安徽省青少年科技活动中心
安徽省数学会文件安徽省数学会中数竞赛[2015]03号
关于公布2015年度全国高中数学联赛
安徽省获奖情况的通知
各市科协、教育局、数学会:
根据安徽省数学会中数竞赛[2015]02号文件通知的要求,2015年度全国高中数学联赛工作已顺利完成。
现将获奖情况通知如下:
经安徽省数学会竞赛委员会评卷,全国高中数学联赛组织委员会审定,评出“2015年度全国高中数学联赛”一等奖52名、二等奖487名、三等奖853名。
附:2015年度全国高中数学联赛安徽省获奖名单
安徽省青少年科技活动中心安徽省数学会
二○一五年十月二十二日
2015年度全国高中数学联赛安徽省获奖名单
一等奖
二等奖
三等奖
41
42。
2015年全国高中数学联赛(WORD,含答案)
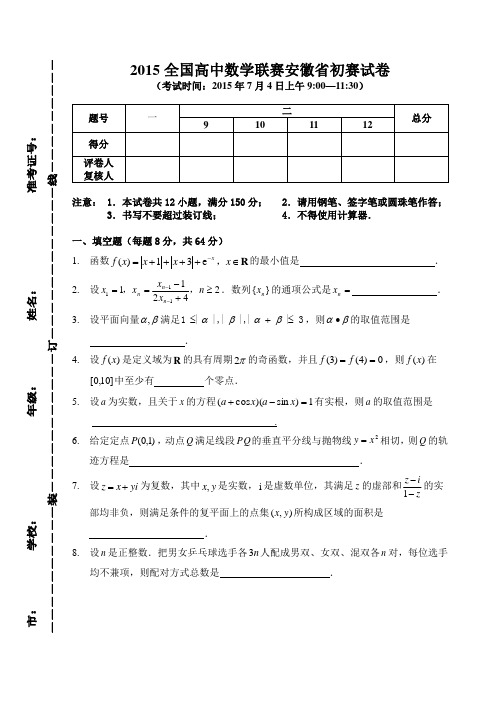
2015全国高中数学联赛安徽省初赛试卷(考试时间:2015年7月4日上午9:00—11:30)注意: 1.本试卷共12小题,满分150分; 2.请用钢笔、签字笔或圆珠笔作答;3.书写不要超过装订线; 4.不得使用计算器.一、填空题(每题8分,共64分)1. 函数R ∈++++=-x x x x f x ,e 31)(的最小值是 .2. 设24211111≥+-==--n x x x x n n n ,.数列}{n x 的通项公式是=n x .3. 设平面向量βα,满足3|||,||,|1≤+≤βαβα,则βα∙的取值范围是.4. 设)(x f 是定义域为R 的具有周期π2的奇函数,并且0)4()3(==f f ,则)(x f 在]10,0[中至少有 个零点.5. 设a 为实数,且关于x 的方程1)sin )(cos (=-+x a x a 有实根,则a 的取值范围是.6. 给定定点)1,0(P ,动点Q 满足线段PQ 的垂直平分线与抛物线2x y =相切,则Q 的轨迹方程是 . 7. 设z x yi =+为复数,其中,x y 是实数,i 是虚数单位,其满足z 的虚部和1z iz--的实部均非负,则满足条件的复平面上的点集(,)x y 所构成区域的面积是.8. 设n 是正整数.把男女乒乓球选手各n 3人配成男双、女双、混双各n 对,每位选手均不兼项,则配对方式总数是 .二、解答题(第9题20分,第10━12题22分,共86分)9. 设正实数b a ,满足1=+b a .求证:31122≥+++bb a a .10. 在如图所示的多面体ABCDEF 中,已知CFBE AD ,,都与平面ABC 垂直.设c CF b BE a AD ===,,,1===BC AC AB .求四面体ABCE 与BDEF 公共部分的体积(用c b a ,,表示).11.设平面四边形ABCD的四边长分别为4个连续的正整数。
证明:四边形ABCD的面积的最大值不是整数。
2015年全国高中数学联赛试题及答案详解(A卷)

(i ) 5 2 ,此时 1 且 5 ,无解;
22
2
4
(ii) 5 9 2 ,此时有 9 5 ;
件等价于:存在整数 k, l (k l) ,使得
2k 2l 2 .
①
2
2
当 4 时,区间[, 2]的长度不小于 4 ,故必存在 k, l 满足①式.
当 0 4 时,注意到[, 2] (0, 8) ,故仅需考虑如下几种情况:
.
答案: 2015 1007i .
解:由已知得,对一切正整数 n ,有
zn2 zn1 1n 1i zn 1 ni 1n 1i zn 2 i , 于是 z2015 z1 10072 i 2015 1007i .
4. 在矩形 ABCD 中, AB 2, AD 1 ,边 DC 上(包含点 D 、 C )的动点 P 与 CB 延 长线上(包含点 B )的动点 Q 满足 DP BQ ,则向量 PA 与向量 PQ 的数量积 PA PQ 的
6. 在平面直角坐标系 xOy 中,点集 K (x, y) x 3y 6 3x y 6 0所对
应的平面区域的面积为
.
答案:24.
解:设 K1 (x, y) x 3y 6 0 .先考虑 K1
在第一象限中的部分,此时有 x 3y 6 ,故这些点对
应于图中的 OCD 及其内部.由对称性知, K1 对应的 区域是图中以原点 O 为中心的菱形 ABCD 及其内部.
同理,设 K2 (x, y) 3x y 6 0 ,则 K2 对
应的区域是图中以 O 为中心的菱形 EFGH 及其内部.
由点集 K 的定义知, K 所对应的平面区域是被
2015年全国高中数学联赛试题答案

…………………20 分
包含 a1 的集合至少有
n− s −t 个.又由于 A1 ⊆ Ci ( i = 1, , t ) ,故 C1 , C2 , , Ct 都 k
n− s −t ,即在剩下的 n − s − t 个集合中, k
包含 a1 ,因此包含 a1 的集合个数至少为
n− s −t n − s + (k − 1)t n − s + t (利用 k ≥ 2 ) = +t ≥ k k k n . ……………40 分 ≥ (利用 t ≥ s ) k
n ≤ (n + 1) ∑ห้องสมุดไป่ตู้ai2 , i =1 所以①得证,从而本题得证.
…………………40 分
证法二:首先,由于问题中 a1 , a2 , , an 的对称性,可设 a1 ≥ a2 ≥ ≥ an .此 n 外,若将 a1 , a2 , , an 中的负数均改变符号,则问题中的不等式左边的 ∑ ai 不 i =1 减,而右边的 ∑ ai2 不变,并且这一手续不影响 ε i = ±1 的选取,因此我们可进一
2t u − 1 2u − 1 m 1 2αt ⋅ 1 2αt ⋅ 1 + 2u + + 2(t −1)u ) =+ =+ ( q q q
…………………10 分
n + 2 ∑ aj n = j +1 2
2
2
n 2 n n n 2 2 ≤ 2 ∑ ai + 2 n − ∑ a j (柯西不等式) …………30 分 2 i =1 2 = n j +1 2 n n 2 2 n + 1 n n n + 1 2 a j (利用 n − = = 2 ∑ ai + 2 ) ∑ 2 2 2 i =1 2 = n j +1 2 n n 2 2 2 ≤ n ∑ ai + (n + 1) ∑ a j (利用 [ x ] ≤ x ) n = i =1 j +1 2
2015年全国高中数学联赛试题及答案解析

5. 已知点 P (1, 2, 5) 是空间直角坐标系 O xyz 内一定点,过 P 作一平面与三坐标轴的正半轴分别交于 A, B, C 三点,则所有这样的四面体 OABC 的体积的最小值为 . x y z 解:设此平面的方程为 1 , a, b, c 0 分别是该平面在 x, y, z 轴上的截距,又点 P 在平面 ABC 内, a b c 3 1 2 5 1 10 1 1 2 5 1 1 2 5 1 2 5 ,即 ,得 VOABC abc 45 .当 , 故 1 ,由于 1 3 a b c a b c 27 abc a b c 3 a b c 6 即 (a, b, c) (3, 6,15) 时, VOABC 的最小值为 45.
2015 年全国高中数学联赛模拟试题 04 第一试参考解答 一、填空题:本大题共 8 小题,每小题 8 分,共 64 分. 1. 集合 A = {x, y} 与 B = {1, log 3 ( x + 2)} 恰有一个公共元为正数 1 + x ,则 A B = 解:由于 1 + x ¹ x ,故 1 + x = y .由 log 3 ( x + 2) ¹ 1 知 x ¹ 1 ,又因为 1 + x > 0 ,所以 3
2
,
1 tan tan
tan tan
tan .
2 tan 1 3tan 2
2 1 3tan tan
3 , u 的最大值为 . 6 3
4.在单调递增数列 an 中,已知 a1 2 , a2 4 ,且 a2 n 1 , a2 n , a2 n 1 成等差数列, a2 n , a2 n 1 , a2 n 2 成 解:因为 an 单调递增, a1 0 ,所以 an 0 .因为 a2 n 1 , a2 n , a2 n 1 成等差数列, a2 n , a2 n 1 , a2 n 2 成等 比数列,所以 所以 a2 n 所以 a2 n 等比数列, n 1, 2,3, .那么, a100 _________.
【VIP专享】2015年全国高中数学竞赛安徽初赛试题及答案

2015全国高中数学联赛安徽省初赛试卷(考试时间:2015年7月4日上午9:00—11:30)二题号一9101112总分得分评卷人复核人注意:1.本试卷共12小题,满分150分;2.请用钢笔、签字笔或圆珠笔作答;3.书写不要超过装订线;4.不得使用计算器.一、填空题(每题8分,共64分)1.函数的最小值是 .R ∈++++=-x x x x f x ,e 31)(2.设.数列的通项公式是 .24211111≥+-==--n x x x x n n n ,,}{n x =n x 3.设平面向量满足,则的取值范围是βα,3|||,||,|1≤+≤βαβαβα∙ .4.设是定义域为的具有周期的奇函数,并且,则在)(x f R π20)4()3(==f f )(x f 中至少有 个零点.]10,0[5.设为实数,且关于的方程有实根,则的取值范围是a x 1)sin )(cos (=-+x a x a a .6.给定定点,动点满足线段的垂直平分线与抛物线相切,则的)1,0(P Q PQ 2x y =Q 轨迹方程是 .7.设为复数,其中是实数,是虚数单位,其满足的虚部和的实z x yi =+,x y i z 1z iz--部均非负,则满足条件的复平面上的点集所构成区域的面积是(,)x y .8.设是正整数.把男女乒乓球选手各人配成男双、女双、混双各对,每位选n n 3n 手均不兼项,则配对方式总数是 .二、解答题(第9题20分,第10━12题22分,共86分)9.设正实数满足.求证:.b a ,1=+b a 31122≥+++bb a a10.在如图所示的多面体中,已知ABCDEF 都与平面垂直.设CF BE AD ,,ABC ,.求四c CF b BE a AD ===,,1===BC AC AB 面体与公共部分的体积(用表示)ABCE BDEF c b a ,,.ABCD ABCD 11.设平面四边形的四边长分别为4个连续的正整数。
20072015年安徽省高中数学竞赛初赛试题及答案详解

2007年安徽省高中数学竞赛初赛试题一.选择题1.假如集合.A B 同时满意{}1.2.3.4A B ={}1A B =,{}{}1,1A B ≠≠就称有序集对(),A B 为“好集对”。
这里的有序集对(),A B 意指当A B ≠,()(),,A B B A 和是不同的集对,那么“好集对”一共有( )个。
2.设函数()()lg 101x f x -=+,()()122x x f f --=方程的解为( )()()()()2222.log lg21.lg log 101.lg lg21.log log 101A B C D --++3.设100101102499500A =是一个1203位的正整数,由从100到500的全体三位数按依次排列而成那么A 除以126的余数是( ) 4.在直角ABC 中, 90C ∠=,CD 为斜边上的高,D 为垂足.,,1AD a BD b CD a b ===-=.设数列{}k u 的通项为()1221,1,2,3,,kk k k k k u a a b a b b k --=-+-+-=则( )5.在正整数构成的数列1.3.5.7……删去全部与55互质的项之后,把余下的各项按从小到大的依次排成一个新的数列{}n a ,易见123451,3,7,9,13a a a a a =====那么2007____________a =192759.. 55 .. A B C D 2831 95976.设A B ==1+cos871-cos87则():A B =7.边长均为整数且成等差数列,周长为60的钝角三角形一共有______________种.8.设2007n ≥,且n为使得nn a =取实数值的最小正整数,则对应此n 的n a 为9.若正整数n 恰好有4个正约数,则称n 为奇异数,例如6,8,10都是奇异数.那么在27,42,69,111,125,137,343,899,3599,7999这10个数中奇异数有_____________________个.10.平行六面体1111ABCD A B C D -中,顶点A 动身的三条棱1,,AB AD AA 的长度分别为2,3,4,且两两夹角都为60那么这个平行六面体的四条对角线1111,,,AC BD DB CA 的长度(按依次)分别为___________________ 11.函数()(),f x g x 的迭代的函数定义为()()()()()()()12,,f x f x f x f f x ==()()()()()()()()()()()()()()()()()1121,,,n n n n f x f f x g x g x g x g g x g x g g x --====其中n =2,3,4…设()()23,32f x x g x x =-=+,则方程组()()()()()()()()()()()()969696f x g y f y g z f z g x ⎧=⎪⎪=⎨⎪=⎪⎩的解为_________________12.设平行四边形ABCD中,4,2,AB AD BD ===则平行四边形ABCD 绕直线AC 旋转所得的旋转体的体积为_______________三.解答题13.已知椭圆22412:3y x +=Γ与点(),0,Q q 直线,l Q A B Γ过且与交于两点(可以重合).1)若AOB ∠为钝角或平角(O 为原点), 4,q =试确定l 的斜率的取值范围.2)设A 关于长轴的对称点为1A ,,4,F q =为椭圆的右焦点试推断1,A F B 和三点是否共线,并说明理由.3)问题2)中,若14,,,q A F B ≠那么三点能否共线?请说明理由. 14. 数列{}n x 由下式确定: 112,1,2,3,,121nn n x x n x x +===+,试求[]20072007lg lg .x k x =整数部分(注[]a 表示不大于a 的最大整数,即a 的整数局部.)15. 设给定的锐角ABC 的三边长,,,,,a b c x y z 正实数满意,ayz bzx cxyp x y z++=其中p为给定的正实数,试求()()()222s b c a x c a b y a b c z =+-++-++-的最大值,并求出当s 取此最大值时, ,,x y z 的取值.07年安徽省高中数学竞赛初赛答案一、选择题1.C.2.A.3.C.4.A.5.B6.D. 第1题解答过程逐个元素考虑归属的选择. 元素1必需同时属于A 与B .元素2必需至少属于A 、B 中之一个,但不能同时属于A 与B ,有2种选择:属于A 但不属于B ,属于B 但不属于A . 同理,元素3与4也有2种选择.但元素2,3,4不能同时不属于A ,也不能同时不属于B .所以4个元素满意条件的选择共有62222=-⨯⨯种.换句话说,“好集对”一共有6个. 答:C. 第2题解答过程令)110lg(+=-x y ,则0>y ,且y x 10110=+-,11010-=-y x ,)110lg(-=-y x ,)110lg(--=y x .从而)110lg()(1--=-x x f . 令t x =2,则题设方程为)()(1t ft f -=-,即)110lg()110lg(--=+t t ,故 0)]110)(110lg[(=-+t t ,1)110)(110(=-+t t ,2102=t , 2lg 2=t ,解得 2lg 212==t x . 从而 1)2(lg log )2lg 21(log 22-==x . 答:A.第3解答过程留意 972126⨯⨯=,2,7与9两两互质. 因为 0≡A (mod2), 500102101100++++≡ 2401500100÷⨯+≡)(6120300≡≡(mod9), 所以6≡A (mod18). (1) 又因为1103-≡,nn )1(103-≡(mod7),所以ii i A 3400010)500(⨯-=∑=i i i )(1)500(4000-⨯-≡∑=100)101102()495496()497498()499500(+-++-+-+-≡ 6300≡=(mod7). (2),(1),(2)两式以及7与18互质,知6≡A (mod126).答:C.另解:632126⨯=,99999963,1109999996-=,)()(11011066--n ,,3,2,1=n 所以499500104974981010310410101102101006118811941200+⨯++⨯+⨯+⨯= A其中B ,C 为整数.从而6036063+=D A 663+=E ,其中D ,E 为整数.所以A 除以63的余数为6.因为A 是偶数,所以A 除以126的余数也为6. 答:C. 第4解答过程易见BD AD CD ⋅=2,即ab b a =-2)(,又已知1=-b a ,故1=ab ,1)1(=-a a ,012=--a a ;1)1(=+b b ,012=++b b .明显k u 是首项为k a ,公比为abq -=的等比数列的前1+k 项与.故ba b a q q a u k k k k k +--=--=+++111)(1)1(,3,2,1=k .即b a b a b a b a u u k k k k k k +--++--=++++++22111)()(])()([11212++++----++=k k k k b b a a ba故答案为A.(易知其余答案均不成立)另解:易见BD AD CD ⋅=2,即ab b a =-2)(,又已知1=-b a ,故1=ab ,51414)((222=⨯+=+-=+ab b a b a ),5=+b a .解得明显k u 是首项为k a ,公比为abq -=的等比数列的前1+k 项与,故ba b a q q a u k k k k k +--=--=+++111)(1)1(])251()251[(5111++--+=k k ,,3,2,1=k . 于是数列{}k u 就是斐波那契数列1,2,3,5,8,13,21,…,它满意递推关系 ,12k k k u u u +=++ ,3,2,1=k . 所以答案为A. 第5题解答过程{}n a 可看成是在正整数数列1,2,3,4,5,6,7,…中删去全部能被2,5或11整除的项之后,把余下的各项按从小至大依次排成的数列.由三阶容斥原理,1,2,3,4,…,m 中不能被2,5或11整除的项的个数为其中⎣⎦a 不表示不大于a 的最大整数,即a 的整数局部. 估值:设11010225511522007m m m m m m m m x m -+++---≈=)1111)(511)(211(---⨯=m 11105421⨯⨯⨯=m m 114=,故 55194112007≈⨯≈m . 又因⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢+⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-⎥⎦⎥⎢⎣⎢-=1105519105519225519555519115519555192551955195519x=5519-2759-1103-501+100+250+551-50=2007,并且5519不是2,5,11的倍数,从而知55192007=a . 答:B.又解:{}n a 可看成是在正整数数列1,2,3,4,5,6,7,…中删去全部能被2,5 或11整除的项之后,把余下的各项按从小至大依次排成的数列.因为2,5,11是质数,它们的最小公倍数为110.易见,-54,-53,…,0,1,2,3,…,55中不能被2,5,11整除的数为,,;,,,17139731±±±±±±,;2119±± ;,,292723±±±,,,;,,474341393731±±±±±±535149±±±,;,共40个.(或由欧拉公式,1,2,3,…,110中不能被2,5,11整除的数的个数,等于1,2,3,…,110中与110互质的数的个数,等于401111511211110110=-⨯-⨯-⨯=∅)()()()(.)明显1,2,3,…中每连续110个整数,不能被2,5,11整除的数都有40个.所以,1,2,3,…,550050110=⨯中,不能被2,5,11整除的数有20005040=⨯个.大于5500中的数不能被2,5,11整除的,是5500+1,5500+3,5500+7,5500+9,5500+13,5500+17,5500+19,….所以5519是第2007个不能被2,5,11整除的数,亦即所求的55192007=a . 答:B .第6题解答过程 明显 287cos 127cos 123cos 12++++++=A留意到 所以 故5.22cot )22sin 5.22sin 2(:)22sin 5.22cos 2()21sin 2(:)21sin 2(:==⨯⨯=B A B A12+=. 答:D.另解:2A 00005.43cos 5.5cos 5.3cos 5.1cos +++++= ,因为2A 与2B是实数,所以 1sin 5.22cos 22sin 2=A , 1sin 5.22sin 22sin 2=B ,答:D. 第7解答过程解:设△ABC 三边长c b a ,,为整数,c b a c b a c b a ,,,,60≥≥=++成等差数列,A ∠为钝角,则必有c a b +=2,222a c b <+.易解得 b b b c a b c b a 32)(60=+=++=++=,40,20=+=c a b ;222c a b -<))((c a c a -+=,即ca c a -<-<10),(40202.因此a a c a c a <=-++<25,2)()(50,即26≥a .另外,29,30,260,≤<=+>++=>+a a a a a c b a a c b .易检验),,(c b a)11,20,29(),12,20,28(),13,20,27(),14,20,26(=都是钝角三角形. 答:4.第8题解答过程留意到22-=x ,22+=y 满意4)22()22(22=++-=+y x ,0,>y x ,故可令θcos 2=x ,θsin 2=y ,0<θ<2π.从而22cos 42-=θ,-2cos 422-=θ,-θπθ2cos 43cos 1cos 2222==-=,故83πθ=,83cos)83sin 83(cosπππn i a n n =+=+ 83sinπn i . n a 取实数,当且仅当083sin =πn ,当且仅当k n 8=,∈k Z.满意此条件且2007≥n 的最小正整数n 为2008,此时1753cos 820083cos2008-====ππx a a n . 答:-1. 第9题解答过程易见奇异数有两类:第一类是质数的立方3p (p 是质数);第二类是两个不同质数的乘积21p p (21,p p 为不同的质数).由定义可得3327=是奇异数(第一类);73242⨯⨯=不是奇异数;23369⨯=是奇异数(第二类); 373111⨯=是奇异数(第二类); 35125=是奇异数(第一类);137是质数,不是奇异数;37343=是奇异数(第一类);221301900899-=-=)(130+=2931130⨯=-)(是奇异数(第二类); )(16016013600359922+=-=-=5961160⨯=-)(是奇异数(第二类); 42119)12020)(120(120180007999233⨯=++-=-=-=是奇异数(第二类).答:8.第10解答过程解:将向量1AA ,AB ,AD 分别记为a ,b ,c . 2==a 3==b ,4==c ,且易见)(2)(2222⋅+⋅+⋅+++=++=244332432222⨯+⨯+⨯+++==55,故551=AC . 类似地,可算得,191=BD ,151=DB ,271=CA =33.答:55,19,15,33. 第11题解答过程令t x =-3,易见3+=t x ,323)3(232)(+=-+=-=t t x x f ,)32(2)()2(+=t x f 3-32)(,,32)(2+=+=t x f t n n ;令s y =+1,易见1-=s y ,2)1(323)(+-=+=s y y g 13-=s , ,132)13(3)(2)2(-=+-=s s y g ,13)()(-=s y g n n , ,3,2,1=n .因此,题设方程组可化为(1)-(2),(2)-(3),(3)-(1)得 所以)()23()()23()(2339629696y x x z z y y x -=-=-=-⇒0=-⇒=-z y y x z y x ==⇒.代入(1)得所以原方程组的解为31323-===z y x . 答:31323-===z y x . 第12题解答过程.以l T V -表示平面图形T 绕直线l 所得旋转体体积.记直线AC 为l ,作l DN BM ⊥,,交l 于F E ,,分别交CD ,AB 于N M ,.过O 作l PQ ⊥,分别交CD AB ,于Q P ,.由于O 是BD 的中点,所以Q P ,分别是DM BN ,的中点.由对称性,易见所求旋转体体积为)(2l NPQD l ADN l ABCD V V V V --∆-+==平行四边形平行四边形.由于2324===AD BD AB ,,,易见 3090=∠=∠DBA ADB ,,73422=+=+=DO AD AO ,72=AC .明显CAB DCA DAC ∠=∠>∠,FNDF >.且21727322==⨯==∆AO DO AD AO S DF ADO ,74716712422==-=-=DF AD AF .从而由圆锥体积公式得 又71074147472=-=-=-=AF AC CF ,7==AO CO ,QO DF CO CF ::=, 215171021727=÷⨯=⨯=CF DF CO QO .从而由圆锥体积公式得ππππ71225657122534310007)2574940(7)72521710712(3=-⨯=-=⨯-⨯=.从而答:所求体积为1757302π:第13题解答过程解:I )可设l :4+=my x ,与Γ联立得03624)43(22=+++my y m . 这是 y 的一元二次方程,由判别式0≥∆解得42≥m .记)(11,y x A ,)(22,y x B ,则 4324221+-=+m m y y ,4336221+=m y y . 由题设条件,02121<+=⋅y y x x ,即0)4)(4(2121<+++y y my my , 得16)(4)1(21212<++++y y m y y m ,即016432444336)1(222<++-⋅++⋅+m m m m m ,即 0)43(424)1(9222<++-+m m m .得02532<+-m , 3252>m , 253)1(2<m ,5353<<-m . 故l 的斜率的取值范围为)53,53(-. 因为F (1,0),所以)(111,1y x --=,)(22,1y x -=,从而 ∴1FA 与FB 共线, 即1A 与F 、B三点共线.III )假设4≠q ,过)0,(q Q 的直线与Γ交于A 、B ,且A 关于长轴的对称点为1A ,假如1A 、F 、B 三点共线.我们另取点)0,4(P .设直线AP 与Γ交于1B ,那么如II )的证明,1A 、F 、B 三点必共线.故B 与1B 重合,从而直线AB 与1AB 重合,就是AQ 与AP 重合.所以P 与Q 重合,4=q ,与假设冲突.这就是说,4≠q 时,三点1A 、F 、B 不能共线.第14题解答过程 14.解:n n n n n x x x x x 1212121+=+=+, 22211441nn n x x x ++=+,故∑∑==++=-20061220061221)1(4)11(n n n nn x x x,亦即80244112006122122007∑=+=-n n x x x , 由11=x 得 80254120061222007∑=+=n n x x .(*) 由于112121<+=+n n n x x x ,,,3,2,1 =n 且明显0>n x ,故{}n x 是递减数列,且 故∑∑==++=2006322200612)31(1n n n nx x151********911)113(911200632<⨯++=++<∑=n ,由(*)式得 第15题解答过程证明:因为△ABC 是锐角三角形,其三边c b a ,,满意0,,>c b a ,以及 因此,由平均不等式可知 从而22222222222)(])[(])[(])[(P zcxy y bzx x ayz z c b a y b a c x a c b =++≤-++-++-+, 亦即上式取等式当且仅当222z y x ==,亦即===z y x cb a P++.因此所求的S 的最大值为c b a P ++2,当S 取最大值时,===z y x cb a P++.(第13题答图) (第10题答图)(第12题答图)2008年安徽高中数学竞赛初赛试题一、选择题1.若函数()y f x =的图象绕原点顺时针旋转2π后,与函数()y g x =的图象重合,则( ) (A )()()1g x f x -=-(B )()()1g x f x -=(C )()()1g x f x -=--(D )()()1g x f x -=-2.平面中,到两条相交直线的间隔 之与为1的点的轨迹为( ) (A )椭圆 (B )双曲线的一局部 (C )抛物线的一局部(D )矩形3.下列4个数中与cos1cos2cos2008+++最接近的是( )y yA AB CDBCD A BC D Q MP N OF E(A )-2008 (B )-1 (C )1 (D )20084.四面体的6个二面角中至多可能有( )个钝角。
2015全国高中数学联赛
王宝
静海一中
2
王程程
天津市实验中学
2
王铎澄
南开中学
2
王飞宇
汉沽一中
2
王涵斌
大港一中
2
王昊天
宝坻一中
2
王昊文
宝坻一中
2
王昊宇
天津一中
2
王浩然
2
裴兆辰
南开中学
2
彭安頔
杨柳青一中
2
彭启洲
天津第一零二中学
2
彭希
新华中学
2
彭晓菡
耀华中学
2
彭正达
南开中学
2
戚宝玥
天津市实验中学
2
齐长悦
天津市实验中学
2
齐涛
静海一中
2
曲鹏桥
开发区第一中学
2
全婧琳
天津一中
2
任晋辉
耀华中学
2
任云飞
南开中学
2
申佳军
大港一中
2
石浤澔
耀华中学
2
石岩
蓟县一中
2
史书毓
杨村一中
2
宋知遇
静海一中
1
赵川喆
天津一中
1
郑宸
天津一中
1
邹尚宏
天津市实验中学
1
安金旭
南开中学
2Hale Waihona Puke 安睿龙天津市实验中学
2
安泰然
南开中学
2
白洋
耀华中学
2
蔡俊禹
耀华中学
2
蔡明睿
天津市实验中学
2
蔡翔宇
塘沽一中
2
曹体睿
南开中学
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015全国高中数学联赛安徽省初赛试卷(考试时间:2015年7月4日上午9:00—11:30)注意: 1.本试卷共12小题,满分150分; 2.请用钢笔、签字笔或圆珠笔作答;3.书写不要超过装订线; 4.不得使用计算器.一、填空题(每题8分,共64分)1. 函数R ∈++++=-x x x x f x ,e 31)(的最小值是 .2. 设24211111≥+-==--n x x x x n n n ,.数列}{n x 的通项公式是=n x .3. 设平面向量βα,满足3|||,||,|1≤+≤βαβα,则βα∙的取值范围是.4. 设)(x f 是定义域为R 的具有周期π2的奇函数,并且0)4()3(==f f ,则)(x f 在]10,0[中至少有 个零点.5. 设a 为实数,且关于x 的方程1)sin )(cos (=-+x a x a 有实根,则a 的取值范围是.6. 给定定点)1,0(P ,动点Q 满足线段PQ 的垂直平分线与抛物线2x y =相切,则Q 的轨迹方程是 . 7. 设z x yi =+为复数,其中,x y 是实数,i 是虚数单位,其满足z 的虚部和1z iz--的实部均非负,则满足条件的复平面上的点集(,)x y 所构成区域的面积是 .8. 设n 是正整数.把男女乒乓球选手各n 3人配成男双、女双、混双各n 对,每位选手均不兼项,则配对方式总数是 .二、解答题(第9题20分,第10━12题22分,共86分)9. 设正实数b a ,满足1=+b a .求证:31122≥+++bb a a .10. 在如图所示的多面体ABCDEF 中,已知CFBE AD ,,都与平面ABC 垂直.设c CF b BE a AD ===,,,1===BC AC AB .求四面体ABCE 与BDEF 公共部分的体积(用c b a ,,表示).11.设平面四边形ABCD的四边长分别为4个连续的正整数。
证明:四边形ABCD的面积的最大值不是整数。
12.已知31位学生参加了某次考试,考试共有10道题,每位学生解出了至少6道题.求证:存在两位学生,他们解出的题目中至少有5道相同.试题解答一、填空题(每题8分,共64分)1. 当3-≤x 时,,e 42)(x x x f -+--=0e 2)(<--='-x x f , 因此)(x f 单调减;当13-≤≤-x 时,,e 2)(x x f -+= 0e )(<-='-x x f ,此时)(x f 亦单调减;当1-≥x 时,x x x f -++=e 42)(,x x f --='e 2)(. 令0)(='x f 得.2ln -=x 因此)(x f 在2ln -=x 处取得最小值6-2ln2.2. 设x a v x a u sin cos -=+=,.方程有实根⇔双曲线1=uv 与圆1)()(22=-+-a v a u 有公共交点. 注意到圆的圆心位于直线x y =之上,只须找到圆与双曲线相切时圆心的位置即可. 易计算得,圆与双曲线切于A(1,1)点时,圆心坐标为2/21-或2/21+.圆与双曲线切于B(-1,-1)点时,圆心坐标为2/21--或2/21+-.因此,a 的取值范围为⎥⎥⎦⎤⎢⎢⎣⎡+-⎥⎥⎦⎤⎢⎢⎣⎡+---∈221,221221,221 a .3. 由4213111++=+--n n n x x x 和421221211++=+--n n n x x x ,可得2112312123121---⎪⎭⎫ ⎝⎛=++=++n n n n n x x x x .故222223232-----⋅-=n n n n n x . 4. ()217299121222-=--≥--+=∙βαβαβα.()494122≤--+=∙βαβαβα.以上等号均可取到.故βα∙的取值范围是⎥⎦⎤⎢⎣⎡-49,217.5. 由题设可知)()()(x f x f x f --=+-=+πππ。
令x=0得0=)(πf 。
另一方面,0.)4()4()42(=-=-=-f f f π 类似地,03)-f(2=π 因此,)(x f 在]10,0[中的零点一定包含34,3,32,44,2,4,32,,3,420-+---ππππππππ,这11个零点.6. 设PQ 的垂直平分线l 与抛物线2x y =相切于),(2t t ,切向为)2,1(t . 则l 的方程为2)(2t t x t y +-=.设),(y x Q ,由PQ 与l 垂直且PQ 中点在l 上,可得⎩⎨⎧-=+=-+②①221)1(0)1(2t tx y y t x . 由①解得yxt 22-=,代入②得Q 的轨迹方程为 0)1)(1(2)12(22=-++-y y x y ,⎥⎦⎤⎢⎣⎡-∈21,1y .7. 0)1()1()1(i 1i )1(Re 1i Re22≥+----=---+=--yx yy x x y x y x z z 等价于 21221221)()(≤-+-y x . 又由于0≥y,故满足条件的点集构成了圆的一部分,计算得其面积为823+π.8. 从3n 名男选手中选取2n 人作为男双选手有23n n C 种选法,把他们配成n 对男双选手有(2)!2!n n n 种配对方式。
女选手类似。
把n 个男选手和n 个女选手配成n 对混双有n!种配对方式。
因此,配对方式总数是n n n nn n n n n n C C 2322232)!()!3(!2!=⎪⎭⎫ ⎝⎛.二、 解答题(第9题20分,第10━12题每题22分,共86分)9. 证明:对任意)1,0(∈a ,由均值不等式有 .414214=⨯≥+aa aa ----------------------------------(5分)因此,a a a aa a a a a -=+-≥++-=+2441441222.------------(15分)同理,对于任意)1,0(∈b ,.212b bb -≥+因此,3221122=-+-≥+++b a bb a a .---------------------(20分)10. 设H CE BF G BD AE == ,,则四面体BEGH 是ABCE 与BDEF 的公共部分.-----------------------------------------------------(5分) 易计算得:G 到直线AB 的距离ba abd +=1,---------------------------------(10分) G 到平面BCFE 的距离ad d 2312=, ------------------------------------------(15分) H 到直线BC 的距离c b bc d +=3,23d b S BEH -=∆.----------------(20分) 因此,))((123332c b b a bd S V BEH BEGH ++==∆.---------------------(22分)11. 不妨设ABCD 是凸四边形,其面积为S .记DA d CD c BC b AB a ====,,,。
由Dcd d c B ab b a AC D cd B ab S cos 2cos 2,sin 21sin 2122222-+=-+=+=, 可得Dcd B ab d c b a D cd B ab S cos cos 2/)(,sin sin 22222-=--++=,--------------(8分)两遍平方和得.))()()((41)(41)()(41)cos(2)()(422222222222222d c b a c d b a b d c a a d c b d c b a cd ab d c b a D B abcd cd ab S -++-++-++-++=--+-+≤--+-+-+= 等号成立当且仅当π=+D B ,即D C B A ,,,四点共圆--------------------(16分)现根据假设d c b a ,,,为四个连续整数).1(3,2,1,≥+++n n n n n 由此)3)(2)(1(+++=n n n n S . 显然 .13322++<<+n n S n n 因此,S 不是整数。
----------------------------------------------------(22分)12. 证明:设S 是所有试题的集合,i S 是第i 位学生解出的试题的集合,i i S S T \=.题目即证存在j i ≠使得5≥j i S S .--------------------------------(5分)不妨设i T S i i ∀==,,4 6.S 共有120310=C 个三元子集,每个i T 恰包含4个三元子集.因此,存在j i ≠使得j i T T ,包含相同的三元子集,3≥j i T T .---(15分)从而,52≥+=-+=j i j i j i j i T T S S S S S S .-----------------(22分)。
