高二数学竞赛培训 第九讲 立体几何体
高中数学竞赛专题讲义之立体几何(传统方法和向量方法)
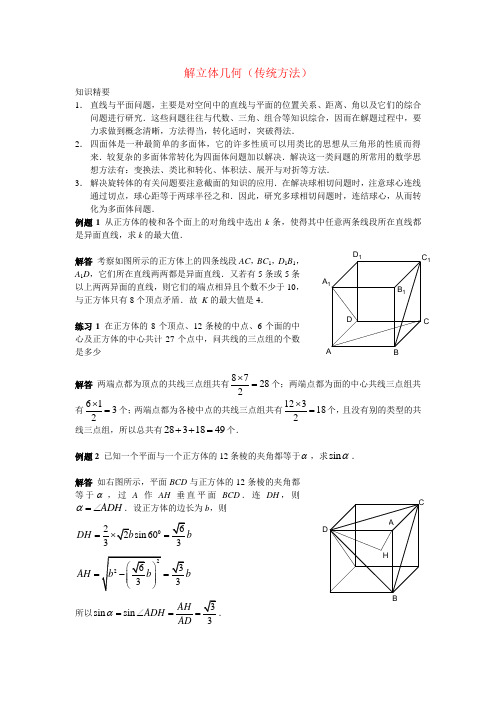
解立体几何(传统方法)知识精要1.直线与平面问题,主要是对空间中的直线与平面的位置关系、距离、角以及它们的综合问题进行研究.这些问题往往与代数、三角、组合等知识综合,因而在解题过程中,要力求做到概念清晰,方法得当,转化适时,突破得法.2.四面体是一种最简单的多面体,它的许多性质可以用类比的思想从三角形的性质而得来.较复杂的多面体常转化为四面体问题加以解决.解决这一类问题的所常用的数学思想方法有:变换法、类比和转化、体积法、展开与对折等方法.3.解决旋转体的有关问题要注意截面的知识的应用.在解决球相切问题时,注意球心连线通过切点,球心距等于两球半径之和.因此,研究多球相切问题时,连结球心,从而转化为多面体问题.例题1 从正方体的棱和各个面上的对角线中选出k条,使得其中任意两条线段所在直线都是异面直线,求k的最大值.解答考察如图所示的正方体上的四条线段AC,BC1,D1B1,A1D,它们所在直线两两都是异面直线.又若有5条或5条以上两两异面的直线,则它们的端点相异且个数不少于10,与正方体只有8个顶点矛盾.故K的最大值是4.练习1 在正方体的8个顶点、12条棱的中点、6个面的中心及正方体的中心共计27个点中,问共线的三点组的个数是多少解答两端点都为顶点的共线三点组共有87282⨯=个;两端点都为面的中心共线三点组共有6132⨯=个;两端点都为各棱中点的共线三点组共有123182⨯=个,且没有别的类型的共线三点组,所以总共有2831849++=个.例题2 已知一个平面与一个正方体的12条棱的夹角都等于α,求sinα.解答如右图所示,平面BCD与正方体的12条棱的夹角都等于α,过A作AH垂直平面BCD.连DH,则ADHα=∠.设正方体的边长为b,则2sin603DH==3AH==所以sin sin3AHADHADα=∠==.练习2 如图所示,正四面体ABCD 中,E 在棱AB 上,F 在棱CD 上,使得(0)AE CFEB FDλλ==<<+∞,记()f λλλαβ=+,其中λα表示E F 与AC 所成的角,λβ表示E F 与BD 所成的角,证明()0f λ'=,即()f λ为常数. 解答 因ABCD 是正四面体,故AC 垂直BD ,作EG 平行AC 交BC 于G ,连G F ,则GEF λα=∠,且CG AE CFGB FD FD==,所以G F 平行BD .所以G F 垂直EG ,且EFG λβ=∠.所以()f λ为常数.例题3 三棱锥P -ABC 中,若棱P A =x ,其余棱长均为1,探讨x 是否有最值.解答当P -ABC 为三棱锥时,x 的最小极限是P 、A 重合,取值为0,若PBC ∆绕BC 顺时针旋转,P A 变大,最大极限是P 、A 、B 、C 共面时,P A 为菱形ABPC 的对角线,.所以无最值.练习3若正三棱锥底面棱长棱长均为1,探讨其侧棱否有最值.解答 若P 在底面的射影为O ,易知PO 越小,侧棱越小.故P 、O 重合时,侧棱取最小极限值3,PO 无穷大时,侧棱也无穷大.所以无最值. 例题4在单位正方体ABCD -A 1B 1C 1D 1的面对角线A 1B 上存在一点P 使得AP +D 1P 最短,求AP +D 1P 的最小值.解答 将等腰直角三角形AA 1B 沿A 1B 折起至1A A B ',使三角形1A A B '与四边形A 1BCD 1共面,联结1A D ',则1A D '的长即为AP +D 1P 的最小值,所以,1A D '==练习4已知单位正方体ABCD -A 1B 1C 1D 1的对棱BB 1、D 1上有两个动点E 、F ,BE =D 1F=λ(102λ<≤).设E F 与AB 所成的角为α,与BC 所成的角为β,求αβ+的最小值. 解答 当12λ=时,2παβ+=.不难证明()f αβλ+=是单调减函数.因此αβ+的最小值为2π.例题5 在正n 棱锥中,求相邻两侧面所成的二面角的取值范围.解答 当顶点落在底面的时候,相邻两侧面所成的二面角为π.当顶点在无穷远处的时候,正n 棱锥变为正n 棱柱,这时相邻两侧面所成的二面角为(2)n nπ-.练习5 已知直平行六面体ABCD -A 1B 1C 1D 1的各条棱长均为3,角BAD =600,长为2的线段MN 的一个端点M 在DD 1上运动,另一端点N 在底面ABCD 上运动,求MN 的中点P 的轨迹(曲面)与共一顶点D 的三个面所围成的几何体的体积.解答 联结DP 、DN ,在三角形MDN 为直角三角形,且DP =MN /2=1,又由已知角BAD =600,角ADC =1200,所以点P 的轨迹以点D 为球心,半径为1的1/6球面,所以其与顶点D 以及三个面围成的几何体的体积为31421639ππ⨯⨯=.立体几何(向量方法)知识精要4. 证明两条直线平行,只需证明这两条直线上的向量共线(即成倍数关系).证明两条直线平行,只需证明这两条直线上的向量的数量积等于零.5. 通过法向量,把线面、面面的角转化为线线的角.从而可以利用公式cos ||||θαβαβ=求解.6. 建立空间直角坐标系.例题1如图,在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =12PA ,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC .(Ⅰ)求证OD ∥平面PAB ;(Ⅱ) 求直线OD 与平面PBC 所成角的大小. 解答OP ABC OA OC AB BC ⊥== 平面,,,.OA OB OA OP OB OP ∴⊥⊥⊥ ,,()O OP z O xyz -以为原点,射线为非负轴,建立空间直角坐标系如图,,0,0,,0,,0,0AB a A B C ⎫⎛⎫⎛⎫=⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭设,则 ()0,0,.OP h P h =设,则 ()D PC 为的中点,Ⅰ212,0,,,0,422OD a h PA a h ⎛⎫⎛⎫∴=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭又,1...2OD PA OD PA OD PAB ∴=-∴∴ 平面∥∥()2,PA a =Ⅱ,h ∴=,OD ⎛⎫∴=- ⎪ ⎪⎝⎭,PBC n ⎛=- ⎝可求得平面的法向量210cos ,OD n OD n OD n ⋅∴〈〉==⋅ OD PBC θ设与平面所成的角为,210sin cos ,OD n θ=〈〉=则 OD PBC ∴ 与平面所成的角为. 练习1如图,已知长方体1111ABCD A B C D -,12,1AB AA ==,直线BD 与平面11AA B B 所成的角为030,AE 垂直BD 于,E F 为11A B 的中点. (Ⅰ)求异面直线AE 与BF 所成的角;(Ⅱ)求平面BDF 与平面1AA B 所成二面角(锐角)的大小; (Ⅲ)求点A 到平面BDF 的距离解答 在长方体1111ABCD A B C D -中,以AB 所在直线为x 轴,AD 所在直线为y 轴,1AA 所在直线为z 轴建立空间直 角坐标系如图.由已知12,1AB AA ==,可得(0,0,0),(2,0,0),(1,0,1)A B F .又AD ⊥平面11AAB B ,从面BD 与平面11AA B B 所成的角即为030DBA ∠=又2,,1,3ABAE BD AE AD =⊥==从而易得1(2E D (Ⅰ)13(,,0),(1,0,1)2AE BF ==-cos ,AE BF AEBF AE BF∴<>=14-==即异面直线AE 、BF 所成的角为4(Ⅱ)易知平面1AA B 的一个法向量(0,1,0)m =(,,)n x y z =是平面BDF 的一个法向1量.(BD =-由n BF n BD ⎧⊥⎪⎨⊥⎪⎩n BF n BD ⎧=⎪⇒⎨=⎪⎩203x x x y -+=⎧⎪⇒⎨-=⎪⎩x zy=⎧⎪⇒=取(1,3,1)n =∴3cos ,15m n m n m n <>===⨯即平面BDF 与平面1AA B 所成二面角(锐角)大小为(Ⅲ)点A 到平面BDF 的距离,即AB 在平面BDF 的法向量n 上的投影的绝对值所以距离||cos ,d AB AB n =<>||||||AB n AB ABn =||||55AB n n ===所以点A 到平面BDF 5例题2 如图1,已知ABCD 是上.下底边长分别为2和6,高为3的等腰梯形,将它沿对称轴OO 1折成直二面角,如图2(Ⅰ)证明:AC ⊥BO 1;(Ⅱ)求二面角O -AC -O 1的大小.解答(I )证明 由题设知OA ⊥OO 1,OB ⊥OO 1.所以∠AOB 是所折成的直二面角的平面角, 即OA ⊥OB . 故可以O 为原点,OA 、OB 、OO 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图3,则相关各点的坐标是A (3,0,0),B (0,3,0),C (0,1,3)O 1(0,0,3).从而.0333),3,3,0(),3,1,3(11=⋅+-=⋅-=-=BO BO 所以AC ⊥BO 1.(II )解:因为,03331=⋅+-=⋅OC BO 所以BO 1⊥OC ,由(I )AC ⊥BO 1,所以BO 1⊥平面OAC ,1BO 是平面OAC 的一个法向量.设),,(z y x =是0平面O 1AC 的一个法向图1量,由,3.0,033001=⎩⎨⎧==++-⇒⎪⎩⎪⎨⎧=⋅=⋅z y z y x C O n 取得)3,0,1(=n . 设二面角O —AC —O 1的大小为θ,由、1BO 的方向可知=<θ,1BO >,所以COS <=cos θ,1BO .43||||1=⋅BO n 即二面角O —AC —O 1的大小是.43arccos练习2 如图, 在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== ,点D 为AB 的中点(Ⅰ)求证1AC BC ⊥; (Ⅱ) 求证11AC CDB 平面;(Ⅲ)求异面直线1AC 与1B C 所成角的余弦值解答∵直三棱锥111ABC A B C -底面三边长3,4,5A C B C A B ===,1,,AC BC CC 两两垂直如图建立坐标系,则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0),B 1(0,4,4),D (32,2,0) (Ⅰ)11(3,0,0),(0,4,4)AC BC =-=,11110,AC BC AC BC ∴⋅=∴⊥(Ⅱ)设1CB 与1C B 的交点为E ,则E (0,2,2)13(,0,2),(3,0,4)2DE AC =-=-111,//2DE AC DE AC ∴=∴111,,DE CDB AC CDB ⊂⊄平面平面1//AC CDB ∴平面(Ⅲ)11(3,0,4),(0,4,4),AC CB =-=1111112cos ,5||||AC CBAC CB AC CB ∴<>==∴异面直线1AC 与1B C 5例题3 在ΔABC 中,已知66cos ,364==B AB ,AC 边上的中线BD =5,求SINA .1A解答 以B 为坐标原点,为x 轴正向建立直角坐标指法,且不妨设点A 位于第一象限由630sin =B,则44(cos ,sin )()3BA B B ==,设=(x ,0),则43(,6x BD +=,由条件得5)352()634(||22=++=x BD ,从而x=2,314-=x (舍去),故2(,33CA =-.于是 141439809498091698098||||cos =+⋅++-=⋅=CA BA A ∴1470cos 1sin 2=-=A A 练习3 在平面上给定ABC ∆,对于平面上的一点P ,建立如下的变换 :f AP 的中点为Q ,BQ 的中点为R ,CR 的中点为'P ,'()f P P =,求证 f 只有一个不动点(指P 与'P 重合的点).解答:依提意,有12AQ AP =,且111()224AR AB AQ AB AP =+=+,'1111()2248AP AC AR AC AB AP =+=+++,要使'P 与P 重合,应111248AP AC AB AP =++,得1(42)7AP AC AB =+,对于给定的ABC ∆,满足条件的不动点P 只有一个.例题4 如图,在四棱锥P —ABCD 中,底面ABCD 为矩形,PD ⊥底面ABCD ,E 是AB 上一点,PE ⊥EC . 已知,21,2,2===AE CD PD 求 (Ⅰ)异面直线PD 与EC 的距离; (Ⅱ)二面角E —PC —D 的大小.解答 (Ⅰ)以D 为原点,DA 、、DP 分别为x 、y 、z 轴建立空间直角坐标系.由已知可得D (0,0,0),P (0,0,)2, C (0,2,0)设),0,2,(),0)(0,0,(x B x x A 则>).0,23,(),2,21,(),0,21,(-=-=x x x E由0=⋅⊥CE PE 得,即.23,0432==-x x 故 由CE DE CE DE ⊥=-⋅=⋅得0)0,23,23()0,21,23(, 又PD ⊥DE ,故DE 是异面直线PD 与CE 的公垂线,易得1||=,故异面直线PD 、CE 的距离为1.(Ⅱ)作DG ⊥PC ,可设G (0,Y ,Z ).由0=⋅得0)2,2,0(),,0(=-⋅z y ,即),2,1,0(,2==y z 故可取作EF ⊥PC 于F ,设F (0,M ,N ),则 ).,21,23(n m EF --= 由0212,0)2,2,0(),21,23(0=--=-⋅--=⋅n m n m PC EF 即得, 又由F 在PC 上得).22,21,23(,22,1,222-===+-=n m m n 故 因,,PC DG PC EF ⊥⊥故平面E —PC —D 的平面角θ的大小为向量与的夹角. 故,4,22||||cos πθθ===EF DG 即二面角E —PC —D 的大小为.4π练习4如图,在三棱柱ABC —A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,EA ⊥EB 1,已知AB =2,BB 1=2,BC =1,∠BCC 1=3π,求: (Ⅰ)异面直线AB 与EB 1的距离;(Ⅱ)二面角A —EB 1—A 1的平面角的正切值.解答(I )以B 为原点,1BB 、BA 分别为Y 、Z 轴建立空间直角坐标系. 由于BC =1,BB 1=2,AB =2,∠BCC 1=3π,在三棱柱ABC —A 1B 1C 1中有B (0,0,0),A (0,0,2),B 1(0,2,0),11)0,23,23(),0,21,23(1C C - 设即得由,0,),0,,23(11=⋅⊥EB EA EB EA a E )0,2,23()2,,23(0a a --⋅--=,432)2(432+-=-+=a a a a .,04343)02323()0,21,23()0,21,23(),(2321,0)23)(21(11EB BE EB BE E a a a a ⊥=+-=⋅⋅-⋅=⋅===--即故舍去或即得又AB ⊥面BCC 1B 1,故AB ⊥BE . 因此BE 是异面直线AB 、EB 1的公垂线, 则14143||=+=BE ,故异面直线AB 、EB 1的距离为1. (II )由已知有,,1111EB A B EB ⊥⊥故二面角A —EB 1—A 1的平面角θ的大小为向量A B 与11的夹角..22tan ,32||||cos ),2,21,23(),2,0,0(111111===--===θθ即故因A B EA A B。
高中数学竞赛辅导课件:立体几何

1
竞赛辅导─立体几何
关于求距离、求角、求面积与体积,以及位 置关系的判定等问题,需要用到的知识点见教程 介绍.
今天我们主要是通过一些例题来体会处理这 些问题的基本思想方法:
一、学会转化;二、掌握基本功法.(如坐标 法、作出图形求解法)
2
一、点、线、面间关系的转化
立体几何的知识告诉我们,最核心的内 容是线面间的的垂直、平行关系,而它们又 通过判定定理、性质定理而相互转化。定理 的应用过程实质上就是下述诸关系的联系与 转化。
=MC2 = ,从而∠
M3 Aa2C,=在6∆00A,MC即中二,面由角余α—弦定
BD1—β 的度数为600。
思考一. 如图,设正三棱锥 S—ABC 的底面边长 为 a,侧棱长为 2a,过 A 作与侧棱 SB、SC 都相 交的截面 AEF,求这个截面周长的最小值. 分析:沿侧棱 SA 将三棱锥的侧面 展开如图,求 AEF 周长最小值 问题就转化成了求 A、A'两点间 的最短距离.
面BDE的距离就是AC到BD的 距离.
这时,AC上任一点到面BDE的距离
就是所求.
由DC⊥α知,DC⊥AC;又AD⊥ AB,根据三垂线定理 , AC⊥ AB.但AB∥AC,故AC ⊥ CE.从而AC ⊥ 面CDE 。又 BE∥AC ,得BE ⊥ 面CDE, 进而面BDE⊥面CDE,
在Rt∆CDE上作高CH,由Rt∆ACD中, ∠ CAD = 300为二
1、 截面法 2、隔离法 3、展平法 4、投影法
例2、 在正方体ABCD—A1B1C1D1中,设∆C1 D1 B
所在的半平面为α ,∆C D1 B所在的半平面为 β,BD1
所在的直线是 α与 β 的交线。求二面角
分析的度数因为二面角的平面角的度数是 D1
数学竞赛教案讲义立体几何

数学竞赛教案讲义-立体几何第一章:立体几何基础1.1 空间点、线、面的位置关系点、直线、平面的基本性质点与直线、直线与直线、直线与平面、平面与平面的位置关系1.2 立体几何的基本概念棱柱、棱锥、棱台、球的定义与性质底面、侧面、顶点的概念空间角、二面角的概念与计算第二章:空间几何图形2.1 棱柱直棱柱、斜棱柱的性质棱柱的面积、体积计算2.2 棱锥直棱锥、斜棱锥的性质棱锥的面积、体积计算2.3 棱台棱台的性质棱台的面积、体积计算2.4 球球的性质球的面积、体积计算第三章:立体几何中的线面关系3.1 直线与平面的关系直线与平面平行、直线在平面内的判定与性质直线与平面相交的性质3.2 直线与直线的关系平行线、相交线的性质异面直线、共面直线的性质3.3 平面与平面的关系平面与平面平行的判定与性质平面与平面相交的性质第四章:立体几何中的角与距离4.1 空间角线线角、线面角、面面角的定义与计算空间角的性质与计算方法4.2 距离点与点、点与直线、点与平面的距离计算直线与直线、直线与平面的距离计算第五章:立体几何的综合应用5.1 立体几何图形的放缩与旋转放缩与旋转的性质与方法放缩与旋转在立体几何中的应用5.2 立体几何中的定理与性质欧拉公式、施瓦茨公式等定理的应用立体几何中的重要性质与定理5.3 立体几何与解析几何的综合应用利用解析几何的知识解决立体几何问题立体几何与解析几何的相互转化第六章:立体几何中的立体角与对角线6.1 立体角立体角的定义与性质立体角的计算方法6.2 对角线多面体的对角线长度计算对角线与几何体的性质关系第七章:立体几何中的不等式与最值7.1 立体几何中的不等式利用立体几何图形性质证明不等式利用不等式解决立体几何问题7.2 立体几何中的最值问题利用几何方法求解最值问题利用代数方法求解最值问题第八章:立体几何中的视图与投影8.1 视图正视图、侧视图、俯视图的定义与性质利用视图研究几何体的性质8.2 投影平行投影、中心投影的性质利用投影解决立体几何问题第九章:立体几何中的定理与性质(续)9.1 立体几何中的定理与性质布雷特施奈德定理、莫恩定理等定理的应用立体几何中的其他重要性质与定理9.2 立体几何中的特殊几何体圆柱、圆锥、球台的性质与应用利用特殊几何体解决立体几何问题第十章:立体几何与实际应用10.1 立体几何在实际应用中的案例分析利用立体几何解决工程、物理、艺术等领域的问题立体几何在现实生活中的应用举例10.2 立体几何竞赛题解析分析历年数学竞赛中的立体几何题目讲解解题思路与方法,提高解题能力10.3 立体几何练习题与答案解析提供立体几何练习题,巩固所学知识分析练习题答案,讲解解题过程与思路第十一章:立体几何中的坐标计算11.1 空间点的坐标空间直角坐标系的建立点的坐标表示与运算11.2 空间向量向量的定义与运算向量与立体几何的关系11.3 空间几何体的坐标表示棱柱、棱锥、棱台、球的坐标表示利用坐标解决立体几何问题第十二章:立体几何中的向量计算12.1 向量的线性运算向量的加法、减法、数乘运算向量共线与垂直的判定与性质12.2 向量的数量积与向量积向量的数量积定义与性质向量的向量积定义与性质12.3 空间向量在立体几何中的应用利用向量计算空间角与距离利用向量解决立体几何中的线面关系问题第十三章:立体几何中的解析几何方法13.1 解析几何与立体几何的关系利用解析几何方法解决立体几何问题解析几何在立体几何中的应用举例13.2 参数方程与极坐标方程立体几何图形的参数方程表示利用参数方程与极坐标方程解决立体几何问题第十四章:立体几何中的不等式与最值(续)14.1 立体几何中的不等式问题利用不等式性质解决立体几何问题不等式在立体几何中的应用举例14.2 立体几何中的最值问题(续)利用几何方法求解最值问题利用代数方法求解最值问题第十五章:立体几何的综合与应用15.1 立体几何与其他数学学科的综合立体几何与代数、分析、概率等学科的关系立体几何在交叉学科中的应用15.2 立体几何在实际应用中的案例分析(续)立体几何在工程、物理、艺术等领域中的应用案例立体几何在其他领域中的应用举例15.3 立体几何竞赛题解析与练习题答案解析(续)分析历年数学竞赛中的立体几何题目讲解解题思路与方法,提高解题能力提供立体几何练习题,巩固所学知识分析练习题答案,讲解解题过程与思路重点和难点解析重点:理解并掌握立体几何的基本概念、立体几何图形、空间几何图形、立体几何中的线面关系、立体几何中的角与距离、立体几何中的立体角与对角线、立体几何中的不等式与最值、立体几何中的视图与投影、立体几何中的定理与性质、立体几何中的坐标计算、立体几何中的向量计算、立体几何中的解析几何方法、立体几何中的不等式与最值(续)、立体几何的综合与应用。
2021-2022年高中数学竞赛辅导资料《立体图形,空间向量》

2021-2022年高中数学竞赛辅导资料《立体图形,空间向量》一. 直线,平面之间的平行与垂直的证明方法1.运用定义证明(有时要用反证法); 2.运用平行关系证明;3.运用垂直关系证明; 4.建立空间直角坐标系,运用空间向量证明.例如,在证明:直线直线时.可以这样考虑(1)运用定义证明直线与所成的角为; (2)运用三垂线定理或其逆定理; (3)运用“若平面,,则”; (4)运用“若且,则”; (5)建立空间直角坐标系,证明. 二. 空间中的角和距离的计算 1.求异面直线所成的角(1)(平移法)过P 作,,则与的夹角就是与的夹角; (2)证明(或),则与的夹角为(或);(3)求与所成的角(),再化为异面直线与所成的角(). 2,求直线与平面所成的角(1) (定义法)若直线在平面内的射影是直线,则与的夹角就是与的夹角; (2) 证明(或),则与的夹角为(或);(3) 求与的法向量所成的角,则与所成的角为或. 3.求二面角(1) (直接计算)在二面角的半平面内任取一点,过P 作AB 的垂线,交AB 于C,再过P 作的垂线,垂足为D,连结CD,则,故为所求的二面角. (2) (面积射影定理)设二面角的大小为(),平面内一个平面图形F 的面积为,F 在内的射影图形的面积为,则.(当为钝角时取“”).(3) (异面直线上两点的距离公式):22222cos EF d m n mn θ=++-,其中是二面角 的平面角,EA 在半平面内且于点A,BF 在半平面内且FB AB 于B,而,,.(4) (三面角的余弦定理),三面角中,,,,又二面角,则cos cos cos cos sin sin αβγθβγ-=.(5)(法向量法)平面的法向量与平面的法向量所成的角为,则所求的二面角为 (同类)或(异类). 4.求两点A,B 间距离(1)构造三角形进行计算; (2),导面直线上两点间的距离公式; (3),求. 5.求点到直线的距离(1)构造三角形进行计算; (2)转化为求两平行红色之间的距离. 6.求点到平面的距离(1)直接计算从点到平面所引垂线段的长度; (2)转化为求平行线面间的距离或平行平面间的距离; (3) (体积法)转化为求一个棱锥的高,其中V 为棱锥体积,S 为底面面积,为底面上的高.(4)在平面上取一点A,求与平面的法向量的夹角的余弦,则点P 到平面 的距离为.7.求异面直线的距离(1)(定义法)求异面直线公垂线段的长; (2)(体积法)转化为求几何体的高; (3)(转化法)转化为求平行线面间的距离或平行平面间的距离;(4)(最值法)构造异面直线上两点间距离的函数,然后求函数的最小值;(5)(射影法)如果两异面直线在同一平面内的射影分别是一个点P 和一条直线, 则与的距离等于P 到的距离; (6)(公式法)22222cos d EF m n mn θ=--±.8.求平行的线线,线面,面面之间的距离的方法,通常是转化为求点与线或点与面之间的距离. 三.多面体与旋转体 1.柱体(棱柱和圆柱)(1)侧面积(为直截面周长,为侧棱或母线长)(2)体积(为底面积,为高) 2.锥体(棱锥与圆锥)(1)正棱锥的侧面积(为底面周长,为斜高)(2)圆锥的侧面积: (为底面周长,为母线长)(3)锥体的体积:(为底面面积,为高). 3.锥体的平行于底面的截面性质:. 4.球的表面积:; 球的体积:. 四.解题思想与方法导引1.空间想象能力;2.数形结合能力;3.平几与立几间的相互转化;4.向量法例题讲解1.正四面体的内切球和外接球的半径之比为( )A,1:2 B,1:3 C,1:4 D,1:92.由曲线,,,围成的图形绕轴旋转一周所得的几何体的体积为;满足,,的点组成的图形绕 轴旋转一周所得的几何体的体积为,则( )A, B, C, D,3.如右图,底面半径,被过A,D 两点的倾斜平面所截,截面是离心 率为的椭圆,若圆柱母线截后最短处,则截面以下部分的 几何体体积是( )AB A BC A 1B 1C 1ABCD M K N S A, B, C, D,4.在四面体ABCD 中,设,,直线AB 与CD 的距离为2,夹角为,则四 面体ABCD 的体积等于( )A, B, C, D,5.三个圆柱侧面两两相切,且它们的轴也两两相互垂直,如果每个圆柱底面半径都是1, 那么,与这三个圆柱侧面都相切的最小球的半径是( ) A, B, C, D,6.四面体ABCD 的顶点为A,B,C,D,其6条棱的中点为,共10个 点,任取4个点,则这4个点不共面的概率是( )A, B, C, D,7.正方体的棱长为,则异面直线C 与BD 间的距离等于 .8.正四棱锥中,,二面角为且,(,为整数),则 .9.在正三棱锥中,,,过A 作平面分别交平面PBC 于DE.当截面的周长最小时, ,P 到截面ADE 的距离为 .10.空间四个球,它们的半径分别是2,2,3,3.每个球都与其他三个球外切.另一个小球与这 四个球都相切,则这个小球的半径等于 .11.三个的正方形都被连接两条邻边的中点的直线分成A,B 两片,如图,把这六片粘在一个正六边形的外面,然后折成多面体,则这个 多面体的体积为 .12.直三棱柱中,平面平面,且=,则AC 与平面所成的角的取值范围是 .13.如图,直三棱柱中,,连接,, ,若,求证:14.如图,设是一个高为3,底面边长为2的正四棱锥,K 是棱SC 的中点,过AK 作平面与线段SB,SD 分别交于M,N (M,N 可以是线段的端点).试求四棱锥的体积V 的最大值与最小值.AB DEF CDF15.有一个的长方体盒子,另有一个的长方体盒子,其中均为正整数(),并且前者的体积是后者一半,求的最大值.课后练习1.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四 面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一 个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为,则以四个氢原子为顶点 的这个正四面体的体积为( )A, B, C, D,2.夹在两个平行平面之间的球,圆柱,圆锥在这两个平面上的射影都是圆,则它们的体积之 比为( )A,3:2:1 B,2:3:1 C,3:6:2 D,6:8:3 3.设二面角的大小是,P 是二面角内的一点,P 点到的距离分别为1cm, 2cm,则点P 到棱的距离是( )A, B, C, D,4.如图,E,F 分别是正三棱锥ABCD 的棱AB,BC 的中点,且DEEF.若BC=,则此正三棱锥的体积是( ) A, B, C, D,5.棱长为的正八面体的外接球的体积是( )A, B, C, D,6.若线段AB 的两端点到平面的距离都等于2,则线段AB 所在的直线和平面的位置关系是 .7.若异面直线所原角为,AB 是公垂线,E,F 分别是异面直线上到A,B 距离为 2和平共处的两点,当时,线段AB 的长为 . 8.如图(1),在直四棱柱中,当底面四边形满足条件时,有C(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)9.如图(2),是一个正方体的展开图,在原正方体中,有下列命题: ①AB 与EF 所连直线平行; ②AB 与CD 所在直线异面; ③MN 与BF 所在直线成; ④MN 与CD 所在直线互相垂直. 其中正确命题的序号为 .(将所有正确的都写出)A BCDA BC D图(1)A BENM 图(2)AB C D E OA A BCD PQ10.如图,在中,AB=AC=13,BC=10,DE//BC 分别交AB,AC 于D,E.将沿 DE 折起来使得A 到,且为的二面角,求到直线BC 的最小距离.11.如图,已知矩形ABCD 中,AB=1,BC=,PA 平面ABCD,且PA=1. (1)问BC 边上是否存在点Q 使得PQQD?并说明理由;(2)若边上有且只有一个点Q,使得PQQD,求这时二面角Q 的正切.课后习题答案1.过顶点A,V 与高作一截面交BC 于点M,点O 为正四面体的中心,为底面ABC 的中心, 设正四面体VABC 的棱长为,则AM==VM,=,,13VO m ==,得113OO VO VO m a =-=- 在中,,即222()()33a m a m =-+,得. 则,有203111(sin 60)3227V ABC V m VO -=⋅⋅⋅⋅=.选B. 温馨提示:正四面体外接球的半径:内切球的半径=. 2. 32212341::():(2):(2)2:3:133V V V R R R R R πππ=⋅⋅⋅=,选B. 3.设PA 棱于点A,PM 平面于点M,PN 平面于点N,PA=,,则,得,有或(舍去),所以,选B.4.由DEEF,EF//AC,有DEAC,又ACBD,DEBD=D,得AC 平面ABD. 由对称性得090BAC CAD BAD ∠=∠=∠=,于是.311()3222224B ACD V a a a -=⋅⋅⋅⋅=,选B.5.可由两个相同的四棱锥底面重合而成,有,得,外接球的体积,选D.6.当时,AB//;当时,AB//或AB;当时,AB//或与斜交. 7.由,得22222cos EFEA AB BF EA BF θ=+++⋅⋅(1)当时,有219412212AB =+++⋅⋅⋅,得; (2)当时,有219412212AB =++-⋅⋅⋅,得.8. ACBD.(或ABCD 是正方形或菱形等)9.将展开的平面图形还原为正方体,可得只②,④正确. 10.解:设的高AO 交DE 于点,令, 由AO=,有,在中,,有222011111112cos 60A O A O O O A O O O =+-⋅⋅⋅得.当时,到直线BC 的最小距离为6.11.解:(1)(如图)以A 为原点建立空间直角坐标系,设,则 Q,P(0,0,1),D 得,由,有,得 ①若方程①有解,必为正数解,且小于.由,,得. (i)当时,BC 上存在点Q,使PQQD; (ii)当时, BC 上不存在点Q,使PQQD.(2)要使BC 边上有且只有一个点Q,使PQQD,则方程①有两个相等的实根, 这时,,得,有.又平面APD 的法向量,设平面PQD 的法向量为 而,(0,2,0)(0,0,1)(0,2,1)PD =-=-, 由,得,解得有,则121212cos ,n n n n n n ⋅<>===⋅,则所以二面角的正切为.例题答案:1,B 设棱长为,外接球的半径为R,内切球的半径为,则222))33R a a R -=-ACDE A ’ P解得,,有:R=1:3.2,C 设,则过A 的两个截面都是圆环,面积分别是和222222212(){(4)[2(2)]}(44)x x a a a πππ-=----=-,于是.3,B 在椭圆中,又,得,所求的体积22111(12)22V πππ=⋅⋅+⋅⋅= 4,B 过C 作,以为底面,BC 为侧棱作棱柱,则所求四面体的体积等于上述棱柱体积的,而的面积1sin 2S CE CD ECD =⨯⨯∠,AB 与CD 的公垂线MN 就是棱柱的高,于是21sin 2V MN CE CD ECD =⨯⨯⨯∠=,因此.5,A 三个圆柱的轴为三条两两垂直的异面直线,而异面直线的距离都为2,则所求球的半径为 .6,D 441064106631414727070C C C ---==. 7, 设E 是上的点,过E 作EH 于H,所以EH 面ABCD,过H 在面ABCD内作HF,连接EF,所以EFBD,令,,,所以EF=3==≥.8,5 因各侧面为全等的等腰三角形.在内作高AE,则CE 也是的高,故.设则,,=02458sin 4(1cos 45)42=-=-222cos 32AE CE AC AE CEθ+-==-+⋅得.9, ; 将三棱锥的侧棱PA 剪开,当的周长最小时,其展开图如图 的周长即是展开图中线段的长.易证 ∽,又PA=2AB=,故, ,.中,DE上的高8AH a ==.于是21264ADE S AH DE ∆=⨯⨯=; 从P 向底面作高PO.则PO==.于是23133412P ABC V a a -=⋅⋅=. 又,得33991616A PDE A PBC V V --===.设P 到截面的距离BC DE F O ABCA 1B 1C 1 S HH 1 为,则31364A PDE P ADE ADE V V d S --∆==⋅=,于是. 10, 设半径为3的球心为A,B,半径为2的球心为C,D.则易知AB=6,CD=4,AC=AD=BC=BD=5.设小球中心为O,半径为,则O 在四面体ABCD 内且AO=BO=3+,CO=DO=2+.取AB 中点E,连结 CE,DE,则CEAB,DEAB,故平面CDE 为线段AB 的垂直平分面,所以O 在平面CDE 内,又由OC=OD=2+知O 在CD 的垂直平 分面内,故O 在等腰底边CD 上的高EF 上(F 为CD 中点),易算出ED=EC=,得为等边三角形.于是EF=.而==.OE===,代入OE+OF=EF=2=解得.11,864 将几何体补成一个棱长为12的正方体,几何体的体积为正方体体积的一半,为. 12, 作AD 于D,易证AD 平面,所以.设, ,则sin AD θ==⋅,故.易证BC 平面,故,从而,即,于是,, 又,得.13,证明:设D,分别为AB,的中点.连结CD,及,.因为,所以 四边形为平行四边形,得//.因AC=BC,于是.又D, 分别为 AB,的中点,故CDAB,,而在平面ABC(或)内的射影为AB (或),得CD,,又已知,所以平面B,从而 ,又//,所以.又,得平面CD,从而得证.14,解:为了建立V 与原四棱锥的关系.我们先引用 下面的事实:(如图)设分别在三棱锥的侧棱SA,SB,SC 上, 又与的体积分别是和V,则.事实上,设C,在平面SAB 的射影分别是H,.则,又,所以111111111313SA B SAB C H SV SA SB SC V SA SB SC CH S ∆∆⋅⋅⋅⋅==⋅⋅⋅⋅.下面回到原题. 设,,因的体积为.于是由上面的事实有012S AMN S KMN S AMK S ANK S ABD S CBD S ABC S ADC V V V V VV V V V V --------=+=+.得2V SM SN SA SM SN SK SB SD SA SB SD SC ⋅⋅⋅⋅=+⋅⋅⋅⋅= SM SK SA SN SK SASB SC SA SD SC SA⋅⋅⋅⋅+⋅⋅⋅⋅=,于是,而由,,得.则,().又得'2213(32)1(31)(31)x x V x x -=-=--.所以 (1)当时,,V 为减函数,(2)当时,,V 为增函数.所以得,又,得.15,解:由题意,2(2)(2)(2)mnp m n p =+++,得. (1)当时,由,则32222(1)(1)(1)(1)28m n p +++≤+<,矛盾! (2)当时,,矛盾!(3)当时,则,即.所以的最大值为130; (4)当时,则,即.所以的最大值为54; (5)当时,222(1)2222(1)(1)(1)(1)55p m n +=>++++,得. 综上所述:的最大值为130.33529 82F9 苹36655 8F2F 輯28533 6F75 潵32190 7DBE 綾LGi 36570 8EDA 軚P26023 65A7 斧22005 55F5 嗵27640 6BF8 毸241535E59 幙{。
全国高中数学联赛竞赛大纲稿及全部定理内容

全国高中数学联赛竞赛大纲及全部定理内容一、平面几何1、数学竞赛大纲所确定的所有内容; 补充要求:面积和面积方法;2、几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理;3、几个重要的极值:到三角形三顶点距离之和最小的点--费马点;到三角形三顶点距离的平方和最小的点--重心;三角形内到三边距离之积最大的点--重心;4、几何不等式;5、简单的等周问题;了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大; 在周长一定的简单闭曲线的集合中,圆的面积最大;在面积一定的n边形的集合中,正n边形的周长最小; 在面积一定的简单闭曲线的集合中,圆的周长最小;6、几何中的运动:反射、平移、旋转;7、复数方法、向量方法; 平面凸集、凸包及应用;二、代数1、在一试大纲的基础上另外要求的内容:周期函数与周期,带绝对值的函数的图像;三倍角公式,三角形的一些简单的恒等式,三角不等式;2、第二数学归纳法;递归,一阶、二阶递归,特征方程法; 函数迭代,求n次迭代,简单的函数方程;3、n个变元的平均不等式,柯西不等式,排序不等式及应用;4、复数的指数形式,欧拉公式,棣美弗定理,单位根,单位根的应用;5、圆排列,有重复的排列与组合,简单的组合恒等式;6、一元n次方程多项式根的个数,根与系数的关系,实系数方程虚根成对定理;7、简单的初等数论问题,除初中大纲中所包括的内容外,还应包括无穷递降法,同余,欧几里得除法,非负最小完全剩余类,高斯函数,费马小定理,欧拉函数,孙子定理,格点及其性质;三、立体几何1、多面角,多面角的性质;三面角、直三面角的基本性质;2、正多面体,欧拉定理;3、体积证法;4、截面,会作截面、表面展开图;四、平面解析几何1、直线的法线式,直线的极坐标方程,直线束及其应用;2、二元一次不等式表示的区域;3、三角形的面积公式;4、圆锥曲线的切线和法线;5、圆的幂和根轴;五、其它抽屉原理; 容斤原理; 极端原理; 集合的划分; 覆盖;数学竞赛中涉及的重要定理1、第二数学归纳法:有一个与自然数n有关的命题,如果:1当n=1时,命题成立;2假设当n≤k时命题成立,由此可推得当n=k+1时,命题也成立;那么,命题对于一切自然数n来说都成立;2、棣美弗定理:设复数z=rcosθ+isinθ,其n次方z^n = r^n cosnθ+isinnθ,其中n为正整数;3、无穷递降法:证明方程无解的一种方法;其步骤为:假设方程有解,并设X为最小的解;从X推出一个更小的解Y;从而与X的最小性相矛盾;所以,方程无解;4、同余:两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余,记作a ≡ b mod m ,读作a同余于b模m,或读作a与b关于模m同余; 比如26 ≡ 14 mod 12定义设m是大于1的正整数,a,b是整数,如果m|a-b,则称a与b关于模m同余,记作a≡bmod m,读作a同余于b模m.;有如下事实:1若a≡0mod m,则m|a;2a≡bmod m等价于a与b分别用m去除,余数相同.5、欧几里得除法:即辗转相除法; 详见高中数学课标人教B版必修三6、完全剩余类:从模n的每个剩余类中各取一个数,得到一个由n个数组成的集合,叫做模n的一个完全剩余系;例如,一个数除以4的余数只能是0,1,2,3,{0,1,2,3}和{4,5,-2,11}是模4的完全剩余系;可以看出0和4,1和5,2和-2,3和11关于模4同余,这4组数分别属于4个剩余类;7、高斯函数:fx=ae-x-b^2/c^2 其中a、b与c为实数常数 ,且a > 0.8、费马小定理:假如p是质数,且a,p=1,那么 a^p-1 ≡1mod p 假如p是质数,且a,p互质,那么 a的p-1次方除以p的余数恒等;9、欧拉函数:φ函数的值:通式:φx=x1-1/p11-1/p21-1/p31-1/p4…..1-1/pn,其中p1, p2…pn为x的所有质因数,x是不为0的整数;φ1=1唯一和1互质的数就是1本身;若n是质数p的k次幂,φn=p^k-p^k-1=p-1p^k-1,因为除了p的倍数外,其他数都跟n互质;欧拉函数是积性函数——若m,n互质,φmn=φmφn;特殊性质:当n为奇数时,φ2n=φn, 证明于上述类似;10、孙子定理:此定理的一般形式是设m = m1 ,… ,mk 为两两互素的正整数,m=m1,…mk ,m=miMi,i=1,2,… ,k ;则同余式组x≡b1modm1,…,x≡bkmodmk的解为x≡M'1M1b1+…+M'kMkbk modm;式中M'iMi≡1 modmi,i=1,2,…,k ;11、裴蜀定理:对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性丢番图方程称为裴蜀等式:若a,b是整数,且a,b=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立;它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.11、梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F 三点共线,则FB AF EA CE DC BD ••=1 12、梅涅劳斯定理的逆定理: 如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F,且满足FB AF EA CE DC BD ••=1,则D 、E 、F 三点共线; 13、塞瓦定理:设O 是△ABC 内任意一点,AO 、BO 、CO 分别交对边于N 、P 、M,则1=••PA CP NC BN MB AM14、塞瓦定理的逆定理:设M 、N 、P 分别在△ABC 的边AB 、BC 、CA 上,且满足1=••PA CP NC BN MB AM ,则AN 、BP 、CM 相交于一点;15、广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和;推论2:设△ABC 三边长分别为a 、b 、c,对应边上中线长分别为m a 、m b 、m c则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+16、三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有AC AB DCBD = 外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D,则有AC AB DC BD = 17、托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD18、三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P19、正弦定理、在△ABC 中有R C c B b A a 2sin sin sin ===R 为△ABC 外接圆半径余弦定理:a 、b 、c 为△ABC 的边,则有:a 2=b 2+c 2-2bc ·cosA; b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;20、西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC,PE ⊥AC,PF ⊥AB,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线;21、欧拉定理:△ABC 的外接圆圆心为O,半径为R,内切圆圆心为I,半径为r,记OI=d,则有:d 2=R 2-2Rr.22、巴斯加线定理:圆内接六边形ABCDEF不论其六顶点排列次序如何,其三组对边AB与DE、BC与EF、CD与FA的交点P、Q、R共线;。
数学竞赛教案讲义立体几何

数学竞赛教案讲义-立体几何教案章节:一、立体几何基本概念1.1 空间点、线、面的基本定义及性质1.2 平面、直线、圆锥、球等基本几何体的性质和方程1.3 空间向量与立体几何的关系二、立体几何中的角度和距离2.1 点与点、点与线、点与面之间的距离公式2.2 线与线、线与面之间的角度和距离公式2.3 空间中的平行公理和推论三、立体几何中的体积和表面积3.1 棱柱、棱锥、圆柱、圆锥等几何体的体积计算公式3.2 棱柱、棱锥、圆柱、圆锥等几何体的表面积计算公式3.3 空间几何体的对称性和轴截面四、立体几何中的定理和性质4.1 线面垂直、线面平行、面面垂直、面面平行等定理及其应用4.2 三垂线定理、射影定理等的重要性质和应用4.3 空间几何中的等体积转换和等角转换五、立体几何在数学竞赛中的应用题型及解题策略5.1 立体几何与解析几何的综合题型5.2 立体几何中的构造题型5.3 立体几何中的极限与最值问题5.4 立体几何中的几何计数问题六、立体几何中的坐标系和变换6.1 空间直角坐标系的定义和性质6.2 坐标变换公式及应用6.3 利用坐标系解决立体几何问题七、立体几何中的视图和投影7.1 平行投影和中心投影的定义和性质7.2 三视图的画法和性质7.3 利用视图和投影解决立体几何问题八、立体几何中的定积分和面积计算8.1 立体几何中的定积分定义和性质8.2 利用定积分计算立体几何体的表面积和体积8.3 立体几何中的面积计算方法和技巧九、立体几何中的概率和组合问题9.1 立体几何中的几何概率定义和性质9.2 利用几何概率解决立体几何问题9.3 立体几何中的组合问题和解题策略十、立体几何在数学竞赛中的应用实例解析10.1 立体几何与解析几何的综合实例解析10.2 立体几何中的构造实例解析10.3 立体几何中的极限与最值问题实例解析10.4 立体几何中的几何计数问题实例解析重点和难点解析一、立体几何基本概念重点和难点解析:空间点、线、面的关系及性质是立体几何的基础,理解并熟练运用这些基本概念对于解决复杂立体几何问题至关重要。
立体几何基本概念

1基本概念数学上,立体几何(solid geometry)是3维欧氏空间的几何的传统名称。
立体几何一般作为平面几何的后续课程,暂时在人教版数学必修二中出现。
立体测绘(Stereometry)是处理不同形体的体积的测量问题。
如:圆柱,圆锥,圆台,球,棱柱,棱锥等等。
立体几何空间图形毕达哥拉斯学派就处理过球和正多面体,但是棱锥,棱柱,圆锥和圆柱在柏拉图学派着手处理之前人们所知甚少。
立体几何形戒指尤得塞斯(Eudoxus)建立了它们的测量法,证明锥是等底等高的柱体积的三分之一,可能也是第一个证明球体积和其半径的立方成正比的。
2基本课题课题内容包括:各种各样的几何立体图形(10张)- 面和线的重合- 二面角和立体角- 方块, 长方体, 平行六面体- 四面体和其他棱锥- 棱柱- 八面体, 十二面体, 二十面体- 圆锥,圆柱- 球- 其他二次曲面: 回转椭球, 椭球,抛物面,双曲面公理立体几何中有4个公理公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.公理2 过不在一条直线上的三点,有且只有一个平面.公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理4 平行于同一条直线的两条直线平行。
各种立体图形表面积和体积一览表注:初学者会认为立体几何很难,但只要打好基础,立体几何将会变得很容易。
学好立体几何最关键的就是建立起立体模型,把立体转换为平面,运用平面知识来解决问题,立体几何在高考中肯定会出现一道大题,所以学好立体是非常关键的。
三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和穿过这个平面的一条斜线垂直,那么它也和这条斜线在平面的射影垂直。
1,三垂线定理描述的是PO(斜线),AO(射影),a(直线)之间的垂直关系.2,a与PO可以相交,也可以异面.3,三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理.关于三垂线定理的应用,关键是找出平面(基准面)的垂线.至于射影则是由垂足,斜足来确定的,因而是第二位的.从三垂线定理的证明得到证明a⊥b的一个程序:一垂,二射,三证.即几何模型第一,找平面(基准面)及平面垂线第二,找射影线,这时a,b便成平面上的一条直线与一条斜线.第三,证明射影线与直线a垂直,从而得出a与b垂直.注:1.定理中四条线均针对同一平面而言2.应用定理关键是找"基准面"这个参照系用向量证明三垂线定理已知:PO,PA分别是平面a的垂线,斜线,OA是PA在a内的射影,b属于a,且b 垂直OA,求证:b垂直PA证明:因为PO垂直a,所以PO垂直b,又因为OA垂直b 向量PA=(向量PO+向量OA)所以向量PA乘以b=(向量PO+向量OA)乘以b=(向量PO 乘以b)加(向量OA 乘以b )=O,所以PA垂直b。
数学竞赛之立体几何专题精讲(例题+练习)

数学竞赛中的立体几何问题立体几何作为高中数学的重要组成部分之一,当然也是每年的全国联赛的必然考查内容.解法灵活而备受人们的青睐,竞赛数学当中的立几题往往会以中等难度试题的形式出现在一试中,考查的内容常会涉及角、距离、体积等计算.解决这些问题常会用到转化、分割与补形等重要的数学思想方法.一、求角度这类题常以多面体或旋转体为依托,考查立体几何中的异面直线所成角、直线与平面所成角或二面角的大小 解决这类题的关键是 ,根据已知条件准确地找出或作出要求的角.立体几何中的角包括异面直线所成的角、直线与平面所成的角、二面角三种.其中两条异面直线所成的角通过作两条异面直线的平行线找到表示异面直线所成角的相交直线所成的角,再构造一个包含该角的三角形,解三角形即可以完成;直线和平面所成的角则要首先找到直线在平面内的射影,一般来讲也可以通过解直角三角形的办法得到,其角度范围是[]0,90︒︒;二面角在求解的过程当中一般要先找到二面角的平面角,三种方法:①作棱的垂面和两个半平面相交;②过棱上任意一点分别于两个半平面内引棱的垂线;③根据三垂线定理或逆定理.另外还可以根据面积射影定理cos S S θ'=⋅得到.式中S '表示射影多边形的面积,S 表示原多边形的面积,θ即为所求二面角.例1 直线OA 和平面α斜交于一点O ,OB 是OA 在α内的射影,OC 是平面α内过O 点的任一直线,设,,.AOC AOB BOC αβγ∠=∠=∠=,求证:cos cos cos αβγ=⋅.分析:如图,设射线OA 任意一点A ,过A 作AB α⊥于点B ,又作BC OC ⊥于点C ,连接AC .有:cos ,cos ,cos ;OC OB OCOA OA OBαβγ=== 所以,cos cos cos αβγ=⋅.评注:①上述结论经常会结合以下课本例题一起使用.过平面内一个角的顶点作平面的一条斜线,如果斜线和角的两边所成的角相等,那么这条斜线在平面内的射影一定会落在这个角的角平分线上.利用全等三角形即可证明结论成立.②从上述等式的三项可以看出cos α值最小,于是可得结论:平面的一条斜线和平面内经过斜足的所有直线所成的角中,斜线与它的射影所成的角最小.例、(1997年全国联赛一试)如图,正四面体ABCD 中,E 在棱AB 上, F 在棱CD 上,使得:()0AE CFEB FDλλ==<<∞,记()f λλλαβ=+, αOC BAF EDCBAG其中λα表示EF 与AC 所成的角,其中λβ表示EF 与BD 所成的角,则: (A )()f λ在()0,+∞单调增加;(B )()f λ在()0,+∞单调减少; (C )()fλ在()0,1单调增加;在()1,+∞单调减少;(D )()f λ在()0,+∞为常数.` 分析:根据题意可首先找到与,λλαβ对应的角.作EG ∥AC ,交BC 于G ,连FG .显然 FG ∥BD ,∠GEF=λα,∠GFE=λβ.∵AC ⊥BD ,∴EG ⊥FG ∴90λλαβ+=︒例五、(1994年全国联赛一试)已知一个平面与一个正方体的12条棱的夹角都等于α,则sin α= .分析:正方体的12条棱可分为三组,一个平面与12条棱的夹角都 等于α只需该平面与正方体的过同一个顶点的三条棱所成的角都等于α即可.如图所示的平面A BD '就是合乎要求的平面,于是:sin 3α=二、求体积这类题常是求几何体的体积或要求解决与体积有关的问题 解决这类题的关键是 ,根据已知条件选择合适的面作为底面并求出这个底面上的高例十五、(2003年全国联赛一试)在四面体ABCD 中,设1,AB CD ==直线AB 与CD 的距离为2,夹角为3π,则四面体ABCD 的体积等于 ()()()(11 ; ; 23A B C D 分析:根据锥体的体积公式我们知道:1V=3S h ⋅⋅.从题目所给条件看,已知长度的两条线段分别位于两条异面直线上,而已知距离是两条异面直线之间的距离而非点线距.显然需要进行转化.作BE ∥CD,且BE=CD ,连接DE 、AE ,显然,三棱锥A —BCD 与三棱锥A —BDE 底面积和高都相等,故它们有相等的体积.于是有:111sin 362A BCD A BDE D ABE BDE V V V S h AB BE ABE h ---∆====⋅⋅∠⋅=例十六、(2002年全国联赛一试)由曲线224,4,4,4x y x y x x ==-==-围成的图形绕y 轴旋转一周所ODCBAD 'C 'B ' A 'EDCBA得旋转体的体积为V 1,满足()()22222216,24,24x y x y x y +≤+-≥++≥的点(),x y 组成的图形绕y 轴旋转一周所得旋转体的体积为V 2,则: (A )V 1=12V 2; (B )V 1=23V 2; (C )V 1=V 2; (D )V 1=2V 2; 分析:我国古代数学家祖暅在对于两个几何体体积的比较方面作出了卓越的贡献,祖暅原理告诉我们: 对于两个底面积相同,高 相等的几何体,任做一个 平行于底面的截面,若每 一个截面的面积相等,则这两个几何体的体积相等.运用祖 原理的思想我们可以将不规则的几何体的体积计算转化为规则几何体的体积计算.如计算球的体积时我们可以将半球转化为圆柱与圆锥的组合体.显然,本题中的两个几何体符合祖暅原理的条件,比较其截面面积如下:取()44y a a =-≤≤,则:()21162164S aa ππππ=-⋅⋅=-当0a <时:()()()22221642164S aa a ππππ=⋅--⋅-+=+ 当0a >时:()()()22221642164S a a a ππππ=⋅--⋅--=-显然,12S S =,于是有:12V V =.例十七、(2000年全国联赛一试)一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积是 .分析:由正四面体的图象的对称性可知,内切球的球心必为正四面体的中心,球与各棱相切,其切点必为各棱中点,考查三组对棱中点的连线交于一点,即为内切球的球心,所以每组对棱间的距离即为内切球的直径,于是有:222r a =∴3343424V a a π⎛⎫=⋅⋅= ⎪ ⎪⎝⎭练习:同样可用体积法求出棱长为a 的正四面体的外 接球和内切球的半径.分析可知,正四面体的内切球 与外接球球心相同,将球心与正四面体的个顶点相连,可将正四面体划分为四个全等的正三棱锥,于是可知内切球的半径即为正四面体高度的四分之一,外接球半径即为高度的四分之三.故只要求出正四面体的高度即可.又:3h a ===,所以,,412R a r ==.例十八、(1999年全国联赛一试)已知三棱锥S--ABC 的底面为正三角形,A 点在侧面SBC 上的射影H 是∆SBC 的垂心,二面角H-AB-C 的平面角等于30︒,SA=.那么,三棱锥S-ABC 的体积为 .分析:在求解立体几何问题时,往往需要首先明白所要 考查对象的图形特点.连接BH 并延长交SC 于D ,连AD . ∵H 为∆SBC 的垂心∴BD ⊥SC , 且 HD ⊥SC ,故 AD ⊥SC ,SC ⊥平面ABC ∴SC ⊥AB作SO ⊥平面ABC 于O ,连接CO 并延长交AB 于E ,易知:CE ⊥AB ,连DE . ∵AB=AC∴HB=HC ,即A 在平面SBC 内的射影H 在线段BC 的垂直平分线上,而点H 是∆SBC 的垂心,可知∆SBC 为SB=SC 的等腰三角形.∴S 在平面ABC 内的射影O 在线段BC 的垂直平分线上.故射影O 为∆ABC 的中心,三棱锥S —ABC 为正三棱锥.设底面边长为2a ,则,ROEDC APrOED HCAS B∵SA=SB=SC=23 ∴SO=3,OC=233=CE=233a ∴11139333333224S ABCABC V S h -∆==⨯⨯⨯⨯⨯=例十九、(1998年全国联赛一试)ABC ∆中,90,30,2C B AC ∠=︒∠=︒=,M 是AB 的中点.将ACM ∆沿CM 折起,使A 、B 两点间的距离为22A —BCM 的体积等于 .分析:关于折叠问题,弄清折叠前后线段之间的变与不变的关系往往是我们解决问题的关键,问题中经常会涉及折叠图形形成二面角,在折叠前作一条直线与折叠线垂直相交,于交点的两侧各取一点形成一个角,于是在折叠过程中,此角始终能代表图形折叠所形成的二面角的大小.此外,通过分析可知解决本例的另一个关键是需要得到棱锥的高,其实只要能找到二面角,高也就能迎刃而解了.如图,作BD⊥CM的延长线相交于D,AF⊥CM于F,并延长到E,使EF=BD,连BE.显然,AF=EF=BD= EB=DF=2,所以:A E2=AB2-EB2=8-4=4三棱锥A—BCM的高即点A到平面BCM的距离也就是等腰∆AEF中点A到边EF的距离.根据面积相等可求得:3h==∴111323V=⋅⋅=例二十、(1995年全国联赛一试)设O是正三棱锥P—ABC底面△ABC的中心,过O的动平面与P—ABC的三条侧棱或其延长线的交点分别记为Q、R、S,则和式111PQ PR PS++(A)有最大值而无最小值;(B)有最小值而无最大值;(C)既有最大值又有最小值,且最大值与最小值不等;(D)是一个与平面QRS位置无关的常量.分析:借助于分割思想,将三棱锥P—QRS划分成三个以O为顶点,以三个侧面为FF MMEEDDBB CCAAOSRQCBAP底面的三棱锥O —PQR ,O —PRS ,O —PSQ . 显然三个三棱锥的高相等,设为h ,又设QPR ∠=RPS SPQ α∠=∠=,于是有:()13P QRS O PQR O PRS O PSQ PQR PRS PSQ V V V V S S S h ----∆∆∆=++=++⋅ ()1sin 6PQ PR PR PS PS PQ h α=⋅+⋅+⋅⋅⋅ 又:1sin sin 6P QRS Q PRS V V PQ PR PS αθ--==⋅⋅⋅⋅,其中θ为PQ 与平面PRS 所成的角.()sin sin sin PQ PR PR PS PS PQ h PQ PR PS ααθ∴⋅+⋅+⋅⋅⋅=⋅⋅⋅⋅于是得:111PQ PR PS ++sin hθ= 例二十一、(1993年全国联赛一试)三棱锥S —ABC 中,侧棱SA 、SB 、SC 两两互相垂直,M 为三角形ABC 的重心,D 为AB 中点,作与SC 平行的直线DP . 证明:(1)DP 与SM 相交;(2)设DP 与SM 的交点为D ',则D 为三棱锥S —ABC 的外接球的球心. 分析:根据题中三棱锥的特点,可将三棱锥补形成为一个如图所示的长方体,因为 C 、M 、D 三点共线,显然,点C 、S 、D 、M 在同一平面内.于是有DP 与SM 相交. 又因为:12DD DM SC MC '==,而点D 为长 方体的底面SAEB 的中心,故必有点D '为 对角线SF 的中点,即为长方体的也是三棱 锥的外接球的球心.例二十二、(1992年全国联赛一试)从正方体的棱和各个面的面对角线中选出k 条,使得其中任意两条线段所在的直线都是异面直线,则k 的最大值是 . 分析:本题可以采用构造法求解.考查图中的 四条线段:A 1D 、AC 、BC 1、B 1D 1,显然其中任意GFMED 'DCBA SH A 1DCD 1C 1B 1两条都是异面直线.另一方面,如果满足题目 要求的线段多于4条,若有5条线段满足要求, 因为5条线段中任意两条均为异面直线,所以其中任意两条没有公共点,于是产生这些线段的端点几何体的顶点的个数必定大于或等于10个,这与题中的正方体相矛盾.故:4k =.例二十三、(1991年全国联赛一试)设正三棱锥P —ABC 的高为PO ,M 为PO 的中点,过AM 作与棱BC 平行的平面,将三棱锥截为上、下两个部分,试求此两部分的体积比. 分析:取BC 的中点D ,连接PD 交AM 于G ,设 所作的平行于BC 的平面交平面PBC 于EF ,由 直线与平面平行的性质定理得:EF ∥BC ,连接AE ,AF ,则平面AEF 为合乎要求的截面. 作OH ∥PG ,交AG 于点H ,则:OH=PG .51112BC PD PG GD GD GD AD EF PG PG PG OH AO +===+=+=+=; 故:2425A PEF PEF A PBC PBC V S EF V S BC -∆-∆⎛⎫=== ⎪⎝⎭;于是:421A PEF A EFBC V V --=. 三、求面积这类题常设计为求几何体中某一特殊位置的截面面积 解决这类题的关键是 ,封断出截面的形状及截面和已知中相关图形的关系F E OM D CBAPHG四、求距离这类题常是以几何体为依托 ,求其中的某些点 、线 、面之间的距离 解决这类题的关键在于 ,根据已知条件判断出或作出符合题意的线段 ,其长度就是符合题意的距离4、(1996年全国联赛一试)已知将给定的两个全等的正三棱锥的底面粘在一起,恰得到一个所有二面角都相等的六面体,并且该六面体的最短棱的长为2,则最远的两顶点间的距离是________.解:该六面体的棱只有两种,设原正三棱锥的底面边长为2a ,侧棱为b .取CD 中点G ,则AG ⊥CD ,EG ⊥CD ,故∠AGE 是二面角A —CD —E 的平面角.由BD ⊥AC ,2ababbGEFBCDA作平面BDF ⊥棱AC 交AC 于F ,则∠BFD 为二面角B —AC —D 的平面角.AG=EG=b 2-a 2,BF=DF=2a b 2-a 2b,AE=2b 2-(233a )2=2b 2-43a 2.由cos ∠AGE=cos ∠BFD ,得2AG 2-AE 22AG 2=2BF 2-BD 22BF 2.∴ 4(b2-432a 2)b 2-a 2=4a 2b 24a 2(b 2-a 2)⇒9b 2=16a 2,⇒b=43a ,从而b=2,2a=3.AE=2.即最远的两个顶点距离为3.分析:设正三棱锥的底面边长为a ,侧棱长为b ,则:2222223244a a b a a a b b b-=⋅--即:2223b a b =- 化简得: 32ba =所以,3,2a b ==.于是可求得线段PP '的长:2432pp '=-=.于是有最远距离为底边长3.ACBD EFOP 'P五、求元素个数这类题常以长方体或三棱锥等几何体为背景,通过计算符合题意的元素个数,来考查学生对计数问题的理解程度解决这类题的关键是计数时要有规律的数,作到不重复、不遗漏8、如果空间三条直线a ,b ,c 两两成异面直线,那么与a ,b ,c 都相交的直线有(A ) 0条 (B ) 1条 (C )多于1 的有限条 (D ) 无穷多条 解:在a 、b 、c 上取三条线段AB 、CC '、A 'D ',作一个平行六面体ABCD —A 'B 'C 'D ',在c 上取线段A 'D '上一点P ,过a 、P 作 一个平面,与DD '交于Q 、与CC '交于R ,则QR ∥a ,于是PR 不与a 平行,但PR 与a 共面.故PR 与a 相交.由于可以取无穷多个点P .故选D .9、给定平面上的5个点A 、B 、C 、D 、E ,任意三点不共线. 由这些点连成4条线,每点至少是一条线段的端点,不同的连结方式有 种.解:图中,4种连结方式都满足题目要求.(图中仅表示点、线间连结形式,不考虑点的位置) .情况(1),根据中心点的选择,有5种其连结方式;情况(2),可视为5个点A 、B 、C 、D 、E 的排列,但一种排列与其逆序排列是同一的,且两者是一一对应的,则有连结方式5!602=种;情况(3),首先是分歧点的选择有5种,其次是分叉的两点的选择有246C =种,最后是余下并连两点的顺序有别,有2!种,共计56260⨯⨯=种;情况(4),选择3点构造三角形,有3510C =种. 共有5606010135+++=种连结方式.B‘C’D’A‘BCDASQ PR acb(1) (2) (3) (4)3. 设四棱锥P ABCD -的底面不是平行四边形, 用平面α去截此四棱锥, 使得截面四边形是平行四边形, 则这样的平面 α( )(A) 不存在 (B)只有1个 (C) 恰有4个 (D)有无数多个例一、(1991年全国联赛一试)由一个正方体的三个顶点所能构成的正三角形的个数为 (A )4; (B )8; (C )12; (D )24.分析:一个正方体一共有8个顶点,根据正方体的结构特征可知,构成正三角形的边必须是正方体的面对角线.考虑正方体的12条面对角线,从中任取一条可与其他面对角线构成两个等边三角形,即每一条边要在构成的等边三角形中出现两次,故所有边共出现112224C =次,而每一个三角形由三边构成,故一共可构成的等边三角形个数为2483=个. 例二、(1995年全国联赛一试)将一个四棱锥的每个顶点染上一种颜色,并使同一条棱的两个端点异色,如果只有5种颜色可供使用,那么不同的染色方法的总数是 .分析:就四棱锥P —ABCD 而言,显然顶点P 的颜色必定不同于A 、B 、C 、D 四点,于是分三种情况考虑:① 若使用三种颜色,底面对角线上的两点可同色,其染色种数为:3560A =(种) ② 若使用四种颜色,底面有一对对角线同色,其染色种数为:1425240C A ⋅=(种)③ 若使用五种颜色,则各顶点的颜色各不相同,其染色种数为:55120A =(种)故不同染色方法种数是:420种.六、特殊四面体1.四面体 由于四面体是三角形在空间中的推广,因此三角形的许多性质也可以推广到四面体: (1)连接四面体的棱中点的线段交于一点,且在这里平分这些线段;(2)连接四面体任一顶点与它对面重心的线段交于一点,且这点将线段分成的比为3:1,G 称为四面体的重心.(3)每个四面体都有外接球,球心是各条棱的中垂面的交点.(4)每个四面体都有内切球,球心是四面体的各个二面角的平分面的交点. 例10(1983年全国)在六条棱长分别为2、3、3、4、5、5的所有四面体中,最大的体积是多少?证明你的结论.2.特殊四面体(i )等腰四面体:三组对棱分别相等的四面体.性质(1)等腰四面体各面积相等,且为全等的锐角三角形;(2)体积是伴随长方体的13.(ii )直角四面体 从一个顶点出发的三条棱相互垂直的四面体.性质(1)直角四面体中,不含直角的面是锐角三角形(称该面为底面);(2)任一侧面面积是它在底面投影的面积和地面面积的比例中项,且侧面面积的平方和是底面面积的平方;(3)三个侧面与底面所成三个二面角的余弦的平方和是1.3.正四面体 每个面都是全等的等边三角形的四面体.性质(1)若正四面体的棱长为a ,则四面体的全面积S =3a 2,体积V =212a 3;(2)正四面体对棱中点的连线长d =22a ;(3)正四面体外接球的半径64a ,内切球的半径为612a .七、“ 多球” 问 题在解决立体几何问题时, 常会遇到若干个球按照一定的法则“ 叠加” 的问题, 我们将 这类问题简称为“ 多球” 问题. 对于“ 多球” 问 题, 我们往往可以从多球中提炼出球心所组成的立体图形, 将问题简化, 然后通过解决这简化的问题, 获得原问题的待求结论,这是 解决“ 多球” 问题的一个常用方法.5、将八个半径都为1的球分放两层放置在一个圆柱内,并使得每个球都和其相邻的四个球相切,且与圆柱的一个底面及侧面都相切,则此圆柱的高等于 .解:如图,ABCD 是下层四个球的球心,EFGH 是上层的四个球心.每个球心与其相切的球的球心距离=2.EFGH 在平面ABCD 上的射影是一个正方形.是把正方形ABCD 绕其中心旋转45 而得.设E 的射影为N ,则MN=2-1.EM=3,故EN 2=3-(2-1)2=22.∴ EN=48.所求圆柱的高=2+48.6、底面半径为1cm 的圆柱形容器里放有四个半径为12cm 的实心铁球,四个球两两相切,其中底层两球与容器底面相切. 现往容器里注水,使水面恰好浸没所有铁球,则需要注水 cm 3. 填(13+22)π. 解:设四个实心铁球的球心为O 1,O 2,O 3,O 4,其中O 1,O 2为下层两球的球心,A ,B ,C ,D 分别为四个球心在底面的射影.则ABCD 是一个边长为22的正方形.所以注水高为1+22.故应注水π(1+22)-4×43π(12)3=(13+22)π. 例 1在桌面上放着四个两两相切、 半 径均为r 的球, 试确定其顶端离桌面的高度;并求夹在这四个球所组成图形空隙中与四个 球均相切的小球的半径.例 2 制作一个底圆直径为4 c m的圆柱形容器,要内装直径为2 c m的钢珠2 6 只,那么这容器至少要多高?( 上海市1 9 8 6 年竞赛试题)例 3 在正四面体内装入半径相同的球,使相邻的球彼此相切,且外层的球又和正四面体的面都相切,如此装法,当球的个数无穷大时,求所装球的体积与正四面体体积之比的极限.( 第八届希望杯高二数学培训题)八、体积法及其应用体积法是处理立体几何问题的重要方法.在高中数学竞赛中,利用体积法解题形式简洁、构思容易,内涵深刻,应用广泛,备受青睐.几何体的体积包括基本几何体的体积计算、等积变换等方法,同时有以下常用方法和技巧:( 1 ) 转移法:利用祖咂原理或等积变换,把所求几何体转化为与它等底、等高的几何体的体积.( 2 ) 分割求和法:把所求几何体分割成基本几何体的体积.( 3 ) 补形求差法:通过补形化归为基本几何体的体积.( 4 ) 四面体体积变换法.( 5 ) 算两次法:对同一几何体的体积,从两种方法计算,建立出未知元素的等量关系,从而使问题求解.利用这种方法求点到平面的距离,可以回避作出表示距离的垂线段.另外,体积法中对四面体的体积变换涉及较多应用广泛.关于四面体的体积有如下常用性质:( 1 ) 底面积相同的两个三棱锥体积之比等于对应高之比;( 2 ) 高相同的两个三棱锥的体积比等于其底面积之比;( 3 ) 用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方;九、立体几何中的截面问题截面问题涉及到截面形状的判定、截面面积和周长的计算、截面图形的计数、截面图形的性质及截面图形的最值.本文介绍此类问题的求解方法.1 判断截面图形的形状2 截面面积和周长的计算3 计算截面图形的个数4 确定截面图形的性质5 求截面图形的最值九、综合问题7、顶点为P 的圆锥的轴截面是等腰直角三角形,A 是底面圆周上的点,B 是底面圆内的点,O 为底面圆圆心,AB ⊥OB ,垂足为B ,OH ⊥PB ,垂足为H ,且P A=4,C 为P A 的中点,则当三棱锥O -HPC 的体积最大时,OB 的长为A .53 B .253 C .63 D .263解:AB ⊥OB ,⇒PB ⊥AB ,⇒AB ⊥面POB ,⇒面P AB ⊥面POB .OH ⊥PB ,⇒OH ⊥面P AB ,⇒OH ⊥HC ,OH ⊥PC ,又,PC ⊥OC ,⇒PC ⊥面OCH .⇒PC 是三棱锥P -OCH 的高.PC=OC=2.而∆OCH 的面积在OH=HC=2时取得最大值(斜边=2的直角三角形).当OH=2时,由PO=22,知∠OPB=30︒,OB=PO tan30︒=263.解2:连线如图,由C 为P A 中点,故V O -PBC =12V B -AOP ,而V O -PHC ∶V O -PBC =PHPB =PO 2PB2(PO 2=PH ·PB ).记PO=OA=22=R ,∠AOB=α,则V P —AOB =16R 3sin αcos α=112R 3sin2α,A BP OH CV B -PCO =124R 3sin2α.PO 2PB 2=R 2R 2+R 2cos 2α=11+cos 2α=23+cos2α.⇒V O -PHC=sin2α3+cos2α⨯112R 3.∴ 令y=sin2α3+cos2α,y '=2cos2α(3+cos2α)-(-2sin2α)sin2α(3+cos2α)2=0,得cos2α=-13,⇒cos α=33,∴ OB=263,选D .例19把一个长方体切割成k 个四面体,则k 的最小值是 .例20已知l αβ--是大小为45的二面角,C 为二面角内一定点,且到半平面α和β和6,A ,B 分别是半平面α,β内的动点,则ABC ∆周长的最小值为_____.例21如图所示,等腰ABC △的底边AB =,高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF △的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P ACFE -的体积. (1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值? (3)当()V x 取得最大值时,求异面直线AC 与PF 所成角的余弦值.例六、设锐角,,αβγ满足:222cos cos cos 1αβγ++=.求证:tan tan tan αβγ⋅⋅≥分析:构造长方体模型.构造如图所示的长方体 ABCD —A 1B 1C 1D 1,连接AC 1、A 1C 1、BC 1、DC 1. 过同一个顶点的三条棱AD 、AB 、AA 1与对角线AC 1所成的角为锐角,,αβγ,满足:222cos cos cos 1αβγ++=不妨设长方体过同一个顶点的三条棱AD 、AB 、AA 1的长分别为,,a bc .则:tan tan tan aa b b c cαβγ=≥=≥=≥ 以上三式相乘即可.证明二:因为,,αβγ为锐角,故:2222sin 1cos cos cos 2cos cos ααβγβγ=-=+≥⋅,sin α∴≥同理:sin βγP ED F BCAD 1C 1B 1 A 1DC BA例22已知三棱锥ABC P -的三条侧棱PA 、PB 、PC 两两垂直,侧面PAB 、PBC 、PCA 与底面ABC 所成的二面角的平面角的大小分别为1θ、2θ、3θ,底面ABC 的面积为34. (1)证明:22tan tan tan 321≥⋅⋅θθθ;(2)若23tan tan tan 321=++θθθ,求该三棱锥的体积ABC P V -. 练 习 题例七、(1994年全国联赛一试)在正n 棱锥中,相邻两侧面所成的二面角的取值范围是 (A ) 2,n n ππ-⎛⎫⎪⎝⎭; (B ) 1,n n ππ-⎛⎫ ⎪⎝⎭; (C ) 0,2π⎛⎫ ⎪⎝⎭; (D ) 21,n n n n ππ--⎛⎫⎪⎝⎭.分析:根据正n 棱锥的结构特征,相邻两侧面所成的二面角应大于底面正n 边形的内角,同时小于π,于是得到(A ).例八、(1992年全国联赛一试)设四面体四个面的面积分别为S 1、S 2、S 3、S 4,它们的最大值为S ,记1234S S S S Sλ+++=,则λ一定满足(A ) 24λ<≤; (B ) 34λ<<; (C ) 2.5 4.5λ<≤; (D ) 3.5 5.5λ<<. 分析:因为 i S S ≤ ()1,2,3,4i =所以12344S S S SS+++≤.特别的,当四面体为正四面体时取等号.另一方面,构造一个侧面与底面所成角均为45︒的三棱锥,设底面面积为S 4,则:()()1231231234123cos 451 2.5cos 45S S S S S S S S S S S S S S λ+++++⋅︒+++===+++⋅︒,若从极端情形加以考虑,当三棱锥的顶点落在底面上时,一方面不能构成三棱锥,另外此时有1234S S S S ++=,也就是2λ=,于是必须2λ>.故选(A ).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A BCDEF第九讲 立体几何体一、选择题1、夹在两个平行平面之间的球,圆柱,圆锥在这两个平面上的射影都是圆,则它们的体积之( ) 比为A 、3:2:1B 、2:3:1C 、3:6:2D 、6:8:3 解:32212341::():(2):(2)2:3:133V V V R R R R R πππ=⋅⋅⋅=,选B.2、设二面角a αβ--的大小是060,P 是二面角内的一点,P 点到,αβ的距离分别为1cm,2cm,则点P 到棱a 的距离是( ) A、3 B、3cm C 、23cm D、3 解:设PA ⊥棱a 于点A,PM ⊥平面α于点M,PN ⊥平面β于点N,PA=t ,PAM θ∠=,则sin 1sin(60)2t t αα=⎧⎨-=⎩,5sin αα=,有sin α=或舍去),所以1sin t α==cm ,选B. 3、如图,E,F 分别是正三棱锥A -BCD 的棱AB,BC 的中点,且DE ⊥EF.若BC=a ,则此正三棱锥的体积是( )A 、324a B3aC3 D3a 4、由DE ⊥EF,EF//AC,有DE ⊥AC,又AC ⊥BD,DE BD=D,得AC ⊥平面ABD. 由对称性得090BAC CAD BAD ∠=∠=∠=,于是2AB AC AD ===. 311()32B ACD V -=⋅=,选B.4. 如图2,在正方体1111ABCD A BC D -中,P 为棱AB 上一点,过点 P 在空间作直线l ,使l 与平面ABCD 和平面AB 11C D 均成030角,则这样的直线l 的条数为(B )A. 1 B .2 C. 3 D .45. 设O 是正三棱锥P-ABC 底面是三角形ABC 的中心,过O 的动平面与PC 交于S ,与PA 、PB 的延长线分别交于Q 、R ,则和式PSPR PQ 111++( ) 解:设正三棱锥P-ABC 中,各侧棱两两夹角为α,PC 与面PAB 所成角为β,则v S-PQR =31S △PQR·h=21(31PQ ·PRsin α)·PS ·sin β。
另一方面,记O 到各面的距离为d ,则v S-PQR =v O-PQR +v O-PRS +v O-PQS ,31S △PQR ·d=31△PRS ·d+31S △PRS ·d+31△PQS ·d=213⋅d PQ ·PRsinα+213⋅d PS ·PRsin α+213⋅d PQ ·PS ·sin α,故有:PQ ·PR ·PS ·sin β=d(PQ ·PR+PR ·PS+PQ ·PS),即dPS PR PQ βsin 111=++=常数。
故选D 。
A .有最大值而无最小值B .有最小值而无最大值C .既有最大值又有最小值,两者不等D .是一个与面QPS 无关的常数6.过空间一定点P 的直线中,与长方体1111ABCD A BC D -的12条棱所在直线成等角的直线共有( C )A .0条B .1条C .4条D .无数多条7. 已知P 为四面体ABC S -的侧面SBC 内的一个动点,且点P 与顶点S 的距离等于点P 到底面ABC 的距离,那么在侧面SBC 内,动点P 的轨迹是某曲线的一部分,则该曲线一定是( D )A .圆或椭圆B .椭圆或双曲线C .双曲线或抛物线D .抛物线或椭圆8.四棱锥P ABCD -的底面ABCD 是单位正方形(,,,A B C D 按反时针方向排列),侧棱PB垂直于底面,且PB =3,记APD θ∠=,则sin θ=(C )A .22 B .33C .55D .66 9.正方体的截平面不可能是: (1) 钝角三角形 (2) 直角三角形 (3) 菱形 (4) 正五边形 (5) 正六边形; 下述选项正确的是( B )A .(1)(2)(5)B .(1)(2)(4)C .(2)(3)(4)D .(3)(4)(5)【解】 正方体的截平面可以是锐角三角形、等腰三角形、等边三角形,但不可能是钝角三角形,直角三角形(证明略);对四边形来讲,可以是梯形(等腰梯形)、平行四边形、菱形,矩形、但不可能是直角梯形(证明略);对五边形来讲,可以是任意五边形,不可能是正五边形(证明略);对六边形来讲,可以是六边形(正六边形)。
∴选 【 B 】10.如图,D C B A ABCD ''''-为正方体。
任作平面α与对角线C A '垂直,使得α 与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l .则( ) A .S 为定值,l 不为定值 B .S 不为定值,l 为定值 C .S 与l 均为定值D .S 与l 均不为定值解:将正方体切去两个正三棱锥A A BD '-与C D B C '''-后,得到一个以平行平面A BD DBC '''与为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱B A ''剪开,展平在一张平面上,得到一个11A B B A '',而多边形W 的周界展开后便成为一条与1A A '平行的线段(如图中1E E '),显然11A A E E '=',故l 为定值. 当E '位于B A ''中点时,多边形W 为正六边形,而当E '移至A '处时,W 为正三角形,易知周长为定值l 的正六边形与正三角形面积分别为2243l 与2363l , 故S 不为定值。
选B.二、填空题1、若线段AB 的两端点到平面α的距离都等于2,则线段AB 所在的直线和平面α的位置关系是 .答案:当2AB <时,AB//α;当2AB =时,AB//α或AB ⊥α;当2AB >时,AB//α或与α斜交.2、若异面直线,a b 所原角为060,AB 是公垂线,E,F 分别是异面直线,a b 上到A,B 距离为2和平共处的两点,当3EF =时,线段AB 的长为 .7、由EF EA AB BF =++ ,得22222cos EF EA AB BF EA BF θ=+++⋅⋅(1)当060θ=时,有219412212AB =+++⋅⋅⋅ ,得AB = ;(2)当0120θ=时,有219412212AB =++-⋅⋅⋅ ,得AB = 3、如图(1),在直四棱柱1111A BC D ABCD -中,当底面四边形ABCD 满足条件时,有1A C⊥1B 1D (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形) 答案:AC ⊥BD.(或ABCD 是正方形或菱形等)ABCD4、如图(2),是一个正方体的展开图,在原正方体中,有下列命题: ①AB 与EF 所连直线平行; ②AB 与CD 所在直线异面; ③MN 与BF 所在直线成060; ④MN 与CD 所在直线互相垂直. 其中正确命题的序号为 .(将所有正确的都写出)9、将展开的平面图形还原为正方体NACF EMBD -,可得只②,④正确.5.在一个棱长为5的正方体封闭的盒内,有一个半径等于1的小球,若小球在盒内任意地运动,则小球达不到的空间的体积的大小等于 .33144π-6.在△ABC 中,已知30,105A B ∠=︒∠=︒,过边AC 上一点D 作直线DE ,与边AB 或者BC 相交于点E ,使得60CDE ∠=︒,且DE 将△ABC 的面积两等分,则2CD AC ⎛⎫= ⎪⎝⎭. 7.用6根等长的细铁棒焊接成一个正四面体形框架,铁棒的粗细和焊接误差不计设此框架能容纳得下的最大球的半径为1R ,能包容此框架的最小球的半径为2R ,则12R R 等于 .33 8. 长方体1111ABCD A BC D -中,已知14AB =,13AD =,则对角线1AC 的取值范围是 .()4,5三、解答题1、(如图)在棱长为1的正方体ABCD 1111-A B C D 中, (1)求异面直线1A B 与1B C 所成的角的大小;A BCDA BC D图(1)A BE NM 图(2)CDF(2)求异面直线1A B 与1B C 之间的距离; (3)求直线1A B 与平面1B CD 所成的角的大小; (4)求证:平面1A BD//平面C 1B 1D ;(5)求证:直线A 1C ⊥平面1A BD; (6)求证:平面AB 1C ⊥平面1A BD; (7)求点1A 到平面C 1B 1D 的距离; (8)求二面角1A -1B C -1D 的大小. 12、(1)解:如图,以D 为原点建立空间直角坐标系,有1A (1,0,1),B(1,1,0),1B (1,1,1),C(0,1,0)得1(0,1,1)A B =- ,1(1,0,1)BC =-- ,设1A B 与1BC 所成的角为α,则11111cos 2A B B C A B B Cα⋅===⋅ ,又000180α≤≤,得060α= 所以异面直线1A B 与1B C 所成的角的大小为060.(2)设点M 在1A B 上,点N 在1B C 上,且MN 是1A B 与1B C 的公垂线,令M (1,,1)m m -,N (,1,)n n ,则(1,1,1)MN n m m n =--+-由1100A B MN B C MN ⎧⋅=⎪⎨⋅=⎪⎩,得(0,1,1)(1,1,1)0(1,01)(1,1,1)0n m m n n m m n -⋅--+-=⎧⎨--⋅--+-=⎩,解得23m =,n =23 所以111(,,)333MN =- ,得MN =,即异面直线1A B 与1B C.(3)解:设平面1B CD 的法向量为1(,,,)n x y z = ,而(0,1,0)DC =,由1n DC ⊥ ,11n B C ⊥ , 有(,,,)(0,1,0)0(,,,)(1,0,1)0x y z x y z ⋅=⎧⎨⋅--=⎩,得0x zy =-⎧⎨=⎩,于是1(1,0,1)n =- ,设1n 与1A B 所成的角为β,则11111cos 2A B n A B n β⋅===-⋅ ,又000180β≤≤,有0120β=. 所以直线1A B 与平面1B CD 所成的角为060.(4)证明:由1A B //C 1D ,C 1D ⊂平面C 1B 1D ,得1A B //平面C 1B 1D , 又BD//1B 1D ,1B 1D ⊂平面C 1B 1D ,得BD//平面C 1B 1D ,AA而1A B BD B = ,于是平面1A BD//平面C 1B 1D .(5)证明:A(1,0,0),1C (0,1,1),1(1,1,1)AC =- ,(1,1,0)DB =,有11(1,1,1)(0,1,1)0AC AB ⋅=-⋅-= 及1(1,1,1)(1,1,0)0AC DB ⋅=-⋅= ,得 11AC AB ⊥ ,1AC DB ⊥ ,1AB BD B = , 于是,直线A 1C ⊥平面1A BD.(6)证明:由(5)知1AC ⊥平面1A BD,而1AC ⊂平面AB 1C ,得平面AB 1C ⊥平面1A BD. (7)解:可得1B C=C 1D =11D B有11201sin 602B CD S ∆=⋅⋅=由11111A B CD C A B D V V --=,得11111(11)1332B CD S h ∆⋅⋅=⋅⋅⋅⋅,即122h =,得3h = 所以点1A 到平面11CB D的距离为3. (8)解:由(3)得平面1B CD 的法向量为1n=(1,0,1)-,它即为平面11A B C 的法向量.设平面11B CD 的法向量为2(,,,)n x y z = ,则21n B C ⊥ , 211n B D ⊥又11B D(0,0,1)(1,1,1)(1,1,0)=-=--由(,,,)(1,0,1)0(,,,)(1,1,0)0x y z x y z ⋅--=⎧⎨⋅--=⎩,得y xz x =-⎧⎨=-⎩,所以2(1,1,1)n =--设1n与2n所成的角为γ,则1212cos n n n n γ⋅===⋅ 所以二面角111A B C D --的大小为arccos3. 2、如图,在ABC ∆中,AB=AC=13,BC=10,DE//BC 分别交AB,AC 于D,E.将ADE ∆沿 DE 折起来使得A 到1A ,且1A DE B --为060的二面角,求1A 到直线BC 的最小距离. 10、解:设ABC ∆的高AO 交DE 于点1O ,令1AO x =,A BCD PQ由12=,有112OO x =-,在11AOO ∆中,01160AOO ∠=, 有222011111112cos60AO AO OO AO OO =+-⋅⋅⋅得1AO =当6x =时,1A 到直线BC 的最小距离为6.3、如图,已知矩形ABCD 中,AB=1,BC=a (0)a >,PA ⊥平面ABCD,且PA=1. (1)问BC 边上是否存在点Q 使得PQ ⊥QD?并说明理由;(2)若边上有且只有一个点Q,使得PQ ⊥QD,求这时二面角Q PD A --的正切. 11、解:(1)(如图)以A 为原点建立空间直角坐标系,设BQ x =,则 Q (1,,0)x ,P(0,0,1),D (0,,0)a得(1,,1)PQ x =- ,(1,,0)QD a x =--由PQ QD ⊥ ,有(1,,1)(1,,0)0x a x -⋅--=,得210x ax -+= ①若方程①有解,必为正数解,且小于a .由2()40a ∆=--≥,0a >,得2a ≥. (i)当2a ≥时,BC 上存在点Q,使PQ ⊥QD;(ii)当02a <<时, BC 上不存在点Q,使PQ ⊥QD.(2)要使BC 边上有且只有一个点Q,使PQ ⊥QD,则方程①有两个相等的实根,这时,2()40a ∆=--=,得2a =,有1x =.又平面APD 的法向量1(1,0,0)n =,设平面PQD 的法向量为2(,,)n x y z = 而(1,1,0)QD =- ,(0,2,0)(0,0,1)(0,2,1)PD =-=-,由2200n QD n PD ⎧⋅=⎪⎨⋅=⎪⎩,得(,,)(1,1,0)0(,,)(0,2,1)0x y z x y z ⋅-=⎧⎨⋅-=⎩,解得,2x y z y == 有2(1,1,2)n =,则121212cos ,n n n n n n ⋅<>===⋅,则12tan ,n n <所以二面角Q PD A --ACB ABC4、已知斜三棱柱ABCD 1111A B C D -的侧面1A AC 1C 与底面垂直,090ABC ∠=,2BC =, AC =且A 1A ⊥1A C, A 1A =1A C.(1)求侧棱A 1A 和底面ABC 所成的角的大小; (2)求侧面1A AB 1B 和底面ABC 所成二面角的大小; (3)求顶点C 到侧面1A AB 1B 的距离.13、解:建立如图所示的空间直角坐标系,由题意知A ,B(0,0,0),C(0,2,0).又由面1A AC 1C ⊥面ABC,且A 1A =1A C,知点1A,1(AA =, 平面ABC 的法向量(0,0,1)n =.(1)111cos ,21AA n AA n AA ⋅<>===⋅ ,得01,45AA n <>=于是,侧棱1AA 和底面ABC 所成的角的大小是045.(2)(AB =-设面1A AB 1B 的法向量1(,,,)nx y z =,则由11(,,,)(0n AA x y z y ⋅=⋅=+=1(,,,)(0n AB x y z ⋅=⋅-=-=得0x =,y =.于是,1(0,)n =,又平面ABC 的法向量(0,0,1)n =,得1111cos ,2n n n n n n ⋅<>===⋅,有01,60n n <>=. 所以侧面1A AB 1B 和底面ABC 所成二面角的大小是060. (3)从点C 向面1A AB 1B 引垂线,D 为垂足,则060CBD ∠=11BC kn BC DC CD DC kn ⋅⋅====所以点C 到侧面1A AB 1B。
