11-12学年度下学期高一数学练习3(03)12-2-1
福建师大附中11-12学年度下学期高一数学期末模块测试新人教A版

某某师大附中2011—2012学年度下学期末模块测试高一数学试题本试卷共4页.满分150分,考试时间120分钟.注意事项:将答案填写在答卷纸上,考试结束后只交答案卷.一、选择题:本大题有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求. 1.sin 300tan 240oo+的值是 A .23-B .23C .321+-D .321+ 2.函数2cos 2y x =+是A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为2π的偶函数D .最小正周期为2π的奇函数 3.已知(2,3)A ,(3,0)B ,且2AC CB =-,则点C 的坐标为 A .(3,4)-B .(4,3)-C .8(,1)3D .8(1,3-4.已知a b a ,2||,1||==与b 的夹角为600,若ka b +与b 垂直,则k 的值为A .4-B .4C .43-.435.若把函数cos y x =的图象上所有点的横坐标缩小到原来的一半(纵坐标不变),然后再把图象向左平移6π个单位,则所得图象对应的函数解析式为 A .1cos(26y x π=+B .1cos()212y x π=+C .cos(2)6y x π=+D .cos(2)3y x π=+6.已知扇形的周长是6cm ,面积是22cm ,则扇形的中心角的弧度数是 A .1 B .4 C .1 或4D .2 或47.若,αβ为锐角,且满足45cos ,cos(),513ααβ=+= 则sin β的值是 A .1665B .3365C .5665D .63658.已知函数sin()y A x B ωϕ=++的一部分图象如图所示,如果2||,0,0πϕω<>>A ,则第14题图A .4=AB .1=ωC .6πϕ=D .4=B9.已知以原点O 为圆心的单位圆上有一质点P ,它从初始位置013()2P 开始,按逆时针方向以角速度1/rad s 做圆 周运动.则点P 的纵坐标y 关于时间t 的函数关系为 A .sin(),03y t t π=+≥B .sin(),06y t t π=+≥ C .cos(),03y t t π=+≥D .cos(),06y t t π=+≥ 10.若(010,)4k k k Z πθ=≤≤∈,则sin cos 1θθ+≥的概率为 A .15B .25C .211D .61111.设()2sin()f x x m ωϕ=+-,恒有()()2f x f x π+=-成立,且(14f π=-,则实数m的值为A .1±B .3±C .-3或1D .-1或312.若两个函数的图象仅经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出下列三个函数:1()22f x x =,2()sin cos f x x x=+,3()2)16f x x π=++,则A .123(),(),()f x f x f x 两两为“同形”函数B .12(),()f x f x 为“同形”函数,且它们与3()f x 不为“同形”函数C .23(),()f x f x 为“同形”函数,且它们与1()f x 不为“同形”函数D .123(),(),()f x f x f x 两两不为“同形”函数二、填空题:本大题有5小题,每小题4分,共20分,把答案填在答卷的相应位置. 13.已知5sin()6x π+=,则2cos()3x π+的值为 *** ; 14.如图,在平行四边形ABCD 中,,,3AB a AD b AN NC ===,则BN = *** (用,a b 表示) ;15.设a =)sin ,23(α,b =31,(cos α,且a ∥b ,则锐角α的大小为 *** ;16.定义在R 上的函数()f x 既是偶函数又是周期函数,若()f x 的最小正周期是2π,且当[0,]4x π∈ 时,()cos f x x =,则()3f π= *** ;17.定义平面向量之间的一种运算“⊗”如下:对任意的向量(,),(,)a m n b p q ==,令a b mq np ⊗=-,给出下面四个判断:①若a 与b 共线,则0a b ⊗=; ② 若a 与b 垂直,则0a b ⊗=;③a b b a ⊗=⊗; ④2222()()||||a b a b a b ⊗+⋅=.其中正确的有 *** (写出所有正确的序号).三、解答题:本大题有6题,共70分,解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分10分)已知||2,||1,(23)(2)9a b a b a b ==⋅+=-. (Ⅰ)求a b 与的夹角θ; (Ⅱ)求向量a 在()a b +上的投影.19.(本小题满分12分)如图,在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A 、B 两点.已知A 、B 的横坐标分别为102,552.(Ⅰ)求)tan(βα+的值;(Ⅱ)求22sin sin 26cos cos 2αααα++的值.20.(本小题满分12分)已知向量(cos 2,4),(1,cos )a x b x λ=-=,其中,[0,]2R x πλ∈∈.设函数()f x a b =⋅.(Ⅰ)求)(x f 的解析式; (Ⅱ)若()f x 的最小值是23-,求λ的值.21.(本小题满分12分) (Ⅰ)已知:3sin cos 5αβ+=,4cos sin 5αβ-=,求sin()αβ-的值; (Ⅱ)类比(Ⅰ)的过程与方法,将(Ⅰ)中已知条件中两个等式的左边进行适当改变,写出改变后的式子,并求cos()αβ-的值.22.(本小题满分12分)如图,在半径为1,圆心角为6π的扇形OAB 的弧上任取一点C ,作CD OA ,交OB 于点D ,求OCD ∆的最大面积.23.(本小题满分12分)已知函数()cos 2(),(0,0,0)222A A f x x A πωϕωϕ=-+>><<的图象过点(1,2),相邻两条对称轴间的距离为2,且()f x 的最大值为2. (Ⅰ)求()f x 的单调递增区间; (Ⅱ)计算(1)(2)(2012)f f f +++;(Ⅲ)设函数()()1g x f x m =--,试讨论函数()g x 在区间[1,4]上的零点情况.参考答案一、选择题:1-12:BABADCBCADDC 二、填空题: 13.5-.1344a b -+ 15.4π16.2 17. ①④ 三、解答题:18.解: (Ⅰ)22(23)(2)4439a b a b a a b b +=-⋅-=-, 即16439a b -⋅-=∴1a b ⋅=∴1cos 2||||a b a b θ⋅==∵[0,]θπ∈∴3πθ=(Ⅱ)222||27a b a a b b +=+⋅+= ∴||7a b +=,设a 与()a b +的夹角为α∴向量a 在()a b+上的投影为2()()5||cos ||7||||||||7a ab a a b a a b a a a a b a b a b α⋅+⋅++⋅=====+++ 19.解:由条件得102cos =α,552cos =β,∵α,β为锐角, ∴1027cos 1sin 2=-=αα,55cos 1sin 2=-=ββ, 因此7cos sin tan ==ααα,21cos sin tan ==βββ. (1)32171217tan tan 1tan tan )tan(-=⨯-+=-+=+βαβαβα. (2)2222222sin sin 2sin 2sin cos tan 2tan 491436cos cos 27cos sin 7tan 7492αααααααααααα++++====-+--- 20.解:(Ⅰ),cos 42cos )(x x x f λ-=]2,0[π∈x(Ⅱ)∵()cos 24cos f x x x λ=-222(cos )12.x λλ=---]2,0[π∈x∵]2,0[π∈x , ∴.1cos 0≤≤x设cos ,0 1.t x t =≤≤则222()12,0 1.y t t λλ=---≤≤01<'λ当、时,当且仅当min 0,1t y ==-时,这与已知矛盾. 101≤≤''λ当、时,当且仅当2min ,12t y λλ==--时.由已知得23212-=--λ,解得.21=λ 11>'''λ当、时,当且仅当min 1,14t y λ==-时.由已知得2341-=-λ,解得85=λ,这与1>λ相矛盾.综上所述,21=λ为所求. 21.解:(Ⅰ)∵53cos sin =+βα①54sin cos =-βα②①的平方+②的平方,得22(sin cos cos sin )1αβαβ+-=21)sin(-=-∴βα(Ⅱ)可将(Ⅰ)(1)中已知条件改为,3sin sin 5αβ+=,54cos cos =+βα,将两式平方后求和得1)cos cos sin (sin 22=++βαβα21)cos(-=-∴βα22.解:作DE OA ⊥于点E ,CF OA ⊥于点F ,设AOC α∠=,则0π在Rt OCF∆中,sin CFα=,cos OF α= 在Rt ODE ∆中,∴OE α===∴cos EF OFOE αα=-= ∴21111sin (cos )sin cos 2222OCD S CD CF EF CF αααααα∆=⋅=⋅=⋅=1cos 2)1sin 2sin 2cos 244444αααα-=-=+-1sin(2)234πα=+-,06πα<<. ∵06πα<<,所以22333πππα<+<∴当232ππα+=,即12πα=时,OCD S ∆有最大值且为124- 23.解:(Ⅰ)22,4,02224T T T πππωωω==>∴==∴=, 由于()f x 的最大值为2且A>0, ∴ 所以222A A+=即A=2∴()1cos 2()4f x x πϕ=-+,又函数()f x 的图象过点(1,2)则cos 2()1sin 21422,,24024k k k Zπϕϕππϕπϕππϕπϕ+=-∴=∴=+=+∈<<∴=∴()1cos 2()1sin 442f x x x πππ=-+=+ 由22(),222k x k k Z πππππ-≤≤+∈得1414(),2k x k k Z π-+≤≤+∈∴)(x f 的单调增区间是[14,14]().k k k Z -++∈ (Ⅱ)由(Ⅰ)知()1sin2f x x π=+,∴()f x 的周期为4,而2012=4×503 且(1)2,(2)1,(3)0,(4)1f f f f ==== ∴原式45032012=⨯=(Ⅲ)()()1cos()sin 222g x f x m x m x m πππ=--=-+-=-函数()g x 的零点个数即为函数sin2y x π=的图象与直线y m =的交点个数.在同一直角坐标系内作出这两个函数的图象(如下图所示),由图象可知:x1) 当1m >或1m <-时,函数sin 2y x π=的图象与直线y m =无公共点,即函数()g x 无零点;2) 当01m <≤或1m =-时,函数sin2y x π=的图象与直线y m =有一个公共点,即函数()g x 有一个零点; 3) 当10m -<≤时,函数sin2y x π=的图象与直线y m =有两个公共点,即函数()g x 有两个零点.。
两条直线的位置关系9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版)

专题39两条直线的位置关系9题型分类1.两条直线的位置关系直线l 1:y =k 1x +b 1,l 2:y =k 2x +b 2,l 3:A 1x +B 1y +C 1=0,l 4:A 2x +B 2y +C 2=0(其中l 1与l 3是同一条直线,l 2与l 4是同一条直线)的位置关系如下表:位置关系l 1,l 2满足的条件l 3,l 4满足的条件平行k 1=k 2且b 1≠b 2A 1B 2-A 2B 1=0且A 1C 2-A 2C 1≠0垂直k 1·k 2=-1A 1A 2+B 1B 2=0相交k 1≠k 2A 1B 2-A 2B 1≠02.三种距离公式(1)两点间的距离公式①条件:点P 1(x 1,y 1),P 2(x 2,y 2).②结论:|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2.③特例:点P (x ,y )到原点O (0,0)的距离|OP |=x 2+y 2.(2)点到直线的距离点P (x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2.(3)两条平行直线间的距离两条平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0间的距离d=|C1-C2| A2+B2.常用结论1.直线系方程(1)与直线Ax+By+C=0平行的直线系方程是Ax+By+m=0(m∈R且m≠C).(2)与直线Ax+By+C=0垂直的直线系方程是Bx-Ay+n=0(n∈R).(3)过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R),但不包括l2.2.五种常用对称关系(1)点(x,y)关于原点(0,0)的对称点为(-x,-y).(2)点(x,y)关于x轴的对称点为(x,-y),关于y轴的对称点为(-x,y).(3)点(x,y)关于直线y=x的对称点为(y,x),关于直线y=-x的对称点为(-y,-x).(4)点(x,y)关于直线x=a的对称点为(2a-x,y),关于直线y=b的对称点为(x,2b-y).(5)点(x,y)关于点(a,b)的对称点为(2a-x,2b-y).(一)判断两条直线位置关系的注意点(1)斜率不存在的特殊情况.(2)可直接利用直线方程系数间的关系得出结论.(二)利用距离公式应注意的点(1)点P(x0,y0)到直线x=a的距离d=|x0-a|,到直线y=b的距离d=|y0-b|.(2)两条平行线间的距离公式要把两条直线方程中x,y的系数化为相等.y (三)对称问题的求解策略(1)解决对称问题的思路是利用待定系数法将几何关系转化为代数关系求解.(2)中心对称问题可以利用中点坐标公式解题,两点轴对称问题可以利用垂直和中点两个条件列方程组解题.求直线l 关于直线0l 对称的直线'l 若直线0//l l ,则//'l l ,且对称轴0l 与直线l 及'l 之间的距离相等.此时0,,'l l l 分别为00,0,++=++=Ax By C Ax By C 22'0(0)++=+≠Ax By C A B ,由002222|||'|--=++C C C C A B A B ,求得'C ,从而得'l .若直线l 与0l 不平行,则0= l l Q .在直线l 上取异于Q 的一点11(,)P x y ,然后求得11(,)P x y 关于直线0l 对称的点22'(,)P x y ,再由,'Q P 两点确定直线'l (其中0'= l l l Q ).题型6:点线对称6-1.(2024高二上·全国·课后作业)若直线定点()2,0A.35B.6-3.(2024高二上·四川遂宁-A.(1,4)--C.(3,4)题型7:线点对称7-1.(2024高二·全国·单元测试)直线7-2.(2024高三上·辽宁营口时,点M到直线2l的距离为7-3.(2024高二上·江苏苏州的直线方程为.7-4.(2024高二上·全国·课后作业)直线题型8:线线对称8-1.(2024高三·全国·专题练习)已知直线直线为2l,则直线2l的方程为8-2.(2024高二上·湖北黄石的距离是25,则直线1l关于直线(四)一、单选题1.(2024高二上·浙江·期中)已知点(,2)(0)a a >到直线:30l x y -+=的距离为1,则a 等于()A B .2C 1D 12.(2024高二上·黑龙江哈尔滨·期末)已知两条直线1:3460l x y -+=,2:3440l x y --=,则这两条直线之间的距离为()A .2B .3C .5D .103.(2024高二·全国·课后作业)求直线x +2y -1=0关于直线x +2y +1=0对称的直线方程()A .x +2y -3=0B .x +2y +3=0C .x +2y -2=0D .x +2y +2=04.(2024高二·全国·课后作业)直线0ax by c ++=关于直线0x y -=对称的直线为()A .0ax by c -+=B .0bx ay c -+=C .0bx ay c ++=D .0bx ay c +-=5.(2024·浙江温州·三模)已知直线12:0,:10l x y l ax by +=++=,若12l l ⊥,则a b +=()A .1-B .0C .1D .26.(2024·安徽蚌埠·三模)已知直线1l :210ax y ++=,2l :()30a x y a --+=,则条件“1a =”是“12l l ⊥”的()A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不必要也不充分条件7.(2024高二上·全国·课后作业)直线220x y ++=与420ax y +-=互相垂直,则这两条直线的交点坐标为()A .()1,4-B .()0,2-C .()1,0-D .0,12⎛⎫⎪⎝⎭8.(2024高二下·四川广元·期中)若直线2mx ny +=过点()2,2A ,其中m ,n 是正实数,则12m n+的最小值是()A .3B .3+C .92D .59.(2024高二上·全国·课后作业)若直线230x y --=与420x y a -+=,则a 的值为()A .4B6C .4或16-D .8或16-10.(2024高二上·全国·课后作业)抛物线214y x =的焦点关于直线10x y --=的对称点的坐标是()A .(2,1)-B .(1,1)-C .11,44⎛⎫- ⎪⎝⎭D .11,1616⎛⎫- ⎪⎝⎭11.(2024·四川)设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则PA PB +的取值范围是A .B .C .D .12.(2024·全国)点(0,﹣1)到直线()1y k x =+距离的最大值为()A .1B CD .213.(2024·北京东城·二模)已知三条直线1:220l x y -+=,2:20l x -=,3:0+=l x ky 将平面分为六个部分,则满足条件的k 的值共有()A .1个B .2个C .3个D .无数个14.(2024高二上·辽宁沈阳·阶段练习)两直线方程为1:3260l x y --=,22:0x y l --=,则1l 关于2l 对称的直线方程为()A .3240x y --=B .2360x y +-=C .2340x y --=D .3260x y --=15.(2024高一下·海南·期末)设,,a b c 分别是ABC V 中,,A B C ∠∠∠所对边的边长,则直线sin 0A x ay c ⋅++=与sin sin 0bx B y C -⋅+=的位置关系是()A .平行B .重合C .垂直D .相交但不垂直16.(2024高三下·江西·开学考试)费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形三个内角均小于120°时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等且均为120°.根据以上性质,.则(,)F x y =的最小值为()A .4B .2+C .3+D .4+17.(2024·贵州毕节·模拟预测)直线()()1:11l x a y a a R ++=-∈,直线21:2l y x =-,下列说法正确的是()A .R a ∃∈,使得12l l ∥B .R a ∃∈,使得12l l ⊥C .R a ∀∈,1l 与2l 都相交D .R a ∃∈,使得原点到1l 的距离为318.(2024·全国)如果直线2y ax =+与直线3y x b =-关于直线y x =对称,那么()A .1,63a b ==B .1,63a b ==-C .3,2a b ==-D .3,6a b ==19.(2024高一·全国·课后作业)已知ΔA 的顶点()2,1B ,()6,3C -,其垂心为()3,2H -,则其顶点A 的坐标为A .()19,62--B .()19,62-C .()19,62-D .()19,6220.(2024高三·全国·课后作业)若动点A ,B 分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 的中点M 到原点的距离的最小值为()A .B .C .D .21.(2024高二上·湖北·阶段练习)在等腰直角三角形ABC 中,3AB AC ==,点P 是边AB 上异于A B 、的一点,光线从点P 出发,经BC CA 、反射后又回到点P ,如图,若光线QR 经过ABC V 的重心,则AP =()A .32B .34C .1D .222.(2024高一上·湖南长沙·开学考试)如下图,一次函数4y x =+的图象与x 轴,y 轴分别交于点A ,B ,点(2,0)C -是x 轴上一点,点E ,F 分别为直线4y x =+和y 轴上的两个动点,当CEF △周长最小时,点E ,F 的坐标分别为()A .53,22E ⎛⎫- ⎪⎝⎭,(0,2)F B .(2,2)E -,(0,2)F C .53,22E ⎛⎫- ⎪⎝⎭,20,3F ⎛⎫ ⎪⎝⎭D .(2,2)E -,20,3F ⎛⎫⎪⎝⎭23.(2024高二上·广东深圳·期中)过定点A 的动直线0x ky +=和过定点B 的动直线210kx y k --+=交于点M ,则MA MB +的最大值是()A .B .3C D24.(2024高二下·陕西西安·期末)设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ,则PA PB ⋅的最大值是()AB C .5D .1025.(河北省张家口市2023-2024学年高二上学期期末数学试题)已知0x y +=,则)AB .CD .26.(2024·贵州·模拟预测)已知,x y +∈R ,满足22x y +=,则x 的最小值为()A .45B .85C .1D .1327.(2024·上海静安·二模)设直线1:220l x y --=与2l 关于直线:240l x y --=对称,则直线2l 的方程是()A .112220x y +-=B .11220x y ++=C .5110x y +-=D .10220x y +-=28.(2024高三·北京·+的最小值所属区间为()A .[10,11]B .(11,12]C .(12,13]D .前三个答案都不对29.(2024·北京)在平面直角坐标系中,记d 为点()cos ,sin P θθ到直线20x my --=的距离,当θ、m 变化时,d 的最大值为A .1B .2C .3D .4二、多选题30.(2024高二下·江苏南京·期末)已知动点,A B 分别在直线1:3460l x y -+=与2:34100l x y -+=上移动,则线段AB 的中点P 到坐标原点O )A B .75C D 31.(24-25高二上·全国·单元测试)已知两条直线1l ,2l 的方程分别为34120x y ++=与8110ax y +-=,下列结论正确的是()A .若12//l l ,则6a =B .若12//l l ,则两条平行直线之间的距离为74C .若12l l ⊥,则323a =D .若6a ≠,则直线1l ,2l 一定相交32.(24-25高二上·全国·课后作业)已知直线l 10y -+=,则下列结论正确的是()A .直线l 的一个法向量为)B .若直线m :10x +=,则l m ⊥C .点)到直线l 的距离是2D .过()2与直线l 40y --=33.(2024高二下·江西南昌·阶段练习)已知曲线e 2xy =和直线:240l x y --=,则()A .曲线上与直线l 平行的切线的切点为e 1,2⎛⎫⎪⎝⎭B .曲线上与直线l 平行的切线的切点为10,2⎛⎫⎪⎝⎭C .曲线上的点到直线lD .曲线上的点到直线l 的最短距离为(3e 5+34.(福建省莆田第三中学,励志学校2023-2024学年高二上学期期中联考数学试卷)以下四个命题叙述正确的是()A .直线210x y -+=在x 轴上的截距是1B .直线0x ky +=和2380x y ++=的交点为P ,且P 在直线10x y --=上,则k 的值是12-C .设点(,)M x y 是直线20x y +-=上的动点,O 为原点,则OM 的最小值是2D .直线()12:310:2110L ax y L x a y ++=+++=,,若12//L L ,则3a =-或2三、填空题35.(2024高二·全国·课后作业)已知(),6A a ,()2,B b -,点()2,3P 是线段AB 的中点,则a b +=.36.(2024高二·江苏·假期作业)已知点(),4M x -与点()2,3N 间的距离为x =.37.(2024高三上·河北廊坊·阶段练习)与直线:2310l x y -+=关于点()4,5对称的直线的方程为.38.(2024高一·全国·课后作业)已知直线l 与直线1:1l y =及直线2:70l x y +-=分别交于点P ,Q .若PQ 的中点为点()1,1M -,则直线l 的斜率为.39.(2024高二上·辽宁大连·阶段练习)设点A 在x 轴上,点B 在y 轴上,AB 的中点是1(2)P -,,则AB 等于40.(2024高三上·黑龙江哈尔滨·期中)点()0,1-到直线()2y k x =+的距离的最大值是.41.(2024高二上·江苏南通·期中)已知点A 在x 轴上,点B 在y 轴上,线段AB 的中点M 的坐标为()2,1-,则线段AB 的长度为.42.(2024高二·全国·课堂例题)已知点()2,1A ,()3,4B ,()2,1C --,则ABC V 的面积为.43.(2024·云南保山·一模)已知坐标原点为O ,过点()P 2,6作直线()2mx 4m n y 2n 0(m,-++=n 不同时为零)的垂线,垂足为M ,则OM 的取值范围是.44.(2024高二上·全国·课后作业)已知点(),2P a 、()2,3A --、()1,1B ,且PA PB =,则a =.45.(2024高二上·安徽六安·期中)已知两直线1110a x b y +-=和2210a x b y +-=的交点为(1,2)P ,则过111(,),Q a b 222(,)Q a b 两点的直线方程为.46.(2024高三上·上海青浦·阶段练习)在平面直角坐标系xOy 中,若动点(,)P a b 到两直线1:l y x =和2:2l y x =-+,则22a b +的最大值为.47.(2024·四川)在平面直角坐标系内,到点A (1,2),B (1,5),C (3,6),D (7,﹣1)的距离之和最小的点的坐标是.48.(2024高三·陕西·阶段练习)若直线m 被两平行线1:10l x y -+=与2:30l x y -+=所截得的线段的长为m 的倾斜角可以是①15°,②30°,③45°,④60°,⑤75°.其中正确答案的序号是(写出所有正确答案的序号).49.(2024高三·全国·专题练习)在平面直角坐标系xOy 中,将直线l 沿x 轴正方向平移3个单位长度,沿y 轴正方向平移5个单位长度,得到直线l 1.再将直线l 1沿x 轴正方向平移1个单位长度,沿y 轴负方向平移2个单位长度,又与直线l 重合.若直线l 与直线l 1关于点(2,3)对称,则直线l 的方程是.50.(2024高三·全国·专题练习)点()0,0,()3,4到直线l 的距离分别为1和4,写出一个满足条件的直线l 的方程:.51.(2024高一·全国·课后作业)经过直线3x+2y+6=0和2x+5y-7=0的交点,且在两坐标轴上的截距相等的直线方程为.52.(2024高二上·全国·课后作业)经过点(1,0)P 和两直线1:220l x y +-=;2:3220l x y -+=交点的直线方程为.53.(2024·黑龙江哈尔滨·模拟预测)已知实数1212,,,x x y y ,满足22114x y +=,22229x y +=,12120x x y y +=,则112299x y x y +-++-的最小值是.四、解答题54.(2024高二上·广东东莞·期中)在平面直角坐标系xOy 中,已知ABC V 的三个顶点(,),(2,1),(2,3)A m n B C -.(1)求BC 边所在直线的方程;(2)若ABC V 的面积等于7,且点A 的坐标满足2360-+=m n ,求点A 的坐标.55.(24-25高二上·全国·课后作业)已知直线l 经过点()2,1P -,且平行于向量()1,1.(1)求直线l 的方程;(2)若直线m 与l 平行且点P 到直线mm 的方程.56.(2024高二上·天津河西·阶段练习)已知直线()():12360m a x a y a -++-+=,:230n x y -+=.(1)若坐标原点O 到直线m ,求a 的值;(2)当0a =时,直线l 过m 与n 的交点,且它在两坐标轴上的截距相反,求直线l 的方程.57.(2024高二·全国·课后作业)已知点()()1,3,5,2A B -,点P 在x 轴上使AP BP -最大,求点P 的坐标.。
河北省衡水中学11-12学年高一下学期二调考试(数学文)

2011—2012学年度第二学期第二次调研考试高一年级数学(文科)试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)注意事项:1.答卷Ⅰ前,考生将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.答卷Ⅰ时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
一、 选择题(每小题5分,共60分。
下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)1. 下列两个变量之间的关系是相关关系的是 ( )A.正方体的棱长和体积B.单位圆中角的度数和所对弧长C.单产为常数时,土地面积和总产量D.日照时间与水稻的亩产量2.在下列各数中,最小的数是 ( )A 、)9(85B 、)6(210C 、)4(1000D 、)2(111113.阅读右侧程序:如果输入x =2,则输出结果y 为 ( )A .π-5B .-π-5C .3+πD .3-π4.与01303终边相同的角是 ( )A .0763B .0493C .0371-D .047-5. 已知点A (1,2,-1),点C 与点A 关于xOy 面对称,点B 与点A 关于x 轴对称,则|BC |的值为 ( ) A. 2 5 B. 4 C. 2 2 D. 276.图1是某地参加2011年高考的学生身高统计图,从左到右的各长方形表示的学生人数依次记为1021,A A A ,,(如2A 表示身高(单位:cm )在[)150,155内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~185cm (含160cm ,不含185cm )的学生人数,那么在流程图中的判断框内应填写的条件是 ( ) A.9i < B.8i < C.7i < D.6i <第3题7.有四个游戏盘面积相等,将它们水平放稳后,在上面扔一颗玻璃小球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是 ( )8.某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为( ) A .63.6万元 B .65.5万元 C .67.7万元 D .72.0万元9. 执行如图所示的程序框图,若输出的n =6,则输入整数p 的最大值是( )A.32B.31C.15D.1610.已知圆的方程为08622=--+y x y x 设该圆中过点(3,5)的最长 弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积是 ( )A .610B .620C .630D .640第9题图S=S+2 n-111.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案.使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,195,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中,正确的是 ( )A .②、③都不能为系统抽样B .②、④都不能为分层抽样C .①、④都可能为系统抽样D .①、③都可能为分层抽样12. 对任意实数,a b ,定义运算“*”如下:x x f b a b b a a b a 221log )23(log )().(),(*-=⎩⎨⎧>≤=*则函数 x x x f b a b b a a b a 221log )23(log )().(),(*-=⎩⎨⎧>≤=*则函数的值域为 ( ) A .[)+∞,0 B .(]0,∞- C .)0,32(log 2 D .),32(log 2+∞ 第Ⅱ卷(非选择题 共90分)二、 填空题(每题5分,共20分。
2011-2012学年度初一第二学期课表(2月10日)
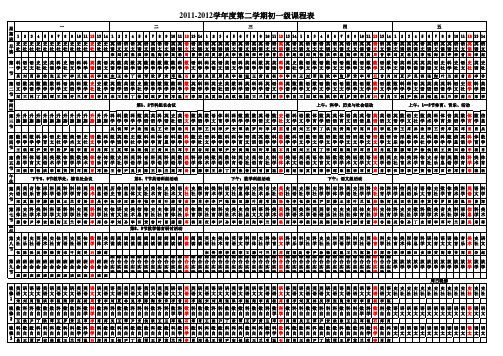
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 实 践
综 合 放 放 放 放 放 放 放 放 放 放 放 放 实 学 学 学 学 学 学 学 学 学 学 学 学 践 周日晚修
吴 刘 周 孙 徐 张 王 叶 李 兰 温 杨 李 赵 宋 王 林 丁 洪 谭 欧 罗 黄 邓 温 石 曾 郑 吴 夏 周 吴 李 候 温 王 黄 高 杨 李 李 谷 王 刘 谭 张 欧 李 陶 罗 黄 李 邓 石 曾 肖 刘 夏 尹 吴 洪 张 陶 叶 兰 郭 曾 茹
第 语 数 英 数 数 数 科 语 英 科 数 史 史 数 英 数 英 数 史 数 数 数 数 数 科 数 英 科 科 英 史 英 数 科 英 科 科 英 语 科 英 数 数 语 数 语 数 语 语 数 数 语 数 数 语 数 数 科 科 语 英 英 英 英 科 语 史 数 二 文 学 语 学 学 学 学 文 语 学 学 社 社 学 语 学 语 学 社 学 学 学 学 学 学 学 语 学 学 语 社 语 学 学 语 学 学 语 文 学 语 学 学 文 学 文 学 文 文 学 学 文 学 学 文 学 学 学 学 文 语 语 语 语 学 文 社 学 节 刘 王 林 丁 欧 谭 王 陶 许 兰 邓 茹 谷 肖 宋 王 林 丁 徐 谭 欧 罗 黄 邓 温 石 李 郑 吴 夏 孙 吴 欧 候 温 王 兰 高 曾 李 李 肖 王 刘 谭 张 欧 李 陶 罗 黄 李 邓 石 曾 肖 王 候 尹 张 洪 张 温 宋 兰 李 茹 石 课 第1、2节科组长会议 上午:科学、历史与社会活动 上午:1--3节体育、音乐、活动 间 操 第 升 升 升 升 升 升 升 升 升 升 升 升 升 升 科 科 数 科 数 英 英 科 英 史 英 语 数 英 数 语 体 科 科 数 数 数 英 语 数 史 语 科 语 数 体 数 英 英 体 语 英 英 信 英 英 语 英 数 语 史 数 美 科 体 音 英 数 体 三 旗 旗 旗 旗 旗 旗 旗 旗 旗 旗 旗 旗 旗 旗 学 学 学 学 学 语 语 学 语 社 语 文 学 语 学 文 育 学 学 学 学 学 语 文 学 社 文 学 文 学 育 学 语 语 育 文 语 语 息 语 语 文 语 学 文 社 学 术 学 育 乐 语 学 育 节 吴 候 谭 尹 欧 张 温 王 许 郭 杨 周 肖 李 王 刘 李 尹 安 谭 欧 罗 许 李 邓 茹 曾 郑 刘 王 李 丁 洪 张 黄 陶 许 高 田 杨 李 赵 宋 王 周 孙 欧 李 王 黄 邓 高 邓 曾 第 数 科 数 科 体 语 史 数 美 语 史 语 数 科 数 英 数 史 数 科 科 体 信 科 数 科 数 史 语 科 数 科 科 体 语 英 英 数 科 数 数 科 语 数 语 数 语 数 数 语 语 数 语 语 数 语 音 形 数 科 史 科 数 科 数 信 英 科 四 学 学 学 学 育 文 社 学 术 文 社 文 学 学 学 语 学 社 学 学 学 育 息 学 学 学 学 社 文 学 学 学 学 育 文 语 语 学 学 学 学 学 文 学 文 学 文 学 学 文 文 学 文 文 学 文 乐 体 学 学 社 学 学 学 学 息 语 学 节 王 候 谭 尹 黄 李 昝 罗 蒋 李 茹 周 肖 郑 王 夏 谭 孙 欧 候 王 黄 田 兰 邓 李 肖 谷 刘 候 谭 尹 安 黄 陶 宋 许 邓 温 石 肖 郑 刘 王 周 丁 李 谭 欧 陶 李 邓 曾 周 肖 赵 陈 滕 谭 尹 徐 侯 欧 王 黄 田 杨 李 第 信 科 体 语 英 美 数 体 数 数 美 体 音 体 数 史 科 英 科 音 科 英 科 英 数 英 科 形 美 数 英 数 体 英 史 英 体 史 科 形 美 语 英 英 语 体 语 数 数 美 语 数 语 语 数 英 史 体 美 科 体 史 音 信 英 数 体 科 五 息 学 育 文 语 术 学 育 学 学 术 育 乐 育 学 社 学 语 学 乐 学 语 学 语 学 语 学 体 术 学 语 学 育 语 社 语 育 社 学 体 术 文 语 语 文 育 文 学 学 术 文 学 文 文 学 语 社 育 术 学 育 社 乐 息 语 学 育 学 节 田 候 李 张 洪 李 欧 黄 黄 邓 蒋 曾 邓 杨 王 昝 尹 吴 安 陈 王 宋 兰 高 邓 杨 郑 滕 李 王 林 丁 黄 张 昝 宋 曾 郭 温 滕 蒋 赵 宋 夏 周 李 李 谭 欧 蒋 李 邓 曾 周 肖 李 伍 李 李 尹 黄 徐 邓 田 许 邓 曾 李 午 休 下午8、9节教学处、德育处会议 第6、7节英语科组活动 下午:数学科组活动 下午:语文组活动
【师说】2021-2022学年高一人教版数学必修二练习:第3章 章末检测 3 Word版含答案

C.(1,1) D.(-2,0)
解析:∵l1:kx=x+y-2,由 得l1恒过定点(0,2),记为点P,∴与l1关于直线y=x+1对称的直线l2也必恒过肯定点,记为点Q,且点P和Q也关于直线y=x+1对称.令Q(m,n),则 ⇒ 即Q(1,1),∴直线l2恒过定点(1,1),故选C.
即 ×|- |×b= (1-b)× .
整理得 = .
∴ = ,
∴ -1= ,∴ = +1,
(1) (2)
即b= ,可以看出,当a增大时,b也增大.
当a→+∞时,b→ ,即b< .
当a→0时,直线y=ax+b接近于y=b.
当y=b时,如图(2ห้องสมุดไป่ตู้, = = = .
∴1-b= ,∴b=1- .
∴b>1- .
(2分)
当x=y时,|x|= ,
即x2-4x+2=0,
解得x=2+ 或x=2- ;(6分)
当x=-y时,|x|= ,
解得x= 或x=- .(10分)
所以点P的横坐标为2+ ,2- , 或- .
(12分)
19.(本小题满分12分)已知△ABC的顶点A(3,-1),AB边上的中线所在直线方程为6x+10y-59=0,∠B的平分线所在直线方程为x-4y+10=0,求BC边所在直线的方程.
(2)设所求的直线方程为2x+3y-5+λ(7x+15y+1)=0,即(2+7λ)x+(3+15λ)y+λ-5=0,由已知- =- ,解得λ=1.
故所求的直线方程为9x+18y-4=0.(10分)
18.(本小题满分12分)点P(x,y)到x轴、y轴和直线x+y-2=0的距离相等,求点P的横坐标.
解析:由题意可知|x|=|y|= .
人教版数学高一-2012年高一数学暑假补充练习十二 综合试卷2
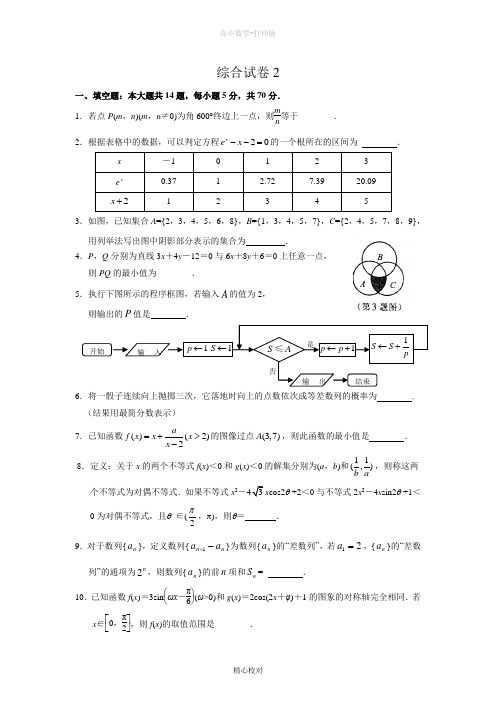
综合试卷2一、填空题:本大题共14题,每小题5分,共70分.1.若点P (m ,n )(m ,n ≠0)为角600°终边上一点,则mn等于________.2.根据表格中的数据,可以判定方程20x e x --=的一个根所在的区间为 .x-1 0 1 2 3 x e0.37 1 2.72 7.39 20.09 2x +123453.如图,已知集合A ={2,3,4,5,6,8},B ={1,3,4,5,7},C ={2,4,5,7,8,9}, 用列举法写出图中阴影部分表示的集合为 .4.P ,Q 分别为直线3x +4y -12=0与6x +8y +6=0上任意一点, 则PQ 的最小值为________.5.执行下图所示的程序框图,若输入A 的值为2, 则输出的P 值是 .6.将一骰子连续向上抛掷三次,它落地时向上的点数依次成等差数列的概率为 . (结果用最简分数表示) 7.已知函数()(2)2af x x x x =+>-的图像过点(3,7)A ,则此函数的最小值是 _ . 8.定义:关于x 的两个不等式f (x )<0和g (x )<0的解集分别为(a ,b )和11(,)b a,则称这两个不等式为对偶不等式.如果不等式x 2-43x cos2θ +2<0与不等式2x 2-4x sin2θ +1<0为对偶不等式,且θ ∈(2π,π),则θ= . 9.对于数列{n a },定义数列{n n a a -+1}为数列{n a }的“差数列”,若21=a ,{n a }的“差数列”的通项为n2,则数列{n a }的前n 项和n S = .10.已知函数f (x )=3sin ⎝⎛⎭⎫ωx -π6(ω>0)和g (x )=2cos(2x +φ)+1的图象的对称轴完全相同.若x ∈⎣⎡⎦⎤0,π2,则f (x )的取值范围是________. 否是输出输入结束开始 1p ←1S ←S A≤1p p ←+1S S p←+11.若不等式组⎩⎪⎨⎪⎧x ≥0x +3y ≥43x +y ≤4所表示的平面区域被直线y =kx +43分为面积相等的两部分,则k 的值是______ .12.设()y f x =函数在(,)-∞+∞内有定义,对于给定的正数K ,定义函数:()()(),()1,()K f x f x Kf x f x Kf x ⎧⎪=⎨>⎪⎩≤,取函数()x f x a -=(a >1),当1K a =时,函数()K f x 值域是______ .13.已知△ABC 所在平面上的动点M 满足222AM BC AC AB ⋅=-,则M 点的轨迹过△ABC的心.14.若不等式a +21x x -≥2log 2x在x ∈(12,2)上恒成立,则实数a 的取值范围为 .二、解答题:本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70),…,[90,100)后画出如下部分..频率分布直方图.观察图形的信息,回答下列问题: (1)求出物理成绩低于50分的学生人数;(2)估计这次考试物理学科及格率(60分及以上为及格);(3)从物理成绩不及格的学生中任选两人,求他们成绩至少有一个不低于50分的概率.16.(本小题满分14分)已知向量(sin ,cos sin )x x x =+a , (2cos ,cos sin )x x x =-b ,x R ∈,设函数()f x =⋅a b (1)求函数)(x f 的最大值及相应的自变量x 的取值集合;(2)当0(0,)8x π∈且0()f x =0()3f x π+的值.17.(本小题满分14分)已知三条直线l 1:2x -y +a = 0 (a >0),直线l 2:-4x +2y +1 = 0和直线l 3:x +y -1= 0 ,且l 1与l 2. (1)求a 的值;(2)能否找到一点P ,使得P 点同时满足下列三个条件:①P 是第一象限的点;②P 点到l 1的距离是P 点到l 2的距离的21;③P 点到l 1的距离与P 点到l 3若能,求P 点坐标;若不能,说明理由.18.(本小题满分16分)已知函数()1x f x a =-(0a >且1)a ≠. (1)求函数()f x 的定义域、值域;(2)是否存在实数a ,使得函数()f x 满足:对于任意[1,)x ∈-+∞,都有()0f x ≤?若存在,求出的取值范围;若不存在,请说明理由.19.(本小题满分16分)如图,某市市区有过市中心O 南北走向的解放路,为了解决南徐新城的交通问题,市政府决定修建两条公路:延伸从市中心O 出发北偏西60°方向的健康路至B 点;在市中心正南方向解放路上选取A 点,在A 、B 间修建南徐新路.(1)如果在A 点处看市中心O 和B 点视角的正弦值为35,求在B 点处看市中心O 和A 点视 角的余弦值;(2) 如果△AOB 区域作为保护区,已知保护区的面积为1543 km 2,A 点距市中心的距离为3 km ,求南徐新路的长度;(3) 如果设计要求市中心O 到南徐新路AB 段的距离为4 km ,且南徐新路AB 最短,请你确定A 、B 两点的位置.20.(本小题满分16分)定义数列{}n a :11a =,当2n ≥ 时,11,2,,2,21,.n n n a r n k k N a a n k k N *-*-⎧+=∈⎪=⎨=-∈⎪⎩ 其中, 0r ≥为常数.(1)当0r =时, 123n n S a a a a =++++.①求:n S ; ②求证:数列{}2n S 中任意三项均不能够成等差数列;(2)求证:对一切n N *∈及0r ≥,不等式121224knk k ka a =-<∑恒成立.。
河北衡水中学11—12学度高一下学期三调考试(数学理)

河北衡水中学11—12学度高一下学期三调考试(数学理)高一年级数学〔理科〕试卷本试卷分第一卷〔选择题〕和第二卷(非选择题)两部分,共150分。
考试时间120分钟。
第一卷〔选择题 共60分〕本卷须知1.答卷Ⅰ前,考生将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.答卷Ⅰ时,每题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
一、 选择题〔每题5分,共60分。
以下每题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上〕 1、cos600°的值等于( )、 AB 、-21C、D 、-23A 、→→→→≥⋅ba b a B 、关于任意向量,,→→b a 有→→→→+≥+ba b aC 、假设→→=ba ,那么→→=ba 或→→-=ba D 、关于任意向量,,→→b a 有→→→→-≥+ba b a3、设250cos 1,13tan 113tan 2,6sin 236cos 212︒-=︒-︒=︒-︒=c b a ,那么a 、b 、c 的大小顺序是()A.c b a <<B.b c a <<C.c a b <<D.a c b << 4、记cos(80),tan 80k -︒=︒那么= () A、C、21k k --5、假设02πα<<,02πβ-<<,1cos()43πα+=,cos()42πβ-=cos()2βα+=〔〕AB、CD、6、设平面上有四个互异的点A 、B 、C 、D ,,0)()2(=-⋅-+→→→→→AC AB DA DC DB 那么△ABC的形状是〔〕A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形 7、函数)sin()(ϕω+=x A x f (2||,0,0,πϕω<>>∈A R x )的图象〔部分〕如下图,那么)(x f 的解析式是() A 、))(6sin(2)(R x x x f ∈+=ππB 、))(62sin(2)(R x x x f ∈+=ππC 、))(3sin(2)(R x x x f ∈+=ππD 、))(32sin(2)(R x x x f ∈+=ππ8、设向量),25sin ,25(cos ),55sin ,55(cos ︒︒=︒︒=→→b a 假设t 是实数,那么→-a 值为()A.22B 、2C 、1D 、219、设O 为△ABC 的外心,平面上的点P 使OP OA OB OC→→→→=++,那么点P 是△ABC 的〔〕A 、外心B 、垂心C 、内心D 、重心10、扇形OAB 的半径为2,圆心角060AOB ∠=,点D 是弧AB 的中点,点C 在线段OA 上,且OC =,那么CD OB →→⋅的值为() A 、B 、CD11、方程,02→→→→=++c x b x a 其中→→→cb a 、、是非零向量,且→→ba 、不共线,那么该方程()A 、至少有一个解B 、至多有一个解C 、至多有两个解D 、可能有许多个解12、如图,半径为2的⊙M 切直线AB 于O 点,射线OC 从OA 动身绕着O 点顺时针方向旋转到OB .旋转过程中, OC 交⊙M 于P ,记PMO ∠为x ,弓形PNO 的面积为 )(x f S =,那么)(x f 的图象是〔〕ABCD第二卷〔非选择题共90分〕二、填空题〔每题5分,共20分。
河北省衡水中学11—12学年高一下学期三调考试(数学理)

2011—2012学年度第二学期三调考试高一年级数学(理科)试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)注意事项:1.答卷Ⅰ前,考生将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.答卷Ⅰ时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
一、选择题(每小题5分,共60分。
下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上) 1、cos600°的值等于( ).A B .-21C .D .-23 2、下列命题中,正确的是( )A .→→→→≥⋅b a b a B .对于任意向量,,→→b a 有→→→→+≥+b a b aC .若→→=b a ,则→→=b a 或→→-=b a D .对于任意向量,,→→b a 有→→→→-≥+b a b a3、设250cos 1,13tan 113tan 2,6sin 236cos 212︒-=︒-︒=︒-︒=c b a ,则a 、b 、c 的大小顺序是( )A.c b a <<B. b c a <<C.c a b <<D. a c b << 4、记cos(80),tan 80k -︒=︒那么= ( )A. C .21kk --5、若02πα<<,02πβ-<<,1cos()43πα+=,cos()42πβ-=cos()2βα+=( )A B .C D .6、设平面上有四个互异的点A 、B 、C 、D ,已知,0)()2(=-⋅-+→→→→→AC AB DA DC DB 则△ABC的形状是( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形7、已知函数)sin()(ϕω+=x A x f (2||,0,0,πϕω<>>∈A R x )的图象(部分)如图所示,则)(x f 的解析式是 ( ) A .))(6sin(2)(R x x x f ∈+=ππ B .))(62sin(2)(R x x x f ∈+=ππ C .))(3sin(2)(R x x x f ∈+=ππ D .))(32sin(2)(R x x x f ∈+=ππ8、设向量),25sin ,25(cos ),55sin ,55(cos ︒︒=︒︒=→→b a 若t 是实数,则→-a ( )A.22 B .2 C .1 D .219、设O 为△ABC 的外心,平面上的点P 使OP OA OB OC →→→→=++,则点P 是 △ABC 的( )A .外心B .垂心C .内心D .重心10、扇形OAB 的半径为2,圆心角060AOB ∠=,点D 是弧AB 的中点,点C 在线段OA 上,且OC =,则CD OB →→⋅的值为( )A .B .CD11、已知方程,02→→→→=++c x b x a 其中→→→c b a 、、是非零向量,且→→b a 、不共线,则该方程( ) A .至少有一个解B .至多有一个解C .至多有两个解D .可能有无数个解12、如图,半径为2的⊙M 切直线AB 于O 点,射线OC 从OA 出发绕着O 点顺时针方向旋转到OB .旋转过程中, OC 交⊙M 于P ,记PMO ∠为x ,弓形PNO 的面积为)(x f S =,那么)(x f 的图象是( )A B C D第Ⅱ卷(非选择题 共90分)二、填空题(每题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11-12学年度下学期高一数学练习3(03)12-2-14直线与圆的方程的应用、空间直角坐标系一.选择题.共6题小题,每题5分.每题有且仅有一个选项正确,所选答案填写到后面指定的表中.1.如图所示空间直角坐标系的直观图中,正确的个数为 ()A .1B .2C .3D .42.点M (3,-3,1)关于xOy 平面的对称点是 ( ) A . (3,-3,-1) B . (-3, 3,1) C . (3,3,-1) D . (-3,-3, 1) 3.两圆x 2+y 2-2x +10y +1=0,x 2+y 2-2x +2y -m =0相交,则m 的取值范围是( )A .(-2,39)B .(0,81)C .(0,79)D .(-1,79)4.已知半径为1的动圆与圆C :(x -5)2+(y +7)2=16相切,则动圆圆心的轨迹方程是( )A .(x -5)2+(y +7)2=25B .(x -5)2+(y +7)2=25或(x -5)2+(y +7)2=9C .(x -5)2+(y +7)2=9D .(x -5)2+(y +7)2=17或(x -5)2+(y +7)2=155.若集合A ={(x ,y )|x 2+y 2≤16},B ={(x ,y )|x 2+(y -2)2≤a -1}且A ∩B =B ,则a 的取值范围是 ( )A .a ≤5B .a ≥5C .1≤a ≤5D . 15a <≤ 6.函数()f t = ( ) A.[2,4]B. [-C.D.题号 1 2 3 4 5 6答案二.填空题.共4道小题每小题5分.将最简答案填在本大题后面指定的横线上.7.若A (3,3,1),B (1,0,5),C (0,1,0),则AB 的中点M 与点C 间的距离为___ _____.8.在空间直角坐标系中,正方体ABCD -A 1B 1C 1D 1的顶点A (3,-1,2),其中心M 的坐标为(0,1,2),则该正方体的棱长等于___ _____.9.由动点P 向圆x 2+y 2=1引两条切线PA 、PB ,切点分别为A 、B ,且∠APB =60°,则动点P 的轨迹方程为____ ____.10.点P 在圆O: x 2+y 2=1上运动,点Q 在圆C :(x -3)2+y 2=1上运动,则PQ 的最小值为____ ____.高一__ __班 学号_____ 姓名__________ 成绩__________三.解答题.解答应写出文字说明、证明过程或演算步骤.共50分.11.矩形ABCD 中,AB ∶BC =4∶3,点E 在边CD 上,且CE ∶ED =1∶7,试用坐标法确定以BC 为直径的圆与直线AE 的位置关系.12. 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.(1)求点P的轨迹方程;(2)求|PQ|的最小值;(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.13.已知方程x2+y2-2x-4y+m=0.(1)此方程表示圆,求m的取值范围;(2) 直线x+2y-4=0 与(1)中的圆交于M、N,且OM⊥ON(O为坐标原点),求m的值;(3)在(2)的条件下,求以MN为直径的圆的方程.14.某地即将受到台风的影响.台风中心位于该地气象台A正西方向300千米处,它以每小时40千米的速度向东北方向移动,距台风中心250千米以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台A所在地将遭受台风影响?持续多长时间?15.在直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.(1)斜率分别等于2 、12的直线1l、2l都通过点(,)M a b,且1l被圆C1截得的弦长与2l被圆C2截得的弦长都等于为5,求点(,)M a b的坐标;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被C2截得的弦长相等.试求所有满足条件的点P 的坐标.高 一 数 学 周 练 答 案第3周练习:直线与圆的方程的应用、空间直角坐标系一.选择题. CAD BAC 提示:1.解析:图(3)不符合右手系的要求,图(4)中水平坐标平面上的,x y 轴按135︒的情况所作出,符合斜二侧画法.只有(3)不符合要求,选 C.2.解析:空间中的一点关于xOy 对称的点的坐标是x ,y 不变,z 变为原来的相反数,即所求的点是(3,-3,-1). 答案:(3,-3,-1)3.解析:选D.两圆的方程分别可化为(x -1)2+(y +5)2=25,(x -1)2+(y +1)2=m +2. 由此,20m +>,2m >-,又两圆相交,得|5-m +2|<4<5+m +2,解之得-1<m <79. 综合知,选D.4.解析:选B.设动圆圆心为M (x ,y ),因为动圆M 与定圆C 相切.所以|MC |=1+4=5或|MC |=4-1=3,代入坐标整理,得(x -5)2+(y +7)2=25或(x -5)2+(y +7)2=9.5.解析:选A.由A ∩B =B 知B ⊆A ,故a -1≤4,即a ≤5. 注意,因为B =∅也可以,所以不需限定1a ≥.6.解析:定义域为[1,-,设,()2t y f t x y c=-==+=,由于有 22134x y t t +=++-=,0,0x y ≥≥,于是由图中的四分之一圆周与直线2x y c +=2≤,所以,c -≤≤,又当直线2x y c +=过点(0,2)时,其在y 轴上的截距c 最小,最小截距等于2,于是2c ≤≤选C.二.填空题.7.532 8.23939.x 2+y 2=4 10.1 提示:7.解析:利用中点坐标公式得M ⎝⎛⎭⎫2,32,3,再利用空间两点间的距离公式求解.答案:532 8.解析:∵AM =(3-0)2+(-1-1)2+(2-2)2=13,∴正方体的体对角线长为213, ∵3a 2=52(a 为正方体的棱长),∴a =2393. 答案:2393.9.解析:由题意得满足条件的图形,如图所示.∵∠APB =60°,∠OPB =30°,即|OP |=2|OB |=2.∴点P 的轨迹是以原点为圆心,半径为2的圆,其方程为x 2+y 2=4. 答案:x 2+y 2=410.解析:如图.设连心线OC 与圆O 交于点P ′,与圆C 交于点Q ′,当点P在P ′处,点Q 在Q ′处时PQ 最小,最小值为P ′Q ′=OC -r 1-r 2=1. 答案:1.三.解答题.11.解:如图,分别以AB 、AD 所在直线为x ,y 轴建立平面直角坐标系.不妨设∴直线AE 的方程为y =67x , 即6x -7y =0.BC 中点为M (8,3),∴以BC 为直径的圆的方程为(x -8)2+(y -3)2=9.M (8,3)到AE 的距离d =|6×8-7×3|62+(-7)2=2785<2781=3=r .∴直线AE 与圆相交.12. 解:(1)设点P 的坐标为(,)x y ,连接OQ 、OP ,则△OQP 为直角三角形, 又|PQ |=|PA |, 所以|OP |2=|OQ |2+|PQ |2 =1+|PA |2,所以x 2+y 2=1+(x -2)2+(y -1)2, 故2x +y -3=0.即为点P 的轨迹方程.(2)由(1)知,P 在直线l :2x +y -3=0上, 所以|PQ |min =|PA |min ,为A 到直线l 的距离,所以|PQ |min =|2×2+1-3|22+12=255.(或由|PQ |2=|OP |2-1=x 2+y 2-1=x 2+9-12x +4x 2-1=5x 2-12x +8=5(x -1.2)2+0.8,得|PQ |min =255.)(3)以P 为圆心的圆与圆O 有公共点,半径最小时为与圆O 相切的情形,而这些半径的最小值为圆O 到直线l 的距离减去圆O 的半径,圆心P 为过原点与l 垂直的直线l ′与l 的交点P 0,所以r =322+12-1=355-1, 又l ′:x -2y =0,联立l :2x +y -3=0得P 0(65,35). 所以所求圆的方程为(x -65)2+(y -35)2=(355-1)2.13.解:(1)方程x 2+y 2-2x -4y +m =0,可化为 (x -1)2+(y -2)2=5-m ,∵此方程表示圆, ∴5-m >0,即m <5.(2)⎩⎪⎨⎪⎧x 2+y 2-2x -4y +m =0,x +2y -4=0,消去x 得(4-2y )2+y 2-2×(4-2y )-4y +m =0, 化简得5y 2-16y +m +8=0.设M (x 1,y 1),N (x 2,y 2),则⎩⎨⎧y 1+y 2=165, ①y 1y 2=m +85. ②由OM ⊥ON 得y 1y 2+x 1x 2=0 , 即y 1y 2+(4-2y 1)(4-2y 2)=0, ∴16-8(y 1+y 2)+5y 1y 2=0.将①②两式代入上式得 16-8×165+5×m +85=0, 解之得m =85.且满足0∆>,所以所求的值为m =85.(3)由m =85,代入5y 2-16y +m +8=0,化简整理得25y 2-80y +48=0,解得y 1=125,y 2=45.∴x 1=4-2y 1=-45,x 2=4-2y 2=125.∴M ⎝⎛⎭⎫-45,125,N ⎝⎛⎭⎫125,45, MN 的中点C 的坐标为⎝⎛⎭⎫45,85. 又|MN |= ⎝⎛⎭⎫125+452+⎝⎛⎭⎫45-1252=855, ∴所求圆的半径为455. ∴所求圆的方程为⎝⎛⎭⎫x -452+⎝⎛⎭⎫y -852=165. 14.思路:遭受台风影响实际就是点在圆上或圆内的问题.利用“解析法”来解决.以A 为圆心,半径等于250千米圆方程为222(300)250x y -+=,直线BC 的方程为(0)y x x =≥. 当且仅当直线BC 与圆A 有公共点时,气象台A 所在地将遭受台风影响,由222(300)250x y y x⎧-+=⎨=⎩得,22600275000x x -+= 260042275001400000∆=-⨯⨯=>,所以直线BC 与圆A 相交,设两交点B 、C 的横坐标分别为12,x x ,则1212300,13750x x x x +==BC ===O 直线BC 中点M的距离cos 45300OM OA =︒==,于是,12OB OM BC =-==1.99≈(小时)后气象台A 开始受台风影响6.61=≈(小时)答:气象台大约在2小时后受到台风影响,持续时间大约6小时37分钟. 解法二 以气象台为坐标原点,正东方向为x 轴正方向,建立直角坐标系如图,则现在台风中心B 的坐标为(-300,0).根据题意,可知,t 小时后,台风中心B ′的坐标为(-300+40tcos45°,40tsin45°),即(-300+202t ,202t ).因为以台风中心为圆心,以250千米为半径的圆上或圆内的点将遭受台风影响,所以B ′在圆上或圆内时,气象台将受台风影响.所以令|AB ′|≤250,即(-300+202t )2+(202t )2≤2502,理得16t 2-1202t+275≤0,解得475215475215+≤≤-t ,1.99≤t ≤8.61. 故大约2小时后,气象台A 所在地将遭受台风影响,大约持续6小时37分. 15. 解:(1)设直线1l 的方程为2y x m =-+,直线2l 的方程为12y x n =+,两圆半径相等,它们圆心分别到两直线的距离相等,设为d,则d ==. 由点到直线的距离公式得d==从而4m =-或6m =-,52n =或72n =所以直线1l 的方程为26y x =--或24y x =--.直线2l 的方程为1522y x =+或1722y x =+,由它们联立,可解得点M 的坐标为:198(,)55-、174(,)55-、136(,)55-或(3,2)- (2)设点P (a ,b )满足条件,不妨设直线l 1的方程为y -b =k (x -a ),k ≠0,则直线l 2的方程为y -b相等,所以圆C 1的圆心到直线l 1的距离和圆C 2的圆心到直线l 2的距离相等,即|1-k (-3-a )-b |1+k 2=|5+1k (4-a )-b |1+1k2,整理得|1+3k +ak -b |=|5k +4-a -bk |,从而1+3k +ak -b =5k +4-a -bk 或1+3k +ak -b =-5k -4+a +bk ,即(a +b -2)k =b -a +3或(a -b +8)k =a +b -5,因为k 的取值有无穷多个,所以⎩⎪⎨⎪⎧ a +b -2=0,b -a +3=0,或⎩⎪⎨⎪⎧a -b +8=0,a +b -5=0, 解得⎩⎨⎧a =52,b =-12,或⎩⎨⎧a =-32,b =132.这样点P 只可能是点P 1⎝⎛⎭⎫52,-12或点P 2⎝⎛⎭⎫-32,132. 经检验点P 1和P 2满足题目条件.。
