徐州市2014届初中毕业生升学模拟考试数学试题(B卷)及答案
2014年徐州市树人中学9年级三模数学试卷

徐州市树人中学2014年初中毕业生第三次模拟考试数学试题(全卷满分:140分考试时间:120分钟)一、选择题:(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母填在答题框内.)1.6-的绝对值是()A.6-B.6C.16D.16-2.下列计算正确的是()A. a2+a3=a5B. a6÷a3=a2C. 4x2-3x2=1D. (-2x2y)3=-8 x6y33.如图所示的物体由两个紧靠在一起的圆柱体组成,它的主视图是()4.如图,直线AB、CD相交于点E,DF∥AB,若∠D=70°,则∠CEB等于( )A.70°B.80°C.90°D.110°5.五箱苹果的质量分别为(单位:千克):18,20,21,22,19.则这五箱苹果质量的平均数和中位数分别为()A.19和20 B.20和19 C.20和20 D.20和216.已知反比例函数的图象经过点P(1,-2),则这个函数的图象位于()A.第一、三象限B.第二、三象限C.第二、四象限D.第三、四象限7.如果两个相似三角形的相似比是1∶2,那么它们的面积比是()A.1∶2 B.1∶2C.1∶4 D.2∶18.如图,平行四边形纸片ABCD,CD=5,BC=2,∠A=60°,将纸片折叠,使点A落在射线AD上(记为点A'),折痕与AB交于点P,设AP的长为x,折叠后纸片重叠部分的面积为y,可以表示y与x之间关系的大致图象是()A.B.C.D.二、填空题(本大题共10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)9.4的平方根是.10.H7N9禽流感病毒颗粒有多种形状,其中球形直径约为0.00000012m.将0.00000012用科学记数法表示为11.如果∠A=55°,那么∠A的余角等于°.第4题图FCBADE第3题图主视方向D.A. B. C.第8题图D CA P BA'(第13题) 12.使x -2有意义的x 的取值范围是 .13.如图,人民币旧版壹角硬币内部的正多边形每个内角度数是 °.14.已知1y x =-,则2()()1x y y x -+-+的值为 .15.已知两圆的半径分别为2和3,两圆的圆心距为4,那么这两圆的位置关系是 _____16.如图,在Rt △ABC 中,∠ACB =90°,D 、E 、F 分别是AB 、BC 、CA 的中点,若CD =5cm ,则EF =cm .17.如图,已知正方形ABCD 的边长为12cm ,E 为CD 边上一点,DE =5cm .以点A 为中心,将△ADE按顺时针方向旋转得△ABF ,则点E 所经过的路径长为 cm .18.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数是三、解答题(本大题共10小题,共86分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或解题步骤))19.(本题10分)(1)计算:0)32013(221245cos 4--⨯÷-︒ ;(2)先化简,再求值:)4()2(2++-a a a ,其中a =3.20.(本题10分)(1)解不等式组:⎪⎩⎪⎨⎧+<-<-21123321x x x , (2)解方程:33112+-=+x x x x . F ED CB A (第17题)第18题并把解集在数轴上表示出来.21.(本题7分)王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和; (2)试通过计算各自的方差来说明,哪个山上的杨梅产量较稳定?22.(本题7分)将正面分别标有数字1、2、3、4、6,背面花色相同的五张卡片洗匀后,背面朝上放在桌面上,从中随机抽取两张。
江苏省徐州市2014年第一次质量检测(一模)

江苏省徐州市2014年第一次质量检测(一模)九年级数学试卷一、选择题(本大题共有8小题,每小题3分,共24分)..2.在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=2,则点D到AB 的距离是()324.下列根式中,与是同类二次根式的是()....5.如图,AB∥CD,AD、BC交于O点,∠BAD=35°,∠BOD=75°,则∠C的度数是()7.一个不透明的布袋中有10个大小形状质地完全相同的小球,从中随机摸出1球恰是黄球8.如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是()....二、填空题(本大题共有10小题,每小题3分,共30分)9.因式分解:y3﹣4y= _________.10.当a<2时,化简= _________.11.已知∠α=80°,则α的补角等于_________.12.中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于_________.13.如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF 与BD交于点O,若FO﹣EO=5,则BC﹣AD= _________.14.已知+|a+b+1|=0,则a﹣b的值等于_________.15.若两圆的半径分别为5和3,圆心距为6,则两圆位置关系是_________.16.已知x﹣=1,则x2+= _________.17.如图,在矩形ABCD中,AB=2,AD=4,E为CD边的中点,P为BC边上的任一点,那么,AP+EP的最小值为_________.18.如图,在直角坐标系xOy中,直线L:y=﹣x﹣1,双曲线y=.在L上取点A,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交L于点A2,再过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交L于点A3,…,这样依次得到L上的点A1,A2,A3,…,A n,….记点A n的横坐标为a n,若a1=2,则a2014= _________.三、解答题(本大题共有10小题,共86分)19.(1)计算:﹣12014+|﹣2|﹣(π﹣3)0;(2)解不等式组:.20.(1)解分式方程:﹣1=;(2)化简求值:(a﹣)÷.(选取一个合适的a的值代入求值)21.(7分)已知,如图,AC∥DE,AC=DE,BE=CF,求证:∠B=∠F.22.(7分)某校学生会计划在“五•一”前夕举行班级歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A、B、C、D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如图所示的两幅不完整的统计图.请根据图①、图②所提供的信息,解答下列问题:(1)本次抽样调查的学生有_________名;(2)请将图②补充完整;(3)若该校共有900名学生,试估计喜欢歌曲C的学生人数?23.(8分)某班45学生协商共建“和谐班委”议案,第一轮无记名方式海选出A、B、C、D四名同学;第二轮A、B、C、D中的2名自由组建“和谐班委”轮回值周,用列表或树状图法解决下列问题:(1)学生A、B获得首次值周的概率是多少?(2)学生A首次不值周的概率是多少?24.(8分)(2014•徐州一模)如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40m,小明的眼睛离地面为1.6m,求楼的高度.25.(8分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.26.(8分)如图,直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.(1)若⊙O的半径为8,求CD的长;(2)求证:PE=PF.27.(10分)某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图.(1)求日均销售量p(桶)与销售单价x(元)的函数关系;(2)若该经营部希望日均获利1350元,那么日均销售多少桶水?28.(10分)在△ABC中,AB=4,BC=6,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△CBC1的面积为3,求△ABA1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按顺时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.∴-x=0 ∴x=0………………………4分经检验x=0是原分式方程的根………………………5分(2)(a -a 1)÷1122+++a a a =a 1a 2-·121+++a a a ………………………1分=a a a )1)(1(-+·2)1(1++a a =a a 1-………………………3分 求值时a 不能的取值有0和-1………………………5分21.证:∵AC ∥DE ∴∠BCA=∠FED ………………………2分∵BE=CF ∴BC=FE ………………………4分又∵AC=DE ∴△ABC ≌△DFE ………………………6分 ∴∠B=∠F ………………………7分22.(1)180………………………2分(2)高度为72………………………5分(3)360人………………………7分 23.(1)列表: …………3分P (AB 首次值周)=61…………6分(2)P (A 首次不值周)=63=21…………8分 24.在Rt △DEF 中 ∵∠DFE=60°∴EF=33DE ………2分 在Rt △DEG 中 ∵∠DGE=30°∴EG=3DE …………4分 ∴GF=EG-EF=3DE-33DE=(3-33)DE又∵GF=AB=403 ∴(3-33)DE=403…………6分 ∴DE=60 ∴DC=DE+EC=60+1.6=61.6即楼的高度为6106米. …………8分25. 解(1)把A (-2,-4)、O (0,0)、B (2,0)三点的坐标代入y=ax 2+bx+c 中,得⎪⎩⎪⎨⎧==++-=+-002442a 4c c b a c b ………2分 解得a=﹣21,b=1,c=0 ∴解析式为y=﹣21x 2+x ………4分 (2)由y=﹣21x 2+x=﹣21(x ﹣1)2+21,可得 抛物线的对称轴为x=1,并且对称轴垂直平分线段OB ∴OM=BM ∴OM+AM=BM+AM………6分 连接AB 交直线x=1于M 点,则此时OM+AM 最小 过点A 作AN⊥x 轴于点N ,在Rt△ABN 中,AB=42∴OM+AM 最小值为42………8分 26. 解:(1)连接OD∵直线PD 垂直平分⊙O 的半径OA 于点B ,⊙O 的半径为8 ∴OB=OA=4,BC=BD=12CD ………2分∴在Rt △OBD中,BD ∴CD=2BD=4分(2)∵PE 是⊙O 的切线,∴∠PEO=90°∴∠PEF=90°-∠AEO ,∠PFE=∠AFB=90°-∠A ………6分 ∵OE=OA ,∴∠A=∠AEO ,∴∠PEF=∠PFE ,∴PE=PF ………8分27. 设日均销售量p (桶)与销售单价x (元)的函数关系为p=kx+b ,根据题意得⎩⎨⎧=+=+25012500k 7b k b ………2分 解得k=-50,b=850,∴p=-50x+850 ………4分(2)由题意得(x-5)(-50x+850)-250=1350………7分 x 1=9,x 2=13(不合题意,舍去) ………9分当 x=9时,p=-50x+850=400(桶)答:若该经营部希望日均获利1350元,那么日均销售400桶水.………10分 28. 解:(1) ∠CC 1A 1 = 60°………2分(2)如图2,由(1)知:△A 1C 1B ≌△ACB.∴A 1B = AB ,BC 1 = BC ,∠A 1BC 1 =∠ABC. ∴∠1 = ∠2,114263A B AB C B BC === ∴ △A 1BA ∽△C 1BC ………4分 ∴112ΔΔ2439A BA C BCS S ⎛⎫== ⎪⎝⎭. ∵1Δ3C BC S =, ∴1Δ43A BA S =. ………6分 (3)在旋转过程中点P 1与线段EB 有三种情况: ①点P 1与线段EB 形成△P 1EB ∴P 1B- EB < P 1E <P 1B+ EB ②点P 1在射线EB 延长线上P 1E=P 1B+ EB ③点P 1在射线BE 延长线上P 1E=P 1B- EB ∴P 1B- EB ≤ P 1E ≤P 1B+ EB ………8分在△ABC 中, BC=6,∠ACB=30°∵点P 是线段A C 上的动点∴3≤ P 1B ≤6 又∵BE=21AB=2∴P 1B- EB 的最小值为1, P 1B+ EB 的最大值为8∴线段EP 1长度的最大值为8,EP 1长度的最小值1. ………10分21C 1CBA 1A图2。
2014初三数学二模
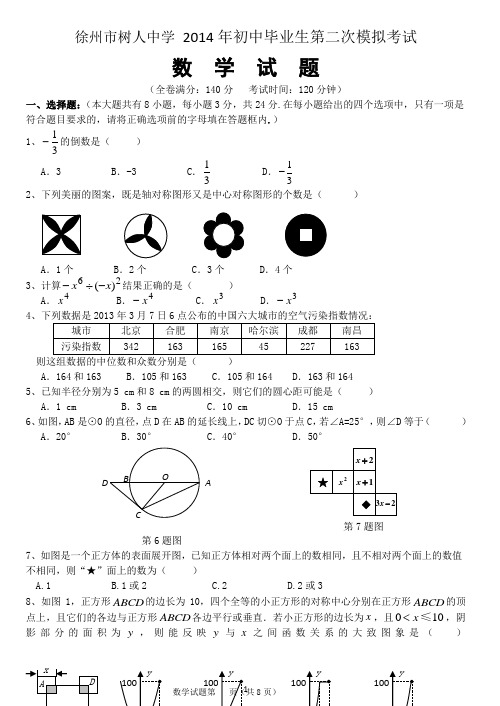
AB D O C徐州市树人中学 2014年初中毕业生第二次模拟考试数 学 试 题(全卷满分:140分 考试时间:120分钟)一、选择题:(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母填在答题框内.) 1、31-的倒数是( ) A .3B .-3C .31D .13-2、下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )A .1个B .2个C .3个D .4个3、计算26)(x x -÷-结果正确的是( ) A .4x B .4x - C .3x D .3x -4则这组数据的中位数和众数分别是( )A .164和163B .105和163C .105和164D .163和1645、已知半径分别为5 cm 和8 cm 的两圆相交,则它们的圆心距可能是( ) A .1 cm B .3 cm C .10 cm D .15 cm6、如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于点C ,若∠A=25°,则∠D 等于( ) A .20° B .30° C .40° D .50°第6题图7、如图是一个正方体的表面展开图,已知正方体相对两个面上的数相同,且不相对两个面上的数值不相同,则“★”面上的数为( )A.1B.1或2C.2D.2或3 8、如图1,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x ,且010x <≤,阴影部分的面积为y ,则能反映y 与x 之间函数关系的大致图象是( )第7题图第18题图D DA B二、填空题:(每小题3分,共30分.请将答案填在答题纸相应的横线上). 9、已知地球距离月球表面约为383900千米,那么这个距离用科学记数法表示为 .10、若2,3,a a b =+=则2a ab += .11、多边形的每个外角的度数都等于40°,则这个多边形的边数为 . 12、如图△ABC 中,∠A=90°点D 在AC 边上,DE ∥BC ,若 ∠1=155°,则∠B 的度数为 . 13、已知反比例函数xk y 1-=(自变量)0≠x ,当自变量0>x 时,函数值y 随x 的增大而减小,请你写出一个符合条件的k 的值 .14、已知一个圆锥的母线长为10cm ,将侧面展开后所得扇形的圆心角是144°,则这个圆锥的底面圆的半径是 cm . 15、如图,在Rt △ABC 中,∠ACB=90°,D 、E 、F 分别是AB 、BC 、CA 的中点,若CD=5cm ,则EF= cm .第15题16、如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心0处,折痕为EF.若菱形ABCD 的边长为2cm ,∠A=1200,则EF= cm . 17、如图,在平面直角坐标系中,点A 的坐标为(0,3),将△OAB 沿x 轴向右平移后得到△O ′A ′B ′,点A 的对应点A ′在直线y =34x 上,那么点B 与对应点B ′之间的距离 为 .18、如图,以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点,交直角边AC 于点E ,B 、E 是半圆弧的三等分点,弧BE 的长为π,则图中阴影部分的面积为 .三、解答题:(本大题共10小题,共86分.请在答题卡指定区域内作答,解答时要写出必要的文字说明、证明过程或运算步骤)19、(本题满分10分)1)计算:202145sin 458-⎪⎭⎫ ⎝⎛-⨯--+ (2)计算:2)3()2)(2(---+x x x 20、(本题满分10分)(1)解不等式组:()52315x x x x +⎧>⎪⎨⎪--≤⎩第12题图(第17题)(2)先化简22)1111(2-÷+--a aa a ,然后从1、-1、32-中选一个你认为合适的数作为a 的值代入求值.21、(本题满分7分)阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某中学全校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:(1)求该校九年级的人数占全校总人数的百分率. (2)求出表(1)中a 、b 的值.(3表(1)22、(本题满分7分)四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上. (1)求随机抽取一张卡片,恰好得到数字2的概率;(2)小丽和小刚想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.23、(本题满分8分)小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤. 妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”; 爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”; 小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?” 请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤). 236224、(本题满分8分)如图所示,已知AB 为⊙O 的直径,CD 是弦,且AB ⊥CD 于点E .连接AC 、OC 、BC .(1)求证:∠ACO=∠BCD .(2)若EB=8cm ,CD=24cm ,求⊙O 的直径.25、(本题满分8分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE 的高度,他们按如下步骤操作:第一步:小亮在测点A 处测得树顶端D 的仰角为30°;第二步:小红在台阶下的点C 处测得树顶端D 的仰角为60°.此时工人师傅告诉他们A 点的高度AB 为3米,台阶AC 的坡度为1B 、C 、E 三点在同一条直线上.请根据以上条件求出树DE 的高度.第25题图26、(本题满分8分)如图①,一条笔直的公路上有A 、B 、C 三地,B 、C 两地相距 150 千米,甲、乙两辆汽车分别从B 、C 两地同时出发,沿公路匀速相向而行,分别驶往C 、B 两地.甲、乙两车到A 地的距离1y 、2y (千米)与行驶时间 x (时)的关系如图②所示.根据图象进行以下探究:(1)请在图①中标出 A 地的位置,并作简要的文字说明; (2)求图②中M 点的坐标,并解释该点的实际意义;(3)在图②中补全甲车的函数图象,求甲车到 A 地的距离1y 与行驶时间x 的函数关系式.y (千米)x (时)乙 甲 图② 图①27、(本题满分10分)已知,如图1,矩形ABCD 中,AD=6,DC=8,矩形EFGH 的三个顶点E 、G 、H 分别在矩形ABCD 的边ABCD 的边AB 、CD 、DA 上,H 为定点,且AH=2,连接CF. (1)如图2,当四边形EFGH 为正方形时,求AE 的长和△FCG 的面积;(2)如图1,设AE=x ,△FCG 的面积=y ,求y 与x 之间的函数关系式及函数值y 的最大值.28、(本题满分10分)如图,抛物线22y ax ax c =-+(0a ≠)交x 轴于A 、B 两点,A 点坐标为(3,0),与y 轴交于点C (0,4),以OC 、OA 为边作矩形OADC 交抛物线于点G . (1)求抛物线的解析式;(2)抛物线的对称轴l 在边OA (不包括O 、A 两点)上平行移动,分别交x 轴于点E ,交CD 于点F ,交AC 于点M ,交抛物线于点P ,若点M 的横坐标为m ,请用含m 的代数式表示PM 的长;(3)在(2)的条件下,连结PC ,则在CD 上方的抛物线部分是否存在这样的点P ,使得以P 、C 、F 为顶点的三角形和AEM △相似?若存在,求出此时m 的值,并直接判断PCM △的形状;若不存在,请说明理由.图2A B C D E F G H F E G H D C B A 图1。
徐州市2014年初中毕业、升学考试数学试题(WORD版、带答案、重新制图排版优化)全国通用
徐州市2014年初中毕业、升学考试数 学 试 题一、选择题(本大题共有8小题。
每小题3分,共24分。
在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1. 2-1等于A.2B.-2C.21 D.-21 2. 右图使用五个相同的立方体搭成的几何体,其主视图...是 3. 抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率 A.大于21 B.等于21 C.小于21D.不能确定 4. 下列运算中错误..的是 A.532=+ B.632=⨯ C.228=÷ D.3)3(2=- 5. 将函数y =-3x 的图像沿y 轴向上平移2个单位长度后,所得图像对应的函数关系式为 A.23+-=x y B.23--=x y C.)2(3+-=x y D.)2(3--=x y姓名 考试证号注意事项1. 本卷满分为140分,考试时间为120分钟。
2. 答题前,请将自己的姓名、考试证号用0.5毫米黑色墨水签字笔写在本试卷及答题卡指定的位置。
3. 答案全部涂、写在答题卡上,写在本试卷上无效。
考试结束后,请将本试卷和答卡一并交回。
A B C D6. 顺次连接正六边形的三个不相邻的顶点。
得到如图所示的图形,该图形 A.既是轴对称图形也是中心对称图形 B.是轴对称图形但并不是是中心对称图形 C.是中心对称图形但并不是轴对称图形 D.既不是轴对称图形也不是中心对称图形7. 若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是 A.矩形 B.等腰梯形C.对角线相等的四边形D.对角线互相垂直的四边形8. 点A 、B 、C 在同一条数轴上,其中点A 、B 表示的数分别为-3、1,若BC =2,则AC 等于 A.3 B.2 C.3或5 D.2或6 二、填空题(本大题共有10小题。
每小题3分,共30分。
不需要写出解答过程,请把答案直接写在答题卡的相应位置上) 9. 函数12-=x y 中,自变量x 的取值范围为 ▲ . 10. 我国“钓鱼岛”周围海域面积约170 000km 2,该数用科学计数法可表示为 ▲ . 11. 函数y =2x 与y =x +1的图像交点坐标为 ▲ .12. 若ab =2,a -b =-1,则代数式22ab b a -的值等于 ▲ . 13. 半径为4cm ,圆心角为60°的扇形的面积为 ▲ cm 2. 14. 下图是某足球队全年比赛情况统计图:(第14题) 根据图中信息,该队全年胜了 ▲ 场.15. 在平面直角坐标系中,将点A (4,2)绕原点逆时针方向旋转90°后,其对应点A ’的坐标为 ▲ .(第6题)16. 如图,在等腰三角形纸片ABC 中,AB =AC ,︒=∠50A ,折叠该纸片,使点A 落在点B 处,折痕为DE ,则=∠CBE ▲ °.17. 如图,以O 为圆心的两个同心圆中,大圆与小圆的半径分别为3cm 和1cm ,若圆P 与这两个圆都相切,则圆P 的半径为 ▲ cm.18. 如图①,在正方形ABCD 中,点P 沿边DA 从点D 开始向点A 以1cm/s 的速度移动;同时,点Q 沿边AB 、BC 从点A 开始向点C 以2cm/s 的速度移动.当点P 移动到点A 时,P 、Q 同时停止移动.设点P 出发x s 时,△P AQ 的面积为y cm 2,y 与x 的函数图像如图②所示,则线段EF 所在的直线对应的函数关系式为 ▲ .图① 图②(第18题)三、解答题(本大题共有10小题,共86分。
江苏省徐州市2014届九年级第二次质量检测数学试卷(含答案)(扫描版)

解得:x=20…………………………5 分 经检验:x=20 是原方程的解…………………………6 分 ∴公交巴士的速度为 20km/h,小汽车的速度为 60km/h…………………………7 分 23.∵四边形 ABCD 是平行四边形 ∴AB∥CD 即 AF∥DC AB=CD…………………………1 分 ∴∠AFE=∠DCE…………………………3 分 ∵E 为 AD 的中点 ∴AE=DE 又∵∠AEF=∠DEC ∴△AEF≌△DEC…………………………6 分
化 简 得 : 3t -64t+500=0 无 解 ③ 若 ∠OQP=90°有 PQ⊥x 轴 ∴
1 4 t= t+1 2 5
2
∴ t=
10 3
∵ t=
10 满 足 0< t< 10 条 件 3 10 . …………………………7 分 3
∴ t 值 存 在 且 t=
当 点 P 在 BC 上 运 动 时 10< t< 20 作 PM⊥y 轴交 y 轴于点 M,PN⊥x 轴交 x 轴于点 N 由 题 意 得 : BP=t-10 OQ=4t-34
∴FA=CD ∴FA=AB…………………………8 分 24.(1)2…………………………3 分 (2)列表或树状图正确…………………………6 分 (3)P(两次摸球颜色相同)=
4 …………………………8 分 25
25.(1)∵∠APD 是△APC 的外角 ∴∠APD=∠A+∠C ∵∠CAB=50°,∠APD=80° ∴∠C=80°-∠A=30°…………………………2 分 ∵∠C、∠B 所对的是同弧 ∴∠B=30°…………………………4 分 (2)过 O 作 OE⊥BD 交 BD 于 E 在 Rt△OEB 中 ∠B=30°OB=5cm ∴BE=
江苏省徐州市沛县2014届九年级中考打靶卷数学试题全国通用

27. (本题 10 分)某次海军舰艇演习中,甲、乙两舰艇同时从 A、B 两个港口出发,均沿直 线匀速驶向演习目标地海岛 C,两舰艇都到达 C 岛后演习第一阶段结束.已知 B 港位于 A 港、C 岛之间,且 A、B、C 在一条直线上. 设甲、乙两舰艇行驶 x(h)后,与 B 港的距 离分别为 y1 和 y2(km),y1、y2 与 x 的函数关系如图所示. (1)求 A 港与 C 岛之间的距离; (2)分别求出甲、乙两舰艇的航速及图中点 M 的坐标; (3)若甲、乙两舰艇之间的距离不超过 20km 时就属于最佳通讯距离,试求出两舰艇在 演习第一阶段处于最佳通讯距离时的 x 的取值范围. y/km 160
x 2, 方程组的解为 y 1.
………………………1 分
(2) 解:解①得: x 2 ……………………………………………………………2 分 解②得: x 3 ………………………………………………………………3 分 在数轴上表示不等式①、②的解集: ……………………………………………………4 分 3 不等式组的解集为 2 x 3 …………………………………………5 分 21. (1)200 …………………………………………………………………2 分 (2) 图略;54° …………………………………………………………………7 分 (4)1020
1 a 1
………………………………………………3 分
………………………………………………………4 分
……………………………………………………………5 分 ………………………………………2 分 ………………………2 分
20.(1)解:①+②,得: 4 x 8 ; x 2
将 x 2 代入①,得: 2 2 y 0 ; y 1
【精校】2014年江苏省徐州市中考真题数学

2014年江苏省徐州市中考真题数学一、选择题(本大题共有8小题.每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的)1.(3分)2-1等于( )A. 2B. -2C.D. -解析:2,答案:C.2.(3分)如图使用五个相同的立方体搭成的几何体,其主视图是( )A.B.C.D.解析:从正面看:上边一层最右边有1个正方形,下边一层有3个正方形.答案:D.3.(3分)抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率( )A. 大于B. 等于C. 小于D. 不能确定解析:∵硬币由正面朝上和朝下两种情况,并且是等可能,∴第3次正面朝上的概率是.答案:B.4.(3分)下列运算中错误的是( )A. +=B. ×=C. ÷=2D. =3解析:A、+无法计算,故此选项正确;B、×=,正确,不合题意;C、÷=2,正确,不合题意;D、=3,正确,不合题意.答案:A.5.(3分)将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )A. y=-3x+2B. y=-3x-2C. y=-3(x+2)D. y=-3(x-2)解析:∵将函数y=-3x的图象沿y轴向上平移2个单位长度,∴平移后所得图象对应的函数关系式为:y=-3x+2.答案:A.6.(3分)顺次连接正六边形的三个不相邻的顶点.得到如图的图形,该图形( )A. 既是轴对称图形也是中心对称图形B. 是轴对称图形但并不是中心对称图形C. 是中心对称图形但并不是轴对称图形D. 既不是轴对称图形也不是中心对称图形解析:此图形是等边三角形,等边三角形是轴对称图形但并不是中心对称图形,答案:B.7.(3分)若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )A. 矩形B. 等腰梯形C. 对角线相等的四边形D. 对角线互相垂直的四边形解析:如图,根据题意得:四边形EFGH是菱形,点E,F,G,H分别是边AD,AB,BC,CD的中点,∴EF=FG=CH=EH,BD=2EF,AC=2FG,∴BD=AC.∴原四边形一定是对角线相等的四边形.答案:C.8.(3分)点A、B、C在同一条数轴上,其中点A、B表示的数分别为-3、1,若BC=2,则AC等于( )A. 3B. 2C. 3或5D. 2或6解析:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.点A、B表示的数分别为-3、1,AB=4.第一种情况:在AB外,AC=4+2=6;第二种情况:在AB内,AC=4-2=2.答案:D.二、填空题(本大题共有10小题.每小题3分,共30分)9.(3分)函数y=中,自变量x的取值范围为.解析:由题意得,x-1≠0,解得x≠1.答案:x≠1.10.(3分)我国“钓鱼岛”周围海域面积约170 000km2,该数用科学记数法可表示为.解析:170 000=1.7×105,答案:1.7×105.11.(3分)函数y=2x与y=x+1的图象交点坐标为 .解析:解方程组得,所以函数y=2x与y=x+1的图象交点坐标为(1,2).答案:(1,2).12.(3分)若ab=2,a-b=-1,则代数式a2b-ab2的值等于 .解析:∵ab=2,a-b=-1,∴a2b-ab2=ab(a-b)=2×(-1)=-2.答案:-2.13.(3分)半径为4cm,圆心角为60°的扇形的面积为cm2.解析:半径为4cm,圆心角为60°的扇形的面积为:=π(cm2).答案:π.14.(3分)如图是某足球队全年比赛情况统计图:根据图中信息,该队全年胜了场.解析:全年比赛场次=10÷25%=40,胜场:40×(1-20%-25%)=40×55%=22场.答案:22.15.(3分)在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .解析:如图A′的坐标为(-2,4).答案:(-2,4).16.(3分)如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=°.解析:∵AB=AC,∠A=50°,∴∠ACB=∠ABC=(180°-50°)=65°,∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,∴∠ABE=∠A=50°,∴∠CBE=∠ABC-∠ABE=65°-50°=15°.答案:15.17.(3分)如图,以O为圆心的两个同心圆中,大圆与小圆的半径分别为3cm和1cm,若圆P与这两个圆都相切,则圆P的半径为cm.解析:由题意,圆P与这两个圆都相切,若圆P与两圆均外切,如图①所示,此时圆P的半径=(3-1)=1cm;若圆P与两圆均内切,如图②所示,此时圆P的半径=(3+1)=2cm.综上所述,圆P的半径为1cm或2cm.答案:1或2.18.(3分)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A 时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为.解析:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC从点A 开始向点C以2cm/s的速度移动.∴当Q到达B点,P在AD的中点时,△PAQ的面积最大是9cm2,设正方形的边长为acm,∴×a×a=9,解得a=6,即正方形的边长为6,当Q点在BC上时,AP=6-x,△APQ的高为AB,∴y=(6-x)×6,即y=-3x+18.故答案为:y=-3x+18.三、解答题(本大题共有10小题,共86分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤)19.(10分)(1)计算:(-1)2+sin30°-;(2)计算:(a+)÷(1+).解析:(1)原式第一项利用乘方的意义化简,第二项利用特殊角的三角函数值计算,最后一项利用立方根定义化简,计算即可得到结果;(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果.答案:(1)原式=1+-2=-;(2)原式=÷=•=a-1.20.(10分)(1)解方程:x2+4x-1=0;(2)解不等式组:.解析:(1)利用配方法求出x的值即可.(2)分别求出各不等式的解集,再求出其公共解集即可.答案: (1)原式可化为(x2+4x+4-4)-1=0,即(x+2)2=5,两边开方得,x+2=±,解得x1=-2+,x2=-2-;(2),由①得,x≥0,由②得,x<2,故此不等式组的解集为:0≤x<2.21.(7分)已知:如图,在平行四边形ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.解析:根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.答案:如图,连接BC,设对角线交于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵AE=DF,OA-AE=OC-DF,∴OE=OF.∴四边形BEDF是平行四边形.22.(7分)甲、乙两人在5次打靶测试中命中的环数如下:甲:8,8,7,8,9乙:5,9,7,10,9(1)填写下表:(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差.(填“变大”、“变小”或“不变”).解析:(1)根据众数、平均数和中位数的定义求解;(2)根据方差的意义求解;(3)根据方差公式求解.答案:(1)甲的众数为8,乙的平均数=(5+9+7+10+9)=8,乙的中位数为9;(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.故答案为:8,8,9;变小.23.(8分)某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.(1)如果随机抽取1名同学单独展示,那么女生展示的概率为;(2)如果随机抽取2名同学共同展示,求同为男生的概率.解析:(1)4名学生中女生1名,求出所求概率即可;(2)列表得出所有等可能的情况数,找出同为男生的情况数,即可求出所求概率.答案:(1)如果随机抽取1名同学单独展示,那么女生展示的概率为;(2)列表如下:所有等可能的情况有12种,其中同为男生的情况有6种,则P==.24.(8分)几个小伙伴打算去音乐厅观看演出,他们准备用360元购买门票.下面是两个小伙伴的对话:根据对话的内容,请你求出小伙伴们的人数.解析:设票价为x元,根据图中所给的信息可得小伙伴的人数为:,根据小伙伴的人数不变,列方程求解.答案:设票价为x元,由题意得,=+2,解得:x=60,则小伙伴的人数为:=8.答:小伙伴们的人数为8人.25.(8分)如图,轮船从点A处出发,先航行至位于点A的南偏西15°且点A相距100km 的点B处,再航行至位于点B的北偏东75°且与点B相距200km的点C处.(1)求点C与点A的距离(精确到1km);(2)确定点C相对于点A的方向.(参考数据:≈1.414,≈1.732)解析:(1)作辅助线,构造直角三角形,解直角三角形即可;(2)利用勾股定理的逆定理,判定△ABC为直角三角形;然后根据方向角的定义,即可确定点C相对于点A的方向.答案:(1)如图,过点A作AD⊥BC于点D,∠ABE=∠BAF,由图得,∠ABC=∠EBC-∠ABE=∠EBC-∠BAF=75°-15°=60°,在Rt△ABD中,∵∠ABC=60°,AB=100,∴BD=50,AD=50,∴CD=BC-BD=200-50=150,在Rt△ACD中,由勾股定理得:AC==100≈173(km).答:点C与点A的距离约为173km.(2)在△ABC中,∵AB2+AC2=1002+(100)2=40000,BC2=2002=40000,∴AB2+AC2=BC2,∴∠BAC=90°,∴∠CAF=∠BAC-∠BAF=90°-15°=75°.答:点C位于点A的南偏东75°方向.26.(8分)某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?解析:(1)根据待定系数法,可得二次函数解析式,根据顶点坐标,可得答案;(2)根据函数值大于或等于16,可得不等式的解集,可得答案.答案:(1)y=ax2+bx-75图象过点(5,0)、(7,16),∴,解得,y=-x2+20x-75的顶点坐标是(10,25)当x=10时,y最大=25,答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;(2)∵函数y=-x2+20x-75图象的对称轴为直线x=10,可知点(7,16)关于对称轴的对称点是(13,16),又∵函数y=-x2+20x-75图象开口向下,∴当7≤x≤13时,y≥16.答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.27.(10分)如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y 轴相交于点E、F.已知B(1,3).(1)k= ;(2)试说明AE=BF;(3)当四边形ABCD的面积为时,求点P的坐标.解析:(1)根据反比例函数图象上点的坐标特征易得k=3;(2)设A点坐标为(a,),易得D点坐标为(0,),P点坐标为(1,),C点坐标为(1,0),根据图形与坐标的关系得到PB=3-,PC=-,PA=1-a,PD=1,则可计算出==,加上∠CPD=∠BPA,根据相似的判定得到△PCD∽△PBA,则∠PCD=∠PBA,于是判断CD∥BA,根据平行四边形的判定方法易得四边形BCDE、ADCF都是平行四边形,所以BE=CD,AF=CD,则BE=AF,于是有AE=BF;(3)利用四边形ABCD的面积=S△PAB-S△PCD,和三角形面积公式得到•(3-)•(1-a)-•1•(-)=,整理得2a2+3a=0,然后解方程求出a的值,再写出P点坐标.答案:(1)把B(1,3)代入y=得k=1×3=3;故答案为3;(2)反比例函数解析式为y=,设A点坐标为(a,),∵PB⊥x于点C,PA⊥y于点D,∴D点坐标为(0,),P点坐标为(1,),C点坐标为(1,0),∴PB=3-,PC=-,PA=1-a,PD=1,∴==,=,∴=,而∠CPD=∠BPA,∴△PCD∽△PBA,∴∠PCD=∠PBA,∴CD∥BA,而BC∥DE,AD∥FC,∴四边形BCDE、ADCF都是平行四边形,∴BE=CD,AF=CD,∴BE=AF,∴AF+EF=BE+EF,即AE=BF;(3)∵四边形ABCD的面积=S△PAB-S△PCD,∴·(3-)·(1-a)-·1·(-)=,整理得2a2+3a=0,解得a1=0(舍去),a2=-,∴P点坐标为(1,-2).28.(10分)如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.(1)试说明四边形EFCG是矩形;(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;②求点G移动路线的长.解析:(1)只要证到三个内角等于90°即可.(2)易证点D在⊙O上,根据圆周角定理可得∠FCE=∠FDE,从而证到△CFE∽△DAB,根据相似三角形的性质可得到S矩形EFCG=2S△CFE=.然后只需求出CF的范围就可求出S矩形EFCG的范围.根据圆周角定理和矩形的性质可证到∠GDC=∠FDE=定值,从而得到点G的移动的路线是线段,只需找到点G的起点与终点,求出该线段的长度即可.答案:(1)证明:如图1,∵CE为⊙O的直径,∴∠CFE=∠CGE=90°.∵EG⊥EF,∴∠FEG=90°.∴∠CFE=∠CGE=∠FEG=90°.∴四边形EFCG是矩形.(2)①存在.连接OD,如图2①,∵四边形ABCD是矩形,∴∠A=∠ADC=90°.∵点O是CE的中点,∴OD=OC.∴点D在⊙O上.∵∠FCE=∠FDE,∠A=∠CFE=90°,∴△CFE∽△DAB.∴=()2.∵AD=4,AB=3,∴BD=5,S△CFE=()2·6S△DAB=××3×4=.∴S矩形EFCG=2S△CFE=.∵四边形EFCG是矩形,∴FC∥EG.∴∠FCE=∠CEG.∵∠GDC=∠CEG,∠FCE=∠FDE,∴∠GDC=∠FDE.∵∠FDE+∠CDB=90°,∴∠GDC+∠CDB=90°.∴∠GDB=90°Ⅰ.当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′)处,如图2①所示. 此时,CF=CB=4.Ⅱ.当点F在点D(F″)处时,直径F″G″⊥BD,如图2②所示,此时⊙O与射线BD相切,CF=CD=3.Ⅲ.当CF⊥BD时,CF最小,如图2③所示.S△BCD=BC·CD=BD·CF,∴4×3=5×CF,∴CF=.∴≤CF≤4.∵S矩形EFCG=,∴×()2≤S矩形EFCG≤×42.∴≤S矩形EFCG≤12.∴矩形EFCG的面积最大值为12,最小值为.②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,如图2②所示,∴点G的移动路线是线段DG″.∵∠G″DC=∠BDA,∠DCG″=∠A=90°,∴△DCG″∽△DAB.∴=.∴=.∴DG″=.∴点G移动路线的长为.考试高分秘诀是什么?试试这四个方法,特别是中考和高考生谁都想在考试中取得优异的成绩,但要想取得优异的成绩,除了要掌握好相关的知识定理和方法技巧之外,更要学会一些考试技巧。
2014徐州中考数学试卷(带答案版)

徐州市2014年初中毕业、升学考试数学试题一、选择题(本大题共有8小题,每小题3分,共24分。
在每小题所给的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1、2−1等于A 、2B 、-2C 、12 D- 12 选C2、右图是用5个相同的立方块搭成的几何体,其主视图是考点:简单组合体的三视图.分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中. 解答:解:此几何体的主视图从左往右分3列,小正方形的个数分别是1,1,2 故选:D .点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图.3、抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率A 、大于1⁄2B 、等于1⁄2C 、小于1⁄2D 、无法确定考点:概率的意义.分析:由掷一枚均匀的硬币,可得掷得的等可能的结果有:正面与反面两种情况,则可求得掷得正面朝上的概率;注意这与做实验的次数无关.解答:解:∵掷一枚均匀的硬币,可得掷得的等可能的结果有:正面与反面, ∴掷得正面朝上的概率为:1⁄2 . 故答案为:B .点评:此题考查了概率的意义.注意概率是频率(多个)的波动稳定值,是对事件发生可能性大小的量的表现.4、下列运算中错误的是A 、√2+√3=√5B 、√2*√3=√6C 、√8÷ √2=2D 、(−√3)2=3考点:二次根式的混合运算. 专题:计算题.分析:根据二次根式的加减法对A 进行判断; 根据二次根式的乘法法法则对B 进行判断; 根据二次根式的除法法法则对C 进行判断; 根据二次根式的性质对D 进行判断. 解答:选A .点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.5、将函数y=-3x的图像沿y轴向上平移2个单位长度后,所得图像对应的函数关系式为A、y=-3x+2B、y=-3x-2C、y=-3(x+2)D、y=-3(x-2)考点:一次函数图象与几何变换.专题:常规题型.分析:根据平移法则上加下减可得出平移后的解析式.y=-3x+2解答:解:由题意得:平移后的解析式为:故答案为:A点评:本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标左移加,右移减;纵坐标上移加,下移减.6、顺次连接正六边形的三个不相邻的顶点,得到如图所示的图形,该图形A、既是轴对称图形也是中心对称图形B、是轴对称图形但不是中心对称图形C、是中心对称图形但并不是轴对称图形D、既不是轴对称图形也不是中心对称图形考点:中心对称图形;轴对称图形.分析:根据轴对称图形与中心对称图形的概念求解.解答:选B点评:本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.7、若顺次连接四边形的各边中点所得到的四边形是菱形,则该四边形一定是A、矩形B、等腰梯形C、对角线相等的四边形 D 对角线互相垂直的四边形考点:菱形的判定;三角形中位线定理.分析:根据三角形中位线的性质及菱形的性质,可证四边形的对角线相等.解答:解:∵四边形EFGH是菱形,∴EH=FG=EF=HG=1⁄2BD=1⁄2AC,故AC=BD.故选:C点评:本题很简单,考查的是三角形中位线的性质及菱形的性质.8、点A、B、C、在同一条数轴上,其中点A、B表示的数分别为-3、1.,若BC=2,则AC等于A、3 B、2 C、3或5 D、2或6考点:数轴.分析:此题注意考虑两种情况:要求的点在已知点的左侧或右侧.解答:选D点评:考查了数轴,注意数轴上距离某个点是一个定值的点有两个,左右各一个,不要漏掉任一种情况.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的思想.二、填空题(本大题共有10小题,每小题3分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
徐州市2014中考押题卷B 卷
参考答案
一、选择题
二、
填
空
题
9.答案不惟一,如矩形、圆等 10.0 11.x ≥21
12.
13.)3)(3(4y x y x -+ 14.4 15.190 16.π380
17.70 18.1和2
三、解答题
19.(1)解:原式=1-1+3(3分)=3(5分)
(2)解:0222=--x x (1分) 222=-x x (2分)3)1(2=-x (3分)
311+=x (4分) 312-=x (5分)(其他解法酌情给分)
20.(1)解:①×5,得 401510=-y x ③(1分)
②×3,得 151521-=-y x ④(2分)
④-③,得5-=x (3分)
把5-=x 代入①得,6-=y (4分) ∴⎩⎨⎧-=-=65y x .(5
分)
(2)解:原式=)1(1
1-+⋅+x x x x x
(3分)=11
-x (5分)
21.(1)16;(1分) (2)90;(3分) (3)87;(5分)
(2)综合成绩=87×10%+90×30%+96×60%=93.3分.(7分)
22.解:根据题意,做树状图可得.(4分)
由图可知,共12种等可能情况.(5分)其中有B 的共6种情况,故摸到的两张卡片 有一张的图案是自行车项目的概率为P =126
7分)
23.解:设每个小组有x 名学生.(1分) 根据题意得,563604360=-x
x (4分) 解得x =6,(6分) 经检验x =6是原方程的解.(7分)
答:每个小组有6名学生.(8分)
24.解:AC 与⊙O 相切.(1分)
证明:如图,连接BE .(2分)
∵AB 是直径,∴∠AEB =90°,∴∠DBE +∠EFB =90°.(3分)
又∵E 是弧BD 的中点,∴弧DE =弧BE ,∴∠BAE =∠DBE .(4分)
又∵CA =CF ,∴∠CAF =∠CF A .(5分) ∵∠CF A =∠EFB ,
∴∠CAF =∠EFB .(6分)∴∠EAB +∠CAF =90°,即∠CAB =90°.(7分) ∴CA ⊥AB ,又∵AB 是直径,∴AC 与⊙O 相切.(8分)
25.解:(1)设小路的宽度应为x m .(1分)由题意得5.10)4)(5.4(=--x x .(3分)
解得,1x =7.5(舍) 2x =1.(4分) 答:小路的宽度应为1m .(5分)
(2)长里面350÷60=5块余50cm ,宽里面300÷60=5块.(6分),
∴还剩余50×300的空隙,∵50>40,∴300÷60=5块.
∴空隙处至少要5块整砖,∴至少要5×5+5=30块地砖.(7分)
答:小明家至少需要块30地砖.(8分)
26.证明:(1)∵BA =BC ,MA =MN ,∴MA BA =MN
BC .(2分) 又∵∠ABC =∠AMN ,∴△BAC ∽△MAN .(3分)
(2)由(1)知,∵∠BAC =∠MAN ,∴∠BAM =∠CAN .(5分)
(3)由(2)知∠BAM =∠CAN ,由(1)知MA BA =AN
AC ,(6分) ∴△BAM ∽△CAN .(7分)∴∠ABC =∠ACN .(8分)
27.解:(1)设y =kx +b ,将A (-1,0)、B (3,2)代入得,
⎩⎨⎧=+=+-230b k b k ,(1分)解得⎪⎪⎩⎪⎪⎨⎧==2121b k .(2分)
∴线段AB 的解析式为2
121+=
x y (-1≤x ≤3).(3分) (2)设直线AB 向下平移m 个单位后的解析式为m x y -+=2121.(4分) 与直线y =2x -4组成方程组得,⎪⎩⎪⎨⎧-=-+=4
22121x y m x y ,(5分) 解得⎪⎪⎩
⎪⎪⎨⎧-=-=m y m x 342323.(6分) 由于两直线的交点位于第四象限, ∴m 323-
>0, m 342-<0.解得23<m <2
9.(8分) (3)当线段AB 最短时,点B 的坐标为(57,56-).(10分) 当AB ⊥直线y =2x -4时,线段AB 最短.设点B 的坐标为(a ,2a -4),显然a >0,利用三角形的相似可得,a +1=2(2a -4),解得a =
57, 代入y =2x -4得y =56-
,故点B 的坐标为(57,56-). 28.解:(1)∵1)1(2---=x m mx y ,∴[])1(4)1(422-⋅---=-m m ac b (1分)
22)1(412+=++-=m m m m ≥0.
(2分) ∴二次函数的图像一定与x 轴有交点.(3分)
(2)对于1)1(2---=x m mx y ,由顶点坐标公式可知,当x =m
m 21-时, y 有最值m
m 4)1(2
+-,(5分)∵二次函数有最大值0,∴m =-1.(6分)
(3)∵)1)(1(1)1(2-+=---=x mx x m mx y ,该二次函数的图象与x 轴的交点坐标
为(1,0)和(m
1-,0),且m ≠-1.(7分) 由定义知“规范交点”应该位于x 轴的正半轴,∴m 1-
>0,解得m <0. ①当-1<m <0时,m 1->1,∴2
1x x =m 1-.
当-6<m
1-<6时,有6>m 1>-6,∴-1<m <61-.(8分) ②当m <-1时,1>m 1-,∴21x x =-m . 当-6<m -<6时,有6>m >-6,∴-6<m <-1.(9分) 由①、②知,当-6<m <-1或-1<m <6
1-时,二次函数2(1)1y mx m x =---与x 轴都有两个“规范交点” .
(10分)。
