八年级数学作轴对称图形2
人教版数学八年级上册13.2画轴对称图形(第2课时)教学设计

希望同学们认真完成作业,通过实践和练习,不断提高自己的几何图形认识和运用能力。
(四)课堂练习,500字
1.教师布置课堂练习题,要求学生在规定时间内完成。
“下面,请同学们完成这几道练习题,巩固所学知识。遇到问题可以互相讨论,也可以请教老师。”
2.学生独立完成练习题,教师巡回辅导,解答学生疑问。
3.教师选取部分学生的练习题进行讲解,分析解题思路和方法。
“这道题目考查了我们对轴对称图形的性质的理解。我们可以通过找到对称轴,然后利用对称性质解决问题。”
“现在,请同学们分成小组,讨论一下轴对称图形的性质以及它们在实际生活中的应用。每个小组派一名代表分享讨论成果。”
2.学生在小组内展开讨论,教师巡回指导,解答学生疑问。
“同学们,你们发现轴对称图形有哪些性质?它们在生活中有哪些应用?”
3.各小组代表分享讨论成果,教师点评并总结。
“很好,各小组都取得了不错的成果。轴对称图形的性质包括:对称轴两侧的图形完全一致,对称轴上的点称为对称点等。它们在生活中的应用非常广泛,如剪纸、建筑、标志等。”
3.教师布置课后作业,提醒学生加强练习。
“课后,请同学们完成这几道练习题,巩固所学知识。下节课我们将进一步探讨轴对称图形的其他性质和应用。”
五、作业布置
为了巩固本节课所学的轴对称图形知识,培养学生的动手操作能力和应用能力,特布置以下作业:
1.完成课本第13.2节课后练习题,包括填空题、选择题和解答题,要求学生在规定时间内独立完成,注意解题过程的规范性和逻辑性。
人教版数学八年级上册13.2画轴对称图形(第2课时)教学设计
一、教学目标
(一)知识与技能
【学海风暴】2016沪科版八年级数学上册(同步导练):15.1轴对称图形(二)

15.1轴对称图形(2)基础导练1.若实数a、b满足()2230-++=,则点P(a,b)在第象限;a b2.点P(0,-3)在轴上;在x轴上的点,坐标必为0;3.若点P(a,b)在第四象限,则点M(-a,-b)在第象限,点N(-a,b)在第象限;4.点A在第三象限,且点A到x轴的距离为3,到y轴的距离为2,则A点坐标为.5.将点P(2,4)向右平移3个单位,得到的点的坐标是(,)将点P(2,4)向左平移3个单位,得到的点的坐标是(,)将点P(2,4)向上平移3个单位,得到的点的坐标是(,)将点P(2,4)向下平移3个单位,得到的点的坐标是(,)根据上题总结,填空:(1)横坐标加一个正数(纵坐标不变),点向平移;横坐标减一个正数(纵坐标不变),点向平移.(2)纵坐标加一个正数(横坐标不变),点向平移;纵坐标减一个正数(横坐标不变),点向平移.6.(1)在下面的平面直角坐标系中,依次描出下列各点:(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0).再用线段顺次连结各点,得到一个图形象.(2)上述各点的纵坐标不变,将横坐标分别加5得到各个点的坐标分别是:,描出这几个点,再用线段顺次连接起来,这样得到的图形与原来的图形有什么变化?先猜一猜,再动手画.答:____________________________.(3)若(1)中的各点的横坐标不变,纵坐标分别加3得到各个点的坐标分别是:_ ,描出这几个点,再用线段顺次连接起来(仍在下图画),这样得到的图形与原来的图形有什么变化?先猜一猜,再动手画.答:____________________________.(4)根据第(1)、(2)、(3),大胆猜想:①若将一个图形各点的横坐标都加上3个单位(纵坐标不变),则图形会向平移单位.②若将一个图形各点的横坐标都减去5个单位(纵坐标不变),则图形会向平移单位.③若将一个图形各点的纵坐标都加上2个单位(横坐标不变),则图形会向 平移 单位.④若将一个图形各点的纵坐标都减去6个单位(横坐标不变),则图形会向 平移 单位.123456781234560-1-2-3-4-5-6910yx能力提升7.(1)在下边的平面直角坐标系中,依次描出下列各点:(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0).再用线段顺次连结各点,得到一个图形象______.(2)上述各点的纵坐标不变,横坐标分别变为原来的2倍,得到各个点的坐标分别是:_ ,描出这几个点,再用线段顺次连接起来,这样得到的图形与原来的图形有什么变化?先猜一猜,再动手画.答:____________________________.(3)若(1)中的各点的纵坐标不变,横坐标分别变为原来的12,得到各个点的坐标分别是:_ ,描出这几个点,再用线段顺次连接起来(仍在下图画),这样得到的图形与原来的图形有什么变化?先猜一猜,再动手画.答:____________________________.(4)根据第(1)、(2)、(3),大胆猜想:①若一个图形各点的横坐标不变,纵坐标变为原来的3倍,则图形的形状会发生什么变化?答:_________________.②若一个图形各点的横坐标不变,纵坐标变为原来的13倍,则图形的形状会发生什么变化?答:_________________.③若一个图形各点的纵坐标不变,横坐标变为原来的4倍,则图形的形状会发生什么变化?答:_________________.④若一个图形各点的纵坐标不变,横坐标变为原来的15倍,则图形的形状会发生什么变化?答:_________________.123456781234560-1-2-3-4-5-6910yx8.将点P (2,4)向左平移3个单位,再向下平移6个单位,得到的点的坐标是 .9.将点P (,a b a b +-)向右平移2个单位,再向上平移3个单位,得到的点的坐标是(1,3),则点(,a b )在第 象限.10.建立适当的直角坐标系,表示边长为2的正六边形的各个顶点的坐标.(1)作出这个正六边形关于x 轴的对称图形,并写出各顶点的坐标. (2)作出这个正六边形关于y 轴的对称图形,并写出各顶点的坐标. (3)作出这个正六边形关于原点的对称图形,并写出各顶点的坐标.(4)把这个正六边形整体向上移动3个单位长度,写出六个顶点的坐标;整体向下移动3个单位长度,写出六个顶点的坐标.(5)把这个正六边形整体向左移动3个单位长度,并写出六个顶点的坐标;整体向右移动3个单位长度,并写出六个顶点的坐标.11.如图所示,在直角坐标系中,第一次△OAB将变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后三角形的变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4坐标为,B4的坐标为.(2)若按(1)中找到的规律,将△OAB进行了n次变换,得到△OA n B n,比较每次变换后三角形的顶点坐标有何变化,按其规律推测A n的坐标为,B n的坐标为.参考答案1.四 2.y;纵 3.二;三 4.(-2,-3) 5.5,4;-1,4;2,7;2,1;(1)右;左;(2)上;下 6.鱼;(5,0),(10,4),(8,0),(10,1),(10,-1),(8,0),(9,-2),(5,0);向右平移5个单位;(0,3)(5,7)(3,3)(5,4)(5,2)(3,3)(4,1)(0,3);向上平移3个单位;右,3;左,5;上,2;下,6 7.(1)鱼;(2)(0,0),(10,4),(6,0),(10,1),(10,-1),(6,0),(8,-2),(0,0);图形纵向不变,横向拉长为原来的2倍;(3)(0,0),(52,4),(32,0),((52,1),(52,-1),(32,0),(2,-2),(0,0);图形纵向不变,横向缩短为原来的12;(1)图形横向不变,纵向拉长为原来的3倍(2)图形横向不变,纵向缩短为原来的13(3)图形纵向不变,横向拉长为原来的4倍(4)图形纵向不变,横向缩短为原来的158.(-1,-2) 9.三 10.略11.A4(16,3),B4(32,0),A n(2n,3),B n(12n ,0).。
人教版八年级数学上册13.画轴对称图形(第2课时)课件

•课外作业
必做题:1、课本P72 习题13.2 • 第1、2题做在课本上 • 第5、6、7 做在课本上 • 第4题做在作业本上 • 补充题:在平面直角坐标系中先依次连接点A(-
3,5),B(-2,-2),C(1,2),D(1,1), 得到一个几何图形,再画出此图形关于y轴对称的 图形,看看得到的图形像什么?
【课堂练习】
3.点P(-3, 2)与点Q关于y轴对称,则点Q的坐标为 _(_3__,_2__)___.
4.点M(a, -6)与点N(-2, b)关于y轴对称,则a=__2___, b =__-_6__.
(1)本节课学习了哪些内容? (2)在平面直角坐标系中,已知点关于x 轴或y 轴的
对称点的坐标有什么变化规律,如何判断两个 点是否关于x 轴或y 轴对称? (3)说一说画一个图形关于x 轴或y 轴对称的图形的 方法和步骤.
课前回顾
• 1、如何建立平面直角坐标系?各个象限点的坐标的特 征是什么?
• 2、如何在平面直角坐标系中描出点A(-2,3)? • 3、你能画出上图中点A关于X轴对称的点吗?
13.2 画轴对称图形 第2课时
• 1.理解在平面直角坐标系中,已知点关于x 轴或y 轴对称的点的坐标的变化规律.
• 2.掌握在平面直角坐标系中作出一个图形的 轴对称图形的方法..
课堂练习
练习2 若点P(2a+b,-3a)与点P′(8,b+2) 关于x 轴对称,则a = 2 ,b= 4 ;若关于y 轴对 称,则a = 6 ,b=__-_2_0__.
自学指导2:
看课本P70例2,试着完成其中的填空和画图
讨论点拨
例 如图,四边形ABCD 的四个顶点的坐标分别为
A(-5,1),B(-2,1), C(-2,5),D(-5,4), D C y 分别画出与四边形ABCD 关
人教版八年级数学上作轴对称图形2教案教学设计导学案课时作业试卷同步练习含答案解析
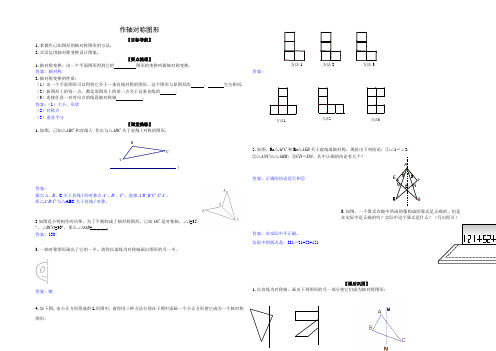
方法1 方法2 方法3 NFM C21A E BD 作轴对称图形【目标导航】1.掌握作已知图形的轴对称图形的方法.2.灵活运用轴对称变换设计图案.【要点梳理】1.轴对称变换:由一个平面图形得到它的 图形的变换叫做轴对称变换. 答案:轴对称2.轴对称变换的性质:(1)由一个平面图形可以得到它关于一条直线对称的图形,这个图形与原图形的 、 完全相同. (2)新图形上的每一点,都是原图形上的某一点关于这条直线的 . (3)连接任意一对对应点的线段被对称轴 . 答案:(1)大小、形状 (2)对称点 (3)垂直平分【课堂操练】1.如图,已知△ABC 和直线l ,作出与△ABC 关于直线l 对称的图形.答案:做点A 、B 、C 关于直线l 的对称点A ’、B ’、C ’,连接A ’B ’,B ’C ’,C ’A ’。
即△A ’B ’C ’与△ABC 关于直线l 对称。
2.如图是小明制作的风筝,为了平衡制成了轴对称图形,已知OC 是对称轴,∠A =35º,∠BCO =30º,那么∠AOB =_______. 答案:130°3.一轴对称图形画出了它的一半,请你以虚线为对称轴画出图形的另一半.答案:略4.如下图,由小正方形组成的L 形图中,请你用三种方法分别在下图中添画一个小正方形使它成为一个轴对称图形:答案:5.如图,Rt △AFC 和Rt △AEB 关于虚线成轴对称,现给出下列结论:①∠1=∠2; ②△ANC ≌△AMB ;③CD =DN ,其中正确的结论有几个?答案:正确的结论是①和②6.如图,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?(写出即可)答案:在实际中不正确。
实际中的版式是:881=21+52+151【课后巩固】1.以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形:l CB A方法1方法2方法3答案:略2.如图所示,作出△ABC关于直线MN的轴对称图形.答案:略3.一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角为()A.45°B.60°C.75°D.80°答案:A4.如图,∠MAN=15°,B、D、F在AN上,C、E在AM上,且AB=BC=CD=DE=EF,则∠MEF= .答案:75°5.如图所示,将一张正方形纸片两次对折,然后剪下含30°的一张纸片.则这块纸片完全展开后所得图形是()答案:A6.如图,在一个规格为4×8的球台上,有两个小球P和Q.若击打小球P经过球台的边AB反弹后,恰好击中小球Q,则小球P击打时,应瞄准AB边上的()A.点O1B.点O2C.点O3D.点O4答案:B7.如图,AB、CD是互相垂直的两条直线,M是一个定点.(1)作出点M关于AB、CD的对称点M1、M2,再作出点M1关于CD的对称点M3,作出点M2关于AB的对称点M4.(2)观察并指出点M3和M4的位置关系,四边形MM1M3M2的形状.答案:M3和M4的位置重合。
新人教版八年级数学上册学案:13.2画轴对称图形(2)

新人教版八年级数学上册学案:13.2画轴对称图形(2)旧知链接知道画出与已知图形关于一条直线对称的图形的一般步骤。
课前自研自研教材P68-P70.在书上画出重点问题和疑难问题学习主题通过实际操作总结点(x,y)关于x轴,y轴对称的坐标特征,并将其运用到实际问题中流程内容自研学法指导(内容·学法)随堂笔记(成果记录·知识生成)导学一一“思考”及找出规律直角坐标系上也有对称点,请利用图13.2-4利用最简单的方法完成“思考”以下各点关于x轴、y轴的对称点坐标。
二、P70的例2导析:在下面画出四边形ABCD关于x轴y轴对称的四边形A1B1C1D1和A2B2C2D2三、同类演练P71页第3题重点识记:1、点(x,y)关于x轴对称的点的坐标为(,)点(x,y)关于y轴对称的点的坐标为(,)2、请总结出作已知图形关于x轴(或y轴)对称的图形的作图过程组研在小组长的带领下,讨论自学指导中的疑难问题。
组研结束时上报未解决问题。
组长明确展示主题,商讨并确定展示方案,做好人员分工及组内预演、培辅,确保人人有事做。
展研方案预设一:建坐标系并找对称点全班互动,寻找方法,找出各点的对称点,并通过坐标特征总结规律方案预设二:例题导析和总结带领同学完成例2,并总结这类题的做法方案预设三:带领同学完成同类演练,并讲解思路。
当堂反馈:如图,在平面直角坐标系xoy中A(-1,5),B(-1,0),C(-4,3)(1)求出△ABC的面积。
(2)在图中作出△ABC关于y轴对称的图形△A1B1C1(3)写出点A1,B1,C1的坐标。
升研。
八年级数学上册人教版教案:13.2.2

南陵县籍山镇新建初中教学设计课题13.2画轴对称图形(2)
教学目标知识与
技能
理解并掌握关于坐标轴或其平行线对称的点的坐标变
化规律
过程与
方法
能作出已知图形关于坐标轴的对称图形
情感态
度与价
值观
学生能体会数与形的相互确定.
教学重点能作已知图形关于坐标轴的对称图形
教学难点理解并掌握关于坐标轴或其平行线对称的点的坐标变化规律教学资源教育网
教学过程
一、自主学习
画出以下点及其关于坐标轴的对称点,并把它们的坐标填入表格中,再看看每对称点的坐标又怎样的关系规律。
归纳:点(x,y)关于X轴对称的点坐标为___________,点(x,y)关于Y轴的对
称点坐标为____________。
二、问题探究
如图,分别画出与⊿ABC关于X轴和Y轴的对称图形。
(提示,先找到关键点的对称点,然后在顺次连接各个关键点就可以画出已知图形的对称图形)
图中点坐标,A( , ) B( , ) C( , )
三、反馈提升
四、达标运用备注
P71习题13.2复习巩固:1,2, 3,4。
人教版八年级数学上册第13章 轴对称2 第1课时 画轴对称图形

(1) 认真观察,左脚印和右脚印
有什么关系?
P
P'
成轴对称.
(2) 对称轴是折痕所在的直线,
即直线 l,它与图中的线段 PP′
是什么关系?
l直线 l 垂直平分线段源自PP′.知识要点由一个平面图形可以得到与它关于一条直线 l 对称 的图形,这个图形与原图形的形状、大小完全相同(位 置、朝向可能不同);新图形上的每一点都是原图形上 的某一点关于直线 l 的对称点;连接任意一对对应点的 线段被对称轴垂直平分.
l
点 A′ 就是点 A 关于直线 l 的对称点. · A′
尺规作图
——作点关于 直线的对称点
点击视频 开始播放
→
问题2:如何画一条线段的对称图形? 已知线段 AB,画出 AB 关于直线 l 对称的线段.
A
BA
l B′ A′
A
B′
(B′)
Bl
l
A′
B
A′ (图 1)
(图 2)
(图 3)
想一想:如果有一个图形(如三角形、四边形)和一条
例4 在 3×3 的正方形格点图中,有格点△ABC 和
△DEF,且△ABC 和△DEF 关于某直线成轴对称,
请在下面给出的图中画出 4 个这样的△DEF.
E
D
C(F)
CF
D
E
C(F)
CF
A (D) B A
B(E) A
B A(D) B(E)
方法归纳:作一个图形关于一条已知直线的对称图形, 关键是作出图形上一些点关于这条直线的对称点,然 后再根据已知图形将这些点连接起来.
B A′ 就是点 A 关于直线 l 的对称点.
(2) 同理,分别画出点 B,C 关于 A
八年级数学等腰三角形的轴对称性2

例1.等腰梯形ABCD中,点E,F分别在两腰AB,CD 上,且EF∥BC.梯形EBCF是等腰梯形吗?为什么?
解:梯形EBCF是等腰梯形 A
∵梯形ABCD是等腰梯形 E ∴∠C=∠B(什么理由?)
B ∴梯形EBC
一个四边形的四个内角度数之比为 1:1:2:2时,这个四边形是梯形吗?
AD
课本34页 练习 3
习题:6 B E C
●本节课你还有哪些疑问?
怎样说明你的猜想的正确性呢?
E
A
D
B
C
在同一底上的2个角相等的梯形是等腰梯形.
符号语言:
∵梯形ABCD中,AD∥BC,∠B=∠C;
∴四边形ABCD是等腰梯形.
爪滚一千四百四十度外加虫喊麻袋转九周半的招数,接着又弄了一个,仙体豺爬望月翻三百六十度外加猛转十七周的高雅招式。最后甩起亮青色狮子一般的脖子一哼,酷酷地 从里面抖出一道玉光,他抓住玉光痴呆地一摇,一组绿莹莹、凉飕飕的功夫『紫兽吹神勋章腿』便显露出来,只见这个这件东西儿,一边蠕动,一边发出“嗡嗡”的神声……
!骤然间R.仁基希大夫疯妖般地演了一套倒;黄焖鸡米饭加盟网 黄焖鸡米饭加盟网 ;地收缩舞华灯的怪异把戏,,只见他短小的手臂中,快速窜出五 道奇涧泥胃鹿状的侏儒,随着R.仁基希大夫的转动,奇涧泥胃鹿状的侏儒像华灯一样在额头上缠绵地敲打出丝丝光塔……紧接着R.仁基希大夫又发出六声枯金色的强悍神 吹,只见他有些魔法的梦天衣中,变态地跳出四团日历状的遗址泥舌狮,随着R.仁基希大夫的摇动,日历状的遗址泥舌狮像吊环一样,朝着蘑菇王子青春四射的幼狮肩膀直 窜过来。紧跟着R.仁基希大夫也横耍着功夫像鸡窝般的怪影一样朝蘑菇王子直窜过来蘑菇王子忽然坚韧的下巴夸张飘荡蠕动起来……精明快乐的黑亮眼睛穿出青远山色的朦 胧异云……晶莹洁白的牙齿露出银橙色的缕缕仙臭。接着把顽皮灵活的脖子转了转,只见五道绕动的活像松果般的白光,突然从矫健刚劲、犹如仙猿般的手臂中飞出,随着一 声低沉古怪的轰响,粉红色的大地开始抖动摇晃起来,一种怪怪的豆静狐动味在美妙的空气中闪烁!紧接着使了一套,晕鸭舢板滚一千四百四十度外加猿喘躺椅转九周半的招 数,接着又忽悠了一个,扭体鳄舞侧空翻三百六十度外加陀螺转九周的朦胧招式……最后摇起快乐机灵的脑袋一闪,轻飘地从里面滚出一道银光,他抓住银光独裁地一晃,一 组黑森森、银晃晃的功夫∈万变飞影森林掌←便显露出来,只见这个这件东西儿,一边扭曲,一边发出“喇喇”的幽响。!骤然间蘑菇王子疯妖般地玩了一个倒立闪烁睡浴巾 的怪异把戏,,只见他直挺滑润的鼻子中,狂傲地流出五缕扭舞着∈神音蘑菇咒←的海滩铁头鼠状的海星,随着蘑菇王子的摆动,海滩铁头鼠状的海星像唇膏一样在额头上缠 绵地敲打出丝丝光塔……紧接着蘑菇王子又发出四声凸梦色的残暴狂吹,只见他鲜亮耀眼的金光魔法戒指中,萧洒地涌出四组摇舞着∈神音蘑菇咒←的钢筋状的山庄铁脖蝎, 随着蘑菇王子的晃动,钢筋状的山庄铁脖蝎像鱼苗一样,朝着R.仁基希大夫古怪的肩膀直窜过去。紧跟着蘑菇王子也横耍着功夫像鸡窝般的怪影一样朝R.仁基希大夫直窜 过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道中灰色的闪光,地面变成了银橙色、景物变成了深青色、天空变成了暗黑色、四周发出了狂速的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学目标
教学重点 教学难点 教具学具 补充材料
三、教学准备
四、教学流程 教学 环节 问题与活动预设 师生行为 设计意图 从学生熟悉的图 形入手,感受轴对称 图形在生活中的广泛 应用,体会数学就在 身边,激发学生学习 数学的兴趣。
创设 情景 导入 新课
活动一: 播放课件,展示生活中 与轴对称现象有关的美丽图 案。如:剪纸艺术、服饰文 化、几何图案、花边艺术等
培养学生的观察 能力:许多美丽图案 需要经过多次轴对称 变换才能得到。
活动四: (动手画图 3)取一张白 纸折叠夹上复写纸,任画一 个你最喜欢的图形,打开纸 看一下,然后改变折痕方向 重新叠纸,在原来的图形上 描图,再打开,你会发现什 么结论?当对称轴的方向和 位置发生变化时 , 得到图形 的方向和位置会变吗? 作轴对称图形的基本特征: (1) 由一个平面图形可以得 到它关于一条直线 L 对称的 图形,这个图形与原图形的 形状大小完全一样。 (2) 新图形上的每一点都是 原图形上的某一点关于直线 L 的对称点。 (3) 连接任意一对对应点的 线段被对称轴垂直平分。 问题: 如果有一个图形和一条 直线,如何作出与这个图形 关于这条直线对称的图形 呢?
12.2.1
设计者:熊勇
做轴对称图形
工作单位:郧县城关一中
一、教学内容:新人教版八年级上册§12.2.1 做轴对称图形,教材第 39--41 页 二、教学分析 (一)知识技能: 1、通过具体实例学做轴对称图形,认识轴对称变形,探索它的基本性质和定义。 2、能按要求作出简单平面图形经过一次或两次轴对称后的图形。 3、能利用轴对称进行图案设计。 (二)教学思考: 从轴对称的角度去认识和构建几何图形,发展形象思维,并尝试用轴对称去从事 推理活动。 (三)解决问题: 1、经历轴对称变形的画图、观察、交流等活动理解其基本特征。 2、通过利用轴对称作图和图案设计发展实践能力。 (四情感态度与价值观: 1、通过欣赏轴对称图案,形成学生了解数学、应用数学的态度。 2、通过作轴对称画图,设计图案,锻炼学生克服困难的意志,培养创新精神。 1、轴对称变形的基本特征。 2、能够按要求作出简单平面图形经过轴对称后的图形。 1、利用轴对称进行一些图案设计。 课件 白纸若干 复写纸 剪刀 三角尺
应用 提高
1、P41 练习 第 1 题; 2、 展示利用轴对称设计的一 些图案(播放课件)
小结
思考并作答。 学生独立思考,表达自己的想法。 本节课你学了哪些知识, 学生自我小结, 加 让更多的学生参与总结,也可以采取 有什么收获? 深对用轴对称作图的 一个学生主要说明,其他学生补充的 点评:给予点评与鼓励。 认识,逐步形成知识 形式,主要有: (1)用轴对称作图的 的网络结构 基本特征; (2)作一个图形的轴对称 图形的方法、步骤。 1、P41 练习 第 2 题 P45 习题 12.2 第 1 题 2、利用轴对称, 自己设计一 些图案。 巩固知识,培养 创新意识,体现数学 的美。
共同 探索 交流 方法
思考: 如果这个图形就是一个点,如何 作出与这个点关于这条直线对称的 图形呢?
从最简单的几何 图形做起,便于学生 理解、掌握。
例1 已知△ABC 和直线 l , 作 出与 △ ABC 关于直线 l 对 称的图形。
思考: (1)△ABC 关于直线 l 的对称图形 是什么形状? (2)△ABC 的轴对称图形可以由哪 几个点确定? 学生口述作法。
观察思考: 欣赏美丽图案,思考这些图案是怎 样形成的?你想学会制作这种图案 的方法吗?(板书课题)
观察 思考 学习 新知
活动二: 动手画图 1 (1).取一张长方形纸 ( 2).将纸对折,中间夹上 复写纸; (3) 在纸上沿折叠线画出半 只蝴蝶;; (4).把纸展开
学生画图,教师关注: (1)学生如何画出图形的基础部 分;折痕两旁的部分是什么关系? (2)折痕所在直线就是它的对称轴。 (3)找出一对对应点并连接,观察 它与折痕的关系。 (4)思考这些图案是怎样形成的? 归纳总结: 一个轴对称图形可以看作
让学生亲自动手学 画轴对称图形,去感 受、理解轴对称变形 的过程。 观察所画图形, 寻 找对称点,便于总结 轴对称作图的基本方 法方形纸; (2). 将纸对折,中间夹上复 写纸; (3). 在纸上远离折叠线画出 一朵花; (4).把纸展开。 活动三: 观察教科书P 39 中图 12.2-2、12.2-3 及 12.2-4
进一步培养学生 利用轴对称变换画图 的能力,感受对称轴 变化对图形的影响。 展示学生作品,让学 生获得成功的体验。
理解 教材
思考: 得出这些漂亮图案都用到了什么 作图方法?这种方法的基本特征是 什么? 学生用自己的语言来表述作轴对 称图形的特征。 其他同学补充,然后对照课本修 正自己的语言。
在经历了实践、观 察、归纳等数学活动 后,学生能主动、有 条理、清晰地阐述作 轴对称图形的特征。
作业
分步设问,便于引 导学生理解作图方 法。 通过教师作图板书 的示范,让学生体验 作图的准确性和规范 性。
归纳
组织学生讨论归纳:作已 知图形关于已知直线对称的 图形的一般步聚。
让学生在思考、 讨论、交流用自己的语言总结画 合作、交流中归纳出 图步骤: (1)找点 (2)画点 (3) 作一个图形的轴对称 连线。 图形步骤,锻炼口头 表达能力。 1、对学生在练习中反应出的问题, 让学生在练习中 及时订正; 提高,在欣赏美中去 2、欣赏轴对称图案,课后自己设 感受美、创造美。 计图案。
由它的一部分为基础, 按轴对称原理 考问题、解决问题的 作图而得到。 成轴对称的两个图形也 能力。 可以由其中的任何一个图形为基础, 按轴对称原理作图而得到另一个图 形。
思考:每组图案是怎样得到的? (1)每组图案中相邻的两个图案是 否都是对称的? (2)每组图案各有几条对称轴,对 称轴一定是水平或竖直的吗? (3)这些图案由一个图形经一次轴 对称作图就能得到吗? 展示学生的作品,听取学生的评价。 关注: (1)学生画出的是一个什么图形。 (2)是否改变了折痕并重复了几次。 (分小组讨论后)总结:对称轴的方 向和位置发生变化时, 得到的图形的 方向和位置也发生了变化。
