Signal processing for melody transcription
signalprocessing latex模板 -回复

signalprocessing latex模板-回复英文文章标题: Introduction to Signal Processing and its LaTeX TemplateIntroduction:Signal processing is a field of study that deals with the analysis, manipulation, and transmission of signals. It plays a crucial role in various applications such as telecommunications, medical imaging, audio and video processing, and control systems. In this article, we will dive into the fundamentals of signal processing and discuss the use of LaTeX templates for writing documents related to this field.Section 1: Understanding Signal ProcessingSignal processing involves the transformation of signals to extract meaningful information or enhance their quality. Signals can be of different types, including analog, digital, continuous-time, or discrete-time. The main objective of signal processing is to manipulate these signals using mathematical techniques to achieve specific goals.Section 2: Basic Concepts in Signal ProcessingTo understand signal processing, it is important to grasp somefundamental concepts. These include:1. Time Domain vs. Frequency Domain:Signals can be represented in either the time domain or the frequency domain. The time domain represents a signal as a function of time, while the frequency domain represents a signal as a function of frequency. Fourier analysis is the mathematical tool used to transform signals between these domains.2. Filtering:Filtering is a vital component of signal processing. It involves the modification of a signal by removing or enhancing specific frequency components. Filters can be classified as low-pass,high-pass, band-pass, or band-reject, depending on the desired frequency response.3. Sampling:Sampling is the process of converting continuous analog signals into discrete digital signals. This is accomplished by measuring the amplitude of the analog signal at regular intervals known as sampling points. The Nyquist-Shannon sampling theorem defines the minimum sampling rate required to accurately reconstruct theoriginal signal.Section 3: LaTeX Template for Signal ProcessingLaTeX, a typesetting system widely used for scientific and technical publications, offers numerous templates dedicated to signal processing. Below, we will outline steps to create a signal processing document using LaTeX:1. Choose a LaTeX Compiler:There are different LaTeX compilers available, such as TeX Live, MiKTeX, and MacTeX. Select the one suitable for your operating system and install it.2. Create a New LaTeX Document:Start by creating a new LaTeX document with the ".tex" extension. Use the "\documentclass" command to specify the type of document you want to create, such as an article or a book.3. Include Required Packages:To enable signal processing-related functionalities, include the necessary packages in the preamble section of the LaTeX document. These packages might include "amsmath," "amssymb," and"graphicx."4. Begin the Document Body:Within the document body, begin by defining the title, author, and date using the "\title," "\author," and "\date" commands, respectively.5. Write the Content:Write the content of your signal processing article using LaTeX syntax. Utilize the mathematical notation and equations provided by LaTeX to correctly represent signal processing concepts and formulas.6. Include Figures and Graphs:LaTeX facilitates the inclusion of figures and graphs within your document. Use the "\includegraphics" command to insert images and the "tikz" package to create graphs.7. Compile the Document:Once the content is complete, compile the LaTeX document using your selected LaTeX compiler. This process transforms your source code into a beautifully formatted document in PDF format.Conclusion:Signal processing plays a crucial role in various technological applications. Understanding the basic concepts of signal processing allows us to analyze, manipulate, and transmit signals effectively. LaTeX provides a convenient platform for writing signal processing-related documents due to its extensive mathematical notation and formatting capabilities. Utilizing LaTeX templates dedicated to signal processing can significantly ease the document creation process and ensure a high-quality output.。
SIGNAL PROCESSING SYSTEM, SIGNAL PROCESSING METHOD
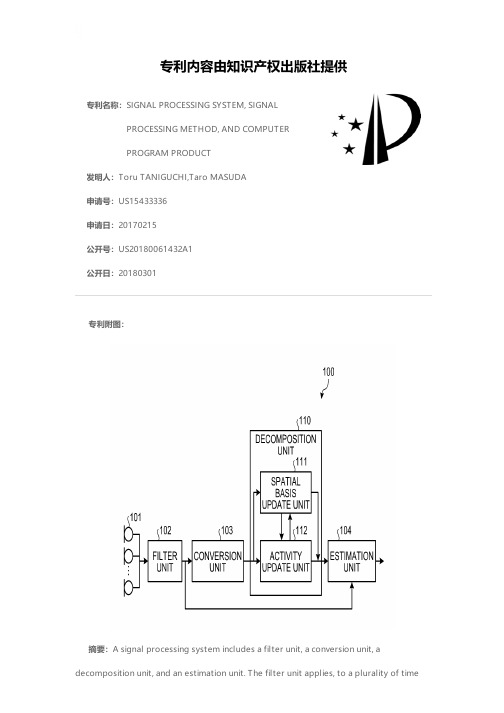
专利名称:SIGNAL PROCESSING SYSTEM, SIGNALPROCESSING METHOD, AND COMPUTERPROGRAM PRODUCT发明人:Toru TANIGUCHI,Taro MASUDA申请号:US15433336申请日:20170215公开号:US20180061432A1公开日:20180301专利内容由知识产权出版社提供专利附图:摘要:A signal processing system includes a filter unit, a conversion unit, adecomposition unit, and an estimation unit. The filter unit applies, to a plurality of timeseries input signals, N filters estimated by independent component analysis of the input signals to output N output signals. The conversion unit converts the output signals into nonnegative signals each taking on a nonnegative value. The decomposition unit decomposes the nonnegative signals into a spatial basis that includes nonnegative three-dimensional elements, that is, K first elements, N second elements, and I third elements, a spectral basis matrix of I rows and L columns that includes L nonnegative spectral basis vectors expressed by I-dimensional column vectors, and a nonnegative L-dimensional activity vector. The estimation unit estimates sound source signals representing signals of the signal sources based on the output signals using the spatial basis, the spectral basis matrix, and the activity vector.申请人:Kabushiki Kaisha Toshiba地址:Tokyo JP国籍:JP更多信息请下载全文后查看。
Signal processing apparatus
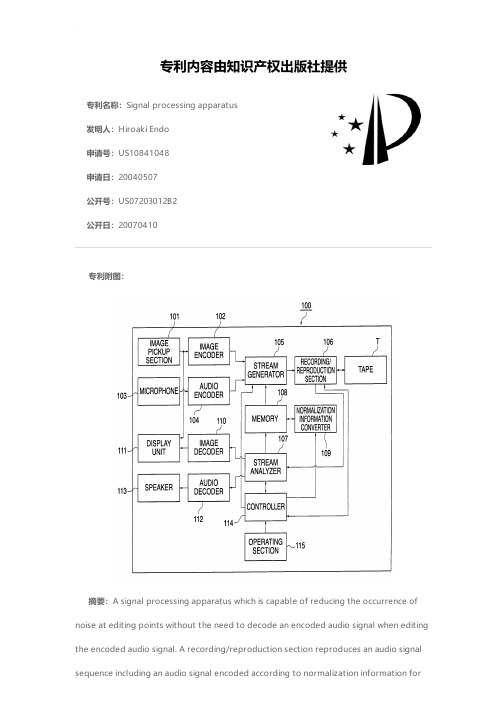
专利名称:Signal processing apparatus发明人:Hiroaki Endo申请号:US10841048申请日:20040507公开号:US07203012B2公开日:20070410专利内容由知识产权出版社提供专利附图:摘要:A signal processing apparatus which is capable of reducing the occurrence of noise at editing points without the need to decode an encoded audio signal when editing the encoded audio signal. A recording/reproduction section reproduces an audio signal sequence including an audio signal encoded according to normalization information forcontrolling amplitude of the audio signal, and the normalization information. A normalization information converter changes the normalization information of the reproduced audio signal sequence. At least one of a first normalization information corresponding to a first encoded audio signal of a first audio signal sequence as the reproduced audio signal sequence and a second normalization information corresponding to a second encoded audio signal of a second audio signal sequence as the reproduced audio signal sequence are changed by the normalization information converter, such that the value of the first normalization information and the value of the second normalization information become equal.申请人:Hiroaki Endo地址:Tokyo JP国籍:JP代理机构:Rossi, Kimms & McDowell LLP.更多信息请下载全文后查看。
改进型music算法 相干信号

改进型music算法相干信号英文回答:Improving the music algorithm for coherent signals is an interesting challenge. Currently, the music algorithm is widely used for signal processing in various applications, including audio processing, radar systems, and wireless communications. However, there is always room for improvement to enhance its performance and accuracy.One possible improvement to the music algorithm is to incorporate machine learning techniques. By training a machine learning model with a large dataset of coherent signals, the algorithm can learn to better identify and extract relevant features from the signals. This can lead to improved accuracy and robustness in detecting and classifying coherent signals.Another improvement could be the integration of deep learning algorithms. Deep learning models, such asconvolutional neural networks (CNNs) or recurrent neural networks (RNNs), have shown great success in various signal processing tasks. By incorporating deep learning into the music algorithm, it can potentially improve the algorithm's ability to handle complex and non-linear coherent signals.Furthermore, optimizing the parameter selection process can also enhance the music algorithm's performance. The music algorithm relies on selecting the number of signal sources and the signal subspace dimension. By developing more efficient and accurate methods for determining these parameters, the algorithm can better adapt to different signal scenarios and improve its overall performance.To illustrate the potential improvements, let's consider the example of music source separation. Currently, the music algorithm is used to separate different sourcesin an audio signal. However, it may struggle when the sources are highly correlated or when there are overlapping sources. By incorporating machine learning techniques, the algorithm can learn to better distinguish between different sources and separate them more accurately.For instance, let's say we have a music recording with vocals and instruments playing simultaneously. The current music algorithm may have difficulty separating the vocals from the instruments if they are highly correlated. However, by training a machine learning model with a large datasetof vocal and instrumental tracks, the algorithm can learnto differentiate between the two and successfully separate them in the given recording.中文回答:改进相干信号的music算法是一个有趣的挑战。
纹理物体缺陷的视觉检测算法研究--优秀毕业论文

摘 要
在竞争激烈的工业自动化生产过程中,机器视觉对产品质量的把关起着举足 轻重的作用,机器视觉在缺陷检测技术方面的应用也逐渐普遍起来。与常规的检 测技术相比,自动化的视觉检测系统更加经济、快捷、高效与 安全。纹理物体在 工业生产中广泛存在,像用于半导体装配和封装底板和发光二极管,现代 化电子 系统中的印制电路板,以及纺织行业中的布匹和织物等都可认为是含有纹理特征 的物体。本论文主要致力于纹理物体的缺陷检测技术研究,为纹理物体的自动化 检测提供高效而可靠的检测算法。 纹理是描述图像内容的重要特征,纹理分析也已经被成功的应用与纹理分割 和纹理分类当中。本研究提出了一种基于纹理分析技术和参考比较方式的缺陷检 测算法。这种算法能容忍物体变形引起的图像配准误差,对纹理的影响也具有鲁 棒性。本算法旨在为检测出的缺陷区域提供丰富而重要的物理意义,如缺陷区域 的大小、形状、亮度对比度及空间分布等。同时,在参考图像可行的情况下,本 算法可用于同质纹理物体和非同质纹理物体的检测,对非纹理物体 的检测也可取 得不错的效果。 在整个检测过程中,我们采用了可调控金字塔的纹理分析和重构技术。与传 统的小波纹理分析技术不同,我们在小波域中加入处理物体变形和纹理影响的容 忍度控制算法,来实现容忍物体变形和对纹理影响鲁棒的目的。最后可调控金字 塔的重构保证了缺陷区域物理意义恢复的准确性。实验阶段,我们检测了一系列 具有实际应用价值的图像。实验结果表明 本文提出的纹理物体缺陷检测算法具有 高效性和易于实现性。 关键字: 缺陷检测;纹理;物体变形;可调控金字塔;重构
Keywords: defect detection, texture, object distortion, steerable pyramid, reconstruction
II
Digital Signal Processing

Digital Signal Processing Digital Signal Processing (DSP) is a crucial aspect of modern technology, playing a vital role in various applications such as communication systems, audio processing, image and video processing, and control systems. As the demand for digital signal processing continues to grow, it is important to understand the challenges and opportunities that come with it. One of the primary challenges in digital signal processing is the need for high-speed and efficient processing of large amounts of data. With the increasing complexity of DSP algorithms and the demand for real-time processing, there is a constant pressure to develop faster and more efficient hardware and software solutions. This requires a deep understanding of algorithms, architectures, and implementation techniques to meet the performance requirements of modern DSP systems. Another challenge in digital signal processing is the need for robust and reliable signal processing algorithms that can handle noisy and uncertain input data. In real-world applications, signals are often corrupted by noise, interference, and other disturbances, which can degrade the performance of signal processing systems. Developing algorithms that can effectively mitigate these effects and provide accurate results is a significant challenge in DSP. Furthermore, the rapid advancements in technology and the increasing demand for high-performance signal processing systems create opportunities for innovation and growth in the field of digital signal processing. The development of new algorithms, hardware architectures, and implementation techniques can lead to significant improvements in the performance andcapabilities of DSP systems, opening up new possibilities for applications in areas such as healthcare, automotive, and consumer electronics. From a practical perspective, digital signal processing has revolutionized various industries, enabling the development of advanced communication systems, high-quality audio and video processing, and sophisticated control systems. The impact of DSP can be seen in everyday devices such as smartphones, digital cameras, and smart home appliances, where signal processing algorithms play a crucial role in delivering a seamless and high-quality user experience. Moreover, the interdisciplinary nature of digital signal processing brings together concepts from mathematics, engineering, and computer science, creating a diverse and dynamic field thatattracts professionals from various backgrounds. The collaborative nature of DSP research and development fosters innovation and creativity, as experts from different disciplines work together to solve complex problems and push the boundaries of what is possible in signal processing. In conclusion, digital signal processing presents both challenges and opportunities in the modern technological landscape. As the demand for high-performance signal processing systems continues to grow, there is a need for innovative solutions that can address the complexities of real-world applications. By leveraging advancements in algorithms, hardware, and interdisciplinary collaboration, the field of digital signal processing is poised to make significant contributions to the advancement of technology and its impact on society.。
Digital Signal Processing

Digital Signal Processing Digital Signal Processing (DSP) is a field of study that deals with the manipulation of signals in the digital domain. It is an essential aspect of modern electronics, as most signals in the real world are analog in nature, and must be converted to digital signals before they can be processed by computers. DSP is used in a wide range of applications, including audio and video processing, telecommunications, control systems, and biomedical engineering. In this essay, we will explore the various aspects of DSP, including its history, principles, and applications. The history of DSP can be traced back to the early days of computing, when researchers first began to explore the possibilities of digital signal processing. In the 1960s, digital signal processing techniques were first developed for use in military applications, such as radar and sonar systems. These early systems were based on simple algorithms, such as the Fast Fourier Transform (FFT), which allowed signals to be analyzed and manipulated in the frequency domain. Over time, these techniques were refined and expanded, and DSP became an essential part of modern electronics. One of the key principles of DSP is the concept of sampling. In order to process analog signals in the digital domain, they must first be sampled at regular intervals. This process involves taking discrete measurements of the signal at specific points in time, and then converting these measurements into digital values. The frequency at which the signal is sampled is known as the sampling rate, and it is an important parameter that affects the quality of the digital signal. Higher sampling rates generally result in better quality signals, but they also require more processing power and storage capacity. Another important principle of DSP is the use of digital filters. These filters are used to manipulate the frequency content of a signal, and they can be used to remove unwanted noise or enhance specific features of the signal. There are many different types of digital filters, including low-pass, high-pass, band-pass, and notch filters, each of which is designed to perform a specific function. Digital filters can be implemented using a variety of algorithms, including Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. DSP has many applications in a wide range of fields. One of the most common applications of DSP is in audio processing, where it is used tomanipulate and enhance sound signals. DSP techniques can be used to remove unwanted noise from audio recordings, enhance the clarity of speech, and improve the overall quality of music recordings. DSP is also used in video processing, where it is used to enhance the quality of images and video streams. In telecommunications, DSP is used to encode and decode digital signals, and it is an essential component of modern digital communication systems. Another important application of DSP is in control systems, where it is used to manipulate signals to control the behavior of machines and systems. DSP techniques can be used to control the speed of motors, adjust the position of robotic arms, and regulate the temperature of industrial processes. In biomedical engineering, DSP is used to analyze and manipulate signals from medical devices, such as ECG machines and MRI scanners. DSP techniques can be used to detect abnormalities in medical signals, enhance the quality of medical images, and improve the accuracy of medical diagnoses. In conclusion, Digital Signal Processing is an essential aspect of modern electronics, with applications in a wide range of fields. Its principles are based on the manipulation of signals in the digital domain, using techniques such as sampling and digital filtering. DSP has a rich history, dating back to the early days of computing, and it has evolved to become a vital component of modern technology. Its applications are diverse, including audio and video processing, telecommunications, control systems, and biomedical engineering. As technology continues to advance, DSP will continue to play a critical role in shaping the future of electronics and communications.。
用Processing将声音视觉化

用Processing将声音视觉化作者:张敬云谢作如来源:《中国信息技术教育》2018年第21期你见过声音的样子吗?在文学作品中,常常会将声音进行视觉化,如白居易《琵琶行》中的“嘈嘈切切错杂弹,大珠小珠落玉盘”,形象而生动地描述出声音的样子。
在互动艺术作品中,也常常会看到艺术家尝试将不同的感官进行转换。
将声音视觉化或者把图像转为声音,是常见的艺术表达形式,如将一段或欢快或优美或震撼的音乐视觉化,以跳动的柱形或流水般的霓虹灯展示出来;将如仙乐般美妙的海豚之声视觉化,以花团锦簇的图像展示出来,带给我們听觉视觉的双重体验(如图1)。
而实现这类创意,肯定要选择Mit的Processing软件。
这是一款艺术家用来“画画”的编程语言,能够将各种奇妙的声音变幻为美轮美奂的图像,让受众感受到艺术创作的魅力。
原理分析声音是一种模拟信号,而计算机处理的只能是数值,所以存储在计算机中的声音文件都是经过处理之后的数字化文件。
声音的数字化是通过“采样”和“量化”的方式,实现波形声音模拟量的数字化。
那么Processing又是如何实现声音的视觉化呢?只要能够获得声音的响度、频率等信息,借助傅立叶变换之类的算法,解析出更多的信息,就能将其以柱形、圆形、线形或者任何你想描绘的图形唯美地展现出来。
Processing是一个开源的编程语言,有很多人为其开发了各种开源的库。
声音处理方面功能最强大、应用也最广的是Minim库。
借助这个Minim库,我们不需要理解傅立叶变换,就能够分析出声音的频率、振幅、节奏等信息。
Processing 3.3.6版本已内置了Minim库,我们可以从“贡献管理器”中安装它。
通过“速写本—引用库文件—添加库文件”打开贡献管理器的Libraries选项卡,在Filter框中键入Minim,从列表中选择库,然后单击Install即可。
基本代码首先我们来看一个用Processing将声音视觉化的例子,基本代码如上页表1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Proceedings of the 19th Australasian Computer Science Conference, Melbourne, Australia, January 31–February 2 1996.Signal Processing for Melody TranscriptionRodger J. McNab, Lloyd A. Smith and Ian H. Witten Department of Computer Science, University of Waikato,Hamilton, New Zealand.{rjmcnab, las, ihw}@AbstractM T is a melody transcription system that accepts acoustic input, typically sung by the user, and displays it in standard music notation. It tracks the pitch of the input and segments the pitch stream into musical notes, which are labelled by their pitches relative to a reference frequency that adapts to the user’s tuning. This paper describes the signal processing operations involved, and discusses two applications that have been prototyped: a sightsinging tutor and a scheme for acoustically indexing a melody database.Keywords Music transcription, pitch tracking,computer assisted instruction, sight reading.1IntroductionWith advances in digital signal processing, music representation techniques, and computer hardware technology, it is becoming feasible to transcribe melodies automatically from an acoustic waveform to a written representation, using a small personal computer. For example, a person could sing a tune and have it printed in ordinary musical notation.Such a scheme would have novel and interesting applications for professional musicians, music students, and non-musicians alike. Songwriters could compose tunes easily without any need for a MIDI keyboard; students could practice sight-singing with a computer tutor; and ordinary people could identify those elusive melodies by humming a few bars and having the tune’s name retrieved from a database.Although pitch trackers, which identify the fundamental frequency of a waveform and follow its evolution over time, have been around for 30 years or more, only a few projects have undertaken the systems engineering required to create a music transcription system, and they have invariably suffered from serious restrictions. Askenfelt [1]describes the use of a real-time hardware pitch tracker to notate folk songs from tape recordings.People listened to output synthesised from the pitch track and used a music editor to correct errors.However, it is not clear how successful the system was: Askenfelt reports that “the weakest points in the transcription process at present are in pitch detection and assignment of note values.” Pitch trackers have been used to transcribe instrumental music, but require the input to have constant pitch—no vibrato or glissando. This restriction rules out vocal sources. For example, Moorer [9] describes a system that transcribes two-part music, and his example inputs were violin and guitar duets. He reported problems in finding the beginnings and ends of notes. Piszczalski and Galler [13] restricted input to recorders and flutes playing at a consistent tempo. These instruments are relatively easy to track because they have strong fundamental frequencies and weak harmonics.More recently, Kuhn [8] described a system that transcribes singing by displaying the evolution of pitch as a thick horizontal line on a musical staff to show users the notes they are producing. No attempt is made to identify the boundary between one note and the next: the only way to create a musical score is for users to tap the computer’s keyboard at the beginning of each note. There are at least two commercial systems that claim to teach sightsinging—but they generate the melodies randomly, which inevitably creates very bad examples for users to work with. More fundamentally, they require the user to keep mercilessly to the tempo set by the machine, and the overall success measure is calculated from the accumulated amount of time that he or she is not singing the correct pitch. Such partial solutions to the melody transcription problem are not very useful in practice.Considerable work is required to build a useable melody transcription system that works with the singing voice. Pitch trackers suffer from well-known problems of accuracy, particularly at the beginnings and ends of notes and at transitions between frequencies, and very large errors (e.g. octave displacement) are common. Most people are not good singers, which introduces another source of variability that must be addressed for a transcription device to be useful. Furthermore, there are different ways of defining musical intervals from pitch, and it is an open research question as to which kind of scale people adhere to when singing unaccompanied. Determining the boundaries between notes is not easy, particularly for vocal input, although users can help by singing da or ta .The relationship between pitch acquisition time and the duration of the shortest expected note is an important factor in assigning rhythm.This paper describes MT , a prototype system for melody transcription that runs on an Apple Macintosh PowerPC using its built-in sound capture capability. Although still in an early stage ofdevelopment, MT is able to identify a sung melody, in real time, and transcribe it into Common Music Notation, familiar to most people in European countries as the system in use for several hundred years to notate Western music. Applications include transcribing folk songs or ephemeral musical performances such as jazz improvisations, computer assisted instruction in music, music information retrieval from acoustic input, and even intonation training for the deaf.The structure of the paper is as follows. Section 2 lays the foundation by discussing background requirements for sound capture and music representation. Section 3 examines the problem of pitch tracking, with a brief review of the well-known Gold-Rabiner algorithm that MT uses, and a more extensive discussion of the post-processing that is required to obtain a meaningful pitch contour. Section 4 considers the question of note segmentation, and introduces two separate methods, one based on amplitude and the other on the pitch contour. Section 5 considers how the notes so identified can be labelled with musical note names. Section 6 describes two applications we have prototyped using melody transcription, and the final section presents conclusions from current work and plans for future development.2PreliminariesBefore describing the pitch tracking and note identification processes, let us dispense with some preliminaries regarding sound capture and note representation. The first step in melody transcription is to capture the analog input and convert it to digital form, filtering it to remove unwanted frequencies. The next is to identify its frequency, as described in Section 3. Whereas frequency is a physical attribute of a periodic or quasi-periodic signal, pitch is a perceptual attribute evoked in the auditory system. In general, there is an orderly and well-behaved correspondence between frequency and pitch which is only breached under carefully-controlled conditions in the psychoacoustic laboratory; hence in this paper the terms frequency and pitch are used synonymously. In order to represent the pitches musically, it is necessary to consider how musical scales are defined.2.1Sampling and filteringM T runs on an Apple Macintosh PowerPC 8100, which has built-in sound I/O. The acoustic waveform is filtered at 10 kHz, sampled at 22.05 kHz, and quantised to an 8-bit linear representation. For music transcription, we are interested only in the fundamental frequency of the input. Harmonics, which occur at integral multiples of frequency, often confuse pitch trackers and make it more difficult to determine the fundamental. Therefore the input is filtered to remove as many harmonics as possible, while preserving the fundamental frequency. Reasonable limits for the singing voice are defined by the musical staff, which ranges from F2 (87.31 Hz) just below the bass staff, to G5 (784 Hz) just above the treble staff. While ledger lines are used to extend the staff in either direction, these represent extreme pitches for singers and lie beyond the scope of most applications of melody transcription.Input is low-pass filtered with cutoff frequency of 1000 Hz, stopband attenuation –14 dB, and passband ripple of 2 dB. These are not stringent design requirements, and can be met by a ninth-order finite impulse response (FIR) filter. The filtered signal is passed to the pitch tracker, which identifies its fundamental frequency.2.2The musical scaleA musical scale is a logarithmic organisation of pitch based on the octave, which is the perceived distance between two pitches when one is twice the frequency of the other. For example, middle C (C4) has frequency 261.6 Hz; the octave above (C5) is 523.2 Hz and above that is soprano high C (C6) at 1046.4 Hz. The octave below middle C (C3) is 130.8 Hz, and below that, at 65.4 Hz, is C2—which has ensured the fortunes of a few extraordinary jingle-singing basses.Although the octave seems to be a perceptual unit in humans [4], pitch organisation within the octave takes different forms across cultures. In Western music, the primary organisation since the time of Bach has been the equal-tempered scale, which divides the octave into twelve equally spaced semitones. The octave interval corresponds to a frequency doubling and semitones are equally spaced in a multiplicative sense, so ascending one semitone multiplies the frequency by the twelfth root of 2, or approximately 1.059.The semitone is the smallest unit of pitch in Western music, but smaller units can easily be perceived and are used in the music of some cultures. Physicists and psychologists have agreed on the logarithmic unit of cent, defined as one hundredth of a semitone in the equal tempered scale. An octave, then, is 1200 cents. The smallest pitch difference between two consecutive tones that can be perceived by humans is about 3 Hz; this yields a pitch discrimination of about five cents at 1000 Hz. Above 1000 Hz discrimination stabilises at about 4 cents.While pitch may be perceived categorically in terms of octaves, semitones and cents, frequency is continuous. Assigning a musical pitch to a given frequency involves quantisation. In order to quantise pitches in Western music based on a particular tuning standard (for example, A-440), semitone resolution is sufficient. To accommodate different tuning systems, however—including adapting to users, who inevitably sing slightly sharp or flat—higher resolution is essential. We have designed the system around a pitch resolution of five cents, which is about the limit of its pitch tracking accuracy. 2.3The MIDI note representation Since musical units—octaves, cents and so forth—are relative measures, a distance in cents could be calculated between each individual interval sung by the user. It is useful, however, to set a fixed reference point, making for easier development and debugging. MIDI (Musical Instruments DigitalInterface) is a standard for controlling and communicating with electronic musical instruments. It has many facets, the one most germane to our melody transcription sytem being its standard representation of the Western musical scale. MIDI assigns an integer to each note of the scale. Middle C (C4) is assigned 60, the note just above (C#4) is 61, and that below (B3) is 59. Although it makes little sense to assign pitch labels to frequencies below about 15 Hz, MIDI note 0 is 8.176 Hz, an octave below C0. The highest defined note, 127, is 13344 Hz, again not likely to be perceived as a musical note. The standard piano keyboard ranges from notes 21 to 108.All pitches are related internally to MIDI notes, each being expressed as a distance in cents from 8.176 Hz. Notes on the equal tempered scale relative to A-440 occur at multiples of one hundred cents: C4, for example, is 6000 cents. This scheme easily incorporates alternative (non-equitempered) tunings of Western music, such as the “just” or Pythagorean system, simply by changing the relationship between cents and note name. It can also be adapted to identify notes in the music of other cultures.3Pitch trackingPitch determination is a common operation in signal processing. Unfortunately it is difficult, as testified by the hundreds of different pitch tracking algorithms that have been developed [7]. These algorithms may be loosely classified into three types, depending on whether they process the signal in the time domain (sampled waveform), frequency domain (amplitude or phase spectrum) or cepstral domain (second order amplitude spectrum). One of the best known pitch tracking algorithms, and one against which other methods are often compared, is the Gold-Rabiner scheme [6]. This is a time-domain method: it determines frequency by examining the structure of the waveform. Because it is well understood and well documented, we chose to implement it as the pitch determination method.3.1Gold-Rabiner algorithmA sound that has pitch is periodic (or, more accurately, quasi-periodic)—its waveform is made up of repeating segments or pitch periods. This observation is the rationale for time-domain pitch trackers, which attempt to find the repeating structure of the waveform. In music and speech, a pitch period is usually characterised by a high-amplitude peak (caused by a puff of air from a vibrating reed or buzzing vocal folds) at the beginning of the pitch period, followed by peaks of diminishing amplitude as the sound dies away. The high-amplitude peak at the beginning of each pitch period is the primary waveform feature used by time-domain pitch trackers.The Gold-Rabiner algorithm uses six independent pitch estimators, each working on a different measurement obtained from local maxima and minima of the signal. The goal is to take into account both the regularity and “peakedness” of a periodic signal, and to provide a large measure of fault tolerance. The final pitch estimate is chosen on the basis of a voting procedure among the six estimators. When the voting procedure is unable to agree on a pitch estimate, the input is assumed to be aperiodic—silence, or an unvoiced sound such as s or sh.The algorithm was designed for speech applications, and performs over a range of input frequencies from 50 Hz to 600 Hz. Our implementation allows the higher frequencies necessary for singing (up to 1000 Hz) by changing the manner in which pitch period lengths are determined. We also made modifications in implementation to speed up pitch tracking.3.2PostprocessingNo pitch tracker returns perfect output. Figure 1 illustrates the various stages in pitch tracking, from raw output to musical notes. Figure 1a shows the output directly from the Gold-Rabiner algorithm, which consists of a pitch estimate at every sample location. Errors can be characterised as gross or fine [7]. We define gross errors to be estimates greater than 10% (about a whole tone) from the input frequency, while fine errors are less than 10% from the true frequency.Gross errors generally occur at times when the signal is unstable, at the start or end of pitched sound, for example, or during note transitions. The most common is an octave error, which occurs when the pitch estimate is twice or one half the true frequency; a problem for all pitch trackers [2]. In time-domain pitch trackers, octave errors occur when the pitch tracker locks onto the first overtone (twice the frequency) or misses a pitch period and estimates the period to be twice its true length (half the frequency).We use a simple “island building” strategy to deal with gross errors. First, areas of stability are found within the sequence of pitch estimates. A stable area consists of two or more consecutive pitch periods with no gross errors in the estimated pitch. The post-processor then extends these areas of stability in both directions, correcting octave errors and labelling the pitch of other gross errors as undefined. Figure 1b shows the pitch track after island building.Most fine errors are caused by sampling resolution. Because digital algorithms deal with discrete samples, the resolution of the pitch estimate depends on fundamental frequency. Sampling at 22 kHz, a pitch period of 100 Hz is sampled 220 times, whereas a pitch period of 1000 Hz is sampled 22 times. Since the sample chosen as the beginning of a pitch period may be half a sample away (on either side) from the true beginning, the pitch estimate may be off by as much as 5%, or about a semitone, at 1000 Hz. A common way to increase the resolution of time-domain pitch estimates is to interpolate between samples [3, 8]. We chose an alternative approach of averaging pitch estimates over a given time period; the result is a perceptually constant resolution, independent of frequency. Pitch estimates are averaged over 20 ms time frames, giving a resolution of approximately 5 cents (0.29%). An undefined pitch value is assigned the average pitch of the frame that it falls within.1002003004005000123456789F r e q u e n c y (H z )Time (seconds)(a) Raw output from the pitch tracker.1002003004005000123456789F r e q u e n c y (H z )Time (seconds)(b) Pitch track after island building.1002003004005000123456789F r e q u e n c y (H z )Time (seconds)(c) Pitch track after averaging.(d) Notes identified from averaged pitch track.Figure 1: Pitch tracking.Figure 1c illustrates the pitch track after averaging and interpolation of undefined pitch estimates, and Figure 1d shows the corresponding musical notes.Averaging over time frames is equivalent to the solution inherently employed by frequency domain pitch trackers, where the time/frequency resolution tradeoff is a well known constraint. At a tempo of 120 beats/minute the duration of a semiquaver is 125 ms, and six pitch frame estimates will be calculated.As a final step before segmentation, the (averaged) frequency of each 20 ms time frame is represented by its distance in cents above MIDI note 0.4Note segmentationTwo methods of note segmentation have been developed, one based on amplitude and the other on pitch. Amplitude segmentation is simpler and more straightforward to implement. The user is required to separate each note, which is accomplished by singing da or ta . Amplitude segmentation has the advantage of distinguishing repeated notes of the same pitch. However, segmenting on pitch is more suitable for real-time implementation and relaxes constraints on the user’s singing. In either case,rhythmic values are determined by simply quantising the note duration according to the tempo set by the user. The most appropriate rhythmic unit for quantisation depends on the application and on tempo restrictions. A program intended for coloratura vocal training, for example, might require quantisation to the nearest 64th note in order to capture trills or other rapid musical ornaments. For our current applications—sightsinging tuition and song retrieval—we believe quantisation to the nearest semiquaver is sufficient, and we have designed the system accordingly. This parameter can easily be changed for future applications.4.1Segmentation based on amplitudeAmplitude segmentation depends on a drop in amplitude between notes in the input signal. This is most easily accomplished by asking the user to sing a syllable such as da or ta —the consonant will cause a drop in amplitude of 60 ms or more at each note boundary.The first step is to obtain the root-mean-squared power of the input signal. This is calculated over 10ms time frames, and the resulting signal is used to segment notes in the input stream. The simplest way to segment notes is to set a threshold, denoting a note start when the power exceeds it, and a note end when the power drops below it. There are three problems with this simple segmentation procedure.First, an extraneous sound, such as a crackling microphone lead or door slam, may send the power shooting above the threshold for a very short time.Second, a signal may cross the threshold several times as it ramps up to or down from its “steady state” level. Third, a fixed threshold may not suffice for all microphones and recording conditions.The first problem is solved by weeding out short spikes with a time threshold: if the note is not long enough, ignore it. Given semiquaver rhythm quantisation, we assume that each note lasts for at least 100 ms, a threshold that can be reduced for music with shorter note values or faster tempos. The second problem is dealt with using hysteresis: a high threshold is set for the note start boundary and a lower one for the end boundary. The third problem calls for adaptive thresholds. Having calculated the power over 10 ms frames, an overall power figure is calculated for the entire input signal and the note start and end thresholds are set to 50% and 30% of this value. These values were arrived at through experimentation. Figure 2 illustrates the use of thresholds in segmentation. The lines in the Figure are note begin and end thresholds—the note starts when its rising amplitude crosses the upperthreshold, and ends when its falling amplitude crosses the lower threshold.1000123456789Time (seconds)101L o g a m p l i t u d eFigure 2: Using thresholds to segment notes fromthe amplitude signal.4.2Segmentation based on pitchThe alternative to amplitude segmentation is to segment notes directly from the postprocessed pitch track by grouping and averaging frames. Frames are first grouped from left to right. A frame whose frequency is within fifty cents of the average of the growing segment is included in the average. Any segment longer than 100 ms is considered a note.For the purpose of determining note durations, notes are extended first by incorporating any contiguous short segments on the right until encountering a change in direction of frequency gradient, unvoiced segments or another note. These newly incorporated segments are considered transitional regions—their frequency estimates are not modified. Notes are then similarly extended on the left. Figure 3 shows the effect of pitch-based segmentation on a sung glissando.10020030040050001234567F r e q u e n c y (H z )Time (seconds)(a) Smoothed pitch track400045005000550060006500700001234567P i t c h (c e n t s )Time (seconds)(b) Segmented pitch trackFigure 3: Pitch-based segmentation on a sungglissando.5Musical pitch identificationLabelling the pitch with a musical note name may seem a simple operation, but mapping frequency,which is continuous, onto a musical scale, which isdiscrete, causes problems because the pitch within a given note may vary over its duration. Seashore [14]reports that professional singers vary frequency in several ways, often starting a long note up to 90cents flat, but that the average over the note is usually the notated pitch. Notes with a regular vibrato are perceived at the average pitch of the vibrato [15]; similarly, a short slide, or glissando, is perceived as the geometric mean of its extremes [11].5.1 Identifying note frequenciesPitch-based segmentation assigns each note the weighted average of its component frequencies.Amplitude segmentation, however, leaves each note as a sequence of individual frames. A single pitch estimate is assigned to these frames using a histogram with bins one semitone wide overlapped at five cent intervals. The range of histograms to be computed for a given note is determined during segmentation. For example, given a note whose frame pitches fall between 4000 and 4750 cents above MIDI note 0, a histogram is calculated with bins at 4000–4100 cents, 4005–4105 cents, 4010–4110 cents, and so forth. For efficiency, a sliding window is used to calculate the histogram. The bin with the highest number of occurrences is chosen as the basis for calculating note frequency. Figure 4displays a note histogram, with the winning bin indicated by a broken line. Note frequency is the weighted average of frequencies falling within the winning bin.05000100001500020000250003000050005500600065007000N u m b e r o f f r a m e sPitch (cents)Figure 4: Using a histogram to determine frequency.5.2Adapting to the user’s tuningM T labels a note by its MIDI number according to its frequency and the current reference frequency. In some applications it is desirable to tie note identification to a particular standard of tuning. In others it is more desirable to adapt to the user’s own tuning and tie note identification to musical intervals rather than to any standard. M T is able to do either.For example, the sightsinging tutor is normative,using a fixed reference frequency of A-440, while the melody indexing application is adaptive,adjusting its reference according to the user’s singing.In adaptive tuning mode, the system assumes that the user will sing to A-440, but then adjusts by referencing each note to its predecessor. For example, if a user sings three notes, 5990 cents,5770 cents and 5540 cents above MIDI note 0, the first is labelled C4 (MIDI 60) and the reference is moved down 10 cents. The second note is labeled Bb3, which is now referenced to 5790 (rather than5800) cents, and the reference is lowered a further 20 cents. The third note is labeled Ab3, referenced now to 5570 cents—even though, by the A-440 standard, it is closer to G3. Thus the beginning of Three Blind Mice will be transcribed. This scheme is not only compassionate in dealing with untrained singers—it also allows the user to sing in the other commonly espoused tunings for Western music, just and Pythagorean.While constantly changing the reference frequency may sound computationally expensive, it is efficiently implemented as an offset in MIDI note calculation. If tuning is tied to a particular standard, the offset is fixed—to use a fixed A-440 tuning, for example, the offset is fixed at 0.6 ApplicationsTwo applications of MT have been prototyped. The first is computer-aided tuition in sightsinging—teaching the skill of singing a melody without prior study. The other is music retrieval from acoustic input. Both applications currently use amplitude-based note segmentation, with the user singing da or ta.6.1 Sightsinging tutorThe sightsinging application displays a melody and evaluates the user’s attempt to sing it. Melodies are drawn from a database of 100 Bach chorales. First, the system displays a melody on the screen. Users are able to set the tempo and hear the starting note using pull-down menus. Then they sing the melody, using the mouse to start and stop recording. Next the system matches the input against the test melody using a dynamic programming algorithm designed to match discrete musical sequences [10]. Dynamic programming finds the best match between two strings, allowing for individual elements to be inserted or deleted.Figure 5 shows the result of matching a user’s sung input with the test melody. A global score is calculated which takes account of both pitch and rhythm, and returns an alignment showing the best match between the two strings. Notes are penalised for each semitone difference in pitch (by 0.1 units), and for each semiquaver difference in duration (by 0.05 units). The sightsinging tutor accepts melodies sung in any octave. The individual pitch and rhythm scores from the best alignment are accumulated to determine a global distance: a perfect score of zero represents no difference between the input and the test melody.Figure 5: Display from the sight-singing tutor.6.2Melody indexingThe indexing application listens to the user sing a few notes of a melody, then returns all melodies that contain that phrase. The current database comprises a set of 1700 North American folk songs.Given the user’s input, it would be easy to match the sung phrase directly against all songs in the database. However, the fact that a melody is equally recognisable whatever key it is played in indicates that the search should be conducted on the basis of pitch ratios, or intervals. Furthermore, a number of experiments have shown that interval directions, independent of interval sizes, are an important factor in the recognition of melodies [5]—indeed, Parsons [12] has produced an index of melodies based entirely on the sequence of interval directions, which is called the “melodic contour” or “pitch profile.” This suggests the possibility of accessing the database according to contour alone. One cardinal advantage of searching on contour, at least for casual singers, is that it releases them from having to sing accurate intervals.The prototype melody indexing program allows the user the option of indexing on contour or on musical intervals; at this point, rhythm is not used for indexing. The user starts singing on any note, and the input is notated in the key that yields the fewest accidentals given the notes sung by the user. Because retrieval is based on musical intervals rather than on absolute pitches, the system will return melodies with those intervals regardless of their keys as stored in the database.Figure 6 shows the melody indexing screen following a search. The names of matching melodies are displayed in a text window, with the first displayed in a melody window. The user may select other melodies from the list for display. In the Figure, the user has selected Three Blind Mice.Figure 6: Display from the melody indexing system.So far, our work on melody indexing has focused on developing and utilising the signal processing front end. In the future we intend to pay more attention to search and indexing functions. For example, we anticipate offering users the option of taking account of rhythm when matching the database. More importantly, we plan to use approximate string matching, as in the sightsinging tutor. This dispenses with the requirement that the user separate each note by singing da or ta, because it is no longer necessary to distinguish repeated notes. It is especially advantageous for accessing folk songs since a given song has many variants—and even for a database of popular or classical。
