第十二章全等三角形复习课

合集下载

全等三角形单元复习课 —初中数学课件PPT

（ C）
A. 7 cm B. 5 cm C. 8 cm D. 无法确定
知识点2：全等三角形的判定方法【例2】（2017宜宾）如图1-12-18-3，已知点B,E,C,F在同一条直线上，AB=DE，∠A=∠D，AC∥DF. 求证：BE=CF.
证明：∵AC∥DF，∴∠ACB=∠F. 在△ABC和△DEF中，
解：(1)∵t＝1 s， ∴BP＝CQ＝3×1＝3(cm). ∵AB＝10 cm，点D为AB的中点， ∴BD＝5 (cm). 又∵BC＝8 cm， ∴PC＝BC-BP=8－3＝5(cm). ∴PC＝BD. 又∵∠B＝∠C,∴△BPD≌△CQP （SAS）. (2)∵vP≠vQ，∴BP≠CQ. 又∵△BPD与△CQP全等，∠B＝∠C，则BP＝PC＝4(cm)，CQ＝BD＝5(cm). ∴点P，点Q运动的时间
∴△BOE≌△COF(SAS). ∴∠E＝∠F. ∴EB∥CF.
拓展提升
8. 如图1-12-18-11,在△ABC中,AB=AC,BE⊥AC于点
E,CF⊥AB于点F,且BE，CF交于点D,则下列结论:①△ABE≌△ACF；②△B源自F≌△CDE；③D点在∠BAC的平分
线上.其中正确的是
（
）D
A. ① B. ①② C. ②③ D. ①②③
第一部分新课内容
第十二章全等三角形
全等三角形单元复习课
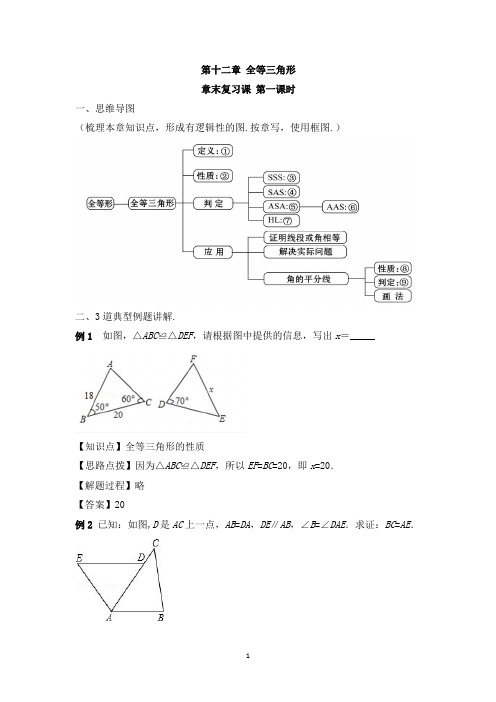
核心知识
1. 全等三角形的定义及性质. 2. 全等三角形的判定方法. 3. 角的平分线的性质及相关证明.
典型例题
知识点1：全等三角形的定义及性质
【例1】如图1-12-18-1,△ABC≌△CDA，AC=7 cm,AB=5
cm，BC=8 cm，则AD的长是
A. 15° B. 30° C. 45° D. 60°

人教版八年级数学上册第十二章：全等三角形复习课件(共15张PPT)

O
\ PD = PE
用途：证线段相等
E
角平分线性质的逆定理到一个角的两边的距离相等的点，在这个角的平分线上。
∵ PD OA PE OB
PD = PE
\ OP 是 AOB 的平分线
用途：判定一条射线是角平分线
A C
P B
一、已知:如图∠B=∠DEF,BC=EF,补充条件求证:ΔABC≌ ΔDEF (1)若要以“SAS”为依据，还缺条件＿A＿B=＿D＿E ＿； (2) 若要以“ASA”为依据，还缺条件∠＿A＿CB＿= ＿∠D；FE
E
O
B
C
6. 已知：BD⊥AM于点D，CE⊥AN于点E， BD、CE交于点F，CF=BF，求证：点F在∠A的平分线上。
CM D
F
A
N EB
7、如图所示，DC=EC，AB∥CD，∠D=90°， AE⊥BC于E，求证：∠ACB=∠BAC．
8. 如图，四边形ABCD中，AC平分∠BAC， CE⊥AB于E，AD+AB=2AE，求证：∠B与∠ADC互补。
2.如图（2），点D在AB上，点E在AC上， B
D
CD与BE相交于点O，且AD=AE,AB=AC.若 O
A
∠B=20°,CD=5cm，则 ∠C= 20°,BE= 5.说cm说理由.
E C 图（2）
3.如图（3），AC与BD相交于o,若
A
D
OB=OD，∠A=∠C，若AB=3cm3c，m 则
CD=
友情. 说提说示理：由公. 共边，公共角，B
(3) 若要以“AAS”为依据，还缺条件∠＿A＿=＿∠＿＿D ；
AD
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据，还缺条件＿A＿C=＿D＿F ＿

人教版八年级数学上册第12章全等三角形单元复习课件

∵BF∥AC，DE⊥AC，∴BF⊥DF，
∵BC平分∠ABF，DH⊥AB，DF⊥BF，∴DH＝DF，
∴DE＝DF，
∴点D为EF的中点．
(2)∵BF∥AC，∴∠C＝∠DBF，
∵BC平分∠ABF，∴∠ABD＝∠DBF，∴∠C＝∠ABD，
∵AD平分∠BAC，∴∠CAD＝∠BAD，
又AD＝AD，∴△DCA≌△DBA，∴∠CDA＝∠BDA，
应角与对角的概念．一般地，对应边、对应角是对两个三
角形而言，而对边、对角是对同一个三角形的边和角而言，
对边是指角的对边，对角是指边的对角．
1．已知△ABC≌△A1B1C1，A和A1对应，B和B1对应，
∠A＝70°，∠B1＝50°，则∠C的度数为( D )
A．70°
B．50°
C．120°
D．60°
2．(全国视野)(2022南京模拟)如图，四边形ABCD的对角
证明：(1)在Rt△BOF和Rt△COE中，
∵OF＝OE，OB＝OC，
∴Rt△BOF≌Rt△COE(HL)．
∴∠FBO＝∠ECO，即∠ABO＝∠ACO．
(2)连接AO．∵OF⊥AB，OE⊥AC，且OF＝OE，
∴∠BAO＝∠CAO．
∵∠ABO＝∠ACO，AO＝AO，
∴△BOA≌△COA(AAS)，∴AB＝AC．
则BD＝
1 ．
22．如图，过点B，D分别向线段AE作垂线段BQ和DF，
点Q和F是垂足，连接AB，DE，BD，BD交AE于点C，且
AB＝DE，AF＝EQ．
(1)求证：△ABQ≌△EDF；
(2)求证：点C是BD的中点．
证明：(1)∵AF＝EQ，∴AQ＝EF，在Rt△ABQ和Rt△EDF中，
＝

人教版八年级上册第十二章全等三角形(复习课)课件

3
4
考点3. 角平分线的性质与判定
1、作已知角的平分线？作法：（1）以点O为圆心，适当长为半径画弧线，交OA 于点N，交OB于点M.
1 2
（2）分别以M、N为圆心，大于 MN的长为半径画弧，两弧在∠AOB的内部相交于点C.
（3）画射线OC，射线OC即为所求.
2. 角的平分线的性质角的平分线的判定
∴DM⊥AM.
4.如图，在△ABC中，点D在边BC上，DE⊥AB，DF⊥AC，垂足分别为E，F，请你添
加一个条件使得AD⊥EF.
（1）你添加的条件是（
），并证明AD⊥EF.
（2）如图，AD为∠BAC的平分线，当有一点G从点D向点A运动时，GE⊥AB，
GF⊥AC，垂足分别为E、F.这时AD是否垂直于EF？
∠CMA＝∠BMN， CM＝BM，
3．在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN 于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证： ①△ADC≌△CEB；②DE＝AD+BE；（2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．
（1）证明：①∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°， ∴∠DAC＝∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°， ∴△ADC≌△CEB．②∵△ADC≌△CEB，∴CD＝BE，AD＝ CE．∴DE＝CE+CD＝AD+BE．（2）△ADC≌△CEB成立，DE＝
AD+BE．不成立，此时应有DE＝AD﹣BE．证明： ∵∠ACD+∠BCE＝90°∠DAC+∠ACD＝90°，∴∠DAC＝ ∠BCE．又AC＝BC，∠ADC＝∠BEC＝90°， ∴△ADC≌△CEB．∴CD＝BE，AD＝CE．∴DE＝AD﹣BE．

京改版八年级上册第十二章《全等三角形的判定与性质复习课》优秀教学案例

2.合作探究：引导学生运用全等三角形的判定与性质，共同探究问题，提高他们的实际问题解决能力。
3.成果展示：各小组展示自己的讨论成果，其他小组进行评价，教师进行指导，促进学生之间的交流与学习。
（四）总结归纳
1.引导学生总结全等三角形的判定与性质的关键点，帮助他们巩固知识，提高他们的归纳总结能力。
2.让学生反思自己在学习过程中的优点和不足，明确今后的学习方向。
固所学知识，提高他们的实际问题解决能力。
2.要求学生在作业中运用全等三角形的判定与性质，培养他们的实践能力。
作为一名特级教师，我将以导入新课、讲授新知、学生小组讨论、总结归纳和作业小结五个环节为主线，环环相扣，注重知识的系统性、实践性和探究性，努力提高学生的综合素质，为他们的全面发展奠定基础。
（二）问题导向
1.提出问题：教师针对全等三角形的判定与性质，设计具有引导性的问题，引导学生深入思考，自主探索。
2.分析问题：教师引导学生从全等三角形的判定方法和性质出发，分析问题的本质，培养学生解决问题的能力。
3.解决问题：教师组织学生进行小组讨论，共同解决问题，培养学生的团队协作能力和沟通能力。
4.总结问题：教师引导学生总结问题的解决过程和答案，帮助学生巩固知识，提高他们的归纳总结能力。
（三）情感态度与价值观
1.培养学生对数学学科的兴趣，激发他们学习数学的内在动力。
2.培养学生的自主学习能力，使他们养成良好的学习习惯。
3.引导学生认识到全等三角形在实际生活中的重要性，提高他们学以致用的能力。
4.培养学生严谨的逻辑思维态度，使他们形成科学的思维方式。
作为一名特级教师，我深知教学目标的重要性。在教学过程中，我将始终关注学生的知识掌握情况、过程与方法的应用以及情感态度与价值观的培养，努力提高他们的综合素质，为他们的全面发展奠定基础。

人教版八年级数学上学期第十二章《全等三角形》章末复习名师教案

°.
【知识点】三角形全等的性质；三角形内角和定理. 【思路点拨】由△ABC≌△A′B′C′，其中∠C′＝24°可得∠C＝24°，所以∠ B=180°-∠A-∠C=180°-36°-24°=1200 【解答过程】解：∵△ABC≌△A′B′C′， ∴∠C＝∠C′＝24° ∵∠A+∠B+∠C=1800
∠A＝36° ∴∠B=180°-∠A-∠C=180°-36°-24°=1200 【答案】1200 14．如图 BC=EF，AC=DF，要证明△ABC≌△DEF，还需添加一个条件：（1）若以“ ”为依据，需添加的条件是；（2）若以“ ”为依据，需添加的条件是．
【考点】全等三角形的判定与性质．【思路点拨】延长 BA 交 CE 的延长线于 F，证明△BCE≌△BFE，由全等可证 CE=EF，再证△ACF≌△ABD，可得 BD=CF 【数学思想】截长补短. 【解答过程】证明：延长 BA 交 CE 的延长线于 F， ∵BE 平分∠ABC，CE⊥BE， ∴△BCE≌△BFE， ∴CE=EF， ∵在△ABC 中，∠BAC=90°，CE⊥BE， ∴∠FCA=∠ABD，又∵ AB=AC ∠FAC=∠BAD ∴△ACF≌△ABD， ∴BD=CF， ∴BD=2CE.
2
三、章末检测题
一、选择题（每题 4 分，共 48 分）
1.如图，在△ABC 和△DEF 中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍
然不能证明△ABC≌△DEF，这个条件是( )
A.∠A=∠D
B.BC=EF
C.∠ACB=∠F
D.AC=DF
【知识点】三角形全等的判定【思路点拨】已知有一条边和相邻的一个角对应相等，可以添∠A=∠D（依据 ASA）或∠ACB=∠F(依据 AAS)，也可以添边 BC=EF(依据 SAS) 【解答过程】选项 A 的依据为 ASA；选项 B 的依据为 SAS；选项 C 的依据为 AAS；选项 D 不能判断两个三角形全等. 【答案】D 2.下列说法正确的是（） A.周长相等的两个三角形全等； B.有两边和其中一边的对角对应相等的两个三角形全等； C.面积相等的两个三角形全等； D.有两角和其中一角的对边对应相等的两个三角形全等. 【知识点】三角形全等的判定和性质. 【思路点拨】三角形全等的判定方法有：SSS；SAS；AAS；ASA；HL. 【解答过程】选项 A 周长相等不能判断三角形全等；选项 B 两边和一个角对应相等，只能是两边和两边的夹角对应相等才能判定三角形全等；选项 C 面积相等的两个三角形不一定全等；选项 D 对，依据为 AAS.

第十二章全等三角形复习课件

E
F B
返回
练习
1：如图，已知，AB∥DE，AB=DE，AF=DC。请问图中有那几对全
等三角形？请任选一对给予证明。 E F C B
答：
D
△ABF≌△DEC △ABC≌△DEF △CBF≌△FEC
A
练2
练习
1：如图，已知，AB∥DE，AB=DE，AF=DC。请问图中有那几对全
等三角形？请任选一对给予证明。 E F C B
∵ QD⊥OA,QE⊥OB, QD＝QE ∴ 点Q在∠AOB的平分线上
角平分线的几何定义： • 角的平分线是到角的两边距离相等的所有点的集合.
记住三个知识点：
• 三角形的三条角平分线相交于一点，这一点到三边的距离相等。 • 三角形的两条外角平分线相交于一点，这一点在第三角的平分线上，并且到三边的距离相等。.
例2：如图，AC和BD相交于点O,OA=OC,OB=OD 求证：DC∥AB
D
O A B
C
证明：在△ABO和△CDO中 OA=OC
∠AOB= ∠COD
OB=OD ∴ △ABO≌△CDO （SAS） ∴ ∠A= ∠C ∴ DC∥AB
例3：如图，OB⊥AB,OC⊥AC,垂足为B,C,OB=OC
AO平分∠BAC吗？为什么？答： AO平分∠BAC
C O B
A
D
例7：如图所示，AB=AD，∠E=∠C
要想使△ABC≌△ADE可以添加的条件是
∠EDA=∠B AAS A ∠DAE=∠BAC ∠BAD=∠EAC
依据是
E
B
D
C
例8：如图，已知AB=CD,DE⊥AC,BF⊥AC,AE=CF 求证：△ABF≌△CDE
D

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十二章全等三角形复习课
1、全等三角形的定义：能够完全重合的两个三角形叫做全等三角形.
一个三角形经过平移、翻折、旋转可以得到它的全等三角形.
2、全等三角形的性质：（1）全等三角形的对应边相等、对应角相等。

（2）全等三角形的周长、面积相等。

（3）全等三角形的对应边上的对应中线、角平分线、高分别相等。

3、全等三角形的判定: ①一般三角形全等的判定方法：SAS 、ASA 、AAS 、SSS
②直角三角形全等的判定方法：SAS 、ASA 、AAS 、SSS 、HL
注意：AAA 、SSA 不能证明两个三角形全等
4、角平分线的性质：角的平分线上的点到角的两边的距离相等.
几何语言：∵ QD ⊥OA,QE ⊥OB,点Q 在∠AOB 的平分线上 ∴ QD ＝QE
角平分线的判定：角的内部到角的两边的距离相等的点在角的平分线上。

几何语言： ∵ QD ⊥OA ，QE ⊥OB ，QD ＝QE ． ∴点Q 在∠AOB 的平分线上．
5、证明两个三角形全等应注意以下几个问题：
（1）表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上.
（2）时刻注意图形中的隐含条件：如 “公共角” 、“公共边”、“对顶角”
练一练：
1、如图，在△ABC 中，两条角平分线BD 和CE 相交于点O ，若∠BOC=120°，那么∠A 的度数是 .
B
C D E
O A
2、如图，已知AB=CD ，AD=CB ，E 、F 分别是AB ，CD 的中点，且DE=BF ，证明下列两个结论： ①△ADE ≌△CBF ；②∠A=∠C
3、如图，E ，F 在BC 上，已知BE=CF ，AB=CD ，AB ∥CD ，求证：AF ∥DE
4、如图，AB ∥CD ，AD ∥BC ，那么AB=CD 吗？为什么？AD 与BC 呢？
A
D
E B A
C
D
E
F
B C A
B D
C F
5、如图，已知AC=AE ，∠B=∠D ，∠1=∠2，求证：BC=DE
6、已知：如图,在△ABC 和△ABD 中，AC ⊥BC, AD ⊥BD,垂足分别为C,D,AD=BC,求证：BD=AC.
7、如图CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 与CD 相交于点O ，且∠1＝∠2，求证：OB ＝OC 。

A
C E
1 2 A D C
B
8、在Rt △ABC 中，∠C ＝90°，AD 平分∠BAC ，交BC 于D ，若BC ＝32，且BD ：CD ＝9：7，则点D 到AB 的距离为（）
A. 18
B. 16
C. 14
D. 12
9、已知：∠ACB=∠ADB=90°，AC=AD ，P 是AB 上任意一点，求证：CP=DP
A
B
C D E C A
B
D P。

第十二章 全等三角形 复习课

全等三角形单元复习课 —初中数学课件PPT

人教版 八年级数学上册第十二章：全等三角形复习课件(共15张PPT)

人教版八年级数学上册第12章 全等三角形 单元复习 课件

人教版八年级上册第十二章 全等三角形(复习课)课件