苏科版2015-2016学年七年级数学下学期期中试题及答案
2015-2016第二学期期中七年级数学参考答案

2015—2016学年度第二学期期中质量评估试题七年级数学参考答案及评分标准11. 9; 12. 80°; 13.(5,0); 14. 4; 15. 100°;16. 一 三、解答题(一)17. 解:34)2(3-----=3+2-2-3 ……………4分 =0 ……………6分 18. 解:∵a ∥b∴∠2=∠3 ……………2分 ∵∠1+∠3=180°∴∠1+∠2=180° ……………4分 ∴∠2=180°-∠1 ∵∠1=118°∴∠2=180°-118°=62° ……………6分 19.(1)图(略) 图……………4分(2)A 1(0,6);B 1(-1,2) ……………6分 四、解答题(二) 20. 解: )223(328)2(32---+-+-=2232322+--+- ……………4分 =2 ……………7分 21. 解:∵∠1=∠2∴AB ∥CD ……………2分 ∴∠3+∠4=180° ……………4分 ∴∠4=180°-∠3 ……………6分 ∵∠3=108°∴∠4=180°-108°=72° ……………7分 22.(每空1分)∵AB ∥DC (已知)∴∠1=∠CFE (两直线平行,同位角相等)……………2分 ∵AE 平分∠BAD (已知)∴∠1=∠2(角平分线的定义) ……………4分 ∴∠2=∠CFE ……………5分 ∵∠CFE=∠E (已知)∴∠2=∠E …………6分 ∴AD ∥BC (内错角相等,两直线平行). …………7分五、解答题(三) 23. 解:100)1(2=-x101±=-x …………4分 110+±=x11=x …………7分或9-=x …………9分24. 证明:∵DE ‖BC (已知)∴∠ADE =∠ABC (两直线平行,同位角相等) …………2分 ∵DF 、BE 分别平分∠ADE 、∠ABC ∴∠ADF =12∠ADE∠ABE =12∠ABC (角平分线的定义) …………4分∴∠ADF =∠ABE …………5分∴ DF ‖BE (同位角相等,两直线平行) …………7分 ∴∠FDE =∠DEB. (两直线平行,内错角相等) …………9分 25. 解:(1)C (0,2),D (4,2),…………2分(2)依题意,得S 四边形ABDC =AB ×OC=4×2=8; …………3分 (3)存在. …………4分。
江苏省苏州市昆山市2015-2016学年七年级数学下学期期中试题(含解析) 苏科版

某某省某某市某某市2015-2016学年七年级数学下学期期中试题一、选择题(本大题共10小题,每小题3分.请将下列各小题唯一正确的选项代号填涂在答题卡相应的位置上)1.计算2x2•x3的结果是()A.2x5B.2x C.2x6D.x52.甲型H1N1流感病毒的直径大约是0.000000081米,用科学记数法可表示为()A.8.1×10﹣9米B.8.1×10﹣8米C.81×10﹣9米D.0.81×10﹣7米3.以下列各组线段为边,能组成三角形的是()A.2cm、2cm、4cm B.8cm、6cm、3cm C.2cm、6cm、3cm D.11cm、4cm、6cm 4.一个多边形的内角和是720°,这个多边形的边数是()A.4 B.5 C.6 D.75.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为()A.①④ B.②③ C.①③ D.①③④6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于()A.40°B.45°C.50°D.60°7.如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余部分剪拼成一个长方形(如图②),则上述操作所能验证的公式是()A.(a+b)(a﹣b)=a2﹣b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2D.a2+ab=a(a+b)8.在下列条件中,①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=∠C;④∠A=∠B=2∠C;⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有()A.2个B.3个C.4个D.5个9.计算10﹣(0.5)2015×(﹣2)2016的结果是()A.﹣2 B.﹣1 C.2 D.310.如果等式(2x﹣3)x+3=1,则等式成立的x的值的个数为()A.1 B.2 C.3 D.4二、填空题(本大题共8小题,每小题3分,共24分)11.若x m=3,x n=5,则x m+n=.12.若a+b=1,ab=﹣2,则(a+1)(b+1)的值为.13.等腰三角形的两边长为4,9.则它的周长为.14.计算:20152一2014×2016=.15.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为.16.如果(x+1)(x+m)的乘积中不含x的一次项,则m的值为.17.如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF 的度数为.18.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2,则S阴影=cm2.三、解答题(本大题共11小题,共76分,应写出必要的计算过程、推理步骤或文字说明)19.计算:(1)|﹣2|﹣(2﹣π)0+(﹣)﹣1(2)﹣2xy•3x2y﹣x2y(﹣3xy+xy2)(3)(2a+b)(b﹣2a)﹣(a﹣3b)2.20.如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移3格.(1)请在图中画出平移后的△A′B′C′;(2)在△ABC中画出中线BD;(3)在△ABC中画出AB边上高(图中标上字母).21.已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.22.先化简再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中a=,b=﹣3.23.如图,在△ABC中,BD⊥AC,EF⊥AC,垂足分别为D、F,且∠1=∠2,试判断DE与BC的位置关系,并说明理由.24.已知:x+y=6,xy=4,求下列各式的值(1)x2+y2(2)(x﹣y)2.25.如图,已知△ABC中,AD是高,AE是角平分线.(1)若∠B=20°,∠C=60°,求∠EAD度数;(2)若∠B=α,∠C=β(β>a),则∠EAD=.(用α、β的代数式表示)26.图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)将图②中的阴影部分面积用2种方法表示可得一个等式,这个等式为.(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.27.如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.28.观察下列关于自然数的等式:32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92﹣4×2=;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.29.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.2015-2016学年某某省某某市某某市七年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分.请将下列各小题唯一正确的选项代号填涂在答题卡相应的位置上)1.计算2x2•x3的结果是()A.2x5B.2x C.2x6D.x5【考点】单项式乘单项式.【分析】据同底数幂相乘,底数不变指数相加进行计算即可得解.【解答】解:2x2•x3=2x2+3=2x5.故选A.2.甲型H1N1流感病毒的直径大约是0.000000081米,用科学记数法可表示为()A.8.1×10﹣9米B.8.1×10﹣8米C.81×10﹣9米D.0.81×10﹣7米【考点】科学记数法—表示较小的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:0.000 000 081=8.1×10﹣8米.故选B.3.以下列各组线段为边,能组成三角形的是()A.2cm、2cm、4cm B.8cm、6cm、3cm C.2cm、6cm、3cm D.11cm、4cm、6cm 【考点】三角形三边关系.【分析】根据已知三角形的两边,则第三边的X围是:大于已知的两边的差,而小于两边的和,分别判断即可.【解答】解:根据三角形的三边关系,知A、2+2=4,不能组成三角形,故此选项错误;B、3+6>8,能够组成三角形,故此选项正确;C、2+3<6,不能组成三角形,故此选项错误;D、4+6<11,不能组成三角形,故此选项错误.故选B.4.一个多边形的内角和是720°,这个多边形的边数是()A.4 B.5 C.6 D.7【考点】多边形内角与外角.【分析】根据内角和定理180°•(n﹣2)即可求得.【解答】解:∵多边形的内角和公式为(n﹣2)•180°,∴(n﹣2)×180°=720°,解得n=6,∴这个多边形的边数是6.故选C.5.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为()A.①④ B.②③ C.①③ D.①③④【考点】平行线的判定.【分析】直接根据平行线的判定定理对各小题进行逐一分析即可.【解答】解:①∵∠1=∠2,∴AB∥CD,故本选项正确;②∵∠3=∠4,∴BC∥AD,故本选项错误;③∵∠A=∠CDE,∴AB∥CD,故本选项正确;④∵∠A+∠ADC=180°,∴AB∥CD,故本选项正确.故选D.6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于()A.40°B.45°C.50°D.60°【考点】平行线的性质.【分析】根据三角形外角性质求出∠4,根据平行线性质得出∠2=∠4,代入求出即可.【解答】解:如图所示,∵∠4=∠1+∠3,∴∠4=30°+20°=50°,∵AB∥CD,∴∠2=∠4=50°,故选C.7.如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余部分剪拼成一个长方形(如图②),则上述操作所能验证的公式是()A.(a+b)(a﹣b)=a2﹣b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2D.a2+ab=a(a+b)【考点】平方差公式的几何背景.【分析】由大正方形的面积﹣小正方形的面积=矩形的面积,进而可以证明平方差公式.【解答】解:大正方形的面积﹣小正方形的面积=a2﹣b2,矩形的面积=(a+b)(a﹣b),故a2﹣b2=(a+b)(a﹣b).故选A.8.在下列条件中,①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=∠C;④∠A=∠B=2∠C;⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有()A.2个B.3个C.4个D.5个【考点】三角形内角和定理.【分析】根据直角三角形的判定对各个条件进行分析,从而得到答案.【解答】解:①、∵∠A+∠B=∠C=90°,∴△ABC是直角三角形,故小题正确;②、∵∠A:∠B:∠C=1:2:3,∴∠A=30°,∠B=60°,∠C=90°,△ABC是直角三角形,故本小题正确;③、设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,解得x=30°,故3x=90°,△ABC是直角三角形,故本小题正确;④∵设∠C=x,则∠A=∠B=2x,∴2x+2x+x=180°,解得x=36°,∴2x=72°,故本小题错误;⑤∠A=2∠B=3∠C,∴∠A+∠B+∠C=∠A+∠A+A=180°,∴∠A=°,故本小题错误.综上所述,是直角三角形的是①②③共3个.故选B.9.计算10﹣(0.5)2015×(﹣2)2016的结果是()A.﹣2 B.﹣1 C.2 D.3【考点】幂的乘方与积的乘方;零指数幂.【分析】直接利用零指数幂的性质结合积的乘方运算法则将原式变形求出答案.【解答】解:10﹣(0.5)2015×(﹣2)2016=1﹣[0.5×(﹣2)]2015×(﹣2)=1﹣2=﹣1.故选:B.10.如果等式(2x﹣3)x+3=1,则等式成立的x的值的个数为()A.1 B.2 C.3 D.4【考点】零指数幂;有理数的乘方.【分析】由于任何非0数的0次幂等于1和1的任何指数为1,所以分两种情况讨论.【解答】解:当x+3=0时,x=﹣3;当2x﹣3=1时,x=2.∴x的值为2,﹣3,当x=1时,等式(2x﹣3)x+3=1,故选C二、填空题(本大题共8小题,每小题3分,共24分)11.若x m=3,x n=5,则x m+n= 15 .【考点】同底数幂的乘法.【分析】由x m=3,x n=5,又由x m+n=x m•x n,即可求得答案.【解答】解:∵x m=3,x n=5,∴x m+n=x m•x n=3×5=15.故答案为:1512.若a+b=1,ab=﹣2,则(a+1)(b+1)的值为0 .【考点】整式的混合运算—化简求值.【分析】原式利用多项式乘以多项式法则计算,整理后把a+b与ab的值代入计算即可求出值.【解答】解:原式=ab+a+b+1=ab+(a+b)+1,当a+b=1,ab=﹣2时,原式=1﹣2+1=0,故答案为:013.等腰三角形的两边长为4,9.则它的周长为22 .【考点】等腰三角形的性质;三角形三边关系.【分析】由于题目没有说明4和9,哪个是底哪个是腰,所以要分类讨论.【解答】解:当腰长为4,底长为9时;4+4<9,不能构成三角形;当腰长为9,底长为4时;9﹣4<9<9+4,能构成三角形;故等腰三角形的周长为:9+9+4=22.故填22.14.计算:20152一2014×2016= 1 .【考点】平方差公式.【分析】把2014×2016写成×,然后利用平方差公式计算即可得解.【解答】解:20152﹣2014×2016=20152﹣×=20152﹣=20152﹣20152+1=1.故答案是:1.15.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的角平分线相交于点P,则∠BPC的度数为115°.【考点】三角形内角和定理;三角形的外角性质.【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.【解答】解:∵∠A=50°,∴∠ABC+∠ACB=180°﹣50°=130°,∵∠ABC与∠ACB的角平分线相交于P,∴∠PBC+∠PCB=(∠ABC+∠ACB)=×130°=65°,在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣65°=115°.故答案为:115°.16.如果(x+1)(x+m)的乘积中不含x的一次项,则m的值为﹣1 .【考点】多项式乘多项式.【分析】把式子展开,找到所有x项的所有系数,令其和为0,可求出m的值.【解答】解:(x+1)(x+m)=x2+(1+m)x+m,∵结果不含x的一次项,∴1+m=0,解得:m=﹣1.故答案为:﹣1.17.如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=40°,则∠ABF 的度数为50°.【考点】翻折变换(折叠问题).【分析】根据翻折的性质可得∠BEF=∠BEC,∠EBF=∠EBC,然后求出∠BEC,再根据直角三角形两锐角互余求出∠EBC,然后根据∠ABF=90°﹣∠EBF﹣∠EBC代入数据进行计算即可得解.【解答】解:补全正方形如图,由翻折的性质得,∠BEF=∠BEC,∠EBF=∠EBC,∵∠DEF=30°,∴∠BEC===70°,∴∠EBC=90°﹣∠BEC=90°﹣70°=20°,∴∠ABF=90°﹣∠EBF﹣∠EBC=90°﹣20°﹣20°=50°.故答案为:50°.18.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2,则S阴影= 1 cm2.【考点】三角形的面积.【分析】根据三角形的面积公式,知△BCE的面积是△ABC的面积的一半,进一步求得阴影部分的面积是△BEC的面积的一半.【解答】解:∵点E是AD的中点,∴△BDE的面积是△ABD的面积的一半,△CDE的面积是△ACD的面积的一半.则△BCE的面积是△ABC的面积的一半,即为2cm2.∵点F是CE的中点,∴阴影部分的面积是△BCE的面积的一半,即为1cm2.三、解答题(本大题共11小题,共76分,应写出必要的计算过程、推理步骤或文字说明)19.计算:(1)|﹣2|﹣(2﹣π)0+(﹣)﹣1(2)﹣2xy•3x2y﹣x2y(﹣3xy+xy2)(3)(2a+b)(b﹣2a)﹣(a﹣3b)2.【考点】整式的混合运算;零指数幂;负整数指数幂.【分析】(1)根据绝对值、零指数幂、负指数幂计算即可;(2)根据同底数幂的乘法、单项式乘以多项式进行计算即可;(3)根据平方差公式和完全平方公式进行计算即可.【解答】解:(1)原式=2﹣1﹣3=﹣2;(2)原式=﹣6x3y2+3x3y2﹣x3y3=﹣3x3y2﹣x3y3;(3)原式=b2﹣4a2﹣a2+6ab﹣9b2=﹣5a2+6ab﹣8b2.20.如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移3格.(1)请在图中画出平移后的△A′B′C′;(2)在△ABC中画出中线BD;(3)在△ABC中画出AB边上高(图中标上字母).【考点】作图-平移变换.【分析】(1)分别作出点A、B、C向左平移2格,再向上平移3格的点,然后顺次连接;(2)作出AC的中点D,然后连接BD;(3)过点C作CD⊥AB延长线于点E,然后连接CE.【解答】解:(1)所作图形如图所示:(2)如图所示,BD即为所作中线;(3)如图所示,CE即为AB的高.21.已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.【考点】整式的混合运算—化简求值.【分析】原式利用幂的乘方运算法则变形,将已知等式代入计算即可求出值.【解答】解:∵n为正整数,且x2n=4,∴原式=(x2n)3﹣2(x2n)2=43﹣2×42=64﹣32=32.22.先化简再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中a=,b=﹣3.【考点】整式的混合运算—化简求值.【分析】原式第一项利用完全平方公式展开,第二项利用平方差公式计算,最后一项利用多项式乘多项式法则计算,去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=a2﹣4ab+4b2+a2﹣b2﹣2a2+8ab﹣6b2=4ab﹣3b2,当a=,b=﹣3时,原式=﹣6﹣27=﹣33.23.如图,在△ABC中,BD⊥AC,EF⊥AC,垂足分别为D、F,且∠1=∠2,试判断DE与BC的位置关系,并说明理由.【考点】平行线的判定与性质.【分析】根据平行线的判定求出EF∥BD,根据平行线的性质得出∠1=∠BDE,求出∠2=∠BDE,根据平行线的判定得出即可.【解答】解:DE∥BC,理由是:∵BD⊥AC,EF⊥AC,∴∠EAF=∠BDF=90°,∴EF∥BD,∴∠1=∠BDE,又∵∠1=∠2,∴∠2=∠BDE,∴DE∥BC.24.已知:x+y=6,xy=4,求下列各式的值(1)x2+y2(2)(x﹣y)2.【考点】完全平方公式.【分析】(1)根据完全平方公式可得x2+y2=(x+y)2﹣2xy,然后把x+y=6,xy=4整体代入进行计算即可;(2)根据完全平方公式可得(x﹣y)2=(x+y)2﹣4xy,然后把x+y=6,xy=4整体代入进行计算即可.【解答】解:(1)∵x2+y2=(x+y)2﹣2xy,∴当x+y=6,xy=4,x2+y2=(x+y)2﹣2xy=62﹣2×4=28;(2)∵(x﹣y)2=(x+y)2﹣4xy,∴当x+y=6,xy=4,(x﹣y)2=(x+y)2﹣4xy=62﹣4×4=20.25.如图,已知△ABC中,AD是高,AE是角平分线.(1)若∠B=20°,∠C=60°,求∠EAD度数;(2)若∠B=α,∠C=β(β>a),则∠EAD=(β﹣α).(用α、β的代数式表示)【考点】三角形内角和定理;三角形的角平分线、中线和高.【分析】(1))根据∠B=20°,∠C=60°,得出∠BAC的度数,再根据AE是角平分线,AD 是高,分别得出∠EAC和∠DAC的度数,从而求出答案;(2)证明过程同(1),只不过把∠B和∠C的度数用字母代替,从而用字母表示出各个角的度数.【解答】解:(1)∵∠B=20°,∠C=60°,∴∠BAC=180°﹣20°﹣60°=100°,∵AE是角平分线,∴∠EAC=50°,∵AD是高,∴∠ADC=90°,∴∠DAC=30°,∴∠EAD=∠EAC﹣∠DAC=50°﹣30°=20°;(2))∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β,∵AE是角平分线,∴∠EAC=90°﹣α﹣β,∵AD是高,∴∠ADC=90°,∴∠DAC=90°﹣β,∴∠EAD=∠EAC﹣∠DAC=(90°﹣α﹣β)﹣(90°﹣β)=(β﹣α).26.图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)将图②中的阴影部分面积用2种方法表示可得一个等式,这个等式为(m+n)2﹣4mn=(m﹣n)2.(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.【考点】完全平方公式的几何背景.【分析】(1)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m﹣n)2、mn之间的等量关系;(2)根据(1)所得出的关系式,可求出(m﹣2n)2,继而可得出m﹣2n的值.【解答】解:(1)(m+n)2﹣4mn=(m﹣n)2;故答案为:(m+n)2﹣4mn=(m﹣n)2(2)(m﹣2n)2=(m+2n)2﹣8mn=25,则m﹣2n=±5.27.如图,正方形ABCD的边长为a,面积为6;长方形CEFG的长、宽分别为a,b,长方形的面积为2,其中点B、C、E在同一直线上,连接DF.求△BDF的面积.【考点】整式的混合运算.【分析】由图形得三角形BDF的面积=正方形ABCD的面积+梯形DCEF﹣三角形ABD的面积﹣三角形BEF,再计算即可.【解答】解:S△BDF=S正方形ABCD+S梯形DCEF﹣S△ABD﹣S△BEF=a2+(a+b)•a﹣a2﹣•2a•b=a2﹣ab;由题意得:a2=6,ab=2,则S△BDF=6﹣×2=5.28.观察下列关于自然数的等式:32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92﹣4× 4 2= 17 ;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.【考点】规律型:数字的变化类;完全平方公式.【分析】由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.【解答】解:(1)32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…所以第四个等式:92﹣4×42=17;(2)第n个等式为:(2n+1)2﹣4n2=4n+1,左边=(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1,右边=4n+1.左边=右边∴(2n+1)2﹣4n2=4n+1.29.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= 140 °;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:∠1+∠2=90°+α;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:∠2=90°+∠1﹣α.【考点】三角形内角和定理;三角形的外角性质.【分析】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;(2)利用(1)中所求得出答案即可;(3)利用三角外角的性质得出∠1=∠C+∠2+α=90°+∠2+α;(4)利用三角形内角和定理以及邻补角的性质可得出.【解答】解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;故答案为:140°;(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α故答案为:∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由:∵∠2+∠α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+α=90°+∠2+α.(4)∵∠PFD=∠EFC,∴180°﹣∠PFD=180°﹣∠EFC,∴∠α+180°﹣∠1=∠C+180°﹣∠2,∴∠2=90°+∠1﹣α.故答案为:∠2=90°+∠1﹣α.。
苏科版2015-2016学年初一下数学期中测试卷及答案

2015-2016学年第二学期期中考试初一数学试卷(考试时间:100分钟满分:100分)一、选择题:(请把每题的答案填在答题卷...相应的表格中,每题2分,共20分)1.下列计算中正确的是( )A.a2+a3=2a5 B.a2·a3=a5 C.a2·a3=a6D.a2+a3=a5 2.下列各式中与2mn-m2-n2相等的是( )A.(m+n)2B.-(m+n)2C.(m-n)2D.-(m-n)2 3.以下列各组线段为边,能组成三角形的是( )A.2cm、2cm、4cm B.8cm、6cm、3cmC.2cm、6cm、3cm D.11cm、4cm、6cm4.氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示这个距离为( )A.5.29×10-8 cm B.5.29×10-9cmC.0.529×10-8 cm D.52.9×10-10 cm5.下列各多项式中,能用公式法分解因式的是 ( )A.a2-b2+2ab B.a2+b2+ab C.4a2+12a+9 D.25n2+15n+9 6.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为2:3,则这个多边形为( )A.三角形B.四边形 C.五边形 D.六边形7.如果a=(-0.1)0,b=(-0.1)-1,c=253-⎛⎫- ⎪⎝⎭,那么a,b,c的大小关系为( )A.a>b>c B.c>a>b C.c>b>a D. a>c>b 8.在如下图的△ABC中,正确画出AC边上的高的图形是 ( ) .9.如图,下列条件中:(1)∠B +∠BCD =180°;(2)∠1=∠2; (3)∠3=∠4;(4)∠B =∠5;能判定AB//CD 的条件个数有( ) A .1 B .2 C .3 D .410. 如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 的外部时,则与和之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )A .3212A ∠=∠-∠B .32(12)A ∠=∠-∠C .212A ∠=∠-∠D .12A ∠=∠-∠二、填空(请把每题的答案填在答.题卷..相应的横线上每小题2分,共20分) 11.某人从P 点出发,向前走5米后即向右转向30°,按转后方向再走5米后又向右转30°,如此反复,当他回到P 点时,共走了_______米. 12. 多项式233342-39-6x y z x y z x yz +的公因式是 . 13.若2236x ax ++是完全平方式,则a = .14.一个等腰三角形周长是16,其中一边长是6,则另外两条边长分别 是 .15.已知2320x y --=,则23(10)(10)x y ÷=_______.16.如果)5)(1(2a ax x x +-+的乘积中不含2x 项,则a 为 .17.计算:20142013)5.1()32(-⨯-= .18.将一直角三角形与两边平行的纸条如图所示放置,下列结论①∠1=∠2,②∠3=∠4,③∠2+∠4=90°,④∠4+∠5=180°,其中正确的有 (填序号).19.如图,在四边形ABCD 中,∠A=45°,直线l 与边AB 、AD 分别相交于点M 、N 。
2015-2016学年第二学期期中教学调研卷七年级数学(苏科版)及答案

2015-2016学年第二学期期中教学调研卷七年级数学(苏科版)2016.4.29 一、选择题(每小题2分,共20分)1、下列图形可由平移得到的是 ( )2、甲型H7N9.流感病毒的直径大约为0.00000008米,用科学记数法表示为( ) A .0.8×10-7米 B .8×10-8米 C .8×10-9米 D .8×10-7米3、下列4个算式中,计算错误的有 ( )(1)()()-=-÷-24c c 2c (2)336)()(y y y -=-÷-(3)303z z z =÷ (4)44a a am m=÷A.4个B.3个C.2个D.1个4、下列命题中,不正确的是( ).A .如果两条直线都和第三条直线平行,那么这两条直线也互相平行B .两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行C .两条直线被第三条直线所截,那么这两条直线平行D .两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行 5、△ABC 的高的交点一定在外部的是( ). A .锐角三角形 B .钝角三角形C .直角三角形D .有一个角是60°的三角形 6、下列条件中,能判定△ABC 为直角三角形的是( ). A .∠A=2∠B 一3∠C B .∠A+∠B=2∠CC .∠A 一∠B=30°D .∠A=12∠B=13∠C7、在四边形的4个内角中,钝角的个数最多为( ).A .1B .2C .3D .4 8、如图,已知直线AB ∥CD ,∠C =115°,∠A=25°,∠E=( ). A .70° B .80° C .90° D .100°(第8题)9、若△ABC 的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为( ).A .7B .6C .5D .410、若a =-0.32,b =-3-2,c =(-13)-2,d =(-13)0,则它们的大小关系是( )A .a <b <c <dB .b <a <d <cC .a <d <c <bD .c <a <d <b二、填空题(每小题2分,共16分)11、一个凸多边形的内角和与外角和相等,它是_________边形.12、已知a 、b 、c 为△ABC 的三边,化简:||a +b -c +||a -b -c -||a -b +c = . 13、已知2m +5n -3=0,则4m ×32n 的值为 .14、若22(32)(32)x y x y A +=-+,则代数式A 为 . 15、如图:∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数为_________第15题 16、如图,边长为4cm 的正方形ABCD 先向上平移2cm ,再向右平移1cm ,得到正方形A ’B ’C ’D ’,此时阴影部分的面积为cm2.17、如图,在△ABC 中,∠ABC =∠ACB ,∠A =40°,P 是△ABC 内一点,且∠ACP =∠PBC ,则∠BPC = .18、如图,已知点P 是射线ON 上一动点(即P 可在射线ON 上运动),∠AON =30°,当∠A = 时,△AOP 为直角三角形. 三、解答题(共10题,共64分)19、(共12分)计算(1) 错误!未找到引用源。
七年级数学下学期期中模拟试卷(一)(含解析) 苏科版-苏科版初中七年级全册数学试题

2015-2016学年某某省某某市丰县宋楼中学七年级(下)期中数学模拟试卷(一)一、精心选一选:(每题3分,共30分)1.计算2x3•3x2的结果是()A.5x5B.6x6C.5x6D.6x52.下列运算正确的是()A.(2a3﹣2a2)÷(2a2)=a B.a2+a2=a4C.(a+b)2=a2+b2+2ab D.(2a+1)(2a﹣1)=2a2﹣13.如图,已知AB∥CD,∠B=120°,∠D=150°,则∠O等于()A.50° B.60° C.80° D.90°4.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是()A.1,2,3 B.2,2,4 C.1,2,4 D.3,4,55.如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,设∠ABD和∠DBC的度数分别为x°、y°,那么下面可以求出这两个角的度数的方程组是()A.B.C.D.6.如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为()A.24° B.26° C.34° D.36°7.已知关于x的二次三项式4x2﹣mx+25是完全平方式,则常数m的值为()A.10 B.±10 C.﹣20 D.±208.下列不是二元一次方程的是()①3m﹣2n=5 ②③④2x+z=3 ⑤3m+2n ⑥p+7=2.A.1个B.2个C.3个D.4个9.甲、乙二人按3:2的比例投资开办了一家公司,约定除去各项支出外,所得利润按投资比例分成.若第一年甲分得的利润比乙分得的利润的2倍少3千元,求甲、乙二人各分得利润多少千元.若设甲分得x千元,乙分得y千元,由题意得()A.B.C.D.10.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.40° B.35° C.30° D.20°二、耐心填一填:(每空3分,共33分)11.把方程2x﹣y﹣3=0化成含y的式子表示x的形式:x=______.12.一种细菌的半径是0.000039m,用科学记数法表示这个数是______m.13.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=______度.14.已知x2+y2=10,xy=2,则(x﹣y)2=______.15.已知x m=4,x2n=6,则x m+2n=______.16.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段______是△ABC中AC边上的高.17.一个多边形的内角和是它外角和的2倍,则它的边数是______.18.方程2x n﹣3﹣y3m+n﹣2+3=0是二元一次方程,则m=______n=______.19.已知是方程组的解,则a﹣b=______.20.若(4x2+2x)(x+a)的运算结果中不含x2的项,则a的值为______.三、细心算一算:(本题共8题,共57分)21.计算题:(1)(﹣2015)0+22×|﹣1|×(﹣)﹣2(2)(x+y﹣2z)(x﹣y+2z)22.先化简,后求值:[(x﹣y)2+2y(y﹣x)﹣(x+y)(x﹣y)]÷(2y),其中x﹣y=2.23.分解因式:(1)2x2﹣8y2;(2)2x3y﹣4x2y2+2xy3.24.解下列方程组:(1)(2).25.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′;(2)若连接AA′,CC′,则这两条线段之间的关系是______.26.如图,已知AE平分∠BAC,过AE延长线一点F作FD⊥BC于D,若∠F=6°,∠C=30°,求∠B的度数.27.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,求每块长方形的长和宽分别是多少?28.阅读下文,寻找规律:已知x≠1时,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4…(1)(1﹣x)(______)=1﹣x8(2)观察上式,并猜想:①(1﹣x)(1+x+x2+…+x n)=______.②(x﹣1)(x10+x9+…+x+1)=______.(3)根据你的猜想,计算:①(1﹣2)(1+2+22+23+24+25)=______.②1+2+22+23+24+…+22007=______.2015-2016学年某某省某某市丰县宋楼中学七年级(下)期中数学模拟试卷(一)参考答案与试题解析一、精心选一选:(每题3分,共30分)1.计算2x3•3x2的结果是()A.5x5B.6x6C.5x6D.6x5【考点】单项式乘单项式.【分析】原式利用单项式乘以单项式法则计算即可得到结果.【解答】解:2x3•3x2=6x5.故选D.2.下列运算正确的是()A.(2a3﹣2a2)÷(2a2)=a B.a2+a2=a4C.(a+b)2=a2+b2+2ab D.(2a+1)(2a﹣1)=2a2﹣1【考点】整式的除法;合并同类项;完全平方公式;平方差公式.【分析】分别利用整式的除法运算法则以及合并同类项法则和完全平方公式、平方差公式计算得出即可.【解答】解:A、(2a3﹣2a2)÷(2a2)=a﹣1,故此选项错误;B、a2+a2=2a2,故此选项错误;C、(a+b)2=a2+b2+2ab,正确;D、(2a+1)(2a﹣1)=4a2﹣1,故此选项错误;故选:C.3.如图,已知AB∥CD,∠B=120°,∠D=150°,则∠O等于()A.50° B.60° C.80° D.90°【考点】平行线的性质.【分析】根据邻补角的定义求出∠B+∠O+∠D=360°,再根据已知角的度数即可求出答案.【解答】解:作OE∥AB,由AB∥CD,则OE∥CD,∴∠B+∠1=180°,∠D+∠2=180°;∴∠B+∠BOD+∠D=360°.又∵∠B=120°,∠D=150°,∴∠BOD=360°﹣∠B﹣∠D=90°.故选:D.4.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是()A.1,2,3 B.2,2,4 C.1,2,4 D.3,4,5【考点】三角形三边关系.【分析】根据三角形的三边关系:三角形两边之和大于第三边,计算两个较小的边的和,看看是否大于第三边即可.【解答】解:A、1+2=3,不能组成三角形,故A选项错误;B、2+2=4,不能组成三角形,故B选项错误;C、1+2<4,不能组成三角形,故C选项错误;D、3+4>5,能组成三角形,故D选项正确;故选:D.5.如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,设∠ABD和∠DBC的度数分别为x°、y°,那么下面可以求出这两个角的度数的方程组是()A.B.C.D.【考点】由实际问题抽象出二元一次方程组.【分析】根据两角互余和题目所给的关系,列出方程组.【解答】解:设∠ABD和∠DBC的度数分别为x°、y°,由题意得,.故选B.6.如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为()A.24° B.26° C.34° D.36°【考点】平行线的性质.【分析】先根据平行线的性质得∠1=∠C=50°,然后根据三角形外角性质计算∠A的度数.【解答】解:∵直线a∥b,∴∠1=∠C=50°,∵∠1=∠A+∠B,∴∠A=50°﹣16°=34°.故选C.7.已知关于x的二次三项式4x2﹣mx+25是完全平方式,则常数m的值为()A.10 B.±10 C.﹣20 D.±20【考点】完全平方式.【分析】符和a2+2ab+b2形式的式子叫完全平方式,要明确,常数项是一次项系数一半的平方,进而求出即可.【解答】解:∵关于x的二次三项式4x2﹣mx+25是完全平方式,∴﹣m=±20,即m=±20.故选:D.8.下列不是二元一次方程的是()①3m﹣2n=5 ②③④2x+z=3 ⑤3m+2n ⑥p+7=2.A.1个B.2个C.3个D.4个【考点】二元一次方程的定义.【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.【解答】解:①3m﹣2n=5是二元一次方程;②是二元一次方程;③是分式方程;④2x+z=3是二元一次方程;⑤3m+2n是多项式;⑥p+7=2是一元一次方程;故选:C.9.甲、乙二人按3:2的比例投资开办了一家公司,约定除去各项支出外,所得利润按投资比例分成.若第一年甲分得的利润比乙分得的利润的2倍少3千元,求甲、乙二人各分得利润多少千元.若设甲分得x千元,乙分得y千元,由题意得()A.B.C.D.【考点】由实际问题抽象出二元一次方程组.【分析】设甲分得x千元,乙分得y千元,根据甲、乙二人的比例为3:2,甲分得的利润比乙分得的利润的2倍少3千元,列方程组即可.【解答】解:设甲分得x千元,乙分得y千元,由题意得,,故选C.10.如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于()A.40° B.35° C.30° D.20°【考点】对顶角、邻补角;角平分线的定义.【分析】根据角平分线的定义求出∠AOC,再根据对顶角相等解答即可.【解答】解:∵OA平分∠EOC,∠EOC=70°,∴∠AOC=∠EOC=×70°=35°,∴∠BOD=∠AOC=35°.故选B.二、耐心填一填:(每空3分,共33分)11.把方程2x﹣y﹣3=0化成含y的式子表示x的形式:x=.【考点】解二元一次方程.【分析】把方程2x﹣y﹣3=0写成用含y的式子表示x的形式,需要把含有x的项移到等号一边,其他的项移到另一边,然后合并同类项,系数化1就可用含y的式子表示x的形式:x=【解答】解:移项得2x=y+3系数化为1得:x=12.一种细菌的半径是0.000039m,用科学记数法表示这个数是×10﹣5m.【考点】科学记数法—表示较小的数.【分析】小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】×10﹣5m.×10﹣5m.13.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= 54 度.【考点】平行线的性质;角平分线的定义.【分析】两直线平行,同旁内角互补,可求出∠FEB,再根据角平分线的性质,可得到∠BEG,然后用两直线平行,内错角相等求出∠2.【解答】解:∵AB∥CD,∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,又∵EG平分∠BEF,∴∠BEG=∠BEF=×108°=54°,故∠2=∠BEG=54°.故答案为:54.14.已知x2+y2=10,xy=2,则(x﹣y)2= 6 .【考点】完全平方公式.【分析】利用(x﹣y)2=x2+y2﹣2xy求解即可.【解答】解:∵x2+y2=10,xy=2,∴(x﹣y)2=x2+y2﹣2xy=10﹣4=6.故答案为:6.15.已知x m=4,x2n=6,则x m+2n= 24 .【考点】幂的乘方与积的乘方;同底数幂的乘法.【分析】根据同底数幂的乘法,底数不变指数相加,即可解答.【解答】解:x m+2n=x m•x2n=4×6=24,故答案为:24.16.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段BE 是△ABC中AC边上的高.【考点】三角形的角平分线、中线和高.【分析】根据过三角形的一个顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:∵BE⊥AC,∴△ABC中AC边上的高是BE.故答案为:BE17.一个多边形的内角和是它外角和的2倍,则它的边数是 6 .【考点】多边形内角与外角.【分析】根据多边形的内角和公式(n﹣2)•180°以及外角和定理列出方程,然后求解即可.【解答】解:设这个多边形的边数是n,根据题意得,(n﹣2)•180°=2×360°,解得n=6.答:这个多边形的边数是6.故答案为:6.18.方程2x n﹣3﹣y3m+n﹣2+3=0是二元一次方程,则m= ﹣n= 4 .【考点】二元一次方程的定义.【分析】根据二元一次方程的定义,从二元一次方程的未知数的个数和次数方面考虑求常数m、n的值.【解答】解:根据二元一次方程的定义,得,解得,故答案为:﹣,4.19.已知是方程组的解,则a﹣b= ﹣1 .【考点】二元一次方程组的解.【分析】根据方程组解的定义,把解代入方程组得到关于a、b的方程,然后求解得到a、b 的值,再代入代数式进行计算即可得解.【解答】解:根据题意得,,解得,所以a﹣b=2﹣3=﹣1.故答案为:﹣1.20.若(4x2+2x)(x+a)的运算结果中不含x2的项,则a的值为﹣.【考点】多项式乘多项式.【分析】原式利用多项式乘以多项式法则计算,根据结果不含x2的项,求出a的值即可.【解答】解:原式=4x3+(4a+2)x2+2ax,由结果中不含x2的项,得到4a+2=0,解得:a=﹣.故答案为:﹣.三、细心算一算:(本题共8题,共57分)21.计算题:(1)(﹣2015)0+22×|﹣1|×(﹣)﹣2(2)(x+y﹣2z)(x﹣y+2z)【考点】整式的混合运算;零指数幂;负整数指数幂.【分析】(1)根据零次幂、乘方定义、绝对值性质、负整数指数幂计算,再计算乘法可得;(2)将原式变形运用平方差公式计算,再根据完全平方公式计算即可.【解答】解:(1)原式=1+4×1×9=1+36=37;(2)原式=[x+(y﹣2z)][x﹣(y﹣2z)]=x2﹣(y﹣2z)2=x2﹣y2+4yz﹣4z2;22.先化简,后求值:[(x﹣y)2+2y(y﹣x)﹣(x+y)(x﹣y)]÷(2y),其中x﹣y=2.【考点】整式的混合运算—化简求值.【分析】原式中括号中利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算,去括号合并后利用多项式乘以单项式法则计算得到最简结果,把x﹣y=2代入计算即可求出值.【解答】解:∵x﹣y=2,∴原式=(x2﹣2xy+y2+2y2﹣2xy﹣x2+y2)÷2y=(﹣4xy+4y2)÷2y=﹣2x+2y=﹣2(x﹣y)=﹣4.23.分解因式:(1)2x2﹣8y2;(2)2x3y﹣4x2y2+2xy3.【考点】提公因式法与公式法的综合运用.【分析】(1)原式提取2,再利用平方差公式分解即可;(2)原式提取公因式,再利用完全平方公式分解即可.【解答】解:(1)原式=2(x2﹣4y2)=2(x+2y)(x﹣2y);(2)原式=2xy(x2﹣2xy+y2)=2xy(x﹣y)2.24.解下列方程组:(1)(2).【考点】解二元一次方程组.【分析】(1)利用①×3﹣②可解出y,再把y的值代入①可求出x,从而得到方程组的解;(2)利用①×3+②×2得9x+10x=48+66,可求出x,再把x的值代入①可求出y,从而得到方程组的解.【解答】解:(1),①×3﹣②得5y=﹣5,解得y=﹣1,把y=﹣1代入①得x+1=3,解得x=2,所以方程组的解为;(2),①×3+②×2得9x+10x=48+66,解得x=6,把x=6代入①得18+4y=16,解得y=﹣,所以方程组的解为.25.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′;(2)若连接AA′,CC′,则这两条线段之间的关系是平行且相等.【考点】作图-平移变换.【分析】(1)利用平移规律得出平移后对应点位置进而求出即可;(2)利用平移的性质得出两条线段之间的关系.【解答】解:(1)如图所示:△A′B′C′即为所求;(2)连接AA′,CC′,则这两条线段之间的关系是:平行且相等.故答案为:平行且相等.26.如图,已知AE平分∠BAC,过AE延长线一点F作FD⊥BC于D,若∠F=6°,∠C=30°,求∠B的度数.【考点】三角形内角和定理;三角形的外角性质.【分析】由FD⊥BC以及∠F=6°利用三角形内角和定理即可求出∠DEF的度数,再利用三角形的外角性质即可求出∠CAE的度数,结合角平分线的性质以及三角形内角和定理即可得出∠B的度数.【解答】解:∵FD⊥BC,∠F=6°,∴∠DEF=90°﹣6°=84°,∴∠CAE=∠DEF﹣∠C=84°﹣30°=54°,∵AE平分∠BAC,∴∠BAC=2∠CAD=108°,∴∠B=180°﹣∠BAC﹣∠C=180°﹣108°﹣30°=52°.27.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,求每块长方形的长和宽分别是多少?【考点】二元一次方程组的应用.【分析】本题可以通过看图找出两个等量关系:长方形的长+宽=50cm,长方形的长×2=长+宽×4,据此可以设未知数列方程组求解.【解答】解:设每块长方形的长是xcm,宽是ycm,根据题意得解得答:长是40cm,宽是10cm.28.阅读下文,寻找规律:已知x≠1时,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4…(1)(1﹣x)(1+x+x2+x3+x4+x5+x6+x7)=1﹣x8(2)观察上式,并猜想:①(1﹣x)(1+x+x2+…+x n)= 1﹣x n+1.②(x﹣1)(x10+x9+…+x+1)= x11﹣1 .(3)根据你的猜想,计算:①(1﹣2)(1+2+22+23+24+25)= ﹣63 .②1+2+22+23+24+…+22007= 22008﹣1 .【考点】平方差公式.【分析】(1)仿照已知等式得到一般性规律,写出即可;(2)利用得出的规律化简两式即可;(3)利用得出的规律化简两式即可.【解答】解:(1)(1﹣x)(1+x+x2+x3+x4+x5+x6+x7)=1﹣x8;(2)观察上式,并猜想:①(1﹣x)(1+x+x2+…+x n)=1﹣x n+1;②(x﹣1)(x10+x9+…+x+1)=x11﹣1;(3)根据你的猜想,计算:①(1﹣2)(1+2+22+23+24+25)=1﹣26=﹣63;②1+2+22+23+24+…+22007=﹣(1﹣2)(1+2+22+23+24+…+22007)=22008﹣1.故答案为:(1)1+x+x2+x3+x4+x5+x6+x7;(2)①1﹣x n+1;②x11﹣1;(3)①﹣63;②22008﹣1.。
七年级数学下学期期中试题一(含解析)苏科版2

2015-2016学年江苏省扬州市七年级(下)期中数学试卷一、选择题:(每题3分,共24分)1.已知三角形的三边分别为2,a,4,那么a的取值范围是()A.1<a<5 B.2<a<6 C.3<a<7 D.4<a<62.下列各式从左到右的变形,是因式分解的是()A.x2﹣9+6x=(x+3)(x﹣3)+6x B.(x+5)(x﹣2)=x2+3x﹣10C.x2﹣8x+16=(x﹣4)2D.6ab=2a•3b3.若4a2+kab+9b2是完全平方式,则常数k的值为()A.6 B.12 C.±6 D.±124.下列计算正确的是()A.a+a2=2a3B.a2•a3=a6C.(2a4)4=16a8D.(﹣a)6÷a3=a35.下列各式能用平方差公式计算的是()A.(3a+b)(a﹣b)B.(﹣3a﹣b)(﹣3a+b)C.(3a+b)(﹣3a﹣b)D.(﹣3a+b)(3a﹣b)6.如图,AB∥CD,EG⊥AB,∠1=50°,则∠E的度数等于()A.30° B.40° C.50° D.60°7.一个正多边形的每个外角都等于40°,则它的内角和是()A.1000°B.1620°C.1260°D.1080°8.如图所示,两个正方形的边长BC、CG在同一直线上,且BC=10,那么阴影部分(即△BDF)的面积是()A.50 B.100 C.200 D.无法确定二、填空题(每题3分,共30分)9.有一句谚语说:“捡了芝麻,丢了西瓜.”意思是说有些人办事只抓一些无关紧要的小事,却忽略了具有重大意义的大事.据测算,一粒芝麻重量约有0.0000021kg,将这一数据可以用科学记数法表示为.10.把多项式﹣16x3+40x2y提出一个公因式﹣8x2后,另一个因式是.11.三个数()﹣1、(﹣2)0、(﹣3)2中,最小数与最大数的差是:.12.若a x=8,a y=3,则a x﹣y= .13.计算(﹣a2b)3= .14.如图,将含有45°角的三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2= °.15.如果(x﹣1)x+4=1成立,那么满足它的所有整数x的值是.16.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,则图中阴影部分的面积是cm2.17.如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了m.18.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,则△BEF的面积是 cm2.三、解答题(共96分):19.计算:①30﹣2﹣3②(﹣2a 2b 3)4+(﹣a )8﹣(2b 4)3③x (x ﹣1)(x+3)﹣x 2(x+1)+3x ﹣1④(﹣y )2﹣(x+y )(x ﹣y )20.把下列各式分解因式:(1)16t 2﹣25(2)4m (x ﹣y )﹣2n (y ﹣x )(3)81(a+b )2﹣25(a ﹣b )2(4)16x 4﹣8x 2y 2+y 4.21.先化简,再求值:(a ﹣2b )(a+2b )﹣(a ﹣5b )(a+3b ),其中a=﹣1,b=1.22.如图,AB ∥DE ,∠A=∠D .AC 与DF 平行吗?请说明理由.23.如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A+∠1=74°,求∠D 的度数.24.探究应用:(1)计算(a ﹣2)(a 2+2a+4)= ;(2x ﹣y )(4x 2+2xy+y 2)= .(2)上面的整式乘法计算结果很简洁,你又发现一个新的乘法公式: (请用含a .b的字母表示).(3)下列各式能用你发现的乘法公式计算的是.A.(a﹣3)(a2﹣3a+9)B.(2m﹣n)(2m2+2mn+n2)C.(4﹣x)(16+4x+x2) D.(m﹣n)(m2+2mn+n2)(4)直接用公式计算:(3x﹣2y)(9x2+6xy+4y2)= ;(2m﹣3)(4m2+6m+9)= .25.阅读下列材料:一般地,n个相同的因数a相乘:a×a×a×a×…×a记作a n,如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).此时,3叫做以2为底8的对数,记为log28(log28=3).一般地,若a n=b,则n叫做以a为底的b的对数,记为log a b=n,如34=81,则4叫做以3为底的81的对数,记为log381=4.(1)下列各对数的值:log24= ;log216= ;log264= ;(2)观察(1)中三数4,16,64之间满足怎样的关系式,写出log24,log216,log264满足的关系式;(3)由(2)的结果,你能归纳出一个一般性的结果吗?log a M+log a N= ;(a>0且a≠1,M>0,N>0)(4)根据上述结论解决下列问题:已知,log a2=0.3,求log a4和log a8的值.(a>0且a≠1)26.如图1的图形,像我们常见的风筝.我们不妨把这样图形叫做“筝形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX= °;②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE= °;②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A= °.2015-2016学年江苏省扬州市教育学院附属中学七年级(下)期中数学试卷参考答案与试题解析一、选择题:(每题3分,共24分)1.已知三角形的三边分别为2,a,4,那么a的取值范围是()A.1<a<5 B.2<a<6 C.3<a<7 D.4<a<6【考点】三角形三边关系.【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求解.【解答】解:由于在三角形中任意两边之和大于第三边,∴a<2+4=6,任意两边之差小于第三边,∴a>4﹣2=2,∴2<a<6,故选B.2.下列各式从左到右的变形,是因式分解的是()A.x2﹣9+6x=(x+3)(x﹣3)+6x B.(x+5)(x﹣2)=x2+3x﹣10C.x2﹣8x+16=(x﹣4)2D.6ab=2a•3b【考点】因式分解的意义.【分析】根据分解因式就是把一个多项式化为几个整式的积的形式的定义,利用排除法求解.【解答】解:A、右边不是积的形式,故A选项错误;B、是多项式乘法,不是因式分解,故B选项错误;C、是运用完全平方公式,x2﹣8x+16=(x﹣4)2,故C选项正确;D、不是把多项式化成整式积的形式,故D选项错误.故选:C.3.若4a2+kab+9b2是完全平方式,则常数k的值为()A.6 B.12 C.±6 D.±12【考点】完全平方式.【分析】先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定k 的值.【解答】解:∵4a2+kab+9b2=(2a)2+kab+(3b)2,∴kab=±2•2a•3b,解得k=±12.故选:D.4.下列计算正确的是()A.a+a2=2a3B.a2•a3=a6C.(2a4)4=16a8D.(﹣a)6÷a3=a3【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.【分析】利用合并同类项、同底数幂的乘法、积的乘方、幂的乘方以及同底数幂的除法的知识求解即可求得答案.注意排除法在解选择题中的应用.【解答】解:A、a与a2不能合并,故本选项错误;B、a2•a3=a5,故本选项错误;C、(2a4)4=16a16,故本选项错误;D、(﹣a)6÷a3=a6÷a3=a3,故本选项正确.故选D.5.下列各式能用平方差公式计算的是()A.(3a+b)(a﹣b)B.(﹣3a﹣b)(﹣3a+b)C.(3a+b)(﹣3a﹣b)D.(﹣3a+b)(3a﹣b)【考点】平方差公式.【分析】运用平方差公式(a+b)(a﹣b)=a2﹣b2时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.【解答】解:A、中不存在互为相反数的项,B、﹣3a是相同的项,互为相反项是b与﹣b,符合平方差公式的要求;C、D中不存在相同的项;因此A、C、D都不符合平方差公式的要求.故选B.6.如图,AB∥CD,EG⊥AB,∠1=50°,则∠E的度数等于()A.30° B.40° C.50° D.60°【考点】平行线的性质.【分析】首先根据平行线的性质得到∠EFG的度数,然后利用直角三角形两锐角互余求得∠E的度数即可.【解答】解:∵∠A=50°,AB∥CD,∴∠EFG=50°,∵EG⊥AB,∴∠E=90°﹣∠EFG=90°﹣50°=40°,故选B.7.一个正多边形的每个外角都等于40°,则它的内角和是()A.1000°B.1620°C.1260°D.1080°【考点】多边形内角与外角.【分析】根据任何多边形的外角和都是360°,利用360除以外角的度数就可以求出多边形的边数;n边形的内角和是(n﹣2)•180°,把多边形的边数代入公式,就得到多边形的内角和.【解答】解:360÷40=9,则它是九边形;内角和是:(9﹣2)•180°=1260度.故选C.8.如图所示,两个正方形的边长BC、CG在同一直线上,且BC=10,那么阴影部分(即△BDF)的面积是()A.50 B.100 C.200 D.无法确定【考点】整式的混合运算.【分析】由两正方形面积之和减去三角形ABD与三角形BFG面积之和即可确定出阴影部分面积.【解答】解:设正方形EFGC边长为a,根据题意得:102+a2+a(10﹣a)﹣×102﹣a(a+10)=100+a2+5a﹣a2﹣50﹣a2﹣5a=50,故选A二、填空题(每题3分,共30分)9.有一句谚语说:“捡了芝麻,丢了西瓜.”意思是说有些人办事只抓一些无关紧要的小事,却忽略了具有重大意义的大事.据测算,一粒芝麻重量约有0.0000021kg,将这一数据可以用科学记数法表示为 2.1×10﹣6.【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.0000021=2.1×10﹣6,故答案为:2.1×10﹣6.10.把多项式﹣16x3+40x2y提出一个公因式﹣8x2后,另一个因式是2x﹣5y .【考点】因式分解-提公因式法.【分析】根据提公因式法分解因式解答即可.【解答】解:﹣16x3+40x2y=﹣8x2•2x+(﹣8x2)•(﹣5y)=﹣8x2(2x﹣5y),所以另一个因式为2x﹣5y.故答案为:2x﹣5y.11.三个数()﹣1、(﹣2)0、(﹣3)2中,最小数与最大数的差是:8 .【考点】实数大小比较;零指数幂;负整数指数幂.【分析】根据乘方,可得幂,根据有理数的大小比较,可得最大数、最小数,根据有理数的减法,可得答案.【解答】解;()﹣1=6,(﹣2)0=1,(﹣3)2=9,9﹣1=8,故答案为:8.12.若a x=8,a y=3,则a x﹣y= .【考点】同底数幂的除法.【分析】根据同底数幂的除法底数不变指数相减,可得答案.【解答】解:a x﹣y=a x÷a y=8÷3=,故答案为:.13.计算(﹣a2b)3= ﹣a6b3.【考点】幂的乘方与积的乘方.【分析】根据积的乘方的运算方法:(ab)n=a n b n,求出(﹣a2b)3的值是多少即可.【解答】解:(﹣a2b)3=•(a2)3•b3=﹣a6b3.故答案为:﹣a6b3.14.如图,将含有45°角的三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2= 25 °.【考点】平行线的性质.【分析】利用两直线平行,内错角相等作答.【解答】解:根据题意可知,两直线平行,内错角相等,∴∠1=∠3,∵∠3+∠2=45°,∴∠1+∠2=45°∵∠1=20°,∴∠2=25°.故答案为25.15.如果(x﹣1)x+4=1成立,那么满足它的所有整数x的值是﹣4,0,2 .【考点】零指数幂.【分析】分情况讨论:当x+4=0时;当x﹣1=1时,分别讨论求解.还有﹣1的偶次幂都等于1.【解答】解:如果(x﹣1)x+4=1成立,则x+4=0或x﹣1=1即x=﹣4或x=2当x=0时,(﹣1)4=1故本题答案为:﹣4、2或0.16.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,则图中阴影部分的面积是44 cm2.【考点】二元一次方程组的应用.【分析】设小长方形的长、宽分别为xcm,ycm,根据图示可以列出方程组,然后解这个方程组即可求出小长方形的面积,接着就可以求出图中阴影部分的面积.【解答】解:设小长方形的长、宽分别为xcm,ycm,依题意得,解之得,∴小长方形的长、宽分别为8cm,2cm,∴S阴影部分=S四边形ABCD﹣6×S小长方形=14×10﹣6×2×8=44cm2.17.如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了240 m.【考点】多边形内角与外角.【分析】由题意可知小亮所走的路线为正多边形,根据多边形的外角和定理即可求出答案.【解答】解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,则一共走了24×10=240米.故答案为:240.18.如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为20cm2,则△BEF的面积是 5 cm2.【考点】三角形的面积.【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答即可.【解答】解:∵点E是AD的中点,∴S△ABE=S△ABD,S△ACE=S△ADC,∴S△ABE+S△ACE=S△ABC=×20=10cm2,∴S△BCE=S△ABC=×20=10cm2,∵点F是CE的中点,∴S△BEF=S△BCE=×10=5cm2.故答案为:5.三、解答题(共96分):19.计算:①30﹣2﹣3②(﹣2a2b3)4+(﹣a)8﹣(2b4)3③x(x﹣1)(x+3)﹣x2(x+1)+3x﹣1④(﹣y)2﹣(x+y)(x﹣y)【考点】整式的混合运算.【分析】①分别根据0指数幂及负整数指数幂的运算法则、数的乘方法则计算出各数,再根据实数混合运算的法则进行计算即可;②分别根据幂的乘方与积的乘方法则计算出各数即可;③、④先算乘方,再算乘法,最后算加减即可.【解答】解:①原式=1﹣+9﹣4=5;②原式=16a8b12+a8﹣8b12;③原式=(x2﹣x)(x+3)﹣x3﹣x2+3x﹣1=x3+3x﹣x2﹣3x﹣x3﹣x2+3x﹣1=6x﹣2x2﹣1;④原式=+y2﹣xy﹣(x2﹣y2)=+y2﹣xy﹣x2+y2=y2﹣xy.20.把下列各式分解因式:(1)16t2﹣25(2)4m(x﹣y)﹣2n(y﹣x)(3)81(a+b)2﹣25(a﹣b)2(4)16x4﹣8x2y2+y4.【考点】提公因式法与公式法的综合运用.【分析】(1)直接利用平方差公式分解因式即可;(2)直接提取公因式2(x﹣y),进而分解因式即可;(3)直接利用平方差公式分解因式得出答案;(4)直接利用完全平方公式分解因式,进而利用平方差公式分解因式即可.【解答】解:(1)16t2﹣25=(4t+5)(4t﹣5);(2)4m(x﹣y)﹣2n(y﹣x)=2(x﹣y)(2m+n);(3)81(a+b)2﹣25(a﹣b)2=[9(a+b)﹣5(a﹣b)][9(a+b)﹣5(a﹣b)]=4(7a+2b)(2a+7b);(4)16x4﹣8x2y2+y4=(4y2﹣y2)2=(2x+y)2(2x﹣y)2.21.先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣5b)(a+3b),其中a=﹣1,b=1.【考点】整式的混合运算—化简求值.【分析】先根据平方差公式和多项式乘以多项式法则算乘法,再合并同类项,最后代入求出即可.【解答】解:(a﹣2b)(a+2b)﹣(a﹣5b)(a+3b)=a2﹣4b2﹣a2﹣3ab+5ab+15b2=11b2+2ab,当a=﹣1,b=1时,原式=9.22.如图,AB∥DE,∠A=∠D.AC与DF平行吗?请说明理由.【考点】平行线的判定与性质.【分析】先利用平行线的性质和等量代换证明∠D=∠EGC,再利用平行线的判定说明.【解答】解:平行.∵AB∥DE∴∠A=∠EGC.(两直线平行,同位角相等)∵∠A=∠D,(已知)∴∠D=∠EGC.(等量代换)∴AC∥DF.(同位角相等,两直线平行)23.如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A+∠1=74°,求∠D的度数.【考点】平行线的性质.【分析】根据平行线的性质由AB∥CD得到∠1=∠A=×74°=37°,再根据对顶角相等得∠ECD=∠1=37°,由DE⊥AE得到∠DEC=90°,然后根据三角形内角和定理计算∠D的度数.【解答】解:∵AB∥CD,∴∠1=∠A,∵∠A+∠1=74°,∴∠1=×74°=37°,∴∠ECD=∠1=37°,∵DE⊥AE,∴∠DEC=90°,∴∠D=90°﹣37°=53°.24.探究应用:(1)计算(a﹣2)(a2+2a+4)= a3﹣8 ;(2x﹣y)(4x2+2xy+y2)= 8x3﹣y3.(2)上面的整式乘法计算结果很简洁,你又发现一个新的乘法公式:(a﹣b)(a2+ab+b2)=a3﹣b3(请用含a.b的字母表示).(3)下列各式能用你发现的乘法公式计算的是 C .A.(a﹣3)(a2﹣3a+9)B.(2m﹣n)(2m2+2mn+n2)C.(4﹣x)(16+4x+x2) D.(m﹣n)(m2+2mn+n2)(4)直接用公式计算:(3x﹣2y)(9x2+6xy+4y2)= 27x3﹣8y3;(2m﹣3)(4m2+6m+9)= 8m3﹣27 .【考点】整式的混合运算.【分析】(1)本题先根据多项式乘多项式法则,计算出两式的值即可解答.(2)根据上题所给的结果推理即可得到公式;(3)在四个选项中分析哪一个最符合题意即可解答;(4)步直接套用公式即可.【解答】解:(1)①(a﹣2)(a2+2a+4),=a3+2a2+4a﹣2a2﹣4a﹣8,=a3﹣8;②(2x﹣y)(4x2+2xy+y2),=8x3+4x2y+2xy2﹣4x2y﹣2xy2﹣y3=8x3﹣y3;(2)如②中,(2x)3=8x3,y3=y3,2xy=﹣(2x•y),所以发现的公式为:(a﹣b)(a2+ab+b2)=a3﹣b3;(3)C符合公式,选C;(4)根据公式:(3x﹣2y)(9x2+6xy+4y2)=(3x)3﹣(2y)3=27x3﹣8y3;(2m﹣3)(4m2+6m+9)=(2m)3﹣33=8m3﹣27.故答案为:a3﹣8;8x3﹣y3;(a﹣b)(a2+ab+b2)=a3﹣b3;C;27x3﹣8y3;8m3﹣27.25.阅读下列材料:一般地,n个相同的因数a相乘:a×a×a×a×…×a记作a n,如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).此时,3叫做以2为底8的对数,记为log28(log28=3).一般地,若a n=b,则n叫做以a为底的b的对数,记为log a b=n,如34=81,则4叫做以3为底的81的对数,记为log381=4.(1)下列各对数的值:log24= 2 ;log216= 4 ;log264= 6 ;(2)观察(1)中三数4,16,64之间满足怎样的关系式,写出log24,log216,log264满足的关系式log24+log216=log264 ;(3)由(2)的结果,你能归纳出一个一般性的结果吗?log a M+log a N= log a MN ;(a>0且a≠1,M>0,N>0)(4)根据上述结论解决下列问题:已知,log a2=0.3,求log a4和log a8的值.(a>0且a≠1)【考点】同底数幂的乘法.【分析】根据题目给出的定义即可求出答案.【解答】解:(1)∵22=4,24=16,26=64∴log24=2;log216=4,log264=6(2)log24+log216=log2(4×16)=log264(3)log a M+log a N=log a MN(4)log a2+log a2=log a4=0.3+0.3=0.6,log a2+log a4=log a8=0.6+0.3=0.9故答案为:(1)2;4;6(2)log24+log216=log264(3)log a MN26.如图1的图形,像我们常见的风筝.我们不妨把这样图形叫做“筝形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:观察“筝形”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=58°,则∠ABX+∠ACX= 32 °;②如图3,已知DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=150°,则∠DCE= 105 °;②如图4,已知∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠B G1C=77°,则∠A= 70 °.【考点】三角形内角和定理;三角形的外角性质.【分析】根据三角形外角性质得∠3=∠B+∠1,∠4=∠2+∠C,然后把两式相加即可得到∠BDC=∠A+∠B+∠C;①由前面的结论得∠BXC=∠A+∠ABX+∠ACX,所以∠ABX+∠ACX=90°﹣58°=32°;②由前面的结论得到∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,再根据角平分线的定义得∠ADC=∠BDC,∠ACE=∠BEC,所以∠DBE﹣∠DCE=∠DCE﹣∠A,然后把∠DAE=60°,∠DBE=150°代入计算即可;③由前面的结论得∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,则∠ABG1=∠ABD,∠ACG1=∠ACD,所以10∠BG1C=10∠A+∠ABD+∠ACD,利用等式的性质得到10∠BG1C﹣∠BDC=9∠A,即有∠A=(10×77°﹣140°)=70°.【解答】解:∠BDC=∠A+∠B+∠C.理由如下:作射线AD,如图,∵∠3=∠B+∠1,∠4=∠2+∠C,∴∠3+∠4=∠1+∠2+∠B+∠C,即∠BDC=∠A+∠B+∠C;①∵∠BXC=∠A+∠ABX+∠ACX,∴∠ABX+∠ACX=90°﹣58°=32°;②∵∠DCE=∠A+∠ADC+∠AEC,∠DBE=∠DCE+∠BDC+∠BEC,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=∠BDC,∠ACE=∠BEC,∴∠DBE﹣∠DCE=∠DCE﹣∠A,∴∠DCE=(∠DBE+∠A)=×=105°;③∵∠BDC=∠A+∠ABD+∠ACD,∠BG1C=∠A+∠ABG1+∠ACG1,而∠ABD,∠ACD 的10等分线相交于点G1、G2…、G9,∴∠ABG1=∠ABD,∠ACG1=∠ACD,∴10∠BG1C=10∠A+∠ABD+∠ACD,∴10∠BG1C﹣∠BDC=9∠A,∴∠A=(10×77°﹣140°)=70°.故答案为32,105,70.。
苏科版2015-2016第二学期期中七年级数学试卷

苏科版2015-2016第二学期期中七年级数学试卷一选择题(本大题共18分每题3分)1地球与月球的平均距离大约为384000km ,将384000用科学记数法表示应为( ) A 60.38410⨯ B 63.8410⨯ C 53.8410⨯ D 338410⨯2已知等腰三角形一边长为3,一边长是方程的解,则这个三角形周长为 ( ) A 6 B 7 C 8 D 7或83下列各式中,计算正确的是------------------------------------------( )A 347a b a =B 632a a a ÷= C 347()a a = D 33(ab)ab =4在△ABC 中,∠A 、∠B 、∠C 的度数比为4:5:6,那么△ABC 是 ( ),A 锐角三角形B 直角三角形C 钝角三角形D 等腰三角形5已知2(0.2)a =- ,22b -=- ,21()2c -=- ,01()2d =- ,则a 、b 、c 、d 的大小关系是( )a b d c <<< B. b a d c <<< C. a b c d <<< D.b a c d <<< 6已知9ma = 13na = 则m na- 的值为 -------------( ),A. 4B. —4C. 913D. 1397已知三角形的三边长分别为3、x 、14,若x 为正整数,则这样的三角形共有( )个 A . 2个 B. 3个 C. 5个 D. 7个8不论x 、y 为何有理数时,2212440x y x y +-++ 的值均为( ) 正数 B. 零 C. 负数 D. 非负数三填空题(本大题共24分,每题3分)9.计算2302(48)-⨯⨯ =________ 10.已知2(x 1)2-= ,则代数式2245x x -+ =_______ 11.一个多边形的每个内角都相等,且一个外角等于一个内角13 ,这个多边形是____形12.写出一个多项式,使这个多项式中含有因式2a + 和2a - ,_________13.如图,在△ABC 中,E 是BC 上一点,EC=2BE,点D 是AC 中点,设△ABC 、△ADF 、△BEF 的面积为分为S △ABC 、S △ADF 、S △BEF ,且S △ABC=12、则S △ADF —S △BEF=______FA BCD EA DCBC'D'ABCDP14.如图,△ABC 的外角∠ACD 的平分线与内 角∠ABC 平分线交于点P ,若∠BPC=25°, 则∠BAC 的度数是________15.如图,将一长方形纸片沿EF 折叠后,点DC 分别落在点D ’、C ’的位置 ,若∠EFB=68°,则∠AED ’=_____16.观察下列各式:3211= ,332123+= ,33321236++=,33332123410+++=…猜想:3333123....10++++=__________三解答题(本大题共10小题,共72分,请在相应的指定区域作答,解答时应写出必要的文字说,证明过程或演算步骤) 17(本题满分6分)计算0224231(3)()22(2)3π---+⨯+- , 用简便方法计算2500499501-⨯18(本题满分6分)因式分解(1)481x - (2)226(1b)2(b 1)a ---19(本题满分6分)如图,AB ∥CD,∠A=∠D ,判断AF 与ED 的位置关系,并说明理由ABDCFE20题(本题6分)先化简再求值:22(1)(1)(2)x x x +--- ,其中x=—121.(本题满分6分)如图,AD 是△ABC 的高,BE 平分∠ABC 交AD 于点E ,∠C=70°,∠BED=64°,求∠BAC 的度数ABCDE22.(本题6分)已知10224nm == ,其中m 、n 为正整数,求nm 的值23题(本题8分)已知如图,O 是△ABC 内一点,求证:∠AOB=∠1+∠2+∠C24题(本题8分).)如图,每个小正方形的边长为1个单位. (1) 画出△ABC 的AB边上的中线CD ;(2) 画出△ABC 向右平移4个单位后得到的△A1B1C1; (3) 图中AC 与A1C1的关系是: ; (4) 找出图中能使S △ABC =S △ABQ 的所有格点Q . (分别用Q1、Q2、……分别表示)A BC25题(本题10分) 阅读下列材料:1×2=31(1×2×3-0×1×2); 2×3=31(2×3×4-1×2×3); 3×4=31(3×4×5-2×3×4);将这三个等式的俩边相加,可以得到1×2+2×3+3×4=31×3×4×5=20.读完这段材料,请你计算:(1)1×2+2×3+…+10×11;(写出计算过程)(2)1×2+2×3+…+ n (n+1)=________(3)1×2×3+2×3×4+…+ n (n+1)(n+2)=_________26题(本题10分)用四块完全相同的小长方形拼成的一个“回形”正方形. 用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式,试用乘法公式说明这个等式成立(2利用(1)中的结论计算:32,4a b ab +==、 求a b -(3)根据(1)中的结论,直接写出1x x +和 1x x -之间的关系若2310x x -+= , 分别求出1x x +和21()x x -的值ba。
2015—2016学年度第二学期期中考试七年级数学试卷及答案
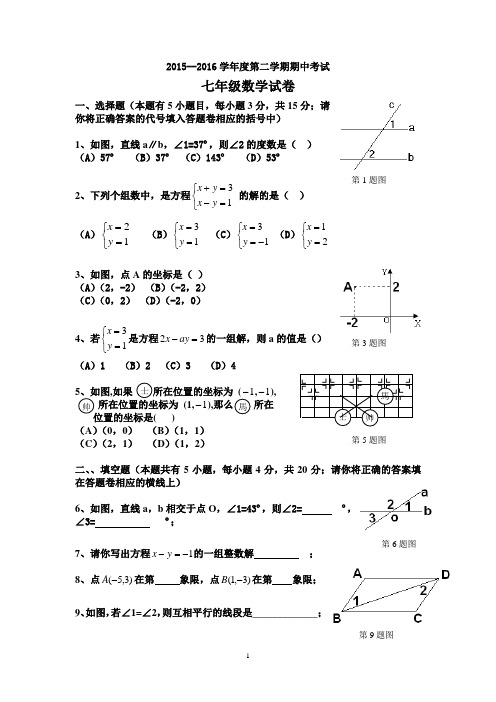
2015--2016学年度第二学期期中考试七年级数学试卷一、选择题(本题有5小题目,每小题3分,共15分;请你将正确答案的代号填入答题卷相应的括号中)1、如图,直线a ∥b ,∠1=37º,则∠2的度数是( )(A )57º (B )37º (C )143º (D )53º2、下列个组数中,是方程⎩⎨⎧=-=+13y x y x 的解的是( ) (A )⎩⎨⎧==12y x (B )⎩⎨⎧==13y x (C )⎩⎨⎧-==13y x (D )⎩⎨⎧==21y x3、如图,点A 的坐标是( )(A )(2,-2) (B )(-2,2)(C )(0,2) (D )(-2,0)4、若⎩⎨⎧==13y x 是方程32=-ay x 的一组解,则a 的值是()(A )1 (B )2 (C )3 (D )4,如果,1-), 所在位置的坐标为 (1,1-),所在() (A )(0,0) (B )(1,1)(C )(2,1) (D )(1,2)二、、填空题(本题共有5小题,每小题4分,共20分;请你将正确的答案填在答题卷相应的横线上)6、如图,直线a ,b 相交于点O ,∠1=43º,则∠2= º,∠3= º;7、请你写出方程1-=-y x 的一组整数解;8、点)3,5(-A 在第 象限,点)3,1(-B 在第 象限;9、如图,若∠1=∠2,则互相平行的线段是_____________;10、把点A (-4,2)向右平移3个单位长度得A1的坐标是 ;把点B (-4,2)向下平移3个单位长度得B2的坐标是 ;三、解答题(本题共5题,每小题6分,共30分)11、如图,直线a 、b 被直线c 所截若∠1=30°,∠2=150°,试说明a 与b 的位置关系。
12、解方程组 ⎩⎨⎧+==+y x y x 293213、解方程组 ⎩⎨⎧=-=+827y x y x14、如图,AD ∥BC ,AD 平分∠EAC ,∠EAD=50°,求∠B 和∠C 的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级期中数学测试卷(满分:150分;时间:120分钟) 得分一、精心选一选(每题3分,共24分) 1.()22a - 的计算结果是 ( )A.24a -B.22aC.4aD.24a 2.有下列长度的三条线段,其中能组成三角形的是:( ) A .3、5、10 B .10、4、6 C .4、6、9 D .3、1、1 3.(-3)100×(-13)101等于 ( ) A .-1 B .1 C .-13 D .134. 下列各式能用平方差公式计算的是( )A .()()23a b a b +-B .⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛+121121x x C .()()n m n m +--- D .()()y x y x +--335.已知x+y=6,xy=4,则x 2y+xy 2的值为 ( )A.12B.-12C.-24D.24 6.如果)5)(1(2a ax x x +-+的乘积中不含2x 项,则a 为 ( )A.-5B.5C.51D.51-7. 小明同学在计算某n 边形的内角和时,不小心多输入一个内角,得到和为2005°,则n 等于( ) A .11 B .12 C .13 D .14 8.如图,AB∥CD,∠ABE 和∠CDE 的平分线相交于点F ,∠F=1250, 则∠E 的度数为( )A .120B .115C .110D .1050二、认真填一填(每题3分,共30分) 9. 计算:(-p)2·p 3= .10.研究表明,甲型H1N1流感球形病毒细胞的直径约为0.00000156米,用科学记数法表示这个数是米。
11.等腰三角形的两边长分别是5cm 和10cm ,则它的周长是 cm 。
12.若一个多边形的每个内角都为135°,则它的边数为13.若(x-y)2=(x+y)2+M,则M 等于14. 如果()2219x m x +-+是一个关于x 的完全平方式,则m=_________.ABCDEF第8题15. 若34,24==y x ,则4x y+=a ,b ,c17.如图,在△ABC 中,已知点D 、E 、F 分别是边BC 、AD 、CE 上的中点,且S △ABC =4,则S △BFF 18. 一机器人以0.5m/s 的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止三、解答题:19.计算:(每题4分,共8分)① ()()1312223π-⎛⎫---++- ⎪⎝⎭② ()()2323a b c a b c +--+20.把下列各式分解因式:(每题4分,共12分) ①()()4m x y n x y ---;②2250t - ; ③ 242436x x -+21. (本题8分)先化简,再求值:2(2)(2)4()a b a b a b +---,其中1a =,2b =-.22.(本题8分)如下图,在每个小正方形边长为1的方格纸中,第18题第17题△ABC 的顶点都在方格纸格点上.将△ABC 向左平移2格, 再向上平移4格.(1)请在图中画出平移后的△A ′B ′C ′,(2)再在图中画出△A ′B ′C ′的高C ′D ′,并求出△ABC 的面积。
23.(本题8分)已知3,2a b ab -==,求(1)()2a b +,(2)226a ab b -+的值.24.(本题10分)如图,已知∠1=∠C, ∠2=∠3,BE 是否平分∠ABC ?请说明理由。
25.(本题10分)如图,在△ABC 中,∠A =40°,∠B =72°,CD 是AB 边上的高,CE 是∠ACB 的平分线,DF ⊥CE 于F ,求∠CDF 的度数.26.(本题10分) 阅读下面材料,解决下列问题:333331218912912121233636+=+=+=+=+++==222,而(),所以(),,而(1+2+3) 21ED A33312121233636+=+++==22以(),,而(1+2+3) 所以3332312312312341001234++=+++++=+++(),,而()233332312312341001234100+=+++++=+++=(),,而(),所以33331234+++=21234+++() 3333312345++++=2( )=_____________求:(1)填空: 333322123...(_______)[__________](n n ++++==为整数) (2)计算: 333331112131415++++27.(本题10分)如图,有足够多的边长为a 的小正方形(A 类)、长为a 宽为b 的长方形(B 类)以及边长为b 的大正方形(C 类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a +2b )(a +b )=a 2+3ab +2b 2(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a +b )(a +2b ),在下面虚框中画出图形....,并根据图形回答(2a +b )(a +2b )= . (2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a 2+5ab +6b 2. ① 你画的图中需C 类卡片_____张.② 可将多项式a 2+5ab +6b 2分解因式为 (3) 如图③,大正方形的边长为m ,小正方形的边长为n ,若用x 、y 表示四个矩形的两边长(x >y ),观察图案并判断, 将正确关系式的序号填写在横线上________ _____(填写序号)......①.224m n xy -= ②.x y m += ③.22x y mn -= ④.22222m n x y ++=28.(本题12分)好学的小红在学完三角形的角平分线及内角和后,钻研了下列3个问题,请你一起参与,共同进步.(1)、如图(1),在△ABC 中,∠ABC 、∠ACB 的平分线相交于点O ,图①∠A=40°,求∠BOC的度数。
(2)、如图(2),△DEF两个外角的平分线相交于点G,∠D=40°,求∠EGF的度数。
P Q(3)、由(1)、(2)可以发现∠BOC与∠EGF有怎样的数量关系?设∠A=∠D=n°, ∠B OC与∠EGF是否还具有这样的数量关系?为什么?2015-2016学年邗江区七年级(下)数学期中试卷答题卡(满分:150分;时间:120分钟) 得分二、填空题(每题3分,共30分)9.5p ; 10.61.5610-⨯; 11. 25 ; 12. 八 ;; 14.3.5或-2.5; 15. 6 ;17 18 三、解答题:19.计算:(每题4分,共8分)① ()()1312223π-⎛⎫---++- ⎪⎝⎭② ()()2323a b c a b c +--+ 解:原式= 2-1+3-8 …… ( 2 分 ) 解:原式= 22(23)a b c -- …… ( 2 分 ) = -4 …… ( 2分 ) = 222(4129)a b bc c --+ …… ( 1分 ) =2224129a b bc c -+- …… ( 1分 ) 20.把下列各式分解因式:(每题4分,共12分) ①()()4m x y n x y ---;②2250t - ; ③242436x x -+解:原式=()()4x y m n -- 解:原式=()2225t - 解:原式=()2469x x -+ … ( 2 分 )=()()255t t +- =()243x - … ( 2 分 ) 21. (本题8分)先化简,再求值:2(2)(2)4()a b a b a b +---,其中1a =,2b =-. 解:原式=222244(2)a b a ab b ---+ =22224484a b a ab b --+- =285ab b - …… ( 4 分 )当a=1,b=-2时原式=()()281252⨯⨯--⨯-= -16-20 = -36 …… ( 4分 )22.(本题8分)如下图,在每个小正方形边长为1的方格纸中,△ABC 的顶点都在方格纸格点上.将△ABC 向左平移2格,再向上平移4格.(1)请在图中画出平移后的△A ′B ′C ′,(2)再在图中画出△A ′B ′C ′的高C ′D ′,并求出△ABC 的面积。
解:(1)如图…… ( 4分 ) (2)14482ABC S ∆=⨯⨯= …… (8分 )23.(本题8分)已知3,2a b ab -==,求(1)()2a b +,(2)226a ab b -+的值.解:(1)当3,2a b ab -==时 (2)当3,2a b ab -==时()()224a b a b ab +=-+…… (2 分) ()22264a ab b a b ab -+=-- …… ( 2分 )=2342+⨯ =2342-⨯= 98+ = 9-8=17 ……( 2 分 ) = 1 …… ( 2分 )24.(本题8分)如图,已知∠1=∠C, ∠2=∠3, BE 是否平分∠ABC ?请说明理由。
解: BE 平分∠ABC ,理由如下: ∵ ∠1=∠C∴ DE ∥BC …… ( 2分 ) ∴ ∠2=∠EBC …… ( 2分 )∵ ∠2=∠3∴ ∠EBC=∠3…… ( 2分 )∴ BE 平分∠ABC …… ( 2分 ) 25.(本题10分)如图,在△ABC 中,∠A =40°,∠B =72°,CD 是AB DF ⊥CE 于F ,求∠CDF 的度数. 解:∵∠A=40°,∠B =72°∴∠ACB=180°-40°-72°=68°…… ( 2分 )∵CE 是∠ACB 的平分线, ∴∠BCE=12∠ACB=12× 68°=34°…… ( 2分 ) ∵CD ⊥AB∴∠CDB=90°∴∠BCD=180°-90°-72°=18°…… ( 2分 )∴∠DCE=∠BCE-∠BCD=34°-18°=16°…… ( 2分 )∵DF ⊥CE∴∠DFC=90°∴∠CDF=180°-90°-16°=74°…… ( 2分 ) 26.(本题10分) 阅读下面材料,解决下列问题:333331218912912121233636+=+=+=+=+++==222,而(),所以(),,而(1+2+3) 33312121233636+=+++==22以(),,而(1+2+3) 所以3332312312312341001234++=+++++=+++(),,而()3B233332312312341001234100+=+++++=+++=(),,而(),所以33331234+++=21234+++() 3333312345++++=()212345++++= 225 (每空一分)求:(2)填空:()3333221123...(12)[2n n n n +++++=++∙∙∙+=(n 为整数)(每空两分)(3)计算(4分): 333331112131415++++原式=()()333333331231512310+++∙∙∙+-+++∙∙∙+ …… ( 2分 )=()()221231512310+++∙∙∙+-+++∙∙∙+=()()22115151101022+⨯+⨯⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭=()()22120551205512055-=+-=17565⨯ =11375…… (4分 )27.(本题10分)如图,有足够多的边长为a 的小正方形(A 类)、长为a 宽为b 的长方形(B 类)以及边长为b 的大正方形(C 类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a +2b )(a +b )=a 2+3ab +2b 2(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b )(a +2b ),在下面虚框中画出图形....,并根据图形回答(2a +b )(a +2b )=22252a ab b ++.…… ( 2+2分 ) (2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a 2+5ab +6b 2. ③ 你画的图中需C 类卡片__6__张.…… ( 2分 )④ 可将多项式a 2+5ab +6b 2分解因式为()()23a b a b ++…… ( 2分 )(3) 如图③,大正方形的边长为m ,小正方形的边长为n ,若用x 、y 表示四个矩形的两边长(x >y ),观察图案并判断,将正确关系式的序号填写在横线上_____①②③④___ _____(填写序号)......…… ( 2分 ) ①.xy =m 2-n 24②.x +y =m ③.x 2-y 2=m·n ④.x 2+y 2=m 2+n 2228.(本题12分)好学的小红在学完三角形的角平分线及内角和后,钻研了下列3个问题,请你一起参与,共同进步.(1)、如图(1),在△ABC 中,∠ABC 、∠ACB 的平分线相交于点O , ∠A=40°,求 ∠BOC 的度数。
