§5.4两角和与差的余弦、正弦和正切(二)
两角和与差的正弦余弦正切公式

两角和与差的正弦余弦正切公式下面我们将分别介绍两角和与差的正弦、余弦和正切公式。
1.正弦的两角和与差公式:设角A和角B的正弦值分别为sinA和sinB,那么有:sin(A + B) = sinA * cosB + cosA * sinBsin(A - B) = sinA * cosB - cosA * sinB证明:我们考虑一个单位圆(半径为1),圆心为O,且角A对应的弧与x 轴的交点为点P,角B对应的弧与x轴的交点为点Q。
根据单位圆上的点的坐标表示,我们有:点P的坐标为(cosA, sinA)点Q的坐标为(cosB, sinB)以O为起点,连接OP和OQ,将其延长到圆的边缘,分别交于点M和点N。
由于所有的角度都是以弧度来表示的,因此我们可以使用三角函数的定义来表示OP和OQ的长度。
通过定义我们有:sinA = PMcosA = OMsinB = QNcosB = ON现在我们来计算sin(A + B)。
根据三角形的正弦定理,我们可以得到:sin(A + B) = PN(即三角形OPN的高)通过几何推导我们可以发现,三角形OPN的底边的长度为cosB * cosA。
同样地,通过几何推导我们可以发现,三角形OPN的高为sinA * cosB + cosA * sinB。
因此,我们得到sin(A + B) = sinA * cosB + cosA * sinB。
同理,可以推导得到sin(A - B) = sinA * cosB - cosA * sinB。
2.余弦的两角和与差公式:设角A和角B的余弦值分别为cosA和cosB,那么有:cos(A + B) = cosA * cosB - sinA * sinBcos(A - B) = cosA * cosB + sinA * sinB证明:我们考虑一个单位圆(半径为1),圆心为O,且角A对应的弧与x 轴的交点为点P,角B对应的弧与x轴的交点为点Q。
根据单位圆上的点的坐标表示,我们有:点P的坐标为(cosA, sinA)点Q的坐标为(cosB, sinB)以O为起点,连接OP和OQ,将其延长到圆的边缘,分别交于点M和点N。
两角和与差的正弦余弦和正切公式

利用三角函数的倍角公式推导
总结词
通过三角函数的倍角公式,我们可以推导出 两角和与差的正弦、余弦和正切公式。
详细描述
三角函数的倍角公式指出,对于任意角度α, sin(2α)、cos(2α)和tan(2α)的值可以通过
sin(α)、cos(α)、tan(α)的函数关系来表达。 利用这个公式,我们可以推导出两角和与差
总结词
通过三角函数的减法定理,我们可以推导出 两角和与差的正弦、余弦和正切公式。
详细描述
三角函数的减法定理指出,对于任意角度α、 β,sin(α-β)、cos(α-β)和tan(α-β)的值可 以通过sin(α)、cos(α)、sin(β)、cos(β)、 tan(α)和tan(β)的函数关系来表达。利用这 个定理,我们可以推导出两角和与差的正弦、 余弦和正切公式。
地理学问题
在地理学中,很多问题涉及到地 球的自转、公转等角度计算,如 时差、太阳高度角等,利用三角 函数公式可以方便地计算。
经济学问题
在经济学中,很多问题涉及到利 率、汇率等与角度相关的问题, 利用三角函数公式可以方便地描 述这些变化规律。
04
三角函数公式的扩展
利用三角函数的和差化积公式扩展
总结词
利用三角函数的积化和差公式扩展
总结词
利用三角函数的积化和差公式,可以将两角和与差的 正弦、余弦和正切公式进行扩展,得到更一般化的公 式形式。
详细描述
三角函数的积化和差公式可以将两个角度的正弦或余 弦的乘积转化为其他角度的正弦、余弦和正切的和或 差的形式,从而扩展了原有的公式。例如,利用积化 和差公式,可以将两角和的余弦表示为单个角度余弦 的函数,进一步推导得到更一般化的公式。
VS
详细描述
5.4 两角和与差的余弦、正弦和正切
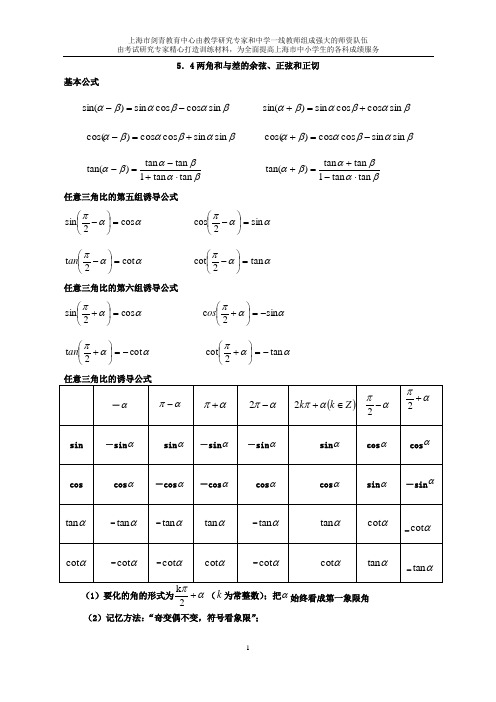
5.4两角和与差的余弦、正弦和正切基本公式βαβαβαsin cos cos sin )sin(-=- βαβαβαsin cos cos sin )sin(+=+βαβαβαsin sin cos cos )cos(+=- βαβαβαsin sin cos cos )cos(-=+βαβαβαtan tan 1tan tan )tan(⋅+-=- βαβαβαtan tan 1tan tan )tan(⋅-+=+ 任意三角比的第五组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛- ααπsin 2cos =⎪⎭⎫⎝⎛- ααπcot 2t =⎪⎭⎫ ⎝⎛-an ααπtan 2cot =⎪⎭⎫⎝⎛- 任意三角比的第六组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛+ ααπsin 2c -=⎪⎭⎫⎝⎛+os ααπcot 2t -=⎪⎭⎫ ⎝⎛+an ααπtan 2cot -=⎪⎭⎫⎝⎛+ 任意三角比的诱导公式(1)要化的角的形式为α+2(k 为常整数);把α始终看成第一象限角 (2)记忆方法:“奇变偶不变,符号看象限”;理解公式:a sin α+b cos α=22b a +sin (α+ϕ) (其中,ϕ通常取πϕ20<≤,2222sin ,cos b a b b a a +=+=ϕϕ,ab=ϕtan α为任意角). 例1.求证:)4cos(2)cos (sin 2)3()4sin(2sin cos )2()6sin(cos 21sin 23)1(ππθθθπααα-=++=++=+x x x例2.利用和(差)角公式化简:)3cos(66)3sin(62)4(cos sin 3)3(cos 53sin 153)2(cos 21sin 23)1(x x x x x x x x -+---+ππ)6sin(cos 21sin 23πααα+=+例3.求证:)4tan(cos sin cos sin π-=+-x xx x x例4.若0<α<β<4π,sin α+cos α=a ,sin β+cos β=b ,则( )A.ab <1B.a >bC.a <b D.ab >2 【当堂练习】1.化简)sin()sin()cos()cos(γββαγββα-----为 ( )A .)2sin(γβα+-B .)sin(γα- .cos()C αγ-D .)2cos(γβα+- 2.已知3tan =α,则αααα22cos 9cos sin 4sin 2-+的值为( )A .3B .2110C .13 D .1303.已知4sin 25α=-,(,)44ππα∈-,sin 4α的值为 ( )A .2425B .2425-C .45D .7254.已知sin αcos α=38,且4π<α<2π,则cos α-sin α的值为 ( ) A .12 B .—12 C .14- D .12±5.已知α+ β =3π, 则cos αcos β–sin αcos β–cos αsin β – sin αsin β 的值为( )A.B .–1C .1 D.6. 已知1tan 23α=,求tan α的值.7.已知4sin 5α=,(,)2παπ∈5cos 13β=-,β是第三象限角,求cos()αβ-的值.【家庭作业】 一、选择题1.tan 70°+tan 50°-3tan 70°·tan 50°= ( )A. 3B.33C .-33D .- 32.若3sin x -3cos x =23sin(x -φ),φ∈(-π,π),则φ=( )A .-π6 B.π6 C.5π6 D .-5π63.已知sin ⎝ ⎛⎭⎪⎫π4-x =35,则sin 2x 的值为( )A.725B.1625C.1425D.19254.已知cos ⎝ ⎛⎭⎪⎫π6-α=33,则sin2⎝ ⎛⎭⎪⎫α-π6-cos ⎝ ⎛⎭⎪⎫5π6+α的值是 ( )A.2+33B .-2+33C.2-33D.-2+33二、填空题5.函数y =2cos2x +sin 2x 的最小值是________.6.若0<α<π2<β<π,且cos β=-13,sin(α+β)=13,则cos α=________.7.已知α、β为锐角,且cos α=17,cos(α+β)=-1114,则β的值为________.三、解答题8.已知tan ⎝ ⎛⎭⎪⎫π4+α=12.(1)求tan α的值; (2)求sin 2α-cos2α1+cos 2α的值.【综合】 一、选择题1.有四个关于三角函数的命题:p1:∃x ∈R ,sin2x 2+cos2x 2=12; p2:∃x 、y ∈R ,sin(x -y)=sin x -sin y ;p3:∀x ∈[0,π],1-cos 2x 2=sin x ; p4:sin x =cos y ⇒x +y =π2. 其中的假命题是 ( )A .p1,p4B .p2,p4C .p1,p3D .p2,p4 二、填空题2. 3-sin 70°2-cos210°=________.3.若cos(α+β)=15,cos(α-β)=35,则tan α·tan β=________.三、解答题4.如图在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐 角α、β,它们的终边分别与单位圆相交于A 、B 两点.已 知A 、B 两点的横坐标分别为210、255. (1)求tan(α+β)的值; (2)求α+2β的大小.5.已知函数f(x)=4cos4x -2cos 2x -1cos 2x .(1)求f ⎝ ⎛⎭⎪⎫-1112π的值;(2)当x ∈⎣⎢⎡⎭⎪⎫0,π4时,求g(x)=f(x)+sin 2x 的最大值和最小值.6.sin14cos16cos14sin16︒︒+︒︒=7.比较大小:036cos 36sin + 038cos 38sin +;8.已知tan2α=2,求:(1)tan()4πα+的值; (2)6sin cos 3sin 2cos αααα+-的值.9.设α、β为锐角, sinα求α+β.10.(1) 已知tan (α+β)=1, tan α=3, 求tan β. (2) 设cos(α-2β)=19-, sin(2α-β)=23, 且2παπ<<, 0<β<2π,求cos(α+β).11.求值:(1) 已知sinθ=35, θ为锐角,求sin 2θ; (2) 已知sinθ=35,sin2θ<0, 求tan 2θ.参考答案:例1(1))6sin(cos 21sin 23πααα+=+ 证法一:左边=sin αcos 6π+cos αsin 6π=sin (α+6π)=右边 证法二:右边=sin αcos 6π+cos αsin 6π=23sin α+21cos α=左边 (2)cos θ+sin θ=2sin (θ+4π)证法一:左边=2(22cos θ+22sin θ)=2(sin 4πcos θ+cos 4πsin θ) =2sin (θ+4π)=右边证法二:右边=2(sin θcos 4π+cos θsin 4π)=2(22sin θ+22cos θ)=cos θ+sin θ=左边(3) 2(sinx+cosx )=2cos (x-4π)证法一:左边=2(sinx +cosx )=2(22sinx +22cosx )=2(cosxcos 4π+sinxsin 4π) =2cos (x -4π)=右边证法二:右边=2cos (x -4π)=2(cosxcos 4π+sinxsin 4π)=2(22cosx +22sinx )=2(cosx +sinx )=左边例2.解:(1) 23sinx +21cosx =sinxcos 6π+cosxsin 6π=sin (x +6π)或:原式=sinxsin 3π+cosxcos 3π=cos (x -3π)(2)315sinx -35cosx =65(23sinx -21cosx )=65(sinxcos 6π-cosxsin 6π) =65sin (x -6π)或:原式=65(sin 3πsinx -cos 3πcosx )=-65cos (x +3π)(3) 3sinx -cosx =2(23sinx -21cosx )=2sin (x -6π)=-2cos (x +3π)(4) 26sin (3π-x )+66cos (3π-x ) =32[21sin (3π-x )+23cos (3π-x )] =32[sin 6πsin (3π-x )+cos 6πcos (3π-x )] =32cos [6π-(3π-x )]=32cos (x -6π)或:原式=32[sin (3π-x )cos 3π+cos (3π-x )sin 3π]=32sin [(3π-x )+3π]=32sin(32π-x )例3证明:左边=)4tan()4cos(2)4sin(2πππ-=--x x x =右边或:右边=tan (x -4π)=xx xx x x x x x x cos sin cos sin 4sinsin 4cos cos 4sincos 4cos sin )4cos()4sin(+-=+-=--ππππππ=左边例4:解:sin α+cos α=2sin (α+4π)=a sin β+cos β=2sin (β+4π)=b 又∵0<α<β<4π∴0<α+4π<β+4π<2π∴sin (α+4π)<sin (β+4π) ∴a <b答案:C 当堂练习 1答案:C解析:利用两角差的余弦公式的逆用 2答案:B解析:二倍角的应用 3答案:B解析:三角函数基本关系式的平方关系的应用 4答案:B解析:平方关系、倍角公式的应用 5答案:B6解析:1tan 23α=,由此得2tan 6tan 10αα+-=解得tan 2α=-+tan 2α=-7答案:33cos()65αβ-=-解析:因为,(,)2παπ∈由此得4sin 5α=所以3cos 5α=-又因为5cos 13β=-,β是第三象限角,所以12sin 13β=-所以33cos()65αβ-=-家庭作业:1 解析:tan 70°+tan 50°-3tan 70°·tan 50° =tan 120°(1-tan 70°·tan 50°)-3tan 70°·tan 50° =- 3. 答案:D2 解析:23sin(x -φ)=23(sin xcos φ-cos xsin φ) =3sin x -3cos x ,∴cos φ=32,sin φ=12. 又φ∈(-π,π),∴φ=π6. 答案:B3 解析:sin 2x =cos ⎝ ⎛⎭⎪⎫π2-2x =cos 2⎝ ⎛⎭⎪⎫π4-x =1-2sin2⎝ ⎛⎭⎪⎫π4-x =1-2×⎝ ⎛⎭⎪⎫35 2=725. 答案:A 4 解析:sin2⎝ ⎛⎭⎪⎫α-π6-cos ⎝ ⎛⎭⎪⎫5π6+α =1-cos2⎝ ⎛⎭⎪⎫π6-α+cos ⎝ ⎛⎭⎪⎫π6-α=2+33.答案:A5 解析:y =(2cos2x -1)+sin 2x +1=cos 2x +sin 2x +1=2sin ⎝ ⎛⎭⎪⎫2x +π4+1 ∴y 的最小值为1- 2.答案:1- 26 解析:∵0<α<π2<β<π,∴π2<α+β<3π2, ∴sin β=223,cos(α+β)=-223,∴cos α=cos[(α+β)-β] =cos(α+β)cos β+sin(α+β)sin β =⎝ ⎛⎭⎪⎫-223×⎝ ⎛⎭⎪⎫-13+13×223 =49 2.答案:4297 解析:cos β=cos[(α+β)-α] =cos(α+β)cos α+sin(α+β)sin α =17×⎝ ⎛⎭⎪⎫-1114+437×5314=12. ∴β=π3. 答案:π38 解:(1)由tan ⎝ ⎛⎭⎪⎫π4+α=1+tan α1-tan α=12.解得tan α=-13. (2)sin 2α-cos2α1+cos 2α=2sin αcos α-cos2α2cos2α =tan α-12=-56.综合训练1 解析:p1:∃x ∈R ,sin2x 2+cos2x 2=12是假命题;p2是真命题,如x =y =0时成立;p3是真命题, ∵∀x ∈[0,π],sin x≥0, ∴1-cos 2x2=sin2x =|sin x|=sin x ;p4是假命题,如x =π2,y =2π时; sin x =cos y ,但x +y≠π2. 答案:A 2 解析:3-sin 70°2-cos210°=3-sin 70°2-1+cos 20°2=23-sin 70°3-cos 20°=23-cos 20°3-cos 20°=2. 答案:23 解析:∵cos(α+β)=cos αcos β-sin αsin β=15,cos(α-β)=cos αcos β+sin αsin β=35, ∴cos αcos β=25,sin αsin β=15. ∴sin αsin βcos αcos β=12,即tan α·tan β=12. 答案:124 解:(1)由已知条件及三角函数的定义可知,cos α=210,cos β =255.因为α为锐角,故sin α>0, 从而sin α=1-cos2α=7210,同理可得sin β=55,因此tan α=7,tan β=12. 所以tan(α+β)=tan α+tan β1-tan αtan β=7+121-7×12=-3. (2)tan(α+2β)=tan[(α+β)+β]=-3+121--3×12=-1. 又0<α<π2,0<β<π2,故0<α+2β<3π2,从而由tan(α+2β)=-1得α+2β=3π4. 5 解:f(x)=2cos2x -12cos2x +1-2cos2x cos 2x =cos 2x 2cos2x +1-2cos 2x cos 2x =2cos2x +1-2=2cos2x -1=cos 2x.(1)f ⎝ ⎛⎭⎪⎫-11π12=cos 2⎝ ⎛⎭⎪⎫-11π12=cos 11π6=cos π6=32. (2)g(x)=cos 2x +sin 2x =2sin ⎝⎛⎭⎪⎫2x +π4. 由0≤x<π4,故π4≤2x+π4<3π4, ∴22≤sin ⎝ ⎛⎭⎪⎫2x +π4≤1,1≤2sin ⎝⎛⎭⎪⎫2x +π4≤ 2.即g(x)的最小值是1,最大值是 2.6. 答案:12解析:sin14cos16cos14sin16︒︒+︒︒=sin 30︒=127. 答案:<8. 解析:(1)∵ tan 2α=2, ∴4tan 3α=-; 所以tan tan 4tan()41tan tan 4παπαπα++=-=17-; (2)由(1), 4tan 3α=-;6sin cos 6tan 173sin 2cos 3tan 26αααααα++==--. 9.答案:α+β=4π 解析:α、β为锐角, sinα∴ cosα, ∴cos(α+β)=cosαcosβ-sinαsinβ∴α+β=4π 10. 答案:tan β=12- cos(α+β) =239729- 解析:(1) ∵tan (α+β)=1, tan α=3,∴tan β=tan [(α+β)-β]=12-. (2) ∵cos(α-2β)=19-, sin (2α-β)=23, 且2παπ<<, 0<β<2π, ∴α-2β∈(4π, π), 2α-β∈(4π-, 2π), sin(α-2β)=92α-β)=3 ∴ cos 2αβ+=cos[(α-2β)-(2α-β)]+β)=2cos 22αβ+-1=239729- 11.答案:sin2θ==. t a n 32θ= 解析:(1) ∵sinθ=35, θ为锐角, ∴ cosθ=45, sin 2θ==. (2) ∵sinθ=35,sin2θ<0, ∴cosθ<0, cosθ=-45,tan 32θ=.。
两角和与差的正弦余弦正切公式

两角和与差的正弦余弦正切公式在三角函数中,我们经常需要计算两个角的和或差的正弦、余弦或正切值。
这些公式被广泛应用于数学、物理、工程等领域的问题求解中。
本文将详细介绍两角和与差的正弦、余弦和正切公式。
一、两角和与差的正弦公式首先,我们来讨论两个角的和的正弦公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道正弦的定义为一个角的对边与斜边之比,可以表示为sin(x)=opposite/hypotenuse。
根据这个定义,我们可以得到如下的两角和的正弦公式:sin(A+B) = sinA*cosB + cosA*sinB这个公式很重要,可以帮助我们计算两个角的和的正弦值。
在实际应用中,我们经常需要计算两个角的和的正弦,而不是两个角分别的正弦。
所以这个公式非常有用。
接下来,我们来讨论两个角的差的正弦公式。
设有两个角A和B,那么它们的差角记为(A-B)。
根据三角函数的定义,我们可以得到如下的两角差的正弦公式:sin(A-B) = sinA*cosB - cosA*sinB这个公式与两角和的正弦公式类似,也非常有用。
二、两角和与差的余弦公式类似于正弦公式,我们也可以推导出两角和与差的余弦公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道余弦的定义为一个角的邻边与斜边之比,可以表示为cos(x)=adjacent/hypotenuse。
根据这个定义,我们可以得到如下的两角和的余弦公式:cos(A+B) = cosA*cosB - sinA*sinB同样地,我们也可以得到两角差的余弦公式:cos(A-B) = cosA*cosB + sinA*sinB这两个公式和两角和与差的正弦公式一样重要,经常被应用于实际问题中。
三、两角和与差的正切公式最后,我们来讨论两角和与差的正切公式。
设有两个角A和B,那么它们的和角记为(A+B)。
根据三角函数的定义,我们知道正切的定义为一个角的对边与邻边之比,可以表示为tan(x)=opposite/adjacent。
两角和与差的余弦正弦和正切

10
10
10
D 、- 3 2 10
8、在 ABC 中,已知 sin Asin B
的形状是( ) A、等腰三角形 B 、直角三角形
sin Acos B cos Asin B cos A cos B 2 ,则
C 、等腰直角三角形 D 、等腰或直角三角形
ABC
9、计算: sin(54 x)cos(24 x) cos(54 x)sin(24 x) =
( 1) sin(
) sin cos cos sin
( 2) sin(
) sin cos cos sin
( 3) cos(
) cos cos cos sin
( 4) cos(
) cos cos cos sin
( 5) tan(
tan tan )
1 tan tan
( 6) tan(
tan tan )
1 tan tan
2
2
(2)若 为锐角,且 sin(
、- 2 2
D 、- 1 2
) 1 ,则 cos 等于( ) 63
2、 2 6 1 B 、 2 6 1 C 、 2 3 1
6
6
4
(7)下列等式成立的是(
)
D 、2 3 1 4
A、 sin( x) cos( x) B 、 sin(2x) sin x
cot( 3 2
) tan
-------------------------------------------------------------------------
【例题精讲 】
例 1、求 150 及 750 的 6 个三角比。
解:
--------------------------------------
0504两角和与差的余弦、正弦和正切(2)

5.4两角和与差的余弦、正弦和正切(2)教学目标:理解和掌握两角和与差的正弦和正切公式.能正确、熟练、灵活的运用公式进行三角变换,会应用于求值、化简、证明等有关问题.初步认识用“构造法”解决问题的思想.理解公式的来源,把握它们之间的内在关系和转化规律.体验“转化”的数学思想.重点难点:重点:两角和与差的余弦、正弦和正切公式.难点:两角和与差的余弦、正弦和正切公式.教学过程:1、 两角和与差的正弦公式下面我们来求两角和与差的正弦公式.sin(α+β)=cos[2π-(α+β)]=cos[(2π-α)-β]=cos(2π-α)cos β+sin(2π-α)sin β=sin αcos β+sin αcos β.即:sin(α+β)=sin αcos β+cos αsin β.它对于任意角α和β都成立.这个恒等式叫做两角和的正弦公式(sine formula of thesum between toe angles ).把上述公式中的β换成-β,得两角差的正弦公式:(sine formula of the difference between toe angles )sin(α-β)=sin αcos β-cos αsin β.例 1 求下列各三角比:(1)sin75°;(2)sin15°.例 2 求sin27°cos72°-cos63°sin18°的值.例 3 (课本P 55例6) 求5cos()cos()cos()cos()126123ππππαααα+⋅++−⋅−的值.例 4 (课本P 56例7)已知:cos α=53,α∈(0,2π),求sin(α-6π).例 5 (课本P56例8)求证:cos(α+β)cos(α-β)=cos 2α-sin 2β.练 1 (课本P 57练习5.4(2)/1、2、3、4、5)练 2 求证:sin(α+β)sin(α-β)=sin 2α-sin 2β.练 3 求证:2222sin()sin()1cot tan sin cos αβαβαβαα+−=−⋅⋅.例 6 (课本P 56例9)在△ABC 中,已知cos A =54,cos B =1312,求sin C 和cos C 的值.★在△ABC 中,有A +B +C =π,可有∠A 、∠B 、∠C 都大于0°小于180°,而且至多一个钝角(直角).★根据诱导公式又有:(1)sin C =sin[180°-(A +B )]=sin(A +B ),同样:cos C =-cos(A +B ),tan C =-tan(A +B );(2)sin 2C =sin[()22A B π+−]=cos(2A B +), 同样:cos2C =sin(2A B +),tan 2C =cot(2A B +). ☆上例改为(1)sin A =35,cos B =1312,求sin C 的值.(2)cos A =54,sin B =135,求sin C 的值.★注意两个解,以及两个解之后的检验.2、 两角和与差的正切公式应用两角和与差的正弦、余弦公式:sin(α+β)=sin αcos β+cos αsin β;cos(α+β)=cos α·cos β-sin α·sin β可以推得两角和与差的正切公式. 由sin()sin cos cos sin tan()cos()cos cos sin sin αβαβαβαβαβαβαβ+++==+−, 当cos α≠0,cos β≠0时,等式右边的分子分母都除以cos αcos β得两角和的正切公式tan tan tan()1tan tan αβαβαβ++=−⋅; 同理可得(或把上述公式中的β换成–β,的两角差的正切公式),tan tan tan()1tan tan αβαβαβ−−=+⋅. ★在两角和与差的正切公式中,α、β和α±β的值都不能取到2π+k π(k ∈Z ).例 7 (课本P 58例10) 已知tan α=31,tan β=-2,求下列三角比的值:(1)tan(α+β);(2)cot(α-β).例 8 (课本P 58例11) 运用两角和的正切公式,求1tan 751tan 75+−的值.例 9 (课本P 59例12)如图,等腰直角三角形ABC 中,∠C=90°,点D 、C 分别是BC 的三等分点, 求tan α、tan β、tan γ的值.练 4 (课本P 59练习5.4(3)/1、2、3、4)例 10 设tan α和tan β是一元二次方程3x 2+5x +1=0的两个根,求cot(α+β)的值.★要注意到两角和的正切公式与韦达定理的形似之处.练 5 已知tan θ和tan()4πθ−是方程x 2+px +q =0的两个根,求证:p -q +1=0.练 6 已知tan α,tan β是关于x 的一元二次方程x 2+px +2=0的两实根,求sin()cos()αβαβ+−值. ★体验推导两角和的正切的方法:分子分母都除以cos αcos β.3、 两角和与差的余弦、正弦和正切公式的混合应用,辅助角公式例 11 (1)已知cot α=2,tan(α-β)=25−,求tan(β-2α)的值; (2)已知sin(30°+α)=53,60°<α<150°,求tan(75°+α)的值.例 12 求值:练 7 在斜三角形△ABC 中,求证:tan A +tan B +tan C =tan A ·tan B ·tan C .练 8 若tan α=3x ,tan β=3x −,且α-β=6π,求x 的值.例 13 (课本P 60例13) 已知2sin 3α=,3cos 4β=−,且α∈(2π,π),β∈(2π,π). 求sin(α-β)和cos(α-β)的值,并判别α-β是第几象限的角.★(1)此题给我们提供了判断一个角在哪个象限的一个方法. ★(2)如果只求α-β所在的象限,还可以这样:∵β∈(2π,π),∴–β∈(-π,-2π),∴-2π<α-β<2π,又∵sin(α-β)=356+−<0,∴α-β∈(-2π,0).所以α-β为第四象限角.例 14 (课本P 60例14)把下列各式化为A sin(α+φ)(A>0)的形式:(1)2sin α+2cos α; (2)sin α-3cos α (3)a sin α+b cos α(a 、b 都不为0).★上述变形方法通常称之为:辅助角公式,常见的有:sin α±cos α=2sin(α±4π);3sin α±cos α=2sin(α±6π);sin α±3cos α=2sin(α±3π).。
两角和与差的正弦、余弦与正切公式

2
(sin
2
A.a>b>c
C.c>a>b
(2)已知
56°-cos 56°),c=
1-ta n 2 39°
,则 a,b,c 的大小关系是(
1+ta n 2 39°
B.b>a>c
D.a>c>b
π
cos(α-6 )+sin
4 3
α= 5 ,则
π
si(nα+6 )=
.
)
答案 (1)D
4
(2)
5
解析 (1)a=cos 50°cos 127°+cos 40°cos 37°
1
D.
2
.
答案 (1)B (2)D (3) 3
解析 (1)根据两角和的正弦公式展开得 sin
3
θ= sin
2
3
θ+ cos
2
θ=1,即
π
3sin(θ+ )=1,解得
6
π
θ+sin(θ+ )=sin
3
1
θ+ sin
2
π
3
sin(θ+ )= .故选
6
3
B.
(2)∵t=2sin 18°,
2cos2 27°-1
.
1+cos
5.积化和差公式
sin αcos
1
β=
2
sin( + ) + sin(-) ,
cos αsin
1
β=2
sin( + )-sin(-) ,
cos αcos
1
β=2
5.4(4)两角和与差的余弦、正弦和正切

cos( ) cos cos sin sin
tan( ) ?
能否用 tan , tan 表示 tan( )?
一、两角和与差的正切
sin cos cos sin sin( ) tan( ) cos( ) cos cos sin sin
1 1 证: tan , tan ,且 , (0, ) 2 2 3 tan tan tan( ) 1 1 tan tan , (0, ) (0, ) 2 在区间 (0, )内,正切值为1的角只有一个, 证毕 即 tan 1 ,因此 4 4
tan17 tan 43 (1) tan 75 (2) 1 tan17 tan 43 解: (1) tan 75 tan(45 30 ) 3 1 tan 45 tan 30 3 2 3 1 tan 45 tan 30 3 1 3 (2)原式= tan(17 43 ) tan 60 3
4
tan 5 cot 50 1 tan 75 (3) (1) tan15 (2) 1 tan 5 cot 50 1 tan 75 2.已知 tan( ) 2, tan 3 ,求 tan
3.在 ABC 中,若 tan A, tan B 是方程
课堂练习: 1. 求下列各式的精确值:
解毕
例2.已知 tan(
3 tan 3 2 解: tan( ) 6 3 1 tan 3 解得 tan 8 5 3
解法二:tan tan[(
