省锦州市实验学校2015届九年级数学下学期质量检测试题(二)(扫描版) 北师大版
辽宁省锦州市九年级下学期数学中考二模试卷

辽宁省锦州市九年级下学期数学中考二模试卷姓名:________ 班级:________ 成绩:________一、选择题(本大题共10小题,每小题3分,共30分) (共10题;共30分)1. (3分)下列运算正确的是()A .B .C .D .2. (3分)(2017·苏州模拟) 有一种细胞直径约为0.000 058cm.用科学记数法表示这个数为()A . 5.8×10﹣6B . 5.8×10﹣5C . 0.58×10﹣5D . 58×10﹣63. (3分)(2019·广西模拟) 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是()A .B .C .D .4. (3分) (2018七下·于田期中) 下列条件中不能判定的是()A .B .C .D .5. (3分)如果点M(3a﹣9,1+a)是第二象限的点,则a的取值范围在数轴上表示正确的是()A .B .C .D .6. (3分)(2018·苏州) 如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是()A .B .C .D .7. (3分)(2019·河池模拟) 如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是()A . 25°B . 30°C . 40°D . 50°8. (3分)如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是()A . 3B . 5C .D .9. (3分)在半径为18的圆中,120°的圆心角所对的弧长是()A . 12πB . 10πC . 6πD . 3π10. (3分) (2016九上·徐闻期中) 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使点A′恰好落在AB上,则旋转角度为()A . 30°B . 45°C . 60°D . 90°二、填空题(本大题共8小题,每小题3分,共24分) (共8题;共24分)11. (3分) (2019九下·温州竞赛) 若代数式在实数范围内有意义,则x的取值范围是________。
辽宁省锦州市实验学校九年级数学下学期质量检测试题(

辽宁省锦州市实验学校2015届九年级数学下学期质量检测试题(二)第18题2014~2015学年度第二学期九年级质量检测(二)数学试题参考答案及评分标准(注:若有其他正确答案请参照此标准赋分)一、选择题(本大题共8个小题,每小题3分,共24分)二、填空题(本大题共8个小题,每小题3分,共24分)9. a(a+2)(a-2) 10. x=1 11. 6.8 12. 43 13.5或6或7 14. 22.5° 15. 154 16. 1155三、解答题(本大题共2个小题,每小题8分,共16分)17. 解:原式=223121)2+()22--+⨯( ·············· 4分=912124-++- ················· 6分=14- ························ 8分18. 解:(1)如图所示:111C B A ∆作图正确 ········· 2分221A B C ∆作图正确 ········· 4分(2)由勾股定理,得A 1C 1=23110+=,∴点A 1所经过的路径长为:9010180π⨯=102π. ·········· 8分四、解答题(本大题共2个小题,每小题10分,共20分)19.解:(1)120; ·························· 2分(2)42; ······························ 4分(3)126; ····························· 6分(4)每天体育锻炼时间不少于1小时的学生人数占被调查人数的百分比为:1-10%-25%=65%. 所以1200×65%=780(人).答:估计该校1200名学生中每天体育锻炼时间不少于1小时的学生为780人.·································· 10分20.(1)用树状图表示摸牌所有可能出现的结果如下:题号 1 2 3 4 5 6 7 8 答案 B C B A D C D A A B C DB B BC C CD D D A A A·································· 6分列表法表示摸牌所有可能出现的结果如下:································· 6分(2)由(1)中树状图或列表法可知,摸出的两张牌共有12种可能结果,且每种结果出现的可能性相同,其中两张牌为相同颜色的结果有4种,则P (摸出的两张牌为相同颜色)=412=13. ············ 10分 五、解答题(本大题共2个小题,每小题10分,共20分)21.解:设每辆汽车的定价应为x 元, ················· 1分(x -15)[8+2(25-x )]=90 ················ 4分整理方程,得x 2-44x+480=0解得x 1=20, x 2=24. ····················· 8分当x=20时,4S 每周进货汽车为8+2×5=18(辆),当x=24时,4S 每周进货汽车为8+2×1=10(辆),为使成本尽可能的低,则x=24.答:每辆汽车的定价应为24元. ················· 10分22.(1)证明:∵∠BAC=12∠BOC, ∠ABC=12∠AOC ,∠BOC=2∠AOC ∴∠BAC =∠AOC=2∠ABC. ··············· 3分 (2)解:①∵∠BAC=12∠BOC ,∠BAC =40°, ∴∠BOC =2∠BAC =80°.由(1)知,∠BAC=2∠ABC ,∴∠ABC=20°.∴∠ACD=∠BAC+∠ABC=60°.∵四边形AFBC 是⊙O 的内接四边形,∴∠F=∠ACD=60°.∵OB =OC ,∴∠OBC =∠OCB =12(180°-80°)=50°. ∵DF ∥OC ,∴∠D =∠OCB =50°.∵∠DBF=180°-∠F -∠D ,∴∠DBF=180°-60°-50=70°. . ·············· 7分②由①∠ABC=20°,∠D =50°,∴∠BAF=∠ABD+∠D =20°+50°=70°.∵∠DBF==70°,∴∠BAF =∠DBF .∵∠F=∠F ,∴△ABF ∽△BDF .A B C D A AB AC ADB BA BC BDC CA CB CDD DA DB DC图2第23题∴AB AFBD BF=. ∵AB=3.2, BD=4, ∴AB AF BD BF ==3.24=45(或0.8). ·············· 10分六、解答题(本大题共2个小题,每小题10分,共20分)23.解:(1)如图1,过点B 作BF ∥AD ,交DC 于点F ,. ····· 1分 又∵AB ∥DF , ∴四边形ABFD 为平行四边形. ∴AB=DF=2米,AD ∥BF.∴∠BFE =∠D =30°,EF =DE -DF =4. 在Rt △BCF 中,设BC =x 米, 则BF =2x ,CF =3x ,在Rt △BCE 中,∠BEC =60°, CE =tan 60BC︒=33x . ∴EF =CF -CE =3x -33x =2343x =. 解得:x =23.∴AD =BF =2x =43(米).答:AD 的长为43米. ···················· 5分(2)∵DH ∥PG ,HG ∥PD ,∴四边形DHGP 是平行四边形. ∴HG=DP.由题意知,∠BPE =45°,在Rt △BCP 中,BC =CP =23, 由(1)知EC=2. ∴PE =PC ―EC =23-2. ∵HG =DP =DE ﹣PE ,∴HG =6-(23-2)=(8-23)米.答:遮阳篷的宽为(8-23)米. ················ 10分 24.解:(1)设每台A 型洗衣机的销售利润为a 元,每台B 型洗衣机的销售利润b 元,由题意,得15a 10b 6000,10a 15b=6500.+=⎧⎨+⎩ 解得a=200,b=300.⎧⎨⎩答:每台A 型洗衣机的销售利润为200元,每台B 型洗衣机的销售利润为300元.································ 3分 (2)①根据题意得y =200x +300(160-x),即y =-100x +48000. ······················ 5分 ②根据题意得160-x ≤2x ,解得x ≥1533. ············· 7分 ∵y =-100x+48000,k=-100<0,∴y 随x 值的增大而减小. ∵x 为正整数,∴当x=54最小时,y 取最大值,此时160-x=106.答:商店购进A 型洗衣机54台,B 型洗衣机106台时,才能使销售总利润最大.图1yN 第25题································ 10分 七、解答题(本题共12分)25.(1)BC= PE+PF . ······················ 1分 证明:如图1,过点P 作PH ⊥BC 于点H , ·············· 2分∴∠P HB =90°.∵PE⊥AD,∴∠P EB =90°. ∵∠ABC =90°,∴四边形BEPH 为矩形. ····················· 5分∴PE=BH ,AB ∥PH.∴∠A=∠C PH.∵A D=CD , ∴∠A=∠DCA. ∴∠CP H =∠DCA. ························ 8分 ∵P F ⊥CD ,∴∠PH C=∠PFC=90°. ∵PC=PC,∴△P C H≌△CPF. ∴CH=PF. ∵ BC=BH+CH , ∴BC=PE+PF . ························· 10分 (2)AB=PE -PF 的结论. ······················ 11分补全图形. ··························· 12分八、解答题(本题共14分)26.解:(1)设所求的二次函数的表达式为y=ax 2+bx+c ,∵二次函数的图象与y 轴交于点C(0,2),∴c=2. ∵CB ∥x 轴,∴点B (4,2). ∵B (4,2),E(6,0),则根据题意,得0=3662,2164 2.a b a b ++⎧⎨=++⎩解得1,62.3a b ⎧=-⎪⎪⎨⎪=⎪⎩则所求的表达式为212263y x x =-++.································ 3分 将二次函数表达式配方: 212263y x x =-++=218(2)63x --+, 则抛物线对称轴为x=2. ····················· 5分(2)如图1,过M 作MN ⊥OC 于点N ,设PC 与AB 交于点G ,由轴对性可得BM=BG.. ∵OA=BC=4,AB=OC=2, ∴AP=m -4.图1 E PF D C B 图2 B C F PE易得△A PG ∽△BCG. ∴AP AGBC BG=, 即424m BG BG --=.∴BM=BG=8m. 则点M 的坐标为(4,2+8m).S △PCM =S 梯形OPMN -S △OPC -S △CMN =12(4+m)(2+8m)-12×2m-12×8m ×4=8. ∴△PCM 的面积与m 无关,即当点P 在线段AE 上运动时,△PCM 的面积始终为8.································ 9分 (3)由(2)知,当点P 与点重合时, ∴BM=43, 点M 的坐标为(4,103). ∵BQ∥AE,易得△MBQ∽△MAE . ∴MB BQ MA AE =,即431023BQ=. ∴BQ=45.∴CQ=BC+BQ=4+45=245. ················· 10分①当0≤t <245时,如图2,设C 1O 1与CP 交于点F ,C 1P 1与ME 交于点H ,∵CC 1=t ,∴C 1Q=245﹣t ,EP 1=t.∵OP ∥BC ,∴易得△C 1QH ∽△P 1EH. ∵相似三角形对应高的比等于相似比, 设△P 1EH 边EP 1上的高为h ,则△C 1QH 边C 1Q 上的高为2﹣h ,∴2425h th t=--.解得h=512t.∴S △P1EH =12EP 1•h=12t•512t.=524t 2. ∵∠ECB=∠CEO, ∴tan ∠BCM=tan ∠CEO=21=63.在Rt△CC 1F 中,CF= CC 1tan∠EAB=13t. ∴S △CC1F =12 CC 1•CF=t•13t=16t 2.∴S=S □C 1C EP1-S △P1EH -S △CC1F =2t -524t 2﹣16t 2=2328t t -+,即S=2328t t -+. ························ 12分图2, ②当245≤t<6时, 如图3,设C 1O 1与ME 交于点K ,与CE 交于点R , ∵CC 1=t ,∴C 1Q=t -245,O 1E=6-t, 易得△C 1QK ∽△EO 1K..∴1111C Q C K O E O K =,即1124256t O K t O K --=-.解得O 1K=10-53t. ∴S △O1EK =12EO 1•EK=12(6-t) (10-53t)= 56t 2-10t+30. 在Rt△RO 1E 中,RO 1=EO 1tan∠CEO=13(6-t).∴S △O1ER =12EO 1•RE 1 =12(6-t) ×13(6-t)=16t 2-2t+6.∴S= S △O1EK -S △O1ER =56t 2-10 t+30-(16t 2-2t+6)=23t 2-8t+24.综上所述,所求的S 与t 的函数关系式为S=223242(0),85224824(6).35t t t t t t ⎧-+≤<⎪⎪⎨⎪-+≤<⎪⎩(说明:不写最后结论不扣分)······························· 14分图3。
辽宁省锦州市实验学校2015届九年级下学期质量检测(二)英语试题(扫描版)

2014—2015学年度第二学期九年级质量检测(二)英语参考答案及评分标准Ⅰ. 选择题(共15分, 每小题1分)1~5 CBABC 6~10 ABBDD 11~15 CADCDⅡ. 补全对话(共5分, 每小题1分)16~20 EDBACⅢ. 完形填空(共10分, 每小题1分)21~25 CABCA 26~30 DBDCBⅣ. 阅读理解(共20分, 每小题1分)31~35 CCAAD 36~40 CBDAA 41~45 DBABC 46~50 CAEBD Ⅴ. 口语交际(共5分, 每小题1分)51. May/Could/ Can I speak to Jack52. How is it going/How is everything going/How are you53. What’s the matter?/ What’s wrong?/What’s your problem?54. Don’t worry.55. When and where shall we meet(注:本题有一定的开放度,除了所给答案外,评卷教师视具体情况酌情赋分!)Ⅵ.短文填空(共10分, 每小题1分)56. was built 57. window 58. Suddenly 59. scared 60. to61. thought 62. catch 63. herself 64. until 65. will eatⅦ.任务型阅读(共30分, 每小题2分)66. over 67. more international help 68. safe 69. test the vaccine 70. France71. No, she isn’t./No.72. More than 73 million73. In 2013. /Three years later.74. Those in need. / Those people in need75. Because she wants her child to grow up in a better environment76. into, because77. The left hemisphere78. both, and79. quicker , stronger80. lefties/ left-handedness(注: 66~80小题中,有些题答案比较灵活,除了所给答案外,评卷教师视具体情况酌情赋分)Ⅷ.书面表达(共25分) 评分标准参考考试说明( A ) 范文样例Dear Baby,I’d like to invite you to spend your summer vacation in Jinzhou. Jinzhou is a good place for fun. Y ou are welcome to visit interesting places such as the EXPO Park, the Mount Bijia. W e can also go fishing in the Linghe River. That’s very fantastic. In the evening we can have some barbecue at the night mark. I am sure you will enjoy yourself here. Please remember to take your cool clothes and sunglasses, because it is very hot in the day. I’m looking forward to your reply.Y ours,Katie ( B ) 范文样例Ladies and gentlemen, my dear teachers and classmates,How fast the time went by! I remember meeting all of you 3 years ago at this school. I was full of energy and thirsty for knowledge at that time. Overcoming lots of difficulties, I have grown up and been talented. Surely, first I am very thankful to all my teachers. Without their help, I can’t make so big progress. And second, to my parents, they supported me silently in my life. T hey’ve done so much for me.I will begin a new life soon. I’m going to senior high school and work hard. Maybe there will be much more difficult tasks ahead of me, but I will never give up.For you new students, I’d like to say junior high school is just the beginning of the new journey. Y ou’ll make mistakes along the way, but the key is to learn from your mistakes and believe yourselves. Please be responsible for your decisions and actions. There will also be many exciting things waiting for you.Good luck and hope to see you again soon! Thank you!。
2015初三二模数学试题参考答案

初三二模数学试题参考答案一.选择题:1-5:BDCAC ,6-10:BDCDA二.填空题:11. 1,-1 ;12. 12 ;13.A. 120°;B. 2.64;14. 3324-.17.解:原式=÷=•=﹣, ……2分解方程x 2﹣4x +3=0得,(x ﹣1)(x ﹣3)=0,x 1=1,x 2=3.……3分 当x =1时,原式无意义; ……4分当x =3时,原式=﹣=﹣51.……5分18.(1)证明:∵DF ∥BE , ∴∠FDO=∠EBO ,∠DFO=∠BEO , ∵O 为AC 的中点, ∴OA=OC , 又∵AE=CF ,∴OA ﹣AE=OC ﹣CF ,即OE=OF , 在△BOE 和△DOF 中,,∴△BOE ≌△DOF (AAS );……3分(2)若OD=AC ,则四边形ABCD 是矩形,理由如下: 证明:∵△BOE ≌△DOF ,∴OB=OD ,∵OD=AC∴OA=OB=OC=OD ,即BD=AC , ∴四边形ABCD 为矩形.……6分≈0.9,sin44°=,,的图象过 y=,的图象上,=,解得y=,+22.(1)2……3分(2)树状图(或列表法)略.共有16种等可能结果,其中两张卡片都是中心对称图形的有4种 P (两张都是中心对称图形)=164=41………8分23.(1)证明:连接OB∵OB =OA ,CE =CB ,∴∠A =∠OBA ,∠CEB =∠又∵CD ⊥OA ,∴∠A +∠AED =∠A +∠CEB =90° ∴∠OBA+∠ABC =90°,∴OB ⊥BC ∴BC 是⊙O 的切线 ………3分 (2)过点C 作CG ⊥BE 于点G , ∵CE =CB ,∴EG =12BE =5 又Rt △ADE ∽Rt △CGE ,∴sin ∠ECG =sin A = 5 13∴CE =EGsin ∠ECG=13,∴CG =CE 2-EG 2=12又CD =15,CE =13,∴DE =2 由Rt △ADE ∽Rt △CGE ,得 ADCG =DEGE∴AD =DE GE·CG =245∴⊙O 的半径为2AD =485……8分24.解:(1)∵y=2x+2, ∴当x=0时,y=2, ∴B(0,2).当y=0时,x=﹣1, ∴A(﹣1,0).∵抛物线y=﹣x 2+bx+c 过点B (0,2),D (3,﹣4), ∴解得:,∴y=﹣x 2+x+2; ……4分(2)E(49,21) ……6分(3)设直线BD 的解析式为y=kx+b ,由题意,得,解得:,∴直线BD 的解析式为:y=﹣2x+2; 设P (b ,﹣b 2+b+2),H (b ,﹣2b+2).如图3,∵四边形BOHP 是平行四边形, ∴BO=PH=2.∵PH=﹣b 2+b+2+2b ﹣2=﹣b 2+3b . ∴2=﹣b 2+3b ∴b 1=1,b 2=2.当b=1时,P (1,2), 当b=2时,P (2,0)∴P 点的坐标为(1,2)或(2,0).……10分 25.解:∵AB=10cm,AC=8cm ,BC=6cm ,∴由勾股定理逆定理得△ABC 为直角三角形,∠C 为直角. (1)BP=2t ,则AP=10﹣2t . ∵PQ∥BC,∴,即,解得t=,∴当t=s 时,PQ∥BC. ……3分(2)如答图1所示,过P 点作PD⊥AC 于点D . ∴PD∥BC,∴,即,解得PD=6﹣t .S=×AQ×PD=×2t×(6﹣t )=﹣t 2+6t=﹣(t ﹣)2+,∴当t=s 时,S 取得最大值,最大值为cm 2.……6分(3)假设存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分, 则有S △AQP =S △ABC ,而S △ABC =AC•BC=24,∴此时S △AQP =12.由(2)可知,S △AQP =﹣t 2+6t ,∴﹣t 2+6t=12,化简得:t 2﹣5t+10=0, ∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解,∴不存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分.……9分 (4)假设存在时刻t ,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t . 如答图2所示,过P 点作PD⊥AC 于点D ,则有PD∥BC, ∴,即,解得:PD=6﹣t ,AD=8﹣t ,∴QD=AD﹣AQ=8﹣t﹣2t=8﹣t.在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,即(8﹣t)2+(6﹣t)2=(2t)2,化简得:13t2﹣90t+125=0,解得:t1=5,t2=,∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=.由(2)可知,S△AQP=﹣t2+6t∴S菱形AQPQ′=2S△AQP=2×(﹣t2+6t)=2×[﹣×()2+6×]=cm2.所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为cm2.…12分。
2015年辽宁省锦州市中考数学二模试卷和解析答案

2015年辽宁省锦州市中考数学二模试卷一、选择题(共8小题,每小题3分,满分24分)1.(3分)下列二次根式为最简二次根式地是()A.B.C.D.2.(3分)下列四个分子结构模型地平面图中,是轴对称图形但不是中心对称图形地是()A.B.C.D.3.(3分)下列各式计算正确地是()A.2x2y+3xy=5x3y2B.(2x2y)3=8x6y3C.2x2y•3xy=6x2y D.2x2y÷3xy=xy4.(3分)一元二次方程﹣2x2+x﹣7=0地根地情况是()A.没有实数根B.有两个相等地实数根C.有两个不相等地实数根D.无法确定5.(3分)下列各组数作为三条线段地长,使它们能构成三角形地一组是()A.2,3,5 B.4,4,8 C.14,6,7 D.15,10,96.(3分)如图是某班45名同学爱心捐款额地频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多地一组是()A.5~10元B.10~15元C.15~20元D.20~25元7.(3分)如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上地一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=.其中正确地结论是()A.①②③B.①②C.②③D.①③8.(3分)如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上地一个动点(不与点A、B重合),过点D作CD地垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x地函数关系图象大致是()A.B.C.D.二、填空题(共8小题,每小题3分,满分24分)9.(3分)因式分解:a3﹣4a=.10.(3分)分式方程地解是.11.(3分)在某中学举行地演讲比赛中,七年级5名参赛选手地成绩及平均成绩如下表所示:那么根据表中提供地数据,计算这5名选手比赛成绩地方差是.12.(3分)如图,气象局预报某市6月10日地空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中地某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染地概率是.13.(3分)如图,这是由若干个相同地小立方体搭成地几何体俯视图和左视图,则小立方体地个数可能是.14.(3分)如图,正八边形ABCDEFGH内接于⊙O,则∠DAE地度数是.15.(3分)如图,在平面直角坐标系中,直线y=﹣4x+4与x轴,y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m地值为.16.(3分)如图,下列各方格中地三个数之间按照一定地规律排列,如果按照这个规律继续排列下去,那么图中n地值为.三、解答题(共2小题,每小题8分,满分16分)17.(8分)计算:(1﹣)0﹣|1﹣|+2cos45°﹣()﹣2.18.(8分)如图,方格纸中地每个小方格都是边长为1个单位长度地正方形,每个小正方形地顶点叫格点,△ABC地顶点均在格点上,请按要求完成下列步骤:(1)画出将△ABC向右平移3个单位后得到地△A1B1C1,再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到地△A2B1C2;(2)求线段B 1C1旋转到B1C2地过程中,点C1所经过地路径长.四、解答题(共2小题,每小题10分,满分20分)19.(10分)近年来,中学生地身体素质普遍下降,某校为了提高本校学生地身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”地文件精神,对部分学生地每天体育锻炼时间进行了调查统计,以下是本次调查结果地统计表和统计图.(1)本次被调查地学生数为人;(2)统计表中a地值为;(3)扇形统计图中C组所在扇形圆心角为度;(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时地学生人数.20.(10分)如图,有四张背面相同地纸牌A、B、C、D,正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色,小明将这4张纸牌洗匀后(正面朝下),随机摸出两张牌.(1)用树状图(或列表法)表示摸牌所有可能出现地结果(纸牌用A、B、C、D 表示);(2)求摸出地两张牌为相同颜色地概率.五、解答题(共2小题,每小题10分,满分20分)21.(10分)某汽车4S店销售某种型号地汽车,每辆进货价为15万元,该店经过一段时间地市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周地销售利润为90万元,并且使成本尽可能地低,则每辆汽车地定价应为多少万元?22.(10分)如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF ∥OC,交BC地延长线于点D,交⊙O于点F,连接BF.(1)求证:∠BAC=2∠ABC;(2)若∠BAC=40°,AB=3.2,BD=4.①求∠BAF地度数;②求地值.六、解答题(共2小题,每小题10分,满分20分)23.(10分)如图1,四边形ABCD是某市凌河休闲广场一个供市民休息和观赏地看台侧面示意图.已知:在四边形ABCD中,AB∥CD中,AB∥CD,AB=2米,BC⊥DC,∠ADC=30°.从底边DC上点E测得点B地仰角∠BEC=60°,且DE=6米.(1)求AD地长度;(2)如图2,为了避免白天市民在看台AB和AD地位置受到与水平面成45°角地光线照射,想修建一个遮阳篷,求这个遮阳篷地宽度HG是多少米?(计算结果都保留根号)24.(10分)某家电商店销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B型洗衣机地利润6500元.(1)问A型和B型洗衣机每台地销售利润各是多少元;(2)该商店计划一次购进两种型号地洗衣机共160台,其中B型洗衣机地进货量不超过A型洗衣机地2倍,设购进A型洗衣机为x台,这160台洗衣机地销售总利润为y元.①求y与x之间地函数表达式;②该商店购进A型、B型洗衣机各多少台,才能使销售利润最大?七、解答题(共1小题,满分12分)25.(12分)在△ABC中,∠ABC=90°,D是AB边上地一点,且AD=CD,P是直线AC上任意一点,过点P作PE⊥AD于点E,PF⊥CD于点F.(1)如图1,当点P在线段AC上,猜想:线段PE、PF与BC地数量关系,并证明你地猜想;(2)当点P在AC地延长线上时,其它条件不变,请你在图2中补全图形,并标记相应地字母,并根据补全地图形猜想PE、PF与BC又有怎样地数量关系?直接写出结论,不用证明.八、解答题(共1小题,满分14分)26.(14分)如图1,二次函数地图象与y轴交于点C(0,2),与x轴地正半轴交于点E(6,0),直线CB∥x轴,与抛物线交于点B,点B地横坐标为4,过点B作BA⊥x轴于点A,点P是线段上一点,把射线CP沿直线BC翻折,交射线AB于点M.(1)求二次函数地表达式及抛物线地对称轴;(2)设OP=m,求△PCM地面积,并观察计算结果,你发现什么规律?(3)如图2,当点P与点E重合时,直线CB与MP交于点Q,将△POC以每秒1个单位地速度沿x轴正方向平移,直到点O与点E(P)重合时停止,设运动地时间为t,平移后地△O1C1P1与△CEM地重叠部分地面积为S,求S与t之间地函数表达式.2015年辽宁省锦州市中考数学二模试卷参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.(3分)下列二次根式为最简二次根式地是()A.B.C.D.【分析】根据最简二次根式地两个条件是否同时满足,同时满足地就是最简二次根式,否则就不是进行判断即可.【解答】解:A、,被开方数含分母,不是最简二次根式;B、,是最简二次根式;C、,被开方数含字母,不是最简二次根式;D、=,被开方数含能开得尽方地因数,不是最简二次根式.故选:B.2.(3分)下列四个分子结构模型地平面图中,是轴对称图形但不是中心对称图形地是()A.B.C.D.【分析】根据轴对称图形与中心对称图形地概念结合各图形地特点求解.【解答】解:A、是轴对称图形,也是中心对称图形,故错误;B、是轴对称图形,也是中心对称图形,故错误;C、是轴对称图形,不是中心对称图形,故正确;D、是轴对称图形,也是中心对称图形,故错误;故选:C.3.(3分)下列各式计算正确地是()A.2x2y+3xy=5x3y2B.(2x2y)3=8x6y3C.2x2y•3xy=6x2y D.2x2y÷3xy=xy【分析】A:根据合并同类项地方法判断即可.B:根据积地乘方地运算方法判断即可.C:根据单项式乘以单项式地方法判断即可.D:根据整式地除法地运算方法判断即可.【解答】解:∵2x2y+3xy≠5x3y2,∴选项A不正确;∵(2x2y)3=8x6y3,∴选项B正确;∵2x2y•3xy=6x3y2,∴选项C不正确;∵2x2y÷3xy=x,∴选项D不正确.故选:B.4.(3分)一元二次方程﹣2x2+x﹣7=0地根地情况是()A.没有实数根B.有两个相等地实数根C.有两个不相等地实数根D.无法确定【分析】求出△地值即可判断.【解答】解:一元二次方程﹣2x2+x﹣7=0中,∵△=1﹣4×(﹣2)×(﹣7)<0,∴原方程无解.故选:A.5.(3分)下列各组数作为三条线段地长,使它们能构成三角形地一组是()A.2,3,5 B.4,4,8 C.14,6,7 D.15,10,9【分析】根据“三角形任意两边之和大于第三边,任意两边之差小于第三边”对各选项进行进行逐一分析即可.【解答】解:根据三角形地三边关系,得A、3+2=5,不能组成三角形,不符合题意;B、4+4=8,不能够组成三角形,不符合题意;C、6+7<13,不能够组成三角形,不符合题意;D、10+9>15,能够组成三角形,符合题意.故选:D.6.(3分)如图是某班45名同学爱心捐款额地频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多地一组是()A.5~10元B.10~15元C.15~20元D.20~25元【分析】根据图形所给出地数据直接找出捐款人数最多地一组即可.【解答】解:根据图形所给出地数据可得:捐款额为15~20元地有20人,人数最多,则捐款人数最多地一组是15﹣20元.故选:C.7.(3分)如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上地一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=.其中正确地结论是()A.①②③B.①②C.②③D.①③【分析】先判断出四边形CFHE是平行四边形,再根据翻折地性质可得CF=FH,然后根据邻边相等地平行四边形是菱形证明,判断出①正确;根据菱形地对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;点H与点A重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF地值,判断出③正确.【解答】解:∵FH与CG,EH与CF都是矩形ABCD地对边AD、BC地一部分,∴FH∥CG,EH∥CF,∴四边形CFHE是平行四边形,由翻折地性质得,CF=FH,∴四边形CFHE是菱形,故①正确;∴∠BCH=∠ECH,∴只有∠DCE=30°时EC平分∠DCH,故②错误;点H与点A重合时,设BF=x,则AF=FC=8﹣x,在Rt△ABF中,AB2+BF2=AF2,即22+x2=(4﹣x)2,解得x=,故③正确.故选:D.8.(3分)如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上地一个动点(不与点A、B重合),过点D作CD地垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x地函数关系图象大致是()A.B.C.D.【分析】本题需先根据题意,求出BC,AC地长,再分别计算出当x=0和x=2时,y地值,即可求得y与x地函数图象.【解答】解:解法一、∵∠ACB=90°,∠BAC=30°,AB=2,∴BC=1,AC=,∴当x=0时,y地值是,当x=1时,y地值是,∵当x=2时CD地垂线与CA平行,虽然x不能取到2,但y应该是无穷大,∴y与x地函数关系图象大致是B,过点D作点DG⊥AC于点G,过点D作点DF⊥BC于点F,∴CF=DG=,DF=CG=(2﹣x),∴EG=y﹣CG,分别在直角三角形CDF、直角三角形DGE、直角三角形CDE中利用勾股定理,DF2+CF2+DG2+GE2=CE2,y=.解法二、∵∠ACB=90°,∠BAC=30°,AB=2,∴BC=1,AC=.∴当x=0时,y=;当x=1时,y=∵当x=2时,CD地垂线与CA平行,虽然x不能取到2,但y应该是无穷大,∴y与x地函数关系图象大致是B选项.故选:B.二、填空题(共8小题,每小题3分,满分24分)9.(3分)因式分解:a3﹣4a=a(a+2)(a﹣2).【分析】首先提取公因式a,进而利用平方差公式分解因式得出即可.【解答】解:a3﹣4a=a(a2﹣4)=a(a+2)(a﹣2).故答案为:a(a+2)(a﹣2).10.(3分)分式方程地解是1.【分析】公分母为(x﹣2),两边同乘以公分母,转化为整式方程求解,结果要检验.【解答】解:去分母,得2x﹣5=﹣3,移项,得2x=﹣3+5,合并,得2x=2,化系数为1,得x=1,检验:当x=1时,x﹣2≠0,所以,原方程地解为x=1.11.(3分)在某中学举行地演讲比赛中,七年级5名参赛选手地成绩及平均成绩如下表所示:那么根据表中提供地数据,计算这5名选手比赛成绩地方差是 6.8.【分析】根据七年级5名参赛选手地成绩及平均成绩表,应用方差地计算公式,求出这5名选手比赛成绩地方差是多少即可.【解答】解:根据成绩统计表,可得5名选手地平均成绩为91分,∴这5名选手比赛成绩地方差是:[(90﹣91)2+(95﹣91)2+(93﹣91)2+(89﹣91)2+(88﹣91)2]=[1+16+4+4+9]==6.8.故答案为:6.8.12.(3分)如图,气象局预报某市6月10日地空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中地某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染地概率是.【分析】首先分别判断出6月1日至6月8日这8天中,有几天使得此人在该市停留期间遇到空气为重度污染,然后根据概率公式,求出此人在该市停留期间遇到空气为重度污染地概率是多少即可.【解答】解:此人6月3日﹣6月8日地这6天中地任意一天到达该市,在该市停留期间都能遇到空气为重度污染,所以此人在该市停留期间遇到空气为重度污染地概率是:6÷8=.故答案为:.13.(3分)如图,这是由若干个相同地小立方体搭成地几何体俯视图和左视图,则小立方体地个数可能是5个或6个或7个.【分析】易得这个几何体共有2层,由俯视图可得第一层立方体地个数,由左视图可得第二层最多和最少小立方体地个数,相加即可;【解答】解:由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3个小立方体和最少有1个小立方体,那么小立方体地个数可能是5个或6个或7个.故答案为:5个或6个或7个.14.(3分)如图,正八边形ABCDEFGH内接于⊙O,则∠DAE地度数是22.5.【分析】连接OD,根据正多边形和圆地知识求出正八边形地中心角地度数,根据圆周角定理求出∠DAE地度数.【解答】解:连接OD,∠DOE=360°÷8=45°,∠DAE=∠DOE=22.5°,故答案为:22.5°.15.(3分)如图,在平面直角坐标系中,直线y=﹣4x+4与x轴,y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m地值为.【分析】作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F,易证△OAB ≌△FDA≌△BEC,求得A、B地坐标,根据全等三角形地性质可以求得C、D地坐标,从而利用待定系数法求得反比例函数地解析式,进而求得N地坐标,则a 地值即可求解.【解答】解:作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.在y=﹣4x+4中,令x=0,解得:y=4,即B地坐标是(0,4).令y=0,解得:x=1,即A地坐标是(1,0).则OB=4,OA=1.∵∠BAD=90°,∴∠BAO+∠DAF=90°,又∵直角△ABO中,∠BAO+∠OBA=90°,∴∠DAF=∠OBA,在△OAB和△FDA中,,∴△OAB≌△FDA(AAS),同理,△OAB≌△FDA≌△BEC,∴AF=OB=EC=4,DF=OA=BE=1,故D地坐标是(5,1),C地坐标是(4,5).代入y=得:k=5,则函数地解析式是:y=.则C地横坐标是4,把x=4代入y=得:y=,则N点坐标为:(4,),故CN=5﹣=,∴将正方形沿y轴向下方平移个单位长度后,点C恰好落在该双曲线上.故答案为:.16.(3分)如图,下列各方格中地三个数之间按照一定地规律排列,如果按照这个规律继续排列下去,那么图中n地值为1155.【分析】首先根据上面地数值变化规律求出m地值为34,然后根据每隔方格中数地规律求n即可,规律为:每个方格中地上面地数乘以下面左侧地数再加上上面地数得下面右侧地数.【解答】解:从方格上方地数地数1、2、3、4、5、6、33…可以推出m=34,第一个方格中:3=1×2+1第二个方格中:15=3×4+3第三个方格中:35=5×6+5∴第n个方格中:n=33×34+33=1155.三、解答题(共2小题,每小题8分,满分16分)17.(8分)计算:(1﹣)0﹣|1﹣|+2cos45°﹣()﹣2.【分析】原式第一项利用零指数幂法则计算,第二项利用绝对值地代数意义化简,第三项利用特殊角地三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果.【解答】解:原式=1﹣+1+﹣=﹣.18.(8分)如图,方格纸中地每个小方格都是边长为1个单位长度地正方形,每个小正方形地顶点叫格点,△ABC地顶点均在格点上,请按要求完成下列步骤:(1)画出将△ABC向右平移3个单位后得到地△A1B1C1,再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到地△A2B1C2;(2)求线段B1C1旋转到B1C2地过程中,点C1所经过地路径长.【分析】(1)根据平移地性质得出对应点位置以及利用旋转地性质得出对应点位置画出图形即可;(2)根据弧长计算公式求出即可.【解答】解:(1)如图所示:(2)点C1所经过地路径长为:=2π.四、解答题(共2小题,每小题10分,满分20分)19.(10分)近年来,中学生地身体素质普遍下降,某校为了提高本校学生地身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”地文件精神,对部分学生地每天体育锻炼时间进行了调查统计,以下是本次调查结果地统计表和统计图.(1)本次被调查地学生数为120人;(2)统计表中a地值为42;(3)扇形统计图中C组所在扇形圆心角为126度;(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时地学生人数.【分析】(1)根据A组有12人,所占地百分比是10%,据此即可求得调查地总人数;(2)用总人数减去其它组地人数即可求得a地值;(3)利用360°乘以对应地比例即可求解;(4)利用1200乘以对应地比例即可求解.【解答】解:(1)本次被调查地学生数是:12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42(人);(3)扇形统计图中C组所在圆心角地度数是:360×=126°;(4)该校1200名学生每天体育锻炼时间不少于1小时地学生人数是:1200×=780(人).20.(10分)如图,有四张背面相同地纸牌A、B、C、D,正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色,小明将这4张纸牌洗匀后(正面朝下),随机摸出两张牌.(1)用树状图(或列表法)表示摸牌所有可能出现地结果(纸牌用A、B、C、D 表示);(2)求摸出地两张牌为相同颜色地概率.【分析】(1)利用树状图展示所有可能出现地结果;(2)由(1)中树状图可得共有12种等可能地结果数,再找出两张牌为相同颜色地结果数,然后根据概率公式求解.【解答】解:(1)画树状图:(2)由(1)中树状图可得,摸出地牌共有12种等可能地结果数,其中两张牌为相同颜色地结果数为4,所以两张牌为相同颜色地概率==.五、解答题(共2小题,每小题10分,满分20分)21.(10分)某汽车4S店销售某种型号地汽车,每辆进货价为15万元,该店经过一段时间地市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周地销售利润为90万元,并且使成本尽可能地低,则每辆汽车地定价应为多少万元?【分析】销售利润=一辆汽车地利润×销售汽车数量,一辆汽车地利润=售价﹣进价,降低售价地同时,销售量就会提高,“一减一加”,根据每辆地盈利×销售地件数=90万元,即可列方程求解.【解答】解:设每辆汽车地降价为x万元,根据题意得:(25﹣x﹣15)(8+)=90,解得x 1=1,x2=5,当x=1时,总成本为15×(8+2×1)=150(万元);当x=5时,总成本为15×(8+2×5)=270(万元),为使成本尽可能地低,则x=1,即25﹣x=25﹣1=24(万元),答:每辆汽车地定价应为24万元.22.(10分)如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF ∥OC,交BC地延长线于点D,交⊙O于点F,连接BF.(1)求证:∠BAC=2∠ABC;(2)若∠BAC=40°,AB=3.2,BD=4.①求∠BAF地度数;②求地值.【分析】(1)根据圆周角定理和等量代换即可得到结论.(2)①根据∠BAC=∠BOC,∠BAC=40°,求得∠BOC=2∠BAC=80°,由(1)知,∠BAC=2∠ABC,于是得到∠ABC=20°,∠ACD=∠BAC+∠ABC=60°,由四边形AFBC是⊙O地内接四边形,得到∠F=∠ACD=60°,由于OB=OC,求得∠OBC=∠OCB=(180°﹣80°)=50°,根据平行线地性质得到∠D=∠OCB=50°,由于∠DBF=180°﹣∠F﹣∠D,于是求得∠DBF=180°﹣60°﹣50°=70°;②由①得∠ABC=20°,∠D=50°,证得∠BAF=∠DBF,由于∠F=∠F,推出△ABF∽△BDF,即可得到结论.【解答】(1)证明:连接AC,∵∠BAC=∠BOC,∠ABC=∠AOC,∠BOC=2∠AOC,∴∠BAC=∠AOC=2∠ABC;(2)解:①∵∠BAC=∠BOC,∠BAC=40°,∴∠BOC=2∠BAC=80°,由(1)知,∠BAC=2∠ABC,∴∠ABC=20°,∴∠ACD=∠BAC+∠ABC=60°,∵四边形AFBC是⊙O地内接四边形,∴∠F=∠ACD=60°,∵OB=OC,∴∠OBC=∠OCB=(180°﹣80°)=50°,∵DF∥OC,∴∠D=∠OCB=50°,∵∠DBF=180°﹣∠F﹣∠D,∴∠DBF=180°﹣60°﹣50°=70°,②由①得∠ABC=20°,∠D=50°,∴∠BAF=∠ABD+∠D=20°+50°=70°,∵∠DBF=70°,∴∠BAF=∠DBF,∵∠F=∠F,∴△ABF∽△BDF,∴==.六、解答题(共2小题,每小题10分,满分20分)23.(10分)如图1,四边形ABCD是某市凌河休闲广场一个供市民休息和观赏地看台侧面示意图.已知:在四边形ABCD中,AB∥CD中,AB∥CD,AB=2米,BC⊥DC,∠ADC=30°.从底边DC上点E测得点B地仰角∠BEC=60°,且DE=6米.(1)求AD地长度;(2)如图2,为了避免白天市民在看台AB和AD地位置受到与水平面成45°角地光线照射,想修建一个遮阳篷,求这个遮阳篷地宽度HG是多少米?(计算结果都保留根号)【分析】(1)作BF⊥AD角CD于F,证明四边形ABFD是平行四边形,得到DF=2,BC=x,在Rt△BCE中,根据正切求出CE,列方程求出x,得到答案;(2)证明四边形DHGP是平行四边形,得到HG=DP,求出DP即可.【解答】解:(1)如图1,作BF⊥AD角CD于F,又∵AB∥CD,∴四边形ABFD是平行四边形,∴AB=DF=2,AD∥BF,∴∠BFE=∠D=30°,EF=DE﹣DF=4,在Rt△BCF中,设BC=x米,则BF=2x,CF=x,在Rt△BCE中,∠BEC=60°,∴CE==x,∴EF=CF﹣CE=x﹣x=4,解得:x=2,∴AD=BF=2x=4;(2)∵DH∥PG,HG∥PD,∴四边形DHGP是平行四边形,∴HG=DP,由题意得,∠BPE=45°,在Rt△BCE中,BC=CP=2,由(1)知,EC=2,∴PE=PC﹣EC=2﹣2,∵HG=DP=DE﹣PE,∴HG=6﹣(2﹣2)=8﹣2.24.(10分)某家电商店销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B型洗衣机地利润6500元.(1)问A型和B型洗衣机每台地销售利润各是多少元;(2)该商店计划一次购进两种型号地洗衣机共160台,其中B型洗衣机地进货量不超过A型洗衣机地2倍,设购进A型洗衣机为x台,这160台洗衣机地销售总利润为y元.①求y与x之间地函数表达式;②该商店购进A型、B型洗衣机各多少台,才能使销售利润最大?【分析】(1)设A型和B型洗衣机每台地销售利润各是a元和b元,根据销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B 型洗衣机地利润6500元,即可列方程组求得a和b地值;(2)①根据两种型号地利润地和就是总利润即可列出函数解析式;②根据一次函数地性质,即可求解.【解答】解:(1)设A型和B型洗衣机每台地销售利润各是a元和b元.则,解得:.答:A型和B型洗衣机每台地销售利润各是200元和300元;(2)①根据题意得y=200x+300(160﹣x),即y=﹣100x+48000;②根据题意得:160﹣x≤2x,解得:x≥53,∵y=﹣100x+48000中,k=﹣100<0,∴y随x地增大而减小.∵x为正整数,∴当x=54时,y取得最大值,此时160﹣x=106.答:该商店购进A型、B型洗衣机各54台和106台时,才能使销售利润最大.七、解答题(共1小题,满分12分)25.(12分)在△ABC中,∠ABC=90°,D是AB边上地一点,且AD=CD,P是直线AC上任意一点,过点P作PE⊥AD于点E,PF⊥CD于点F.(1)如图1,当点P在线段AC上,猜想:线段PE、PF与BC地数量关系,并证明你地猜想;(2)当点P在AC地延长线上时,其它条件不变,请你在图2中补全图形,并标记相应地字母,并根据补全地图形猜想PE、PF与BC又有怎样地数量关系?直接写出结论,不用证明.【分析】(1)BC=PE+PF.如图1,过点P作PH⊥BC于点H,所以∠PHB=90°,由PE⊥AD,得到∠PEB=90°,因为∠ABC=90°,所以四边形BEPH为矩形,得到PE=BH,AB∥PH,再证明△PCH≌△CPF,得到CH=PF,由BC=BH+CH,所以BC=PE+PF.(2)根据题意补全图形,猜想并得到结论:AB=PE﹣PF.【解答】解:(1)BC=PE+PF.证明:如图1,过点P作PH⊥BC于点H,∴∠PHB=90°,∵PE⊥AD,∴∠PEB=90°,∵∠ABC=90°,∴四边形BEPH为矩形,∴PE=BH,AB∥PH,∴∠A=∠CPH,∵AD=CD,∴∠A=∠DCA,∴∠CPH=∠DCA,∵PF⊥CD,∴∠PHC=∠PFC=90°,在△PCH和△CPF中,,∴△PCH≌△CPF,∴CH=PF,∵BC=BH+CH,∴BC=PE+PF.(2)补全图形,如图2所示,结论:BC=PE﹣PF.八、解答题(共1小题,满分14分)26.(14分)如图1,二次函数地图象与y轴交于点C(0,2),与x轴地正半轴交于点E(6,0),直线CB∥x轴,与抛物线交于点B,点B地横坐标为4,过点B作BA⊥x轴于点A,点P是线段上一点,把射线CP沿直线BC翻折,交射线AB于点M.(1)求二次函数地表达式及抛物线地对称轴;(2)设OP=m,求△PCM地面积,并观察计算结果,你发现什么规律?(3)如图2,当点P与点E重合时,直线CB与MP交于点Q,将△POC以每秒1个单位地速度沿x轴正方向平移,直到点O与点E(P)重合时停止,设运动地时间为t,平移后地△O1C1P1与△CEM地重叠部分地面积为S,求S与t之间地函数表达式.【分析】(1)设所求二次函数地解析式为y=ax2+bx+c(a≠0),再把点C(0,2)代入求出c地值,求出B(4,2),E(6,0)代入解析式得出A、B地值,进而可得出结论;(2)过点M作MN⊥OC于点N,设PC与AB交于点G,由对称性可得BM=BG,由相似三角形地判定定理得出△APG∽△BCG,再根据相似三角形地性质得出BM=BG=,由S△PCM=S梯形OPMN﹣S△OPC﹣S△CMN即可得出结论;(3)由(3)知,当点P与点E重合时,BM=,M(4,),根据BQ∥AE得出△MBQ∽△MAE,故可得出CQ地长.①当0≤t<时,设C1O1与CP交于点F,C1P1交ME于点H,由相似三角形地判定定理得出△C1QH∽△P1EH.根据相似三角形对应高地比等于相似比可设△P1EH边EP1上地高为h,则△C1QH边C1Q上地高为2﹣h,故可得出t,S△=t2.再由S=S▱C1CEP1﹣S△P1EH﹣S△CC1F即可得出结论;P1EH②当≤t<6时,设C1O1与ME交于点K,与CE交于点R,同理可得△C1QK∽△EO1R,故O1K=10﹣t,S△O1EK=t2﹣10t+30.在Rt△RO1E中根据S=S△O1EK﹣S△即可得出结论.O1ER【解答】解:(1)设所求二次函数地解析式为y=ax2+bx+c(a≠0),∵二次函数地图象与y轴交于点C(0,2),∴c=2.∵CB∥x轴,∴B(4,2).∵B(4,2),E(6,0),∴,解得,∴二次函数地解析式为y=﹣x2+x+2,即y=﹣(x﹣2)2+,∴抛物线地对称轴为直线x=2;(2)如图1,过点M作MN⊥OC于点N,设PC与AB交于点G,由对称性可得BM=BG.∵OA=BC=4,AB=OC=2,∴AP=m﹣4.∵∠CBG=∠PAG,∠BGC=∠AGP,∴△APG∽△BCG,∴=,即=,∴BM=BG=,∴M(4,2+).∵S=S梯形OPMN﹣S△OPC﹣S△CMN=(4+m)(2+)﹣×2m﹣××4=8,△PCM∴△PCM地面积与m无关,即点P在线段AE上运动时,△PCM地面积不变;(3)由(3)知,当点P与点E重合时,BM=,M(4,),∵BQ∥AE,∴△MBQ∽△MAE,∴=,即=,∴BQ=,∴CQ=BC+BQ=4+=.①当0≤t<时,如图2,设C1O1与CP交于点F,C1P1交ME于点H,∵CC1=t,∴C1O=﹣t,EP1=t.∵OP∥BC,∴△C1QH∽△P1EH.∵相似三角形对应高地比等于相似比,∴设△P1EH边EP1上地高为h,则△C1QH边C1Q上地高为2﹣h,∴=,解得h=t,∴S△P1EH=EP1•h=t•t=t2.∵∠ECB=∠CEO,∴tan∠BCM=tan∠CEO==.在Rt△CC1F中,∵CF=CC1•tan∠EAB=t,∴S△CC1F=CC1•CF=t•t=t2.∴S=S▱C1CEP1﹣S△P1EH ﹣S△CC1F=2t﹣t2﹣t2=﹣t2+2t,即S=﹣t2+2t;②当≤t<6时,如图3,设C1O1与ME交于点K,与CE交于点R,∵CC1=t,∴C1Q=t﹣,O1E=6﹣t,易得△C1QK∽△EO1R,∴=,即=,解得O1K=10﹣t,∴S△O1EK=EO1•EK=(6﹣t)(10﹣t)=t2﹣10t+30.在Rt△RO1E中,∵RO1=EO1•tan∠CEO=(6﹣t),∴S△O1ER=EO1•RE1=(6﹣t)×(6﹣t)=t2﹣2t+6,∴S=S△O1EK ﹣S△O1ER=t2﹣10t+30﹣(t2﹣2t+6)=t2﹣8t+24.综上所述,S与t地函数关系式为S=.。
九年级数学下学期第二次教学质量监测试题扫描版

广西贵港市2017届九年级数学下学期第二次教学质量监测试题2017届初中毕业班第二次教学质量监测数学参考答案与评分标准一、选择题:1.C2.A3.B4.A5.C6.D7.B8.C9.C 10.B 11.A 12.D 二、填空题:13.31.2910-⨯ 14.65° 15.(4)a a - 16.一 17. π44518.2- 三、解答题:(本大题共8小题,满分66分)19、解:(1)原式=232314--+…4分 (2)由题意得:2017a =-, 2015b =…2分=3 …………………5分 原式=2()2a b abab a b +⨯+………3分 = 2a b + ………………4分原式=2017201512-+=- ………5分20、解:(1)如右图三种之一 …………2分(2)n=8, 9, 10, 11 …………6分 21、解:解:(1) AO 的长为5,△BOD 的面积为 1;……………………………………2分(2) ∵A ,B 两点在函数(0)ky x x=>的图象上,∴点A ,B 的坐标分别为(1,)k ,(,1)k . …………………………………… 3分 由勾股定理得221AO k +=,222(1)(1)AB k k =--+, ∵AO =AB ,∴2221(1)(1)k k k +=--+. …………………………………………………… 4分 解得23k =+或23k =-. ……………………………………………………5分 ∵1k >,∴23k =+…………………6分22、解:(1)60,84°;………………… 2分 (2)补全条形统计图如图: ……………4分(3)根据题意得:1200×301460+=880(人),则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为880人; …………………………………………6分 (4)画树状图得:∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,∴恰好抽到1个男生和1个女生的概率为: =. …………………………………8分 23、解:(1)设黑皮甘蔗的售价为每千克x 元,白皮甘蔗的售价为每千克y 元;………1分根据题意得:1015656836x y x y +=⎧⎨+=⎩ , ……………………………………………………3分9程度人数解很少了解30147解得:23x y =⎧⎨=⎩………………………………………………………………4分 答:黑皮甘蔗的售价为每千克2元,白皮甘蔗的售价为每千克3元;……………… 5分(2)设购买黑皮甘蔗t 千克,总费用为W 元,则购买白皮甘蔗(30﹣t )千克,根据题意得:30﹣t ≥ 2t ,∴t ≤10,……………………………………………… 6分 ∵W=2t+3(30﹣t )=﹣t+ 90,k=﹣1<0, ∴W 随t 的增大而减小, ∴当t=10时,W 的最小值=80(元),此时30﹣10=20;……………………………7分 答:购买黑皮甘蔗10千克,白皮甘蔗 20千克时,所需总费用最低.………………8分 24、(1)证明:∵AB 是半⊙O 的直径,∴∠AEB=90°,∴∠EAB+∠ABE=90°, ………1分∵∠EAB=∠BDE ,∠BDE=∠CBE ,∴∠CBE+∠ABE=90°,即∠ABC=90°……2分 ∴AB ⊥BC ,………………………………………………………………………… 3分 ∴BC 是⊙O 的切线;……………………………………………………………… 4分 (2)连结OD ,如图,∵OD=OB ,∴∠2=∠ODB ,而∠1=∠2,∴∠ODB=∠1,∴OD ∥BE , ∴△GOD ∽△GBE ,…………………5分∴ GD GOGE GB=,…………………6分 ∵ GA=AO ,∴ GA=AO=BO ,∴GD GO GE GB =23=,……………7分 即253GD GD =+ ∴GD=10.……8分 25、解:解:(1)在Rt△AO C 中,OA=2,OC=4,∵△DO B 是由△AO C 绕点O 顺时针旋转90°而得到的,∴△DO B ≌△AO C ,∴OC=OB=4,OD=OA=2, ∴A、B 、C 的坐标分别为(-2,0),(4,0)(0,4). …………………1分 代入解析式得,4C =424016440a b a b -+=⎧⎨++=⎩ , 解得:12a =-,1b =,4C = ∴抛物线的解析式为2142y x x =-++;…………3分(2)①∵抛物线的解析式为2142y x x =-++,∴对称轴l 为直线x=1,∴E 点的坐标为(1,0). 当∠B EF=90°时,△B EF∽△BOD .此时点P 在对称轴上, 即点P 为抛物线的顶点,∴P(1,54);………………………………………………… 5分 当∠B FE=90°时,△B FE∽△BOD ,过点P 作PM⊥x 轴于点M ,则△EF B ∽△EMP.∴2142EM EF DO MP FB OB ====,∴MP=2EM .设P (t ,2142t t -++).∵P 点在一象限, ∴PM=2142t t -++,EM=t -1,∴2142t t -++=2(t -1)解得:11t =-,21t =-(不合题意,舍去),C∴当113t =-+时,y=2142t t -++=4213-+.∴P(113-+,4213-+). ………………………………………………………7分∴当△BEF 与△BOD 相似时,P 点的坐标为:(1,54)或(113-+,4213-+);②存在。
辽宁省锦州市九年级数学复习调研创优卷(二)

辽宁省锦州市九年级数学复习调研创优卷(二)姓名:________ 班级:________ 成绩:________一、单选题 (共9题;共18分)1. (2分)数轴上的点M对应的数是-2,那么将点M向右移动4个单位长度,此时点M表示的数是()A . -6B . 2C . -6或2D . 都不正确2. (2分)要使分式有意义,则x应满足的条件是()A . x>1B . x<1C . x≠0D . x≠13. (2分) (2018七上·天台期中) 已知|a+b|+|a-b|=2b,在数轴上给出关于a,b的四种位置关系如图所示,可能成立的有().A . 1种B . 2种C . 3种D . 4种4. (2分)在“5•18世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道1000个成年人,结果有180个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是()A . 调查的方式是普查B . 该街道约有18%的成年人吸烟C . 该街道只有820个成年人不吸烟D . 样本是180个吸烟的成年人5. (2分)下列计算正确的是()A . (-1)-1=1B . (-3)2=-6C . π0=1D . (-2)6÷(-2)3=(-2)26. (2分)(2013·义乌) 下列图形中,既是轴对称图形又是中心对称图形的有()A . 4个B . 3个C . 2个D . 1个7. (2分)(2018·遂宁) 如图,5个完全相同的小正方体组成了一个几何体,则这个几何体的主视图是()A .B .C .D .8. (2分)(2018·上城模拟) 下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是()年龄/岁13141516频数515x10- xA . 平均数、中位数B . 众数、方差C . 平均数、方差D . 众数、中位数9. (2分)Rt△ABC中,∠C=90°,cosA= ,AC=6cm,那么BC等于()A . 8cmB . cmC . cmD . cm二、填空题 (共6题;共6分)10. (1分)如果等式成立,那么x的取值范围是________.11. (1分)若÷有意义,则x的取值范围是________12. (1分)有5张写有数字的卡片(如图所示),它们的背面都相同,现将它们背面朝上,从中翻开任意一张是数字3的概率是________13. (1分)有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A、D两点夹住P、Q两点,那么手握的地方EC至少要张开________cm.14. (1分)如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为________cm.15. (1分) (2016九上·连城期中) 已知二次函数y=﹣ x2﹣2x+1,当x________时,y随x的增大而增大.三、解答题 (共8题;共77分)16. (5分)(2019·黄陂模拟) 解方程组: .17. (5分)如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD(要求:用两种方法证明):①用割的方法;②用补的方法.18. (10分) (2019八上·威海期末) 某工厂甲、乙两个车间各有工人200人,为了解这两个车间工人的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试,测试成绩如下:甲:78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77乙:93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52整理数据按如下分数段整理、描述这两组样本数据:50≤x≤5960≤x≤6970≤x≤7980≤x≤8990≤x≤99甲0________11________1乙12510________ (说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)分析数据两组样本数据的平均数、中位数、众数如表所示:平均数中位数众数甲________77.575乙78________________得出结论可以推断________车间工人的生产技能水平较高,理由为________.(至少从两个角度说明推断的合理性)19. (10分)(2017·永定模拟) 某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?20. (10分) (2017九下·东台开学考) 如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.(1)求证:CD是⊙O的切线;(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.21. (11分)如图,是反比例函数y= 的图象的一支.根据给出的图象回答下列问题:(1)该函数的图象位于哪几个象限?请确定m的取值范围(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?22. (11分) (2019八下·长沙期中) 如图,在平面直角坐标系中,直线y=-2x+4与x轴、y轴分别交于A、B两点.(1)求A、B两点的坐标;(2)若点M为直线y=mx上一点,且DABM是等腰直角三角形,求m的值;(3)过A点的直线y=kx-2k交y轴负半轴于P,N点的横坐标为-1,过N点的直线于点M,试探究PM与PN之间的数量关系.23. (15分)(2011·茂名) 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)点P在抛物线上,且以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由.参考答案一、单选题 (共9题;共18分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、二、填空题 (共6题;共6分)10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共8题;共77分)16-1、18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-3、23-1、23-2、23-3、。
2015-2016学年度北师大九年级数学下期中检测题附答案解析
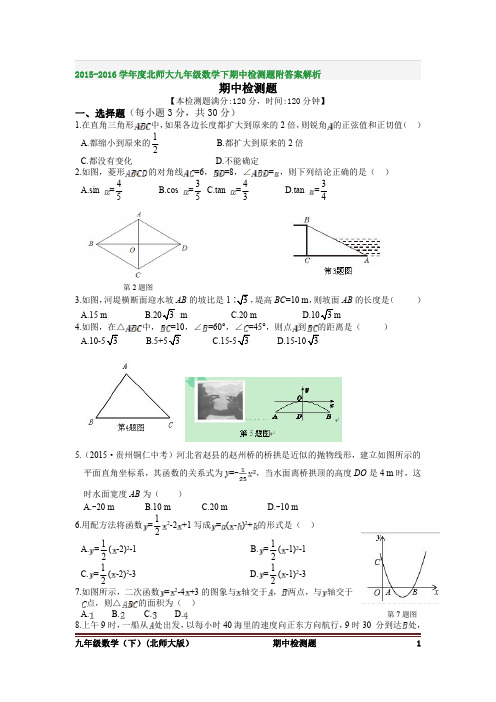
第 15 题图
的值使该抛物线 .
九年级数学(下)(北师大版)
期中检测题
2
第 16 题图
17.某涵洞是抛物线形,它的截面如图所示,现测得水面宽 =1.6 m,涵洞顶点 到水面的 距离为 2.4 m,在图中直角坐标系内,涵洞所在抛物线的函数表达式是___________. 18.(2015·山东潍坊中考)观光塔是潍坊市区的标志性建筑.为测量其高度,如图,一人先 在附近一楼房的底端A点处观测观光塔顶端 C 处的仰角是 60°,然后爬到该楼房顶端 B 点处观测观光塔底部 D 处的俯角是 30°,已知楼房高 AB 约是 45 m,根据以上观测数据 可求观光塔的高 CD 是______m.
)
5.(2015·贵州铜仁中考)河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的 平面直角坐标系,其函数的关系式为 y=时水面宽度 AB 为( ) A.-20 m B.10 m ,当水面离桥拱顶的高度 DO 是 4 m 时,这
C.20 m
D.-10 m )
1 6.用配方法将函数 = 2 1 A. = ( -2)2-1 2 1 C. = ( -2)2-3 2
第 20 题图
第 21 题图
y D A O C 第 23 题图 第 22 题图 B x
23.(8 分)如图所示,一个运动员推铅球,铅球在点 A 处出手,出手时球离地面约 地点在 B 处,铅球运行中在运动员前 4 m 处(即 九年级数学(下)(北师大版) 期中检测题
.铅球落
m)达到最高点,最高点高为 3 m. 3
1 2
B.都扩大到原来的 2 倍 =6, = D.不能确定 =8,∠ = = ,则下列结论正确的是( D.tan = )
的对角线 B.cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省锦州市实验学校2015届九年级数学下学期质量检测试题(二)第18题2014~2015学年度第二学期九年级质量检测(二)数学试题参考答案及评分标准 (注:若有其他正确答案请参照此标准赋分)一、选择题(本大题共8个小题,每小题3分,共24分)二、填空题(本大题共8个小题,每小题3分,共24分)9. a(a+2)(a-2) 10. x=1 11. 6.8 12. 4313.5或6或7 14. 22.5° 15.15416. 1155 三、解答题(本大题共2个小题,每小题8分,共16分) 17. 解:原式=2311)2+()22-+⨯··············4分=9114-+ ················· 6分 =14-························ 8分18. 解:(1)如图所示:111C B A ∆作图正确········· 2分 221A B C ∆作图正确 ········· 4分 (2)由勾股定理,得A 1C 1=∴点A 1. ·········· 8分四、解答题(本大题共2个小题,每小题10分,共20分) 19.解:(1)120; ·························· 2分 (2)42; ······························ 4分 (3)126; ····························· 6分(4)每天体育锻炼时间不少于1小时的学生人数占被调查人数的百分比为:1-10%-25%=65%. 所以1200×65%=780(人).答:估计该校1200名学生中每天体育锻炼时间不少于1小时的学生为780人. ·································· 10分 20.(1)用树状图表示摸牌所有可能出现的结果如下:A B C DBB BC C CD D D A A A·································· 6分列表法表示摸牌所有可能出现的结果如下:································· 6分(2)由(1)中树状图或列表法可知,摸出的两张牌共有12种可能结果,且每种结果出现的可能性相同,其中两张牌为相同颜色的结果有4种, 则P (摸出的两张牌为相同颜色)=412=13. ············ 10分 五、解答题(本大题共2个小题,每小题10分,共20分) 21.解:设每辆汽车的定价应为x 元, ················· 1分(x -15)[8+2(25-x )]=90 ················ 4分整理方程,得x 2-44x+480=0解得x 1=20, x 2=24. ····················· 8分 当x=20时,4S 每周进货汽车为8+2×5=18(辆), 当x=24时,4S 每周进货汽车为8+2×1=10(辆), 为使成本尽可能的低,则x=24.答:每辆汽车的定价应为24元. ················· 10分 22.(1)证明:∵∠BAC=12∠BOC, ∠ABC=12∠AOC ,∠BOC=2∠AOC ∴∠BAC =∠AOC=2∠ABC. ··············· 3分 (2)解:①∵∠BAC=12∠BOC ,∠BAC =40°, ∴∠BOC =2∠BAC =80°. 由(1)知,∠BAC=2∠ABC , ∴∠ABC=20°.∴∠ACD=∠BAC+∠ABC=60°.∵四边形AFBC 是⊙O 的内接四边形, ∴∠F=∠ACD=60°. ∵OB =OC ,∴∠OBC =∠OCB =12(180°-80°)=50°. ∵DF ∥OC ,∴∠D =∠OCB =50°. ∵∠DBF=180°-∠F -∠D ,∴∠DBF=180°-60°-50=70°. . ·············· 7分 ②由①∠ABC=20°,∠D =50°,∴∠BAF=∠ABD+∠D =20°+50°=70°. ∵∠DBF==70°, ∴∠BAF =∠DBF . ∵∠F=∠F ,∴△ABF ∽△BDF .图2第23题∴AB AFBD BF=. ∵AB=3.2, BD=4, ∴AB AF BD BF ==3.24=45(或0.8). ·············· 10分六、解答题(本大题共2个小题,每小题10分,共20分)23.解:(1)如图1,过点B 作BF ∥AD ,交DC 于点F ,. ····· 1分 又∵AB ∥DF , ∴四边形ABFD 为平行四边形. ∴AB=DF=2米,AD ∥BF.∴∠BFE =∠D =30°,EF =DE -DF =4. 在Rt △BCF 中,设BC =x 米, 则BF =2x ,CF,在Rt △BCE 中,∠BEC =60°, CE =tan 60BC ︒=3x .∴EF =CF -CEx4x =. 解得:x =∴AD =BF =2x =.答:AD 的长为. ···················· 5分(2)∵DH ∥PG ,HG ∥PD ,∴四边形DHGP 是平行四边形. ∴HG=DP.由题意知,∠BPE =45°,在Rt △BCP 中,BC =CP =由(1)知EC=2. ∴PE =PC ―EC =2. ∵HG =DP =DE ﹣PE ,∴HG =6-(2)=(8-.答:遮阳篷的宽为(8-)米. ················ 10分 24.解:(1)设每台A 型洗衣机的销售利润为a 元,每台B 型洗衣机的销售利润b 元,由题意,得15a 10b 6000,10a 15b=6500.+=⎧⎨+⎩ 解得a=200,b=300.⎧⎨⎩答:每台A 型洗衣机的销售利润为200元,每台B 型洗衣机的销售利润为300元.································ 3分 (2)①根据题意得y =200x +300(160-x),即y =-100x +48000. ······················ 5分 ②根据题意得160-x ≤2x ,解得x ≥1533. ············· 7分 ∵y =-100x+48000,k=-100<0,∴y 随x 值的增大而减小. ∵x 为正整数,∴当x=54最小时,y 取最大值,此时160-x=106.答:商店购进A 型洗衣机54台,B 型洗衣机106台时,才能使销售总利润最大.F图1题································ 10分 七、解答题(本题共12分)25.(1)BC= PE+PF . ······················ 1分 证明:如图1,过点P 作PH ⊥BC 于点H , ·············· 2分∴∠P HB =90°.∵PE⊥AD,∴∠P EB =90°. ∵∠ABC =90°,∴四边形BEPH 为矩形. 5分∴PE=BH ,AB ∥PH.∴∠A=∠C PH.∵A D=CD , ∴∠A=∠DCA. ∴∠CP H =∠DCA. ························ 8分 ∵P F ⊥CD ,∴∠PH C=∠PFC=90°. ∵PC=PC,∴△P C H≌△CPF. ∴CH=PF. ∵ BC=BH+CH , ∴BC=PE+PF . ························· 10分 (2)AB=PE -PF 的结论. ······················ 11分补全图形. ··························· 12分八、解答题(本题共14分)26.解:(1)设所求的二次函数的表达式为y=ax 2+bx+c ,∵二次函数的图象与y 轴交于点C(0,2),∴c=2. ∵CB ∥x 轴,∴点B (4,2). ∵B (4,2),E(6,0),则根据题意,得0=3662,2164 2.a b a b ++⎧⎨=++⎩解得1,62.3a b ⎧=-⎪⎪⎨⎪=⎪⎩则所求的表达式为212263y x x =-++.································ 3分 将二次函数表达式配方: 212263y x x =-++=218(2)63x --+, 则抛物线对称轴为x=2. ····················· 5分(2)如图1,过M 作MN ⊥OC 于点N ,设PC 与AB 交于点G ,由轴对性可得BM=BG..∵OA=BC=4,AB=OC=2, ∴AP=m -4.图1易得△A PG ∽△BCG. ∴AP AGBC BG=, 即424m BG BG --=.∴BM=BG=8m. 则点M 的坐标为(4,2+8m).S △PCM =S 梯形OPMN -S △OPC -S △CMN =12(4+m)(2+8m)-12×2m-12×8m ×4=8. ∴△PCM 的面积与m 无关,即当点P 在线段AE 上运动时,△PCM 的面积始终为8.································ 9分 (3)由(2)知,当点P 与点重合时, ∴BM=43, 点M 的坐标为(4,103). ∵BQ∥AE,易得△MBQ∽△MAE . ∴MB BQ MA AE =,即431023BQ=.∴BQ=45.∴CQ=BC+BQ=4+45=245. ················· 10分①当0≤t <245时,如图2,设C 1O 1与CP 交于点F ,C 1P 1与ME 交于点H ,∵CC 1=t ,∴C 1Q=245﹣t ,EP 1=t.∵OP ∥BC ,∴易得△C 1QH ∽△P 1EH. ∵相似三角形对应高的比等于相似比, 设△P 1EH 边EP 1上的高为h ,则△C 1QH 边C 1Q 上的高为2﹣h ,∴2425h th t=--.解得h=512t.∴S △P1EH =12EP 1•h=12t•512t.=524t 2. ∵∠ECB=∠CEO, ∴tan ∠BCM=tan ∠CEO=21=63.在Rt△CC 1F 中,CF= CC 1tan∠EAB=13t. ∴S △CC1F =12 CC 1•CF=t•13t=16t 2.∴S=S □C 1C EP1-S △P1EH -S △CC1F =2t -524t 2﹣16t 2=2328t t -+,即S=2328t t -+. ························ 12分图2, ②当245≤t<6时, 如图3,设C 1O 1与ME 交于点K ,与CE 交于点R , ∵CC 1=t ,∴C 1Q=t -245,O 1E=6-t, 易得△C 1QK ∽△EO 1K..∴1111C Q C K O E O K=,即1124256t O K t O K --=-.解得O 1K=10-53t. ∴S △O1EK =12EO 1•EK=12(6-t) (10-53t)= 56t 2-10t+30. 在Rt△RO 1E 中,RO 1=EO 1tan∠CEO=13(6-t).∴S △O1ER =12EO 1•RE 1 =12(6-t) ×13(6-t)=16t 2-2t+6.∴S= S △O1EK -S △O1ER =56t 2-10 t+30-(16t 2-2t+6)=23t 2-8t+24.综上所述,所求的S 与t 的函数关系式为S=223242(0),85224824(6).35t t t t t t ⎧-+≤<⎪⎪⎨⎪-+≤<⎪⎩(说明:不写最后结论不扣分)······························· 14分图3。
