正四面体性质及其应用
正四面体知识

正四面体知识
正四面体是一种三维几何体,由四个等边等角三角形组成。
以下是有关正四面体的一些基本知识:
1. 定义:正四面体是一种具有四个等边等角三角形为侧面的多面体。
它的四个顶点和六条棱之间都是等长的,每个内角都是完全相等的。
2. 基本特征:
- 顶点:正四面体有四个顶点,每个顶点都与其他三个顶点相连。
- 棱:正四面体有六条棱,每个顶点都与两条棱相连。
- 面:正四面体有四个面,每个面都是一个等边等角三角形。
- 角:正四面体有四个内角,每个内角都相等。
3. 对称性:正四面体具有多种对称性质:
- 旋转对称性:正四面体可以进行120度的旋转,使其中一个顶点重合于另一个顶点。
- 镜像对称性:正四面体可通过某个面进行镜像反射。
4. 其他性质:
- 高度:正四面体的高度是指从一个顶点到相对的面上的垂直距离。
- 体积:正四面体的体积可以通过公式V = (a³ * √2) / 12来计算,其中a为等边三角形的边长。
- 表面积:正四面体的表面积可以通过公式S = √3 * a²来计算,其中a为等边三角形的边长。
- 对角线:正四面体的对角线是指连接不相邻顶点的线段。
正四面体有四条对角线。
5. 应用:
- 几何学:正四面体是基本的多面体之一,对于研究几何学和立体几何具有重要意义。
- 物理学:正四面体的对称性被广泛应用于物理学中的结构分析和量子力学领域。
希望这些基本知识能够帮助你更好地理解正四面体。
正四面体结构的物质

正四面体结构的物质
正四面体结构是指一种由四个六面体组成的特殊空间结构,可以被看作由六个正四边形和四个八边形组成的一个更大的正八边形结构,而这种正四面体结构可以被用在各种物质中。
一种常见的正四面体结构可以在金属硅中找到,金属硅是一种金属元素和硅元素的结合物,其中的硅原子以一种特殊的正四面体结构来构成自己的晶格,这种晶格模式与金属离子反应并结合形成一个特殊的结构,从而使金属硅具有了独特的物理性质。
此外,正四面体结构也可以被发现在页岩石和固体分子中,页岩石主要由铁、氧和碳组成,其中碳原子以一种正四面体晶格结构排布,这种晶格模式起着关键的作用,既可以保持页岩石物理性质的稳定,又可以增强页岩石的耐腐蚀性和减少它的暴露于外界环境中条件下的腐蚀。
而在固体分子中,此类晶格结构被用来维持分子结构的稳定性,并维护不同化学物质之间的平衡性。
正四面体结构也能被用于石墨烯的制备,石墨烯是一种非常新兴的材料,它以一种非常特殊的正四面体结构来构成自己的晶格,这种晶格不仅可以使石墨烯具有非常高的弹性和伸缩性,而且还使它具有非常好的电子导电性,因此,它是一种非常有用的材料,可用于制造各种新型电子设备。
总之,正四面体结构可以被用于多种不同的物质中,这种结构不仅能够改善物质的物理性质,而且还可以作为增强许多材料性能的基础。
正四面体的性质

正四面体的性质:设正四面体的棱长为a,则这个正四面体的(1)全面积S全= 2a;(2)体积V=312a;(3)对棱中点连线段的长d= a;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
)(4)相邻两面所成的二面角α=1 arccos3(5)对棱互相垂直。
(6)侧棱与底面所成的角为β=1 arccos3(7)外接球半径R=4a;(8)切球半径r=12a.(9)正四面体任意一点到四个面的距离之和为定值(等于正四面体的高). 直角四面体的性质有一个三面角的各个面角都是直角的四面体叫做直角四面体.如图,在直角四面体AOCB中,∠AOB=∠BOC=∠COA=90°,OA=a,OB=b,OC=c.则①不含直角的底面ABC是锐角三角形;②直角顶点O在底面上的射影H是△ABC的垂心;③体积V= 16a b c;④底面面积S△ABC⑤S2△BOC=S△BHC·S△ABC;ABCDOH⑥S 2△BOC+S 2△AOB +S 2△AOC =S 2△ABC⑦22221111OH a b c=++; ⑧外接球半径 R=⑨切球半径 r=AOB BOC AOC ABCS S S S a b c∆∆∆∆++-++正四面体的性质:设正四面体的棱长为a ,则这个正四面体的(1)全面积 S 全= 2a ; (2)体积 3; (3)对棱中点连线段的长 d=a ;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
)(4)相邻两面所成的二面角 α=1arccos 3(5)对棱互相垂直。
(6)侧棱与底面所成的角为β=1arccos 3(7)外接球半径 R=4a ; (8)切球半径 r=a . (9)正四面体任意一点到四个面的距离之和为定值(等于正四面体的高). 直角四面体的性质有一个三面角的各个面角都是直角的四面体叫做直角四面体. 如图,在直角四面体AOCB 中,∠AOB=∠BOC=∠COA=90°,OA=a ,OB=b ,OC=c .则①不含直角的底面ABC 是锐角三角形;AO H②直角顶点O 在底面上的射影H 是△ABC 的垂心;③体积 V=16a b c ;④底面面积S △ABC⑤S 2△BOC =S △BHC ·S △ABC ; ⑥S 2△BOC +S 2△AOB +S 2△AOC =S 2△ABC⑦22221111OH a b c=++;⑧外接球半径 R=⑨切球半径 r=AOB BOC AOC ABCS S S S a b c∆∆∆∆++-++正四面体的性质:设正四面体的棱长为a ,则这个正四面体的(1)全面积 S 全= 2a ;(2)体积 3;(3)对棱中点连线段的长 d=2a ;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
正四面体常用结论

正四面体常用结论
正四面体是一种具有四个等边三角形的三维几何体,其常用结论包括以下几个方面。
1. 正四面体的性质
正四面体的四个面都是等边三角形,四个顶点相互连通,其中每个顶点都是三个面的公共点,每条边都是两个面的公共边。
正四面体的底面中心、顶点以及每个面的重心三点共线,且共线比为1:3。
正四面体的每个内角都是70.53度,每个外角为109.47度。
2. 正四面体的体积公式
正四面体的体积公式为V=√2/12a³,其中a为正四面体的棱长。
这个公式可以通过正四面体的高度和底面积来推导得到,也可以通过计算四个棱锥的体积并相加得到。
3. 正四面体的表面积公式
正四面体的表面积公式为S=√3a²,其中a为正四面体的棱长。
这个公式可以通过将正四面体分解成四个等腰三角形和一个正三角形来推导得到。
4. 正四面体的对称性
正四面体具有旋转对称性和镜像对称性。
它有6个旋转对称轴,分
别为通过两个相邻顶点的轴,以及通过中心垂直于某个面的轴。
它也有6个镜像对称面,分别为通过两个相邻顶点和中心的面,以及通过棱中点和面中心的面。
5. 正四面体的嵌入
正四面体可以嵌入到三维空间中的不同形状中。
其中最著名的是嵌入到八面体中,也就是四面体与另外一个四面体共享一个顶点,中心分别连接形成六个正方形。
正四面体作为一种基本几何体,具有独特的性质和应用。
掌握正四面体的常用结论,可以帮助我们更好地理解三维几何空间中的形状和应用。
几何体的正四面体

几何体的正四面体正四面体是一种特殊的几何体,具有很多独特的性质和特点。
在本文中,我将介绍正四面体的定义、属性以及一些有趣的应用。
一、正四面体的定义正四面体是一种具有四个等边等角面的多面体。
它的四个面都是等边三角形,每两个面之间的夹角都是一样的,也都是等于70.53°。
在正四面体中,任意两条边的长度和相等。
这些特点使得正四面体在几何学中有着重要的地位。
二、正四面体的性质1. 对称性:正四面体具有很高的对称性。
它有24个对称操作,包括旋转和翻转等。
这些对称性使得正四面体在立体几何中有广泛的应用,例如建筑设计和立体模型制作等。
2. 共面性:正四面体的四个顶点共面。
这意味着可以通过这四个顶点构成一个平面。
而且在这个平面上,正四面体可以被视为一个等边三角形。
3. 体积和表面积:正四面体的体积和表面积可以通过简单的公式计算得到。
其中,体积公式为V = (a³√2) / 12,表面积公式为S = a²√3,其中a表示正四面体一个面的边长。
4. 空间分割:正四面体可以将三维空间分割成四个完全相同的四面体。
这种空间分割在某些科学领域中非常有用,例如晶体结构的研究和分子模拟等。
三、正四面体的应用1. 立体几何学研究:正四面体是立体几何学中的一个基本概念,它的研究可以帮助我们理解和解决各种与几何学相关的问题,例如立体投影、体积计算等。
2. 建筑设计:正四面体的对称性和美观性使得它成为建筑设计中的常用元素。
例如,一些摩天大楼的外形可以采用正四面体的结构,使得建筑物更加稳定和美观。
3. 教育和娱乐:正四面体的独特性质和形状可以作为教学和娱乐的工具。
通过搭建正四面体模型或者使用虚拟现实技术,人们可以更直观地了解和体验正四面体的一些特点和性质。
总结:正四面体作为一种特殊的几何体,具有对称性、共面性以及特定的体积和表面积等性质。
它在几何学研究、建筑设计和教育娱乐等领域有着广泛的应用。
通过深入研究和探索正四面体,我们可以进一步拓展对几何学的理解和应用。
正四面体的性质及应用
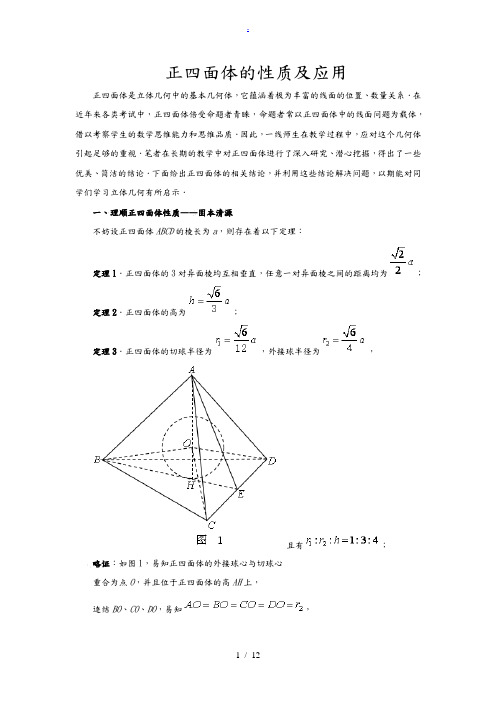
正四面体的性质及应用正四面体是立体几何中的基本几何体,它蕴涵着极为丰富的线面的位置、数量关系.在近年来各类考试中,正四面体倍受命题者青睐,命题者常以正四面体中的线面问题为载体,借以考察学生的数学思维能力和思维品质.因此,一线师生在教学过程中,应对这个几何体引起足够的重视.笔者在长期的教学中对正四面体进行了深入研究、潜心挖掘,得出了一些优美、简洁的结论.下面给出正四面体的相关结论,并利用这些结论解决问题,以期能对同学们学习立体几何有所启示.一、理顺正四面体性质——固本清源不妨设正四面体ABCD的棱长为a,则存在着以下定理:定理1.正四面体的3对异面棱均互相垂直,任意一对异面棱之间的距离均为;定理2.正四面体的高为;定理3.正四面体的切球半径为,外接球半径为,且有;略证:如图1,易知正四面体的外接球心与切球心重合为点O,并且位于正四面体的高AH上,连结BO、CO、DO,易知,且,从而AO、BO、CO、DO两两所确定的平面将正四面体分割成四个形状相同的正三棱锥:,,且每一个小正三棱锥的高都是切球的半径,于是有,即,亦即有,所以,.故定理4.正四面体的全面积为,体积为;定理5.正四面体底面任一点O到三个侧面的距离的之和;正四面体任意一点到四个侧面的距离之和(仿定理3利用体积分割法易证).定理6.正四面体的侧棱与其底面所成的线面角大小为;定理7.正四面体相邻侧面所成的二面角的大小为;略证:设相邻两个侧面所成的角为,由于四个侧面的面积均相等,所以由射影面积公式知.定理8.设正四面体的侧棱与底面所成的角为,相邻两个侧面所成的二面角记为,则有略证:如图1所示,易知,,由H为的中心,易知,从而.定理9.正四面体的外接球的球心与切球的球心O重合且为正四面体的中心;中心与各个顶点的四条连线中两两夹角相等,其大小为,此角即为化学中甲烷分子结构式中的键位角.略证:如图1,在三角形AOB中,,,由余弦定理可求得,于是.同理可得.定理10.正四面体接于一正方体,且它们共同接于同一个球,球的直径等于正方体的对角线.二、运用正四面体性质——化繁为易1.巧算空间距离例1.一个球与正四面体的6条棱都相切,若正四面体的棱长为a,则求此球的体积.分析一:由定理10知,将正四面体嵌于正方体的部,然后再利用正四面体的棱与球相切,则该半径与正方体的切半径相等进行求解.解法一.如图2所示,将正四面体补成正方体,易知与正四面体的各棱相切的球即为正方体的切球.∵正四面体的棱长为a,∴正方体的棱长为.∴正方体的切球半径.∴.分析二:根据正四面体的对称性,结合定理1可知,该球的球心应位于正四面体的中心,其直径即为正四面体相对棱之间的距离.解法二.∵正四面体的棱长为a,∴由定理1可知,相对棱间的距离为.即该球的半径为.∴.例2.在棱长为2的正四面体木块ABCD的棱AB上有一点P(),过P点要锯出与棱AB垂直的截面,当锯到某个位置时因故停止,这时量得在面ABD上锯痕,在面ABC上的锯缝,求锯缝MN的值.解:如图3,取AB的中点E,连结CE,DE,则为正四面体相邻两面的二面角的平面角,由条件知∠MPN也是正四体相邻两面的二面角的平面角,即∠NPM=∠CED,由定理7可知,于是,在中,由余弦定理得,∴2.妙求空间角例3.设P为空间一点,PA、PB、PC、PD是四条射线,若PA、PB、PC、PD两两所成的角相等,则这些角的余弦值为.解:如图4,构造正四面体ABCD,设P为四面体的中心,则PA、PB、PC、PD两两所成的角相等,设,由正四面体的性质,可知余弦值为例4.如图5,在正四面体ABCD中,E、F分别为棱AD、BC的中点,连结AF、CE.⑴求异面直线直线AF和CE所成的角;⑵求CE与面BCD所成的角.解:⑴连结FD,在平面AFD,过点E作EG∥AF交DF于点G.则是异面直线AF与CE所成的角(或其补角).设正四面体ABCD的棱长为a,可得,,.由余弦定理可求得.故异面直线AF与CE所成的角为.⑵由已知易知平面AFD⊥平面BCD,在平面AFD,过点E作EH⊥FD于点H,连结CH,则∠ECH为CE与平面BCD所成的角.∵EH为正四面体高的一半,由正四面体性质的定理2知.∴.∴CE与底面BCD所成的角为.例5.如图6,正四面体ABCD的四个顶点在同一个球面上,CC1和DD1是该球的直径,求面ABC与面AC1D1所成角的正弦值.解:由正四面体性质定理10知正四面体接于一球,该正方体也接于此球,且正方体的对角线为此球的直径,如图所示,即CC1、DD1为该球的直径.连结C1D1,交AB于点M,连结MC.∵MC⊥AB,MD1⊥AB,∴∠CMD1为平面ABC与平面AC1D1所成的角.设正方体棱长为a,在中,.∴平面ABC与平面ACD所成的角的正弦值为.归纳反思:正四面体是立体几何中一个重要的数学问题载体,在平时的学习过程中若能有意识地研究它、利用它,就能较好地培养我们数学思维的“方向感”和思路的“归属感”,有助于促进自己数学思维空间的拓展、数学品质的提升.1.在正四面体P ABC-中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是②.①//BC面PDF;②面PDF⊥面ABC;③DF⊥面PAE;④面PAE⊥面ABC.2.正四面体ABCD中,AB与平面ACD所成角的余弦值为3.3.如图,正四面体ABCD的棱长为2,点E,F分别为棱AD,BC的中点,则EF BA的值为()A.4B.4-C.2-D.24.以下说法 ①三个数20.3a =,2log 0.3b =,0.32c =之间的大小关系是b a c <<;②已知:指数函数()(0,1)x f x a a a =>≠过点(2,4),则log 41a y =;③已知正四面体的边长为2cm ,则其外接球的体积为33cm π; ④已知函数()y f x =的值域是[1,3],则()(1)F x f x =-的值域是[0,2];⑤已知直线//m 平面α,直线n 在α,则m 与n 平行.其中正确的序号是①③.5.在正四面体A BCD -中,M 为AB 的中点,则直线CM 与AD 所成角的余弦值为()A .12B .2C .3D .23选:C .6.在正四面体ABCD 中,E 、F 分别为棱AD 、BC 的中点,连接AF 、CE ,则异面直线AF 和CE 所成角的正弦值为()A .13B .23C .24D .5 选:D .【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.本题易错点在于要看清是求异面直线AF 和CE 所成角的正弦值,而不是余弦值,不要错选答7.如图所示,在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +的最小值为7,则该正四面体的外接球的体积是()A 6πB .6πC 36D .32π 选:A .8.棱长为1的正四面体ABCD 中,E 为棱AB 上一点(不含A ,B 两点),点E 到平面ACD 和平面BCD 的距离分别为a ,b ,则11a b +的最小值为6 【考点】7F :基本不等式及其应用【专题】31:数形结合;35:转化思想;5F :空间位置关系与距离;5T :不等式【分析】设点O 是正三角形ACD 的中心,连接OB ,作EF AO ⊥,垂足为点F .AO 交CD 于点M ,则点M 为CD 的中点.设(01)AE AB λλ=<<.23AO AM =,3AM ,22BO AB AO =-.由//EF BO ,可得6EF BO a λ===.同理可得:6)b EN λ=-.代入利用基本不等式的性质即可得出. 【解答】解:如图所示,设点O 是正三角形ACD 的中心,连接OB ,作EF AO ⊥,垂足为点F .AO 交CD 于点M ,则点M 为CD 的中点.设(01)AE AB λλ=<<.223333AO AM ===, 226BO AB AO ∴=- //EF BO ,6EF BO a λ∴===. 同理可得:6)b EN λ==-.∴21111161()11(1)()2a b λλλλλλ+=+=⨯=+---当且仅当12λ=时取等号.故答案为:9.已知M 是正四面体ABCD 棱AB 的中点,N 是棱CD 上异于端点C ,D 的任一点,则下列结论中,正确的个数有()(1)MN AB ⊥;(2)若N 为中点,则MN 与AD 所成角为45︒;(3)平面CDM ⊥平面ABN ;(4)存在点N ,使得过MN 的平面与AC 垂直.A .1个B .2个C .3个D .4个【考点】LM :异面直线及其所成的角;LO :空间中直线与直线之间的位置关系;LW :直线与平面垂直;LY :平面与平面垂直【专题】14:证明题【分析】连接CM 、DM ,可证明出AB ⊥平面CDM ,从而MN AB ⊥,得(1)正确;取AC 中点E ,连接EM 、EN ,利用三角形中位线定理证明出EN 、NM 所成的直角或锐角,就是异面直线MN 、AD 所成的角,再通过余弦定理,可以求出MN 与AD 所成角为45︒,故(2)正确;根据(1)的正确结论:MN AB ⊥,结合平面与平面垂直的判定定理,得到(3)正确;对于(4),若存在点N ,使得过MN 的平面与AC 垂直,说明存在N 的一个位置,使MN AC ⊥.因此证明出“不论N 在线段CD 上的何处,都不可能有MN AC ⊥”,从而说明不存在点N ,使得过MN 的平面与AC 垂直.【解答】解:(1)连接CM 、DM正ABC ∆中,M 为AB 的中点CM AB ∴⊥同理DM AB ⊥,结合MC M D M =AB ∴⊥平面CDM ,而MN ⊆平面CDMMN AB ∴⊥,故(1)是正确的;(2)取AC 中点E ,连接EM 、ENADC ∆中,E 、N 分别是AC 、CD 的中点//EN AD ∴,12EN AD =. EN ∴、NM 所成的直角或锐角,就是异面直线MN 、AD 所成的角设正四面体棱长为2a ,在MCD ∆中,2CM DM a === 则Rt MNC ∆中122CN a a =⨯=∴MN = 在MNE ∆中,122ME EN a a ==⨯=∴222cos 2EN MN EM ENM EN MN +-∠==⨯⨯ 45ENM ∴∠=︒,即异面直线MN 、AD 所成的角是45︒,故(2)正确;(3)由(1)的证明知:AB ⊥平面CDMAB ⊂平面ABN∴平面ABN ⊥平面CDM ,故(3)正确;(4)若有MN AC ⊥,根据(1)的结论MN AB ⊥,因为AB 、AC 相交于A 点,所以MN ⊥平面ABCMCD ∆中,CM MD ==,2CD a =2221cos 023CM MD CD CMD CM MD +-∴∠==> 可得CMD ∠是锐角,说明点N 在线段CD 上从C 到D 运动过程中, CMN ∠的最大值是锐角,不可能是直角,因为CM ⊂平面ABC ,CM 与NM 不能垂直,以上结论与MN ⊥平面ABC 矛盾,故不论N 在线段CD 上的何处,都不可能有MN AC ⊥.因此不存在点N ,使得过MN 的平面与AC 垂直.综上所述,正确的命题为(1)(2)(3)故选:C .10.棱长为a 的正四面体中,给出下列命题:①正四面体的体积为324a V =;②正四面体的表面积为2S ;③切球与外接球的表面积的比为1:9;④正四面体的任意一点到四个面的距离之和均为定值.上述命题中真命题的序号为②③④.【考点】LE :棱柱、棱锥、棱台的侧面积和表面积;LF :棱柱、棱锥、棱台的体积【专题】31:数形结合;35:转化思想;49:综合法;5F :空间位置关系与距离【分析】①正四面体的高h ==,体积为213V =,计算即可判断出正误;②正四面体的表面积为24S a =,即可判断出正误;③分别设切球与外接球的半径为r ,R ,则23143r ⨯,解得r ;R +=,解得R ,即可判断出正误; ④正四面体的任意一点到四个面的距离之和为H,则221133H ⨯=【解答】解:①正四面体的高h =,体积为3231324a V ==≠,因此不正确;②正四面体的表面积为224S a =,正确;③分别设切球与外接球的半径为r ,R ,则2314312r ⨯=,解得r =;R +=,解得R . :1:3r R ∴=,因此表面积的比为1:9,正确;④正四面体的任意一点到四个面的距离之和为H ,则221133H ⨯=化简可得:H =,即为正四面体的高,均为定值,正确.上述命题中真命题的序号为②③④.。
正四面体的总曲率

正四面体的总曲率正四面体是一种非常重要的多面体,它在几何学、物理学和数学中都有广泛的应用。
正四面体的总曲率是描述其表面弯曲程度的一个数学量,它可以帮助我们更好地理解正四面体的几何特性。
1. 正四面体的定义和特性正四面体是由四个等边三角形构成的多面体,每个三角形都是一个侧面,四个顶点都位于同一球面上。
正四面体的边长等于其高度,且所有角的度数为109.471°23′。
正四面体是一种对称图形,具有高度的旋转对称性和反射对称性。
2. 总曲率的计算正四面体的总曲率可以通过高斯曲率来计算。
高斯曲率是描述二维表面在一点处弯曲程度的量,对于正四面体,我们可以通过对每个侧面进行曲率计算,然后求和得到总曲率。
①侧面的曲率首先,我们来计算正四面体一个侧面的曲率。
我们可以将侧面看作是一个等边三角形的边界,使用黎曼曲率公式来计算:其中,是侧面的边长,是侧面的面积,是侧面的法向量。
对于正四面体,边长,面积可以通过海伦公式计算得到:其中,是边长,是半周长。
②总曲率正四面体有四个侧面,因此总曲率为:3. 总曲率的物理意义正四面体的总曲率具有重要的物理意义。
在物理学中,曲率与引力有关,正四面体的总曲率可以用来描述其表面引力的大小。
在数学中,曲率也是研究几何图形性质的重要工具,正四面体的总曲率可以帮助我们更好地理解其几何特性。
4. 总曲率与几何性质的关系正四面体的总曲率与其几何性质密切相关。
例如,正四面体的总曲率越大,其表面引力越大,这可能导致正四面体在物理场中的行为发生变化。
此外,正四面体的总曲率还可以用来研究其稳定性,曲率越大,稳定性越差。
5. 总结总之,正四面体的总曲率是描述其表面弯曲程度的一个重要数学量。
通过计算正四面体的总曲率,我们可以更好地理解其几何性质和物理性质。
正四面体的总曲率在几何学、物理学和数学中都有广泛的应用,对于研究正四面体的性质和发展相关理论具有重要意义。
正四面体的性质

(1)全面积 S 全2a ; (2)体积3; (3)对棱中点连线段的长d=2a ;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
)(4)相邻两面所成的二面角 α=1arccos 3(5)对棱互相垂直。
(6)侧棱与底面所成的角为β=1arccos 3(7)外接球半径a ; (8)内切球半径r=12a . (9)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高). 直角四面体的性质有一个三面角的各个面角都是直角的四面体叫做直角四面体.如图,在直角四面体AOCB 中,∠AOB=∠BOC=∠COA=90°,OA=a ,OB=b ,OC=c .则①不含直角的底面ABC 是锐角三角形;②直角顶点O 在底面上的射影H 是△ABC 的垂心;③体积 V= 16a b c ;④底面面积S △ABC⑤S 2△BOC=S △BHC ·S △ABC ;⑥S 2△BOC +S 2△AOB +S 2△AOC =S 2△ABC⑦22221111OH a b c =++; ⑧外接球半径⑨内切球半径 r=AOB BOC AOC ABCS S S S a b c∆∆∆∆++-++ABCDO H(1)全面积 S 全2a ; (2)体积3; (3)对棱中点连线段的长d=2a ;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
)(4)相邻两面所成的二面角 α=1arccos 3(5)对棱互相垂直。
(6)侧棱与底面所成的角为β=1arccos 3(7)外接球半径a ; (8)内切球半径r=12a . (9)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高). 直角四面体的性质有一个三面角的各个面角都是直角的四面体叫做直角四面体.如图,在直角四面体AOCB 中,∠AOB=∠BOC=∠COA=90°,OA=a ,OB=b ,OC=c .则①不含直角的底面ABC 是锐角三角形;②直角顶点O 在底面上的射影H 是△ABC 的垂心;③体积 V= 16a b c ;④底面面积S △ABC⑤S 2△BOC=S △BHC ·S △ABC ;⑥S 2△BOC +S 2△AOB +S 2△AOC =S 2△ABC⑦22221111OH a b c =++; ⑧外接球半径⑨内切球半径 r=AOB BOC AOC ABCS S S S a b c∆∆∆∆++-++ABCDO H(1)全面积 S 全2a ; (2)体积3; (3)对棱中点连线段的长d=2a ;(此线段为对棱的距离,若一个球与正四面体的6条棱都相切,则此线段就是该球的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正四面体性质及其应用 Revised by Jack on December 14,2020
正四面体的性质及其应用
正四面体是四个面都是等边三角形的凸多面体,它是一个很规则的几何体,因此具有一些特有的性质,设正四面体的棱长为a ,则 (1) 全面积S 全= 3 a 2; (2) 高h = 6
3a ;
(3) 体积V = 2
12 a 3;
(4) 对棱中点的连线是对棱的公垂线,其长为d = 2
2a
(5) 相邻两面所成的二面角α=arccos 1
3; (6) 棱与其相交的面所成的角 β=arctan 2 ;
(7) 正四面体的内切球和外接球的球心重合,内切球半径 r = 6
12a ,外接球半径R =
6
4a ,r ︰R =1︰3;
(8) 正四面体内任一点到四个面的距离之和为定值(等于正四面体的高)。
将正四面体置于正方体中,结合正方体的性质以上诸性质容易得到证明。
考查正四面体的性质多出选择或填空题,熟记以上八条性质对快速求解相关问题有很大帮助,例如:
例1:已知半径为1的球面上有A 、B 、C 三个点,且它们之间的球面距离都为π
3,则球心O 到平面ABC 的距离为( ) A 3 2 B 6 3 C 12 D 21 7
解析:如右图所示,OA=OB=OC =1 又3
π
=
==⌒
⌒
⌒
CA BC AB ,球的半径r =1
∴∠AOB=∠BOC=∠COA =π
3,则AB=BC=CA =1
所以O -ABC 为棱长为1的正四面体,则由正四面体的性质得球心O 到平面ABC 的
距离即其高为 6
3,答案B 。
例2:(05年湖南省十所示范校联考)已知棱长为a 的正四面体ABCD 有内切球O ,经过该棱锥A -BCD 的中截面为M ,则O 到平面M 的距离为( ) A a 4 B 6 6a C 6 12a D 2 8a
解析:直接运用正四面体的性质,内切球的半径r = 6
12a ,中截面到底面的距离为高
的一半 6 6a ,则O 到平面M 的距离为 6 6a - 6 12a = 6
12a ,因此选C 。
例3:(06年陕西卷)将半径为R
的球心到桌面的距离为 。
解析A 、B 、C 、D
,因为四个球两两相切,则ABCD 2R 的正四面体,A 到面BCD
的距离为2 6
3R ,则上面一个球的球心A 到桌面的距
离为R +2 6 3R =(1+2 6
3)R 。
例4:(06年山东卷)如图1,在等腰梯形ABCD 中,AB =2DC =2,∠DAB =60○,E 为AC 的中点,将△ADE 与△BEC 分别沿ED P ,则三棱锥P -DCE 的外接球的体积为( )
A 4 3 27π
B 6 2π
C 6 8π
D 解析:三棱锥P -DC
E 实质上是棱长为1的正四面体, 则其外接球的体积为 V = 43πR 3= 43π( 6 4)3= 6 8π。
例5:(06年湖南卷)棱长为2球心的一个截面如图1
A
2 2
B
3 2
C 2
D 3
解析:由截面图形可知,正四面体恰好有两个顶点在球面上, 且截面圆经过其外接球的球心(正四面体的中心),由 正四面体的对称性可知M 为AB 对棱CD 的中点,M 到AB 的距离即为正四面体对棱公垂线的长 2
2a ,所以
S △ABC = 1
2×2× 2 ×2= 2 。
例6:(07年安徽卷)半径为1的球面上的四点A 、B 、C 、D 是正四面体的顶点,则A 与B 两点间的球面距离为( )
A )3
3
arccos(-
B )36arccos(-
C )31arccos(-
D )4
1arccos(- 解析:由题意可知,此球O 为正四面体的外接球,且外接球的半径为1,则正四面体的棱长为2 6 3,根据余弦定理得cos ∠AOB =1+1-(2 6
3)2
2×1×1=-1
3,所以∠AOB =arccos(-
13),因此A 与B 两点间的球面距离为l =αR = arccos(-13)×1= arccos(-13)。
