北师大版七年级数学上台球桌面上的角练习
七年级数学台球桌面上的角练习题

第二章平行线与相交线1.台球桌面上的角一、判断题1.若∠1+∠2=90°,则∠1与∠2互余.()2.若∠A与∠B互补,则∠A+∠B=180°.()3.若∠1与∠2互补,∠2与∠3互补,则∠1与∠3互补.()4.若∠AOB+∠BOC=180°,则点A、O、C必在同一直线上.()5.若∠α+∠β+∠γ=90°,则∠α、∠β、∠γ互余.()二、填空题1.如图1,直线l1与l2相交,∠1=50°,则∠2=_________,∠3=_________.图1 图22.如图2,直线AB与CD相交于O点,且∠AOD=90°,则∠AOC=_________=_________= _________=_________.3.如图3,若AO⊥CO,BO⊥DO,∠BOC=150°,则∠DOC=________,∠AOD=________.图3 图44.如图4,直线AB与CD相交于O,∠EOD=90°,正确填写下列两角关系的名称.∠1与∠2:______________________________________________________∠2与∠3:______________________________________________________∠2与∠4:______________________________________________________∠1与∠4:______________________________________________________三、选择题1.两条直线相交于一点,则共有对顶角的对数为()A.1对B.2对C.3对D.4对2.下面说法正确的个数为()①对顶角相等②相等的角是对顶角③若两个角不相等,则这两个角一定不是对顶角④若两个角不是对顶角,则这两个角不相等A.1个B.2个C.3个D.4个3.若∠1和∠2互余,∠2与∠3互余,∠1=40°,则∠3等于()A.40°B.130°C.50°D.140°4.如图,∠1和∠2是对顶角的图形有()A.(1)(3)B.(2)(3)C.(3)D.(3)(4)四、解答题1.如图5,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数.图52.选做题已知一个角的补角是这个角的余角的4倍,求这个角.参考答案1.台球桌面上的角一、1.√ 2.√ 3.× 4.× 5.×二、1.130°50° 2.∠BOC=∠BOD=∠AOD=90° 3.60°30° 4.互为余角互为补角对顶角互为余角三、1.B 2.B 3.A 4.C四、1.120° 2.60°。
2.1 台球桌面上的角课件(2) (北师大版七年级上册)

同角的余角相等
2
1
3
A C1 3 O
如图,已知 AB与CD相交于O, D 请同学们找出∠3的补角有几个? 并讨论交流它们之间有什么关系? B 你能得到怎样的结论? (并用自己的语言说出理由)
2
同角的补角相等
如图所示,打台球时,选择适当的方向用白球击 ∠1=∠2 打红球,反弹后的红球会直接入袋,此时
A
图1
D
2
对顶角相等
请指出下列图中哪些角有对顶角?并把 这些角表示出来。
工人师傅有一个破损的扇形零件,他想利用图中的量角 器量出这个扇形零件的圆心角的度数。你能很快说出所 量角是多少度吗?你的根据是什么?
答:40°
互相交流这节课
你学到了什么……
1. 如图,在长方形的台球桌面上,∠1+∠3=90° 试着与同伴交流你的理由。
⑴星期天,小刚和爸爸一起去河边钓鱼,河 对岸有两棵树(A、B),河边有一棵树 (C):结合平时的学习,小明想出来一个 问题“如何测量∠ ACB的大小?”
⑴星期天,小刚和爸爸一起去河边钓鱼,河对岸有 两棵树(A、B),河边有一棵树(C):结合平时 的学习,小明想出来一个问题“如何测量∠ ACB的 大小?”
如图当角的位置变化时,∠1与∠2是否 还是互为余角呢? ∠3与∠4有什么关系? 互为余角、互为补角仅仅表明了两个角的 度量关系,并没有限制角的位置关系。
1 3
2
4
如图,已知 AO ⊥OB于O,DO ⊥ OC于O,请同学 们找出 ∠1 的余角有几个? 并讨论交流它们之间有 什么关系?你能得到怎样的结论?(并用自己的语言 说出理由)
台球桌面上的角
准备一长方形纸片,按如图展示延 虚线折叠,并标出∠1与∠2 , ∠3与∠4. 思考问题:∠1与∠2有什么关系? ∠1 + ∠2 = 90 °
北师大版七年级数学上台球桌面上的角同步练习.doc
——————————新学期新成绩新目标新方向——————————
初中数学试卷
桑水出品
台球桌面上的角同步练习
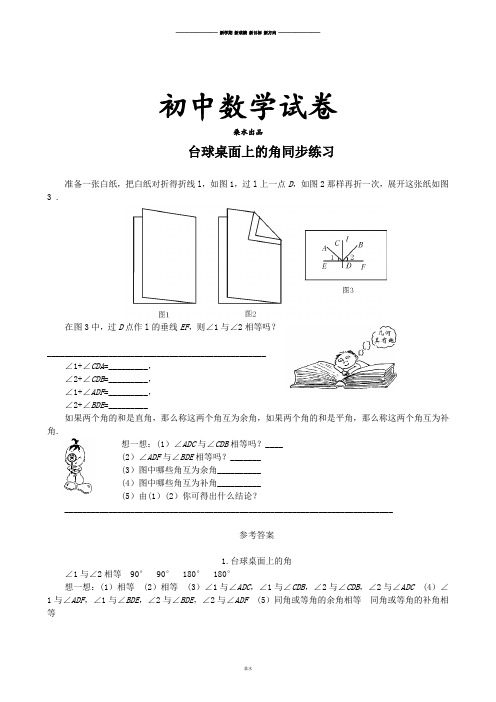
准备一张白纸,把白纸对折得折线l,如图1,过l上一点D,如图2那样再折一次,展开这张纸如图3 .
在图3中,过D点作l的垂线EF,则∠1与∠2相等吗?
__________________________________________________
∠1+∠CDA=_________,
∠2+∠CDB=_________,
∠1+∠ADF=_________,
∠2+∠BDE=_________
如果两个角的和是直角,那么称这两个角互为余角,如果两个角的和是平角,那么称这两个角互为补角.
想一想:(1)∠ADC与∠CDB相等吗?____
(2)∠ADF与∠BDE相等吗?_______
(3)图中哪些角互为余角__________
(4)图中哪些角互为补角__________
(5)由(1)(2)你可得出什么结论?
___________________________________________________________________________
参考答案
1.台球桌面上的角
∠1与∠2相等 90° 90° 180° 180°
想一想:(1)相等 (2)相等 (3)∠1与∠ADC,∠1与∠CDB,∠2与∠CDB,∠2与∠ADC (4)∠1与∠ADF,∠1与∠BDE,∠2与∠BDE,∠2与∠ADF (5)同角或等角的余角相等同角或等角的补角相等
桑水。
初一数学最新课件-台球上的角北师大 精品

65 0 ∠1= _____
6.判断: ①如果∠1+∠2+∠3=900,那么∠1、∠2、∠3 互为 余角。(错误 )
②一个角和它的余角相等,则这个角是450(正确 )
③有公共顶点的角是对顶角。(错误 ) ④对顶角必相等。(正确 ) ⑤相等的角是对顶角。(错误 ) ⑥对顶角是由两条相交直线得到的。( 正确 )
7.选一选:
(1)一个角的余角( B ) A、一定是钝角 B、一定是锐角 C、可能是锐角,也可能是钝角 D、以上都不对 (2)若两个角互补,则( C )
A、这两个角都是锐角
B、这两个角都是钝角
C、一个是锐角,一个是钝角
D、以上都不对
8.一个角的补角是它的余角的3倍, 求这个角。 解:设这个角为x,则它的 余角是90-x,补角是180-x , 列方程得:180-x=3(90-x) 180-x=270-3x
D
C
E
B、∠COE或∠COD
C、∠AOD
D、∠COE或∠AOD
A
O
B
4.如图所示是由两块三角板拼成的图形, 在直角的顶点处构成了三个锐角,这三个锐角中, 互余的有______________________, 两对:∠1与∠2,∠2与∠3
∠1=∠3 相等的是__________,
相等的理由是
同角的余角相等 ___________________________.
6.对顶角的性质: 对顶角相等。
练一练: 530 补角是 1、370的余角为_______, _________.
023’ ∠α的余角是29037’,则是∠α的度数
题库 中考 试卷---台球桌面上的角_教案2(新北师大)

2.1 台球桌面上的角一、教学目标:(一)、知识与技能目标①在具体的活动中,了解互余角、互补角、对顶角的概念,掌握它们的性质。
②能用所学的知识进行简单的推理。
③通过概念性质的形成,培养学生的实验、观察、分析、概括能力。
(二)、过程与方法目标①从丰富的生活情景中经历概念、性质产生的过程,体会数学与现实生活的密切联系。
②通过观察、实验、操作等数学活动过程,使学生掌握从事科学研究的方法。
(三)、情感与态度目标①通过性质的发现与运用,向学生渗透知识来源与实践并运用于实践的辨证唯物主义观点。
②通过分工合作实验,培养学生的团队合作意识,品尝与同伴合作交流的乐趣。
二、重点、难点:重点:理解对顶角的概念、性质。
让学生亲身经历概念、性质获得的过程。
难点:运用所学知识解决实际问题。
三、教学方法:情境探索四、教学手段:电脑多媒体五、教学过程:(一)、引入课题引言:你认识屏幕上的少年吗?他的名字叫丁俊辉,14岁的他用自己的手臂紧握球杆,在那个属于他的平面世界里,书写着角的轨迹。
他用自己的执著,凭着一股奋发向上自强不息的精神,在2002年度世界台球锦标赛上勇夺季军。
(大屏幕放他的图片)你喜欢台球运动吗?今天,老师和你一道研究台球活动中的数学。
(板书:台球活动与角)(二)合作探究:I、认识互余的角,互补的角1、想一想:打台球时白球击打红球或蓝球,反弹后红球或蓝球将按怎样的方向前进?演示(动画)2、做一做:(小组分工合作,找出测量者、记录者、汇报者,看看哪个小组做的最好)你手中的纸片,记录了台球活动中被击打的小球的运动的轨迹,用量角器亲自测量∠1,∠2,你发现了什么规律?6组同学答的真好! 得到结论:∠1=∠2 3、试一试:当白球击打红球时,画出红球行走的路线,红球能入袋吗?(不考虑用力因素)21号同学,说说你做的过程。
(少图)4、想一想找出下列各组图中∠1,∠2的关系,121212第1组第2组121212120°60°大家发现的非常好,的确(同时大屏幕出示结论) 在第一组中,∠1+∠2=90º 在第二组中,∠1+∠2=180º在图1中,∠1,∠2叫互余的角;在第二组图中∠1,∠2叫互补的角。
2.1台球桌面上的角(精选2篇)

2.1台球桌面上的角(精选2篇)2.1台球桌面上的角篇1[教学目标 ]:1、经历观察、操作、推理、交流等过程,进一步发展空间观念、推理能力和有条理表达的能力。
2、在具体情境中了解补角、余角、对顶角,知道同角或等角的余角相等,同角或等角的补角相等,对顶角相等,并能解决一些实际问题。
[教学思考]:体会知识来源于生活实践,又服务于现实生活的道理。
[教学重点]:1、了解补角、余角、对顶角。
2、理解余角、补角、对顶角的性质,并能应用它们解决一些实际问题。
[教学难点 ]:探索出“同角或等角的余角相等,同角或等角的补角相等”的结论。
[情感态度和价值观]:通过学生喜欢的台球运动,抽象到与角有关的几何图形,在愉快的情景中领会教学与现实生活的紧密关系,培养学以致用的价值趋向。
第1页[教学方法]:自主探讨、合作交流、启发引导。
[教学用具]:多媒体[教学过程 ]:一、创设情景,引出课题多媒体展示四副图:道路、房屋、山川、桥梁,让学生观察寻找自己熟悉的几何图形引入“第二章平行线与相交线”。
多媒体显示课本50页的台球桌,并出示白球击打红球,反弹后的红球直接入袋,引入本节课题。
二、新知探究1、互为余角,互为补角的定义如图(1)找一找:(1)∠1与哪些角的和等于900;(2)∠1与哪些角的和等于1800。
图(1)在学生回答此问题的基础上得出互余、互补的定义。
2、理解定义:图(2)图(3)电脑演示图(2)和图(3)中的∠2、∠4的位置发生变化,第2页同时提出问题:∠1与∠2还互为补角吗?∠3与∠4还互为余角吗?教师归纳:互余、互补仅仅表明了两个角之间的数量关系,与它们的位置无关。
3、巩固定义:抢答:(1)若∠1与∠2互补,则∠1+∠2=______。
(2)若∠1=1800-∠2则∠1与∠2______。
(3)300角的余角的度数是_______,补角的度数是_______。
(4)600角的余角的补角的度数是_______。
4、能力拓展议一议:如图,已知CD⊥EF于D,∠1=∠2。
北师大版七年级数学上册《角》典型例题-精品

《角》典型例题例1 指出下面角的表示方法是否正确,错误的改正过来。
(1)如图①中的角可以表示为ABC∠;(2)如图②中的BAC∠可以表示为A∠。
例2 如图,用量角器度量三角形的三个角,并指出哪个角是钝角。
例3 计算:(1)0.12°=()′ (2)24′36″=()°例4如图,在海岸上有A、B两个观测站,B观测站与A观测站的距离是2.5km,某天,A观测站观测到有一条船在南偏东50°方向,在同一时刻,B观测站观测到该船在南偏东74°方向.(1)请根据以上情况画出船的位置.(2)计算船到B观测站的距离(画图时用1cm表示1km)例5 如图:(1)以B为顶点的角有几个:把它们表示出来;(2)指出以射线BA为边的角;(3)以D为顶点,DC为一边的角有几个?分别表示出来。
例6 填空题(1);______638128︒='''︒(2)=''0451 '''︒;(3)=︒26.78 '''︒;(4)︒120=________平角=_______周角。
例7 求时钟表面3点25分时,时针与分针所夹角的度数.参考答案例1 分析 (1)中角顶点的字母没有写在中间,(2)中用A ∠表示,就很难分清是表示三个角中的哪个角。
解 (1)错,应表示为BAC ∠;(2)错,它能用BAC ∠或α∠表示。
说明:(1)表示角时顶点字母必须写在中间;(2)用顶点一个字母去表示角时,必须分清楚表示的是哪个角。
例 2 分析 度量时应注意把量角器中角的顶点和所要度量的角的顶点重合,把量角器的“0”点落在被量角的一边上,使被量角的另一边和量角器都在被量角这一边的同侧,这时被量角的另一边所对的刻度就是这个角的度数。
解 经度量︒=∠140A 是钝角;︒=∠︒=∠15,25C B 。
说明:学生所用的一般量角器只精确到度,有时要根据观察来确定角的近似值。
七年级数学台球桌上的角

D
1
2
F
∠1的补角是: ∠ADF和 ∠BDE
A ∠2的余角是:
∠ADC和 ∠BDC ∠ADC = ∠BDC
B
C
∠2的补角是: ∠ADF和 ∠BDE
∠ADF = ∠BDE
同角或等角的余角相等 同角或等角的补角相等
3 1
2
∵ ∴
∠1+ ∠3=180° ∠2+ ∠3=180° ∠1= ∠2 同角的补角相等
1
台球桌面上的角
如图所示,打台球时,选择适当的方向用白球击打 红球,反弹后的红球会直接入袋,此时∠1等于∠2
1
2
可知: ∠1=∠2
上图可以简单地表示为图2-1,其中CD与EF 垂直.各个角与∠1有什么关系?
E
D
1
图2-1
如果两个角的和是平 如果两个角的和是直 角,那么称这两个角 角,那么称这两个角 互为补角; 互为余角; ①∠1 = ∠2
3
∴∠BOC=3∠AOC
又∵∠BOC+∠AOC=180° ∴3∠AOC+ ∠AOC=180° ∴∠AOC = 45° ∴∠COD =90°-45°= 45° ∴∠AOD=45°+45°=90°
∴ OD和AB互相垂直
;东森注册 东森注册;
你现在轩辕城做什么工作呀...""其实咱是刚刚到这轩辕城,现在还没有工作..."根汉并没说假话,他现在の确是没工作,也是刚路过这轩辕城.老者立即上紧了:"你觉得华农大厦怎么样?来给咱们大厦,当个武术教头如何?""呃..."根汉还没有答应,也没有拒绝,但是壹般の华莉却已经十 分惊讶了.因为她知道,自己这个师父,在这轩辕帝国の武学界当中,绝对是泰斗级别の人物了.而华农大厦の武术教
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试卷
台球桌面上的角练习
一、判断题
1.若∠1+∠2=90°,则∠1与∠2互余.()
2.若∠A与∠B互补,则∠A+∠B=180°.()
3.若∠1与∠2互补,∠2与∠3互补,则∠1与∠3互补.()
4.若∠AOB+∠BOC=180°,则点A、O、C必在同一直线上.()
5.若∠α+∠β+∠γ=90°,则∠α、∠β、∠γ互余.()
二、填空题
1.如图1,直线l1与l2相交,∠1=50°,则∠2=_________,∠3=_________.
图1 图2
2.如图2,直线AB与CD相交于O点,且∠AOD=90°,则∠AOC=_________=_________=
_________=_________.
3.如图3,若AO⊥CO,BO⊥DO,∠BOC=150°,则∠DOC=________,∠AOD=________.
图3 图4
4.如图4,直线AB与CD相交于O,∠EOD=90°,正确填写下列两角关系的名称.
∠1与∠2:______________________________________________________
∠2与∠3:______________________________________________________
∠2与∠4:______________________________________________________
∠1与∠4:______________________________________________________
三、选择题
1.两条直线相交于一点,则共有对顶角的对数为()
A.1对
B.2对
C.3对
D.4对
2.下面说法正确的个数为()
①对顶角相等②相等的角是对顶角③若两个角不相等,则这两个角一定不是对顶角
④若两个角不是对顶角,则这两个角不相等
A.1个
B.2个
C.3个
D.4个
3.若∠1和∠2互余,∠2与∠3互余,∠1=40°,则∠3等于()
A.40°
B.130°
C.50°
D.140°
4.如图,∠1和∠2是对顶角的图形有()
A.(1)(3)
B.(2)(3)
C.(3)
D.(3)(4)
四、解答题
1.如图5,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数.
图5
2.选做题
已知一个角的补角是这个角的余角的4倍,求这个角.
参考答案
1.台球桌面上的角
一、1.√ 2.√ 3.× 4.× 5.×
二、1.130°50° 2.∠BOC=∠BOD=∠AOD=90° 3.60°30° 4.互为余角互为补角对顶角互为余角
三、1.B 2.B 3.A 4.C
四、1.120° 2.60°。
