第08节 分情况语句
扩展语句、压缩语段(专项练习)-【中职专用】中职高考语文一轮复习讲练测(全国通用)

课堂练习
10. 请筛选、整合下面文字中的主要信息,拟写一条“年画”的定义。(不超过40字) 年画是民间很常见的一种图画,大多于农历新年到来时张贴。年画画面线条单纯,色 彩鲜明。传统年画多为木版水印制作,主要产地有天津杨柳青、苏州桃花坞和山东潍坊等; 现代年画则多为机器印制。年画的常见题材有合家欢、看花灯、胖娃娃、五谷丰登等,也 有以神话传说和历史故事为题材的,多含有吉祥喜庆的意义。年画历史悠久,早在宋代就 有相关记载;清代中期,年画尤为盛行;至今还深受人民群众喜爱。
【解析】 本题属于串词成句型扩写题,要探究词语本身的特点, 以及它们之间的相互关系,合理扩展。
课堂练习
2. 下面一段话描写了怎样的景象?请用一句话概括。(不超过20字) 春天来了,太阳温暖大地,青草不但在林荫道旁,还在石板的夹缝里 长出来,绿油油的。桦树、杨树、野樱树长出清香树叶,椴树上鼓起一个 个快要绽裂的花蕾。寒鸦、麻雀、鸽子已经在欢乐地搭巢。植物也罢,鸟 雀也罢,昆虫也罢,一律兴高采烈。
示例:年画是春节时张贴的、画面线条单纯、色彩鲜明,含有吉祥喜庆意义的图画。 【解析】分析题干“下定义”,可知应为一个肯定的判断句“……是……”,为年 画下定义,即“年画是……”,后面加上从文中提取的年画同其他事物相区别的根本特 征即可。
课堂练习
11. 根据下面特定情景扩展一段描写性语段,要求:内容具体、语言优美,不 少于40个字。
课堂练习
6. 运用想象和联想,将下面一句话扩充成一段有情景的话。(不少 于40字)
在一本旧书夹页里,我发现一朵小花。
外研版必修第二册(2019版)专题 08-Unit 2 Let’s celebrate-节假日活动

专题08-Unit 2 Let’s celebrate!-节假日活动Part 1单元话题写作词块背诵1.take place发生,举行2.fall on (节日)落在,适逢3.lunar calendar 农历4.in memory of =in honor of 为了纪念;追念5.in praise of 歌颂6.in celebration of 为了庆祝……7.dress up as 打扮成……8.get together 聚会9.family reunion 家庭团聚10.enjoy the full moon 赏月11.a symbol of reunion 团圆的象征12.light the lantern 点灯笼New Year's Day 元旦(1月1日)The Spring Festival 春节(农历1月1日)The Lantern Festival 元宵节(农历1月15日)International Working Women's Day 国际劳动妇女节(3月8日)Arbor Day 植树节(3月12日)ChingMing Festival; Tomb-sweeping Festival 清明节(4月5日)International Labour Day 国际劳动节(5月1日)Chinese Youth Day 中国青年节(5月4日)Nurses' Festival 护士节(5月12日)The Dragon Boat Festival 端午节(农历5月5日)International Children's Day 国际儿童节(6月1日)The Party's Birthday 建党节(7月1日)Double Seventh Festival 七夕节(农历7月7日)The Army's Day 建军节(8月1日)Mid-autumn(Moon) Festival 中秋节(农历8月15日)Teachers' Day 教师节(9月10日)Double-ninth festival 重阳节(农历9月9日)National Day 国庆节(10月1日)Winter Solstice Festival 冬至节(12月23日)New Year's Eve 除夕(农历12月30日)do Spring Festival shopping 买年货offer sacrifices to one's ancestors 祭祖New Year's visit 拜年propose a toast 敬酒lucky money 压岁钱New Year paintings 年画firecrackers 爆竹fireworks 烟花Part 2元话题写作必备句式1.It’s believed that the moon is a symbol of reunion, luck and fortune.人们认为月亮是团圆、运气和财富的象征。
人教版四年级数学上册第一单元《第08课时_亿以上数的读法》(教学设计)

人教版四年级数学上册第一单元《第08课时_亿以上数的读法》(教学设计)一. 教材分析本节课是人教版四年级数学上册第一单元的第08课时,主要内容是学习亿以上数的读法。
教材通过生动的例题和练习,让学生掌握亿以上数的读法,培养学生的数感和逻辑思维能力。
二. 学情分析四年级的学生已经掌握了整数的读写方法和基本的数数能力,但是对于亿以上数的读法还没有接触过,可能会有一定的陌生感。
因此,在教学过程中,需要通过生动的例题和实际操作,让学生理解和掌握亿以上数的读法。
三. 教学目标1.让学生掌握亿以上数的读法,能够正确地读出亿以上的数。
2.培养学生的数感和逻辑思维能力。
3.提高学生的数学兴趣,使学生在轻松愉快的氛围中学习。
四. 教学重难点1.亿以上数的读法。
2.理解亿以上数的组成和读法规律。
五. 教学方法采用情境教学法、互动教学法和小组合作法,通过生动有趣的例题和实际操作,让学生在轻松愉快的氛围中学习亿以上数的读法。
六. 教学准备1.准备亿以上的数的学习材料和练习题。
2.准备教学课件和教学道具。
七. 教学过程1.导入(5分钟)通过一个有趣的故事,引入亿以上数的读法的学习。
例如,讲述一个小朋友在数学比赛中的有趣经历,他在读一个很大的数时,读错了亿以上的数的读法,导致成绩不理想。
让学生在故事中感受到亿以上数的读法的重要性。
2.呈现(10分钟)通过教学课件和实物道具,呈现亿以上的数,让学生直观地感受亿以上数的读法。
同时,教师可以讲解亿以上数的组成和读法规律,让学生理解亿以上数的读法。
3.操练(10分钟)让学生分成小组,进行亿以上数的读法练习。
教师可以准备一些练习题,让学生在小组内进行讨论和解答。
通过实际操作,让学生掌握亿以上数的读法。
4.巩固(10分钟)通过一些有趣的游戏和练习题,让学生巩固亿以上数的读法。
例如,可以让学生进行亿以上数的接龙游戏,或者让学生在读数比赛中竞争。
5.拓展(10分钟)让学生思考亿以上数的读法在实际生活中的应用。
08 第八节 数学建模——微分方程的应用

第八节 数学建模——微分方程的应用举例微分方程在物理学、力学、经济学和管理科学等实际问题中具有广泛的应用,本节我们将集中讨论微分方程的实际应用,尤其是微分方程经济学中的应用. 读者可从中感受到应用数学建模的理论和方法解决实际问题的魅力.分布图示★衰变问题 ★逻辑斯谛方程 ★价格调整问题 ★人才分配问题内容要点:一、衰变问题镭、铀等放射性元素因不断放射出各种射线而逐渐减少其质量, 这种现象称为放射性物质的衰变. 根据实验得知, 衰变速度与现存物质的质量成正比, 求放射性元素在时刻t 的质量.用x 表示该放射性物质在时刻t 的质量, 则dtdx表示x 在时刻t 的衰变速度, 于是“衰变速度与现存的质量成正比”可表示为.kx dtdx-= (8.1) 这是一个以x 为未知函数的一阶方程, 它就是放射性元素衰变的数学模型, 其中0>k 是比例常数, 称为衰变常数, 因元素的不同而异. 方程右端的负号表示当时间t 增加时, 质量x 减少.解方程(8.1)得通解.ktCex -=若已知当0t t =时, ,0x x =代入通解kt Ce x -=中可得,00kt e x C -= 则可得到方程(8.1)特解,)(00t t k e x x --=它反映了某种放射性元素衰变的规律.注: 物理学中, 我们称放射性物质从最初的质量到衰变为该质量自身的一半所花费的时间为半衰期, 不同物质的半衰期差别极大. 如铀的普通同位素(U 238)的半衰期约为50亿年;通常的镭(Ra 226)的半衰期是上述放射性物质的特征, 然而半衰期却不依赖于该物质的初始量, 一克Ra 226衰变成半克所需要的时间与一吨Ra 226衰变成半吨所需要的时间同样都是1600年, 正是这种事实才构成了确定考古发现日期时使用的著名的碳-14测验的基础.二、 逻辑斯谛方程:逻辑斯谛方程是一种在许多领域有着广泛应用的数学模型, 下面我们借助树的增长来建立该模型.一棵小树刚栽下去的时候长得比较慢, 渐渐地, 小树长高了而且长得越来越快, 几年不见, 绿荫底下已经可乘凉了; 但长到某一高度后, 它的生长速度趋于稳定, 然后再慢慢降下来. 这一现象很具有普遍性. 现在我们来建立这种现象的数学模型.如果假设树的生长速度与它目前的高度成正比, 则显然不符合两头尤其是后期的生长情形, 因为树不可能越长越快; 但如果假设树的生长速度正比于最大高度与目前高度的差, 则又明显不符合中间一段的生长过程. 折衷一下, 我们假定它的生长速度既与目前的高度,又与最大高度与目前高度之差成正比.设树生长的最大高度为H (m), 在t (年)时的高度为h (t ), 则有)]()[()(t h H t kh dtt dh -= (8.2) 其中0>k 是比例常数. 这个方程为Logistic 方程. 它是可分离变量的一阶常数微分方程.下面来求解方程(8.2). 分离变量得,)(kdt h H h dh=-两边积分,)(⎰⎰=-kdt h H h dh得 ,)]ln([ln 11C kt h H h H+=-- 或,21k H t H C k H t e C e hH h==-+ 故所求通解为,11)(22kHtkHt kHt Ce H e C He C t h -+=+=其中的⎪⎪⎭⎫ ⎝⎛>==-0112H C e C C C 是正常数. 函数)(t h 的图象称为Logistic 曲线. 图8-8-1所示的是一条典型的Logistic 曲线, 由于它的形状, 一般也称为S 曲线. 可以看到, 它基本符合我们描述的树的生长情形. 另外还可以算得.)(lim H t h t =+∞→这说明树的生长有一个限制, 因此也称为限制性增长模式.注: Logistic 的中文音译名是“逻辑斯谛”. “逻辑”在字典中的解释是“客观事物发展的规律性”, 因此许多现象本质上都符合这种S 规律. 除了生物种群的繁殖外, 还有信息的传播、新技术的推广、传染病的扩散以及某些商品的销售等. 例如流感的传染、在任其自然发展(例如初期未引起人们注意)的阶段, 可以设想它的速度既正比于得病的人数又正比于未传染到的人数. 开始时患病的人不多因而传染速度较慢; 但随着健康人与患者接触, 受传染的人越来越多, 传染的速度也越来越快; 最后, 传染速度自然而然地渐渐降低, 因为已经没有多少人可被传染了.下面举两个例子说明逻辑斯谛的应用.人口阻滞增长模型 1837年, 荷兰生物学家V erhulst 提出一个人口模型00)(),(y t y by k y dtdy=-= (8.3)其中b k ,的称为生命系数.我们不详细讨论这个模型, 只提应用它预测世界人口数的两个有趣的结果.有生态学家估计k 的自然值是0.029. 利用本世纪60年代世界人口年平均增长率为2%以及1965年人口总数33.4亿这两个数据, 计算得,2=b 从而估计得:(1)世界人口总数将趋于极限107.6亿. (2)到2000年时世界人口总数为59.6亿.后一个数字很接近2000年时的实际人口数, 世界人口在1999年刚进入60亿. 新产品的推广模型 设有某种新产品要推向市场, t 时刻的销量为),(t x 由于产品性能良好, 每个产品都是一个宣传品, 因此, t 时刻产品销售的增长率,dtdx与)(t x 成正比, 同时, 考虑到产品销售存在一定的市场容量N , 统计表明dtdx与尚未购买该产品的潜在顾客的数量)(t x N -也成正比, 于是有)(x N kx dtdx-=(8.4)其中k 为比例系数. 分离变量积分, 可以解得kNtCe Nt x -+=1)((8.5)由,)1()1(,)1(2322222kNt kNt kNt kNt kNt Ce Ce e N Ck dt x d Ce ke CN dt dx -----+-=+= 当N t x <)(*时, 则有,0>dt dx 即销量)(t x 单调增加. 当2)(*N t x =时, ;022=dt x d 当2)(*N t x >时, ;022<dtxd 当2)(*N t x <时, 即当销量达到最大需求量N 的一半时, 产品最为畅销, 当销量不足N 一半时, 销售速度不断增大, 当销量超过一半时, 销售速度逐渐减少.国内外许多经济学家调查表明. 许多产品的销售曲线与公式(8.5)的曲线(逻辑斯谛曲线)十分接近. 根据对曲线性状的分析, 许多分析家认为, 在新产品推出的初期, 应采用小批量生产并加强广告宣传, 而在产品用户达到20%到80%期间, 产品应大批量生产; 在产品用户超过80%时, 应适时转产, 可以达到最大的经济效益.三、价格调整模型在本章第一节例3已经假设, 某种商品的价格变化主要服从市场供求关系. 一般情况下,商品供给量S 是价格P 的单调递增函数, 商品需求量Q 是价格P 的单调递减函数, 为简单起见, 分别设该商品的供给函数与需求函数分别为P P Q bP a P S βα-=+=)(,)( (8.6)其中βα,,,b a 均为常数, 且.0,0>>βb当供给量与需求量相等时, 由(8.6)可得供求平衡时的价格baP e +-=βα 并称e P 为均衡价格.一般地说, 当某种商品供不应求, 即Q S <时, 该商品价格要涨, 当供大于求, 即Q S >时, 该商品价格要落. 因此, 假设t 时刻的价格)(t P 的变化率与超额需求量S Q -成正比, 于是有方程)]()([P S P Q k dtdP-= 其中,0>k 用来反映价格的调整速度.将(8.6)代入方程, 可得)(P P dtdPe -=λ (8.7) 其中常数,0)(>+=k b βλ方程(8.7)的通解为t e Ce P t P λ-+=)(假设初始价格,)0(0P P =代入上式, 得,0e P P C -=于是上述价格调整模型的解为t e e e P P P t P λ--+=)()(0由于0>λ知, +∞→t 时, .)(e P t P →说明随着时间不断推延, 实际价格)(t P 将逐渐趋近均衡价格e P .四、人才分配问题模型每年大学毕业生中都要有一定比例的人员留在学校充实教师队伍, 其余人员将分配到国民经济其他部门从事经济和管理工作. 设t 年教师人数为),(1t x 科学技术和管理人员数目为),(2t x 又设1外教员每年平均培养α个毕业生, 每年人教育、科技和经济管理岗位退休、死亡或调出人员的比率为βδδ),10(<<表示每年大学生毕业生中从事教师职业所占比率),10(<<δ于是有方程111x x dt dx δαβ-= (8.8) 212)1(x x dtdx δβα--= (8.9) 方程(8.8)有通解t e C x )(11δαβ-=(8.10)若设,)0(101x x =则,101x C =于是得特解tex x )(101δαβ-= (8.11) 将(8.11)代入(8.9)方程变为te x x dtdx )(1022)1(δαββαδ--=+ (8.12) 求解方程(8.12)得通解t te x eC x )(122)1(δαβδββ---+= (8.13)若设,)0(202x x =则,110202x x C ⎪⎪⎭⎫⎝⎛--=ββ于是得特解 tt ex e x x x )(101020211δαβδββββ--⎪⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--= (8.14) (8.11)式和(8.14)式分别表示在初始人数分别为)0(),0(21x x 情况, 对应于β的取值, 在t 年教师队伍的人数和科技经济管理人员人数. 从结果看出, 如果取,1=β即毕业生全部留在教育界, 则当∞→t 时, 由于,δα>必有+∞→)(1t x 而,0)(2→t x 说明教师队伍将迅速增加. 而科技和经济管理队伍不断萎缩, 势必要影响经济发展, 反过来也会影响教育的发展. 如果将β接近于零. 则,0)(1→t x 同时也导致,0)(2→t x 说明如果不保证适当比例的毕业生充实教师选择好比率β, 将关系到两支队伍的建设, 以及整个国民经济建设的大局.五、追迹问题设开始时甲、乙水平距离为1单位, 乙从A 点沿垂直于OA 的直线以等速0v 向正北行走; 甲从乙的左侧O 点出发, 始终对准乙以)1(0>n mv 的速度追赶. 求追迹曲线方程, 并问乙行多远时, 被甲追到.建立如图8-8-2所示的坐标系, 设所求追迹曲线方程为).(x y y =经过时刻t , 甲在追迹曲线上的点为),,(y x P 乙在点).,1(0t v B 于是有,1tan 0xyt v y --='=θ (8.15) 由题设, 曲线的弧长OP 为,1002t nv dx y x='+⎰解出t v 0代入(8.15), 得.11)1(02⎰'+=+'-xdx y n y y x两边对x 求导, 整理得.11)1(2y ny x '+=''- 这就是追迹问题的数学模型.这是一个不显含y 的可降阶的方程, 设p y x p y ''=''='),(, 代入方程得211)1(p np x +='- 或 ,)1(12x n dxp dp -=+两边积分, 得|,|ln |1|ln 1)1ln(12C x np p +--=++即 .1112nxC p p -=++ 将初始条件00||==='x x p y 代入上式, 得.11=C 于是,1112nxy y -='++' (8.16) 两边同乘,12y y '+-'并化简得,112n x y y --='+-' (8.17)(8.16)与(8.17)式相加, 得,11121⎪⎭⎫ ⎝⎛---='n n x x y两边积分, 得.)1(1)1(121211C x n n x n n y nn nn +⎥⎦⎤⎢⎣⎡-++---=+- 代入初始条件0|0==x y 得,122-=n nC 故所求追迹曲线方程为 ),1(11)1(1)1(2211>-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-=-+n n n n x n x n y n n n n甲追到乙时, 即曲线上点P 的横坐标,1=x 此时.12-=n n y 即乙行走至离A 点12-n n 个单位距离时被甲追到.。
最新力学漆安慎(第二版)答案08节

力学(第二版)漆安慎习题解答第八章弹性体的应力和应变第八章一、基本知识小结1•弹性体力学研究力与形变的规律;弹性体的基本形变有拉伸压缩形变和剪切形变,弯曲形变是由程度不同的拉伸压缩形变组成,扭转形变是由程度不同的剪切形变组成。
2•应力就是单位面积上作用的内力;如果内力与面元垂直就叫正应力,用c表示; 如果内力方向在面元内,就叫切应力,用T表示。
3•应变就是相对形变;在拉压形变中的应变就是线应变,如果10表示原长,A l表示绝对伸长或绝对压缩,则线应变c =A l/l o;在剪切形变中的应变就是切应变,用切变角书表示。
4.力与形变的基本规律是胡克定律,即应力与应变成正比。
在拉压形变中表示为c = Y c Y是由材料性质决定的杨氏模量,在剪切形变中表示为T = N书,N 是由材料性质决定的切变模量。
5.发生形变的弹性体具有形变势能:拉压形变的形变势能密度E p0弓Y 2,剪切形变的形变势能密度E p01N 26•梁弯曲的曲率与力偶矩的关系12Ybh37•杆的扭转角与力偶矩的关系NR421、思考题解答8.1作用于物体内某无穷小面元上的应力是面元两侧的相互作用力,其单位为N.这句话对不对?答:不对,应力为作用于该无穷小面元两侧单位面积上的相互作用内力,其单位为或。
其面元法向分量称正应力,切向分量称切应力。
8.2(8.1.1)式关于应力的定义当弹性体作加速运动时是否仍然适用?答:适用,(8.1.1)式中的是面元两侧的相互作用内力,它与作用于物体上的外力和物体的运动状态有关。
8.3牛顿第二定律指出:物体所受合力不为零,则必有加速度。
是否合力不为零,必产生变形,你能否举出一个合力不为零但无形变的例子?答:不一定,物体是否发生形变应看物体内应力是否为零,应力为零,则不形变。
自由落体运动,物体受重力作用,但物体内部应力为零,则不发生形变。
8. 4胡克定律是否可叙述为:当物体受到外力而发生拉伸(压缩)形变时,外力与物体的伸长(压缩)成正比,对于一定的材料,比例系数是常数,称作该材料的杨氏模量?答:不对。
08第八节课:绩效管理指标标准的确定2

表现,在评定量表上每一点的相对基准上予以定位,以帮助评估者作评价。
第八课
绩效管理闭环——绩效考评指标标准的确定
绩效考核指标标准确定的“五可”原则
第7 页
可评价 原则
可比较 原则
可实现 原则 可操作 原则
可接受 原则
第八课
绩效管理闭环——绩效考评指标标准的确定
绩效考核指标标准的确定容易出现的误区
第8 页
指标的唯一性与指标之间的制衡之术
一个打字员,其工作标准为60个字每分钟、错误率在1%,在这种情况 下员工就很可能把打字速度提高到120个字没分钟,但是错误率到了5%。因 此在员工执行时会有偏好性,错误率也是打字员的考核指标标准之一。
第八课
绩效管理闭环——绩效考评指标标准的确定
第9 页
四、绩效考核指标标准的确定容易出现的误区
只有确定了绩效考评指标的标准,才能提高绩效考评的质量,更好的发挥绩效管理的功能与作用,使组织
与组织、员工与员工之间,通过横向和纵向的对比,认清优势与差距,取长补短,提升业绩。
第八课
绩效管理闭环——绩效考评指标标准的确定
绩效考评指标标准的设计原则
第3 页
定量标准:用数量作为标度的标准,如工作能力和工作成果,一
2)动态标准,主要有:行为特征标准、目标管理标准、情景评 价和工作模拟标准。 A、行为特征标准: 通过观察分析,选择一例关键行为作为评价 的标准。 B、目标管理标准 : 是以目标管理为基础的评价标准,目标管理 是一种以绩效为目标、以开发能力为重点的评价方法,目标管 理评价准则是把它们具体化和规范化。 C、情景评价标准: 是对领导人员进行评价的标准。它是从领导 者与被领导者和环境的相互关系出发来设计问卷调查表,由下 级对上级进行评价,然后按一定的标准转化为分数。 D、工作模拟标准: 是通过操作表演、文字处理和角色扮演等工 作模拟,将测试行为同标准行为进行比较,从中作出评定。
实验心理学讲义08第8讲 记忆
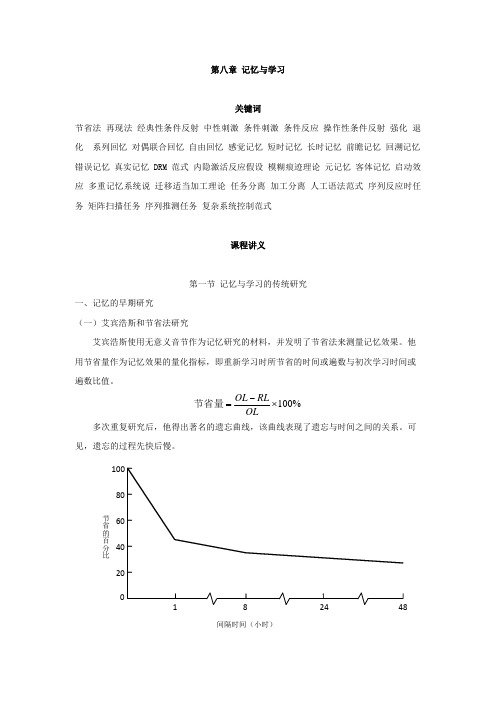
第八章 记忆与学习关键词节省法 再现法 经典性条件反射 中性刺激 条件刺激 条件反应 操作性条件反射 强化 退化 系列回忆 对偶联合回忆 自由回忆 感觉记忆 短时记忆 长时记忆 前瞻记忆 回溯记忆 错误记忆 真实记忆 DRM 范式 内隐激活反应假设 模糊痕迹理论 元记忆 客体记忆 启动效应 多重记忆系统说 迁移适当加工理论 任务分离 加工分离 人工语法范式 序列反应时任务 矩阵扫描任务 序列推测任务 复杂系统控制范式课程讲义第一节 记忆与学习的传统研究一、记忆的早期研究(一)艾宾浩斯和节省法研究艾宾浩斯使用无意义音节作为记忆研究的材料,并发明了节省法来测量记忆效果。
他用节省量作为记忆效果的量化指标,即重新学习时所节省的时间或遍数与初次学习时间或遍数比值。
%100×−=OLRL OL 节省量 多次重复研究后,他得出著名的遗忘曲线,该曲线表现了遗忘与时间之间的关系。
可见,遗忘的过程先快后慢。
节省的百分比2040 60 801001 82448 间隔时间(小时)图8-1 遗忘曲线(采自Ebbinghaus,1885)(二)巴特莱特和再生实验巴特莱特使用故事和图画等有意义的材料进行研究。
研究主要包括两种方法:重复再生和系列再生。
由此发现当信息从一个人传到另一个人时是怎样被扭曲的,而这些扭曲信息的出现是记忆功能不完善的表现。
巴特莱特认为在系列再生过程中人们记忆的变化存在以下几种趋势:①习惯性表征的变形②精心组织③简单化④命名⑤细节的保存。
因此他指出,任何学习和记忆都是在已有图式的基础上进行的,当这些图式与正在记忆的内容相冲突时,人们便会歪曲记忆内容,使之更适合于头脑中已有的图式。
(三)我国心理学家的研究除了国外的一些经典研究,我国心理学家也进行过关于记忆内容变化和遗忘曲线的研究。
(1)对图形记忆变化的研究:曹日昌对这种变化进行了分类,他指出和识记图形相比较,记忆所表现出来的变化大致可以分为:①简略、概括②完整、合理③详细、具体④夸张、突出。
08第八章 斜视

第八章斜视斜视(Strabismus)是双眼视的运动系统异常,导致在双眼视的情况下一眼的视轴偏离,不能和注视目标相交。
斜视在普通人群中的发病率为2%—6%。
第一节斜视的分类一.方向可分为内斜、外斜、上斜、下斜、外旋、内旋。
二.程度(用棱镜度表示)斜视的程度可分为轻、中、重:轻:10Δ中:11-30Δ重:≥30Δ三.眼别可分为右眼、左眼、双眼交替斜视四.时间可分为恒定性、间歇性。
对于见间隙性应在记录时应说明偏斜时间所占百分比。
五.性质:可分为共同性、非共同性。
1、共同性:各注视方向斜视度相差不超过5Δ,其病变部位在核上。
2、非共同性:偏斜角度在各注视方向不同,病变部位可是从神经核到眼外肌的任何水平。
又可分为:(1)麻痹性:眼外肌麻痹所致(2)非麻痹性:机械性六.远-近关系根据在远距离和近距离注视时作三棱镜加遮盖试验测得的斜视度数来分类的,其原因在于调节性集合对视轴相对位置关系的影响。
105例1:右眼40Δ恒定性内斜例2:左眼间歇性15Δ外斜及5Δ上斜,偏斜时间占50%。
记录为:15ΔLX(T),5ΔLH(T)50%(下斜hypotropia=HoT)例3:交替性20Δ外斜;视远时偏斜,视近时正位。
记录为:20pd XT@D,ortho@N第二节病因病因是多元性的,神经支配因素较为重要。
一. 遗传家庭成员里如果有人患斜视,其兄弟姐妹发病率提高。
患斜视的儿童可能其父母或一级血亲有斜视。
孪生子同患斜视且斜视类型相似是遗传影响的有力证明。
尽管可以肯定斜视有遗传倾向,但遗传的确切方式尚不明。
二. 屈光不正高度屈光不正通过对调节的影响成为斜视的重要病因之一。
远视和内斜视密切相关。
屈光参差和一种特殊类型的微斜视有关。
三. 器质性和知觉性原因眼球、视网膜或视神经的任何病变,只要持续时间足够长达到不可逆阶段而且是单侧的,都可能引起斜视。
四. 解剖因素和眼球运动系统解剖结构的异常,包括眼眶和眼球的位置、大小和形状,球后组织的容量和粘性,眼外肌的功能(由其附着部位、长度、弹性和结构决定)以及眼眶筋膜和韧带的解剖结构,均可造成斜视。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八节分情况语句
【教学目标】
掌握case语句的结构、用法
【教学重点】
区别case与if 的差别
【教学内容】
一.格式:
case表达式of
情况标号1:语句1;
情况标号2:语句2;
......
情况标号n:语句n;
[else
语句 ]
end;
二.功能:
1.先计算出表达式的值,然后用表达式的值与各情况标号对照,当找到一个相匹配的情况标号时,就去执行后面的语句,然后跳到与case相对应的end后面的语句继续执行。
2.如果找不到与之匹配的情况标号,则执行else后面的语句,然后继续执行与case 相对应的end后面的语句。
三.说明:
1.情况标号与表达式的类型应一致。
2.所有情况标号互不相同。
3.表达式的值可以是整型、字符型、布尔型,不能是实型。
四.例题
例1.输入1到7之间的某数,输出表示一星期中相应的某一天英文名称。
program lt8_1;
var
n:integer;
w:string;
begin
readln(n);
case n of
1:w:= 'Monday';
2:w:='Tuesday';
3:w:='Wednesday';
4:w:= 'Thursday';
5:w:='Friday';
6:w:='Saturday';
7:w:='Sunday'
else
w:='False';
end;
writeln(w);
end.
例2:编写程序将学生成绩由数字转换为字母标志的五个等级。
100-90:A 89-80:B 79-70:C 69-60:D 59-0:E
要求输入一个学生成绩后,输出一个字母等级。
program lt8_2;
var
a:real;
n:integer;
ch:char;
begin
readln(a);
n:=trunc(a/10);
case n of
9,10:ch:='A';
8:ch:='B';
7:ch:='C';
6:ch:='D';
else
ch:='E'
end;
writeln(ch);
end.
作业8:利用CASE语句编写下列程序(文件命名:×××zy8_题号)
1.键盘输入两个数(均不为零)及一个算术运算符,输出其运算的结果。
2.键盘输入年和月,输出该月有几天。
拓展题
3.给小朋友出计算题,程序运行时,屏幕显示
3+5=
等待小朋友从键盘输入答案。
要求:
1.运算符随机生成:
随机产生一个整数n(1<=n<=4),
如果n:1显示+法,n为2显示-,n为3显示*,n为4显示/。
2.运算数随机生成,0<=a,b<=9
“-”时,a>b
“ /”时,能保证整除,范围在乘法口诀表内
提示:
4.对上题拓展,对小朋友的答案进行判断,正确输入“OK”,错误输出“NO”,并显示正确答案。
