计算流体力学-z1
流体力学计算题及问题详解

第二章例1:用复式水银压差计测量密封容器内水面的相对压强,如下列图。
:水面高程z 0=3m,压差计各水银面的高程分别为z 1=, z 2=, z 3=m, z 4=m, 水银密度 3/13600m kg ρ=',水的密度3/1000m kg ρ= 。
试求水面的相对压强p 0。
解:ap z z γz z γz z γp =-----+)(')(')(3412100)()('1034120z z γz z z z γp ---+-=∴例2:用如下列图的倾斜微压计测量两条同高程水管的压差。
该微压计是一个水平倾角为θ的Π形管。
测压计两侧斜液柱读数的差值为L=30mm ,倾角θ=30∘,试求压强差p 1 – p 2 。
解: 224131)()(p z z γz z γp =-+-- θL γz z γp p sin )(4321=-=-∴例3:用复式压差计测量两条气体管道的压差〔如下列图〕。
两个U 形管的工作液体为水银,密度为ρ2 ,其连接收充以酒精,密度为ρ1 。
如果水银面的高度读数为z 1 、 z 2 、 z 3、z 4 ,试求压强差p A – p B 。
解: 点1 的压强 :p A )(21222z z γp p A --=的压强:点)()(33211223z z γz z γp p A -+--=的压强:点 B A p z z γz z γz z γp p =---+--=)()()(3423211224 )()(32134122z z γz z z z γp p B A ---+-=-∴例4:用离心铸造机铸造车轮。
求A-A 面上的液体总压力。
解: C gz r p +⎪⎭⎫ ⎝⎛-=2221ωρ a p gz r p +⎪⎭⎫ ⎝⎛-=∴2221ωρ在界面A-A 上:Z = - ha p gh r p +⎪⎭⎫⎝⎛+=∴2221ωρ⎪⎭⎫⎝⎛+=-=∴⎰2420218122)(ghR R rdr p p F a Rωπρπ例5:在一直径d= 300mm ,而高度H=500mm 的园柱形容器中注水至高度h 1 = 300mm ,使容器绕垂直轴作等角速度旋转。
流体力学课后答案
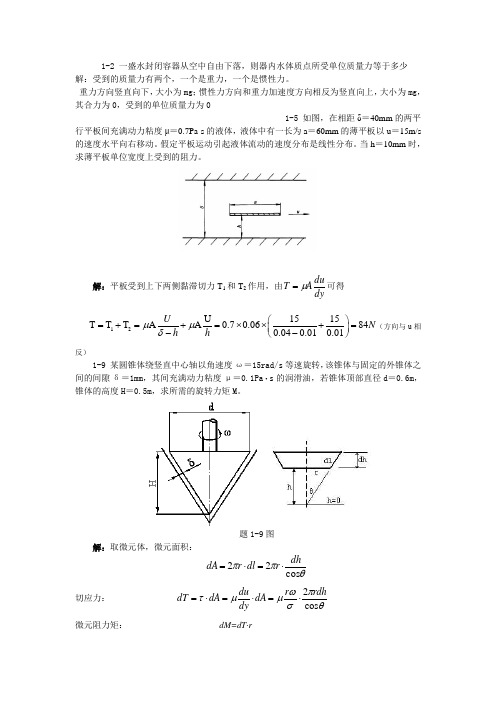
1-2 一盛水封闭容器从空中自由下落,则器内水体质点所受单位质量力等于多少 解:受到的质量力有两个,一个是重力,一个是惯性力。
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-9 某圆锥体绕竖直中心轴以角速度ω=15rad/s 等速旋转,该锥体与固定的外锥体之间的间隙δ=1mm ,其间充满动力粘度μ=0.1Pa ·s 的润滑油,若锥体顶部直径d =0.6m ,锥体的高度H =0.5m ,求所需的旋转力矩M 。
题1-9图解:取微元体,微元面积:θππcos 22dhr dl r dA ⋅=⋅= 切应力: θπσωμμτcos 2rdh r dA dy du dA dT ⋅=⋅=⋅= 微元阻力矩: dM=dT·r阻力矩:2-12 圆柱形容器的半径cm R 15=,高cm H 50=,盛水深cm h 30=,若容器以等角速度ω绕z 轴旋转,试求ω最大为多少时不致使水从容器中溢出。
解:因旋转抛物体的体积等于同底同高圆柱体体积的一半,因此,当容器旋转使水上升到最高时,旋转抛物体自由液面的顶点距容器顶部h’= 2(H-h)= 40cm等角速度旋转直立容器中液体压强的分布规律为0222p gz r p +⎪⎪⎭⎫⎝⎛-=ωρ对于液面,p=p 0 , 则gr z 222ω=,可得出22r gz =ω 将z=h ’,r=R 代入上式得s R gh /671.1815.04.08.92'222=⨯⨯==ω2-13装满油的圆柱形容器,直径cm D 80=,油的密度3/801m kg =ρ,顶盖中心点装有真空表,表的读数为Pa 4900,试求:(1)容器静止时,作用于顶盖上总压力的大小和方向;(2)容器以等角速度120-=s ω旋转时,真空表的读数值不变,作用于顶盖上总压力的大小和方向。
工程流体力学课后习题答案

注:
3-9相对密度为0.85的柴油,由容器A经管路压送到容器B。容器A中液面的表压力为3.6大气压,容器B中液面的表压力为0.3大气压。两容器液面差为20米。试求从容器A输送到容器B的水头损失?
解:列A、B两液面的伯努利方程:
3-10为测量输油管内流量,安装了圆锥式流量计。若油的相对密度为0.8,管线直径D=100毫米,喉道直径d=50毫米,水银压差计读数
解:
又 (2)
由(1)、(2)得
Q1=0.0446m3/s=44.6L/s
Q2=0.0554 m3/s=55.4L/s
5-88图示一管路系统,CD管中的水由A、B两水池联合供应。已知L1=500m,L0=500m,L2=300m,d1=0.2m,d0=0.25m,λ1=0.029,λ2=0.026,λ0=0.025,Q0=100L/s。求Q1、Q2及d2
解:
5-1818水从固定液面的水箱,通过直径d=0.03m的圆柱形外管嘴流出。已知管嘴内的真空度为1.5m水柱,求管嘴出流的流量。
解:
\5-2020水沿T管流入容器A,流经线型管嘴流入容器B,再经圆柱形管嘴流入容器C,最后经底部圆柱形管嘴流到大气中。已知d1=0.008m,d2=0.010m,d3=0.006m。当H=1.2m,h=0.025m时,求经过此系统的流量和水位差h1与h2。
解:法一:h-hD> 0.4 m
h> 1.33 m
法二:
由题意:P1·(0.3-e1)≥P2·(0.2 +e2)
解得:h≥1.33m
流体运动学与动力学基础
6自水箱接出一个水龙头,龙头前有压力表。当龙头关闭时,压力表读数为0.8大气压;当龙头开启时,压力表读数降为0.6大气压。如果管子直径为12毫米,问此时的流量为多少?
化工原理第一章流体力学基础

第一章 流体力学基础
m GA uA
17/37
1.3.1 基本概念
三、粘性——牛顿粘性定律
y x
v
内部存在内摩擦力或粘滞力
v=0
内摩擦力产生的原 因还可以从动量传 递角度加以理解:
v
单位面积上的内摩擦力,N m2
dv x
dy
动力粘度 简称粘度
速度梯度
----------------牛顿粘性定律
(2)双液柱压差计
p1
1略小于2
z1
p1 p2 2 1 gR
p1
R
p2
R
p2
1
z1
R 2
0
倾斜式压差计
浙江大学本科生课程 化工原理
第一章 流体力学基础
读数放大
14/14
幻灯片2目录
1.3 流体流动的基本方程 1.3.1 基本概念 1.3.2 质量衡算方程 1.3.3 运动方程 一、作用在流体上的力 二、运动方程 三、N-S方程 四、欧拉方程 五、不可压缩流体稳定层流时的N-S 方程若干解
v x v y vz 0
t x
y
z
t
vx
x
vy
y
vz
z
v x x
v y y
v z z
0
D
Dt
v x x
v y y
v z z
0
-------连续性方程微分式
若流体不可压缩,则D/Dt=0
v x v y v z 0 x y z
浙江大学本科生课程 化工原理
第一章 流体力学基础
dy
N m2 ms
Ns m2
Pa s
m
1Pa s 10P 1000cP
《流体力学》Ⅰ主要公式及方程式讲解

《流体力学与流体机械》(上)主要公式及方程式1.流体的体积压缩系数计算式:β1dρp=-1dVVdp=ρdp 流体的体积弹性系数计算式:E=-VdpdpdV=ρdρ 流体的体积膨胀系数计算式:βdVT=1VdT=-1dρρdT2.等压条件下气体密度与温度的关系式:ρ0t=ρ1+βt,其中β=1273。
3T=±μAdudy 或τ=TduA=±μdy 恩氏粘度与运动粘度的转换式:ν=(0.0731E-0.0631E)⨯10-4f1∂p⎫x-ρ∂x=0⎪fr-1∂p=0⎫⎪ρ∂r⎪⎪4.欧拉平衡微分方程式: f⎪y-1∂pρ∂y=0⎪⎬和fθ-1∂pρ=0⎬ f1∂p⎪r∂θρ∂z=0⎪⎪⎪⎭f1∂p⎪z-z-ρ∂z=0⎪⎭欧拉平衡微分方程的全微分式:dp=ρ(fxdx+fydy+fzdz) dp=ρ(frdr+fθrdθ+fzdz) 5 fxdx+fydy+fzdz=0frdr+fθrdθ+fzdz=06pγ+z=C 或 p1γ+zp21=γ+z2 或p1+ρgz1=p2+ρgz2相对于大气时:pm+(ρ-ρa)gz=C 或pm1+(ρ-ρa)gz1=pm2+(ρ-ρa)gz27p=p0+γh,其中p0为自由液面上的压力。
8.水平等加速运动液体静压力分布式:p=p0-ρ(ax+gz);等压面方程式:ax+gz=C;自由液面方程式:ax+gz=0。
注意:p0为自由液面上的压力。
1 9.等角速度旋转液体静压力分布式:p=p0+γ(ω2r22g-z);等压面方程式:ω2r22-gz=C;自由液面方程式:ω2r22-gz=0。
注意:p0为自由液面上的压力。
10.静止液体作用在平面上的总压力计算式:P=(p0+γhc)A=pcA,其中p0为自由液面上的相对压力。
压力中心计算式:yD=yc+γsinαIxc (p0+γycsinα)AIxcycA或yD-yc=IxcycA。
当自由液面上的压力为大气压时:yD=yc+矩形截面的惯性矩Ixc计算式:Ixc=圆形截面的惯性矩Ixc计算式:Ixc11bh3;三角形截面的惯性矩Ixc计算式:Ixc=bh3 1236π4=d 6411.静止液体作用在曲面上的总压力的垂直分力计算式:Pz=p0Az+γVP,注意:式中p0应为自由液面上的相对压力。
流体力学课后习题答案龙天渝

方向的投影面积;
的形心的淹没深度;是压力体的体积。
4、浮体的稳定性
设表示定倾半径,表示偏心距,它等于浮体平衡时,重心与浮心的距离,浮体的平衡有三种情况:
稳定平衡
=随遇平衡
不稳定平衡定倾半径的定义是
(2-9)
式中,是浮体被淹没的体积;是浮面对其转轴的面积惯性矩。
二、难点分析
1.通器内不同液体的压强传递
设抛物线方程为
,当
时,
,即
,则:
式中,
正是同高等径圆柱体的体积。
三、习题详解
【2-1】如题2-1所示,已知=20求水深
。
,=240
,
,
【解】设水和水银的密度分别为和
两式相减,化简后算得:
,当地大气压为,则
0,则液深
处的压强为
(2-5)
3、物体壁面受到的静止液体的总压力
计算静止液体对物体壁面的总压力时,只需考虑相对压强的作用。
(1)平面壁总压力
压力中心
= =
ca
(2-6)
+ (2-7)
式中,坐标从液面起算;下标d表示合力作用点;c表示形心。
(2)曲面壁总压力
分力
式中,
别是
,
和
=,
(2-8),
和
分
分别是曲面在
2.什么是流线?流线有哪些重要性质,流线和迹线有无重合的情况?
3.总流连续性方程的物理意义是什么?
4.何谓均匀流及非均匀流?以上分类与过流断面上流速分布是否均匀有无关系?
5.何谓渐变流,渐变哪些有哪些重要性质?引入渐变流概念,对研究流体运动有什么实际意义?
6.动能校正系数及动量校正系数的物理意义是什么?
《计算流体力学》作业答案

计算流体力学作业答案问题1:什么是计算流体力学?计算流体力学(Computational Fluid Dynamics,简称CFD)是研究流体力学问题的一种方法,它使用数值方法对流体流动进行数值模拟和计算。
主要包括求解流体运动的方程组,通过空间离散和时间积分等计算方法,得到流体在给定条件下的运动和相应的物理量。
问题2:CFD的应用领域有哪些?CFD的应用领域非常广泛,包括但不限于以下几个方面:1.汽车工业:CFD可以用于汽车流场的模拟和优化,包括空气动力学性能和燃烧过程等。
2.航空航天工业:CFD可以用于飞机、火箭等流体动力学性能的预测和优化,包括机身、机翼的设计和改进等。
3.能源领域:CFD可以用于燃烧、热交换等能源领域的流体力学问题求解和优化。
4.管道流动:CFD可以用于石油、化工等行业的管道流动模拟和流体输送优化。
5.空气净化:CFD可以用于大气污染物的传输和分布模拟,以及空气净化设备的设计和改进。
6.生物医药:CFD可以用于生物流体输送和生物反应过程的模拟和分析,包括血液流动、药物输送等。
问题3:CFD的数值方法有哪些?CFD的数值方法一般包括以下几种:1.有限差分法(Finite Difference Method,FDM):将模拟区域划分为网格,并在网格上离散化流体运动的方程组,利用有限差分近似求解。
2.有限体积法(Finite Volume Method,FVM):将模拟区域划分为有限体积单元,通过对流体流量和通量的控制方程进行离散化,求解离散化方程组。
3.有限元法(Finite Element Method,FEM):将模拟区域划分为有限元网格,通过对流体运动方程进行弱形式的变分推导,将流动问题转化为求解线性方程组。
4.谱方法(Spectral Method):采用谱方法可以对流体运动方程进行高精度的空间离散,通常基于傅里叶变换或者基函数展开的方式进行求解。
5.计算网格方法(Meshless Methods):不依赖网格的数值方法,主要包括粒子方法(Particle Methods)、网格自适应方法(Gridless Method)等。
流体力学公式总结

工程流体力学公式总结第二章 流体的主要物理性质 流体的可压缩性计算、牛顿内摩擦定律的计算、粘度的三种表示方法。
1.密度 ρ = m /V2.重度 γ = G /V3.流体的密度和重度有以下的关系: γ = ρ g 或 ρ = γ/ g 4.密度的倒数称为比体积,以 υ表示 υ = 1/ ρ = V/m 5.流体的相对密度: d = γ流 /γ水 = ρ流 /ρ 水6.热膨胀性1V VT7.压缩性 . 体积压缩率 κ1V Vp8.体积模量9.流体层接触面上的内摩擦力10.单位面积上的内摩擦力(切应力) (牛顿内摩擦定律)dv dn11. .动力粘度μ:dv/dn12.运动粘度 ν :ν = μ /ρ 13.恩氏粘度° E :°E = t 1 / t 2第三章 流体静力学 重点:流体静压强特性、欧拉平衡微分方程式、等压面方程及其、流体静力学 基本方程意义及其计算、 压强关系换算、 相对静止状态流体的压强计算、流体 静压力的计算(压力体) 。
1.常见的质量力:重力 ΔW = Δ mg 、 直线运动惯性力 ΔFI = Δm ·a 离心惯性力 ΔFR = Δm ·r ω2 .FAd dn2.质量力为 F 。
:F = m ·am = m(fxi+fyj+fzk) am = F/m = fxi+fyj+ fzk 为单位质量力,在数值上就等于加速度 实例:重力场中的流体只受到地球引力的作用, 取 z 轴铅垂向上, xoy 为水平面, 则单位质量力在 x 、y 、 z 轴上的分量为fx= 0 , fy= 0 , fz= -mg/m = -g 式中负号表示重力加速度 g 与坐标轴 z 方向相反 3流体静压强不是矢量,而是标量,仅是坐标的连续函数 得静压强的全微分为 : p pd p p dxpdyxy4.欧拉平衡微分方程式pf y ρdxd ydz dxd ydz 0y pf z ρdxd ydz dxd ydz 0z单位质量流体的力平衡方程为:1p1pyρy1p0 ρz5.压强差公式(欧拉平衡微分方程式综合形式)ρ(f x dx f y dy f z dz) pdx pdy pdz xyz d p ρ( f x dx f y d y f z dz)6.质量力的势函数dp ρ( f x dx f y dy f z dz)dU7.重力场中平衡流体的质量力势函数UUUdU dx d y dz= f x dx f y dy f z dz xyz gdz。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
需要对界面上的被求函数ห้องสมุดไป่ตู้身及其导数的分布作出某种形式的假定。用有限体
积法导出的离散方程可以保证具有守恒特性,而且离散方程系数物理意义明确, 计算量相对较小。1980年,S.V.Patanker在其专著《Numericacl Heat Transfer and Fluid Flow》中对有限体积法作了全面的阐述。此后,该方法 得到了广泛应用,是目前CFD应用最广的一种方法。当然,对这种方法的研 究和扩展也在不断进行,如PChow提出了适用于任意多边形非结构网格的扩 展有限体积法。
– – – – 成本最低 结果最理想 影响因素表达清楚 缺点:局限与非常简单的问题
• 数值方法
– 成本较低:数值实验 – 适用范围宽 – 缺点:可靠性差,表达困难
• 实验研究
– 可靠 – 成本高
将三种方法有 机结合,互为 补充,必然会 取得相得益彰 的效果
6
1.1.2 计算流体动力学的工作步骤 采用CFD的方法对流体流动进行数值模拟,通常包括如下步骤: (1) 建立反映工程问题或物理问题本质的数学模型。具体地说就是要建立反映 问题各个量之间关系的微分方程及相应的定解条件,这是数值模拟的出发点。 没有正确完善的数学模型,数值模拟就毫无意义。流体的基本控制方程通常包 括质量守恒方程、动量守恒方程、能量守恒方程,以及这些方程相应的定解条 件。 (2) 寻求高效率、高准确度的计算方法,即建立针对控制方程的数值离散化方 法,如有限差分法、有限元法、有限体积法等。这里的计算方法不仅包括微分 方程的离散化方法及求解方法,还包括贴体坐标的建立,边界条件的处理等。 这些内容,可以说是CFD的核心。 (3)编制程序和进行计算。这部分工作包括计算网格划分、初始条件和边界条 件的输入、控制参数的设定等。这是整个工作中花时间最多的部分。由于求解 的问题比较复杂,比如N-S方程就是一个十分复杂的非线性方程,数值求解方 法在理论上不是绝对完善的,所以需要通过实验加以验证。正是从这个意义上 讲,数值模拟又叫数值试验。应该指出,这部分工作不是轻而易举就可以完成 的。 (4)显示计算结果。计算结果一般通过图表等方式显示,这对检查和判断分析 质量和结果有重要参考意义。 以上这些步骤构成了CFD数值模拟的全过程。其中数学模型的建立是理论研 究的课题,一般由理论工作者完成。
的近似数值解法。这种方法发展较早,比较成熟,较多地用于求解双曲型和
抛物型问题。在此基础上发展起来的方法有PIC(Particle-in-cell)法、 MAC(Marker-and-Cell)法,以及南美籍华人学者陈景广提出的有限分析法 (Finite Analytic Method)等.
17
有限元法是20世纪80年代开始应用的—种数值解法,它吸收了有限差分法
– 制约因素
• 可靠性检验
– 与分析解对比(简单问题) – 实验结果 – 前人结果 (Benchmark problems)
• 结果表达与分析
– – – – 成品阶段 图线 拟合 分析讨论
10
1.1.3 计算流体动力学的特点 CFD的长处是适应性强、应用面广。首先,流动问题的控制方程一般是非线 性的,自变量多,计算域的几何形状和边界条件复杂,很难求得解析解,而用 CFD方法则有可能找出满足工程需要的数值解;其次,可利用计算机进行各种数 值试验,例如,选择不同流动参数进行物理方程中各项有效性和敏感性试验,从 而进行方案比较。再者,它不受物理模型和实验模型的限制,省钱省时,有较多 的灵活性,能给出详细和完整的资料,很容易模拟特殊尺寸、高温、有毒、易燃 等真实条件和实验中只能接近而无法达到的理想条件。 CFD也存在一定的局限性。首先,数值解法是一种离散近似的计算方法,依 赖于物理上合理、数学上适用、适合于在计算机上进行计算的离散的有限数学模 型,且最终结果不能提供任何形式的解析表达式,只是有限个离散点上的数值解, 并有一定的计算误差;第二,它不像物理模型实验一开始就能给出流动现象并定 性地描述,往往需要由原体观测或物理模型试验提供某些流动参数,并需要对建 立的数学模型进行验证;第三,程序的编制及资料的收集、整理与正确利用,在 很大程度上依赖于经验与技巧。此外,因数值处理方法等原因有可能导致计算结 果的不真实,例如产生数值粘性和频散等伪物理效应。当然,某些缺点或局限性 可通过某种方式克服或弥补,这在本书中会有相应介绍。此外,CFD因涉及大量 数值计算,因此,常需要较高的计算机软硬件配置。 CFD有自己的原理、方法和特点,数值计算与理论分析、实验观测相互联系、 相互促进,但不能完全替代,三者各有各的适用场合,在实际工作中,需要注意 三者有机的结合,争取做到取长补短。
1.1 计算流体动力学概述
1.1.1 什么是计算流体动力学 计算流体动力学(computational Fluid Dynamics,简称CFD)是通过计算 机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统所 做的分析。CFD的基本思想可以归结为:把原来在时间域及空间域上连续的 物理量的场,如速度场和压力场,用一系列有限个离散点上的变量值的集合来 代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数 方程组,然后求解代数方程组获得场变量的近似值。 CFD可以看做是在流动基本方程(质量守恒方程、动量守恒方程、能量守恒 方程)控制下对流动的数值模拟。通过这种数值模拟,我们可以得到极其复杂问 题的流场内各个位置上的基本物理量(如速度、压力、温度、浓度等)的分布,以 及这些物理量随时间的变化情况,确定旋涡分布特性、空化特性及脱流区等。还 可据此算出相关的其他物理星,如旋转式流体机械的转矩、水力损失和效率等。 此外,与CAD联合,还可进行结构优化设计等。
考虑到目前的CFD商用软件大多采用有限体积法,我们后续内容主要讨论
有限体积法。
18
离散方法分类小结
• 有限差分法( Finite difference method) – 用差商与代替导数 – 经典、成熟 – 数学理论基础明确 – 主导方法 • 有限容积法(Finite volume method) – 控制容积法(Control volume method) – 基本上属于有限差分法的范畴 • 有限单元法(Finite element method) – 将求解区域分成若干个小的单元(element) – 设定待求变量在单元上的分布函数 – 适应性强,适用于复杂的求解区域 – 一度有取代有限差分法的趋势 – 程序技巧要求高 – 数学基础不如有限差分法明确
7
CFD:总体步骤
出发点和 基础!
• 给出物理模型(Physical model / description) • 借助基本原理/定律给出数学模型 (Mathematical model)
– – – – – – – 质量守恒(Mass Conservation) 能量守恒(Energy Conservation) 动量守恒(Momentum Conservation) 傅立叶定律(Fourier’s heat conduction law) 菲克定律(Fick’s mass diffusion law) 牛顿内摩擦定律(Newton’s friction law) 。。。。。。。
• •
2
计算流体动力学(CFD)基础知识
流体流动现象大量存在于自然界及多种工程领域中,所有这些过程都受质量 守恒、动量守恒和能量守恒等基本物理定律的支配。本章向读者介绍这些守恒定 律的数学表达式,在此基础上提出数值求解这些基本方程的思想,阐述计算流体 力学的任务及相关基础知识,最后简要介绍目前常用的计算流体动力学商用软件。
中离散处理的内核,又采用了变分计算中选择逼近函数对区域进行积分的合理 方法。有限元法因求解速度较有限差分法和有限体积法慢,因此应用不是特别 广泛。在有限元法的基础上,英国C A.BBrebbia等提出了边界元法和混合 元法等方法。 有限体积法是将计算区域划分为一系列控制体积,将待解微分方程对每一 个控制体积积分得出离散方程。有限体积法的关键是在导出离散方程过程中,
计算流体力学(CFD)
Computational Fluid Dynamics
CFD基础知识
1
主要参考书
• • • • 陶文铨编著. 数值传热学. 西安交通大学出版社 王福军编著 , 《计算流体动力学分析:CFD软件原理与应用》 , 清华大学出 版社 , 2004年09月第1版 Patankar SV. Numerical Heat Transfer and Fluid Flow. N. Y., McGrawHill, 1980 Shih TM. Numerical Heat Transfer, Washington, Hemisphere Publishing Co., 1984 陶文铨著. 计算传热学的近代进展. 科学出版社, 2000年 Anderson JD JR. Computational Fluid Dynamics. McGraw-Hill, 1995
3
CFD方法与传统的理论分析方法、实验测量方法组成了研究流体流动问题的完整体系 图1.1给出了表征三者之间大系的“三维”流体力学示意图。
4
理论分析方法的优点在于所得结果具有普遍性,各种影响因素清晰可见,
是指导实验研究和验证新的数值计算方法的理论基础。但是,它往往要求对计 算对象进行抽象和简化,才有可能得出理论解。对于非线性情况,只有少数流
8
• 对数学模型进行简化和化简
– 简化:物理上的 – 化简:数学上的
Very Important!
求解区域的离散化(discretization) 数学模型的离散化 核心内容,成
败关键 恰当的方法 建立结点(代表点)处待求变量近似值(未知!!) 之间的代数关系:
离散化方程
9
• 求解离散化方程
计算,就好像在计算机上做一次物理实验。例如,机翼的绕流,通过计算并将
其结果在屏幕上显示,就可以看到流场的各种细节:如激波的运动、强度,涡 的生成与传播,流动的分离、表面的压力分布、受力大小及其随时间的变化等。 数值模拟可以形象地再现流动情景,与做实验没有什么区别。
