第四版 徐芝纶第四章_工学_高等教育_教育专区
【9A文】徐芝纶编《弹性力学简明教程》第四版-全部章节课后答案详解

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
华北水利水电学院参考书目

思想政治教育学原理
《思想政治教育学原理》,教育部社会科学研究与思想政治工作司主编,高等教育出版社,2010年3月
948
岩石学
《岩石学》,中国地质大学出版社或《岩石学》,乐昌硕主编,地质出版社,1984
951
应用地球物理学
《应用地球物理学原理》,张胜业、潘玉玲,中国地质大学出版社,2004
955
580
暖通空调
《暖通空调》(第二版),陆亚俊等,中国建筑工业出版社,2009
581
农业生物环境工程
《农业生物环境工程》马承伟主编中国农业出版社2005年版
582
固体废弃物的处理与处置
《固体废物工程》第一版,中国环境科学出版社,李秀金2003.9
584
微机原理与接口技术
《微机原理及应用》,徐晨主编,高等教育出版社
547
经济地理学
《经济地理学》,李小健等,高等教育出版社,1999
548
人力资源管理
《人力资源管理》,黄维德,高等教育出版社,2003
549
马克思主义政治经济学原理
《马克思主义政治经济学原理》(第二版),张雷声主编,中国人民大学出版社,2009年12月
550
思想道德修养与法律基础
《思想道德修养与法律基础》,本书编写组编,高等教育出版社,2010年修订版
528
弹性力学
《弹性力学简明教程》,徐芝纶,高等教育出版社
529
建筑设计
《建筑设计研究》、《绿色建筑》、《建筑高技术研究》、《中外建筑大师作品集》
531
管理信息系统
《管理信息系统》,黄梯云等,高等教育出版社
533
常微分方程
《常微分方程》,王高雄,高等教育出版
弹性力学简明教程 第四 徐芝纶PPT学习教案

第43页/共195页
定 义
§2-5 物理方程
物理方程─表示(微分体上)应力和形变 之间的物理关系。
利用广义胡克定律:
x
1 E
(σ
x
σ
y
σ
z
),
y
1 E
(σ
y
σ
z
σ
x
),
z
1 E
(σ
z
σ
x
σ
y
),
yz
1
G
yz
,
zx
G1
zx
,
xy G1 xy ,
第44页/共195页
所以弹力的平衡条件是严格的、精确的 。
第24页/共195页
V
理力( V )
h
材力(
)
dx dy
弹力(
)
dx
V hdxb
dV dxd y1
第25页/共195页
思考题 1.试检查,同一方程中的各项,其量纲
必然相同(可用来检验方程的正确性)。 2.将条件 M,c改0为对某一角点的 ,将得M 出0什么结果? 3.微分体边上的应力若考虑为不均匀分布,
:
σ x x
yx
y
f
x
0.
(a)
Fy0 ,同理可得:
σ y y
xy
x
f
y
0.
(b)
第20页/共195页
平衡条件
Mc0, 得
xy
1 2
xy
x
d
x
yx
1 2
yx
y
d
y,
当 d x, d y时,0得切应力互等定理,
第1章——绪论

弹性力学A:《弹性力学简明教程》第三版,徐芝纶编,高等教育出版社B:《弹性力学》第四版,徐芝纶编,高等教育出版社1徐芝纶(1911—1999),河海大学)教授2§1-2 弹性力学中的几个基本概念(一)外力按照外力作用的不同分布方式,可分为积力和表面力,分别简称体力和面力。
体力)定义:所谓体力是分布在物体体积内的力,如重力。
)性质:一般情况下,体力随点的位置不同而不同,体力是连续分布的。
P A BCo(o弹性力学材料力学P A BC P30•工程问题的复杂性是诸多方面因素组成的。
如果不分主次考虑所有因素,则问题的复杂,数学推导的困难,将使得问题无法求解。
•根据问题性质,忽略部分暂时不必考虑的因素,提出一些基本假设。
使问题的研究限定在一个可行的范围。
•基本假设是学科的研究基础。
•超出基本假设的研究领域是固体力学其它学科的研究范围。
§1.3 弹性力学的基本假设§1.4 弹性力学的发展和研究方法弹性力学是一门有悠久历史的学科,早期研究可以追溯到1678年,胡克(R.Hooke)发现胡克定律。
这一时期的研究工作主要是通过实验方法探索物体的受力与变形之间的关系。
1807年,Thomas Young(1773~1829,英国物理学家、医生、波动光学的奠基人)做了大量的实验,提出和测定了材料的弹性模量。
3738•近代弹性力学的研究是从19世纪开始的。
•柯西1828年提出应力、应变概念,建立了平衡微分方程、几何方程和广义胡克定律。
•柯西的工作是近代弹性力学的一个起点,使得弹性力学成为一门独立的固体力学分支学科。
柯西(A.L.Cauchy )圣维南(A.J.Saint-Venant)39基尔霍夫(G.R.Kirchoff)41钱学森。
弹性力学讲课文档

因此,即应力与应变关系可用胡克定律表示 (物理线性)。
31
第三十一页,共39页。
(3)均匀性--假定物体由同种材料组成。
因此, E、μ等与位置 无关。 (4)各向同性--假定物体各向同性。
因此, E、μ等与方向无关。
由(3),(4)知E、μ等为常数 符合(1)-(4)假定的称为理想弹性体。
21
第二十一页,共39页。
z
oy x
yz
σy
yx
图1-6
(2)符号规定:
图示单元体面的法线为y,称为y
面,应力分量垂直于单元体面的应 力称为正应力。
正应力记为σy,沿y轴的正向 为正,其下标表示所沿坐标轴的方向
。
平行于单元体面的应力称为切
应下力标,y表用示所在、yx的平面表yz,示第,二其下第标一x
、z分别表示沿坐标轴的方向。如
图1-6所示的 、 yx。 yz
22
第二十二页,共39页。
其它x、z正面上的应力
分量的表示如图1-7所示。
凡正面上的应力沿坐
标正向为正,逆坐标正向
z
为负。
图1-7
oy
x
23
第二十三页,共39页。
z
oy x
图1-8
图1-8所示单元体
面的法线为y的负向,正
应力记为
,沿y轴负向
37
第三十七页,共39页。
《绪论》习题课
[练习2]弹性力学中基本假设是什么?
答:为了简化计算,弹性力学中采用如下基本假设: (1)连续性假设,(2)完全弹性假设,(3)均匀性假 设,(4)各向同性假设,(5)小变形假设。
38
第三十八页,共39页。
河海大学2018年硕士研究生入学考试自命题科目参考范围
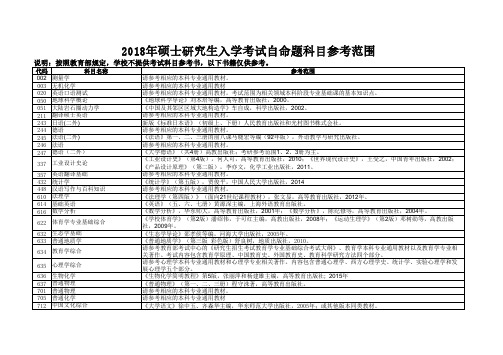
337 工业设计史论 357 432 448 610 614 616 英语翻译基础 统计学 汉语写作与百科知识 法理学 基础英语 数学分析
622 体育学专业基础综合 632 生态学基础 633 普通地质学 634 教育学综合 635 心理学综合 636 637 701 705 712 生物化学 普通物理 普通物理 普通化学 中国文化综合
《理论力学》武清玺、徐鉴等编,高等教育出版社,2010年。
《水文学原理》芮孝芳,中国水利水电出版社,2004年。 《材料力学》(第一版)徐道远等编著,河海大学出版社,2006.1;或《材料力学》(第四版)孙训方主编,高等教育出版 社,2002年。 《水力学》李家星,赵振兴主编,河海大学出版社。 《机械设计》(第八版),濮良贵主编,高等教育出版社。 《社会研究方法》,劳伦斯·纽曼,中国人民大学出版社,2007年版(第一、二部分);《社会研究中的统计应用》,李 沛良,社会科学文献出版社,2002年(第一章到第八章)。 《有机化学》(第四版)汪小兰编,高等教育出版社,2005年 《流体力学基础》王惠民主编,清华大学出版社,2005年。 《误差理论与测量平差基础》武汉大学测绘学院测量平差学科组,武汉大学出版社,2008年。 《电路》(第五版)邱关源主编,高等教育出版社,2006年。 《地理信息系统教程》许捍卫等编,国防工业出版社,2010年;《地理信息系统概论》,黄杏元等编,高等教育出版社, 2001年。 《离散数学》(第2版),屈婉玲 耿素云 张立昂,高等教育出版社,2008.3 参考本科阶段港口航道工程规划、经济、物流、管理等相关教材。 《自动控制原理》(第六版)胡寿松主编,科学出版社。 中国新闻采访写作学(新修版),刘海贵著,复旦大学出版社,2014年; 当代新闻评论教程(第5版),丁法章著,复旦大学出版社,2012年 《固体物理》黄昆,韩汝喜等编,高等教育出版社。
河海大学考博参考书

河海大学考博参考书10294 河海大学2021年博士研究生入学考试参考范围2021年博士研究生入学考试参考范围考试科目代码《科技哲学概论》丁长青、张雁编著,河海大学出版社,2003.10;《科学技术方法》丁长青编著,河海0001 政治理论大学出版社,2003.10;《自然辩证法概论》黄顺基主编,教育部社科与思政司编著,高等教育出版社,2004.5 1001 英语 1002 俄语 1003 日语 1004 德语 1005 法语 2001 数理方程 2002 计算数学 2003 概率论与数理统计《English Through Reading》W.W.S Bhasker and N.S.Prabhu.Macmillan World Publishing;《研究生英语教程》郑亚南主编,河海大学出版社参照相应的硕士专业通用教材参照相应的硕士专业通用教材参照相应的硕士专业通用教材参照相应的硕士专业通用教材《数学物理方程》陈才生等编,东南大学出版社,2002;或《数学物理方程》陈才生等编,科学出版社,2008。
《矩阵论基础》方保镕主编,清华大学出版社,2004;《数值分析》李庆扬等,清华大学出版社,2007 《概率论与数理统计教程》魏宗舒等编,高等教育出版社《应用概率统计》夏乐天等,机械工业出版社,2008 考试科目名称参考范围 2004 应用统计 - 1 -10294 河海大学2021年博士研究生入学考试参考范围考试科目代码 2021 管理综合 2021 数理逻辑 2021 环境化学《现代企业管理一变革的观点》黄速建等主编,经济管理出版社;《战略管理》张阳等主编,科学出版社《计算机科学中的现代逻辑学》王元元主编,科学出版社,2002 《环境化学》戴树桂主编,高等教育出版社,2002;《有机污染化学》陆光华编著,河海大学出版社,2021年7月第一版《社会思想名家》,刘易斯·科塞著,石人译,上海人民出版社,2007年;《新教伦理与资本主义精神》,2021 社会学理论与马克斯·韦伯著,苏国勋等译,社会科学文献出版社,2021年;《社会分工论》,涂尔干著,渠东译,三方法联书店,2000年;《规训与惩罚》,福柯著,刘北成等译,三联书店,2007年;《社会研究方法》,风笑天著,中国人民大学出版社,2009年 2022 政治学原理 2023 常微分方程《政治学概论》孙关宏等主编,复旦大学出版社,2004年;《政治科学》迈克尔·罗斯金等编,华夏出版社,2001年《常微分方程教程》(第二版),丁同仁、李承治编,高等教育出版社《土地经济学》(第六版)毕宝德主编,中国人民大学出版,2021年。
第4章 4.1.2

4.1.2 圆的一般方程【课时目标】 1.正确理解圆的一般方程及其特点.2.会由圆的一般方程求其圆心、半径.3.会依据不同条件利用待定系数法求圆的一般方程,并能简单应用.4.初步掌握点的轨迹方程的求法,并能简单应用.1.圆的一般方程的定义(1)当________________时,方程x 2+y 2+Dx +Ey +F =0叫做圆的一般方程,其圆心为____________,半径为______________________.(2)当D 2+E 2-4F =0时,方程x 2+y 2+Dx +Ey +F =0表示点________________.(3)当__________________时,方程x 2+y 2+Dx +Ey +F =0不表示任何图形.2.由圆的一般方程判断点与圆的位置关系已知点M (x 0,y 0)和圆的方程x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0).,则其位置关系如下表:一、选择题1.圆2x 2+2y 2+6x -4y -3=0的圆心坐标和半径分别为( )A .⎝⎛⎭⎫-32,1和194B .(3,2)和192C .⎝⎛⎭⎫-32,1和192D .⎝⎛⎭⎫32,-1和1922.方程x 2+y 2+4x -2y +5m =0表示圆的条件是( )A .14<m <1 B .m >1 C .m <14D .m <1 3.M (3,0)是圆x 2+y 2-8x -2y +10=0内一点,过M 点最长的弦所在的直线方程是( ) A .x +y -3=0 B .x -y -3=0C .2x -y -6=0D .2x +y -6=04.圆x 2+y 2-2x +4y +3=0的圆心到直线x -y =1的距离为( )A .2B .22C .1D . 2 5.已知圆x 2+y 2-2ax -2y +(a -1)2=0(0<a <1),则原点O 在( )A .圆内B .圆外C .圆上D .圆上或圆外6.若圆M 在x 轴与y 轴上截得的弦长总相等,则圆心M 的轨迹方程是( )A .x -y =0B .x +y =0C .x 2+y 2=0D .x 2-y 2=0二、填空题7.如果圆的方程为x 2+y 2+kx +2y +k 2=0,那么当圆面积最大时,圆心坐标为________.8.已知圆C :x 2+y 2+2x +ay -3=0(a 为实数)上任意一点关于直线l :x -y +2=0的对称点都在圆C 上,则a =________.9.已知圆的方程为x2+y2-6x-8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为________.三、解答题10.平面直角坐标系中有A(-1,5),B(5,5),C(6,-2),D(-2,-1)四个点能否在同一个圆上?11.如果方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0表示一个圆.(1)求t的取值范围;(2)求该圆半径r的取值范围.能力提升12.求经过两点A(4,2)、B(-1,3),且在两坐标轴上的四个截距之和为2的圆的方程.13.求一个动点P在圆x2+y2=1上移动时,它与定点A(3,0)连线的中点M的轨迹方程.1.圆的一般方程x2+y2+Dx+Ey+F=0,来源于圆的标准方程(x-a)2+(y-b)2=r2.在应用时,注意它们之间的相互转化及表示圆的条件.2.圆的方程可用待定系数法来确定,在设方程时,要根据实际情况,设出方程,以便简化解题过程.3.涉及到的曲线的轨迹问题,要求作简单的了解,能够求出简单的曲线的轨迹方程,并掌握求轨迹方程的一般步骤.4.1.2圆的一般方程答案知识梳理1.(1)D 2+E 2-4F >0 ⎝⎛⎭⎫-D 2,-E 2 12D 2+E 2-4F (2)⎝⎛⎭⎫-D 2,-E 2 (3)D 2+E 2-4F <02.> = <作业设计1.C [由一般方程圆心⎝⎛⎭⎫-D 2,-E 2,半径r =12D 2+E 2-4F 两公式易得答案.] 2.D [表示圆应满足D 2+E 2-4F >0.]3.B [过M 最长的弦应为过M 点的直径所在直线.]4.D [先求出圆心坐标(1,-2),再由点到直线距离公式求之.]5.B [先化成标准方程(x -a )2+(y -1)2=2a ,将O (0,0)代入可得a 2+1>2a (0<a <1),即原点在圆外.]6.D [圆心应满足y =x 或y =-x ,等价于x 2-y 2=0.]7.(0,-1)解析 r =12k 2+4-4k 2=124-3k 2. 当k =0时,r 最大,此时圆面积最大,圆的方程可化为x 2+y 2+2y =0,即x 2+(y +1)2=1,圆心坐标为(0,-1).8.-2解析 由题意知圆心⎝⎛⎭⎫-1,-a 2应在直线l :x -y +2=0上,即-1+a 2+2=0,解得 a =-2.9.20 6解析 点(3,5)在圆内,最长弦|AC |即为该圆直径,∴|AC |=10,最短弦BD ⊥AC ,∴|BD |=46,S 四边形ABCD =12|AC |·|BD |=206. 10.解 设过A 、B 、C 三点的圆的方程为x 2+y 2+Dx +Ey +F =0,则⎩⎪⎨⎪⎧ D -5E -F =265D +5E +F =-506D -2E +F =-40,解得⎩⎪⎨⎪⎧D =-4E =-2F =-20. 所以过A 、B 、C 三点的圆的方程为x 2+y 2-4x -2y -20=0.将点D (-2,-1)代入上述方程等式不成立.故A 、B 、C 、D 四点不能在同一个圆上.11.解 (1)方程x 2+y 2-2(t +3)x +2(1-4t 2)y +16t 4+9=0表示一个圆必须有: D 2+E 2-4F =4(t +3)2+4(1-4t 2)2-4(16t 4+9)>0,即:7t 2-6t -1<0,∴-17<t <1. (2)该圆的半径r 满足:r 2=D 2+E 2-4F 4=(t +3)2+(1-4t 2)2-(16t 4+9)=-7t 2+6t +1=-7⎝⎛⎭⎫t -372+167, ∴r 2∈⎝⎛⎦⎤0,167,∴r ∈⎝⎛⎦⎤0,477. 12.解 设圆的一般方程为x 2+y 2+Dx +Ey +F =0,令y =0,得x 2+Dx +F =0,所以圆在x 轴上的截距之和为x 1+x 2=-D ;令x =0,得y 2+Ey +F =0,所以圆在y 轴上的截距之和为y 1+y 2=-E ;由题设,x 1+x 2+y 1+y 2=-(D +E )=2,所以D +E =-2. ①又A (4,2)、B (-1,3)两点在圆上,所以16+4+4D +2E +F =0, ②1+9-D +3E +F =0, ③由①②③可得D =-2,E =0,F =-12,故所求圆的方程为x 2+y 2-2x -12=0.13.解 设点M 的坐标是(x ,y ),点P 的坐标是(x 0,y 0).由于点A 的坐标为(3,0)且M是线段AP 的中点,所以x =x 0+32,y =y 02于是有x 0=2x -3,y 0=2y . 因为点P 在圆x 2+y 2=1上移动,所以点P 的坐标满足方程x 20+y 20=1,则(2x -3)2+4y 2=1,整理得⎝⎛⎭⎫x -322+y 2=14. 所以点M 的轨迹方程为⎝⎛⎭⎫x -322+y 2=14.。
