高考数学课时达标52
2022高考数学总复习(人教A理一轮)课时规范练52 算法初步
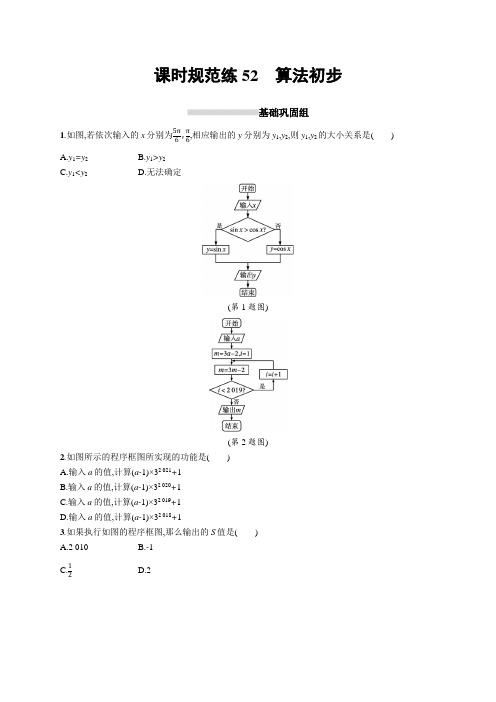
课时规范练52算法初步基础巩固组1.如图,若依次输入的x分别为5π6,π6,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定(第1题图)(第2题图)2.如图所示的程序框图所实现的功能是()A.输入a的值,计算(a-1)×32 021+1B.输入a的值,计算(a-1)×32 020+1C.输入a的值,计算(a-1)×32 019+1D.输入a的值,计算(a-1)×32 018+13.如果执行如图的程序框图,那么输出的S值是()A.2 010B.-1C.12D.2(第3题图)(第4题图)4.秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,a n分别为0,1,2,…,n.若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为()A.248B.258C.268D.2785.执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为()A.0B.1C.2D.3(第5题图)(第6题图)6.按如图所示的程序框图,某同学在区间[0,9]上随机地取一个数作为x输入,则该同学能得到“OK”的概率为()A.12B.19C.1318D.897.某程序框图如图所示,运行该程序后输出S=()A.53B.74C.95D.116(第7题图)(第8题图)8.执行如图的程序框图,如果输入的x∈-π4,π,则输出y的取值范围是() A.[-1,0] B.[-1,√2] C.[1,2] D.[-1,1]综合提升组9.我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是()A.i<20?S=S-1i,i=2iB.i≤20?S=S-1i,i=2iC.i<20?S=S2,i=i+1D.i≤20?S=S2,i=i+110.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.“三分损益”包含“三分损一”和“三分益一”,用现代数学的方法解释如下,“三分损一”是在原来的长度减去一分,即变为原来的三分之二;“三分益一”是在原来的长度增加一分,即变为原来的三分之四,如图的程序是与“三分损益”结合的计算过程,若输入的x的值为1,则输出的x的值为()A.1627B.3227C.89D.2311.条形码是由一组规则排列的条、空及其对应的代码组成,用来表示一定的信息,我们通常见的条形码是“EAN-13”通用代码,它是由从左到右排列的13个数字(用a1,a2,…,a13表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中a13是校验码,用来校验前12个数字代码的正确性.图1是计算第13位校验码的程序框图,框图中符号[M ]表示不超过M的最大整数(例如[365.7]=365).现有一条形码如图2所示(97a37040119917),其中第3个数被污损,那么这个被污损的数字a3是()图1图2A.6B.7C.8D.912.根据某校10位高一同学的身高(单位:cm)画出的茎叶图(图1),其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,设计一个程序框图(图2),用A i(i=1,2,…,10)表示第i个同学的身高,计算这些同学身高的方差,则程序框图①中要补充的语句是()图1图2A.B=B+A iB.B=B+A i 2C.B=(B+A i -A )2D.B=B 2+A i 213.我国南北朝时期的数学家张丘建在《张丘建算经》中给出一个解不定方程的百鸡问题,问题如下:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?用代数方法表述为:设鸡翁、鸡母、鸡雏的数量分别为x ,y ,z ,则鸡翁、鸡母、鸡雏的数量即为方程组{5x +3y +z3=100,x +y +z =100的解.其解题过程可用框图表示如下图所示,则框图中正整数m 的值为 .(第13题图)(第14题图)14.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”.若输入的m,n分别为385,105,执行该程序框图(图中“m MOD n”表示m除以n的余数,例:11 MOD 7=4),则输出的m=.参考答案课时规范练52算法初步1.C由程序框图可知,当输入的x为5π6时,sin5π6>cos5π6成立,所以输出的y1=sin5π6=12;当输入的x为π时,sinπ>cosπ不成立,所以输出的y2=cosπ=√3,所以y1<y2.2.B由程序框图可知a1=a,a n+1=3a n-2,由i的初值为1,末值为2 019可知,此递推公式共执行了2 019+1=2 020(次),又由a n+1=3a n-2,得a n+1-1=3(a n-1),得a n-1=(a-1)×3n-1,即a n=(a-1)×3n-1+1,故a2021=(a-1)×32 021-1+1=(a-1)×32 020+1,故选B.3.D当k=0时,S=-1,k=1时,S=12,当k=2时,S=2,所以S的值呈现周期性变化,周期为3.当k=2 018=3×672+2时,S的值与k=2时的值相等,即S=2.当k=2 019时,k<2 019不成立,输出S=2.故选D.4.B该程序框图是计算多项式f(x)=5x5+4x4+3x3+2x2+x当x=2时的值,f(2)=258,故选B.5.C先画出x ,y 满足的约束条件{x ≥0,y ≥0,x +y ≤1,对应的可行域如图中的阴影部分.平移直线l 0:y=-2x.当直线经过点A (1,0)时,y=-2x+S 中截距S 最大,此时S max =2×1+0=2. 与x ≥0,y ≥0,x+y ≤1不成立时S=1进行比较,可得S max =2. 6.C 当x ∈0,12时,由算法可知y=-2x+2得y ∈[1,2],能得到“OK ”; 当x ∈12,1时,由算法可知y=-2x+2得y ∈(0,1),不能得到“OK ”;当x ∈[1,3)时,由算法可知y=log 3x 得y ∈[0,1),不能得到“OK ”; 当x ∈[3,9]时,由算法可知y=log 3x 得y ∈[1,2],能得到“OK ”;∴P=12+69=1318,故选C .7.D 根据程序框图可知其功能为计算:S=1+11×2+12×3+…+1n (n+1)=1+1-12+12−13+…+1n −1n+1=1+1-1n+1=2n+1n+1,初始值为n=1,当n=6时,输出S ,可知最终赋值S 时n=5,所以S=2×5+15+1=116,故选D .8.B 流程图计算的输出值为分段函数:y={2cos 2x +sin2x -1,x <π2,cos 2x +2sinx -1,x ≥π2,原问题即求解函数在区间[-π4,π]上的值域.当-π4≤x<π2时,y=2cos 2x+sin 2x-1=cos 2x+1+sin 2x-1=√2sin (2x +π4),-π4≤x<π2,则-14π≤2x+π4<54π,此时函数的值域为[-1,√2]. 当π2≤x ≤π时,y=cos 2x+2sin x-1=-sin 2x+2sin x ,π2≤x ≤π,则0≤sin x ≤1,此时函数的值域为[0,1].综上可得,函数的值域为[-1,√2]∪[0,1],即[-1,√2]. 即输出y 的取值范围是[-1,√2].故选B .9.D 根据题意可知,第一天S=12,所以满足S=S 2,不满足S=S-1i,故排除A,B,由框图可知,计算第二十天的剩余时,有S=S 2,且i=21,所以循环条件应该是i ≤20.故选D .10.B 若x=1,则x=23,i=2,则x=89,i=3,则x=3227,i=4,结束循环,输出结果x=3227,故选B . 11.B 由程序框图可知,S 表示的结果为前12项中所有偶数项之和,T 表示的结果为前12项中所有奇数项之和,则 S=7+7+4+1+9+1=29,T=9+a 3+0+0+1+9=19+a 3,M=3×29+19+a 3=106+a 3,由检验码,a 13=7,可知N=10-a 13=3, 结合选项进行检验: 若a 3=6,则N=106+a 3-106+a 310×10=106+6-106+610×10=2,不合题意; 若a 3=7,则N=106+a 3-106+a 310×10=106+7-106+710×10=3,符合题意; 若a 3=8,则N=106+a 3-106+a 310×10=106+8-106+810×10=4,不合题意; 若a 3=9,则N=106+a 3-106+a 310×10=106+9-106+910×10=5,不合题意.故选B .12.B 由s 2=(x 1-x )2+(x 2-x )2+…+(x n -x )2n=x 12+x 22+…+x n 2-2(x 1+x 2+…+x n )x+nx2n=x 12+x 22+…+x n 2-2nx 2+nx 2n=x 12+x 22+…+x n 2n−x 2,循环退出时i=11,知x 2=(A i -1)2.所以B=A 12+A 22+…+A 102,故程序框图①中要补充的语句是B=B+A i 2.故选B .13.4 由{5x +3y +z3=100,x +y +z =100,得y=25-74x ,故x 必为4的倍数,当x=4t 时,y=25-7t ,由y=25-7t>0得t 的最大值为3,故判断框应填入的是“t<4?”,故m=4.14.35 模拟执行程序,可得m=385,n=105,执行循环体,r=70,m=105,n=70,不满足条件r=0,执行循环体;r=35,m=70,n=35,不满足条件r=0,执行循环体;r=0,m=35,n=0,满足条件r=0,退出循环,输出的m 值为35.内容仅供参考后记亲爱的朋友,你好!非常荣幸和你相遇,很乐意为您服务。
高中数学课时达标训练五新人教A版选修1_1

课时达标训练(五)[即时达标对点练]题组1 全称命题、特称命题及其真假判断1.下列四个命题中,既是全称命题又是真命题的是( ) A .斜三角形的内角是锐角或钝角 B .至少有一个实数x ,使x 2>0 C .任意无理数的平方必是无理数 D .存在一个负数x ,使1x>22.以下四个命题既是特称命题又是真命题的是( ) A .锐角三角形的内角是锐角或钝角 B .至少有一个实数x ,使x 2≤0 C .两个无理数的和必是无理数 D .存在一个负数x ,使1x>23.有下列四个命题:①∀x ∈R ,2x 2-3x +4>0;②∀x ∈{1,-1,0},2x +1>0;③∃x 0∈N ,使x 20≤x 0;④∃x 0∈N *,使x 0为29的约数.其中真命题的个数为( )A .1B .2C .3D .4 题组2 全称命题、特称命题的否定4.命题“∀x ∈[0,+∞),x 3+x ≥0”的否定是( ) A .∀x ∈(-∞,0),x 3+x <0 B .∀x ∈(-∞,0),x 3+x ≥0 C .∃x 0∈[0,+∞),x 30+x 0<0 D .∃x 0∈[0,+∞),x 30+x 0≥05.命题“∃x ∈Z ,使x 2+2x +m ≤0”的否定是( ) A .∃x ∈Z ,使x 2+2x +m >0 B .不存在x ∈Z ,使x 2+2x +m >0 C .∀x ∈Z ,使x 2+2x +m ≤0 D .∀x ∈Z ,使x 2+2x +m >06.命题p :“有些三角形是等腰三角形”,则是( )A .有些三角形不是等腰三角形B .所有三角形是等边三角形C .所有三角形不是等腰三角形D .所有三角形是等腰三角形7.命题“∃x ∈R ,使得x 2+2x +5=0”的否定是________________________________. 题组3 全称命题、特称命题的应用8.已知命题“∃x 0∈R ,2x 20+(a -1)x 0+12≤0”是假命题,则实数a 的取值范围是________.9.已知p :∀x ∈R ,2x >m (x 2+1),q :∃x 0∈R ,x 20+2x 0-m -1=0,且p ∧q 为真,求实数m 的取值范围.[能力提升综合练]1.已知命题p :∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≥0,则是( )A .∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0B .∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0C .∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<0D .∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<0 2.下列四个命题中的真命题为( ) A .若sin A =sin B ,则A =B B .∀x ∈R ,都有x 2+1>0 C .若lg x 2=0,则x =1 D .∃x 0∈Z ,使1<4x 0<33.已知命题p :∀x ∈R ,2x 2+2x +12<0;命题q :∃x 0∈R ,sin x 0-cos x 0= 2.则下列判断正确的是( )A .p 是真命题B .q 是假命题C .是假命题 D .是假命题4.已知命题p :∀b ∈[0,+∞),f (x )=x 2+bx +c 在[0,+∞)上为增函数,命题q :∃x 0∈Z ,使log 2x 0>0,则下列结论成立的是( )5.命题p :∃x 0∈R ,x 20+2x 0+5<0是________(填“全称命题”或“特称命题”),它是________命题(填“真”或“假”),它的否定为:________.6.已知a >0,函数f (x )=ax 2+bx +c .若x 0满足关于x 的方程2ax +b =0,则下列四个命题中假命题的序号是________.①∃x ∈R ,f (x )≤f (x 0); ②∃x ∈R ,f (x )≥f (x 0);③∀x ∈R ,f (x )≤f (x 0); ④∀x ∈R ,f (x )≥f (x 0).7.已知p :存在实数x ,使4x +2x·m +1=0成立,若是假命题,求实数m 的取值范围.8.已知p :“∀x ∈[1,2],x 2-a ≥0”,q :“∃x 0∈R ,使x 20+2ax 0+2-a =0”.若命题“p 且q ”是真命题,求实数a 的取值范围.答 案 即时达标对点练1.解析:选A 只有A ,C 两个选项中的命题是全称命题;且A 显然为真命题.因为2是无理数,而(2)2=2不是无理数,所以C 为假命题.2.解析:选BA 中锐角三角形的内角是锐角或钝角是全称命题;B 中x =0时,x 2=0,所以B 既是特称命题又是真命题;C 中因为3+(-3)=0,所以C 是假命题;D 中对于任一个负数x ,都有1x<0,所以D 是假命题.3. 解析:选C 对于①,这是全称命题,由于Δ=(-3)2-4×2×4<0,所以2x 2-3x +4>0恒成立,故①为真命题;对于②,这是全称命题,由于当x =-1时,2x +1>0不成立,故②为假命题; 对于③,这是特称命题,当x 0=0或x 0=1时,有x 20≤x 0成立,故③为真命题; 对于④,这是特称命题,当x 0=1时,x 0为29的约数成立,所以④为真命题. 4. 解析:选C 全称命题:∀x ∈[0,+∞),x 3+x ≥0的否定是特称命题:∃x 0∈[0,+∞),x 30+x 0<0.5. 解析:选D 特称命题的否定为全称命题,否定结论.故选D.6. 解析:选C 在写命题的否定时,一是更换量词,二是否定结论.更换量词:“有些”改为“所有”,否定结论:“是等腰三角形”改为“不是等腰三角形”,故为“所有三角形不是等腰三角形”.故选C.7.解析:“∃x ∈R ,使得x 2+2x +5=0”的否定为“∀x ∈R ,使得x 2+2x +5≠0”. 答案:∀x ∈R ,使得x 2+2x +5≠08. 解析:由题意可得“对∀x ∈R ,2x 2+(a -1)x +12>0恒成立”是真命题,令Δ=(a-1)2-4<0,得-1<a <3.答案:(-1,3)9. 解:由命题p 为真可知2x >m (x 2+1)恒成立, 即mx 2-2x +m <0恒成立,所以⎩⎪⎨⎪⎧m <0,Δ=4-4m 2<0,解得m <-1. 由命题q 为真可得 Δ=4-4(-m -1)≥0, 解得m ≥-2, 因为p ∧q 为真, 所以p 真且q 真,所以由⎩⎪⎨⎪⎧m <-1,m ≥-2,得-2≤m <-1,所以实数m 的取值范围是[-2,-1).能力提升综合练1. 解析:选C 命题p 的否定为“∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<0”.2. 解析:选BA 中,若sin A =sin B ,不一定有A =B ,故A 为假命题,B 显然是真命题;C 中,若lg x 2=0,则x 2=1,解得x =±1,故C 为假命题;D 中,解1<4x <3得14<x <34,故不存在这样的x 0∈Z ,故D 为假命题.3. 解析:选D p :2x 2+2x +12=2⎝⎛⎭⎪⎫x 2+x +14=2⎝ ⎛⎭⎪⎫x +122≥0,∴p 为假命题,为真命题.q :sin x 0-cos x 0=2sin ⎝⎛⎭⎪⎫x 0-π4=2,∴x 0=34π时成立.故q 为真,而为假命题.4. 解析:选D f (x )=x 2+bx +c=⎝ ⎛⎭⎪⎫x +b 22+c -b 24, 对称轴为x =-b2≤0, 所以f (x )在[0,+∞)上为增函数,命题p 是真命题.令x 0=4∈Z ,则log 2x 0=2>0,所以命题q 是真命题,为假命题,p ∨()为真命题.故选D.5. 解析:命题p :∃x 0∈R ,x 20+2x 0+5<0是特称命题.因为x 2+2x +5=(x +1)2+4>0恒成立,所以命题p为假命题,命题p的否定为:∀x∈R,x2+2x+5≥0.答案:特称命题假∀x∈R,x2+2x+5≥06. 解析:由题意:x0=-b2a为函数f(x)图象的对称轴方程,所以f(x0)为函数的最小值,即对所有的实数x,都有f(x)≥f(x0),因此∀x∈R,f(x)≤f(x0)是错误的.答案:③7. 解:∵为假命题,∴p为真命题.即关于x的方程4x+2x·m+1=0有解.由4x+2x·m+1=0,得m=-2x-12x =-⎝⎛⎭⎪⎫2x+12x≤-2.即m的取值范围为(-∞,-2].8. 解:p为真时,x2-a≥0,即a≤x2.∵x∈[1,2]时,上式恒成立,而x2∈[1,4],∴a≤1. q为真时,Δ=(2a)2-4(2-a)≥0,即a≥1或a≤-2.∵p且q为真命题,∴p,q均为真命题.∴a=1或a≤-2.即实数a的取值范围是{a|a=1或a≤-2}.。
高考数学课时达标测试:第1章 第2讲 命题及其关系、充分条件与必要条件

课时达标 第2讲一、选择题1.已知命题p :正数a 的平方不等于0,命题q :若a 不是正数,则它的平方等于0,则q 是p 的( )A .逆命题B .否命题C .逆否命题D .否定B 解析 命题“正数a 的平方不等于0”可写成“若a 是正数,则它的平方不等于0”,从而q 是p 的否命题.2.(2018·天津卷)设x ∈R ,则“⎪⎪⎪⎪x -12<12”是“x 3<1”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件A 解析 由⎪⎪⎪⎪x -12<12得0<x <1,由x 3<1得x <1,而0<x <1⇒x <1,x <1⇒/ 0<x <1.故选A. 3.原命题为“△ABC 中,若cos A <0,则△ABC 为钝角三角形”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( )A .真、真、真B .假、假、真C .真、真、假D .真、假、假B 解析 因为cos A <0,0<A <π,则A 必为钝角,△ABC 为钝角三角形,所以原命题为真,从而逆否命题也为真;△ABC 为钝角三角形,可能是B 或C 为钝角,A 为锐角,则cos A >0,所以逆命题为假,从而否命题也为假.故选B.4.(2018·浙江卷)已知平面α,直线m ,n 满足m ⊄α,n ⊂α,则“m ∥n ”是“m ∥α”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件A 解析 由立体几何知识知m ⊄α,n ⊂α,m ∥n ⇒m ∥α.但m ∥α时,m 与α内的直线n 可能异面.故选A.5.命题“∀x ∈[1,2],x 2-a ≤0”为真命题的一个充分不必要条件是( )A .a ≤4B .a ≥4C .a ≤5D .a ≥5D 解析 命题“∀x ∈[1,2],x 2-a ≤0”为真命题的一个充要条件是∀x ∈[1,2],a ≥x 2恒成立,即a ≥4.故命题“∀x ∈[1,2],x 2-a ≤0”为真命题的一个充分不必要条件是D 项.6.(2019·北京东城期末)下列四个选项中错误的是( )A .命题“若x ≠1,则x 2-3x +2≠0”的逆否命题是“若x 2-3x +2=0,则x =1”B .存在x 0∈R ,使x 20+2x 0+3=0C .“若α=β,则sin α=sin β”的逆否命题为真命题D .“x >2”是“x 2-3x +2>0”的充分不必要条件B解析对于A项,显然正确;对于B项,因为Δ=4-12<0,所以方程无实根,故B项错误;对于C项,“若α=β,则sin α=sin β”为真命题,所以其逆否命题也为真命题,故C项正确;对于D项,x2-3x+2>0的解集是{x|x>2或x<1},故D项正确.二、填空题7.已知命题p:若a>b>0,则log12a<log12b+1,命题p的原命题、逆命题、否命题、逆否命题中真命题的个数为________.解析因为a>b>0,所以log12a<log12b,所以命题p为真命题,其逆命题为:若log12a<log12b+1,则a>b>0,因为a=2,b=2时,log12a<log12b+1,而a=b,所以逆命题为假命题.根据命题与其逆否命题的真假相同,逆命题与否命题的真假相同,知命题p的原命题、逆命题、否命题、逆否命题中只有2个是真命题.答案28.能够说明“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为________.解析取a=-1,b=-2,c=-3,满足a>b>c,但a+b=-3=c,不满足a+b>c,故“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为-1,-2,-3.答案-1,-2,-3(答案不唯一)9.记不等式x2+x-6<0的解集为集合A,函数y=lg(x-a)的定义域为集合B.若“x∈A”是“x∈B”的充分条件,则实数a的取值范围为________.解析由x2+x-6<0得A=(-3,2),由x-a>0得B=(a,+∞),若“x∈A”是“x∈B”的充分条件,则A⊆B,则a≤-3.答案(-∞,-3]三、解答题10.写出“若x=2,则x2-5x+6=0”的逆命题、否命题、逆否命题,并判断其真假.解析逆命题:若x2-5x+6=0,则x=2,是假命题;否命题:若x≠2,则x2-5x+6≠0,是假命题;逆否命题:若x2-5x+6≠0,则x≠2,是真命题.11.已知函数f(x)=lg(x2-2x-3)的定义域为集合A,函数g(x)=2x-a(x≤2)的值域为集合B.(1)求集合A,B;(2)已知p:m∈A,q:m∈B,若綈p是綈q的充分不必要条件,求实数a的取值范围.解析(1)A={x|x2-2x-3>0}={x|(x-3)(x+1)>0}={x|x<-1或x>3},B={y|y=2x-a,x≤2}={y|-a <y≤4-a}.(2)因为綈p是綈q的充分不必要条件,所以q是p的充分不必要条件,所以B A,所以4-a<-1或-a≥3,所以a≤-3或a>5,即实数a的取值范围是(-∞,-3]∪(5,+∞).12.已知p:A={x|x2-2x-3≤0,x∈R},q:B={x|x2-2mx+m2-9≤0,x∈R,m∈R}.(1)若A ∩B =[1,3],求实数m 的值;(2)若p 是綈q 的充分条件,求实数m 的取值范围.解析 (1)由题意得A ={x |-1≤x ≤3,x ∈R },B ={x |m -3≤x ≤m +3,x ∈R ,m ∈R },因为A ∩B =[1,3],所以m -3=1,解得m =4.(2)因为p 是綈q 的充分条件,所以A ⊆(∁R B ),因为∁R B ={x |x <m -3或x >m +3,x ∈R ,m ∈R },所以m -3>3或m +3<-1,解得m >6或m <-4,即实数m 的取值范围是(-∞,-4)∪(6,+∞).13.[选做题](2019·商南高中模拟)在△ABC 中,设p :a sin B =b sin C =c sin A,q :△ABC 是等边三角形,那么p 是q 的( )A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件A 解析 a sinB =b sinC =c sin A ,即2R sin A sin B =2R sin B sin C,R 为△ABC 外接圆半径,所以sin A sin C =sin 2B ①;2R sin B sin C =2R sin C sin A,sin A sin B =sin 2 C ②. ①-②,得(sin C -sin B )(sin A +sin B +sin C )=0,则sin C =sin B ,所以C =B .代入①得C =A ,所以A =B=C ,则△ABC 是等边三角形.当△ABC 为等边三角形时,即A =B =C ,a =b =c 时,a sin B =b sin C =c sin A=2R 成立,所以p 是q 的充要条件.故选A.。
新教材老高考适用2023高考数学一轮总复习课时规范练50二项式定理北师大版

课时规范练50 二项式定理基础巩固组1.(x +12x )6的展开式中的第3项为( ) A.3x 4B.52C.154x 2D.1516x 22.(1x -1)5的展开式中x -2的系数是( ) A.15 B.-15 C.10D.-103.(2021湖南怀化一模)(x 2+1)(1x -2)5展开式的常数项为( ) A.112 B.48 C.-112D.-484.(2021湖北荆门月考)若(x √x3)8的展开式中x 4的系数为7,则展开式的常数项为( )A.716 B.12 C.-716D.-125.(2021广东湛江三模)(1+3x )2+(1+2x )3+(1+x )4=a 0+a 1x+a 2x 2+a 3x 3+a 4x 4,则a 0+a 1+a 2+a 3+a 4= ( )A.49B.56C.59D.646.(x +1x -2)6的展开式中含x 5项的系数为( ) A.12 B.-12 C.24D.-247.对于二项式(1x+x 3)n (n ∈N *),以下判断正确的有( )①存在n ∈N *,展开式中有常数项 ②对任意n ∈N *,展开式中没有常数项 ③对任意n ∈N *,展开式中没有含x 的项 ④存在n ∈N *,展开式中有含x 的项 A.①③B.②④C.②③D.①④8.(2021福建漳州模拟)已知(x+1)6=a 0+a 1(x-1)+a 2(x-1)2+…+a 6(x-1)6,则a 4= . 9.(2021湖南长郡中学模拟三)若(x -12x )n的展开式中只有第5项的二项式系数最大,则展开式中常数项为 .(用数字作答)综合提升组10.(2021河南郑州一模)式子(x -y 2x)(x+y )5的展开式中,x 3y 3的系数为( ) A.3 B.5 C.15 D.2011.已知(ax 2+√x)n(a>0)的展开式中第5项与第7项的二项式系数相等,且展开式的各项系数之和为1 024,则下列说法不正确的是( ) A.展开式中奇数项的二项式系数和为256 B.展开式中第6项的系数最大 C.展开式中存在常数项D.展开式中含x 15的项的系数为45 12.(2021河北石家庄一模)关于(1-2x )2 021=a 0+a 1x+a 2x 2+…+a 2 021x 2 021(x ∈R ),则( )A.a 0=0B.a 1+a 2+a 3+…+a 2 021=32 021C.a 3=8C 20213D.a 1-a 2+a 3-a 4+…+a 2 021=1-32 02113.(2021安徽蚌埠高三开学考试(理))若二项式(x +12)n展开式中第4项的系数最大,则n 的所有可能取值的个数为 .14.(2021福建宁德三模)已知(a +1x)(1+x )5展开式中的所有项的系数和为64,则实数a= ;展开式中常数项为 .创新应用组15.设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(mod m).若a=C200+C201·2+C202·22+…+C2020·220,a≡b(mod 10),则b的值可以是()A.2 018B.2 019C.2 020D.2 02116.“杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律,最早在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现.如下图,在由二项式系数所构成的“杨辉三角”中,第10行中从左至右第5与第6个数的比值为.课时规范练50 二项式定理1.C 解析∵(a+b )n的二项式通项为T k+1=C n k ·a n-k·b k,∴(x +12x )6的展开式中的第3项是T 3=T 2+1=C 62·x 6-2·(12x )2=154x 2. 2.D 解析(1x-1)5的二项式通项T k+1=C 5k (1x )5-k ·(-1)k =(-1)k ·C 5k x k-5,当k=3时,T 4=-C 53x -2=-10x -2,即x -2的系数为-10.3.C 解析由题得,(1x -2)5的二项式通项为T r+1=C 5r (-2)r x r-5,令r=3,r=5,得展开式的常数项为C 53×(-2)3+(-2)5=-112.故选C .4.A 解析(x √x 3)8的二项式通项为T r+1=C 8r x 8-r (√x3)r=C 8r (-a )r x 8-43r .令8-43r=4,解得r=3,所以展开式中x 4的系数为C 83(-a )3=7,解得a=-12,所以(x √x3)8的二项式通项为T r+1=C 8r (12)rx 8-43r .令8-43r=0,解得r=6,所以展开式的常数项为C 86×(12)6=716.故选A .5.C 解析令x=1,a 0+a 1+a 2+a 3+a 4=(1+3)2+(1+2)3+(1+1)4=59.故选C . 6.B 解析由(x +1x -2)6=(x 2-2x+1x)6=(x -1)12x 6,则(x-1)12的二项式通项为T r+1=C 12rx12-r(-1)r=(-1)rC 12rx12-r.当r=1,此时T 2=-1×C 121x 11=-12x 11,可得(x -1)12x 6展开式中x 5项的系数为-12.故选B .7.D 解析设(1x +x 3)n (n ∈N *)的二项式通项为T k+1,则T k+1=C n k (1x )n -k(x 3)k =C n k x4k-n,不妨令n=4,则当k=1时,展开式中有常数项,故①正确,②错误;令n=3,则当k=1时,展开式中有含x 的项,故③错误,④正确.故选D .8.60 解析∵(x+1)6=[(x-1)+2]6,∴展开式通项T r+1=C 6r(x-1)6-r 2r.由题知,a 4对应6-r=4,则可得r=2.∴T 3=C 62(x-1)4·22=4C 62(x-1)4,即a 4=4C 62=60.9.358 解析(x -12x )n的展开式中只有第5项的二项式系数最大,则由二项式系数性质知,展开式共有9项,则n=8.(x -12x )8的二项式通项为T r+1=C 8r x 8-r·(-12x )r =(-12)rC 8rx 8-2r,令8-2r=0,解得r=4.所以展开式中常数项为T 5=(-12)4×C 84=116×70=358.10.B 解析∵(x -y 2x)(x+y )5=x (x+y )5-y 2x (x+y )5, 则x (x+y )5的二项式通项为T k+1=x C 5k x 5-k y k=C 5k x 6-k y k, y 2x(x+y )5的二项式通项为T r+1=y 2xC 5r x 5-r y r=C 5rx 4-r y r+2,由{6-k =3,4-r =3,解得{k =3,r =1. 故式子(x -y 2x)(x+y )5的展开式中,x 3y 3的系数为C 53−C 51=5. 故选B .11.A 解析由二项展开式中第5项与第7项的二项式系数相等可知n=10.又因为展开式的各项系数之和为1024,即当x=1时,(a+1)10=1024,所以a=1.所以二项式为(x 2√x)10=(x 2+x -12)10.二项式系数和为210=1024,则奇数项的二项式系数和为12×1024=512,故A 不正确;由n=10可知展开式共有11项,中间项的二项式系数最大,即第6项的二项式系数最大,因为x 2与x -12的系数均为1,则该二项式展开式的二项式系数与系数相同,所以第6项的系数最大,故B 正确;若展开式中存在常数项,由二项式通项T k+1=C 10k x 2(10-k )·x -12k 可得2(10-k )-12k=0,解得k=8,故C 正确;由二项式通项T k+1=C 10kx2(10-k )x -12k 可得2(10-k )-12k=15,解得k=2,所以展开式中含x 15的项的系数为C 102=45,故D 正确.故选A .12.D 解析令x=0,则12021=a 0,即a 0=1,故A 错误;令x=1,则(1-2)2021=a 0+a 1+a 2+…+a 2021,即a 0+a 1+a 2+a 3+…+a 2021=-1,所以a 1+a 2+a 3+…+a 2021=-2,故B 错误;根据二项式通项得,a 3=C 20213×12018×(-2)3=-8C 20213,故C 错误;令x=1,则a 0+a 1+a 2+a 3+…+a 2021=-1, 令x=-1,则a 0-a 1+a 2-a 3+…-a 2021=(1+2)2021=32021,两式相加可得a 0+a 2+…+a 2020=32021-12, ① 两式相减可得a 1+a 3+…+a 2021=-1-320212,②②-①可得-a 0+a 1-a 2+a 3-a 4+…+a 2021=-1-32021-32021+12=-32021,所以a 1-a 2+a 3-a 4+…+a 2021=1-32021,故D 正确.故选D .13.4 解析因为(x +12)n的二项式通项为C n r x n-r (12)r=C n r (12)r x n-r.由题意可得{C n 3(12)3≥C n 2(12)2,C n 3(12)3≥C n 4(12)4,即{n -2≥6,8≥n -3,故8≤n ≤11.又因为n 为正整数,所以n=8或9或10或11,故n 的所有可能取值的个数为4.14.1 6 解析令x=1,可得(a +1x)(1+x )5展开式中的所有项的系数和为32(a+1)=64,解得a=1.则展开式中常数项为a ×C 50+C 51=1+5=6.15.D 解析a=C 200+C 201·2+C 202·22+…+C 2020·220=(1+2)20=320=(80+1)5,它被10除所得余数为1.又因为a ≡b (mod10),所以b 的值可以是2021.16.56 解析由题意第10行的数就是(a+b )10的展开式中各项的二项式系数,因此从左至右第5与第6个数的比值为C 104C 105=56.。
2020年高考数学(文科)一轮复习 第九单元 听课手册 第52讲随机事件的概率

听课手册第52讲随机事件的概率1.概率和频率(1)频率:在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数n A为事件A出现的频数,称事件A出现的比例f n(A)= 为事件A出现的.(2)概率:对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动并,我们可以用这个常数来刻画随机事件A发生的可能性的大小,并把这个常数称为随机事件A的,记作P(A).(3)频率与概率的关系:频率反映了一个随机事件出现的频繁程度,但频率是随机的,而概率是一个的值,因此,人们用概率来反映随机事件发生的可能性的大小,有时也用频率作为随机事件概率的估计值.2.事件的关系与运算3.概率的几个基本性质(1)概率的取值范围:.(2)必然事件A的概率P(A)= .(3)不可能事件A的概率P(A)= .(4)概率的加法公式:如果事件A与事件B互斥,则P(A∪B)= .(5)对立事件的概率:若事件A与事件B互为对立事件,则P(A)= .题组一常识题1.[教材改编]一次射击训练中,66名队员各射击一次,所得环数统计如下:3环,2人;4环,4人;5环,9人;6环,18人;7环,11人;8环,12人;9环,7人;10环,3人.则不少于7环的频数为;不少于7环的概率约为.2.[教材改编]给出下列命题,其中真命题有个.①有一大批产品,已知次品率为10%,从中任取100件,必有10件是次品;②做7次抛硬币的试验,结果3次出现正面,因此正面出现的概率是;③随机事件发生的频率就是这个随机事件发生的概率.3.[教材改编]如果从不包括大小王的52张扑克牌中随机抽取1张,那么取到红心的概率是,取到方块的概率是,则“取到红心”与“取到方块”是(填“互斥事件”“对立事件”),取到黑色牌的概率是.题组二常错题◆索引:混淆对立事件和互斥事件的概念而判断错误;频率与概率的关系理解不清致错.4.从1,2,3,4,5这五个数中任取两个数,给出下列四组事件:①恰有一个是偶数和恰有一个是奇数;②两个都是偶数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.上述每组事件中,是互斥事件的有;是对立事件的有.5.击中靶心的概率约为.6.同时掷3枚硬币,至少有1枚正面向上的概率是.探究点一事件关系的判断例1 (1)在5张电话卡中,有3张移动卡和2张联通卡,从中任取2张,若事件“2张全是移动卡”的概率是,那么概率为的事件是()A.至多有1张移动卡B.恰有1张移动卡C.都不是移动卡D.至少有1张移动卡(2)口袋里装有1红、2白、3黄共6个形状相同的小球,从中取出2个小球.事件A=“取出的2个小球同色”,事件B=“取出的2个小球中至少有1个黄球”,事件C=“取出的2个小球中至少有1个白球”,事件D=“取出的2个小球不同色”,事件E=“取出的2个小球中至多有1个白球”.下列结论中,正确结论的序号为.①A与D为对立事件;②B与C是互斥事件;③C与E是对立事件;④P(C∪E)=1.[总结反思] 判断事件关系时的常用方法:(1)利用集合观点判断事件关系;(2)写出所有的试验结果,看所求事件中包含哪几个试验结果,从而判断所求事件的关系.变式题(1)口袋中装有形状相同的3个白球和4个黑球,从中任取3个球,则:①恰有1个白球和全是白球;②至少有1个白球和全是黑球;③至少有1个白球和至少有2个白球;④至少有1个白球和至少有1个黑球.在上述事件中,是对立事件的为()A.①B.②C.③D.④(2)有一个游戏,其规则是甲、乙、丙、丁四个人从同一地点随机地向东、南、西、北四个方向前进,每人一个方向.事件“甲向南”与事件“乙向南”是()A.互斥但不对立事件B.对立事件C.相互独立事件D.以上都不对探究点二随机事件的频率与概率例2[2017·全国卷Ⅲ]某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.[总结反思] (1)概率与频率的关系:频率反映了一个随机事件出现的频繁程度,频率随着试验次数的变化而变化,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,有时也用频率作为随机事件概率的估计值.(2)求频率的关键是确定频数,解题时要将已知条件转化为确定频数的条件,从而计算频数.变式题某鲜花店将一个月(30天)某品种鲜花的日销售量与销售天数统计如下表,将日销售量在各区间的销售天数占总天数的值视为概率.(1)求这30(2)若此花店在日销售量低于100枝的时候选择一天做促销活动,求这一天恰好是在日销售量低于50枝时的概率.探究点三互斥事件与对立事件的概率例3 经统计,在某储蓄所一个营业窗口等候的人数及相应的概率如下:求:(1)至多2(2)至少3人排队等候的概率.[总结反思] 求复杂事件概率的两种常用方法:(1)直接法:将所求事件分解为一些彼此互斥的事件的和,运用互斥事件概率的加法公式计算.(2)间接法:先求此事件的对立事件,再用公式P(A)=1-P()求得,即运用逆向思维(正难则反)求解,特别是“至多”“至少”型题目,用间接法往往会比较简便.变式题某商场有奖销售活动中,购满100元商品得1张奖券,多购多得.1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖分别为事件A,B,C,求:(1)P(A),P(B),P(C);(2)1张奖券的中奖概率;(3)1张奖券不中特等奖且不中一等奖的概率.完成课时作业(五十二)。
2019-2020年高中数学《第52课时计数原理和排列组合》教学案新人教A版必修3

2019-2020年高中数学《第52课时计数原理和排列组合》教学案新人教A版必修3基础训练1. 有四位老师在同一年级的4个班级中,各教一个班的数学,在数学考试时,要求每位老师均不在本班监考,则安排监考的方法总数是________种.2. 4位同学从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法有________种.3.从a、b、c、d、e五人中选1名班长,1名副班长,1名学习委员,1名纪律委员,1名文娱委员,但a不能当班长,b不能当副班长.不同选法总数为________种.4.五名学生报名参加四项体育比赛,每人限报一项,则报名方法的种数为________.五名学生争夺四项比赛的冠军(冠军不并列),获得冠军的可能性有________种.5.三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过5次传递后,毽又被踢回给甲,则不同的传递方式共有________种.重点讲解1.分类计数原理完成一件事,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,……,在第n类方式中有m n种不同的方法,则完成这件事情,共有N=m1+m2+…+m n种不同的方法.2.分步计数原理完成一件事,需要分成n个不同的步骤,完成第1步有m1种不同的方法,完成第2步有m2种不同的方法,……,完成第n步有m n种不同的方法,那么完成这件事情共有N =m1×m2×…×m n种不同的方法.3.排列(1)排列的定义:从n个不同的元素中取出m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.(2)排列数的定义:从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号A m n表示.(3)排列数公式:A m n=n(n-1)(n-2)…(n-m+1),其中n、m∈N*,且m≤n.(4)全排列:n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列,A n n=n·(n-1)·(n-2)·…·2·1=n!.排列数公式写成阶乘的形式为A m n=n!(n-m)!,这里规定0!=14.组合(1)组合的定义:从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.(2)组合数的定义:从n 个不同元素中取出m(m ≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m 个元素的组合数,用符号C m n 表示.(3)组合数的计算公式:C m n =A m n A m m =n !m !(n -m )!=n (n -1)(n -2)…(n -m +1)m !,由于0!=1,所以C 0n =1.(4)组合数的性质:①C m n =C n -m n __;②C m n +1=C m n __+C m -1n __. 典题拓展例1.高三一班有学生50人,男生30人,女生20人;高三二班有学生60人,男生30人,女生30人;高三三班有学生55人,男生35人,女生20人。
高考数学(人教文科)总复习(福建专用)配套训练:课时规范练52 Word版含解析

课时规范练52古典概型基础巩固组1.(2017安徽马鞍山一模,文6)从正五边形的5个顶点中随机选择3个顶点,则以它们作为顶点的三角形是锐角三角形的概率是()A. B. C. D.2.同时抛掷两个骰子,则向上的点数之差的绝对值为4的概率是()A. B. C. D.3.从甲、乙等5名学生中随机选出2人,则甲被选中的概率为()A. B. C. D.4.一名同学先后投掷一枚骰子两次,第一次向上的点数记为x,第二次向上的点数记为y,在平面直角坐标系xOy中,以(x,y)为坐标的点落在直线2x+y=8上的概率为()A. B. C. D.5.从集合{2,3,4,5}中随机抽取一个数a,从集合{1,3,5}中随机抽取一个数b,则向量m=(a,b)与向量n=(1,-1)垂直的概率为()A. B. C. D.6.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.7.将一颗质地均匀的骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设任意投掷两次使直线l1:x+ay=3,l2:bx+6y=3平行的概率为p1,不平行的概率为p2,若点(p1,p2)在圆(x-m)2+y2=的内部,则实数m的取值范围是.8.(2017江西宜春中学3月模拟,文19)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.9.(2017辽宁鞍山一模,文18)上周某校高三年级学生参加了数学测试,年级部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);……第六组[90,100],并据此绘制了如图所示的频率分布直方图.(1)估计这次月考数学成绩的平均分和众数;(2)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间[90,100]内的概率.〚导学号24190953〛综合提升组10.设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率为()A. B. C. D.11.(2017湖北武昌1月调研,文14)已知某射击运动员,每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;因为射击4次,所以以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数: 57270293714098570347437386369647141746980371623326168045601136619597742467104281据此估计,该射击运动员射击4次至少击中3次的概率为.12.抛掷两枚质地均匀的骰子,得到的点数分别为a,b,则使得直线bx+ay=1与圆x2+y2=1相交且所得弦长不超过的概率为.13.(2017湖南邵阳一模,文19)空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.现统计邵阳市市区2017年10月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.(1)求这60天中属轻度污染的天数;(2)求这60天空气质量指数的平均值;(3)将频率分布直方图中的五组从左到右依次命名为第一组,第二组,……第五组.从第一组和第五组中的所有天数中抽出两天,记它们的空气质量指数分别为x,y,求事件|x-y|≤150的概率.〚导学号24190954〛创新应用组14.已知M={1,2,3,4},若a∈M,b∈M,则函数f(x)=ax3+bx2+x-3在R上为增函数的概率是()A. B. C. D.15.(2017北京丰台一模,文18)某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表.[90,100]2(1)根据A公司的频率分布直方图,估计该公司满意度评分的中位数;(2)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;(3)请从统计角度,对A,B两家公司做出评价.答案:1.C从正五边形的5个顶点中随机选择3个顶点,基本事件总数为n=10,它们作为顶点的三角形是锐角三角形的方法种数为5,故以它们作为顶点的三角形是锐角三角形的概率是P=.故选C.2.C同时抛掷两枚骰子,基本事件总数为36,记“向上的点数之差的绝对值为4”为事件A,则事件A包含的基本事件有(1,5),(2,6),(5,1),(6,2),共4个,故P(A)=.3.B从甲、乙等5名学生中选2人有10种方法,其中2人中包含甲的有4种方法,故所求的概率为.4.B依题意,以(x,y)为坐标的点共有6×6=36个,其中落在直线2x+y=8上的点有(1,6),(2,4),(3,2),共3个,故所求事件的概率P=.5.A由题意可知m=(a,b)有:(2,1),(2,3),(2,5),(3,1),(3,3),(3,5),(4,1),(4,3),(4,5),(5,1),(5,3),(5,5),共12种情况.因为m⊥n,即m·n=0,所以a×1+b×(-1)=0,即a=b,满足条件的有(3,3),(5,5),共2个,故所求的概率为.6.(方法一)将一颗质地均匀的骰子先后抛掷2次,共有36个基本事件.其中向上的点数之和小于10的基本事件共有30个,所以所求概率为.(方法二)将一颗质地均匀的骰子先后抛掷2次,共有36个基本事件.记A表示“向上的点数之和小于10”,则表示“向上的点数之和不小于10”,的基本事件共有6个,所以P()=,P(A)=1-P()=.7.由题意可知直线l1的斜率k1=-,直线l2的斜率k2=-.∵l1∥l2,∴k1=k2.∴-=-.∴ab=6.∴能使l1∥l2的情况有(1,6),(2,3),(3,2),(6,1),共4种.又总的基本事件有36种,∴能使l1∥l2的概率为p1=,不平行的概率为p2=.∴由-,解得m的取值范围是.8.解(1)从袋中随机取两个球,其一切可能的结果组成的基本事件有1,4和2,1和3,1和4,2和3,2和4,3,共6个.从袋中取出的球的编号之和不大于4的事件共有1,3和2,1两个.因此所求事件的概率P=.(2)先从袋中随机取一个球,记下编号为m,放回后,再从袋中随机取一个球,记下编号为n,其一切可能的结果(m,n)有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.又满足条件n≥m+2的事件为:(1,3),(1,4),(2,4),共3个,所以满足条件n≥m+2的事件的概率为P1=.故满足条件n<m+2的事件的概率为1-P1=1-.9.解(1)因为各组的频率之和为1,所以成绩在区间[80,90)内的频率为1-(0.005×2+0.015+0.020+0.045)×10=0.1,所以平均分为0.05×45+0.15×55+0.45×65+0.20×75+0.10×85+0.05×95=68(分),众数的估计值是65.(2)设A表示事件“在成绩大于等于80分的学生中随机选2名,至少有1名学生的成绩在区间[90,100]内”,由题意可知成绩在区间[80,90)内的学生有:40×0.1=4,记这4名学生分别为a,b,c,d,成绩在区间[90,100]内的学生有0.005×10×40=2(人),记这2名学生分别为e,f,则从这6人中任选2人的基本事件空间为:Ω={(a,b),(a,c),(a,d),(a,e),(a,f),(b,c)(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)}共15种, 事件“至少有1名学生的成绩在区间[90,100]内”的可能结果为:A={(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f)},共9种,故所求事件的概率为P(A)=.10.C因为f(x)=x3+ax-b,所以f'(x)=3x2+a.因为a∈{1,2,3,4},所以f'(x)>0,所以函数f(x)在区间[1,2]上为增函数.若存在零点,则f(1)f(2)≤0,解得a+1≤b≤8+2a.因此,可使函数在区间[1,2]上有零点的有:a=1,2≤b≤10,故b=2,b=4,b=8,共有3种情况;a=2,3≤b≤12,故b=4,b=8,b=12,共有3种情况;a=3,4≤b≤14,故b=4,b=8,b=12,共有3种情况;a=4,5≤b≤16,故b=8,b=12,共有2种情况.所以有零点共有3+3+3+2=11种情况.而构成函数共有4×4=16个,根据古典概型可得有零点的概率为.11.0.75由题意知模拟射击4次的结果,经随机模拟产生了20组随机数,在20组随机数中表示射击4次至少击中3次的有:572702939857034743738636964746986233261680453661959774244281,共15组随机数,故所求概率约为=0.75.12.由题意可知抛掷两枚质地均匀的骰子得到的点数(a,b)有(1,1),(1,2),(1,3),…,(6,6),共36种.因为直线bx+ay=1与圆x2+y2=1相交,且所得弦长不超过,所以1>,即1<a2+b2≤9.故满足直线bx+ay=1与圆x2+y2=1相交,且所得弦长不超过的(a,b)有(1,1),(1,2),(2,1),(2,2),共4种,因此所求的概率为.13.解(1)依题意知,轻度污染即空气质量指数在151~200之间,共有0.003×50×60=9(天).(2)由直方图知这60天空气质量指数的平均值为=25×0.1+75×0.4+125×0.3+175×0.15+225×0.05=107.5.(3)第一组和第五组的天数分别为60×0.1=6,60×0.05=3,则从9天中抽出2天的一切可能结果的基本事件有36种,由|x-y|≤150知两天只能在同一组中,而两天在同一组中的基本事件有18种,用M表示|x-y|≤150这一事件,则P(M)=.14.A记事件A为“函数f(x)=ax3+bx2+x-3在R上为增函数”.因为f(x)=ax3+bx2+x-3,所以f'(x)=3ax2+2bx+1.当函数f(x)在R上为增函数时,f'(x)≥0在R上恒成立.又a>0,所以Δ=(2b)2-4×3a=4b2-12a≤0在R上恒成立,即a≥.当b=1时,有a≥,故a可取1,2,3,4,共4个数;当b=2时,有a≥,故a可取2,3,4,共3个数;当b=3时,有a≥3,故a可取3,4,共2个数;当b=4时,有a≥,故a无可取值.综上,事件A包含的基本事件有4+3+2=9种.又a,b∈{1,2,3,4},所以所有的基本事件共有4×4=16种.故所求事件A的概率为P(A)=.故选A.15.解(1)设A公司调查的40份问卷的中位数为x,则有0.015×10+0.025×10+0.03×(x-70)=0.5,解得x≈73.3,所以,估计该公司满意度得分的中位数为73.3.(2)满意度高于90的问卷共有6份,其中4份评价A公司,设为a1,a2,a3,a4,2份评价B公司,设为b1,b2.从这6份问卷中随机取2份,所有可能的结果有:(a1,a2),(a1,a3),(a1,a4),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2),共有15种.其中2份问卷都评价A公司的有以下6种:(a1,a2),(a1,a3),(a1,a4),(a2,a3),(a2,a4),(a3,a4).设两份问卷均是评价A公司为事件C,则有P(C)=.(3)由所给两个公司的调查满意度得分知:A公司得分的中位数低于B公司得分的中位数,A公司得分集中在[70,80)这组,而B公司得分集中在[70,80)和[80,90)两个组,A公司得分的平均数低于B公司得分的平均数,A公司得分比较分散, 而B公司得分相对集中,即A公司得分的方差高于B公司得分的方差.。
高三江苏专版数学一轮复习课时作业(52)概率综合问题.pdf

课时作业(五十二) [第52讲 概率综合问题] [时间:45分钟 分值:100分] 1.从装有5只红球、5只白球的袋中任意取出3只球,有事件:(1) “取出2只红球和1只白球”与“取出1只红球和2只白球”;(2)“取出2只红球和1只白球”与“取出3只红球”;(3) “取出3只红球”与“取出3只球中至少有1只白球”;(4) “取出3只红球”与“取出3只白球”.其中是对立事件的有________. 2.某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是________. 3.某饭店有11张餐桌.据统计,在就餐时间,在4张或4张以下餐桌上有顾客的概率为0.20 ,在5至8张餐桌上有顾客的概率为0.35;在9至11张餐桌上有顾客的概率为0.30,则顾客到饭店后因没有餐桌而到别的饭店就餐的概率为________. 4.把红,黑,白,蓝四张纸牌随机地分给甲,乙,丙,丁四个人,每人分得一张,事件“甲分得红牌”和事件“乙分得红牌”是________.(填“不是互斥事件”或“互斥但非对立事件”或“对立事件”) 5.甲、乙2人下棋,下成和棋的概率是,乙获胜的概率是,则甲不胜的概率是________. 图K52-1 6.如图K52-1,圆形靶子被分成面积相等的三部分,并分别染上红色、黄色、蓝色.两人分别向靶子上投射一支飞镖,假设一定中靶,且投中靶面上任一点都是等可能的,则两人所投中区域的颜色不同的概率是________. 7.已知某运动员每次投篮命中的概率等于40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数: 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,该运动员三次投篮恰有两次命中的概率为________. 8.甲、乙两人将参加某项测试,他们能达标的概率分别是0.8、0.7,则两人都达标的概率是________,两人中至少有一人达标的概率是________. 9.黄种人群中各种血型的人所占的比如下表所示: 血型ABABO该血型的人所占的比(%)2829835已知同种血型的人可以输血,O型血可以输给任一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.小明是B型血,若小明因病需要输血,任找一个人,其血可以输给小明的概率是________. 10.[2011·南通二模] 把一个体积为27 cm3的正方体木块表面涂上红漆,然后锯成体积为1 cm3的27个小正方体,现从中任取一块,则这一块至少有一面涂有红漆的概率为________. 11.设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,nN),若事件Cn的概率最大,则n的所有可能值为________. 12.[2011·江西卷] 小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于,则周末去看电影;若此点到圆心的距离小于,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为________. 13.(8分)袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为,得到黑球或黄球的概率是,得到黄球或绿球的概率也是,试求得到黑球、得到黄球、得到绿球的概率各是多少? 14.(8分)[2011·东莞一模] 某班主任统计本班50名学生放学回家后学习时间的数据,用条形图表示(如图K52-2). (1)求该班学生每天在家学习时间的平均值; (2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话,求在学习时间为1个小时的学生中选出的人数; (3)假设学生每天在家学习时间为18时至23时,已知甲每天连续学习2 h,乙每天连续学习3 h,求22时甲、乙都在学习的概率. 图K52-2 15.(12分)[2011·南通三模] 某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下: 组号分组频数频率第一组[230,235)80.16第二组[235,240)0.24第三组[240,245)15第四组[245,250)100.20第五组[250,255]50.10合 计501.00(1)写出表中位置的数据; (2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数; (3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率. 16.(12分)某商场有奖销售中,购满100元商品得1张奖券,多购多得,每1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C.求: (1)P(A),P(B),P(C); (2)1张奖券的中奖概率; (3)1张奖券不中特等奖且不中一等奖的概率. 课时作业(五十二) 【基础热身】 1. [解析] 由定义可得互斥事件是,其中“取出3只红球”不发生,则“取出3个球中至少有一个白球”必然发生,因此是对立事件. 2.两次都不中靶 [解析] “连续射击2次”包含的基本事件有“(+,+),(+,-),(-,+),(-,-)”(“+”表示“中靶”,“-”表示“没有中靶”),“至少一次中靶”与“两次都不中靶”不可能同时发生,所以“至少有一次中靶”的互斥事件是“两次都不中靶”. 3.0.15 [解析] 所求的概率为P=1-0.20-0.35+0.30=0.15. 4.互斥但非对立事件 [解析] “甲分得红牌”不发生,事件“乙分得红牌”不一定发生,有可能丙或丁分得红牌. 【能力提升】 5. [解析] 甲不胜包含和棋和乙胜,所以所求的概率为P=+=. 6. [解析] 两人分别向靶子上投射一支飞镖,有9种不同的结果,颜色相同的情况有3种,则颜色相同的概率为=,所以颜色不同的概率为P=1-=. 7.0.25 [解析] 通过阅读可知20组随机数中,只有191,271,932,812,393为恰好有两次命中,据此可知20组中占了5组,故其概率是0.25. 8.0.56 0.94 [解析] 两人均达标为0.8×0.7=0.56,两人都不达标的概率为(1-0.8)×(1-0.7)=0.06,所以两人中至少有一人达标为1-0.06=0.94. 9.0.64 [解析] 对任一人,其血型为A,B,AB,O型血的事件分别记为A′,B′,C′,D′,它们是互斥的.由已知,有P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件B′+D′.根据互斥事件的加法公式,有P(B′+D′)=P(B′)+P(D′)=0.29+0.35=0.64. 10. [解析] 因“至少有一面涂有红漆”的对立事件是“每面都没有红漆”,只有中心一块如此,所以,所求概率为P=1-=. 11.3和4 [解析] 总事件数为6.只要求出当n=2,3,4,5时的基本事件个数即可. 当n=2时,落在直线x+y=2上的点为(1,1); 当n=3时,落在直线x+y=3上的点为(1,2)、(2,1); 当n=4时,落在直线x+y=4上的点为(1,3)、(2,2); 当n=5时,落在直线x+y=5上的点为(2,3). 显然,当n=3,4时,事件Cn的概率最大为. 12. [解析] 设A={小波周末去看电影},B={小波周末去打篮球},C={小波周末在家看书},D={小波周末不在家看书},如图所示,则P(D)=1-P(C)=1-=. 13.[解答] 从袋中任取一球,记事件“得到红球”、“得到黑球”、“得到黄球”、“得到绿球”分别为A、B、C、D, 则有P(B+C)=P(B)+P(C)=; P(C+D)=P(C)+P(D)=; 又P(A)=,P(A)+P(B)+P(C)+P(D)=1, 解得P(B)=,P(C)=,P(D)=. 即得到黑球、得到黄球、得到绿球的概率分别是、、. 14.[解答] (1)平均学习时间为 =1.8小时. (2)20×=4. (3)设甲开始学习的时刻为x,乙开始学习的时刻为y,试验的全部结果所构成的区域为Ω={(x,y)|18≤x≤21,18≤y≤20},面积SΩ=2×3=6.事件A表示“22时甲、乙正在学习”,所构成的区域为A={(x,y)|20≤x≤21,19≤y≤20},面积为SA=1×1=1,这是一个几何概型,所以P(A)==. [点评] 根据以上的解法,我们把此类问题的解决总结为以下四步: (1)构设变量.从问题情景中,发现哪两个量是随机的,从而构设为变量x、y. (2)集合表示.用(x,y)表示每次试验结果,则可用相应的集合分别表示出试验全部结果Ω和事件A所包含试验结果.一般来说,两个集合都是几个二元一次不等式的交集. (3)作出区域.把以上集合所表示的平面区域作出来,先作不等式对应的直线,然后取一特殊点验证哪侧是符合条件的区域. 计算求解.根据几何概型的公式,易从平面图形中两个面积的比求得. 15.[解答] (1)位置的数据分别为12、0.3; (2)第三、四、五组参加考核人数分别为3、2、1; (3)设上述6人为abcdef(其中第四组的两人分别为d,e),则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}, 共有15种. 记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种. 所以P(A)==,故2人中至少有1名是第四组的概率为. 16.[解答] (1)P(A)=,P(B)==, P(C)==. (2)A、B、C两两互斥, P(A+B+C)=P(A)+P(B)+P(C) ==. (3)P()=1-P(A+B)=1-=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时达标 第52讲[解密考纲]对抛物线的定义、标准方程及几何性质的考查是常数,通常在选择题、填空题中单独考查或在解答题中与圆锥曲线综合考查.一、选择题1.(2018·宁夏银川九中月考)已知抛物线的方程为标准方程,焦点在x 轴上,其上点P (-3,m )到焦点的距离为5,则抛物线方程为( B )A .y 2=8xB .y 2=-8xC .y 2=4xD .y 2=-4x解析 设抛物线方程为y 2=-2px (p >0),则p2-(-3)=5,∴p =4,∴抛物线方程为y 2=-8x .故选B .2.(2018·江西九江第一次统考)已知抛物线的方程为y 2=2px (p >0),过抛物线上一点M (p ,2p )和抛物线的焦点F 作直线l 交抛物线于另一点N ,则|NF |∶|FM |=( C ) A .1∶2 B .1∶3 C .1∶2D .1∶3解析 由题意知直线l 的方程为y =22⎝⎛⎭⎫x -p2, 联立方程⎩⎪⎨⎪⎧y 2=2px ,y =22⎝⎛⎭⎫x -p 2,得N ⎝⎛⎭⎫p 4,-22p . 所以|NF |=p 4+p 2=34p ,|MF |=p +p 2=32p ,所以|NF |∶|FM |=1∶2,故选C .3.已知抛物线C :y 2=4x ,顶点为O ,动直线l :y =k (x +1)与抛物线C 交于A ,B 两点,则OA →·OB →=( A )A .5B .-5C .4D .-4解析 设A ⎝⎛⎭⎫y 214,y 1,B ⎝⎛⎭⎫y 224,y 2,由已知得直线l 过定点E (-1,0),因为E ,A ,B 三点共线,所以⎝⎛⎭⎫y 214+1y 2=⎝⎛⎭⎫y 224+1y 1, 即y 1y 24(y 1-y 2)=y 1-y 2,因为y 1≠y 2,所以y 1y 2=4, 所以OA →·OB →=(y 1y 2)216+y 1y 2=5.4.(2018·吉林长春一模)过抛物线y 2=2px (p >0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A 、B 两点,则|AF ||BF |=( A )A .13B .23C .34D .43解析 设抛物线的准线为l :x =-p2,|FB |=m ,|F A |=n ,过A ,B 两点向准线l 作垂线AC ,BD , 由抛物线定义知|AC |=|F A |=n ,|BD |=|FB |=m , 过B 作BE ⊥AC ,E 为垂足,则|AE |=|CE |-|AC |=|BD |-|AC |=m -n , |AB |=|F A |+|FB |=n +m .在Rt △ABE 中,∠BAE =60°,cos 60°=|AE ||AB |=m -n m +n =12, 即m =3n .故|AF ||BF |=n m =m3m =13.5.已知点A (2,1),抛物线y 2=4x 的焦点是F ,若抛物线上存在一点P ,使得|P A |+|PF |最小,则点P 的坐标为( D )A .(2,1)B .(1,1)C .⎝⎛⎭⎫12,1D .⎝⎛⎭⎫14,1 解析 由抛物线定义知,|PF |等于P 到准线x =-1的距离,当P A 与准线垂直时|P A |+|PF |最小,∴P 点的纵坐标为1,代入方程得x =14.6.已知抛物线x 2=4y 上有一条长为6的动弦AB ,则AB 的中点到x 轴的最短距离为( D )A .34B .32C .1D .2解析 由题意知,抛物线的准线l :y =-1,过点A 作AA 1⊥l 于点A 1,过点B 作BB 1⊥l 于点B 1,设弦AB 的中点为M ,过点M 作MM 1⊥l 于点M 1,则|MM 1|=|AA 1|+|BB 1|2. 因为6=|AB |≤|AF |+|BF |,所以|AA 1|+|BB 1|≥6,2|MM 1|≥6,|MM 1|≥3, 故点M 到x 轴的距离d ≥2,故选D . 二、填空题7.(2018·福建福州质检)过抛物线y 2=2px (p >0)的焦点作倾斜角为30°的直线l 与抛物线交于P ,Q 两点,分别过P ,Q 两点作PP 1,QQ 1垂直于抛物线的准线于P 1,Q 1,若|PQ |=2,则四边形PP 1Q 1Q 的面积是__1__.解析 由题意得四边形PP 1Q 1Q 为直角梯形,|PP 1|+|QQ 1|=|PQ |=2,|P 1Q 1|=|PQ |sin 30°=1,∴S =|PP 1|+|QQ 1|2·|P 1Q 1|=1.8.如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽米.解析 如图,建立平面直角坐标系,设抛物线方程为x 2=-2py (p >0).由题意将点A (2,-2)代入x 2=-2py ,得p =1,故x 2=-2y .设B (x ,-3),代入x 2=-2y 中,得x =6,故水面宽为26米. 9.(2017·全国卷Ⅱ)已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则|FN |=__6__.解析 依题意,抛物线C :y 2=8x 的焦点F (2,0),准线x =-2,因为点N 在y 轴上,M 为FN 的中点,所以点M 的横坐标为1,所以|MF |=1-(-2)=3,|FN |=2|MF |=6. 三、解答题10.已知抛物线y 2=4px (p >0)的焦点为F ,圆W :(x +p )2+y 2=p 2的圆心到过点F 的直线l 的距离为p .(1)求直线l 的斜率;(2)若直线l 与抛物线交于A ,B 两点,△WAB 的面积为8,求抛物线的方程.解析 (1)易知抛物线y 2=4px (p >0)的焦点为F (p,0),依题意设直线l 的方程为x =my +p ,因为W (-p,0),所以点W 到直线l 的距离为|-p -p |1+(-m )2=p ,解得m =±3,所以直线l 的斜率为±33.(2)由(1)知直线l 的方程为x =±3y +p ,由于两条直线关于x 轴对称,不妨取x =3y +p ,代入y 2=4px 中,得y 2-43py -4p 2=0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=43p ,y 1y 2=-4p 2,所以|AB |=1+(3)2·(43p )2+4×4p 2=16p , 因为△WAB 的面积为8,所以12p ×16p =8,得p =1,所以抛物线的方程为y 2=4x .11.已知抛物线y 2=2px (p >0),过点C (-2,0)的直线l 交抛物线于A ,B 两点,坐标原点为O ,OA →·OB →=12.(1)求抛物线的方程;(2)当以AB 为直径的圆与y 轴相切时,求直线l 的方程. 解析 (1)设l :x =my -2,代入y 2=2px 中, 得y 2-2pmy +4p =0.(*) 设A (x 1,y 1),B (x 2,y 2),所以y 1+y 2=2pm ,y 1y 2=4p ,所以x 1x 2=y 21y 224p2=4.因为OA →·OB →=12,所以x 1x 2+y 1y 2=12,即4+4p =12, 得p =2,抛物线的方程为y 2=4x . (2)(1)中(*)式可化为y 2-4my +8=0. y 1+y 2=4m ,y 1y 2=8.设AB 的中点为M , 则|AB |=2x M =x 1+x 2=m (y 1+y 2)-4=4m 2-4,① 又|AB |=1+m 2|y 1-y 2|=(1+m 2)(16m 2-32),② 由①②得(1+m 2)(16m 2-32)=(4m 2-4)2, 解得m 2=3,m =±3.所以直线l 的方程为x +3y +2=0或x -3y +2=0.12.(2017·全国卷Ⅲ)已知抛物线:C :y 2=2x ,过点(2,0)的直线l 交C 于A ,B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,-2),求直线l 与圆M 的方程. 解析 (1)设A (x 1,y 1),B (x 2,y 2),l :x =my +2.由⎩⎪⎨⎪⎧x =my +2,y 2=2x可得y 2-2my -4=0,则y 1y 2=-4. 又x 1=y 212,x 2=y 222,故x 1x 2=(y 1y 2)24=4.因此OA 的斜率与OB 的斜率之积为y 1x 1·y 2x 2=-44=-1,所以OA ⊥OB .故坐标原点O 在圆M 上.(2)由(1)可得y 1+y 2=2m ,x 1+x 2=m (y 1+y 2)+4=2m 2+4. 故圆心M 的坐标为(m 2+2,m ), 圆M 的半径r =(m 2+2)2+m 2.由于圆M 过点P (4,-2),因此AP →·BP →=0, 即(x 1-4)(x 2-4)+(y 1+2)(y 2+2)=0, 即x 1x 2-4(x 1+x 2)+y 1y 2+2(y 1+y 2)+20=0. 由(1)可得y 1y 2=-4,x 1x 2=4.所以2m 2-m -1=0,解得m =1或m =-12.当m =1时,直线l 的方程为x -y -2=0,圆心M 的坐标为(3,1),圆M 的半径为10,圆M 的方程为(x -3)2+(y -1)2=10.当m =-12时,直线l 的方程为2x +y -4=0,圆心M 的坐标为⎝⎛⎭⎫94,-12,圆M 的半径为854, 圆M 的方程为⎝⎛⎭⎫x -942+⎝⎛⎭⎫x +122=8516.。
