理论力学常见问题解答:第11章
理论力学(盛冬发)课后习题问题详解ch11

第11章 动量矩定理一、是非题(正确的在括号打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。
(×)2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。
(√)3. 质点系动量矩的变化与外力有关,与力无关。
(√)4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。
(√)5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。
(×)6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。
(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)8. 如图11.23所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+2213ml mr =+,式中m 为AB 杆的质量。
(×) 9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式,而不需附加任何条件。
(×)10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。
(×)图11.23二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的力无关。
5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。
理论力学第11章习题答案
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
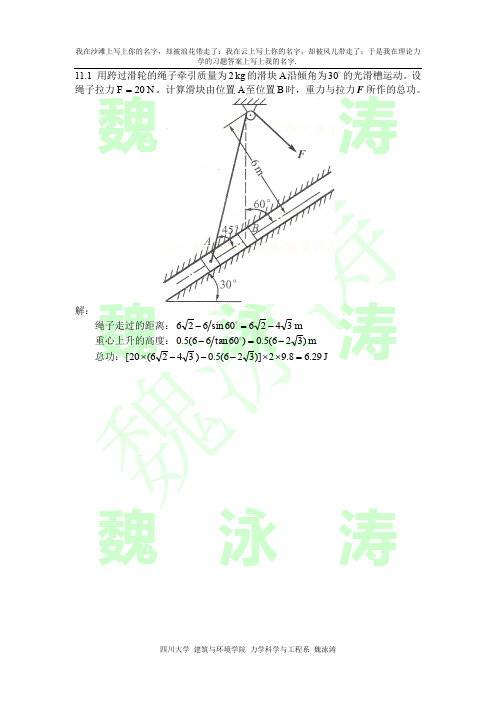
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
11.8 如图所示,重物 M 系于弹簧上,弹簧的另一端则固定在置于铅垂平面内的 圆环的最高点 A 上。重物不受摩擦地沿圆环滑下,圆环的半径为 20 cm ,重物的 质量为 5 kg ,如重物在初位置时 AM 20 cm ,且弹簧具有原长,重物的初速度 等于零,弹簧的重量略去不计,欲使重物在最低处时对圆环的压力等于零,弹簧 刚性系数应为多大?
11.5 计算图示各系统的动能 (1)如图(a)所示,质量为 m 、长为 l 的均质圆盘在自身平面内作平面运动,已知圆 盘上 A 、 B 两点的速度方向, B 点的速度为 vB , 45 ; (2)如图(b)所示,质量为 m1 的均质杆 OA 、一端铰接在质量为 m2 的均质圆盘中心, 另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为 v ; (3)如图(c)所示质量为 m 的均质细圆环半径为 R ,其上固结一个质量也为 m 的质 点 A ,细圆环在水平面上纯滚动,图示瞬时角速度为 。
魏 魏 魏
泳
F ) 2
涛 涛 涛
解: 滚阻力偶: M N (mg 轮转动角度:
x R
将力 F 向 C 简化, F 对 C 主矩: M C Fr
F sin 60 x M C M
3 FR x F x 总功: Fx (mg ) 2 2 R 2 R Fx F x (1 3 ) (mg ) 2 2 R
涛 涛 涛
解:
1 l 2 (2m)l 2 2m ( ) 2 ml 2 12 3 3 滑块 A 的速度: vA l cos sin 滑块 B 的速度: vB l 1 2 1 2 1 2 5 2 2 系统动能: J D mvA mvB ml 2 2 2 6 l 重力功: (sin 0 sin ) 2mg l (sin 0 sin ) mg 2mgl(sin 0 sin ) 2 1 弹性力功: k[l 2 (1 cos 0 ) 2 l 2 (1 cos ) 2 ] 2 根据动能定理: 5 2 2 1 ml 0 2mgl(sin 0 sin ) k[l 2 (1 cos 0 ) 2 l 2 (1 cos ) 2 ] ( 1 ) 6 2 当 0 60 、 0 时,
理论力学第十一章 质点系动量定理讲解

结论与讨论
牛顿第二定律与 动量守恒
牛顿第二定律 动量定理 动量守恒定理
工程力学中的动量定理和动量守恒定理比 物理学中的相应的定理更加具有一般性,应 用的领域更加广泛,主要研究以地球为惯性 参考系的宏观动力学问题,特别是非自由质 点系的动力学问题。这些问题的一般运动中 的动量往往是不守恒的。
结论与讨论
O
第一种方法:先计算各个质点 的动量,再求其矢量和。
第二种方法:先确定系统 的质心,以及质心的速度, B 然后计算系统的动量。
质点系动量定理应用于简单的刚体系统
例题1
y vA
A
O
解: 第一种方法:先计算各个质点 的动量,再求其矢量和。
p mA v A mB vB
建立Oxy坐标系。在角度为任 意值的情形下
p mi vi
i
§11-1 质点系动量定理
动量系的矢量和,称为质点系的动量,又称 为动量系的主矢量,简称为动量主矢。
p mi vi
i
根据质点系质心的位矢公式
mi ri
rC
i
m
mi vi
vC i m
p mvC
§11-1 质点系动量定理
质点系动量定理
对于质点
d pi dt
质点系动量定理应用
动量定理的
于开放质点系-定常质量流 定常流形式
考察1-2小段质量流,其 受力:
F1、F2-入口和出口 处横截面所受相邻质量流 的压力;
W-质量流的重力; FN-管壁约束力合力。
考察1-2小段质量流, v1、v2-入口和出口处质量流的速度; 1-2 :t 瞬时质量流所在位置; 1´-2´ :t + t 瞬时质量流所在位置;
【精品】理论力学参考答案第11章 盛冬发

理论力学参考答案第11章盛冬发__________________________________________________第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”) 1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。
(×)2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。
(√)3. 质点系动量矩的变化与外力有关,与内力无关。
(√)4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。
(√)5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。
(×)6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。
(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)__________________________________________________8. 如图11.23所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+ 2213ml mr =+,式中m 为AB 杆的质量。
(×)9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式,而不需附加任何条件。
(×)10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。
(×)图11.23二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
__________________________________________________4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。
理论力学:第11章 动量矩定理

对瞬心 C': LC IC
11.2 动量矩定理
一、 质点动量矩定理
由牛顿第二定律: ma F
易证:
dmO (mv )
dt
mO
(F)
微分形式动量矩定理
其中 O 为定点。
或
dmO (mv) mO (dS )
LH
P vr
b
1
Q r2
Q vC
r
b
sin
1
Q r2
g 2 2 g
g 2 2g
(P
2Q)r
P
b b
(1
sin
)
vC g
系统外力对 H 的力矩:
11-3
ΣmH
(F
(e)
)
m
P
r
b
Q
b
Q
sin
绳子剪断前为静力学问题,易求反力。
绳子剪断后为定轴转动动力学问题,用质心运动定理求: MaC
F (e)
但需要先求出 aC ,用刚体定轴转动微分方程可求: Iz mz (F (e) )
11-5
解:I. 绳子剪断前,受力如图(a)。 W
由对称性: N A0 2
II. 绳子剪断瞬时,受力、运动如图(b)。
11-2
欲用动量矩定理求 aC , aC 只跟三个运动物体有关,并且有一个“轴”O,如图。 但其中的 N 如何处理?
事实上,滚子沿斜面法向是静平衡的, N = Q cosα。 解:① 求加速度 aC 。
理论力学(盛冬发)课后习题答案ch11资料

127· R O 2 Q (b) (a) R O 1 Q 图11.28 三、选择题 1. 均质杆AB,质量为m,两端用张紧的绳子系住,绕轴O转动,如图11.29所示。则杆AB对O轴的动量矩为 A 。 (A) 265ml (B) 21213ml (C) 234ml (D) 2121ml 2. 均质圆环绕z轴转动,在环中的A点处放一小球,如图11.30所示。在微扰动下,小球离开A点运动。不计摩擦力,则此系统运动过程中 B 。 (A) 不变,系统对z轴的动量矩守恒 (B) 改变,系统对z轴的动量矩守恒 (C) 不变,系统对z轴的动量矩不守恒 (D) 改变,系统对z轴的动量矩不守恒 3. 跨过滑轮的轮绳,一端系一重物,另一端有一与重物重量相等的猴子,从静止开始以速度v向上爬,如图11.31所示。若不计绳子和滑轮的质量及摩擦,则重物的速度 B 。 (A) 等于v,方向向下 (B) 等于v,方向向上 (C) 不等于v (D) 重物不动 A B l O l l r A z 图11.29 图11.30 4. 在图11.32中,摆杆OA重量为G,对O轴转动惯量为J,弹簧的刚性系数为k,杆在铅垂位置时弹簧无变形。则杆微摆动微分方程为 D (设sin)。 (A) GbkaJ2 (B) GbkaJ2 (C) GbkaJ2 (D) GbkaJ2
第11章 动量矩定理 ·129·
129· 示。试求各物体对通过点O并与图面垂直的轴的动量矩。 (a) O A l O R C (c) (b) O R 图11.35 解:(a)杆OA对通过点O并与图面垂直的轴的动量矩为 231mlJLOO (b)圆盘对通过点O并与图面垂直的轴的动量矩为 221mRJLOO (c)圆盘对通过点O并与图面垂直的轴的动量矩为 22223)21(mRmRmRJLOO 11-2 如图11.36所示,鼓轮的质量11800kgm,半径025mr.,对转轴O的转动惯量2853kgmOJ.。现在鼓轮上作用力偶矩0743kNmM.来提升质量22700kgm的物体 A。试求物体A上升的加速度,绳索的拉力以及轴承O的反力。绳索的质量和轴承的摩擦都忽略不计。 解:(1)选整体为研究对象,受力分析如图所示。应用质点系动量矩定理,有 grmMrmJO2022)( 解得鼓轮转动的角加速度为 )/(21.325.027003.8525.08.927007430222220sradrmJgrmMO 物体A上升的加速度为 )/(8.02smraA (2)要求绳索的拉力,可选物体 A为研究对象,受力分析如图所示。应用质点运动微分方程,有 gmFamT22 解得绳索的拉力为 )(62.288.027008.9270022kNamgmFT (3)要求轴承O的反力,可选鼓轮为研究对象,受力分析如图所示。应用质心运动定
哈工大理论力学教案 第11章

解: 设
xC1 = a
m (a s) + m2 (a + esin s) xC2 = 1 m + m2 1
由
xC1 = xC2
,
m2 esin 得 s= m1 + m2
�
p2 p1 = ∑ Ii(e)
i=1
n
--质点系动量定理微分形式的投影式 --质点系动量定理微分形式的投影式
--质点系动量定理的积分形式 --质点系动量定理的积分形式 即在某一时间间隔内, 即在某一时间间隔内,质点系动量的改变量等于在这段
(e) p2y p1y = ∑I y
时间内作用于质点系外力冲量的矢量和. 时间内作用于质点系外力冲量的矢量和.
消去t 消去 得轨迹方程
xc yc 2 2 [ ] +[ ] =1 2(m1 + m2 )l /(2m1 + m2 ) m1l /(2m1 + m2 )
系统动量沿x, 轴的投影为 轴的投影为: 系统动量沿 y轴的投影为:
px = mvCx = mxC = 2(m + m2 )lω sin ω t 1
d(mv) = Fdt
--质点动量定理的微分形式 --质点动量定理的微分形式
即质点动量的增量等于作用于质点上的力的元冲量. 即质点动量的增量等于作用于质点上的力的元冲量. 在
t1~ t2 内, 速度由 v1 ~ v2, 有
mv2 mv1 = ∫ Fdt = I
t1
t2
--质点动量定理的积分形式 --质点动量定理的积分形式 即在某一时间间隔内, 即在某一时间间隔内,质点动量的变化等于作用于质点 的力在此段时间内的冲量. 的力在此段时间内的冲量.
--质点系动量定理的微分形式 --质点系动量定理的微分形式
理论力学第11章的课后习题答案

求:重物A下降的加速度以及轮C与地面接触点处的静摩擦力。
C B rO R
D A
C
B
r OR
m2 g Fs
FN
解:分别选轮子和重物A为研究对象,受力分析和运动分析 如图所示。轮子作平面运动,应用刚体平面运动微分方程,有
C B
FT
Fs
m2aO
D
rO
R
FT r Fs R m2 2
JO g W1R2
g
小车上升的加速度为
aห้องสมุดไป่ตู้
R
M W1R sinR
JO g W1R2
gR
a
FT
W1
FN
由小车的运动微分方程,有
FT
W1 sin
W1 g
a
解得绳子的拉力为
FT
W1 sin
W1 g
a
11-18 如图11.52所示结构中,重物A、B的质量分别为m1和m2 B物体与水平面间摩擦系数为f,鼓轮O的质量为M,
重物A的运动微分方程为 A
m1g FT' m1aA
C B r OR
m2 g Fs
FN
FT
F T'
a
A
m1g
其中: aO R
aA (R r)
FT' FT
联立求解,可得重物A下降的加速度为
aA
m1(R
m1(R r)2 r)2 m2 (R2
2)
g
轮C与地面接触点处的静摩擦力为
Fs
(2
m1(R r)2
FT'A
A
aA
Mg
A
m1g
重物A: m1g FTA m1a A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学常见问题及解答第11单元:动量矩定理及普遍定理综合应用1.直线运动的质点,对一点有动量矩吗?解答:如果该点不在直线上,则运动质点对该点有动量矩。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel). 《理论力学•理论和习题》,科学出版社1983洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:直线运动,质点,动量矩2.动量矩一定对定点定义吗?解答:不一定,可对任意点定义动量矩。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:动量矩,定点,任意点3.质点系对质心的绝对动量矩与相对动量矩有何关系?解答:相等。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995(美)施皮格尔(M.R.Spiegel). 《理论力学•理论和习题》,科学出版社1983范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:质点系,绝对动量矩,相对动量矩,关系4.质点系对定点与对质心动量矩的关系如何?这种关系反映了何种原理?解答:质点系对定点的动量矩(“绝对”动量矩),等于质点系随质心平动时的动量矩(动量对定点的矩,“牵连”动量矩)与质点系相对质心(随质心平动的动系)动量矩(“相对”动量矩)之和,用公式表示:CC C O L v M r L '+⨯= 。
这种关系反映了运动合成(分解)在动量矩定理表达中的应用(类似于动能的表达——柯尼希定理)。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:质点系,动量矩,定点,质心,关系,运动合成(分解)5. 如何求定轴转动刚体对平行轴的动量矩?解答:如图刚体绕z 轴转动,定轴'z 与z 轴平行。
如果z 轴过刚体质心,则刚体对定轴'z 与z 轴的动量矩相等;如果z 轴不过刚体质心,需要先利用平行轴定理求出刚体对过质心平行轴C z (动轴)的动量矩,然后利用对定轴('z )动量矩与对过质心平行轴(动轴C z )的关系求解:C z z z L K m L +=)('' ,式中'z L 和C z L 分别为刚体对'z 和C z 轴的动量矩,)('K m z 为刚体动量K 对'z 轴的矩。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:刚体,定轴转动,动量矩,平行轴6. 动量矩定理可求什么量?求几个?用何种方程?解答:可求解(角)加速度、(角)速度、约束力(偶)、主动力等量。
对平面问题,对点的动量矩定理是一个标量方程,因此可求解1个代数未知量。
z ´如果求(角)加速度、约束力(偶)、主动力等量,宜用动量矩定理的微分形式;如果求解(角)速度,一般宜用动量矩定理的积分形式。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:动量矩定理,求解量,微分形式,积分形式7. 平面运动刚体对质心的动量矩定理是何种形式?对瞬心是否总有类似关系?解答:平面运动刚体对质心的动量矩定理:)()(e C C F m I ∑= 。
对瞬心,类似的形式一般不成立,但有两种情况成立:①均质圆轮作纯滚动;②均质直杆沿直角墙面下滑。
如图。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:刚体,平面运动,质心,瞬心,动量矩定理,条件8. 应用动量矩守恒,如何解释花样滑冰运动员在跳起作空中旋转时,起跳时总是手臂伸直,而起跳后又马上收缩手臂?解答:运动员在空中是动量矩守恒的。
当起跳时手臂伸直,人旋转时的转动惯量最大,并具有一定的旋转速度;随后马上收拢手臂,转动惯量变小,由于动量矩守恒,旋转速度增大,从而在空中能转动更多的圈数。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995C CC 'C '范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:动量矩守恒,花样滑冰,手臂伸缩9. 有动量守恒定律、动量矩守恒定律,为何没有动能守恒定律?解答:事实上,可以谈动能守恒。
但是,动能守恒的条件是所有主动力的功率为零,事实上对应质点系整体作匀速直线平动,而这样特殊而简单的情形实际是一种平衡状态,而无需讨论动能守恒。
另外,机械能守恒倒是值得讨论和使用,它实际上是保守系统的动能定理。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:动量矩守恒,花样滑冰,手臂伸缩10. 下述问题应用“定轴转动微分方程”求解,与应用动量矩求解的结果相同。
问求解过程是否正确?均质圆轮重Q ,半径为r ,其上作用一常力偶M ,重物重P 。
求重物的加速度。
求解:研究整体。
画受力图和运动图。
由定轴转动微分方程)()(e O O F m I ∑= (1)其中,gr P Q r g P r g Q I O 222)2(21+=+= (2) a OX OY Qr P M F m e O -=∑)()( (3)式(2)、(3)代入式(1),解得g r P Q r P M 2)2(+-=ε (4) 从而,重物的加速度g r P Q r P M r a )2(+-==ε (5) 解答:上述求解的结果正确(可用动量矩定理验证),但求解过程有误。
求解时利用了系统对轴O 的“转动惯量”式(2),而这样的表示存在概念错误,因为只有单个刚体才可定义转动惯量,而这样的系统则不能使用式(2)形式的“转动惯量”。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:刚体,定轴转动微分方程,转动惯量11. 刚体平面运动微分方程本质上是哪些普遍定理?解答:本质是动量定理(质心运动定理)和动量矩定理(对质心的转动微分方程)。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)(美)施皮格尔(M.R.Spiegel ). 《理论力学 • 理论和习题》,科学出版社1983关键词:刚体,平面运动微分方程,动量定理,动量矩定理12. 动力学普遍定理在选择使用时有何规律?解答:①求运动:优先考虑动能定理;②求反力或反力偶,必须用动量定理(质心运动定理)或动量矩定理(定轴转动微分方程);③先考察是否是守恒问题;④经常需要补充运动学方程或静力学方程。
参考资料:贾启芬,刘习军. 《理论力学》,机械工业出版社2011第2版萧龙翔等.《理论力学》,天津大学出版社1995范钦珊. 《理论力学》,清华大学出版社2004(美)施皮格尔(M.R.Spiegel). 《理论力学•理论和习题》,科学出版社1983洪嘉振,杨长俊. 《理论力学》,高等教育出版社2008(第3版)关键词:动力学普遍定理,选择,规律。
