振动与波复习题及答案
大学物理振动与波练习题与答案
【解】:(1) y 5cos(20 4x) 厘米
(2) y 5cos(3t 11) 厘米
(3) y 5cos3(t 4 x 5) , c 3 (cm/ s)
33
4
(4) y 5cos(3t 9) , yI 15 sin(3t 9) 0
23、一平面简谐波沿 x 轴正方向传播,波速 c=8 m/s, 若 t=0 时的波形曲线如图 2-23 所示 (1)写出波动方程 (2)画出 t=1.25 s 时的波形曲线 【解】:
t=0 时,y=0, v>0 cm T=5s
所以 2 。 波长= 40
y 4.0 cos[0.4t ] (cm) 2
B 点的振动方程
yA
(t)
5 c os [10
(t
20) 300
2
]
5 c os (10t
7 6
)cm
(2)
A,B 相位相同
(3) 或 O 点的振动方程
yo
(t)
5
cos(10t
2
)
(cm)
O 点相位
o
2
OB,OA 间的相位差
oA
oB
2 3
O 比 A 超前
oA
o
A
2 3
A
7 6
同时 B 点
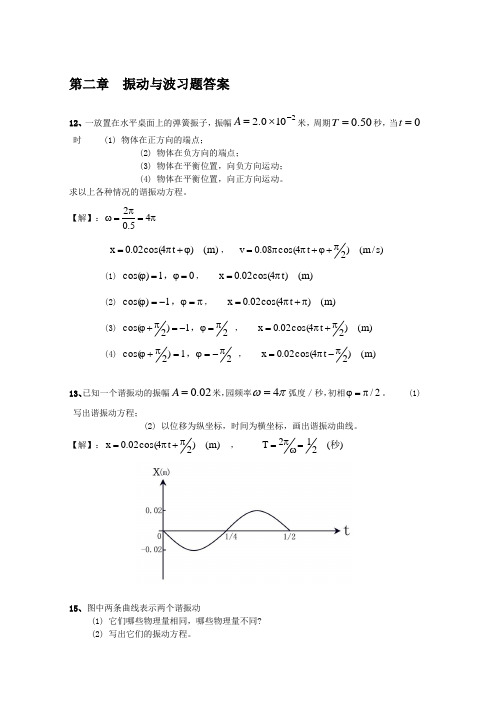
13、已知一个谐振动的振幅 A 0.02 米,园频率 4 弧度/秒,初相 / 2 。 (1)
写出谐振动方程; (2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】: x 0.02cos(4 t 2) (m) ,
T
2
1 2
《大学物理》期末考试复习题(振动与波)

)
(A) 2 ;
答案:(D)
(B)
m1 m2
2
;
(C)
m2 m1
2
;
(D) 2
m2 . m1
一物体作简谐振动,振动方程为
x
A cos(t
1 4
) 。在
t = T/4(T
为周期)时刻,物体的
加速度为 ( )
(A)
2 2
A 2
;
(B)
2 2
A 2 ;
(C)
3 2
A 2
;
(D)
3 2
A 2
。
一弹簧振子,当把它水平放置时,它作简谐振动。若把它竖直放置或放在光滑斜面上,试判
一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的 1/4 时,其动能为振 动总能量的
(A) 7/16 ; (B) 9/16 ; (C) 11/16 ; (D) 15/16 。 []
答案:(D)
第十章 波动
10-1 机械波的几个概念
10-2 平面简谐波的波函数
如图所示,有一平面简谐波沿 x 轴负方向传播,
断下列情况正确的是
(A)竖直放置作简谐振动,在光滑斜面上不作简谐振动;
(B)竖直放置不作简谐振动,在光滑斜面上作简谐振动;
(C)两种情况都作简谐振动;
(D)两种情况都不作简谐振动。
[]
竖直放置 放在光滑斜面上
答案:(C)
同一弹簧振子悬挂相同的质量,分别按如图(a)、(b)、(c)所示的三种方式放置,摩擦力都
(A) 曲线 3,1,2 分别表示 x,v,a 曲线; (B) 曲线 2,1,3 分别表示 x,v,a 曲线; (C) 曲线 1,2,3 分别表示 x,v,a 曲线; (D) 曲线 2,3,1 分别表示 x,v,a 曲线.
新高考物理复习专题八机械振动与机械波练习含答案

专题八机械振动与机械波五年高考考点过关练考点一机械振动1.(2022浙江1月选考,6,3分)图甲中的装置水平放置,将小球从平衡位置O拉到A后释放,小球在O点附近来回振动;图乙中被细绳拴着的小球由静止释放后可绕固定点来回摆动。
若将上述装置安装在太空中的我国空间站内进行同样操作,下列说法正确的是()A.甲图中的小球将保持静止B.甲图中的小球仍将来回振动C.乙图中的小球仍将来回摆动D.乙图中的小球将做匀速圆周运动答案B2.(2022浙江6月选考,11,3分)如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距x。
套在杆上的小球从中点以初速度v向右运动,小球将做周期为T的往复运动,则()A.小球做简谐运动B.小球动能的变化周期为T2C.两根弹簧的总弹性势能的变化周期为T时,其运动周期为2TD.小球的初速度为v2答案B3.[2019课标Ⅱ,34(1),5分]如图,长为l的细绳下方悬挂一小球a,绳的另一端固定在天花板上O点处,在Ol的O'处有一固定细铁钉。
将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,点正下方34并从释放时开始计时。
当小球a摆至最低位置时,细绳会受到铁钉的阻挡。
设小球相对于其平衡位置的水平位移为x,向右为正。
下列图像中,能描述小球在开始一个周期内的x⁃t关系的是()答案A4.[2022重庆,16(1),4分]某同学为了研究水波的传播特点,在水面上放置波源和浮标,两者的间距为L。
t=0时刻,波源开始从平衡位置沿y轴在竖直方向做简谐运动,产生的水波沿水平方向传播(视为简谐波),t1时刻传到浮标处使浮标开始振动,此时波源刚好位于正向最大位移处,波源和浮标的振动图像分别如图中的实线和虚线所示,则()A.浮标的振动周期为4t1B.水波的传播速度大小为L4t1t1时刻浮标沿y轴负方向运动C.32D.水波的波长为2L答案A5.(2023山东,10,4分)(多选)如图所示,沿水平方向做简谐运动的质点,依次通过相距L的A、B两点。
机械振动和波 试题及答案

一、填空题1、质量为0.10kg 的物体,以振幅1cm 作简谐运动,其角频率为110s -,则物体的总能量为, 周期为 。
2、一平面简谐波的波动方程为y 0.01cos(20t 0.5x)ππ=-( SI 制),则它的振幅为 、角频率为 、周期为 、波速为 、波长为 。
3、一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的倔强系数为 ,振子的振动角频率为 。
4、一横波的波动方程是y = 0.02cos2π(100t – 0.4x)( SI 制)则振幅是_________,波长是_ ,频率是 ,波的传播速度是 。
5、两个谐振动合成为一个简谐振动的条件是 。
6、产生共振的条件是振动系统固有频率与驱动力频率 (填相同或不相同)。
7、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
8、弹簧振子系统周期为T 。
现将弹簧截去一半,仍挂上原来的物体,作成一个新的弹簧振子,则其振动周期为 。
9、作谐振动的小球,速度的最大值为 ,振幅为 ,则振动的周期为 ;加速度的最大值为 。
10、广播电台的发射频率为 。
则这种电磁波的波长为 。
11、已知平面简谐波的波动方程式为 ,则 时,在X=0处相位为 ,在 处相位为 。
12、若弹簧振子作简谐振动的曲线如下图所示,则振幅 ;圆频率初相 。
13、一简谐振动的运动方程为2x 0.03cos(10t )3ππ=+( SI 制),则频率ν为 、周期T 为 、振幅A 为 ,初相位ϕ为 。
14、一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为10.05cos(4)()x t SI ωπ=+和20.05cos(1912)()x t SI ωπ=+,其合成运动的方程x = .15、A 、B 是在同一介质中的两相干波源,它们的位相差为π,振动频率都为100Hz ,产生的波以10.0m/s 的速度传播。
波源A 的振动初位相为3π,介质中的P 点与A 、B 等距离,如图所示。
大学物理复习题答案(振动与波动)

大学物理1复习题答案一、单选题(在本题的每一小题备选答案中,只有一个答案是正确的,请把你认为正确答案的题号,填入题干的括号内)1.一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为'T 1和'T 2。
则有 ( B )A .'T T >11且 'T T >22B .'T T =11且 'T T >22C .'T T <11且 'T T <22D .'T T =11且 'T T =222.一物体作简谐振动,振动方程为cos 4x A t ⎛⎫=+⎪⎝⎭πω,在4Tt =(T 为周期)时刻,物体的加速度为 ( B )A. 2ω B 。
2ω C 。
2ω D2ω3.一质点作简谐振动,振幅为A ,在起始时刻质点的位移为/2A -,且向x 轴的正方向 运动,代表此简谐振动的旋转矢量图为 ( D )AAAAAAC)AxxAAxA B C D4。
两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为)cos(1αω+=t A x .当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为 ( B )A. )π21cos(2++=αωt A x B. )π21cos(2-+=αωt A x . C 。
)π23cos(2-+=αωt A x D. )cos(2π++=αωt A x . 5.波源作简谐运动,其运动方程为t y π240cos 100.43-⨯=,式中y 的单位为m ,t 的单位为s ,它所形成的波形以s m /30的速度沿一直线传播,则该波的波长为 ( A )A .m 25.0B .m 60.0C .m 50.0D .m 32.06.已知某简谐振动的振动曲线如图所示,位移的单位为厘米,时间单位为秒.则此简谐振动的振动方程为: ( B )A .cos x t ππ⎛⎫=+ ⎪⎝⎭22233B .cos x t ππ⎛⎫=+ ⎪⎝⎭42233C .cos x t ππ⎛⎫=- ⎪⎝⎭22233D .cos x t ππ⎛⎫=- ⎪⎝⎭42233二. 填空题(每空2分)1. 简谐运动方程为)420cos(1.0ππ+=t y (t 以s 计,y 以m 计),则其振幅为 0.1 m ,周期为 0。
机械振动和机械波测试题及答案

机械振动和机械波一、单选题(每小题提供的四个选项中,只有一个是正确的,每小题5分)1.单摆振动的回复力是 [ ]A.摆球所受的重力B.摆球重力在垂直悬线方向上的分力C.悬线对摆球的拉力D.摆球所受重力和悬线对摆球拉力的合力2.一个做简谐运动的质点,它的振幅是4cm,频率是2.5Hz。
该质点从平衡位置开始经过0.5s后,位移的大小和所通过的路程分别为[ ]A.4cm,10cmB.4cm,20cmC.0,24cmD.100cm,100cm3.图为一列简谐横波在介质中传播的波形图。
在传播过程中,某一质点在10s内运动的路程是16m,则此波的波速是[ ]A.1.6m/sB.2.0m/sC.40m/sD.20m/s4.若单摆的摆长不变,摆球的质量增加为原来的4倍,摆球经过平衡位置时的速度减为原来的1/2,则单摆振动的[ ] A. 频率不变,振幅不变 B.频率改变,振幅变大C.频率改变,振幅不变D.频率不变,振幅变小5. 一列横波沿x轴传播,到达坐标原点时的波形如图。
当此波到达P点时,处于O点处的质点所通过的路程和该时刻的位移是[ ]A.40.5cm,1cmB.40.5cm,-1cmC.81cm,1cmD.81cm,-1cm二、多选题每个题提供的四个选项中至少有一个是正确的(每小题6分,共30分)6.一列波在不同介质中传播,保持不变的物理量是[ ]A. 波长B. 波速C. 频率D. 振幅7.一列机械波在某一时刻的波形如实线所示,经过△t 时间的波形如虚线所示。
已知波的传播速率为1m/s,则下列四个数据中△t的可能值为[ ]A.1sB.8sC.9sD.20s8.图示为简谐横波在某一时刻的波形图线。
已知波的传播速度为2m/s,质点a的运动方向如图。
则下列说法中正确的是[ ]A. 波沿x的负方向传播B. 质点d再经过0.5s第一次到达波峰C. 过去此刻之后,质点b比质点c先回到平衡位置D. 该时刻质点e运动的加速度为零9.一列简谐横波沿x轴正方向传播在t=0的波形如图。
振动与波复习题及答案
第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a .则下列计算该振子劲度系数的公式中,错误的是:(A) 2max 2max /x m k v =. (B) x mg k /=.(C) 22/4T m k π=. (D) x ma k /=. [ B ] 2. 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为(A) g l π2. (B) gl22π.(C) g l 322π. (D) gl 3π. [ C ] 3. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π. (B) π/2. (C) 0 . (D) θ. [ C ]4. 两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(ωt + α).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .(C) )π23cos(2-+=αωt A x . (D) )cos(2π++=αωt A x . [ B ][ ]6. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) π/6. (B) 5π/6. (C) -5π/6. (D) -π/6. (E) -2π/3. [ ]7. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2.将它们拿到月球上去,相应的周期分别为1T '和2T '.则有(A) 11T T >'且22T T >'. (B) 11T T <'且22T T <'.(C) 11T T ='且22T T ='. (D) 11T T ='且22T T >'. [ D ] 8. 一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动.当重物通过平衡位置且向规定的正方向运动时,开始计时.则其振动方程为: (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x(C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A xv 21(E) t m /k A x cos = [ B ] 9. 一质点在x 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为(A) 1 s . (B) (2/3) s .(C) (4/3) s . (D) 2 s . [ B ]10.一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为(A) 2221ωA -. (B) 2221ωA . (C) 2321ωA -. (D)2321ωA . [ B ] 11. 两个同周期简谐振动曲线如图所示.x 1的相位比x 2的相位(A) 落后π/2. (B) 超前π/2. (C) 落后π . (D) 超前π.[ B ]12. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ B ]13. 一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s .(C) 2.20 s .(D) 2.00 s . [ B ]A21-A21-A21 21A21 AA21-A21-2115. 用余弦函数描述一简谐振子的振动.若其速度~时间(v ~t )关系曲线如图所示,则振动的初相位为(A) π/6. (B) π/3.(C) π/2. (D) 2π/3. (E) 5π/6.[ A ]17. 一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为 (A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ D ]18 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A) kA 2. (B)221kA . (C) (1/4)kA 2. (D) 0. [ D ]19. 一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为:(A) 1:4. (B) 1:2. (C) 1:1.(D) 2:1. (E) 4:1. [ D ]20.动的初相为 (A) π23. (B) π.(C) π21. (D) 0. [ B ] 二. 填空题21. 在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为 (a) ______________________________;(b) ______________________________;(c) ______________________________.23. 在两个相同的弹簧下各悬一物体,两物体的质量比为4∶1,则二者作简谐振 动的周期之比为___2:1___.24. 一质点作简谐振动,速度最大值v m = 5 cm/s ,振幅A = 2 cm .若令速度具有 正最大值的那一时刻为t = 0,则振动表达式为_____50.02cos()22x t π=-___.25. 一物体作余弦振动,振幅为15×10-2m ,角频率为6π s -1,初相为0.5 π,则21--(c)A/ -A 2cos()2x A t T ππ=+2cos()2x A t T ππ=+2cos()x A t T ππ=+振动方程为 __0.15cos(6)2x t ππ=+(SI).27. 一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m ,初速度为0.09 m/s ,则振幅A =____0.05m_________ ,初相φ =____3arcsin 5-____________.30. 已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为_______1:1__________.31.则此简谐振动的三个特征量为A =_____0.1m________;ω =_____/6rad s π_____;φ =_____3π__________. .34. 已知三个简谐振动曲线如图所示,则振动方程分别为:x 1 =10cos t π______________________, x 2 =10cos()2t ππ- _____________________,x 3 =10cos()t ππ+_______________________.37.一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初相为_____4π_______.振动方程为__0.02cos()4x t ππ=+____________.41. 一作简谐振动的振动系统,振子质量为2 kg ,系统振动频率为1000 Hz ,振 幅为0.5 cm ,则其振动能量为______1002πJ________.43. 一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,t x (cm)则弹簧的劲度系数为____200N/m_______,振子的振动频率为_5πHZ________. 44.两个同方向的简谐振动曲线如图所示.合振动的振幅 为______21A A -___________,合振动的振动方程 为_____212()cos()2x A A t T ππ=-+______. 50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为)612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI)则其合成振动的振幅为___0.01m________,初相为____6π_____.第十章波复习题一、选择题1. 在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计). (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计)[ C ]2. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则 (A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ B ] 3.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5s 时刻的波形图是 [ A ]·---4. 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻 [ D ](A) A 点振动速度大于零. (B) B 点静止不动. (C) C 点向下运动. (D) D 点振动速度小于零.5. 把一根十分长的绳子拉成水平,用手握其一端.维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长. (B) 振动频率越低,波长越长.(C) 振动频率越高,波速越大. (D) 振动频率越低,波速越大.[ B ] 6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则O 点的振动初相φ 为: (A) 0. (B)π21(C) π (D)π23(或π-21) [ B ]7. 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为(A) ])/(cos[0φω+-=u x t A y .(B) )]/([cos u x t A y +=ω.(C) })]/([cos{0φω+-=u x t A y . (D)})]/([cos{0φω++=u x t A y . [ C ]8.如图所示为一平面简谐波在t = 0 时刻的波形图,该波的波速u = 200 m/s ,则P 处质点的振动曲线为[ C ]9. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是 [ A ]xy Ouy(m)ωSA ϖO ′ωSA ϖO′ωϖO ′ωSAϖO ′(A)(B)(C)(D)S10. 一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是(A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI). (C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI). [ A ]11. 图示一简谐波在t = 0时刻的波形图,波速 u = 200 m/s ,则P 处质点的振动速度表达式为 [ C ](A))2cos(2.0π-ππ-=t v (SI). (B) )cos(2.0π-ππ-=t v (SI). (C) )2/2cos(2.0π-ππ=t v (SI).(D) )2/3cos(2.0π-ππ=t v (SI).12.在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是(A) A 1 / A 2 = 16. (B)A 1 / A 2 = 4.(C) A 1 / A 2 = 2.(D) A 1 / A 2 = 1 /4. [ C ] 13. 一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为最大值的媒质质元的位置是:(A) o ',b ,d ,f . (B) a ,c ,e ,g .(C) o ',d . (D) b ,f . [ B ]14. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [C ] 15. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中(A) 它的势能转换成动能. (B) 它的动能转换成势能. (C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.[ C ] 16. 如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为)212cos(1π+π=t A y ,则S 2的振动方程为(A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y . [ D ]S17. 两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B)π21. (C) π. (D) π23. [ C ] 18. S 1和S 2是波长均为λ 的两个相干波的波源,相距3λ /4,S 1的相位比S 2超前π21.若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,则在S 1、S 2连线上S 1外侧和S 2外侧各点,合成波的强度分别是(A) 4I 0,4I 0. (B) 0,0.(C) 0,4I 0 . (D) 4I 0,0. [ A ] 19 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ] 20 在波长为λ 的驻波中,两个相邻波腹之间的距离为 (A) λ /4. (B) λ /2.(C) 3λ /4. (D) λ . [ B ] 21.沿着相反方向传播的两列相干波,其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=.在叠加后形成的驻波中,各处简谐振动的振幅是 (A) A . (B) 2A .(C))/2cos(2λx A π. (D) |)/2cos(2|λx A π. [ D ]二、填空题22.一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在 该时刻的运动方向.A _____________;B_____________ ;C ______________ . 23. 一平面简谐波的表达式为)37.0125cos(025.0x t y -= (SI),其角频率ω =__________________________,波速u =______________________,波长λ = _________________.24. 频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________.25. 图为t = T / 4 时一平面简谐波的波形曲线,则其波的表达式为 ______________________________________________.26、一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.S 1S 2Pλ/4-xOP 1P 227、一简谐波沿x 轴正方向传播.x 1和x 2两点处的振动曲线分别如图(a)和(b)所示.已知x 2 .> x 1且x 2 - x 1 < λ(λ为波长),则x 2点的相位比x 1点的相位滞后___________________.28、已知某平面简谐波的波源的振动方程为t y π=21sin 06.0(SI),波速为2 m/s .则在波传播前方离波源 5 m 处质点的振动方程为_-______________________.29、(1)一列波长为λ 的平面简谐波沿x 轴正方向传播.已知在λ21=x处振动的方程为y = A cos ω t ,则该平面简谐波的表达式为______________________________________. (2) 如果在上述波的波线上x = L (λ21>L)处放一如图所示的反射面,且假设反射波的振幅为A ',则反射波的表达式为 _______________________________________ (x ≤L ).30、一平面简谐波沿x 轴负方向传播.已知 x = -1 m 处质点的振动方程为)cos(φω+=t A y ,若波速为u ,则此波的表达式为 _________________________________________________________. 31、一个波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2,在两个球面上分别取相等的面积∆S 1和∆S 2,则通过它们的平均能流之比=21P /P ___________________.32、一点波源发出均匀球面波,发射功率为4 W .不计媒质对波的吸收,则距离 波源为2 m 处的强度是__________________.33、如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3λ 和10 λ / 3 ,λ 为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率___________,波源S 1 的相位比S 2 的相位领 先_________________.34、如图所示,S 1和S 2为同相位的两相干波源,相距为L ,P 点距S 1为r ;波源S 1在P 点引起的振动振幅为A 1,波源S 2在P 点引起的振动振幅为A 2,两波波长都是λ ,则P 点振幅A =_________________________________________________________. 35、两相干波源S 1和S 2的振动方程分别是tA y ωcos 1=和)21cos(2π+=t A y ω.S 1距P 点3个波长,S 2距P 点21/4个波长.两波在P 点引起的两个振动的相位差是____________.36、 S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(λ为波长)如图.已知S 1的初相为π21. (1) 若使射线S 2C 上各点由两列波引起的振动均干涉相消,则S 2的初相应为________________________.(2) 若使S 1 S 2连线的中垂线MN 上各点由两列波引起的 振动均干涉相消,则S 2的初位相应为_______________________.(a)(b)PS S1237、 两列波在一根很长的弦线上传播,其表达式为 y 1 = 6.0×10-2cos π(x - 40t ) /2 (SI) y 2 = 6.0×10-2cos π(x + 40t ) /2 (SI)则合成波的表达式为__________________________________________________; 在x = 0至x = 10.0 m 内波节的位置是_____________________________________ __________________________________;波腹的位置是________________________________________________________. 38、设入射波的表达式为)(2cos 1λνxt A y +π=.波在x = 0处发生反射,反射点为固定端,则形成的驻波表达式为____________________________________. 39、 一驻波表达式为t x A y ππ=100cos 2cos .位于x 1 = 3 /8 m 的质元P 1与位于x 2 = 5 /8 m 处的质元P 2的振动相位差为_____________________________. 40、 在弦线上有一驻波,其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________.。
振动和波动要点习题
振动和波一、选择题1.(3分,答D )已知一平面简谐波的表达式为cos()y A at bx =-(,a b 为正值常量),则 (A )波的频率为a (B )波的传播速度为/b a (C )波长为/b π (D )波的周期为2/a π2.(本题3分,答B )一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[]3. (3分,答B )一质点在x 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点,若t =0时刻质点第一次通过x =-2cm 处,且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为(A) 1s (B) (2/3)s (C)(4/3)s (D) 2s4. (3分,答D )一劲度系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为T 1.若将此弹簧截去一半的长度,下端挂一质量为m 21的物体,则系统振动周期T 2等于 (A) 2 T 1 (B) T 1(C)T 12/ (D) T 1 /2 (E) T 1 /45.(本题3分,答A )轴一简谐波沿Ox 轴正方向传播,t = 0 时刻的波形曲线如图所示,已知周期为 2 s ,则 P 点处质点的振动速度v 与时间t 的关系曲线为:6.(3分,答B )一平面简谐波在弹性媒质时,某一时刻媒质中某质元在负最大位移处,则它的能量是(A ) 动能为零 势能最大 (B )动能为零 势能为零 (C ) 动能最大 势能最大 (D )动能最大 势能为零v (m/s)O 1 t (s)ωA(C)· v (m/s)O1 t (s)ω A(A)·1 v (m/s)t (s)(D)O-ω A1 v (m/s) t (s)-ωA(B) O ··x o A x A 21 ω(A)A 21ω(B) A 21-(C) (D)o oo A 21-xxxAxAxAxω ω2O 1 y (m)x (m)t =0 A u图17.(3分,答D )沿相反方向传播的两列相干波,其波动方程为y 1=A cos2π (νt -x /λ)y 2=A cos2π (νt + x /λ) 叠加后形成的驻波中,波节的位置坐标为(A)x =±k λ.(B)x =±k λ/2 .(C)x =±(2k +1)λ/2 .(D)x =±(2k +1)λ/4 . 其中k = 0 , 1 , 2 , 3…….8.(3分,答D )如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为y =A cos(ω t+φ0),则B 点的振动方程为 (A )y =A cos[ω t-(x/u )+φ0] (B )y =A cos ω[ t+(x/u )] (C )y =A cos{ω [t-(x/u ) ]+φ0} (D )y =A cos{ω[ t+(x/u ) ]+φ0}9.(3分,答D )一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:(A )它的动能转换成势能. (B )它的势能转换成动能. (C )它从相邻的一段质元获得能量,其能量逐渐增大. (D )它把自己的能量传给相邻的一段质元,其能量逐渐减小. 10.(3分,答B )在波长为λ的驻波中,两个相邻波腹之间的距离为 (A )λ/4 (B )λ/2 (C )3λ/4 (D )λ11.(3分,答C )某时刻驻波波形曲线如图所示,则a 、b 两点振动的相位差是 (A )0 (B )/2π (C )π (D )5/4π12.(本题3分,答B)在驻波中,两个相邻波节间各质点的振动(A )振幅相同,相位相同 (B )振幅不同,相位相同 (C )振幅相同,相位不同 (D )振幅不同,相位不同 二、填空题1. (3分)已知一个简谐振动的振幅A=2cm, 角频率14s ωπ-=,以余弦函数表达式运动规律时的A -Ayxλ λ/2O ··a b · · · · · · · · ··x 2A A/2x 1初相12φπ=,试画出位移和时间的关系曲线(振动图线) 2.(4分)两个简谐振动方程分别为x 1=Acos(ω t ) ;x 2=Acos(ω t +π/3) 在同一坐标上画出两者的x-t 曲线.3. (3分)有两相同的弹簧,其劲度系数均为k .(1)把它们串联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为;(2)把它们并联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为.[答案:(1)22m k π,(2)22mkπ] 4.(4分)一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的劲度系数,振子的振动频率.[答案:2210N/m,1.6Hz ⨯]5.(3分)一平面机械波沿x =-1m 轴负方向传播,已知处质点的振动方程cos()y A t ωϕ=+,若波速为u ,求此波的波函数.[答案:cos{[(1)/]}y A t x u ωϕ=+++]6.(3分)一作简谐振动的振动系统,振子质量为2kg ,系统振动频率为1000Hz ,振幅为0.5cm ,则其振动能量为.(答案:29.9010J ⨯ )7.(3分)两个同方向同频率的简谐振动211310cos(),3x t ωπ-=⨯+221410cos()(SI)6x t ωπ-=⨯-,它们的合振幅是. (答案:2510m -⨯ )8.(3分)一平面简谐波沿Ox 轴正方向传播,波动表达式为cos[(/)/4]y A t x u ωπ=-+,则1x L =处质点的振动方程是;2x L =-处质点的振动和1x L =处质点的振动相位差为21φφ-=. (答案:1cos[(/)/4]y A t L u ωπ=-+,12()/L L u ω+)9.(5分)一余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在该时刻的运动方向.A 向下 ,B 向上 ,C 向上.10. (本题4分)一平面简谐波的表达式cos (/)cos(/)y A t x u A t x u ωωω=-=-其中/x u 表示,/x u ω表示,y 表示.[答案:波从坐标原点传至x 处所需时间(2分),x 处质点此原点处质点滞后的相位(1分),t 时刻x 处质点的振动位移(1分)]11. (本题3分)如图所示,两相干波源S 1和S 2相距为3λ/4,λ为波长,设两波在S 1 S 2连O Cyxu · · · A B线上传播,它们的振幅都是A ,并且不随距离变化,已知在该直线上S 1左侧各点的合成波强度为其中一个波强度的4倍,则两波源应满足的相位条件是__π/2_ 12. (3分)一驻波的表达式为y =2A cos(2πx/λ) cos(2πνt ),两个相邻波 腹之间的距离是.(答案:λ/2) 三、计算题1. (5分)一质点作简谐运动,其振动方程为110.24cos()()23x t SI ππ=+,试用旋转矢量法求出质点由初始状态运动到x =-0.12 m ,v <0的状态所经过的最短时间. 解:旋转矢量如图所示.图3分 由振动方程可得π21=ω,π=∆31φ1分667.0/=∆=∆ωφt s 1分2(本题10分)一质量m =0.25kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点,弹簧的劲度系数k =25N/m.(1)求振动的周期T 和频率ω. (2)如果振幅A =15cm ,t =0时物体位于x =7.5cm 处,且物体沿x 轴反方向运动,求初速度v 0及初相φ.(3)写出振动的数值表达式. 解:(1)12/10k m s ωπ-== (2分)2/0.63T s πω== (1分)(2) A=15cm , 在t =0时,07.5cm x =,00v < 由2200(/)A x v ω=+得2200 1.3m/s v A x ω=--=- (2分)100(/)/3/3tg v x φωππ-=-=或400,/3x φπ>∴=(3分)(3)21510cos(10/3)(SI)x t π-=⨯+(2分)3.(10分)在一轻弹簧下端悬挂0100g m =砝码时,弹簧伸长8cm. 现在这根弹簧下端悬挂0250g m =物体,构成弹簧振子,将物体从平衡位置向下拉动4cm ,并给以向上的21cm/s 的初速度(令这时t=0).选x 轴向下,求振动方程的数值式.解:k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/mx (m) ωωπ/3π/3t = 0t0.12 0.24 -0.12 -0.24 OAAO xS 1S 211s 7s 25.025.12/--===m k ω(2分) 5cm )721(4/2222020=+=+=ωv x A cm (2分) 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ,φ = 0.64 rad (3分))64.07cos(05.0+=t x (SI) (1分)4.(8分)在一竖直轻弹簧的下端悬挂一小球,弹簧被拉长0 1.2cm l =而平衡.再经拉动后,该小球在竖直方向作振幅为2cm A =的振动,试证此振动为简谐振动;选小球在正最大位移处开始计时,写出此振动的数值表达式.解:设小球的质量为m ,则弹簧的劲度系数(图参考上题)0/k mg l = 选平衡位置为原点,向下为正方向. 小球在x 处时,根据牛顿第二定律得202()d x mg k l x m dt -+=将k 代入整理后得 220d x g x dt l =-所以振动为简谐振动,其角频率为0/28.589.1(rad/s)g l ωπ===(5分)设振动表达式为 c o s ()x A t ωφ=+ 由题意:t=0时,200210m0x A v -==⨯=解得:0φ=2210cos(9.1)x t π-∴=⨯m (3分)5.(10分)在一轻弹簧下端悬挂m 0=100g 的砝码时,弹簧伸长8cm,现在这根弹簧下端悬挂m =250g 的物体, 构成弹簧振子. 将物体从平衡位置向下拉动4cm,并给以向上的21cm/s 的初速度(这时t =0) ,选x 轴向下,求振动方程的数值式. 解:物体受向下的重力和向上的弹性力.k=m 0g/∆l , x 0=4×10-2m, v 0=-21×10-2m/sω=()m l g m m k Δ0==7s -1A=22020ω/v x +=5×10-2m因A cos ϕ=4×10-2m, A sin ϕ=-v 0/ω=3×10-2m,有 ϕ=0.64rad 所以x=5×10-2cos(7t +0.64) (SI)6.(本题5分)一质量为0.2kg 的质点作简谐振动,其振动方程为10.6cos(5)(SI)2x t π=-求:(1)质点的初速度;(2)质点在正向最大位移一半处所受的力.解:(1)003.0sin(5)()0, 3.0m/s 2dx v t SI t v dt π==--==(2分) (2)2F ma m x ==-ω12x A =时, 1.5N F =-(无负号扣1分) (3分) 7.(5分)一平面简谐波沿x 轴正方向传播,波速为1m/s ,在x 轴上某质点的振动频率为1Hz ,振幅为0.01m. t = 0时该质点恰好在正最大位移处,若以该质点的平衡位置为x 轴的原点. 求此一维简谐波的表达式.解. 0.01cos[2()](m)y t x =-π8.(本题10分)某质点作简谐振动,周期为2s ,振幅为0.06m ,t =0时刻,质点恰好处在负最大位移处,求(1)该质点的振动方程.(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长. 解:(1)振动方程 00.06cos(2/2)0.06cos()(SI)y t t ππππ=+=+3分 (2)0.06cos[((/))0.06cos[(/2))(SI)y t x u t x ππππ=-+=-+ 4分(3)波长4m uT λ==9.(10分)一列平面简谐波在以波速5m/s u =,沿x 轴正向传播,原点O 处质点的振动曲线如图所示.1)求解并画出25cm x =处质元的振动曲线 2)求解并画出3s t =时的波形曲线 解:1)原点O 处质元的振动方程为211210cos(),(SI)22y t ππ-=⨯-(2分)波的表达式 (2分)211210cos((/5)),(SI)22y t x ππ-=⨯--x =25m 处质元的振动方程21210cos(3),(SI)2y t ππ-=⨯-振动曲线如右y-t 图 (2分)2)t=3s 时的波形曲线方程2210cos(/10),(SI)y x ππ-=⨯-(2分)波形曲线见右y-x 图 (2分)10.(10分)某质点作简谐振动,周期为2s ,振幅为0.6m ,t =0时刻,质点恰好处在负最大4O2 y(cm)t (s)2位移处,求(1)该质点的振动方程;(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长.解:(1) 振动方程)22cos(06.00π+π=ty )cos(06.0π+π=t (SI) (3分) (2) 波动表达式])/(cos[06.0π+-π=u x t y (4分)])21(cos[06.0π+-π=x t (SI)(3) 波长4==uT λm (3分)11.(5分)如图所示,一简谐波向x 轴正向传播,波速0500/,1,u m s x m P ==点的振动方程为10.03cos(500)(SI)2y t ππ=-. (1) 按图所示坐标系,写出相应的波的表达式; (2) 在图上画出t=0时刻的波形曲线.解:(1) 2m )250/500(/===νλu m 波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y110.03cos[500(1)2/2]0.03cos(500)(SI)22t x t x =π-π--π=π+π-π(3分)(2) t = 0时刻的波形曲线x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI) (2分)12.(10分)图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图(波向左传播).已知波速为u ,波的周期大于2 s ,求(1) 坐标原点处介质质点的振动方程;(2) 该波的波动表达式. 解:(1) 比较t = 0 时刻波形图与t = 2 s 时刻波形图,可知此波向左传播.在t = 0时刻,O 处质点φcos 0A =,φωsin 00A -=<v ,故2πφ-= 又t = 2 s ,O 处质点位移为)24cos(2/ππ-=νA A 所以244πππ-=-ν,ν = 1/16 Hz 振动方程为)28/cos(0ππ-=t A y (SI)(2) 波速u = 20 /2 m/s = 10 m/s,波长λ = u /ν = 160 m 波动表达式]21)16016(2cos[π-+π=x t A y (SI) x (m)uP y (m)O-2-112-0.030.03x (m)O160A y (m)8020t =0t =2 s2A。
高三第一轮复习单元过关试题——振动与波
高三第一轮复习单元过关试题振动和波一、单选题1.关于单摆的运动有下列说法,正确的是( ) ①单摆的回复力是摆线的拉力与重力的合力 ②单摆的回复力是重力沿摆球运动轨迹切向的分力③单摆的周期与质量无关与振幅无关,与摆长和当地的重力加速度有关 ④单摆做简谐运动的条件是摆角很小如小于5o ⑤在山脚下走时准确的摆钟移到高山上走时将变快 A .①③④ B .②③④ C .③④⑤ D .①④⑤2.一弹簧振子做简谐运动,周期为T ,下列叙述中正确的是( )A 、若t 时刻和(t+△t)时刻振子运动位移的大小相等,方向相同,则△t 一定等于T 的整数倍B 、若t 时刻和(t+△t)时刻振子运动速度的大小相等,方向相反,则△t 一定等于T/2的整数倍C 、若△t=T ,则t 时刻和(t+△t)时刻振子运动的加速度一定相等D 、若△t=T/2,则t 时刻和(t+△t)时刻弹簧的长度一定相等3.如图所示在竖直平面内,有一段光滑圆弧轨道MN ,它所对应的圆心角小于10o ,P 是MN 的中点,也是圆弧的最低点,在N 、P 之间一点Q 和P 之间搭一光滑斜面,将两个小球(可视为质点)分别同时由Q 点和M 点静止释放,则两个小球相遇点一定在( ) A .斜面PQ 上一点 B .PM 弧上的一点 C .P 点 D .条件不足,无法判定4.如图两单摆摆长相同,平衡时两摆球刚好接触。
现将摆球A 在两摆线所在平面内向左拉开一小角度后释放,碰撞后,两球分开各自做简谐运动,以m A 、m B 分别表示摆球A 、B 的质量,则( )A .如果m A >mB ,下一次碰撞将发生在平衡位置右侧 B .如果m A <m B ,下一次碰撞将发生在平衡位置左侧C .无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧D .无论两摆球的质量之比是多少,下一次碰撞都只能在平衡位置左侧5.如图所示,下列说法正确的是( ) A 、振动图象是从平衡位置开始计时的MPQ NA右左Bx/cmt/s0 2 -21 32 4 5 6B 、2s 末速度为负方向,加速度最大C 、3s 末,。
高考物理总复习专题练习:振动和波
高考物理复习振动和波专题训练及其答案一、单项选择题1.如图所示为一列简谐横波t时刻的图象,已知波速为0.2m/s,以下说法正确的是()A.经过0.5s,质点a、b、c通过的路程均为75cmB.若从t时刻起质点a比质点b先回到平衡位置,则波沿x轴正方向传播C.图示时刻质点a、b、c所受的回复力大小之比为2∶1∶3D.振源的振动频率为0.4Hz2.一列向右传播的简谐横波在某一时刻的波形如图所示,该时刻,两个质量相同的质点P、Q 到平衡位置的距离相等。
关于P、Q两个质点,以下说法正确的是()A.P较Q先回到平衡位置B.再经14周期,两个质点到平衡位置的距离相等C.两个质点在任意时刻的动量相同D.两个质点在任意时刻的加速度相同3.图为一列简谐波在0=t时刻的波形图,此时质点Q正处于加速运动过程中,且质点N在1st=时第一次到达波峰。
则下列判断正确的是()A.此时质点P也处于加速运动过程B.该波沿x轴负方向传播C.从0=t时刻起,质点P比质点Q晚回到平衡位置D.在0=t时刻,质点N的振动速度大小为1m/s4.如图所示为一列机械波在t=0时刻传播的波形图,此刻图中P点速度沿y轴正方向,t=2s 时刻,图中Q点刚好在x轴上。
则下列说法正确的是()A.该机械波沿x轴正方向传播B.该机械波周期不可能是8s3C.无论周期是多少,当Q点在x轴时,P点一定离x轴最远D.P点振幅是10cm5.如图所示是沿x轴传播的一列简谐横波在t=0时刻的波形图,已知波的传播速度为16.0m/s,从此时起,图中的P质点比Q质点先经过平衡位置.那么下列说法中正确的是()A.这列波一定沿x轴正向传播B.这列波的频率是3.2HzC.t=0.25s时Q质点的速度和加速度都沿y轴负向D.t=0.25s时P质点的速度和加速度都沿y轴负向6.如图(a)所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图(b)为xy 平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图(b)上x=0.4m处的Q点的说法正确的是().A.t=0时,速度最大,其大小为0.1m/s,方向沿y轴正方向B.t=0到t=5s内,通过的路程为20cmC.t=2s时,运动到x=0.2m处D.t=3s时,加速度最大,且方向向下7.一列简谐横波在某时刻的波形图如图所示,已知图中质点b的起振时刻比质点a延迟了0.5s,b和c之间的距离是5m,以下说法正确的是()A.此列波的波长为2.5mB.此列波的频率为2HzC.此列波的波速为2.5m/sD.此列波的传播方向为沿x轴正方向传播8.P、Q、M是某弹性绳上的三个质点,沿绳建立x坐标轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a .则下列计算该振子劲度系数的公式中,错误的是:(A) 2max 2max /x m k v =. (B) x mg k /=.(C) 22/4T m k π=. (D)x ma k /=. [ B ]2. 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为 (A) g l π2. (B) g l22π.(C) gl322π. (D)gl 3π.[ C ]3. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为(A) . (B) /2. (C) 0 . (D) . [ C ]4. 两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(t + ).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .l(C))π23cos(2-+=αωt A x . (D))cos(2π++=αωt A x . [ B ][ ]6. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) /6. (B) 5/6. (C)-5/6.(D) -/6. (E) -2/3. [ ] 7. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2.将它们拿到月球上去,相应的周期分别为1T '和2T '.则有(A) 11T T >'且22T T >'. (B) 11T T <'且22T T <'. (C) 11T T ='且22T T ='. (D) 11T T ='且22T T >'. [ D ]8. 一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动.当重物通过平衡位置且向规定的正方向运动时,开始计时.则其振动方程为: (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x(C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x(E)t m /k A x cos = [ B ]9. 一质点在x 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为 (A) 1 s . (B) (2/3) s . (C) (4/3) s . (D) 2 s . [ B ]10.一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为 (A) 2221ωA -. (B) 2221ωA . (C)2321ωA -. (D)2321ωA . [ B ] v (m/s)t (s)O mm v 2111. 两个同周期简谐振动曲线如图所示.x 1的相位比x 2的相位(A) 落后/2. (B) 超前.(C) 落后. (D) 超前.[ B ] 12. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ B ] 13. 一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s .(C) 2.20 s . (D) 2.00 s .[ B ]x o A ϖ x A 21 ωA 21ωA 21-(D)oo o A 21-xx xA ϖ A ϖx Aϖxω ωx (cm)t (s)O4 21A21-A21-A21 21A21 AA21- oo 2T2T A21- t21 xtx(A)(B)(C)(D)2T2Tottxxx tOx 1x 215. 用余弦函数描述一简谐振子的振动.若其速度~时间(v ~t )关系曲线如图所示,则振动的初相位为 (A) /6. (B) /3.(C) /2. (D) 2/3. (E) 5/6.[ A ] 17. 一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为 (A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ D ]18 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A) kA 2. (B) 221kA . (C) (1/4)kA 2. (D) 0. [ D ]19. 一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为:(A) 1:4. (B) 1:2. (C) 1:1. (D) 2:1. (E) 4:1. [ D ]20. 图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为 (A) π23. (B) π.(C) π21. (D) 0. [ B ]二. 填空题21. 在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为(a) ______________________________;v (m/s)t (s) Om 21- -m(c)v 0v 0v = 0x t O A/-Ax 1x 22cos()2x A t T ππ=+(b) ______________________________; (c) ______________________________.23. 在两个相同的弹簧下各悬一物体,两物体的质量比为4∶1,则二者作简谐振动的周期之比为___2:1___.24. 一质点作简谐振动,速度最大值v m = 5 cm/s ,振幅A = 2 cm .若令速度具有正最大值的那一时刻为t = 0,则振动表达式为_____50.02cos()22x t π=-___.25. 一物体作余弦振动,振幅为15×10-2 m ,角频率为6 s -1,初相为0.5,则振动方程为 __0.15cos(6)2x t ππ=+(SI).27. 一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m ,初速度为0.09 m/s ,则振幅A =____0.05m_________ ,初相 =____3arcsin 5-____________.30. 已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为_______1:1__________. 31. 一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为A=_____0.1m________;=_____/6rad s π_____;x (cm)t (s)105-101471013O4 3 2 -1 1 t (s)o x (cm)x 1 x 2 1 -222cos()2x A t Tππ=+2cos()x A t T ππ=+=_____3π__________..34. 已知三个简谐振动曲线如图所示,则振动方程分别为:x 1 =10cos t π______________________,x 2 =10cos()2t ππ- _____________________,x 3 =10cos()t ππ+_______________________.37.一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初相为_____4π_______.振动方程为__0.02cos()4x t ππ=+____________.41. 一作简谐振动的振动系统,振子质量为 2 kg ,系统振动频率为1000 Hz ,振幅为0.5 cm ,则其振动能量为______1002πJ________.43. 一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为____200N/m_______,振子的振动频率为_5πHZ________.44.两个同方向的简谐振动曲线如图所示.合振动的振幅为______21A A -___________,合振动的振动方程x (cm)t (s)O x 1x 2x 3100-10123x tO AA a b cd e fωωπt xO t =0t = t π/4·xt O x 1(t ) x 2(t )A 1 A 2 -1 -A 2T为_____212()cos()2x A A t T ππ=-+______. 50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为)612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI)则其合成振动的振幅为___0.01m________,初相为____6π_____.第十章波复习题一、选择题1. 在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的.(B) 波源振动的速度与波速相同. (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于计).(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于计)[ C ]2. 机械波的表达式为y = 0.03cos6(t + 0.01x ) (SI) ,则(A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ B ]3.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ A ]4. 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻[ D ](A) A 点振动速度大于零. (B) B 点静止不动. (C) C 点向下运动. (D) D 点振动速度小于零. 5. 把一根十分长的绳子拉成水平,用手握其一端.维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长. (B) 振动频率越低,波长越长.(C)振动频率越高,波速越大. (D) 振动频率越低,波速越大.[ B ]6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则O 点的振动初相为: (A) 0. (B) π21(C)(D) π23(或π-21)[ B ]7. 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为 (A)])/(cos[0φω+-=u x t A y . (B) )]/([cos u x t A y +=ω.x (m)O 20.10y (m)(A)x O 20.10(B)x (m)O 2-0.10y (m)(C)x O 2y (m)(D)-0.10xu ABCD OxyOuxy u BO |x|(C) })]/([cos{0φω+-=u x t A y .(D) })]/([cos{0φω++=u x t A y . [ C ] 8.如图所示为一平面简谐波在t = 0 时刻的波形图,该波的波速u = 200 m/s ,则P 处质点的振动曲线为[ C ] 9. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是[ A ]10. 一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是(A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI).(C) )312cos(10.0π+π=t y P (SI).(D))612cos(10.0π+π=t y P(SI). [ A ]11. 图示一简谐波在t = 0时刻的波形图,波速 u = 200 m/s ,则P 处质点的振动速度表达式为 [ C ] (A) )2cos(2.0π-ππ-=t v (SI). (B) )cos(2.0π-ππ-=t v (SI). (C) )2/2cos(2.0π-ππ=t v (SI).ωA O ′S(D) )2/3cos(2.0π-ππ=t v (SI).12.在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是 (A) A 1 / A 2 = 16. (B) A 1 / A 2 = 4. (C) A 1 / A 2 = 2. (D) A 1 / A 2 = 1 /4. [ C ]13. 一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为最大值的媒质质元的位置是:(A) o ',b ,d ,f . (B) a ,c ,e ,g .(C) o ',d . (D) b ,f . [ B ]14. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零. (C) 动能最大,势能最大. (D) 动能最大,势能为零. [C ]15. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中 (A) 它的势能转换成动能. (B) 它的动能转换成势能. (C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D)它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.[ C ]16. 如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为 (A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C))212cos(2π+π=t A y .(D))1.02cos(22π-π=t A y . [ D ]17. 两相干波源S 1和S 2相距 /4,(为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B)π21. (C) . (D)π23. [ C ] 18. S 1和S 2是波长均为 的两个相干波的波源,相距3 /4,S 1的相位比S 2超前π21.若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,则在S 1、S 2连线上S 1外侧和S 2外侧各点,合成波的强度分别是 (A) 4I 0,4I 0. (B) 0,0. (C) 0,4I 0 . (D) 4I 0,0. [ A ]19 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同. (C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ]20 在波长为 的驻波中,两个相邻波腹之间的距离为 (A)/4. (B)/2.S 1S PS 1S 2Pλ/4(C) 3/4. (D). [ B ]21.沿着相反方向传播的两列相干波,其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=.在叠加后形成的驻波中,各处简谐振动的振幅是 (A) A . (B) 2A .(C) )/2cos(2λx A π. (D) |)/2cos(2|λx A π. [ D ] 二、填空题22.一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在该时刻的运动方向.A _____________;B _____________ ;C ______________ .23. 一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI),其角频率=__________________________,波速u =______________________,波 长 = _________________.24. 频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________.25. 图为t = T / 4 时一平面简谐波的波形曲线,则其波的表达式为______________________________________________.xy u O AB Cx (m)O -0.101u =330 m/sy (m)23426、一平面简谐波沿Ox 轴正方向传播,波长为.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.27、一简谐波沿x 轴正方向传播.x 1和x 2两点处的振动曲线分别如图(a)和(b)所示.已知x 2 .> x 1且x 2 - x 1 < (为波长),则x 2点的相位比x 1点的相位滞后___________________.28、已知某平面简谐波的波源的振动方程为t y π=21sin 06.0 (SI),波速为2 m/s .则在波传播前方离波源 5 m 处质点的振动方程为_-______________________. 29、(1)一列波长为 的平面简谐波沿x 轴正方向传播.已知在λ21=x 处振动的方程为y =A cos t ,则该平面简谐波的表达式为______________________________________.(2) 如果在上述波的波线上x = L (λ21>L )处放一如图所示的反射面,且假设反射波的振幅为A ',则反射波的表达式为_______________________________________ (x ≤L ).30、一平面简谐波沿x 轴负方向传播.已知 x = -1 m 处质点的振动方程为 )cos(φω+=t A y ,若波速为u ,则此波的表达式为 _________________________________________________________. 31、一个波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2,在两个球面上分别取相等的面积S 1和S 2,则通过x O P 1P 2L 1L 2ty 1t y 20(a)(b)xO 反射面波疏媒质波密媒质L它们的平均能流之比=21P /P ___________________.32、一点波源发出均匀球面波,发射功率为4 W .不计媒质对波的吸收,则距离波源为2 m 处的强度是__________________. 33、如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3和103 ,为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率___________,波源S 1的相位比S 2的相位领先_________________.34、如图所示,S 1和S 2为同相位的两相干波源,相距为L ,P 点距S 1为r ;波源S 1在P 点引起的振动振幅为A 1,波源S 2在P 点引起的振动振幅为A 2,两波波长都是,则P 点振幅A =_________________________________________________________. 35、两相干波源S 1和S 2的振动方程分别是t A y ωcos 1=和)21cos(2π+=t A y ω.S 1距P 点3个波长,S 2距P 点21/4个波长.两波在P 点引起的两个振动的相位差 是____________.36、 S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(为波长)如图.已知S 1的初相为π21.(1)若使射线S 2C 上各点由两列波引起的振动均PS 1S 3λ10λ/312LrS 1S 2M NC干涉相消,则S 2的初相应为________________________.(2)若使S 1 S 2连线的中垂线MN 上各点由两列波引起的振动均干涉相消,则S 2的初位相应为_______________________.37、 两列波在一根很长的弦线上传播,其表达式为 y 1 = 6.0×10-2cos (x - 40t ) /2 (SI) y 2 = 6.0×10-2cos (x + 40t ) /2 (SI) 则合成波的表达式为__________________________________________________; 在x = 0至x = 10.0 m 内波节的位置是_______________________________________________________________________;波腹的位置是________________________________________________________.38、设入射波的表达式为 )(2cos 1λνxt A y +π=.波在x = 0处发生反射,反射点 为固定端,则形成的驻波表达式为____________________________________.39、 一驻波表达式为 t x A y ππ=100cos 2cos .位于x 1 = 3 /8 m 的质元P 1与位于x 2 = 5 /8 m 处的质元P 2的振动相位差为_____________________________.40、 在弦线上有一驻波,其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________.。
