等差数列求和及练习题(整理)

合集下载

等差数列的性质、求和知识点及训练

等差数列的性质、求和知识点及训练重点：掌握等差数列的通项公式、求和公式以及等差中项的求法难点:对等差数列的综合考察一知识梳理1.定义：d a a n n =--1（d 为常数）（2≥n ）； 2．等差数列通项公式：*11(1)()n a a n d dn a d n N =+-=+-∈ ，首项:1a ，公差:d ，末项:n a 推广： d m n a a m n )(-+=．从而mn a a d mn --=；3．等差中项（1）如果a ，A ，b 成等差数列，那么A 叫做a 与b 的等差中项．即：2ba A +=或b a A +=2（2）等差中项：数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a4．等差数列的前n 项和公式：1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-2An Bn =+ （其中A 、B 是常数）（当d ≠0时，S n 是关于n 的二次式且常数项为0） 5．等差数列的判定方法（1）定义法：若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列．（2）等差中项：数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a ．（3）数列{}n a 是等差数列⇔b kn a n +=（其中b k ,是常数）。

（4）数列{}n a 是等差数列⇔2n S An Bn =+,（其中A 、B 是常数）。

6．等差数列的证明方法定义法：若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列．7.提醒：（1）等差数列的通项公式及前n 和公式中，涉及到5个元素：1a 、d 、n 、n a 及n S ，其中1a 、d 称作为基本元素。

(完整版)等差等比数列求和与差的练习题

(完整版)等差等比数列求和与差的练习题
题目一：等差数列求和
已知等差数列的首项为$a_1$，公差为$d$，求该等差数列的前$n$项和$S_n$。

解答步骤：
1. 根据公式$S_n = \frac{n}{2}(a_1 + a_n)$计算出结果。

题目二：等差数列差的问题
已知等差数列的首项为$a_1$，公差为$d$，依次计算以下问题：
1. $a_3 - a_2$；
2. $a_5 - a_3$；
3. $a_{10} - a_5$。

解答步骤：
1. 利用公式$a_n = a_1 + (n-1)d$计算出各项的值；
2. 按照题目给定的差问题计算出结果。

题目三：等比数列求和
已知等比数列的首项为$a_1$，公比为$r$，求该等比数列的前$n$项和$S_n$。

解答步骤：
1. 如果公比$r=1$，则$S_n = n \cdot a_1$，直接计算结果；
2. 如果公比$r \neq 1$，则$S_n = a_1 \cdot \frac{1 - r^n}{1 - r}$，按照公式计算结果。

题目四：等比数列差的问题
已知等比数列的首项为$a_1$，公比为$r$，依次计算以下问题：
1. $a_2 - a_1$；
2. $a_4 - a_2$；
3. $a_{10} - a_{5}$。

解答步骤：
1. 利用公式$a_n = a_1 \cdot r^{(n-1)}$计算各项的值；
2. 按照题目给定的差问题计算出结果。

以上是关于等差数列求和与差的练题的完整版文档。

高考数学解答题(新高考)数列求和(裂项相消法)(典型例题+题型归类练)(解析版)

专题06 数列求和（裂项相消法）(典型例题+题型归类练)一、必备秘籍常见的裂项技巧类型一：等差型类型二：无理型类型三：指数型①11(1)11()()n n n n n a a a k a k a k a k++-=-++++如：11211(2)(2)22n n n n n k k k k++=-++++类型四：通项裂项为“+”型如：①()()()21111111nn n n n n n +⎛⎫-⋅=-+ ⎪++⎝⎭ ②()()131222(1)(11)1n nn n nn n n n n +⎛⎫++⋅-=+- ⎝+⎪⎭本类模型典型标志在通项中含有(1)n -乘以一个分式.二、典型例题类型一：等差型例题1．（2022·辽宁·鞍山一中模拟预测）已知n S 是等差数列{}n a 的前n 项和，0n a >，315S =，公差1d >，且___________.从①21a -为11a -与31a +等比中项，②等比数列{}n b 的公比为3q =，1124,b a b a ==这两个条件中，选择一个补充在上面问题的横线上，使得符合条件的数列{}n a 存在并作答. (1)求数列{}n a 的通项公式；(2)设数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求证：16nT <. 【答案】(1)选择条件见解析，21n a n =+(2)证明见解析 (1)若选①，21a -为11a -与31a +的等比中项，则()()()2132111a a a -+=-，由{}n a 为等差数列，315S =，得2315a =，∴25a =，把25a =代入上式，可得()()4616d d -+=，解得2d =或4d =-（舍） ∴13a =，21n a n =+；若选②，3q =为等比数列{}n b 的公比，且1124,b a b a ==，可得213b b =，即413a a =，即有113)3a d a +=（，即123a d =；又315S =，可得11332152a d +⨯⨯=，即15a d +=，解得12,3d a ==，此时21n a n =+；第（2）问解题思路点拨：由（1）知：，设，则，典型的裂项相消的特征，可将通项裂项为：解答过程：由题意知：；(2)∵()()111111212322123n n a a n n n n +⎛⎫==- ⎪++++⎝⎭， ∴11111111112355721232323n T n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅+-=- ⎪ ⎪+++⎝⎭⎝⎭； ∴16n T <，得证例题2．（2022·广东佛山·模拟预测）已知数列{}n a 的前n 项和为n S ，111a =-，29a =-，且()11222n n n S S S n +-+=+≥． (1)求数列{}n a 的通项公式； (2)已知11n n n b a a +=，求数列{}n b 的前n 项和n T ．【答案】(1)213n a n =- (2)122212nn -(1)解：由题意得：由题意知()()112n n n n S S S S +----=，则()122n n a a n +-=≥又212a a -=，所以{}n a 是公差为2的等差数列，则()11213n a a n d n =+-=-；感悟升华（核心秘籍）本例是裂项相消法的等差型，注意裂项，是裂通项，裂项的过程中注意前面的系数不要忽略了.第（2）问解题思路点拨：由（1）知：，，则，典型的裂项相消的特征，可将通项裂项为：解答过程：由题意知：；(2)由题知()()11112132112213211n b n n n n ⎛⎫==- ⎪----⎝⎭则1111111111211997213211211211n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-++-+++-=-- ⎪ ⎪ ⎪ ⎪⎢⎥---⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 122212n n-=类型二：无理型例题3．（2022·重庆八中模拟预测）已知各项均为正数的等差数列{}n a 满足11a =，22112()n n n n a a a a ++=++．(1)求{}n a 的通项公式； (2)记11n n n b a a +=+，求数列{}n b 的前n 项和n S ．【答案】(1)21n a n =-(2)1(211)2n +-(1)解：各项均为正数的等差数列{}n a 满足11a =，22112()n n n n a a a a ++=++，整理得()()()1112n n n n n n a a a a a a ++++-=+，由于10n n a a ++≠，所以12n n a a +-=，故数列{}n a 是以1为首项，2为公差的等差数列．所以21n a n =-．(2)解：由（1）可得111212122121n n n n n b a a n n ++--===+-++，所以11(3153...2121)(211)22n S n n n =⨯-+-+++--=+-．例题4．（2022·福建龙岩·模拟预测）已知等差数列{}n a 的前n 项和为n S ，3518a a +=，648S =.第（2）问解题思路点拨：由（1）知：，，则，典型的裂项相消的无理型特征，可将通项分母有理化为：解答过程：由题意知：；(1)求{}n a 的通项公式； (2)设112n n n b a a +-=+，求数列{}n b 的前n 项和为n T .【答案】(1)21n a n =+；(2)证明见解析﹒(1)由题可知，11261861548a d a d +=⎧⎨+=⎩，解得132a d =⎧⎨=⎩，∴21n a n =+；(2)1122232122321n n n n n b a a n n +-+--===+++-，()()()()()1517395212323212n T n n n n ⎡⎤=-+-+-+++--++--⎣⎦12123132n T n n ⎡⎤=+++--⎣⎦感悟升华（核心秘籍）本例是裂项相消法的无理型，具有明显的特征，其技巧在于分母有理化，注意裂项相消的过程中，是连续相消，还是隔项相消，计算注意细节.类型三：指数型第（2）问解题思路点拨：由（1）知：，，则，典型的裂项相消的无理型特征，可将通项分母有理化为：解答过程：由题意知：；例题5．（2022·全国·模拟预测）已知等差数列{}n a 满足()*10n n a a n +->∈N ，且141015a a a ++=，2a ，4a ，8a 成等比数列．(1)求数列{}n a 的通项公式；(2)若122n a n n n n a b a a ++⋅=⋅，求数列{}n b 的前n 项和n S ．【答案】(1)n a n =(2)n S 1212n n +=-++(1)解：设等差数列{}n a 的公差为d ，因为2a ，4a ，8a 成等比数列，所以()()()211137a d a d a d +=++，整理得()10d a d -=，又因为10n n a a +->，所以0d >，1a d =，又1410131215a a a a d ++=+=，即15d ＝15，所以11a d ==，所以n a n =；感悟升华（核心秘籍）第（2）问解题思路点拨：由（1）知：，，则，具有明显的裂项相消法的特征，但是裂项是难点，在裂项时要把握住“型”，再结合待定系数法解答过程：用待定系数法裂通项：与对比，得通分，逆向求裂项求和．(2)解：由（1）知，n a n =，所以()()12221221n n nn n b n n n n +⋅==-++++，2324312112222222222223243541121n n n n n n n S n n n n n n ---+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1212n n +=-++．例题6．（2022·江西·临川一中模拟预测（理））已知数列{}n a 的前n 项和为n S ，且21,*=-∈n n S a n N .(1)求数列{}n a 的通项公式； (2)若数列{}n b 满足22,(1)*++=∈⋅⋅+n n n b n N a n n ，求数列{}n b 的前n 项和n T .【答案】(1)12n na ；(2)1112(1)2n n T n +=-+⋅. (1)因为21n n S a =-，当1n =时，1121S a =-，解得11a =，当2n ≥时，1121n n S a --=-，所以()()111212122n n n n n n n a S S a a a a ---=-=---=-，即12(2)n n a a n -=≥，所以数列{}n a 是首项为1，公比为2的等比数列.故11122n n n a --=⨯=.(2)，1122211(1)(1)22(1)2n n n n n n n b a n n n n n n +++++===-⋅⋅++⋅+⋅于是12231111111111122222322(1)22(1)2n n n n T n n n ++=-+-++-=-⋅⋅⋅⋅⋅+⋅+⋅类型四：通项裂项为“+”型第（2）问解题思路点拨：由（1）知：，，则，具有明显的裂项相消法的特征，但是裂项是难点，在裂项时要把握住“型”，再结合待定系数法解答过程：用待定系数法裂通项：与对比，得通分，逆向求裂项求和例题7．（2022·吉林辽源·高二期末）已知等差数列{}n a 的前n 项和21,3n S n an b a =++=，数列{}n b 的前n 项和23n n n T b +=，12b =. (1)求数列{}n a 和{}n b 的通项公式； (2)令(1)nnn na cb =-，求数列{}nc 的前n 项和n P .【答案】(1)21n a n =+，()1n b n n =+ (2)2,?1,?1n n n n P n n n +⎧-⎪⎪+=⎨⎪-⎪+⎩为奇数为偶数感悟升华（核心秘籍）第（2）问解题思路点拨：由（1）知：，，则，注意通项中含有明显的裂项的两个特征，①含有分式②含有（注意通项中含有是裂项为“”型的重要标志），但是裂项是难点，在裂项时要把握住“型”，再结合待定系数法解答过程：用待定系数法裂通项：与对比，得则：，注意到通项中含有，需分奇偶讨论通分，逆向求当为偶数（为正），（注意此时为偶数，代入偶数的结论中）当为奇数（为偶数）综上：(1)设等差数列{}n a 的公差为d ，则22113222n n n n d d S na d n n n a b -⎛⎫=+=+-=++ ⎪⎝⎭，所以1,23,20,dd a b ⎧=⎪⎪⎪-=⎨⎪=⎪⎪⎩所以2,2,0,d a b =⎧⎪=⎨⎪=⎩，所以数列{}n a 的通项公式为()32121n a n n =+-=+. 因为23n n n T b +=，当2n ≥时，1113n n n T b --+=，所以112133n n n n n n n b T T b b --++=-=-，所以11133n n n n b b --+=，即111n n b n b n -+=-. 所以1232112321n n n n n n n b b b b b b b b b b b b -----=⨯⨯⨯⋅⋅⋅⨯⨯⨯()11432112321n n n n n n n n +-=⨯⨯⨯⋅⋅⋅⨯⨯⨯=+---. (2)()()()()()11111111nn n n n n n n a c b n n n n ++⎛⎫=-=-⋅=-+ ⎪++⎝⎭，当n 为奇数时，11111111223341n P n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++⋅⋅⋅-+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭12111n n n +=--=-++. 当n 为偶数时，11111111223341n P n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++⋅⋅⋅++ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1111n n n =-+=-++. 综上所述，数列{}n c 的前n 项和2,1,1n n n n P n n n +⎧-⎪⎪+=⎨⎪-⎪+⎩为奇数为偶数.例题8．（2022·陕西·长安一中高二期中（文））已知等差数列{}n a 的公差为2，前n 项和为n S ，且124,,S S S成等比数列．（1）求数列{}n a 的通项公式；（2）令()1141n n n n nb a a -+=-，求数列{}n b 的前n 项和n T ．【答案】（1）21n a n =-；（2）2,2122,21n nn n T n n n ⎧⎪⎪+=⎨+⎪⎪+⎩为偶数为奇数第（2）问解题思路点拨：由（1）知：，，则，注意通项中含有明显的裂项的两个特征，①含有分式②含有（注意通项中含有是裂项为“”型的重要标志），但是裂项是难点，在裂项时要把握住“型”，再结合待定系数法解答过程：用待定系数法裂通项：与对比，得，通分，逆向求当为奇数（为正），（注意此时为奇数，代入奇数的结论中）当为偶数（为奇数）综上：（1）∴等差数列{an }的公差为2，前n 项和为S n ，且S 1、S 2、S 4成等比数列． ∴S n ＝na 1+n （n ﹣1）（2a 1+2）2＝a 1（4a 1+12），a 1＝1，∴an ＝2n ﹣1；（2）∴由（1）可得()()111411112121n n n n n n b a a n n --+⎛⎫=-=-+ ⎪-+⎝⎭，当n 为偶数时，T n ＝11111111113355723212121n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+++-++-+ ⎪ ⎪ ⎪ ⎪ ⎪---+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1212121nn n =-=++．当n 为奇数时，11111111113355723212121n T n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+++-⋯-+++ ⎪ ⎪ ⎪ ⎪ ⎪---+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭12212121n n n +=+=++ ． 2,2122,21n nn n T n n n ⎧⎪⎪+∴=⎨+⎪⎪+⎩为偶数为奇数．三、题型归类练1．（2022·内蒙古·满洲里市教研培训中心模拟预测（理））已知在等差数列{}n a 中，25a =，1033a a =． (1)求数列{}n a 的通项公式; (2)设()21n n b n a =+，求数列{}n b 的前n 项和n S ．【答案】(1)21n a n =+(2)1n n + (1)设等差数列{}n a 的公差为d ，由210353a a a =⎧⎨=⎩，可得()1115932a d a d a d ⎧+=⎪⎨+=+⎪⎩解得13,2a d==，所以()13122n a n n -⨯=++= (2)由（1）可得2111(1)(22)(1)12n n b n a n n n n n n ====-++++所以111111 (22311)n n S n n n ⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭ 2．（2022·山西运城·模拟预测（理））已知单调递增的等差数列{}n a 的前n 项和为n S ，512340,,1,S a a a =-成等比数列，正项等比数列{}n b 满足11631,23b a S b =+=+. (1)求{}n a 与{}n b 的通项公式； (2)设()3123log n n n c a b =+，求数列{}n c 的前n 项和n T .【答案】(1)31n a n =-，3nn b =(2)64n nT n =+ (1)设数列{}n a 的公差为d ，则0d >，由540S =得1545402a d ⨯+=，即128a d +=①，又123,1,a a a -成等比数列，所以()22131a a a -=，所以()()211112a d a a d +-=+，所以21(1)2d a -=②，联立①②及0d >解得12,3a d ==. 所以2(1)331n a n n =+-⨯=-. 所以161653,6572b S a d ⨯==+=，所以35723b =+，解得327b =，又231,0b b q q =>，所以3q =，所以3nn b =.(2)由（1）得()311111(31)23log (31)(32)33132n n c n b n n n n ⎛⎫===- ⎪-+-+-+⎝⎭，所以121111111111325583132323264n n n T c c c n n n n ⎛⎫⎛⎫=+++=-+-+⋅⋅⋅+-=-= ⎪ ⎪-+++⎝⎭⎝⎭. 3．（2022·河南·模拟预测（理））已知正项数列{}n a 的前n 项和为n S ，且()()222220n n S n n S n n -+--+=．(1)求1a 的值和数列{}n a 的通项公式； (2)设21n n n b a a +=，求数列{}n b 的前n 项和n T ．【答案】(1)12a =；2n a n =；(2)()()32316812n n T n n +=-++. (1)由()()222220n n S n n S n n -+--+=得：()()()220n n S S n n +-+=；{}n a 为正项数列，0n S ∴>，2n S n n ∴=+；当1n =时，112a S ==；当2n ≥时，()()221112n n n a S S n n n n n -=-=+----=；经检验：12a =满足2n a n =；()2n a n n N *∴=∈.(2)由（1）得：()()111112224282n b n n n n n n ⎛⎫===- ⎪⋅+++⎝⎭，11111111111832435112n T n n n n ⎛⎫∴=⨯-+-+-+⋅⋅⋅+-+- ⎪-++⎝⎭()()()()1111132332318212821216812n n n n n n n n ⎛⎫++⎛⎫=⨯+--=⨯-=- ⎪ ⎪ ⎪++++++⎝⎭⎝⎭. 4．（2022·河北保定·一模）已知数列{}n a 的前n 项和为n S ，且1332n n S +-=． (1)求数列{}n a 的通项公式； (2)设3314log log n n n b a a +=⋅，求{}n b 的前n 项和n T ．【答案】(1)3nn a =；(2)41n nT n =+. (1)因为1332n n S +-=，故当1n =时，13a =，当2n ≥时，1332n n S --=，则()132nn n n a S S n -=-=≥，当1n =时，13a =满足上式，所以3nn a =.(2)由（1）得()33144114log log 11n n n b a a n n n n +⎛⎫===- ⎪⋅++⎝⎭，所以12311111144141223111n n n T b b b b n n n n ⎛⎫⎛⎫=++++=⨯-+-++-=-= ⎪ ⎪+++⎝⎭⎝⎭. 故数列{}n b 的前n 项和41n nT n =+. 5．（2022·安徽·北大培文蚌埠实验学校高三开学考试（文））已知数列{}n a 的前n 项和为n S ，11a =，525S =，且()*1232n n n n S a S S n ++-=+∈N ．(1)求数列{}n a 的通项公式； (2)设n b =，求数列{}n b 的前n 项和n T ．【答案】(1)21n a n =-(2)n T )112=(1)由1232n n n n S a S S ++-=+得：121211223222n n n n n n n n n n a S S S S S S S a a +++++++-=-+=-+-=-+即122n n n a a a ++=+，所以数列{}n a 为等差数列，由53525S a ==得35a =，设公差为d ，315212a a d d ==+=+，得2d =，所以()11221n a n n =+-⨯=-，故数列{}n a 的通项公式为21n a n =-．(2)12n b =，所以1122n Tn =++)112=．6．（2022·江苏盐城·三模）已知正项等比数列{}n a 满足1330a a +=，请在①4120S =，②481a =，③2211120n n n n a a a a --+-=，2n ≥，*n N ∈中选择一个填在横线上并完成下面问题：(1)求{}n a 的通项公式；(2)设()()12311n n n n b a a +⋅=++，{}n b 的前n 和为n S ，求证：14n S <．【答案】(1)选择见解析；3nn a =(2)证明见解析(1)设正项等比数列{}n a 公比为q ，又1330a a +=，选①，()()41234131120S a a a a a a q =+++=++=，所以3q =；选②，13431130a a a q q ⎛⎫+=+= ⎪⎝⎭，所以()()2310390,3q q q q -++==；选③，()()22111112340n n n n n n n n a a a a a a a a ----+-=-+=，所以13n n a a -=，∴3q =；又1311191030a a a a a +=+==，∴13a =，则3nn a =．(2)因为()()()()1112323111131313131n n n n n n n n n b a a +++⋅⋅===-++++++，所以122231111111313131313131n n n n S b b b +⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪++++++⎝⎭⎝⎭⎝⎭11114314n +=-<+． 7．（2022·浙江金华·模拟预测）已知数列{}{},n n a b ，其中{}n a 为等差数列，且满足11211,,32a b b ===，21141,2n n n n nn a b a b n N *++-=+∈. (1)求数列{}{},n n a b 的通项公式； (2)设212n n nn n a c a a ++=，数列{}n c 的前n 项和为n T ，求证：1n T <【答案】(1)21n a n =-，131(21)22n n b n -⎛⎫=-- ⎪⎝⎭(2)证明见解析(1)解：由数列{}n a 为等差数列，{}n b 且满足11211,,32a b b ===，211412n n n n nn a b a b ++-=+，当1n =时，可得122132a b a b =+，即213322a =⨯+，解得23a =；因为{}n a 是等差数列，所以21n a n =-，所以2141(21)(21)2n n nn n b n b +--=++，所以1121212n n n b b n n +-=+-，所以12132121131532123n n n b b b b b b b b n n n -⎛⎫⎛⎫⎛⎫=+-+-++- ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭11211112211111311222222212n n n ---⎛⎫⎛⎫- ⎪ ⎪⎪⎝⎭⎛⎫⎝⎭=++++=+=- ⎪⎝⎭-所以131(21)22n n b n -⎛⎫=-- ⎪⎝⎭.(2)解：由（1）得12311(21)(21)22(21)2(21)n n n n n c n n n n -+==--+-+，所以12n n T c c c =+++211111112323252(21)2(21)n n n n -=-+-++-⋅⋅⋅-+ 1112(21)n n =-<+.8．（2022·湖北·二模）已知正项等差数列{}n a 满足：()33n n a a n *=∈N ，且1382,1,a a a +成等比数列．(1)求{}n a 的通项公式；(2)设()()1121212n n n a n a a c ++=++，n R 是数列{}n c 的前n 项和，若对任意n *∈N 均有n R λ<恒成立，求λ的最小值．【答案】(1)n a n =(2)最小值为23(1)解：设等差数列的公差为d ，由33n n a a =得[]11(31)3(1)a n d a n d +-=+-，则1a d =，所以1(1)n a a n d nd =+-=．因为12a 、31a +、8a 成等比数列，所以()231812a a a +=⋅，即2(31)28d d d +=⋅，所以27610d d --=，解得1d =或17d =-，因为{}n a 为正项数列，所以0d >，所以1d =，所以n a n =．(2)解：由（1）可得()()()()1111122112121212121212n n n a n n nn a a n n c +++++⎛⎫===- ⎪++++++⎝⎭，所以1223111111111122121212121212312n n n n R ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪⎪ ⎪⎢⎥+++++++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，因为对任意n *∈N 均有23n R <，所以23λ≥，所以实数λ的最小值为239．（2022·江西·临川一中高二期末（理））已知数列{}n a ，0n a >，11a =，n S 为其前n 项和，且满足()()()1112n n n n S S S S n --+-=≥.(1)求数列{}n a 的通项公式； (2)设()11nnn a b =-⋅，求数列{}n b 的前n 项和n T ．【答案】(1)=n a ()1nn T =-(1)由题可知()22112n n S S n --=≥⇒数列是{}2n S 等差数列，所以()2211n S S n n =+-=，)12n n n n S a S S n -=-=≥，又因为11a ==，所以n a(2)()()11nnnnnb a -===-．所以()()311nnn T =-=+-故答案为：n a ()1n- .10．（2022·重庆八中模拟预测）已知n S 是公差不为零的等差数列{}n a 的前n 项和，36S =，2319a a a =⋅.(1)求数列{}n a 的通项公式； (2)设数列()()24141nn n a b n n +=-∈-N ，数列化{}n b 的前2n 项和为2n T ，若2112022n T +<，求正整数n 的最小值. 【答案】(1)*,N na n n =∈(2)505(1)公差d 不为零的等差数列{}n a ，由2319a a a =⋅， ()()211182a a d a d +=+，解得1a d =.又31336S a d =+=，可得11a d ==，所以数列{}n a 是以1为首项和公差的等差数列，所以*,N na n n =∈.(2)解：由（1）可知()()241111412121nn n n b n n n ⎛⎫=-=-+ ⎪--+⎝⎭， 211111111113355743414141n T n n n n ∴=--++--+--++---+1141n =-++，2111412020n T n +=<+，20194n ∴>所以n 的最小值为505.11．（2022·天津市武清区杨村第一中学二模）已知{}n a 是等差数列，{}n b 是等比数列，且114342131,2,2,a b a b b b a a ====+．(1)求数列{}{},n n a b 的通项公式；(2)记{}n b 的前n 项和为n S ，证明：()n n n S a b n *≤⋅∈N ；(3)记()311(1)*++⋅=-∈⋅n n n nnn a b c n a a N ，求数列{}n c 的前2n 项和．【答案】(1)(),2nn n a n b n *=∈=N ；(2)证明见解析；(3)2212221n n T n +=-+(1)设等差数列公差为d ，等比数列公比为q ，所以()2311111132132222222d q d a d b q b q q d q b q a d⎧+==+=⎧⎧⇒⇒⎨⎨⎨=+==+⎩⎩⎩，所以,2n n na b n ==， (2){}n b 的前n 项和为 248222222n n n n n n n n n S n a b =++++≤++++=⋅=⋅，(当1n =时，取等号)命题得证.(3)由（1）得，()()131131222(1)(1)(1)11n nn n n n nn n n n n n a b c a n n a n +++⎛⎫+ ⎪+⋅⋅=-=-=-+⎝+⎭⋅，所以数列{}n c 的前2n 项和2212244881616122()3222241334522nn n n T n n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++++++ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭-⎝⎭，2212221n n T n +=-+12．（2022·黑龙江实验中学模拟预测（理））已知数列{}n a 满足11a =，11n n n n a a a a --=-，且0n a ≠. (1)求数列{}n a 的通项公式； (2)若()()11121n n n n b n a a ++=-+，数列{}n b 前n 项和为nT，求2022T .【答案】(1)1n a n =；(2)20222023. (1)由11n n n n a a a a --=-，0n a ≠得：1111n n a a --=，又111a ，∴数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项，1为公差的等差数列，1n n a ∴=，1n a n ∴=；(2)由（1）知：()()()()1121111111n n n n b n n n n +++=-=-+++；20221111111111223342021202220222023T ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴=++--+++⋅⋅⋅+++-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭12022120232023=-=.13．（2022·湖北·蕲春县第一高级中学模拟预测）已知数列{}n a 的前n 项和为n S ，其中1215a S ==，，当2n ≥时，1124n n n a S S +-，，成等差数列. (1)求数列{}n a 的通项公式.(2)记数列()()2123211n n n a a ++⎧⎫⋅⎪⎪⎨⎬++⎪⎪⎩⎭的前n 项和n T ，求证：121855n T ≤<.【答案】(1)14n n a -=；(2)证明见解析．(1)依题意，当2n ≥时，1144n n n a S S +-+=，故11444n n n n a S S a +-=-=，由1215a S ==，得22144a a a ==，，故数列{}n a 是以1为首项，4为公比的等比数列，则14n n a -=；(2)依题意，()()()()2211123232111141414141n n n n n n n n a a ++++⋅⋅==-++++++，故12231111111111414141414141541n n n n T ++⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪ ⎪+++++++⎝⎭⎝⎭⎝⎭， ∴n *∈N ，∴1112111855415n T +=≤-<+，即121855n T ≤<．。

高二等差数列求和练习题与答案

高二等差数列求和练习题与答案等差数列是数学中的重要概念，也是高中数学中的基础知识点之一。

在高二的学习中，我们要掌握等差数列的求和公式，进一步巩固和应用这一概念。

下面将给出一些高二等差数列求和的练习题，并提供详细的解答。

练习题1：求等差数列1，3，5，7，9的和。

解：根据等差数列的求和公式，我们可以得知，等差数列的和等于首项与末项的和乘以项数再除以2。

这里，首项为1，末项为9，项数为5。

代入公式得：总和 = (首项 + 末项) ×项数 ÷ 2= (1 + 9) × 5 ÷ 2= 10 × 5 ÷ 2= 50 ÷ 2= 25所以，等差数列1，3，5，7，9的和为25。

练习题2：求等差数列2，5，8，11，...，101的和。

解：这是一个公差为3的等差数列，我们需要找到首项、末项和项数，然后代入求和公式进行计算。

首项 a = 2公差 d = 5 - 2 = 3末项 l = 101项数 n = (l - a) ÷ d + 1= (101 - 2) ÷ 3 + 1= 99 ÷ 3 + 1= 33 + 1= 34总和 = (首项 + 末项) ×项数 ÷ 2= (2 + 101) × 34 ÷ 2= 103 × 34 ÷ 2= 3502 ÷ 2= 1751所以，等差数列2，5，8，11，...，101的和为1751。

练习题3：已知等差数列的首项为7，公差为4，和为123。

求该等差数列的项数。

解：我们可以根据求和公式来解题，将已知的数据代入公式求解。

公式为：总和 = (首项 + 末项) ×项数 ÷ 2将已知数据代入得：123 = (7 + l) × n ÷ 2化简得：246 = (7 + l) × n由于等差数列的首项是7，公差是4，所以末项 l = 7 + 4 × (n - 1)。

等差数列求和及练习题(整理).doc

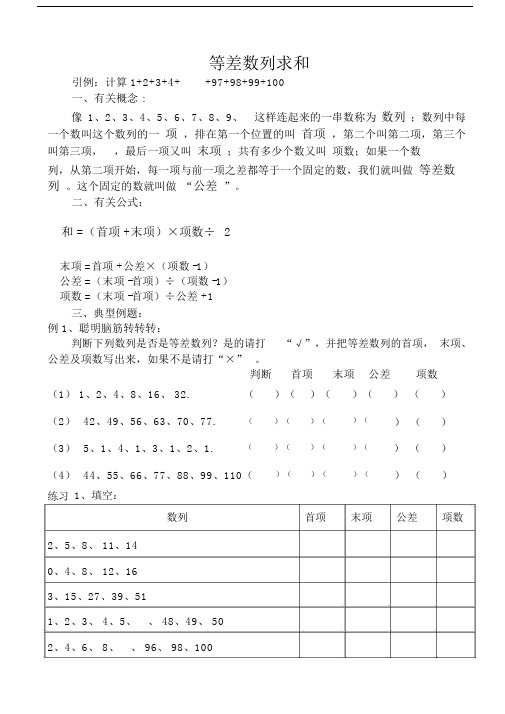
等差数列求和引例：计算 1+2+3+4++97+98+99+100一、有关概念 :像1、2、3、4、5、6、7、8、9、这样连起来的一串数称为数列；数列中每一个数叫这个数列的一项，排在第一个位置的叫首项，第二个叫第二项，第三个叫第三项，，最后一项又叫末项；共有多少个数又叫项数；如果一个数列，从第二项开始，每一项与前一项之差都等于一个固定的数，我们就叫做等差数列。

这个固定的数就叫做“公差”。

二、有关公式：和 =（首项 +末项）×项数÷ 2末项 =首项 +公差×（项数 -1）公差 =（末项 -首项）÷（项数 -1）项数 =（末项 -首项）÷公差 +1三、典型例题：例 1、聪明脑筋转转转：判断下列数列是否是等差数列？是的请打“√”，并把等差数列的首项，末项、公差及项数写出来，如果不是请打“×”。

判断首项末项公差项数（1） 1、2、4、8、16、 32.（）（）（）（）（）（2）42、49、56、63、70、77. （）（）（）（）（）（3）5、1、4、1、3、1、2、1. （）（）（）（）（）（4）44、55、66、77、88、99、110（）（）（）（）（）练习1、填空：数列首项末项公差项数2、5、8、 11、140、4、8、 12、163、15、27、39、511、2、3、 4、5、、 48、49、 502、4、6、 8、、 96、 98、100例 2、已知等差数列 1,8,15, , 78.共 12 项，和是多少？（博易 P27例 2）（看 ppt,推出公式）例 3、计算 1+3+5+7++35+37+39练习 2：计算下列各题（1）6+10+14+18+22+26+30 （3）1+3+5+7++95+97+99（2）3+15+27+39+51+63（4）2+4+6+8++96+98+100（3）已知一列数 4,6,8,10 ，，64，共有 31 个数，这个数列的和是多少？例 5、有一堆圆木堆成一堆，从上到下，上面一层有 10 根，每向下一层增加一根，共堆了 10 层。

四年级奥数等差数列求和一

等差数列的通项公式
定义：等差数列中任意一项都等于前一项加上一个常数
公式：an=a1+(n-1)d，其中an是第n项，a1是第一项，d是公差
特点：每一项与前一项的差等于公差，且差值相等
求解方法：根据已知项和公差，利用通项公式求出任意
一项
02
等差数列求和的方法
公式法求和
适用范围：适用于已知首项和公差的等差数列
公式：S_n = n/2 * (2a_1 + (n1)d)，其中a_1是首项，d是公差， n是项数
推导过程：由等差数列的性质，可以推导出该公式
计算步骤：代入已知数值，计算出等差数列的和
倒序相加法求和
添加标题
定义：将等差数列从前往后和从后往前分别相加，再除以2得到等差数列的和
添加标题
适用范围：适用于等差数列求和问题
+(n-1)d)
变形一： Sn=an^2/2+( n-9)an/2nd/2+n^2/4n/4
变形二： Sn=d/2*n^2+ (a1-d/2)*n
拓展：等差数列求和公式的应用范围和适用条件
05
等差数列求和的练习题
基础练习题
题目：1+2+3+...+99=？题目：求1到100的所有偶数的和。题目：求1到100的所有奇数的和。题目：已知等差数列的前三项分别为a、b、c，求该等差数列的和。
添加标题
举例：对于数列1, 3, 5, 7, 9，倒序相加得到1+9, 3+7, 5+5，结果为 10+10+5=25
添加标题
优势：可以快速求解等差数列求和问题

(完整版)三年级奥数等差数列求和习题及答案

计算（三）等差数列求和知识精讲一、定义：一个数列的前n 项的和为这个数列的和。

二、表达方式：常用n S 来表示。

三：求和公式：和=(首项+末项)⨯项数2÷，1()2n n s a a n =+⨯÷。

对于这个公式的得到可以从两个方面入手：(思路1)1239899100++++++L11002993985051=++++++++L 1444444442444444443共50个101（）（）（）（） 101505050=⨯= (思路2)这道题目，还可以这样理解：23498991001009998973212101101101101101101101+++++++=+++++++=+++++++L L L 和=1+和倍和即，和 (1001)100 2 10150 5050=+⨯÷=⨯=。

四、中项定理：对于任意一个项数为奇数的等差数列，中间一项的值等于所有项的平均数，也等于首项与末项和的一半；或者换句话说，各项和等于中间项乘以项数。

譬如：① 48123236436922091800+++++=+⨯÷=⨯=L （），题中的等差数列有9项，中间一项即第5项的值是20，而和恰等于209⨯； ② 65636153116533233331089++++++=+⨯÷=⨯=L （），题中的等差数列有33项，中间一项即第17项的值是33，而和恰等于3333⨯。

例题精讲：例1：求和：（1）1+2+3+4+5+6 = （2）1+4+7+11+13=（3）1+4+7+11+13＋ (85)分析：弄清楚一个数列的首项，末项和公差，从而先根据项数公式求项数，再根据求和公式求和。

例如（3）式项数=（85-1）÷3+1=29和=（1+85）×29÷2=1247答案：（1）21 （2）36 （3）1247例2：求下列各等差数列的和。

（1）1+2+3+4+…+199（2）2+4+6+…+78（3）3+7+11+15+…+207分析：弄清楚一个数列的首项，末项和公差，从而先根据项数公式求项数，再根据求和公式求和。

综合算式专项练习题等差数列的计算

综合算式专项练习题等差数列的计算综合算式专项练习题：等差数列的计算一、等差数列的概念和性质等差数列是指一个数列中，从第二项起，每一项与它的前一项之差是相等的。

这个相等的差称为公差，通常记为d。

等差数列可以用一般表示式an = a1 + (n-1)d来表示，其中a1表示首项，n表示项数，an表示第n项。

二、等差数列的求解1. 已知首项、公差和项数，求等差数列的和等差数列的和可以用求和公式Sn = n/2 * (a1 + an)来求解。

其中，n表示项数，a1表示首项，an表示第n项。

首先，我们需要确定n、a1和an的值，然后代入求和公式进行计算即可。

2. 已知首项、公差和和数，求等差数列的项数要求解等差数列的项数，我们可以使用求和公式Sn = n/2 * (a1 + an)。

已知Sn，a1和公差d后，我们可以将已知的值代入求和公式中，得到关于项数n的方程，然后解方程即可。

三、综合算式专项练习题1. 某等差数列的首项是3，公差是5，求该等差数列的前10项和。

解：根据求和公式，代入已知的值，得到：S10 = 10/2 * (3 + a10)= 5 * (3 + a1 + 9d) (因为a10 = a1 + 9d)= 5 * (3 + 3 + 9 * 5) (代入a1 = 3，d = 5)= 5 * (6 + 45)= 5 * 51= 255所以，该等差数列的前10项和为255。

2. 某等差数列的首项是2，公差是4，项数是12，求该等差数列的和。

解：根据求和公式，代入已知的值，得到：S12 = 12/2 * (2 + a12)= 6 * (2 + a1 + 11d) (因为a12 = a1 + 11d)= 6 * (2 + 2 + 11 * 4) (代入a1 = 2，d = 4)= 6 * (4 + 44)= 6 * 48= 288所以，该等差数列的和为288.3. 某等差数列的首项是7，和数是93，公差是4，求该等差数列的项数。

数列求和综合练习题(含答案)

数列求和综合练习题一、选择题1．已知数列{}n a 的前n 项和为n S ，若11++=n n a n ，10n S =，则=n （）A ．90B ．121C ．119D ．1202．已知{}n a 是公差为1的等差数列，n S 为{}n a 的前n 项和，若844S S =，则10a =（） A.172 B.192C.10D.12 3．数列{}n a 中,1160,3n n a a a +=-=+，则此数列前30项的绝对值的和为 ( )A.720B.765C.600D.630 4．数列{}n a 的前n 项和为n S ，若1(1)n a n n =+，则6S 等于( )A ．142 B ．45 C ．56 D ．675．设{a n }是由正数组成的等比数列，S n 为其前n 项和．已知a 2·a 4＝1，S 3＝7，则S 5＝( ) A.12 B.314 C.172 D.1526．设是等差数列的前项和，已知，则等于 ( )A. 13B. 35C. 49D. 637．等差数列的前n 项和为= ( ) A ．18 B ．20 C ．21D ．228．等差数列{}n a 的前n 项和为n S ，且336,0S a ==，则公差d 等于（） A.1- B.1 C.2- D.29．设等差数列{}n a 的前n 项和为n S ，若111-=a ，664-=+a a ，则当n S 取最小值时，n 等于（） A ．6 B ．7 C ．8 D ．9 10．在等差数列中，已知，则该数列前11项的和等于（）A ．58B ．88C ．143D ． 17611．已知数列}{n a 的前n 项和为)34()1(2117139511--++-+-+-=+n S n n ,则312215S S S -+的值是（）A ．-76B ．76C ．46D ．1312．等比数列{a n }的前n 项和为S n ，若a 1＋a 2＋a 3＋a 4＝1，a 5＋a 6＋a 7＋a 8＝2，S n ＝15，则项数n 为( ) A ．12 B ．14 C ．15 D ．1613．等差数列{}n a 中，若14739a a a ++=，36927a a a ++=，则{}n a 的前9项和为( ) {}n a 5128,11,186,n S a S a ==则{}n a 4816a a +=11S二、解答题14．已知数列{}n a 的前n 项和()2*,n S n n N =∈. （1）求数列{}n a 的通项公式；（2）若数列{}n b 是等比数列，公比为()0q q >且11423,b S b a a ==+，求数列{}n b 的前n 项和n T .15．已知等差数列{}n a 的前n 项和为n S ，且93=S ，731,,a a a 成等比数列. （1）求数列{}n a 的通项公式；（2）若数列{}n a 的公差不为0，数列{}n b 满足nn n a b 2)1(-=，求数列{}n b 的前n 项和n T .16．设数列{}n a 的前n 项和122nn S ，数列{}n b 满足21(1)log n nb n a =+．（1）求数列{}n a 的通项公式；（2）求数列{}n b 的前n 项和n T ．17．已知数列}{n a 的各项均为正数，n S 是数列}{n a 的前n 项和，且3242-+=n n n a a S ．（1）求数列}{n a 的通项公式；（2）n n n nn b a b a b a T b +++== 2211,2求已知的值．18．已知数列}{n a 的前n 项和nn S 2=，数列}{n b 满足)12(,111-+=-=+n b b b n n ()1,2,3,n =．（1）求数列}{n a 的通项n a ；（2）求数列}{n b 的通项n b ；（3）若nb ac nn n ⋅=，求数列}{n c 的前n 项和n T ．19．已知数列{}n a 的前n 项和为n S ，且2n n S n +=2.（1）求数列}{n a 的通项公式；（2）若*)(,1211N n a a a b n n n n ∈-+=+求数列}{n b 的前n 项和n S .20．已知数列{a n }的前n 项和2n n S a =-，数列{b n }满足b 1=1，b 3+b 7=18，且112n n n b b b -++=（n ≥2）.（1）求数列{a n }和{b n }的通项公式；（2）若nnn a b c =，求数列{c n }的前n 项和T n.21．已知数列}{n a 的前n 项和为n S ，数列}1{+n S 是公比为2的等比数列，2a 是1a 和3a 的等比中项. （1）求数列}{n a 的通项公式；（2）求数列{}n na 的前n 项和n T .22．设数列{}n a 满足11=a )(211*+∈=-N n a a n n n （1）求数列{}n a 的通项公式；（2）令n n b na =，求数列{}n b 的前n 项和n S三、填空题23．已知等比数列{}n a 的各项均为正数，若11a =，34a =，则2________;a =此数列的其前n 项和__________.n S =24．已知等差数列{}n a 中，52=a ，114=a ，则前10项和=10S ．25．设等比数列{}n a 的前n 项和为n S ,已知488,12,S S ==则13141516a a a a +++的值为． 26．设n S 是等差数列{}n a 的前n 项和,且3613S S =，则912S S = ．27．等差数列{}n a 中，10120S =，那么29a a += ．28．[2014·北京海淀模拟]在等比数列{a n }中，S n 为其前n 项和，已知a 5＝2S 4＋3，a 6＝2S 5＋3，则此数列的公比q ＝________.29．在等差数列}{n a 中，5,142==a a ,则}{n a 的前5项和5S = . 30．已知等差数列{}n a 中，已知8116,0a a ==，则18S =________________.31．已知等比数列的前项和为，若，则的值是 .32．已知{a n }是等差数列，a 1=1，公差d≠0，S n 为其前n 项和，若a 1，a 2，a 5成等比数列，则S 8= _________ ． 33．数列{}n an 项和为9n S =，则n =_________．34．[2014·浙江调研]设S n 是数列{a n }的前n 项和，已知a 1＝1，a n ＝－S n ·S n －1(n≥2)，则S n ＝________.}{n a n n S 62,256382-==S a a a a 1a参考答案1．D【解析】n n n n a n -+=++=111 ，()()111...23)12(-+=-+++-+-=∴n n n S n ，1011=-+n ，解得120=n ．【命题意图】本题考查利用裂项抵消法求数列的前n 项和等知识，意在考查学生的简单思维能力与基本运算能力． 2．B 【解析】试题分析：∵公差1d =，844S S =，∴11118874(443)22a a +⨯⨯=+⨯⨯，解得1a =12，∴1011199922a a d =+=+=，故选B. 考点：等差数列通项公式及前n 项和公式3．B 【解析】试题分析：因为13n n a a +=+，所以13n n a a +-=。

等差数列求和基础题

等差数列求和基础题一．选择题1. 等差数列{}n a 的前n 项和为n S ，若142,20,a S ==则6S =A.16B.24C.36D.422. 设等差数列{}n a 的前n 项和为n S ,若111a =-,376a a +=-,则当n S 取最小值时, n 等于A.8B.7C.6D.93. 已知n S 是等差数列{}n a 的前n 项和，且63S =，1118S =，则9a 等于A.3B.5C.8D.154. 已知等差数列{a n }前n 项的和为S n , 233=a , S 3=9，则a 1= A.23 B.29 C.-3 D.6 5. 已知等差数列{}n a 中,256,15a a ==,若2n n b a =,则数列{}n b 的前5项和为A. 90B. 45C. 30D. 1866. 等差数列}{n a 的前n 项和为n S ，若119717,170a a a S ++=则的值为A.10B.20C.25D.307. 设等差数列｛a n ｝前n 项和为S n . 若a 1= -11,a 4+a 6= -6 ,则当S n 取最小值时，n 等于A.6B. 7C.8D.98. 设等差数列{}n a 的前n 项和为n S ，246a a +=，则5S 等于A.10B.12C.15D.309. 已知等差数列{}n a 满足244a a +=，3510a a +=，则它的前10项的和10S =A.138B.135C.95D.2310. 记等差数列的前n 项和为n S ，若244,20S S ==，则该数列的公差d =A.2B.3C.6D.711. 已知等差数列{}n a 中，26a =，515a =，若2n n b a =，则数列{}n b 的前5项和等于A.30B.45C.90D.18612. 设S n 是等差数列{a n }的前n 项和，若S 5 = S 9，则a 3:a 5 =A.5:9B.9:5C.3:5D.5:313. 在等差数列}{n a 中，已知S 3=9，S 9=54，则}{n a 的通项n a 为A.33-=n a nB.n a n 3=C.2+=n a nD.1+=n a n14. 若等差数列}{n a 的前3项和93=S 且11=a ，则2a 等于A.3B.4C.5D.615. 等差数列{}n a 中，11a =，3514a a +=，其前n 项和100n S =，则n =A.9B.10C.11D.1216. 等差数列{a n }的前n 项和为S n ，若等于则442,10,2S S S ==A.12B.18C.24D.4217. 已知{}n a 是等差数列，1010a =，其前10项和1070S =，则其公差d =Ａ.23- Ｂ.13- Ｃ.13 Ｄ.2318. 在等差数列｛a n ｝中，若a 4+a 6 =12, S n 是数列｛a n ｝的前n 项和，则S 9的值为A.48B.54C.60D.6619. 一个只有有限项的等差数列,它的前5项的和为34,最后5项和为146,所有项的和为234,则它的第七项等于A.22B.21C.19D.1820. 已知数列{a n }的通项公式是a n =2n –49 (n ∈N )，那么数列{a n }的前n 项和S n 达到最小值时的n 的值是A.23B.24C.25D.2621. 已知等差数列{a n }中,a 2+a 8=8,则该数列前9项和S 9等于A.18B.27C.36D.4522. 设S n 是等差数列{a n }的前n 项和,若S 7=35,则a 4=A.8B.7C.6D.523. 等差数列{}n a 中，n S 是前n 项和，且38S S =，7k S S =，则k 的值为A.4B.11C.2D.1224. 等差数列{a n }中，若a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27，则前9项的和S 9等于A.66B.99C.144D.29725. 等差数列{a n }中，a 1+a 2+…+a 50＝200，a 51+a 52+…+a 100＝2700，则a 1等于A.－1221B.－21.5C.－20.5D.－2026. 等差数列｛a n ｝的前n 项和为S n ，若a 3+a 17=10，则S 19的值为A.95B.100C.115D.12527. 在等差数列}{n a 中，，，83125S S a =-=则前n 项和n s 的最小值为 txjyA.80-B.76-C.75-D.74-28. 等差数列{a n }中，若a 3+ a 4+ a 5+ a 6+ a 7=450 则前9项和S 9=A.1620B.810C.900D.67529. 已知等差数列{}n a 的前n 项和为n S ，若5418a a =-，则8S 等于A.144B.72C.54D.3630. 在等差数列{a n }中，前n 项和S n =36n －n 2，则S n 中最大的是A.S 1B.S 9C.S 17D.S 1831. 将含有k 项的等差数列插入4和67之间，结果仍成一新的等差数列，并且新的等差数列所有项的和为781，则k 的值为A.20B.21C..22D.2432. 设数列{}n a 是等差数列，且n S a a ,6,682=-=是数列 {}n a 的前n 项和，则A.S 4<S 3B.S 4==S 2C.S 6<S 3D.S 6=S 333. 已知等差数列前n 项和为S n ，若S 15<0,S 14>0,则此数列中绝对值最小的项为A.第6项B.第7项C.第8项D.第9项34. 设等差数列{}n a 的前n 项和为n S ，已知20092007120102010,2,20092007S S a S =--==则 A.2008- B.2008 C.2010- D.201035. 已知等差数列{}n a 中，10795=-+a a a ，记n n a a a S +++= 21，则13S 的值为A.130B.260C.156D.16836. 已知等差数列{}n a 的前n 项和为n S ,且424a a -=，39S =,则数列{}n a 的通项公式为A.n a n =B.2n a n =+C.21n a n =-D.21n a n =+37. 等差数列{}n a 中，14739a a a ++=，36927a a a ++=，则数列{}n a 前9项和9S 等于A.297B.144C.99D.6638. 等差数列{}n a 的前n 项和)3,2,1(⋅⋅⋅=n S n 当首项1a 和公差d 变化时，若1185a a a ++是一个定值，则下列各数中为定值的是A. 15SB. 16SC.17SD.18S39. 在公差为2的等差数列{}n a 中，如果前17项和为1734S =，那么12a 的值为A. 2B. 4C. 6D. 840. 已知等差数列30,240,18,}{49===-n n n n a S S S n a 若项和为的前，则n 的值为A.18B.17C.16D.1541. 已知等差数列854,18,}{S a a S n a n n 则若项和为的前-==A.18B.36C.54D.7242. 设函数()f x =，类比课本推导等差数列的前n 项和公式的推导方法计算(4)(3)...(0)(1)...(4)(5)f f f f f f -+-++++++的值为A.2B. 2C.2D. 243. 在等差数列｛a n ｝中，,3321=++a a a 165302928=++a a a ，则此数列前30项和等于A.810B.840C.870D.90044. 设数列}{n a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项为A.1B.2C.4D.645. 已知等差数列{}n a 的公差0<d ，若10,248264=+=⋅a a a a ，则该数列的前n 项和n S 的最大值为A.50B.45C.40D.3546. 等差数列{}n a 中，11a =,3514a a +=，其前n 项和100n S =,则n =A.9B.10C.11D.1247. 若}{n a 是等差数列，首项01>a ，020082007>+a a ，020082007<⋅a a ，则使数列}{n a 的前n 项和n S 为正数的最大自然数n 是A.4013B. 4014C. 4015D. 401648. 设数列{n a }是等差数列，且n S a a ,6,682=-=是数列{n a }的前n 项和，则A.S 4<S 5B.S 4=S 5C.S 6<S 5D.S 6=S 549. 已知等差数列{}n a 的通项公式()211,2,3n a n n =-=，，记11T a =，1121122,,n n n n n n T a n T T a a n -+-++⎧⎪=⎨++⎪⎩为奇数,为偶数（2,3,n =），那么2n T = A.21n + B.1162n - C.25 436n n n n ⎧⎨-+≠⎩，=1，，1D.232n n + 50. 已知数列2),1(2,}{a a S S n a n n n n 则且项和为的前-=等于A.4B.2C.1D.—2 51. 等差数列1062,}{a a a S n a n n ++若项和为的前为一个确定的常数，则下列各个和中，也为确定的常数的是A.S 6B.S 11C.S 12D.S 1352. 设n S 是等差数列{}n a 的前n 项和，若3163=S S 则=126S S A.310 B.13 C.81 D.91 53. 已知等差数列{}n a 的前n 项和为n S ，若9S =18，n S =240，4n a -=30，则n 的值为A.18B.17C.16D.1554. 若等差数列{}n a 的前5项和525S =，且23a =，则7a =A.12B.13C.14D.1555. 已知{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于A.64B.100C.110D.12056. 等差数列{a n }、{b n }的前n 项和分别为S n 、T n ，且3457-+=n n T S n n ，则使得nn b a 为整数的正整数n 的个数是A.3B.4C.5D.657. 数列{}n a 是公差为2-的等差数列，若509741=+++a a a ，则=++++99963a a a a A.－182 B.－82 C.－148 D.－7858. 设A ．B ．C 三点共线（该直线不过原点O ），数列{a n }是等差数列，S n 是该数列的前n 项和 =a 1+a 200，则S 200=A.200B.100C.50D.30059. 一个等差数列共n 项，其和为90，这个数列的前10项的和为25，后10项的和为75，则项数n 为A.14B.16C.18D.2060. 等差数列{a n }中，a 1>0，公差d <0, S n 为其前n 项和，对任意自然数n ，若点（n, S n ）在以下4条曲线中的某一条上，则这条曲线应是61. 已知等差数列{a n }前n 项和S n 有最大值且11011-<a a ，当S n 是最小正数时，n = A.17 B.18 C.19 D.2062. 记等差数列{}n a 的前n 项和为n S ，若112a =，420S =，则6S = A.16 B.24 C.36 D.4863. 设|a n |是等差数列，若a 2=3,a 7=13,则数列{a n }前8项的和为A.128B.80C.64D.5664. 已知等差数列}{n a 的前n 项和为S n ，若OC a OA a OB 20043+=，且A 、B 、C 三点共线（该直线不过原点O ），则S 2006 ＝A.1003B. 1004C. 2006D.200765. 等差数列{}n a 的前n 项和为n S ，若1697=+a a ，77=S ，则12a 的值是A.15B.30C.31D.6466. 已知数列{a n }、{b n }都是公差为1的等差数列，其首项分别为a 1、b 1，且a 1+b 1=5，a 1、b 1∈N *，设C n =a b （n ∈N *），则数列{C n }前10项和等于A.55B.70C.85D.10067. 已知,)1()1()1(22102nn n x a x a x a a x x x ++++=++++++ 若 ++21a a n a n -=+-291，那么自然数n 的值为A. 3B.4C.5D.668. 已知等差数列{a n }的前n 项和为S n ，若m >1，m ∈N*，且21121,38m m m m a a a S -+-+==，则m 等于A.11B.10C.9D.869. 已知等差数列{a n }中, S n 是它的前n 项和，若S 16>0, S 17<0, 则当S n 取最大值时，n 的值为 A.16 B.9 C.8 D.1070. 已知两个等差数列{}n a 和{}n b 的前n 项和分别为A n 和n B ，且7453n n A n B n +=+，则使得n na b 为整数的正整数n 的个数是 A.2 B.3 C.4 D.571. 设数列}{n a 是等差数列，且n S a a ,6,673=-=是数列}{n a 的前n 项和，则A.54S S =B.56S S =C.64S S >D.56S S <72. 已知数列{－2n+25}，其前n 项和S n 达到最大值时，n 为A.10B.11C.12D.13 73. 若n S 是等差数列{}n a 的前n 项和,其首项10a >,991000a a +>,991000a a ⋅<,则使0n S >成立的最大自然数n 是A.198B.199C.200D.20174. 设等差数列{}n a 满足81335a a =.且10a >.n S 为其前n 项之和.则n S 中最大的是A.10SB.11SC.20SD.21S75. 已知S n 是等差数列{a n }的前n 项和，且a 2＋a 4＋a 7＋a 15＝40，则S 13的值为A.20B.65C.130D.26076. 等差数列{}n a 的通项公式是12+=n a n ，其前n 项和为n S ，则数列⎭⎬⎫⎩⎨⎧n S n 的前10项和为A.75B.70C.120D.10077. 在等差数列}{n a 中，若30,240,1849===-n n a S S ，则n 的值为A.14B.15C.16D.1778. 在等差数列{}n a 中，若C a a a =++1383，则其前n 项和n S 的值等于5C 的是A.15SB.17SC.8SD.7S79. 设{}n a 是等差数列，1359a a a ++=，69a =，则这个数列的前6项和等于Ａ.12 Ｂ.24 Ｃ.36 Ｄ.4880. {}n a 是等差数列，10110,0S S ><，则使n a <0的最小的n 值是A.5B.6C.7D.881. 等差数列}{n a 的前n 项和为n S ，若10173=+a a ，则19S 的值是A.55B.95C.100D.不能确定82. 在等差数列{a n }中，a 1>0,且3a 8=5a 13,则S n 中最大的是A.S 21B.S 20C.S 11D.S 10 83. 设S n 是等差数列前n 项的和，若9535=a a ,则59S S 等于 A.1 B.－1 C.2 D.21 84. 已知等差数列{a n }的公差为正数，且a 3·a 7=－12,a 4+a 6=－4,则S 20为A.180B.－180C.90D.－9085. 若{a n }是等差数列，首项a 1>0,a 2003+a 2004>0,a 2003·a 2004<0,则使前n 项和S n >0成立的最大自然数n 是A.4005B.4006C.4007D.400886. 已知等差数列{}n a 中，247,15a a ==，则前10项的和10S ＝A.100B.210C.380D.40087. 设S n 是等差数列｛a n ｝的前n 项和，若S 3S 6＝13，则S 6S 12＝ A .310 B.13 C.18 D .1988. 设等差数列｛a ｝的前n 项的和为S n ，若a 1＞0，S 4=S 8，则当S n 取得最大值时，n 的值为A.5B.6C.7D.889. 已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝A.100B. 101C.200D.20190. 已知等差数列{a n }的前20项的和为100，那么a 7·a 14的最大值为A.25B.50C.100D.不存在91. 若某等差数列{a n }中，a 2+a 6+a 16为一个确定的常数，则其前n 项和S n 中也为确定的常数的是A.S 17B.S 15C.S 8D.S 792. 在等差数列{a n }中，a 10<0，a 11>0，且a 11>|a 10|，则{a n }的前n 项和S n 中最大的负数为A.S 17B.S 18C.S 19D.S 2093. 等差数列}{n a 的公差为d ，前n 项的和为S n ，当首项a 1和d 变化时，1182a a a ++是一个定值，则下列各数中也为定值的是A.S 7B.S 8C.S 13D.S 1594. 在等差数列{ a n }中，S 4 =1, S 8 =4,则a 17 + a 18 + a 19+ a 20 的值是A ．7B ．8C ．9D ．1095. 设a 1, a 2, a 3,……和b 1, b 2, b 3,……都是等差数列，且a 1=25, b 1=75, a 100＋b 100=100,则数列a 1＋b 1, a 2＋b 2,……的前100项的和是A.0B.100C.10000D.不确定96. 等差数列{a n }中，若前15项的和S 15=90，则a 8等于245D. C.12 445B. 6.A 97. 已知S k 表示数列{a k }前k 项和,且S k + S k+1 = a k +1 (k ∈N*),那么此数列是A ．递增数列B ．递减数列C ．常数列D ．摆动数列98. 设S n 是等差数列{a n }的前n 项和,若31a a =95,则59S S 等于txjy A.-1 B. 21 C.1 D.2 99. 等差数列{a n }中，a n -4=30,且前9项的和S 9=18，前n 项和为S n =240,则n 等于A.15B.16C.17D.18100. 等差数列{a n }中，若a 10=10,a 19=100,前n 项和S n =0,则n 等于A.7B.9C.17D.19参考答案（仅供参考）1 2 3 4 5 6 7 8 9 10 11 12 13 14 15D C A B A D A C C B C B D A B16 17 18 19 20 21 22 23 24 25 26 27 28 29 30C D B D B C D A B C A C B B D31 32 33 34 35 36 37 38 39 40 41 42 43 44 45A B C C A C C A D D D B B B B46 47 48 49 50 51 52 53 54 55 56 57 58 59 60B B B D A B A D B B B B BC C61 62 63 64 65 66 67 68 69 70 71 72 73 74 75C D C A A C B B C D A C A C C76 77 78 79 80 81 82 83 84 85 86 87 88 89 90A B A B B B B A A B B A B A A91 92 93 94 95 96 97 98 99 100B C C C C A C C A C欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

等差数列求和
引例：计算1+2+3+4+……+97+98+99+100
一、有关概念:
像1、2、3、4、5、6、7、8、9、……这样连起来的一串数称为数列；数列中每一个数叫这个数列的一项，排在第一个位置的叫首项，第二个叫第二项，第三个叫第三项，……，最后一项又叫末项；共有多少个数又叫项数；如果一个数列，从第二项开始，每一项与前一项之差都等于一个固定的数，我们就叫做等差数列。

这个固定的数就叫做“公差”。

二、有关公式：
和=（首项+末项）×项数÷2
末项=首项+公差×（项数-1）
公差=（末项-首项）÷（项数-1）
项数=（末项-首项）÷公差+1
三、典型例题：
例1、聪明脑筋转转转：
判断下列数列是否是等差数列？是的请打“√”，并把等差数列的首项，末项、公差及项数写出来，如果不是请打“×”。

判断首项末项公差项数
（1）1、2、4、8、16、32. （）（）（）（）（）（2）42、49、56、63、70、77. （）（）（）（）（）（3）5、1、4、1、3、1、2、1. （）（）（）（）（）（4）44、55、66、77、88、99、110（）（）（）（）（）
例2、已知等差数列1,8,15,…,78.共12项，和是多少？（博易P27例2）
（看ppt,推出公式）
例3、计算1+3+5+7+……+35+37+39
练习2：计算下列各题
（1）6+10+14+18+22+26+30 （3）1+3+5+7+……+95+97+99
（2）3+15+27+39+51+63 （4）2+4+6+8+……+96+98+100
（3）已知一列数4,6,8,10，…，64，共有31个数，这个数列的和是多少？
例5、有一堆圆木堆成一堆，从上到下，上面一层有10根，每向下一层增加一根，共堆了10层。

这堆圆木共有多少根？（博易P27例3）（看ppt）
练习3：
丹丹学英语单词，第一天学了6个单词，以后每一天都比前一天多学会一个，最后一天学会了26个。

丹丹在这些天中共学会了多少个单词？
等差数列求和练习题
一、判断下列数列是否是等差数列？是的请打“√”，并把等差数列的首项，末项
及公差写出来，如果不是请打“×”。

判断首项末项公差
1. 2、4、6、8、10、12、14、16.（）（）（）（）
2. 1、3、6、8、9、11、12、14. （）（）（）（）
3. 5、10、15、20、25、30、35. （）（）（）（）
4. 3、6、8、9、12、16、20、26.（）（）（）（）
二、请计算下列各题。

（1）3+6+9+12+15+18+21+24+27+30+33
（2）4+8+12+16+20+24+28+32+36+40
（3）求3、6、9、12、15、18、21、这个数列各项相加的和。

（4）2+4+6+8+……+198+200
★（5）求出所有三位数的和。

（其他作业：练习册B 1题、4题、6题）。