试按第三和第四强度理论计算单元体的相当应力。图中应力
材料力学作业题集(学院)
一、求图示图形形心的位置。
二、计算半圆形对形心轴 的惯性矩。
三、试确定图示平面图形的形心主惯性轴的位置，并求形心主惯性矩。
一、试求图示各梁中截面1-1、2-2、3-3上的剪力和弯矩，这些截面无限接近于截面 或截面 。设 、 、 均为已知。
五、平面直角折杆在C端受到铅直力P作用，如图所示。材料的[σ]=160MPa。若P=10kN，l=2m，a=1.2m。试根据第四强度理论设计轴AB的直径d。
六、下图示圆轴直径d=15mm，受弯矩My与扭矩Mx共同作用。测得轴表面上点A沿轴线方向的线应变 ，点B沿与轴线成45o方向的线应变 ，E=210GPa， ， MPa。试求My与Mx，并用第四强度理论校核轴的强度。
五、已知受力构件表面某点处沿三个方向的线应变为： ， ， 。材料的弹性模量 ，泊松比 ，试求该点的主应力。
一、从低碳钢零件中某点取出一单元体，其应力状态如图所示，试按第三和第四强度理论计算单元体的相当应力。图中应力单位是 。
(1)、 , ,
(2)、 , ,
二、上题中若材料为铸铁，试按第一和第二强度理论计算单元体的相当应力。图中应力单位是 ，泊松比 。
一、作图示杆的扭矩图
二、已知传动轴为钢制实心轴，最大扭矩MT＝7kN•m，材料的许可切应力[]＝30MPa，切变模量G＝80GPa，许可扭角[]＝0.2/m，试按强度条件和刚度条件设计轴径d。
四、已知圆轴受外力偶矩m＝5kN·m，材料的许可切应力[]＝80MPa。
（1）试设计实心圆轴的直径D1；
（2）若该轴改为=d/D=0.9的空心圆轴，试设计空心圆轴的内、外径d2、D2。
材料力学习题答案
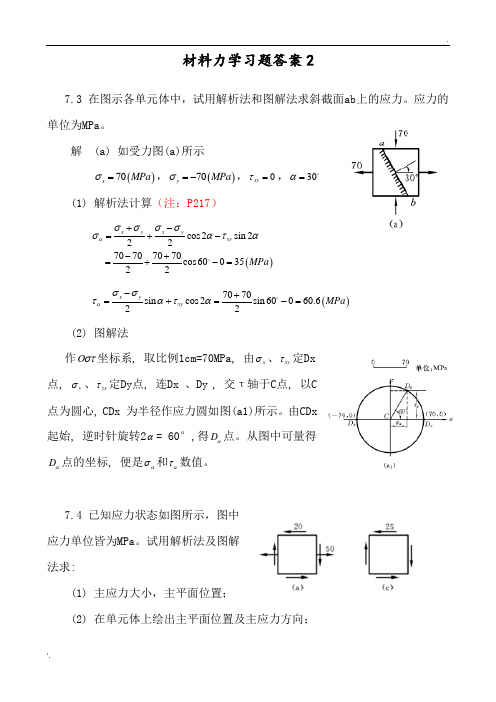
.材料力学习题答案27.3在图示各单元体中，试用解析法和图解法求斜截面ab上的应力。
应力的单位为MPa。
解(a) 如受力图(a)所示()70xMPaσ=，()70yMPaσ=-，0xyτ=，30α=(1) 解析法计算（注：P217）()cos2sin22270707070cos6003522x y x yxyMPaασσσσσατα+-=+--+=+-=()7070sin cos2sin60060.622x yxyMPaασστατα-+=+=-=(2) 图解法作Oστ坐标系, 取比例1cm=70MPa, 由xσ、xyτ定Dx点,yσ、yxτ定Dy点, 连Dx 、Dy , 交τ轴于C点, 以C点为圆心, CDx 为半径作应力圆如图(a1)所示。
由CDx起始, 逆时针旋转2α= 60°,得Dα点。
从图中可量得Dα点的坐标, 便是ασ和ατ数值。
7.4 已知应力状态如图所示，图中应力单位皆为MPa。
试用解析法及图解法求:(1) 主应力大小，主平面位置；(2) 在单元体上绘出主平面位置及主应力方向；.(3) 最大切应力。
解 (a) 受力如图(a)所示()50x MPa σ=，0y σ=，()20xy MPa τ=(1) 解析法 （数P218）2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭()()225750050020722MPa MPa ⎧+-⎪⎛⎫=±+=⎨ ⎪-⎝⎭⎪⎩ 按照主应力的记号规定()157MPa σ=，20σ=，()37MPa σ=-02220tan 20.8500xyx yτασσ⨯=-=-=---，019.3α=-()13max 5773222MPa σστ-+=== (2) 图解法作应力圆如图(a1)所示。
应力圆与σ轴的两个交点对应着两个主应力1σ、3σ 的数值。
由x CD 顺时针旋转02α，可确定主平面的方位。
7月浙江自考材料力学试题及答案解析
浙江省2018年7月自学考试材料力学试题课程代码：02605一、单项选择题(本大题共10小题，每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.图示受力构件中，由力的可传性原理，将力P由位置B移至C，则( )（1）固定端A的约束反力不变；（2）杆件的内力不变，但变形不同；（3）杆件的变形不变，但内力不同；（4）杆件AC段的内力和变形均保持不变。
A.仅(1)正确B.仅(4)正确C.(1)和(4)正确D.仅(3)错误2.图示受力杆件的轴力图正确的为( )13.结构由于温度变化，一般有( )A.静定结构中将引起应力，静不定结构中也将引起应力B.静定结构中将引起变形，静不定结构中将引起应力和变形C.无论静定结构或静不定结构，都将引起应力和变形D.静定结构中将引起应力和变形，静不定结构中将引起应力4.如图，等截面圆轴上装有四个皮带轮，如何安排合理，现有四种答案，正确的是( )A.将C轮与D轮对调B.将B轮与D轮对调C.将B轮与C轮对调D.将B轮与D轮对调，然后再将B轮与C轮对调5.图示圆轴受扭，则A、B、C三个横截面相对于D截面的扭转角，正确的是( )A.φDA＝φDB＝φDCB.φDA＝0，φDB＝φDCC.φDA＝φDB＝2φDCD.φDA＝φDC，φDB＝026.图示梁，剪力等于零的截面位置x之值为( )A.5a/6B.6a/5C.6a/7D.7a/67.关于图示单元体属于哪种应力状态，正确答案为( )A.单向应力状态B.二向应力状态C.三向应力状态D.纯剪应力状态8.三向应力状态中，若三个主应力相等，均为σ，则三个主应变为( )A.等于零B.(1－2ν)σ/EC.3(1－2ν)σ/ED.(1－2ν)σ2/E9.塑性材料的下列应力状态中，基于第三强度理论，哪一种最易发生破坏?( )10.正方形截面细长压杆，横截面边长a和杆长l成比例增加，它的临界应力为( )A.成比例增加B.保持不变C.按(l/a)2变化D.按(a/l)2变化二、填空题(本大题共10小题，每小题2分，共20分)请在每小题的空格中填上正确答案。
河海大学材料力学考研练习题
学号姓名2-1求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A1=A2=1150mm2。
CBAE D2-2求下列各杆内的最大正应力。
（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。
2-4一直径为15mm，标距为200mm的合金钢杆，比例极限内荷载从零缓慢地增加58.4kN时，杆伸长了0.9mm，直径缩小了0.022mm，确定材料的弹性模量E、泊松比ν。
2-6图示短柱，上段为钢制，长200mm，截面尺寸为100×100mm2；下段为铝制，长300mm，截面尺寸为200×200mm2。
当柱顶受F力作用时，柱子总长度减少了0.4mm，试求F值。
已知E钢=200GPa，E铝=70GPa。
2-7图示等直杆AC，材料的容重为ρg，弹性模量为E，横截面积为A。
求直杆B截面的位移ΔB。
学号姓名2-8图示结构中，AB可视为刚性杆，AD为钢杆，面积A1=500mm2，弹性模量1E1=200GPa；CG为铜杆，面积A2=1500mm2，弹性模量E2=100GPa；BE为木杆，面积A3=3000mm2，弹性模量E3=10GPa。
当G点处作用有F=60kN时，求该点的竖直位移ΔG。
2-11图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。
若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB杆所需的直径。
2-12图示结构中的CD杆为刚性杆，AB杆为钢杆，直径d=30mm，容许应力［σ］=160MPa，弹性模量E=2.0×105MPa。
试求结构的容许荷载F。
2-14图示AB为刚性杆，长为3a。
A端铰接于墙壁上，在C、B两处分别用同材料、同面积的①、②两杆拉住，使AB杆保持水平。
在D点作用荷载F后，求两杆内产生的应力。
设弹性模量为E，横截面面积为A。
学号姓名2-15两端固定，长度为l，横截面面积为A，弹性模量为E的正方形杆，在B、C截面处各受一F力作用。
材料力学强度理论
9 强度理论1、 脆性断裂和塑性屈服脆性断裂:材料无明显的塑性变形即发生断裂，断面较粗糙，且多发生在垂直于最大正应力的截面上，如铸铁受拉、扭，低温脆断等。
塑性屈服:材料破坏前发生显著的塑性变形，破坏断面较光滑，且多发生在最大剪应力面上，例如低碳钢拉、扭，铸铁压。
2、四种强度理论(1)最大拉应力理论（第一强度理论）材料发生脆性断裂的主要因素是最大拉应力达到极限值,即：01σσ= (2)最大伸长拉应变理论（第二强度理论）：无论材料处于什么应力状态,只要发生脆性断裂,都是由于最大拉应变（线变形）达 到极限值导致的,即： 01εε=(3)最大切应力理论（第三强度理论）无论材料处于什么应力状态,只要发生屈服,都是由于最大切应力达到了某一极限 值,即： 0max ττ=(4)形状改变比能理论（第四强度理论）无论材料处于什么应力状态,只要发生屈服,都是由于单元体的最大形状改变比能达到一个极限值,即：u u 0dd =强度准则的统一形式 [] σσ≤*其相当应力: r11σ=σr2123()σ=σ-μσ+σ r313σ=σ-σ222r41223311()()()2⎡⎤σ=σ-σ+σ-σ+σ-σ⎣⎦ 3、摩尔强度理论的概念与应用； 4、双剪强度理论概念与应用。
9.1图9.1所示的两个单元体，已知正应力σ =165MPa ，切应力τ=110MPa 。
试求两个单元体的第三、第四强度理论表达式。
图9.1[解] （1）图9.1（a ）所示单元体的为空间应力状态。
注意到外法线为y 及－y 的两个界面上没有切应力，因而y 方向是一个主方向，σ是主应力。
显然，主应力σ 对与y 轴平行的斜截面上的应力没有影响，因此在xoz 坐标平面内可以按照平面应力状态问题对待。
外法线为x 、z 轴两对平面上只有切应力τ，为纯剪切状态，可知其最大和最小正应力绝对值均为τ,则图9.1（a ）所示单元体的三个主应力为：τστσσσ-===321、、,第三强度理论的相当应力为解题范例r4σ=()eq313165110275a σσσστ=-=+=+=MPa第四强度理论的相当应力为：()eq4a σ==252.0== MPa(2)图9.1(b)所示单元体,其主应力为第三强度理论的相当应力为：()eq31322055275b σσσ=-=+=MPa第四强度理论的相当应力为：()eq4a σ=252.0==MPa9.2一岩石试件的抗压强度为[]σ=14OMPa,E=55GPa, μ=0.25, 承受三向压缩。
《材料力学》第7章-应力状态和强度理论-习题解
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。
四个强度理论与其相当应力
由于各向同性材料，正应力仅产生线应变，剪应力 仅产生剪 应变。而两种情况下的正应力和剪应力分 别相 等，因此，
其形状改变比能也相等，故两种情况下的危险程度相
等。
σ
σ
τ τ
(a)
(b)
二、定量计算
状态(a):
1
2
2
2
2
3
2
2
2
2
2 0
第2强度理论
—最大伸长 线应变理论
σ r1 σ1
r 2 1 2 3
第二类强度理论
（屈服失效的 理论）
第3强度理论
—最大剪应 力理论
σr3 σ1 σ3
第4强度理论
—形状改变
r4
1 2
1
2 2
2
3 2
解： （1）对于图 (a) 所示的单元体， 由图知 1= 0，2= 3= –100MPa,
100MPa 100MPa
r3 1 3 0 100 100 MPa
(a)
r4
1
2
1
2 2
2
3 2
3
1
2
[ ( )]
r2
1
2
3
(9-2-2)
第 二 类强度理论
三、 最大剪应力理论 (第三强度理论) 根据：当作用在构件上的外力过大时，其危险点处的材料就会 沿最大剪应力所在截面滑移而发生屈服失效。
基本假说： 最大剪应力 max 是引起材料屈服的因素。
四个强度理论的相当应力表达式
aF
Fa
A
B
C
A
B
C
C
A
B
A
B 1
C1
1
3
3
B
C
对图示的纯剪切应力状态，试按强度理论建立纯剪切状
态下的强度条件，并导出剪切许用应力［τ］与拉伸许用
应力［σ］之间的关系。
1＝， 2＝0，3＝
1 单元体纯剪切强度条件
KK
τ
第三强度理论 第四强度理论
第一强度理论 1
2
τ σ
3
[]为材料在单轴拉伸是的许用拉应力。
材料在纯剪切应力状态下的许用剪应力为
τ σ 0.577σ
3
（10-13）
已知铸铁构件上危险点处的应力状态，如图所示。若铸
铁拉伸许用应力为［σ］＋＝30MPa，试校核该点处的强度
是否安全。
第一强度理论
1 ＋
= 100MPa 。试按强度条件选择工字钢的号码。
（a）
200KN
200KN
A C
0.42
1.66
2.50
单位：m 例题 10-3 图
B D
0.42
解：作钢梁的内力图。 C , D 为危险截面
按正应力强度条件选择截面
200KN
A C
0.42
1.66 2.50
取 C 截面计算 Q c = Qmax = 200kN
( 2
3)2
( 3
1)2
rM
1
t
c
3
在大多数应力状态下,脆性材料将发生脆性断裂.因而应选用 第一强度理论;而在大多数应力状态下,塑性材料将发生屈服和剪 断.故应选用第三强度理论或第四强度理论.但材料的破坏形式不 仅取决于材料的力学行为,而且与所处的应力状态,温度和加载速 度有关.实验表明,塑性材料在一定的条件下低温和三向拉伸,会 表现为脆性断裂.脆性材料在三向受压表现为塑性屈服.
材料力学(上海理工大学)智慧树知到课后章节答案2023年下上海理工大学
材料力学（上海理工大学）智慧树知到课后章节答案2023年下上海理工大学第一章测试1.1、下列结论中是正确的。
A:材料力学主要研究各种材料的力学问题 B:材料力学主要研究杆件受力后变形与破坏的规律 C:材料力学主要研究各类杆件中力与材料的关系 D:材料力学主要研究各种材料的力学性质答案:材料力学主要研究杆件受力后变形与破坏的规律2.2、下列结论中哪些是正确的？答：。
（1）为保证构件能正常工作，应尽量提高构件的强度。
（2）为保证构件能正常工作，应尽量提高构件的刚度。
（3）为保证构件能正常工作，应尽量提高构件的稳定性。
（4）为保证构件能正常工作，应尽量提高构件的强度、刚度和稳定性。
A:全对 B:（1），（2），（3） C:（4） D:全错答案:全错3.3、下列结论中哪些是正确的？答：。
（1）外力是作用在物体外部的力。
（2）杆件的自重不属于外力。
（3）支座约束反力不属于外力。
（4）运动杆件的惯性力不属于外力。
A:（1），（2） B:全错 C:（1），（4） D:全对答案:全错4.4、下列结论中哪些是正确的？答：。
(1)截面法是分析杆件内力的方法。
(2)截面法是分析杆件应力的方法。
(3)截面法是分析杆件截面上内力与应力关系的基本方法。
A:（1） B:全错 C:（3） D:（2）答案:（1）5.5、下列结论中哪些是正确的？答：。
(1)杆件的某个横截面上，若轴力N=0，則各点的正应力σ也为零（既σ=0）。
(2)杆件的某个横截面上，若各点的正应力σ均为零（既σ=0），則轴力必为零（既N=0）。
(3)杆件的某个横截面上，若各点的正应力σ均为零（既σ=0），則弯矩必为零（既M=0）。
A:（2） B:（1） C:（3） D:（2），（3）答案:（2），（3）6.6、构件的强度、刚度、稳定性_______。
A:与二者无关 B:只与材料的力学性质有关 C:与二者都有关 D:只与构件的形状尺寸有关答案:与二者都有关7.7、均匀性假设认为，材料内部各点的_______是相同的。
注册结构工程师(一级基础考试-上午-材料力学)模拟试卷5
注册结构工程师（一级基础考试-上午-材料力学）模拟试卷51．图5—6—1所示单元体，法线与x轴夹角α=45°的斜截面上切应力τ是a ( )。
[2012年真题]A．B．τ=50MPaa=60MPaC．τa=0D．τa2．图5—6—2所示圆轴固定端最上缘A点的单元体的应力状态是( )。
[2011年真题]A．B．C．D．大致指向( )。
3．图5—6—3所示xy坐标系下，单元体的最大主应力σ1[2011年真题]A．第一象限，靠近x轴B．第一象限，靠近y轴C．第二象限，靠近x轴D．第二象限，靠近y轴为4．受力体一点处的应力状态如图5—6—4所示，该点的最大主应力σ1( )。
[2009年真题]A．70MPaB．10MPaC．40MPaD．50MPa5．按照第三强度理论，图5—6—5所示两种应力状态的危险程度是( )。
[2014年真题]A．无法判断B．两者相同C．(a)更危险D．(b)更危险6．按照第三强度理论，图5—6—6所示两种应力状态的危险程度是( )。
[2013年真题]A．(a)更危险B．(b)更危险C．两者相同D．无法判断7．图5—6-7所示圆轴，在自由端圆周边界承受竖直向下的集中力F，按第为( )。
[2009年真三强度理论，危险截面的相当应力σeq3题]A．B．C．D．8．图5—6—8所示正方形截面等直杆，抗弯截面模量为W。
在危险截面上，弯矩为M，扭矩为M，A点处有最大正应力σ和最大剪应力τ。
若材料为低碳a钢，则其强度条件为( )。
A．σ≤[σ]，τ＜[τ]B．C．D．9．图5—6—9所示等腰直角三角形单元体，已知两直角边表示的截面上只有剪应力，且等于τ，则底边表示的截面上的正应力σ和剪应力τ分别为( )。
A．σ=τ0，τ=τB．σ=τ，τ=0C．D．10．求图5—6—10所示平面应力状态的σα、εα。
已知α=45°，E、μ分别为材料的弹性模量和泊松比，则有( )。
A．B．C．D．11．如图5—6—11所示单元体的应力单位为MPa，则其最大剪应力为( )MPa。
[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx
![[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx](https://img.taocdn.com/s3/m/9169fcbc5f0e7cd185253626.png)
应力状态强度理论1.图示单元体，试求 (1) 指定斜截而丄的应力；(2) 主应力大小及主平而位置，并将主平而标在单元体上。
F<T r — CT V解：(1) (y (/ = — ----- + ---------- cos 2a 一 g sin 2& = 76.6 MPar r/ = ----- sin + r v cos2a =-32.7 MPaCc£X-50 ± 加 +(—129.9)2 = _50 ±1506=100 MPa, (r 2 = 0 , 6=-200 MPa解：b 、=150 MPa,「=—120 MPayx由 r = ----------- sin 2Q +「cos 2a = —~~— = -804522得 6 =-10 MPa3.—点处两个互成45°平面上的应力如图所示,其屮<7未知，求该点主应力。
max bmin81.98 MPa-121.98a = 81.98 MPa, <r 2 = 0 , cr 3 = -121.98 MPa^0=larctan(^^) = l arctan2 CT X -cr v 2402.某点应力状态如图示。
试求该点的主应力。
解：取合适坐标轴令6=25 MPa, r x =-129.9 MPa120"-- ----- sin 2a + T cos 2a = 0 得 = -125 MPa 2 -100MPa-200150 MPacr cr + cr所以max= __ ±2214.22MPa一74.226=214.22 MPa, cr2 = 0, <r3 = -74.22 MPa4.图示封闭薄壁圆筒，内径d=100 mm,壁厚f = 2 mm,承受内床“ =4 MPa, 外力偶矩M“=0・192 kN-mo求靠圆筒内壁任一点处的主应力。
解・・r常九严停32a=^- = 5Q MPax 4t<r v二四= 100 MPa、2tmax bmin 100.7MPa 49.356=100.7 MPa, 6=49.35 MPa, (r3 = -4 MPa5.受力体某点平面JL的应力如图示，求其主应力大小。
材料力学作业题集(学院)
台州学院材料力学作业题集专业：班级：姓名：学号：任课教师：前言材料力学是变形体力学的入门课程，是土木工程专业学生必修的技术基础课。
要求学生明确从几何、物理和静力平衡三个方面分析杆件力学问题的基本思路，掌握杆件的强度、刚度和稳定性的基本概念；培养学生具备必要的基础理论知识，比较熟练的计算能力、一定的分析能力和实验能力，为学习结构力学、钢结构、混凝土结构等后续课程提供必要的基础。
为此，为配合课堂教学环节，建筑工程学院材料力学课程组特按教材章节编写了此作业题集，各章包括作图题，简答题，计算题，综合题等题型，重点考查学生对基本概念，基本原理，基本方法的理解和掌握，训练学生的计算能力，建模能力以及思维能力。
建筑工程学院材料力学课程组 2013年6月一、试作出图示各杆的轴力图。
()a P 1=20kN P 3=30kNP 3=10kN二、图示结构中，1、2两杆的横截面直径分别为15mm和20mm，试求两杆的应力。
设两根横梁皆为刚体。
三、图示结构中，AB为刚体，1、2杆的抗拉（压）刚度分别为EA，2EA。
试求两杆的轴力。
四、在图示简易吊车中，BC 为钢杆，AB 为木杆。
木杆AB 的横截面面积21cm 100=A ，许用应力[]MPa 71=σ；钢杆BC 的横截面面积22cm 6=A ，许用应力[]MPa 1602=σ。
试求许可吊重[]F 。
五、图示结构中，BC 由一束直径为2mm 的钢丝组成，若钢丝的许用应力为[]MPa 160=σ，q =20kN/m ，AC 杆长4m 。
试求BC 需由多少根钢丝组成。
BC六、结构尺寸及受力如图所示，AB 可视为刚体，CD 为圆截面钢杆，直径为D=30mm ，材料为Q235钢，许用应力为[]180σ=MPa ，200E GPa =，求许可载荷[]F 。
七、桁架的尺寸及受力如图所示，若F =200kN ，AB 杆的横截面面积A=4000mm 2，试求AB 杆的应力。
八、图示桁架结构，杆AC 由两根L63×10 等边角钢组成，杆CD 由两根L75×10等边角钢组成，已知：L63×10 的横截面为11.657cm 2，L75×10的横截面积为14.126cm 2，[σ]=150MPa 。
试按第三和第四强度理论计算单元体的相当应力。图中应力
一、从低碳钢零件中某点取出一单元体，其应力状态如图所示，试按第三和第四强度理论计算单元体的相当应力。
图中应力单位是MPa 。
(1)、40=ασ,40090=+ασ,60=ατ (2)、60=ασ,80090-=+ασ,40-=ατ （1）max min123r313r41004040MPa202σ=100MPa,σ=0MPa,σ=-20MPa σσσ120MPa σ111.3MPa σ+=±=-=-==（2）max min123r313r470.66080MPa90.6σ=70.6MPa,σ=0MPa,σ=-90.6MPa σσσ161.2MPa σ140.0MPa σ=-±=-=-==二、上题中若材料为铸铁，试按第一和第二强度理论计算单元体的相当应力。
图中应力单位是MPa ，泊松比3.0=μ。
（1）r11r2123σσ100MPaσσ(σσ)106.0MPa μ===-+=（2）r11r2123σσ70.6MPaσσ(σσ)97.8MPaμ===-+=α三、图示短柱受载荷kN 251=F 和kN 52=F 的作用，试求固定端截面上角点A 、B 、C 及D 的正应力，并确定其中性轴的位置。
121i 33121260025100150150100101012121.66106.750F F y F zZy zσ---⨯⨯=++⨯⨯⨯⨯=-++1.668.02.58.84MPa1.668.02.53.84MPa1.668.02.512.16MPa 1.668.0 2.57.16MPaA B C D σσσσ=-++==-+-==---=-=--+=--1.66+106.7y +50z ＝0当z ＝0时，31.661015.5mm 106.70y -=⨯= 当y ＝0时，31.661033.3mm 50y -=⨯=四、图示简支梁选用25a 工字钢，受力及尺寸如图。
已知钢材的弹性模量GPa 210=E ，许用应力[]MPa 160=σ，梁的容许挠度为[]500/l f =1cos 41sin 4z y M Fl M Fl αα==3max 6651040.8660.5()62.57MPa 4401.81048.28310y z z y M M W W σ--⨯⨯=+=+=⨯⨯max 3111.42310500f l===⨯<max 40001.4234 5.69mm []8mm 500f f =⨯=<== F z五、手摇绞车如图所示，钢轴的直径mm 20=d ，其许用应力[]MPa 80=σ。
注册岩土工程师(基础考试-上午-材料力学)模拟试卷8
注册岩土工程师（基础考试-上午-材料力学）模拟试卷8单项选择题共120题，每题1分。
每题的备选项中只有一个最符合题意。
1．某点平面应力状态如图所示，则该点的应力圆为：A．—个点圆B．圆心在原点的点圆C．圆心在(5MPa，0)点的点圆D．圆心在原点、半径为5MPa的圆2．如图所示单元体取自梁上哪一点？A．aB．bC．cD．d3．平面应力状态如图所示，下列结论中正确的是：A．等于：4．如图所示的应力状态单元体若按第四强度理论进行强度计算，则其相当应力σr4A．5．图示矩形截面杆AB，A端固定，B端自由。
B端右下角处承受与轴线平行的集中力F，杆的最大正应力是：A．B．C．D．6．图示圆轴固定端最上缘A点的单元体的应力状态是：A．B．C．D．7．图示T形截面杆，一端固定一端自由，自由端的集中力F作用在截面的左下角点，并与杆件的轴线平行。
该杆发生的变形为：A．绕y和z轴的双向弯曲B．轴向拉伸和绕y、z轴的双向弯曲C．轴向拉伸和绕z轴弯曲D．轴向拉伸和绕y轴弯曲8．图示圆轴，在自由端圆周边界承受竖直向下的集中F，按第三强度理论，危险截面的相当应力A．9．图示为正方形截面等直杆，抗弯截面模量为W，在危险截面上，弯矩为，A点处有最大正应力σ和最大剪应力γ。
若材料为低碳钢，则M，扭矩为Mn其强度条件为：A．B．C．D．10．工字形截面梁在图示荷载作用上，截面m—m上的正应力分布为：A．图(1)B．图(2)C．图(3)D．图(4)11．矩形截面杆的截面宽度沿杆长不变，杆的中段高度为2a，左、右高度为3a，在图示三角形分布荷载作用下，杆的截面m—m和截面n—n分别发生：A．单向拉伸、拉弯组合变形B．单向拉伸、单向拉伸变形C．拉弯组合、单向拉伸变形D．拉弯组合，拉弯组合变形12．一正方形截面短粗立柱（见图a），若将其低面加宽一倍（见图b），原厚度不变，则该立柱的强度：A．提高一倍B．提高不到一倍C．不变D．降低13．图示应力状态为其危险点的应力状态，则杆件为：A．斜弯曲变形B．偏心拉弯变形C．拉弯组合变形D．弯扭组合变形14．折杆受力如图所示，以下结论中错误的为：A．点B和D处于纯剪状态B．点A和C处为二向应力状态，两点处σ1＞0，σ1＝0，σ3＜0C．按照第三强度理论，点A及C比点B及D危险D．点A及C的最大主应力σ1数值相同15．矩形截面拉杆中间开一深为的缺口（见图），与不开缺口时的拉杆相比（不计应力集中影应力是不开口时正应力的多少倍？A．2B．4C．8D．1616．结构如图，折杆AB与直杆BC的横截面面积为A＝42cm2，Wy一Wz＝420cm3，[σ]＝100MPa，则此结构的许可荷载[P]为：A．15kNB．30kNC．45kND．60kN17．矩形截面拉杆两端受线性荷载作用，最大线荷载为q(N/m)，中间开一深为a的缺口（见图），则其最大拉应力为：A．B．C．D．18．图示矩形截面梁，高度h＝120mm，跨度l＝1m，梁中点受集中力P，两端受拉力S＝50kN，此的对称轴y上，距上表面a— 50mm，若横截面内最大正应力与最小正应力之比为5/3，则P为：A．5kNB．4kNC．3kND．2kN19．图示钢制竖直杆DB与水平杆AC刚接于B，A端固定，P、l、a与圆截面杆直径d为已知。
四个强度理论的相当应力表达式
pD ≈ = 90 MPa 4t
( 因为 t «D , 所以 A Dt )
包含直径的纵向截面上的应力
用两个横截面 mm , nn 从圆筒部分 取出
单位长的圆筒研究。
m n
p
m
1
n
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。 包含直径 直径平面
的纵向平
23
11 10
x y
22 2 x yFra bibliotek 2 2 x
29.8MPa 3.72 MPa
(单位 MPa)
1 29.28MPa， 2 3.72MPa， 3 0
1 29.28MPa 30MPa
某结构上危险点处的应力状态如图所示，其中σ＝ 116.7MPa，τ＝46.3MPa。材料为钢，许用应力［σ］＝ 160MPa。试校核此结构是否安全。
1
r3 1 3
rM
c
t
3
在大多数应力状态下,脆性材料将发生脆性断裂.因而应选用 第一强度理论;而在大多数应力状态下,塑性材料将发生屈服和剪 断.故应选用第三强度理论或第四强度理论.但材料的破坏形式不 仅取决于材料的力学行为,而且与所处的应力状态,温度和加载速 度有关.实验表明,塑性材料在一定的条件下低温和三向拉伸,会 表现为脆性断裂.脆性材料在三向受压表现为塑性屈服.
§ 10 - 5 各种强度理论的适用范围及其应用
1、 在三向拉伸应力状态下，会脆断破坏，无论是
脆性或塑性材料，均宜采用最大拉应力理论。 2、对于塑性材料如低C钢，除三轴拉应力状态以外的
复杂应力状态下，都会发生屈服现象，可采用第三、 第四强度理论。
对于图示各点应力状态
对于图示各点应力状态，属于单向应力状态的是： (A) a 点； (B) b 点；(C ) c 点；(D)d 点。
正确答案是 。
H1002ADD对于图示单元体中τmax 有下列四种答案： (A) 100MPa ； (B) 0MPa ； (C) 50MPa ； (D) 200MPa 。
正确答案是 。
H1003ADD关于图示单元体属于哪种应力状态，有下列四种答案： (A )单向应力状态； (B)二向应力状态； (C) 三向应力状态； (D) 纯剪应力状态。
正确答案是 。
关于图示单元体属于哪种应力状态，有下列四种答案： (A )单向应力状态； (B)二向应力状态； (C) 三向应力状态； (D) 纯剪应力状态。
正确答案是 。
H1005ADB矩形截面简支梁受力如图(a)所示，横截面上各点的应力状态如图(b)所 示。
关于他们的正确性，现有四种答案： (A) 点1,2的应力状态是正确的； (B) 点2,3的应力状态是正确的； (C) 点3,4的应力状态是正确的； (D) 点1,5的应力状态是正确的。
正确答案是 。
H1006ADC关于图示梁上a 点的应力状态有下列四种答案： 正确答案是。
(a)H1007ADC对于图示悬臂梁中，A 点的应力状态有下列四种答案：正确答案是 。
H1008ADC微元体的应力状态如图示，关于其主应力有下列四种答案： (A )σ1＞σ2＞０，σ3＝０；(B)σ3＜σ2＜０，σ1＝０；(C)σ1＞０，σ2＝０，σ3＜０，｜σ1｜＜｜σ3｜； (D)σ1＞０，σ2＝０，σ3＜０，｜σ1｜＞｜σ3｜。
正确答案是 。
(A )(B ) (C )(D ) σH1009ADC已知单元体AB 、BC 面上只作用有剪应力τ，现关于AC 面上应力有下列四 种答案：(A) τAC ＝τ/2，σAC ＝0； (B)τAC ＝τ/2，σAC ＝31/2τ/2； (C)τAC ＝τ/2，σAC ＝-31/2τ/2； (D) τAC ＝-τ/2，σAC ＝31/2τ/2。
16172材料力学温习题
一、填空题构件的承载能力包括强度、刚度和___稳固性__3个方面。
工程上通常按延伸率的大小把材料分成两大类，δ大于____5 %__的材料称为塑性材料。
轴向拉伸（紧缩）时，杆中的最大正应力为最大剪应力的____ 2__倍。
静定梁的大体形式有简支梁、外伸梁和悬臂梁。
圆轴受力如图1所示，其危险截面在___ CD __段。
圆杆扭转时，依照切应力互等定理，其纵向截面上也存在切应力。
铸铁试件的紧缩破坏和剪（应力）应力有关。
强度失效的要紧形式有屈服和断裂；。
静定梁的大体形式有简支梁，外伸梁和___悬臂梁__。
如图2所示，铸铁丁字形截面梁的许用应力别离为：许用拉应力［σｔ］＝50ｍpa，许用压应力［σc］=200mpa，那么上下边缘距中性轴的合理比值y1/y2=__4 ___。
(应力为上拉下压，c 为形心)。
单元体各个面上只经受剪应力作用的应力状态，称为纯剪切。
两悬臂梁受力相同，其中一梁横截面为圆形，一梁横截面为正方形，且两梁横截面积相等，材料相同，按正应力强度条件，承载能力较强的梁横截面为__正方形____。
在梁的某一截面上，假设q(x)=dM(x)/dx=___ 0_ __，那么在这一截面上弯矩有一极值。
集中外力偶作用途，M图数值有突变，逆时针；时针方向集中外力偶处，M图自左向右向下突变。
（正向向上）图3所示二向应力状态，其最大应力为______Mpa 。
关于不同柔度的塑性材料压杆，其最大临界应力将不超过材料的 屈服极限 。
以为固体在其整个几何空间毫无间隙地充满了物质，如此的假设称为 均匀性 假设。
10.构件的组合变形适用叠加原理有两个条件，一个是遵从原始尺寸原理，即构件的变形量很小，另一个是__服从胡克定律（材料变形量是线性的）__。
比较第三和第四强度理论，按第 四 强度理论设计的轴的直径小。
如图3所示的外伸梁，已知B 截面的转角216B Fl EI θ=，那么C 截面的挠度C y =216Fal EI。
四大强度理论.
第10章强度理论10.1 强度理论的概念构件的强度问题是材料力学所研究的最基本问题之一。
通常认为当构件承受的载荷达到一定大小时，其材料就会在应力状态最危险的一点处首先发生破坏。
故为了保证构件能正常地工作，必须找出材料进入危险状态的原因，并根据一定的强度条件设计或校核构件的截面尺寸。
各种材料因强度不足而引起的失效现象是不同的。
如以普通碳钢为代表的塑性材料，以发生屈服现象、出现塑性变形为失效的标志。
对以铸铁为代表的脆性材料，失效现象则是突然断裂。
在单向受力情况下，出现塑性变形时的屈服点σ和发生断裂时s的强度极限σ可由实验测定。
sσ和bσ统称为失效应力，以安全系数除失效应力得到b许用应力[]σ，于是建立强度条件[]σσ≤可见，在单向应力状态下，强度条件都是以实验为基础的。
实际构件危险点的应力状态往往不是单向的。
实现复杂应力状态下的实验，要比单向拉伸或压缩困难得多。
常用的方法是把材料加工成薄壁圆筒(图10-1)，在内压p 作用下，筒壁为二向应力状态。
如再配以轴向拉力F，可使两个主应力之比等于各种预定的数值。
这种薄壁筒试验除作用内压和轴力外，有时还在两端作用扭矩，这样还可得到更普遍的情况。
此外，还有一些实现复杂应力状态的其他实验方法。
尽管如此，要完全复现实际中遇到的各种复杂应力状态并不容易。
况且复杂应力状态中应力组合的方式和比值又有各种可能。
如果象单向拉伸一样，靠实验来确定失效状态，建立强度条件，则必须对各式各样的应力状态一一进行试验，确定失效应力，然后建立强度条件。
由于技术上的困难和工作的繁重，往往是难以实现的。
解决这类问题，经常是依据部分实验结果，经过推理，提出一些假说，推测材料失效的原因，从而建立强度条件。
图10－1经过分析和归纳发现，尽管失效现象比较复杂，强度不足引起的失效现象主要还是屈服和断裂两种类型。
同时，衡量受力和变形程度的量又有应力、应变和变形能等。
人们在长期的生产活动中，综合分析材料的失效现象和资料，对强度失效提出各种假说。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、从低碳钢零件中某点取出一单元体，其应力状态如图所示，试按第三和第四强度理论计算单元体的相当应力。
图中应力单位是MPa 。
(1)、40=ασ,40090=+ασ,60=ατ
(2)、60=ασ,80090-=+ασ,40-=ατ （1）
max min
123r313r41004040MPa
202σ=100MPa,σ=0MPa,σ=-20MPa σσσ120MPa σ111.3MPa σ+=
±=-=-==
（2）
max min
123r313r470.66080MPa
90.6σ=70.6MPa,σ=0MPa,σ=-90.6MPa σσσ161.2MPa σ140.0MPa σ=-±=-=-==
二、上题中若材料为铸铁，试按第一和第二强度理论计算单元体的相当应力。
图中应力单位是MPa ，泊松比3.0=μ。
（1）
r11r2123σσ100MPa
σσ(σσ)106.0MPa μ===-+=
（2）
r11r2123σσ70.6MPa
σσ(σσ)97.8MPa
μ===-+=
α
σ
三、图示短柱受载荷kN 251=F 和kN 52=F 的作用，试求固定端截面上角点A 、B 、C 及D 的正应力，并确定其中性轴的位置。
121i 33
121260025100150150100101012121.66106.750F F y F z
Z
y z
σ---⨯⨯=++⨯⨯⨯⨯=-++
1.668.0
2.58.84MPa
1.668.0
2.5
3.84MPa
1.668.0
2.512.16MPa 1.668.0 2.57.16MPa A B C D σσσσ=-++==-+-==---=-=--+=-
-1.66+106.7y +50z ＝0
当z ＝0时，31.66
1015.5mm 106.70y -=⨯=
当y ＝0时，31.66
1033.3mm 50
y -=⨯=
四、图示简支梁选用25a 工字钢，受力及尺寸如图。
已知钢材的弹性模量GPa 210=E ，许用应力[]MPa 160=σ，梁的容许挠度为[]500/l f =
1
cos 4
1
sin 4
z y M Fl M Fl α
α
==
3max 6651040.8660.5()62.57MPa 4401.81048.28310y z z y M M W W σ--⨯⨯=+=+=⨯⨯
max 311
1.42310500
f l
===⨯<
max 4000
1.4234 5.69mm []8mm 500
f f =⨯=<=
= F z
五、手摇绞车如图所示，钢轴的直径mm 20=d ，其许用应力[]MPa 80=σ。
试按第三强度理论求绞车的最大起吊重量F 。
T =0.18F
w 0.40.22F
M F =⨯=
22310.269[]r w M T F W W σσ=+=≤
[]233.5kN 0.269W F σ≤=
即最大荷载为233.5 kN
六、图示，水平放置圆截面直角钢杆（2
ABC π
=
∠），直径mm 100d =，m l 2=，
m N k 1q =，[]MPa 160=σ，试按第四强度理论校核该杆的强度。
2
222
130
221
2AZ AZ A M ql ql ql M T ql =+===
463.6MPa<[]r σσ=
=
七、圆截面直角曲拐ABC 位于水平面内，如图示。
若在自由端C 处作用一集中力P 2，该力作用于xy 平面内，且与y 轴交角为045。
已知KN 5=P ，m 1=a ，m 2=b ，m 1.0=d ，[]MPa 160=σ。
按第三强度理论校核该曲拐的强度。
不考虑轴力的影响。
,,x y z M Pa M Pa M Pb ===
3125MPa []
r z
σσ==
=
=<
强度足够！
八、圆截面等直杆受横向力P 和绕轴线的外力偶0M 作用。
由实验测得杆表面A 处沿轴线方向
的线应变6010400-⨯=ε，杆表面B 处沿与母线成045方向的线应变645103750-⨯=ε。
杆的抗弯截面模量3mm 6000=W ，弹性模量GPa 200=E ，泊松比25.0=μ，许用应力[]MPa 140=σ。
试按第四强度理论校核该杆的强度。
36,200104001080MPa A
A A A E E
σεσε--=
==⨯⨯⨯=
[][]4545451
11()B B B
E
E E εσμσμτμττ-︒︒=
-+=--=
4560MPa 1B E ε
τμ
==+
A 为危险点，且
（注：可编辑下载，若有不当之处，请指正，谢谢!）。