圆锥曲线|圆、椭圆、抛物线、双曲线
高中数学有关圆-椭圆-双曲线-抛物线的详细知识点

<一>圆的方程(x-a)^2+(y-b)^2=r^2,圆心O(a,b),半径r。
(1)圆的一般式方程:x^2+y^2+Dx+Ey+F=0此方程可用于解决两圆的位置关系:配方化为标准方程:(x+D/2)^2.+(y+E/2)^2=(D^2+E^2-4F)/4其圆心坐标:(-D/2,-E/2)半径为r=√[(D^2+E^2-4F)]/2此方程满足为圆的方程的条件是:D^2+E^2-4F>0若不满足,则不可表示为圆的方程(2)点与圆的位置关系点P(X1,Y1) 与圆(x-a)^2+(y-b) ^2=r^2的位置关系:⑴当(x1-a)^2+(y1-b) ^2>r^2时,则点P在圆外。
⑵当(x1-a)^2+(y1-b) ^2=r^2时,则点P在圆上。
⑶当(x1-a)^2+(y1-b) ^2<r^2时,则点P在圆内。
圆与直线的位置关系判断平面内,直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是:1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x^2+y^2+Dx+Ey+F=0,即成为一个关于x的一元二次方程f(x)=0。
利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下:如果b^2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b^2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b^2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x 轴),将x^2+y^2+Dx+Ey+F=0化为 (x-a)^2+(y-b) ^2=r^2。
令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;当x1<x=-C/A<x2时,直线与圆相交;半径r,直径d在直角坐标系中,圆的解析式为:(x-a)^2+(y-b)^2=r^2;x^2+y^2+Dx+Ey+F=0=> (x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4=> 圆心坐标为(-D/2,-E/2)其实只要保证X方Y方前系数都是1就可以直接判断出圆心坐标为(-D/2,-E/2)这可以作为一个结论运用的且r=根号(圆心坐标的平方和-F)<二>椭圆的标准方程椭圆的标准方程分两种情况:当焦点在x轴时,椭圆的标准方程是:x^2/a^2+y^2/b^2=1,(a>b>0);当焦点在y轴时,椭圆的标准方程是:y^2/a^2+x^2/b^2=1,(a>b>0);其中a>0,b>0。
2022年高考复习 椭圆、双曲线、抛物线的方程与性质

轴,则△FAB的周长的取值范围为
圆
锥
曲
线
的
几
何
性
质
(8,12);
抛物线的准线l:直线x=-2, 焦点F(2,0),
由抛物线定义可得|AF|=xA+2,
圆(x-2)2+y2=16的圆心为(2,0),半径为4,
所以△FAB的周长=|AF|+|AB|+|BF|=xA+2+(xB-xA)+4=6+xB,
2
);有相同离心率的椭圆方程为
=1(k>-b
+
2
2
a k b k
y 2 x2
x2 y2
+ 2 =λ1(λ1>0,焦点在 x 轴上)或 2 + 2 =λ2(λ2>0,
2
b
a
a
b
焦点在 y 轴上).
核心考点
(5)等轴双曲线
实轴和虚轴等长的双曲线叫做等轴双曲线,
常用
结论
其方程为 x2-y2=λ(λ≠0),离心率 e= 2 ,
2022
高考复习
椭圆、双曲线、抛物线的方程与性质
目
录
核心
考点
>>
常考
题型
>>
跟踪
检测
核心考点
1.圆锥曲线的定义
(1)椭圆: |MF1|+|MF2|=2a(2a>|F1F2|);
(2)双曲线: ||MF1|-|MF2||=2a(2a<|F1F2|);
(3)抛物线: |MF|=d(d为M点到准线的距离且定点M在准线外).
圆锥曲线的标准方程公式

圆锥曲线的标准方程公式
圆锥曲线的标准方程公式是数学中用于描述圆锥曲线几何性质的方程形式。
圆锥曲线包括圆、椭圆、双曲线和抛物线。
每种曲线都有其独特的标准方程形式。
1. 圆的标准方程公式:
圆的标准方程公式是(x - h)² + (y - k)² = r²,其中圆心坐标为(h, k),半径为r。
这个方程描述了平面上所有到圆心距离等于半径的点的集合。
2. 椭圆的标准方程公式:
椭圆的标准方程公式是(x²/a²) + (y²/b²) = 1,其中a和b分别代表椭圆的长轴
和短轴的半长。
这个方程描述了平面上到椭圆两个焦点的距离之和等于常数2a的
点的集合。
3. 双曲线的标准方程公式:
双曲线的标准方程公式可以分为两种形式:(x²/a²) - (y²/b²) = 1和(y²/a²) - (x²/b²) = 1,其中a和b分别代表双曲线的焦点到中心的距离和横轴/纵轴的半长。
这个方
程描述了平面上到双曲线两个焦点的距离之差等于常数2a的点的集合。
4. 抛物线的标准方程公式:
抛物线的标准方程公式可以分为两种形式:y² = 4ax和x² = 4ay,其中a为抛物线的焦点到顶点的距离。
这个方程描述了平面上到抛物线焦点的距离等于焦点到顶点距离的某个倍数的点的集合。
通过这些标准方程公式,我们可以方便地描述和理解圆锥曲线的形状和性质。
它们在几何、物理、工程等领域中都有广泛的应用。
掌握数学中的圆锥曲线与双曲线

掌握数学中的圆锥曲线与双曲线圆锥曲线与双曲线是数学中重要的概念,它们在几何学、物理学、工程学以及其他应用领域中都有广泛的应用。
掌握圆锥曲线与双曲线的性质和特征对于解决实际问题、推导数学公式以及拓展数学知识都非常重要。
本文将详细介绍圆锥曲线与双曲线的定义、性质以及一些重要的应用。
1. 圆锥曲线的定义圆锥曲线是在平面上由一个动点P和一个固定点F(焦点)确定的几何图形。
当动点P满足定点到动点的距离和定点到直线的距离之比为定值(离心率)时,所生成的曲线就是圆锥曲线。
根据离心率的不同取值,圆锥曲线可以分为四种:椭圆、双曲线、抛物线和直线。
2. 圆锥曲线的性质(1)椭圆:椭圆是圆锥曲线中离心率小于1的情况。
椭圆具有两个焦点,并且动点P到两个焦点的距离之和是一个定值。
(2)双曲线:双曲线是圆锥曲线中离心率大于1的情况。
双曲线同样具有两个焦点,但动点P到两个焦点的距离之差是一个定值。
(3)抛物线:抛物线是圆锥曲线中离心率等于1的情况。
抛物线具有一个焦点,并且动点P到焦点的距离等于焦点到直线的距离。
(4)直线:当离心率趋于无穷大时,圆锥曲线变成一条直线。
3. 双曲线的定义双曲线是一个平面上的点P到两个不相交的固定点F1和F2的距离之差等于一个常量的轨迹。
双曲线的形状可以用以下方程表示:x^2/a^2 - y^2/b^2 = 1,其中a和b分别表示双曲线的横轴和纵轴的长度。
4. 双曲线的性质(1)双曲线具有两条渐近线,与双曲线趋近于无穷远处且永不相交。
(2)双曲线的对称轴是横轴和纵轴的平分线,同时也是双曲线的渐近线。
(3)双曲线的顶点是在横轴和纵轴的交点处,顶点之间的距离等于2a。
(4)双曲线有两个分支,分别位于两个焦点的两侧。
5. 圆锥曲线与双曲线的应用(1)在物理学中,圆锥曲线和双曲线广泛用于描述物体的运动轨迹,如行星绕太阳的轨道等。
(2)在工程学中,圆锥曲线和双曲线可以用于设计道路、桥梁和建筑物等的弧度和曲线形状。
圆锥曲线(椭圆-双曲线-抛物线)的定义、方程和性质知识总结
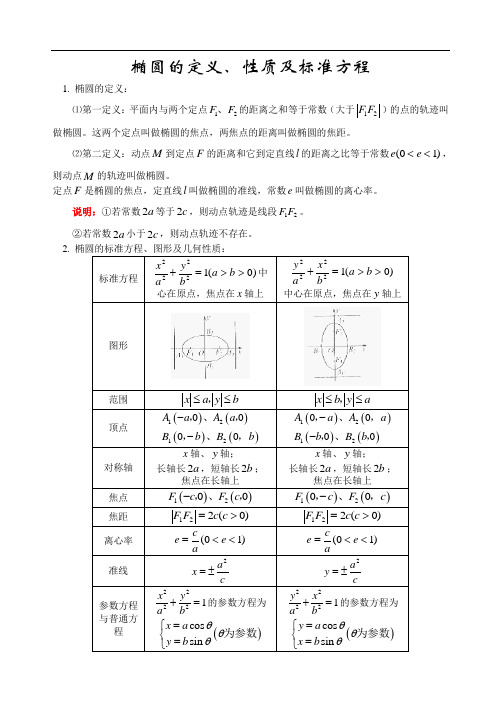
椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a by a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点,焦点在y 轴上图形范围 x a y b ≤≤,x b y a ≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴 x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
圆锥曲线(抛物线、椭圆、双曲线)标准方程推导

圆锥曲线(抛物线、椭圆、双曲线)标准方程推导几何定义是在平面中,由所有满足到一定点与到一定直线距离相等的点所组成的图形,把这个定点称为焦点(focus)、定直线称为准线(directrix)。
为了方便推导,把这一定点放在x轴正方向上,定直线垂直x 轴放在x轴负半轴上,且原点刚好在两者中间。
上面这些都仅仅是为了推导方便而已。
设曲线上的点坐标为(x,y),于是,\begin{aligned} d(F, P) &=d(P, D) \\ \sqrt{(x-a)^{2}+(y-0)^{2}} &=|x+a| \\ (x-a)^{2}+y^{2}&=(x+a)^{2} \\ x^{2}-2 a x+a^{2}+y^{2} &=x^{2}+2 ax+a^{2} \\ y^{2} &=4 a x \end{aligned}四种不同开口的标准型:二、椭圆(Ellipse)几何意义是在平面中,由所有到两个顶点距离之和为定值的点所组成的图形,把这两个定点称为焦点(foci),也是为了推导的方便,把这两个焦点对称放在x轴正负半轴上,令两段距离之和为2a,根据两点之间距离公式进行如下推导:\begin{aligned} d\left(F_{1}, P\right)+d\left(F_{2}, P\right) &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}} &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}=& 2 a-\sqrt{(x-c)^{2}+y^{2}} \\ (x+c)^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+(x-c)^{2}+y^{2} \\x^{2}+2 c x+c^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+x^{2}-2 c x+c^{2}+y^{2} \\ 4 c x-4 a^{2}=&-4 a \sqrt{(x-c)^{2}+y^{2}} \\ c x-a^{2}=&-a\sqrt{(x-c)^{2}+y^{2}} \\ \left(c x-a^{2}\right)^{2}=& a^{2}\left[(x-c)^{2}+y^{2}\right] \\ c^{2} x^{2}-2a^{2} c x+a^{4}=& a^{2}\left(x^{2}-2 cx+c^{2}+y^{2}\right) \\ \left(c^{2}-a^{2}\right)x^{2}-a^{2} y^{2} &=a^{2} c^{2}-a^{4} \\ \left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2} &=a^{2}\left(a^{2}-c^{2}\right) \end{aligned}令 b^2=a^2-c^2 (根据三角形两边之和大于第三边推出c<a)所以,\begin{aligned} b^{2} x^{2}+a^{2} y^{2} &=a^{2} b^{2} \\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1\end{aligned}常见的两种椭圆标准方程,一种是横躺在x轴上,一种是“站立”着,关键就是看x和y下面哪个数值比较大,哪个大,那么长的对称轴就在哪个方向上。
[寒假]圆锥曲线(椭圆-双曲线-抛物线)的定义、方程和性质知识总结
![[寒假]圆锥曲线(椭圆-双曲线-抛物线)的定义、方程和性质知识总结](https://img.taocdn.com/s3/m/6c5fee9fb8f3f90f76c66137ee06eff9aef849f8.png)
椭圆的定义,性质及标准方程1.椭圆的定义:⑴第一定义:平面内与两个定点用、入的距离之和等于常数(大于I耳与I)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M到定点方的距离和它到定直线/的距离之比等于常数e(O<e<1),则动点M的轨迹叫做椭圆。
定点尸是椭圆的焦点,定直线/叫做椭圆的准线,常数e叫做椭圆的离心率。
说明:①若常数2〃等于2c,则动点轨迹是线段4②若常数2。
小于2c,则动点轨迹不存在。
3.焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在X轴上时,设《、耳分别是椭圆的左、右焦点,尸(X0,%)是椭圆上任一点,贝小尸片|二Q+"υ,∖PF2∖=a-ex0o∖PF i∖推导过程:由第二定义得一二e(4为点尸到左准线的距离),d1( 2、a贝IJ1尸耳I二七4 a-∖-ex0;同理得I尸闾二a一%。
=e x0H-----------=CXO+Q<c)简记为:左“+”右“-。
由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。
'-若焦点在y轴上’则为/3=1。
有时为了运算方便,设mx2+ny2-1(m>0,m≠π)o双曲线的定义、方程和性质知识要点:1.定义(1)第一定义:平面内到两定点F1、F2的距离之差的绝对值等于定长2a(小于∣F1F2∣)的点的轨迹叫双曲线。
说明:①I1PF1HPF2∣∣=2a(2a<∣FιF2∣)是双曲线;若2a=∣FF2∣,轨迹是以Fi、F2为端点的射线;2a>∣FF2∣时无轨迹。
②设M是双曲线上任意一点,若M点在双曲线右边一支上,则IMF11>∣MF2∣,∣MHHMF2∣=2a;若M在双曲线的左支上,则IMFI1<∣MF∕∣MFιHMF2∣=-2a,故IMF1HMF2∣=±2a,这是与椭圆不同的地方。
(2)第二定义:平面内动点到定点F的距离与到定直线1的距离之比是常数e(e>1)的点的轨迹叫双曲线,定点叫焦点,定直线1叫相应的准线。
圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a by a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点,焦点在y 轴上图形范围 x a y b ≤≤,x b y a ≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴 x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线|圆、椭圆、抛物线、双曲线
几何开始于最简单的图形-直线和圆。
约公元前350年,梅内克缪斯发现了圆锥曲线。
在约公元前250年,佩尔加的阿波罗尼奥斯对圆锥曲线进行首次定义分析。
阿波罗尼奥斯对圆锥曲线的构造始于圆和圆心正上方的一个点,用直线连接圆周上的每个点与该悬点,得到的面就是圆锥面。
用一个平面去截一个二次锥面,得到的交线就称为圆锥曲线(conic sections)。
圆锥曲线包括椭圆、抛物线、双曲线和圆,通过直角坐标系,它们又与二次方程对应,所以,圆锥曲线又叫做二次曲线。
1 椭圆
圆锥面是最简单的三维图形之一。
但是一些复杂的二维曲线包含于圆锥面内。
阿波罗尼奥斯的问题是:假设你用一个平面截取那个圆锥圆,截线是什么样?一种可能是,如果正好平行截在恰当的地方,你可以重新得到起初的圆。
高一点或低一点,也可得到小一点或大一点的圆。
但是当不是平行截取时,出现的图形看起来像是被拉伸或压扁的圆。
这就是最常见的圆锥曲线-椭圆。
我们生活的地球每时每刻都在环绕太阳的椭圆轨迹上运行,太阳系其他行星也如此,太阳则位于椭圆的一个焦点上。
如果这些行星运行速度增大到某种程度,它们就会沿抛物线或双曲线运行。
人类发射人造地球卫星或人造行星就要遵照这个原理。
相对于一个物体,按万有引力定律受它吸引的另一物体的运动,不可能有任何其他的轨道了。
因而,圆锥曲线在这种意义上讲,它构成了我们宇宙的基本形式。
从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上。
2 抛物线
用一个平行于圆锥的边的平面来截圆锥面,这样生成一条不封闭的“U”形线-抛物线。
我们周围到处是抛物线。
如果你向空中斜抛出一块石头,划出的那条轨迹就是抛物线(忽略空气阻力的影响)。
抛物线也出现在宇宙中。
一些彗星,如哈雷彗星,可预测地、规律性地出现在夜空。
也有其它的一些只出现一次的彗星,通常在绕太阳的抛物轨道上运行。
从抛物线的焦点发出的光,经过抛物线反射后,反射光线都平行于抛物线的对称轴。
一束平行光垂直于抛物线的准线,向抛物线的开口射进来,经抛物线反射后,反射光线汇聚在抛物线的焦点。
3 双曲线
通过垂直地切割对顶圆锥使得平面与两个半平面相交来构造这种图形,使得双曲线有两个独立的分支,这两个分支不相交但完全对称
-双曲线。
哈勃太空望远镜中的镜面形状就是双曲线,可能让天文学家来观测宇宙。
从双曲线一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上。
4 圆锥曲线比较
圆锥
曲线
椭圆双曲线抛物线
标准
方程
x2/a2 y2/b2=1 (a>b>0) x2/a2-y2/b2=1 (a>0,b>0) y2=2px (p>0)
范围x∈[-a,a]y∈[-b,b] x∈(-∞,-a]∪[a, ∞)y∈R x∈[0, ∞)y∈R
对称
性
关于x轴,y轴,原点对称关于x轴,y轴,原点对称关于x轴对称
顶点(a,0),(-a,0),(0,b),(0,-
b)
(a,0),(-a,0) (0,0)
焦点(c,0),(-c,0)【其中
c2=a2-b2】
(c,0),(-c,0)【其中c2=a2
b2】
(p/2,0)
准线x=±a2/c x=±a2/c x=-p/2
渐近
线
——————y=±(b/a)x[4]—————离心
率
e=c/a,e∈(0,1) e=c/a,e∈(1, ∞)e=1
焦半径∣PF?∣=a ex∣PF?∣=a-
ex
∣PF?∣=∣ex
a∣∣PF?∣=∣ex-a∣
∣PF∣=x p/2
焦准
距
p=b2/c p=b2/c p 通径2b2/a 2b2/a 2p。
