重叠部分图形的面积专题
五年级组合图形的面积精选32题
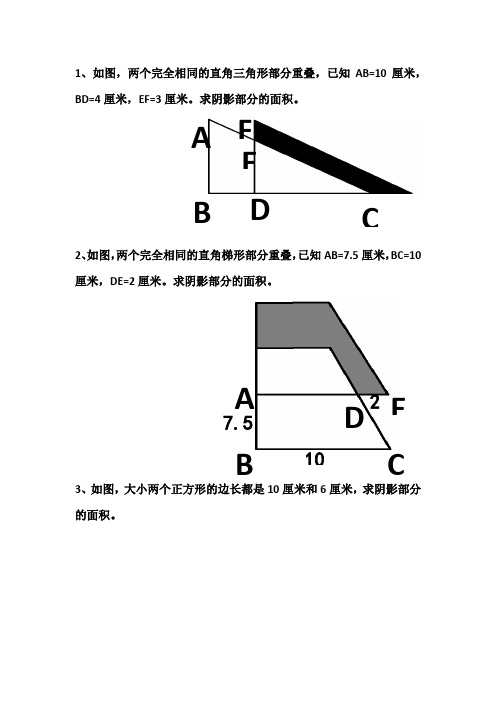
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
图形面积巧计算(附解题思路与参考答案)

图形面积巧计算专项练习 (附解题思路和参考答案)教学内容:巧算图形面积。
教学对象:三、四年级学生。
教学重点:正方形、长方形面积的计算。
教学难点:重叠图形面积的计算。
教学过程: 一 复习教学(一)点学生回答:1.什么叫面积?2.正方形、长方形的公式、3.遇到较复杂的组合图形后又该如何计算?(二)投影出示下列内容,引导学生熟读记牢。
1面积:面积指的是物体所占平面的大小。
2 长方形的面积=长×宽,长方形的面积÷长=宽,长方形的面积÷宽=长。
正方形的面积=边长×边长,正方形的面积÷边长=边长。
3 求复杂图形的面积,需要敏锐的观察力和灵活的思维,运用添加辅助线、割补、转化等方法解答。
二新课教学(一)例题1 在一张长9米,宽7米的长方形铁板上,切割出一个面积最大的正方形,这个正方形铁板的面积是多少平方米?三 巩固练习11. 明明把一张长12厘米,宽8厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米?请根据例题写出解题思路:请列式计算9米 7 米 解题思路:要使切割出的正方形铁板面积最大就要使它的边长最长(如图),那么只能选原来的长方形的宽为边长,即正方形的边长为7米。
解:7×7=49(平方米) 答:这个正方形铁板的面积是49平方米。
2 妈妈把一块长2米,宽6分米的长方形布料裁成一个面积最大的正方形,这个正方形的面积是多少?解题思路: 1. 统一单位:2米=20分米。
2. 再根据正方形的面积公式“边长×边长”可求出基面积。
解:3 将以张长10米,宽8米的长方形铁板切割成一个面积最大的正方形,这个正方形的面积是多少平方米?剩下的部分是什么形状?面积是多少?1.正方形的面积:答:这个正方形的面积是 平方米。
2.剩下的面积:答;剩下的部分是 ,面积是 平方米。
(二)例题2 求下面图形的面积。
(单位:厘米)解题思路:不是规则的长方形要把原图进行割补,使其变成规则的图形解答。
重叠法的经典例题

重叠法的经典例题一、例题在一个长方形中,长为8厘米,宽为6厘米,有两个半径为1厘米的圆重叠放在长方形内(圆与长方形的边相切),求阴影部分(两个圆重叠部分以外的区域)的面积。
二、题目解析1. 首先计算长方形的面积- 根据长方形面积公式S = a× b(其中a为长,b为宽),已知长方形长a = 8厘米,宽b = 6厘米,所以长方形面积S_长方形=8×6 = 48平方厘米。
2. 然后计算两个圆的面积- 根据圆的面积公式S=π r^2(其中r为半径),已知圆半径r = 1厘米,一个圆的面积S_圆=π×1^2=π平方厘米。
- 那么两个圆的面积S_两个圆=2π平方厘米,取π = 3.14,则S_两个圆=2×3.14 = 6.28平方厘米。
3. 接着计算两个圆重叠部分的面积- 两个半径为1厘米的圆重叠部分是一个类似橄榄形的图形。
我们可以先算出两个扇形(圆心角为90^∘,因为圆与长方形边相切)的面积之和,再减去中间正方形的面积。
- 一个扇形的面积是圆面积的(1)/(4),所以一个扇形面积S_扇形=(1)/(4)×π×1^2=(π)/(4)平方厘米。
- 两个扇形面积S_两个扇形=(π)/(2)平方厘米,取π = 3.14,则S_两个扇形=1.57平方厘米。
- 中间正方形的面积S_正方形=1×1 = 1平方厘米。
- 所以两圆重叠部分面积S_重叠=1.57 - 1=0.57平方厘米。
4. 最后计算阴影部分面积- 阴影部分面积S_阴影=S_长方形-S_两个圆+S_重叠- 把S_长方形=48平方厘米,S_两个圆=6.28平方厘米,S_重叠=0.57平方厘米代入可得:- S_阴影=48 - 6.28+0.57 = 42.29平方厘米。
小学奥数图形--重叠求面积

重叠求面积
一、基础达标
1、两个完全一样的长方形,长8厘米,宽3厘米。
重叠后总面积是多少平方厘米 ?
2、如图,一大一小的两个正方形有一部分重合,两块没有重合的阴影部分面积相差多少?
3、有一块菜地长20米,宽12米。
菜地中间留了2米宽的路,把菜地平分成4小块。
每小块地的面积是多少?
4、两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积。
5、如图,以AB为直径作半圆,三角形ABC是直角三角形,AB长40厘米,BC长30厘,求阴影部分①比阴影部分②面积大多少平方厘米?
二、能力提升
1、如右图,两个正方形的边长分别为14厘米和8厘米,甲、乙两块空白区域的面积之和为156平方厘米,那么阴影部分的面积是多少平方豪米。
2、如图,由两个完全一样的直角三角形叠在一起而成的,求阴影部分的面积是多少平方米?
3、如图(单位: 厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
4、如图,直角三角形ABC,AB长是40厘米,图中阴影部分的甲的面积比阴影部分乙的面积大148平方厘米,求:BC的长度。
5、下图的长方形是一块草坪,中同有丙条宽1米的走道,求植草的面枳。
三、竞赛链接
(第九届“走进美妙数学花园”决赛题选)如图所示,四个相叠的正方形,边长分别是11、9、7、5,求红色区与黑色区的面积差。
九年级数学有关图形重叠部分面积的计算

若将半圆上点D 固定,再把半圆往 矩形外旋至A′D处,半圆弧A′D与 B A′
AD交于点P, 设∠ADA′ =α
(1)若AP =2- ,求α的度数; (2)当∠α =30°2 时,求阴影部 A P 分的面积
3
B
6
2
A O
2D
C O
D
C
1、如图,在Rt△ABC中,AC=4,
巩固复习 BC=2,分别以AC、BC为直径画半
D
C
例:如图,己知矩形ABCD中,AB=8,
BC=4,则阴影部分的面积是多少?
基本图形:扇形与矩形。
E
A
B
解题思路: S扇形EAD+S矩形-S三角形EBC
1、正方形ABCD内接于⊙O,⊙O
练一练 的半径为2,分别以正方形各边
为折痕,将劣弧AB、BC、CD、DA
向内对折,则图中阴影部分的面
积为_1_6___4__
O C
A BD
思路:(S直角三角形OBD-S扇形BOD)×2
组合图形 方法2、利用平移来计算重叠部分的面积
例1:己知直经AB=10,点C、D是圆 的三等分点,求阴影部分的面积。
C
D
解题 根据平行线之间距离相等,转 A
O
B
思路: 化求S扇形
计算结果:
25
6
例2、如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于
B
圆,则图中阴影部分的面积为_2____2 3
2、如图,菱形OABC中,A 1200,OA=1,将
菱形OABC绕点O按顺时针方向旋转 900 ,则 A
图分中的由面弧积是BB_,_B_'_A2_' ,__弧__AC,CB围成的阴影部
五年级组合图形的面积精选32题

1、如图,两个完全相同的直角三角形部分重叠,已知
AB=10厘米,
BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分的面积。
A B C
D E
F A
D
E B C
107.52
4、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分
的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?
A
B
C D E F
A
B C D F E G。
等积变形中的面积重叠问题

遇到困难可看下面的解答
图中辅助线是本题最简单的证法
例19. 凸四边形ABCD的两组 对边中点连线EF, GH相交 于O.求证: 两块红色四边形 的总面积=四边形ABCD面 积的一半。
如何证,自己想,试试你的分析能力
例20. 凸四边形ABCD的 两组对边中点连线EF, GH相交于O.连接AH, CG分别交EF与M,N. 则
答: △PAF与△PBG 面积之差是 2.16平方厘米
提示: 连接AG.易知正方形ABCD边长为
4厘米. △ADG面积为8平方厘米.
也就是矩形DEGF的面积为16平方厘米.
所以
DE 16 3.2 5
厘米.
可以求得AE=2.4厘米, CG=3厘米.
由重叠原理, 知S① + S③ = S② + S④.
证明,就是精准简练的实话实说
例17.如右图,已知凸 四边形ABCD中,边AB 和CD的中点为K和M, BM与CK的交点为P, AM与DK的交点为Q.证 明三角形BPC与三角形 AQD的面积之和等于四 边形MQKP的面积.
请先积极、独立地思考
例18.ABCD为任意四边形, M, N分别为 AD, BC中点,MB交AN于 P; MC交DN于Q. 若四边形 ABCD的面积为150,四边 形MPNQ的面积是50,求: 四个三角形APM,DQM, BPN和CQN的面积和是多 少?
3
3
3
SABC1,求 PQR 的面积.
这样添线〉
答:三角形PQR的面积是81/560
例22.如图 ABC 中,A F1A B , B D 1B C , C E1C A .
2
3
6
若 SABC1 ,求 PQR 的面积.
小学奥数几何中的重叠问题

目
1.了解容斥原理二量重叠和三量重叠的内容;
2.掌握容斥原理的在组合计数等各个方面的应用.
目
一、两量重叠问题
在一些计数问题中,经常遇到有关集合元素个数的计算•求两个集合并集的元素的个数,不能简单地
把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个
数,用式子可表示成:AUB A B AI B(其中符号U”读作 并”,相当于中文 和”或者 或”的意思;符 号“I”读作 交”,相当于中文 且”的意思.)则称这一公式为包含与排除原理, 简称容斥原理.图示如下:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:AI B,即阴影面积•图示如下:
二、三量重叠问题
A类、B类与C类元素个数的总和A类元素的个数B类元素个数C类元素个数 既是A类又是B类的元素个数 既是B类又是C类的元素个数 既是A类又是C类的元素个数 同时是A类、B类、C类 的元素个数.用符号表示为:AU BUC A B C AI B BI C AI C AI BI C.图示如下:
另一个长方形长10厘米宽厘米它们中间重叠的部分是个边长4厘米的正几何中的重叠问题两个长方形如图摆放时出现了重叠见图中的阴影部分重叠部分恰好是边长为厘米的正方形如果利用两个长方形面积之和来计算被覆盖桌面的面积那么重叠部分在两个长方形面积中各被计算了一次而实际上这部分只需计算一次就可以了
数学竞赛
小学奥数几何中的
几何中的重叠问题
【难度】2星 【题型】解答
将图中的三个圆标上 圆面积C圆面积)纸片共同重叠的面积,
A、B、C•根据包含排除法,三个纸片盖住桌面的总面积(A圆面积B
(A与B重合部分面积A与C重合部分面积B与C重合部分面积)三个
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
4
B 6
D
O
8
C
x
(2)操作与求解: ①正方形ODEF平行移动过程中,通过操作、观察,试 判断S(S>0)的变化情况是 C ; A.逐渐增大 B.逐渐减少 C.先增大后减少 E D.先减少后增大 y A 4 B F 2 3 6 O 8 C x
D
②当正方形ODEF顶点O移动到点C时,求S的值;
(3)探究与归纳: 设正方形ODEF的顶点O向右移动的距离为x,求重叠部 分面积S与x的函数关系式. y F
D
3
C
A
6
B(M) 图1
9
E
(1)问:矩形ABCD是否可能完全落在等边∆MEF的内 部?若可能,请求出相应的时间t(s)的取值范围;若不可 F 能,请说明理由。
D 3 A 6
C D’ 3 B 3 A’ ( M) 9
C’’ 3
6 3 9 3 t 3 2
B’’ 3 E
6 3 3t
9 t 3 3t
14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 1 x 1 ( x 4) (3)4 x 4.5时, S x ( x 4) 2 2 2 2 1 2 1 2 x ( x 4) 2 x 4 4 4
x 2
C
N
A P
M
D
x
1 O Q R 2 x B E xFC N 2 14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 14 (4)4.5 x 时, 2 3 S 8 x 72 x 166
A P O
M
D
Q R
B
C
N
14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 20 (7) x 时, S 0 3
如图1,在矩形ABCD中,AB=6cm,BC=3cm,AB边刚 好落在直线l上,另有一等边∆MEF,边ME也在直线l上, ME=9cm,M与B重合。将矩形ABCD沿直线l自左向右, 以3cm/s的速度运动,即等边∆MEF的边长以1cm/s的速度 在扩大,如图2所示。设运动时间为t(s),矩形ABCD与等 边∆MEF重叠部分面积为S(cm² ) F
A BE
D
O’ x O C
F
10 x 14 x 14
D C O’ x
O
CD
O’ x
如图,等腰直角三角形纸片ABC中,AC=BC=4, ∠ACB=90º ,直角边AC在x轴上,B点在第二象限,A (1,0),AB交y轴于E,将纸片过E点折叠使BE与EA 所在直线重合,得到折痕EF(F在x轴上),再展开还原 沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点 开始沿射线EA平移,至B点到达A点停止.设平移时间为t (s),移动速度为每秒1个单位长度,平移中四边形 BCFE与△AEF重叠的面积为S. B y (1)求折痕EF的长; 45° 4 2 4 E EF 2
2
C
FO 1 A
x
(2)是否存在某一时刻t使平 移中直角顶点C经过抛物线 y=x2+4x+3的顶点?若存在,求 出t值;若不存在,请说明理由;
B
4 C
y
4 2
E FO 4 P
解:设CP//BA交y轴于P 则点C 在射线CP上运动 PC所在直线的解析式为:y=-x-3
2
A
x
y ( x 2) 1 顶点坐标为D( 2, 1) 把x 2代入y x 3,得 y=-1 点D(-2,-1)在直线CP上 直角顶点C在运动过程中经过此抛物线的顶点。 t= 2 CD 2
F
D 3 A 6
3C (3t 6)
B ( M)
3t 9
E
6 3 (3)2 t 时, 3 9 3 2 39 3 S t 18 3 9 t 2 2
F
D 3 A 6
C
B ( M)
9
E
6 3 9 3 (4) t 时, 3 2
S 18
F
D 3 A 6
C
(3)直接写出S与t的函数关系式及自变量t的取值范围.
B y
4
C
4 2
E FO 4 A x
(3)直接写出S与t的函数关系式及自变量t的取值范围.
B y
4
C
4 2
E FO A x
(3)直接写出S与t的函数关系式及自变量t的取值范围.
B y
4
C
4 2
E FO A x
(3)直接写出S与t的函数关系式及自变量t的取值范围.
A P O Q R
D
M
x
B
E
F N C 14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 14 (5) x 5时, 13 400 2 3 S x 60 x 2 3
A P O
M
D
x
B E CF N
Q R
20 (6)5 x 时, 3
14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3
F
D 3 A 6
C
B ( M)
9
E
15 3 15 (7) t 时, 2 2FD 3 A 6C
B ( M)
9
E
15 (8)t 时, S 0 2
(3)在整个运动过程中,是否存在这样的t,使得重叠 部分面积恰好为矩形ABCD的面积的一半?若存在,请 求出符合条件的t的值;若不存在,请说明理由。 F
(1)0 x 3时, S 0
A P O
M
D
x
B 2 x6 C N
Q 2x R
14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 1 (2)3 x 4时, S (2 x 6) 2(2 x 6) 2 2 4( x 3)
A P O
M
D
x
B
Q R
(3)求PQR与梯形ABCD重叠部分的 面积S与x的函数关系
A P
M D
O
Q R
B
C
N
A P O
M
D
Q R PR : 3,4,4.5,5
14 20 PQ : 4, , 3 3
N C 14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 B
A P O
M
D
Q R
N C 14 20 0 ~ 3 ~ 4 ~ 4.5 ~ ~5~ ~ 3 3 B
9
E A’’’ A’’’’
15 3 6 3 t3 AD : t1 2 t2 2 3
15 t3 2
F
D 3 A 6
C
3 3t
B 3t ( M) 9 E
3 (1)0 t 时, 3
F
D 3 A 6
C
3t 3
9 E
B 3t ( M)
3 3 3 (2) t 2时, S 9t 3 2
9 3 t 2
6 3 t 3
(2)当0<t≤3时,求S与t之间的函数关系式 F
D 3 A 6
C C’
C’’ C’’’
3
B 3 B’ (M) 9 E B’’ B’’’
BC :
3 9 3 t1 t2 3 2
9 t3 2
F
D 3 A 6
C D’’ D’
D’’’
D’’’’
B A’ A’’ ( M)
E
A
B
D
O
C
x
(3)探究与归纳: 设正方形ODEF的顶点O向右移动的距离为x,求重叠部 分面积S与x的函数关系式. y F
E
A
B
D
O
C
x
E
y
FA
P
B
E
y
AF
B
y E
A F B
D
y
0 x4
EA
BF
O O’
C x DO y
O’
C x OD F
4 x6
6 x8
O’C x
AE B
O
y
8 x 10
重叠部分图形的面积
如图,在平面直角坐标系中,直角梯形ABCO的边OC落 在x轴的正半轴上,且AB∥OC,BC⊥OC,AB=4,BC=6, OC=8.正方形ODEF的两边分别落在坐标轴上,且它的 面积等于直角梯形ABCO面积.将正方形ODEF沿x轴的 正半轴平行移动,设它与直角梯形ABCO的重叠部分面 积为S. (1)分析与计算:求正方形ODEF的边长; E y F
2 24 3 t 4 6 3 24 3 综上所述: t 或t 6 4 2
②矩形退出等边三角形时
B y
4
C
4 2
E FO A x
(3)直接写出S与t的函数关系式及自变量t的取值范围.
B y
4
C
4 2
E FO A x
(3)直接写出S与t的函数关系式及自变量t的取值范围.
B y
4
C
4 2
E FO A x
1 如图,已知tanMON , 梯形ABCD在MON内部, 2 且点A在OM上,BC在ON上,AB 2 5,AD 1, 且tanABC 2,tanDCB 4,点P从点O出发以每 秒 5的速度在射线OM上匀速运动,点Q, R在射线ON 上, 且PQ / /AB, PR ON于R,设点P运动了x秒
7 (2)当x 时,PQR与梯形ABCD 2 重叠部分的面积S _____
P’A
2 5
M
1
D
当x 5时,S ?
O
P Q R B
