第二版《材料力学》完整习题解答(华中科大版倪樵主编)
材料力学答案——倪樵、钱勤、李国清
例、平面直角框架及受力如图，已知框架各段的弯曲刚度 EI，试求 |M|max。 平面直角框架及受力如图， B l D l l l m m MF ： 9m /10 m /10 M： m 1 M0 ： l X1 m C m 一次超静定， 解:一次超静定，取静定基 一次超静定
δ 11 X 1 + ∆1F = 0
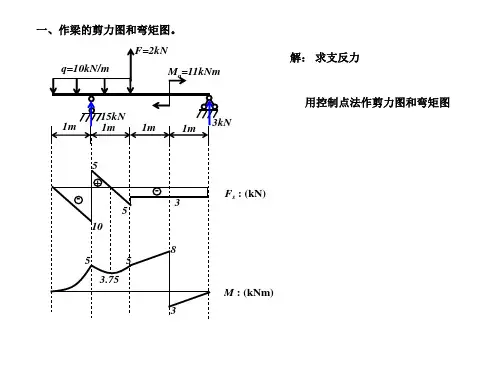
一、作梁的剪力图和弯矩图。 作梁的剪力图和弯矩图。 F=2kN q=10kN/m Mo=11kNm 用控制点法作剪力图和弯矩图 1m 15kN 1m 1m 1m 3kN 解： 求支反力
5 +
5 10
3
Fs : (kN)
8 5 3.75 M : (kNm) 3 5
作用，已知材料的[σ]=10MPa，[τ]=3MPa，横截面 二、图示木梁受一移动载荷 F 作用，已知材料的 ，τ ， 高宽比h/b=3/2，试确定截面尺寸。 高宽比 ，试确定截面尺寸。 最大弯矩在集中力作用处， 解: 最大弯矩在集中力作用处，最大剪 力在支座处截面 F=1kN h x 0.5m b
π 2E π 2 × 200 × 109 λp = = = 99.35 6 σp 200 × 10
λs =
1m
304 − σ s 304 − 235 = = 61.61 1.12 1.12
I d = A 4
(2) 计算压杆的柔度
µ = 0.7 i =
σ cr (MPa )
235 200
λ=
µl
i
=
0.7 ×1 = 80 0.035 / 4
σ 1 = 40MPa σ 2 = 0 σ 3 = −10MPa
tan 2α 0 = − 2τ xy
= 215 ×10
−6
材料力学第2版 课后习题答案 第10章 强度理论
解： t ≥
pD =
2[σ ]
3×106 ×1 2 × 300×106
= 0.01m = 1.0cm
2
9-8 铸铁圆柱形容器外直径D = 20 cm，壁厚t＝2cm，受内压强p＝4MPa，并在容器两端
受轴向压力P＝200 kN作用，设 µ = 0.25 ，
许用拉应力[σ +]＝25 MPa，（1）用第二强
论作强度校核。 解：
σ
4 xd
=
σ 2 + 3τ 2
σ
= 1202 + 3× 402 = 138MPa < [σ ]
τ
σ τ
题 9-3 图
所以安全。
9-4 某梁在平面弯曲下，已知危险截面上作用有弯矩M＝50.9 kN ⋅ m ，剪力FS＝134.6 kN，截面为No. 22b工字钢，[σ ]＝160 MPa，试根据第三强度理对梁作主应力校核。
σ
m xd
=
σ
1
−
σ σ
+ b − b
σ3
= 1.027 −
256 × (−101.027)
625
=
42.4MPa
9-12 内径为d，壁厚为t的圆筒容器，内部盛有比重为γ ，高度为H的液体，竖直吊装如
图示。试按第三强度理论沿容器器壁的母线绘制圆筒的相当应力σ
3 xd
图（不计端部影响）。
解：
σ
y
=
πd2 4
应力校核。
70
(+)
(−) 30
( Q −图)
(−) 20
(−) 30
24.44 (+)
(M −图)
(−) 20
Wz
材力习题册(第二版201008)参考答案(1-9章)
第一章绪论一、选择题1．根据均匀性假设，可认为构件的（C）在各处相同。
A．应力B．应变C．材料的弹性系数D．位移2．构件的强度是指（C），刚度是指（A），稳定性是指（B）。
A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则A点剪应变依次为图(a) （A），图(b) （C），图(c) （B）。
A．0B．r2C．r D．1.5r4.下列结论中( C )是正确的。
A．内力是应力的代数和；B．应力是内力的平均值；C．应力是内力的集度；D．内力必大于应力；5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应力是否相等（B）。
A．不相等；B．相等；C．不能确定；6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（C）。
A. 认为组成固体的物质不留空隙地充满了固体的体积；B. 认为沿任何方向固体的力学性能都是相同的；C. 认为在固体内到处都有相同的力学性能；D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是连续性假设，均匀性假设，各向同性假设。
2．材料力学的任务是满足强度，刚度，稳定性的要求下，为设计经济安全的构件提供必要的理论基础和计算方法。
3．外力按其作用的方式可以分为 表面力 和 体积力 ，按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4．度量一点处变形程度的两个基本量是 （正）应变ε 和 切应变γ。
三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。
（ × ） 2．外力就是构件所承受的载荷。
（ × ） 3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。
（ √ ） 4．应力是横截面上的平均内力。
（ × ） 5．杆件的基本变形只是拉(压)、剪、扭和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。
材料力学第二版第4章习题答案
材料力学_第二版_范钦珊_第4章习题答案第4章 弹性杆件横截面上的切应力分析4－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。
（A ）等截面圆轴，弹性范围内加载； （B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。
正确答案是 A 。
解：p )(I M x ρρτ=在推导时利用了等截面圆轴受扭后，其横截面保持平面的假设，同时推导过程中还应用了剪切胡克定律，要求在线弹性范围加载。
4－2 两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。
试判断下列结论的正确性。
（A ）max 1τ＞max 2τ； （B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ； （D ）若G 1＞G 2，则有max 1τ＜max 2τ。
正确答案是 C 。
解：因两圆轴等长，轴表面上母线转过相同角度，指切应变相同，即γγγ==21由剪切胡克定律γτG =知21G G >时，max 2max 1ττ>。
4－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。
关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。
（A ）234)1(α-； （B ）)1()1(2234αα--； （C ）)1)(1(24αα--； （D ）)1/()1(2324αα--。
正确答案是 D 。
解：由max 2max 1ττ=得)1(π16π1643231α-=d M d M xx 即 31421)1(α-=D d（1） )1(222212121α-==D d A A W W （2）（1）代入（2），得 2324211)1(αα--=W W4－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。
材料力学第2版 课后习题答案 第3章 剪切实用计算
P 30 × 10 3 l≥ = = 8.33cm b[τ ] 24 × 10 −3 × 40 × 10 6
l≥
2P 2 × 30 × 10 3 = = 12.7cm h σ iy 10 × 10 −3 × 90 × 10 6
[ ]
取 l = 127 mm 3-8 销钉式安全联轴器如图所示．允许传递扭矩Mn=300N.m。销钉材料的剪切强度 极限τb＝360 MPa，轴的直径D＝30mm。试确定销订的直径d。 解:
推进轴，其凸缘法兰承 小宽度 b=50mm ，材料 j]=22.5Mpa 。试校合其
3-6 某拖轮的螺旋桨 受总推力P=250KN，凸缘最 为 45 号钢，许用剪应力 [ τ 剪切强度。
解
τ =
P 250 × 10 3 = = 3.979 MPa < [τ ] 2πrb π × 0.4 × 0.05
习
题
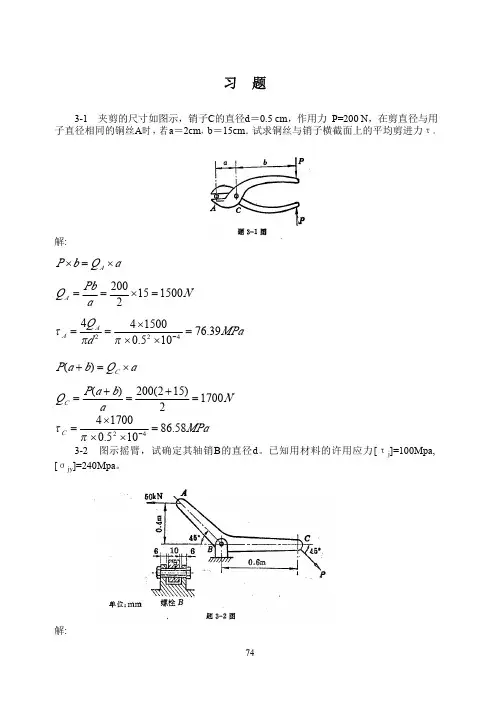
3-1 夹剪的尺寸如图示，销子C的直径d＝0.5 cm，作用力 P=200 N，在剪直径与用 子直径相同的铜丝A时 ， 若 a＝2cm，b＝15cm． 试求铜丝与销子横截面上的平均剪进力τ。
解:
P × b = QA × a QA = τA = Pb 200 = × 15 = 1500 N a 2
3-2 图示摇臂，试确定其轴销 B 的直径 d 。已知用材料的许用应力 [ τ j]=100Mpa, [σjy]=240Mpa。
解:
74
∑MB = 0
P ⋅ cos 45� × 0.6 = 50 × 0.4
P = 47.14 KN
RB = 37.27 KN τ = R ≤ [τ ] 2 d2
π 4
2×3 2 6 πd [τ ] = π × 26 2 × 100 = 318.6 KN 4 4
材料力学第2版 课后习题答案 第12章 变形能法
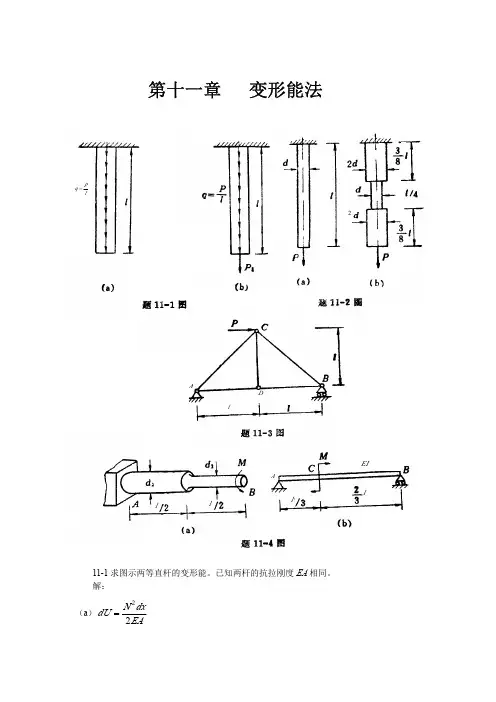
q2 4 ⎞ 2 2 3 ⎜ P x + qPx + x ⎟ ∫0 ⎜ ⎟dx 4 ⎝ ⎠
l⎛
δB =
∂U 1 = ∂P 2 EJ
⎛ 2 3 ql 2 ⎞ Pl 3 ql 4 ⎜ Pl + ⎟= ⎜3 ⎟ 3EJ + 8 EJ 4 ⎝ ⎠
11-6 试求下列图示各梁 A 点的挠度和截面 B 的转角，已知截面抗弯刚度 EI。
L
⎡
⎛L
⎞
⎤
5PL3 96 EJ
11-8 外伸梁的两支座均为弹性支座，弹簧的刚度（引起单位变形所需的力）分别为 k1 和 k2，已知梁的抗弯刚度 EI，试求外伸端 A 的铅直位移。 解：先求设两支座为非弹性支承时，A 端的铅直位移 δ A1 。
∑MB = 0
⎛ b⎞ y c = P ⎜1 + ⎟ ⎝ a⎠
第十一章
变形能法
q=
P l
2
A D l
EI
A
l
l
l
l
11-1 求图示两等直杆的变形能。已知两杆的抗拉刚度 EA 相同。 解：
N 2 dx （a） dU = 2 EA
N = qx =
l
P x t P2 x2 P 2l dx = 0 2 EAl 2 6 EA
l
U = ∫ dU = ∫
0
(b)
x N = P (1 + ) l x⎞ P ⎜1 + ⎟ l 7 P 2l l⎠ ⎝ U =∫ dx = 0 2 EA 6 EA
(
)
=
71qa 4 24 EJ
求 θB
M � ( x1 ) = −1 M � ( x2 ) = 0 θB =
⎤ 1 ⎡ a⎛ 5q 2 1 2 ⎞ ⎜ 2qax1 − a − qx1 ⎟(− 1)dx1 ⎥ ⎢ ∫ 0 EJ ⎣ ⎝ 2 2 ⎠ ⎦ 3 2 1 ⎛5 3 q a a ⎞ ⎜ qa + ⋅ ⎟ = − 2 qa ⋅ ⎟ EJ ⎜ 2 2 3 2 ⎝ ⎠ =−
工程力学工程静力学与学习材料力学第二版本包括答案.doc
1－ 1 图 a 、b 所示，1 1与22分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解OxyOxy和投影，并比较分力与力的投影。
(a) (b)习题 1-1 图yy 2F y 1FFy 2FFy 1Fy 2F x 1xFx 2x 2F x 1Fx 2（c ）（d ）解：（a ），图（ c ）： FFsoc i 1 Fnis j 1分力： Fx1 F cos i 1 ， F y1 F sinj1投影：F x1F cos， F y1 F sin讨论：= 90 °时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（ d ）：分力： F x2 ( F cosF sin tan )i 2 F sinj 2， F y 2sin投影： FF cos ，F y2 F cos()x 2讨论： ≠ 90°时，投影与分量的模不等。
1 －2试画出图 a 、 b 两情形下各物体的受力图，并进行比较。
FAyFAxACDFRDFB(a)(b)(a-1)习题 1－2 图FAyFCF CF AyFF AxF AxACBA CBD'F CF RDF RDD(a-2)(a-3)(b-1)比较：图（ a-1 ）与图（ b-1 ）不同，因两者之 F R D 值大小也不同。
1 －3 试画出图示各物体的受力图。
..习题 1－3 图FDCFDC CBFF BAFAxABFAxBAF AF BFAyF BFAy(a-1)或(a-2)(b-1)CB FBDF DCF BF BABWFAxCAF AF AFAyD或(b-2) (c-1)(d-1)F CDFFCCFAxABCF cAFAyDF ABF AF D(e-1)F B或(d-2) F D(e-2)D FF O 1'CF AF O 1AF OxAFOxOOO 1FOyFOyABF AF AA ..WF B W(f-2)(e-3)(f-1)(f-3)F AF AF B1 －4 图 a 所示为三角架结构。
(完整版)材料力学课后习题答案
xx8-1 试求图示各杆的轴力，并指出轴力的最大值。
取 1-1 截面的左段；(2) (3) F N1取 2-2 截面的右段；F R用截面法求内力，取1-1、2-2、 3-3 截面；(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2；kN 取 2-2 截面的左段；取 3-3 截面的右段；轴力最大值： 用截面法求内力，取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面；38-2 解：8-5 (2) (2) 取 1-1 截面的右段； 取 2-2 截面的右段F ；N112kN 22kN(5) 轴力最大值： 试画出 8-1所示各杆的轴力图。
(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆，承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用， 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ，如欲使 AB 与 BC 段横截面上的正应力相同，试求载荷 F 2 之值。
(2) 求 1-1、 2-2 截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷 F=10 kN 作用，杆的横截面面积 A=1000 mm 2，粘接面的方位 角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。
l 1l 2解： (1) 用截面法求 AB 、 BC 段的轴力；(2) 分段计F 算个杆向变形；FAC 杆缩短。
2F8-22 图示桁架，杆 1与A 杆 2的横截面面积与材料均相B 同，在节点 A 处承受C 载荷 F 作用。
从解： 8-6 解： (1) 用截面法求出 F 11-1、2-2 截面的轴力；(2) 求 1-1、 2-2 截面的正应A 力 ，利用正应力相B 同 ；题 8-5 图所示圆截面杆，已知载荷 1F 1=200 kN ，F 2=1020 kN ，CAB 段的直径 d 1=40 mm ，如 欲使 AB 与 BC 段横截面上的正应力相同，试求 BC 段的直径。
工程材料力学性能 第二版 课后习题答案
《工程材料力学性能》（第二版）课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性：在外加载荷作用下，应变落后于应力现象。
静力韧度：材料在静拉伸时单位体积材科从变形到断裂所消耗的功。
弹性极限：试样加载后再卸裁，以不出现残留的永久变形为标准，材料能够完全弹性恢复的最高应力。
比例极限：应力—应变曲线上符合线性关系的最高应力。
包申格效应：指原先经过少量塑性变形，卸载后同向加载，弹性极限(ζP)或屈服强度(ζS)增加；反向加载时弹性极限(ζP)或屈服强度(ζS)降低的现象。
解理断裂：沿一定的晶体学平面产生的快速穿晶断裂。
晶体学平面－－解理面，一般是低指数，表面能低的晶面。
解理面：在解理断裂中具有低指数，表面能低的晶体学平面。
韧脆转变：材料力学性能从韧性状态转变到脆性状态的现象（冲击吸收功明显下降，断裂机理由微孔聚集型转变微穿晶断裂，断口特征由纤维状转变为结晶状）。
静力韧度：材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。
是一个强度与塑性的综合指标，是表示静载下材料强度与塑性的最佳配合。
二、金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学姓能?答案：金属的弹性模量主要取决于金属键的本性和原子间的结合力，而材料的成分和组织对它的影响不大，所以说它是一个对组织不敏感的性能指标，这是弹性模量在性能上的主要特点。
改变材料的成分和组织会对材料的强度(如屈服强度、抗拉强度)有显著影响，但对材料的刚度影响不大。
三、什么是包辛格效应，如何解释，它有什么实际意义?答案：包辛格效应就是指原先经过变形，然后在反向加载时弹性极限或屈服强度降低的现象。
特别是弹性极限在反向加载时几乎下降到零，这说明在反向加载时塑性变形立即开始了。
包辛格效应可以用位错理论解释。
第一，在原先加载变形时，位错源在滑移面上产生的位错遇到障碍，塞积后便产生了背应力，这背应力反作用于位错源，当背应力(取决于塞积时产生的应力集中)足够大时，可使位错源停止开动。
第二版《材料力学》完整习题解答_(华中科大版_倪樵主编)
g
2
1
x
l2
l 2
0
因此
max
l
3 4
g
此处轴向变形为 l l gl2 3 2ln 2 0.403 gl2
4E
E
2-8
C
B
30 45
A
1m
0.8 m
F
A
45
l2 30
l1
R
P A
Q
对A点列平衡方程：
有两个铆钉，每个铆钉所受剪切力为:
Fs 2
则铆钉剪切面上的切应力为:
Fs / 2 59.3 MPa d2 /4
2-25
C FC
DF
1.5 m
1.5 m
F
2.1 mm 时 l f 所以B端不受约束，此时
FC F FB 0 F 200 kN 80 MPa
0
sin 2 45
50
MPa
各截面受力如图：
b
F
F
h
2-5
n
F
a
粘接面
2-6
1
2
l
3
C
A
l2
F
B
l2
A l1
A
角度为a的斜截面上的正应力和切应力分别为：
F
0 cos2 a
要使 2
1 2
0
sin
2a
则有
0
cos2 a
2
1 2
0
sin 2a
2 0
30 cm
第二版《材料力学》习题解答
A =AR +RP
l2 cos 30
+ Ax
tan
30=1.367
mm
2-9
F A
l
y
y
f ky2
f
对A点列平衡方程：
l
Fy 0 : ky2dy F
0
k
3F l3
在y处截面的内力为：
N
பைடு நூலகம்
y
y 0
ky2dy
1 ky3= 3
F l3
y3
由胡克定律，在y截面的应变为：
E
N y
EA
F EAl3
0
sin
2a
则有
0
cos2 a
2
1 2
0
sin
2a
2 0 sin a
cos a
cosa 2 sin a
a =arctan0.5=arcsin 1 =arccos 2
5
5
对刚性杆AB列平衡方程：
N1 N3
N 2
Fy 0 : N3 0
Fx 0, M ( A) 0 :
A
F
B
N1 N2 F 2
MPa
a=45°时： 45
45
0 1 2
cos2 0 sin
45
2
50
45
MPa 50
MPa
a=-45°时： 45
45
1 2
0 cos2 45 50 MPa 0 sin 2 45 50
MPa
a=135°时： 135
135
0 cos2 135 50 MPa
1 2
0
sin
2
y3
地桩总的缩短量为：
(完整版)材料力学习题册答案..
练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。
（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（ 是 ） （4）应力是内力分布集度。
（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。
（是 ） （6）若物体产生位移，则必定同时产生变形。
（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。
（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。
（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。
（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。
（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。
（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。
根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。
（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。
变形。
（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。
（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
材料力学第2版 课后习题答案 第7章 弯曲变形
解：查自重得：
q = 587.02 N / m
J = 15760cm4 Pl 3 5ql 4 f =− − 48EJ 384EJ −176 × 103 × 113 = 48 × 210 × 109 × 15760 × 10−8 × 4 −587.02 × 5 × 114 + 385 × 210 × 109 × 15760 × 10−8 × 4 = 0.0377 m = 3.77cm
(d) 解：
D A P P E
' yC = y E + θ B ia + y C
C B P
− P ( 2a ) − Pa 3 − Pa3 = − − 3EJ 3EJ 3EJ 3 −10 Pa = 3EJ
3
252
7-5 门式起重机横梁由4根36a工字钢组成如图所示， 梁的两端均可视为铰支， 钢的弹 性模量E=210Gpa。试计算当集中载荷P＝176 kN作用在跨中并考虑钢梁自重时，跨中截面 C的挠度yC。
x=l
∴y =−
'
∴D = 0
y=0
∴C =
− M 0l 6
M 0l 2 ⎛ x x 3 ⎞ ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
M 0l 2 ⎛ 1 3 x 2 ⎞ ∴θ = y = − ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
− M 0l 2 l ；此时挠度最大 f = 3 9 3EJ 2 ⎛ l ⎞ − M 0l 中点挠度 y ⎜ ⎟ = ⎝ 2 ⎠ 16 EJ − M 0l Ml θA = θB = 0 6 EJ 3EJ （b）解： 设中点为C点，则分析CB段
''
C2 = −
D2 = −
a4 24