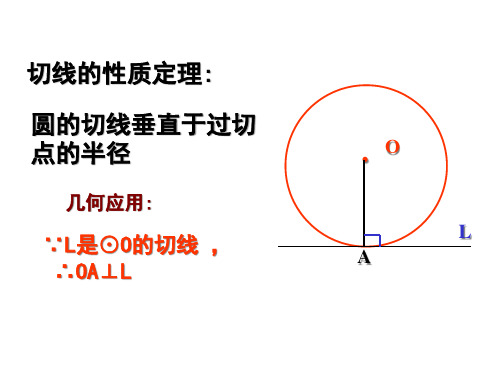
《3.4.2+直线和圆的位置关系切线判定及性质定理》课件2
合集下载
2422直线和圆的位置关系切线的判定1精品PPT课件

(2)直线l和⊙O的位置有什么关系?根据什么? 相切 d=r
(3)由此你发现直线l满足了什么条件时,它是圆的切线?
一:直线l经过半径OA的外端点A
二:直线l垂直于半径OA
判断
1. 过半径的外端的直线是圆的切线( × )
O l
r A
判断
2. 与半径垂直的的直线是圆的切线( × )
O r
l A
判断
直线l与⊙O只有一个公共点
直线l与⊙O相切.
.O
.
l
切点A
二、温故知新
用圆心到直线的 距离d判定切线
直线l 与⊙O相切
d=r
.o dr
┐l
三、探索新知 问:已知⊙O和⊙O上一点A,如何过点A作⊙O的切
线呢?
O
A
作图步骤:
如图,在⊙O上,连结OA,过点A作直线l⊥OA,
O
思考以下问题:
l
A
(1)圆心O到直线l的距离和圆的半径有什么数量关系? 相等
2,已知:如图,在△ABC中,AB=AC,以AB为直径作⊙O 交BC于D,DE⊥AC于E。 求证:DE是⊙O的切线。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
(2)如果已知条件中不知直线与圆是否有公共点, 则过圆心作直线的垂线段为辅助线,再证垂线段长 等于半径长。简记为:作垂直,证半径。
五、挑战自我 〖例3〗
如图,AB是⊙O的直径,点D在AB的延长线上,
BD=OB,点C在⊙O上, ∠CAB=30°, C
求证:DC是⊙O的切线.
《直线和圆的位置关系——切线的判定和性质》PPT课件

A.2.3 B.2.4 C.2.5 D.2.6
【点拨】如图,设切点为 D,连接 CD.∵AB 是⊙C 的切线, ∴CD⊥AB. ∴S△ABC=12AB·CD. 在△ ABC 中,∵AB=5,BC=3,AC=4, ∴AC2+BC2=42+32=52=AB2. ∴∠ACB=90°. ∴S△ABC=12AC·BC=12AB·CD. ∴CD=ACA·BBC=4×53=2.4. ∴⊙C 的半径为 2.4,故选 B. 【答案】B
1. 说得太好了,老师佩服你,为你感到骄傲! 2. 你的设计(方案、观点)富有想象力,极具创造性。 3. 我非常欣赏你的想法,请说具体点,好吗? 4. 某某同学的解题方法非常新颖,连老师都没想到,真厉害! 5. 让我们一起为某某喝彩!同学们在学习过程中,也要敢于猜想,善于猜想,这样才能有所发现,有所创造! 三、表扬类
6.【2019·重庆】如图,AB是⊙O的直径,AC是⊙O的切 线,A为切点,若∠C=40°,则∠B的度数为( B )
A.60° B.50° C.40° D.30°
7.【2019·福建】如图,PA,PB是⊙O的切线,A,B为 切点,点C在⊙O上,且∠ACB=55°,则∠APB等于 ( B)
A.55° B.70° C.110° D.125°
在 Rt△ AOD 中,设 AD=x,则 AO=2x,根据勾股定理
有 AD2+DO2=AO2,即 x2+12=(2x)2,求得 x= 33(负值 舍去),∴AD= 33.在 Rt△ AOD 和 Rt△ AOF 中, OD=OF,OA=OA,∴Rt△ AOD≌Rt△ AOF.
∴∠AOD=∠AOF=30°,S△ AOD=S△ AOF, ∴∠DOF=60°. ∴阴影部分的面积=2S△AOD-S 扇形 ODF =2×12×1× 33-π×12×36600 = 33-π6.
【点拨】如图,设切点为 D,连接 CD.∵AB 是⊙C 的切线, ∴CD⊥AB. ∴S△ABC=12AB·CD. 在△ ABC 中,∵AB=5,BC=3,AC=4, ∴AC2+BC2=42+32=52=AB2. ∴∠ACB=90°. ∴S△ABC=12AC·BC=12AB·CD. ∴CD=ACA·BBC=4×53=2.4. ∴⊙C 的半径为 2.4,故选 B. 【答案】B
1. 说得太好了,老师佩服你,为你感到骄傲! 2. 你的设计(方案、观点)富有想象力,极具创造性。 3. 我非常欣赏你的想法,请说具体点,好吗? 4. 某某同学的解题方法非常新颖,连老师都没想到,真厉害! 5. 让我们一起为某某喝彩!同学们在学习过程中,也要敢于猜想,善于猜想,这样才能有所发现,有所创造! 三、表扬类
6.【2019·重庆】如图,AB是⊙O的直径,AC是⊙O的切 线,A为切点,若∠C=40°,则∠B的度数为( B )
A.60° B.50° C.40° D.30°
7.【2019·福建】如图,PA,PB是⊙O的切线,A,B为 切点,点C在⊙O上,且∠ACB=55°,则∠APB等于 ( B)
A.55° B.70° C.110° D.125°
在 Rt△ AOD 中,设 AD=x,则 AO=2x,根据勾股定理
有 AD2+DO2=AO2,即 x2+12=(2x)2,求得 x= 33(负值 舍去),∴AD= 33.在 Rt△ AOD 和 Rt△ AOF 中, OD=OF,OA=OA,∴Rt△ AOD≌Rt△ AOF.
∴∠AOD=∠AOF=30°,S△ AOD=S△ AOF, ∴∠DOF=60°. ∴阴影部分的面积=2S△AOD-S 扇形 ODF =2×12×1× 33-π×12×36600 = 33-π6.
直线和圆的位置关系切线的判定课件

圆心O到直线L的距
O
离等于半径,直线
L与⊙O相切。
A
•直线和圆的位置关系切线的判定
•2
圆的切线判定定理:
经过半径的外端且垂直于这条半径
的直线是圆的切线。
条件: (1)经过半径的外端;
●
(2)垂直于过该点半径;
O
┐
符
A
l
号
语 ∵l⊥OA,且l 经过⊙O上的A点
言
表 ∴直线l是⊙O的切线
达
•直线和圆的位置关系切线的判定
l是圆的切线 l是圆的切线 l是圆的切线
2. 证明圆的切线常用辅助线作法:
⑴有公共点时,连半径,证垂直 ⑵无公共点时,作垂直,证半径
•直线和圆的位置关系切线的判定
•12
1、矩形的两边长分别为2.5和5,若以较 长一边为直径作半圆,则矩形的各边与半 圆相切的线段最多有( D )
A、0条 B、 1条 C、 2条 D、 3条
O l
r
A
O r
l
A
O l
r
A
•直线和圆的位置关系切线的判定
•5
精彩源于发现
请你总结一下:圆 的切线的判定有几 种方法?
•直线和圆的位置关系切线的判定
•6
知识清单:
1、如何判定一条直线是已知圆的切线? (1)与圆只有一个公共点的直线是圆的切线; (2)到圆心的距离等于半径的直线是圆的
切线;(d=r)
(2)如果已知条件中不知直线与圆是否有公共 点,则过圆心作直线的垂线段为辅助线,再 证垂线段长等于半径长。简记为:(无公
共点时,作垂直,证半径)
•直线和圆的位置关系切线的判定
•11
谈谈今天的收获
2422直线与圆的位置关系之切线长定理课件
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理
几何语言:
反思:切线长定理为证明线段相等、角相等提 供了新的方法
我们学过的切线,常有 五个 性质:1、切线和圆只有一个公共点;2、切线和圆心的距离等于圆的半径;3、切线垂直于过切点的半径;4、经过圆心垂直于切线的直线必过切点;5、经过切点垂直于切线的直线必过圆心。
解:设△ABC的内切圆与三边相切于D、E、F,
连结OA、OB、OC、OD、OE、OF,
则OD⊥AB,OE⊥BC,OF⊥AC.
∴S△ABC=S△AOB+S△BOC +S△AOC
设△ABC的三边为a、b、c,面积为S,则△ABC的内切圆的半径 r=
结论
有关圆的计算问题
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
证明:∵PA,PB与⊙O相切,点A,B是切点 ∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90° ∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
结论
·
A
初中数学九年级上册《切线的概念、切线的判定和性质》PPT课件(共12张PPT)

直线和⊙O相离
d>r (没有公共点)
直线和⊙O相切
d = r (一个公共点)
直线和⊙O相交
d<r (两个公共点)
第2页,共12页。
如图在⊙O中经过半径OA的外端点A 做直线l⊥OA,则圆心O到直线 l 的距离 是多少?
直线 l 和⊙O有什么位置关系?
o
A
l
这时圆心O到直线 l 的距离就是⊙O的半径.
·O
∵ l2切⊙O于B,OB是半径
∴ l2⊥OB.
又∵ AB为直径,
l2
B
∴ l1∥ l2 .
第8页,共12页。
知识拓展
▪ 例2.如图,AB为⊙O的直径,C是⊙O上一点,D在AB
的延长线上,且∠DCB= ∠A.
▪ (1)CD与⊙O相切吗?如果相切,请你加以证明,如果不相 切,请说明理由.
▪ (2)若CD与⊙O相切,且∠D=30°,BD=10,求⊙O的半径.
1.如图 AB是⊙O的直径,∠ABT=45°AT=AB,
求证AT 是⊙O的切线. 证明: ∵ AT=AB,∠ABT = 45°,
∴ ∠ATB = ∠ABT=45 °.
∴ ∠TAB = 180°-∠ATB-∠ABT
B
= 90°.
∴ TA⊥OA.
·O
又∵ OA是⊙O的半径 ∴ AT是⊙O的切线.
T
A
第6页,共12页。
▪ 归纳小结
▪ 本节课应掌握: ▪ 1.直线和圆相交、割线、直线和圆相切,切线、切点、直线和圆
相离等概念. ▪ 2.设⊙O的半径为r,直线L到圆心O的距离为d则有: ▪ 直线L和⊙O相交d<r
▪ 直线L和⊙O相切d=r
▪ 直线L和⊙O相离d>r
初中数学直线与圆的位置关系(2)切线的判定

且∠CAE=∠B,AE与⊙O还相切于点A吗?
D
课堂操练
1.判断下列命题是否正确:
(1)经过半径外端的直线是圆的切线; (× ) (2)垂直于半径的直线是圆的切线; (× )
(3)和圆有一个公共点的直线是圆的切线(√ )
(4)经过半径的一端,并且垂直于一条半径的直线
是圆的切线.
(× )
2.已知圆的直径为10cm,圆心与直线l的距离恰
拓展提高
如图,OA、OB是⊙O中互相垂直的两条半
径,M是OB上任一点,连结AM并延长交⊙O
于C,过C作直线交MB的延长线于D,当
△DMC满足什么条件时CD是⊙O的切线?并
说明理由.
A
BM
D
O
C
合作探究
例1.已知直线AB经过⊙O上的点C,并且OA=OB, CA=CB.求证:直线AB是⊙O的切线.
O
A
C
B
合作探究
例2.如图,已知OA=OB=5厘米,AB=8厘米, ⊙O的直径为6厘米. 求证:AB与⊙O相切.
O
A
C
B
合作探究
例3.如图(a)AB为⊙O的直径,△ABC内接于⊙O, 且∠CAE=∠B. (1)试说明AE与⊙O相切于点A; (2)如图(b),若AB是⊙O的非直径的弦,
直线与圆的位置关系(2) ——切线的判定
离石区江阴高级中学初三数学备课组
回 顾 直线与圆的位置关系
相交
rd 相切
相离
判定切线的方法: 1. 与圆有唯一公共点的直线是圆的切线。 2.与圆心的距离等于半径的直线是圆的切线
探究
如图,OA是⊙O的半径,过A作
直线 l⊥OA,若设圆的半径为r,直
线 l是⊙O的切线吗,为什么?
D
课堂操练
1.判断下列命题是否正确:
(1)经过半径外端的直线是圆的切线; (× ) (2)垂直于半径的直线是圆的切线; (× )
(3)和圆有一个公共点的直线是圆的切线(√ )
(4)经过半径的一端,并且垂直于一条半径的直线
是圆的切线.
(× )
2.已知圆的直径为10cm,圆心与直线l的距离恰
拓展提高
如图,OA、OB是⊙O中互相垂直的两条半
径,M是OB上任一点,连结AM并延长交⊙O
于C,过C作直线交MB的延长线于D,当
△DMC满足什么条件时CD是⊙O的切线?并
说明理由.
A
BM
D
O
C
合作探究
例1.已知直线AB经过⊙O上的点C,并且OA=OB, CA=CB.求证:直线AB是⊙O的切线.
O
A
C
B
合作探究
例2.如图,已知OA=OB=5厘米,AB=8厘米, ⊙O的直径为6厘米. 求证:AB与⊙O相切.
O
A
C
B
合作探究
例3.如图(a)AB为⊙O的直径,△ABC内接于⊙O, 且∠CAE=∠B. (1)试说明AE与⊙O相切于点A; (2)如图(b),若AB是⊙O的非直径的弦,
直线与圆的位置关系(2) ——切线的判定
离石区江阴高级中学初三数学备课组
回 顾 直线与圆的位置关系
相交
rd 相切
相离
判定切线的方法: 1. 与圆有唯一公共点的直线是圆的切线。 2.与圆心的距离等于半径的直线是圆的切线
探究
如图,OA是⊙O的半径,过A作
直线 l⊥OA,若设圆的半径为r,直
线 l是⊙O的切线吗,为什么?
直线和圆的位置关系及切线的性质PPT优秀版

当r = 4cm时,d<r, ⊙ C与AB相交. (来自教材)
知1-练
1 【中考·湘西州】在Rt△ABC中,∠C=90°,BC=
例②1切线[中和考圆·心梅的州距]如离图3等,于cAB半m是径⊙,. O的A弦C,A=C是4⊙Oc的m切,以点C为圆心,以2.5 cm为半径
D.50°
A若.A相B=切12,OA=5,画则B圆C的B,长.为相则(交 ⊙) C与直线AB的位置关系是( A )
(来自《点拨》)
知2-讲
导引: 如图,连接OA,根据切线的性质,先求出∠OAC =90°,再根据等腰三角形的性质和∠B=20°, 可以求出∠AOC=40°,最后根据直角三角形中 两锐角互余就可以求出∠C=50°. 答案:D
(来自《点拨》)
总结
知2-讲
(1)半径处处相等可得等腰三角形,从而底角相等; (2)切线垂直于过切点的半径得直角三角形,从而
两锐角互余.
(来自《点拨》)
知2-练
1 下列说法正确的是( C ) A.圆的切线垂直于半径 B.垂直于切线的直线经过圆心 C.经过圆心且垂直于切线的直线经过切点 D.经过切点的直线经过圆心
(来自《典中点》)
知2-练
2 【中考·吉林】如图,直线l是⊙O的切线,A为 切点,B为直线l上一点,连接OB交⊙O于点C. 若AB=12,OA=5,则BC的长为( D ) A.5 B.6 C.7 D.8
知1-导
思考: 设⊙O的半径为r,圆心O到直线l的距离为d,
在直线和圆的不同位置关系中,你能根据d与r的 大小关系确定直线和圆的位置关系吗?
知1-导
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么
关系?
r ●O ┐d
24.2.2直线和圆的位置关系(2)切线的判定与性质课件(新版)新人教版

求证:AB是⊙O的切线。
【典例精析,提炼方法】
3.归纳:上面的两道例题所添加的辅助线是否相同? 证明思路是否相同? 若不同应如何选用?
【拓展训练,能力提升】
1 、 已 知 : 如 图 , AB 是 ⊙ O 的 直 径 , P 是 ⊙ O 外 一 点 , PA⊥AB,• 弦BC ∥OP,请判断PC是否为⊙O的切线,说 明理由.
推理:圆心到直线的距离d =半径 r O A l 相切
经过半径的外端并且垂直于这条半径的直线是圆的 切线.
二、学习新知--切线的判定
思考:已知一个圆和圆上的一点A,如何过这个点画出圆的切线?
.O . A
l
第一步:连接OA; 第二步:过A点作OA的垂线l.
三、跟踪训练,理解判定
×
1. 过半径的外端的直线是圆的切线(
【拓展训练,能力提升】
【课堂小结,盘点收获】
(1)切线的判定定理与性质定理是什么?它们有怎样 的联系? (2)在应用切线的判定定理和性质定理时,需要注意 什么?
2. 与半径垂直的的直线是圆的切线( 3. 过半径的端点与半径垂直的直线是圆的切线(
O l r A O r A
) )
×
)
O l
×
l
r A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可: (1)直线经过 半径的外端; (2)直线与这半径垂直.
三、巩固训练,运用判定】
三、巩固训练,运用判定】
九年级
上册
24.2.2 直线和圆的位置关系(2) ——切线的判定与性质
• 学习目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题. • 学习重点: 切线的判定定理和性质定理的应用.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
●
C
A
D
议一议 7
切线的性质定理
• 圆的切线垂直于过切点的半径.
驶向胜 利彼岸
∵CD是⊙O的切线,A是切点,OA 是⊙O的半径,∴OA⊥CD.
注意:
学科网
●
O
D
切线的性质定理是证明两线 垂直的重要根据;作过切点的半径 是常做辅助线之一.
C
┑ A
例题欣赏 8
切线的性质定理的应用
如图:大圆的弦AB与小圆相切于点 C,AB=12m,求圆环的面积。
直线和圆的位置关系
----切线的判定定理和性质定理
复习回顾 1
直线与圆的位置关系
r
●
O ┐d
r
●
O
r
●
O
相交
d ┐ 相切
d ┐ 相离
• 直线和圆相交
d < r;
d = r;
直线和圆相切
直线和圆相离
d > r;
思考:怎样利用d=r,过圆上 一点画圆的切线?
1.连接OA
O
2.过A点做OA的垂线m
则直线m就是所求的切线
A
m
做一做
4
切线判定定理的应用
• 1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?
O
●
●
A
2.已知直线AB经过⊙O上的点 C,并且OA=OB,CA=CB,判定 直线AB是否为⊙O的切线,并 证明你的结论
O
A
CB议一议3切线的判定定理• 经过半径的外端,并且垂直于这条半径的直线是 圆的切线.
学科网
∵ OA是⊙O的半径,直线CD经过A 点,且CD⊥OA, ∴ CD是⊙O的切线.
●
O D
• 提示: • 切线的判定定理是证明一条直线是否是圆的切线的根 据;作过切点的半径是常用经验辅助线之一.
C
┑ A
3.应用: 例1 如图,AB是⊙O的直径,⊙O过BC的中点D, DE⊥AC. 求证:DE是⊙O的切线.
补充作业
10
挑战自我
驶向胜利 的彼岸
• 1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切 线,A,B是切点.请你观察猜想,PA,PB有怎样的关系? 并证明你的结论.
学科网
A
P B
●
O
作 业 :
课本习题 2、3、4题
结束寄语:
• 具有丰富知识和经验的人,比 只须一种知识和经验更容易产 生新的联想和独到的见解。
证明:连接OD. ∵BD=CD,OA=OB, ∴OD是△ABC的中位线. ∴OD//AC. ∵ DE⊥AC ∴∠DEC=90°, ∴ ∠ODE=90°.即OD⊥DE 又∵ D在圆周上, ∴ DE是⊙O的切线. C E D B A O
议一议
5
驶向胜利 的彼岸
探索切线性质
• 如图,直线CD与⊙O相切于点A,半径OA与直线CD 有怎样的位置关系?说说你的理由. • 半径OA⊥CD.
●
C
A
D
议一议 7
切线的性质定理
• 圆的切线垂直于过切点的半径.
驶向胜 利彼岸
∵CD是⊙O的切线,A是切点,OA 是⊙O的半径,∴OA⊥CD.
注意:
学科网
●
O
D
切线的性质定理是证明两线 垂直的重要根据;作过切点的半径 是常做辅助线之一.
C
┑ A
例题欣赏 8
切线的性质定理的应用
如图:大圆的弦AB与小圆相切于点 C,AB=12m,求圆环的面积。
直线和圆的位置关系
----切线的判定定理和性质定理
复习回顾 1
直线与圆的位置关系
r
●
O ┐d
r
●
O
r
●
O
相交
d ┐ 相切
d ┐ 相离
• 直线和圆相交
d < r;
d = r;
直线和圆相切
直线和圆相离
d > r;
思考:怎样利用d=r,过圆上 一点画圆的切线?
1.连接OA
O
2.过A点做OA的垂线m
则直线m就是所求的切线
A
m
做一做
4
切线判定定理的应用
• 1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?
O
●
●
A
2.已知直线AB经过⊙O上的点 C,并且OA=OB,CA=CB,判定 直线AB是否为⊙O的切线,并 证明你的结论
O
A
CB议一议3切线的判定定理• 经过半径的外端,并且垂直于这条半径的直线是 圆的切线.
学科网
∵ OA是⊙O的半径,直线CD经过A 点,且CD⊥OA, ∴ CD是⊙O的切线.
●
O D
• 提示: • 切线的判定定理是证明一条直线是否是圆的切线的根 据;作过切点的半径是常用经验辅助线之一.
C
┑ A
3.应用: 例1 如图,AB是⊙O的直径,⊙O过BC的中点D, DE⊥AC. 求证:DE是⊙O的切线.
补充作业
10
挑战自我
驶向胜利 的彼岸
• 1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切 线,A,B是切点.请你观察猜想,PA,PB有怎样的关系? 并证明你的结论.
学科网
A
P B
●
O
作 业 :
课本习题 2、3、4题
结束寄语:
• 具有丰富知识和经验的人,比 只须一种知识和经验更容易产 生新的联想和独到的见解。
证明:连接OD. ∵BD=CD,OA=OB, ∴OD是△ABC的中位线. ∴OD//AC. ∵ DE⊥AC ∴∠DEC=90°, ∴ ∠ODE=90°.即OD⊥DE 又∵ D在圆周上, ∴ DE是⊙O的切线. C E D B A O
议一议
5
驶向胜利 的彼岸
探索切线性质
• 如图,直线CD与⊙O相切于点A,半径OA与直线CD 有怎样的位置关系?说说你的理由. • 半径OA⊥CD.
