2020春七年级数学下册 第八章 一元一次不等式 8.3 一元一次不等式组和它的解(第1课时)课件 (新版)华东
七年级数学下册_8.3一元一次不等式组的应用(第2课时)课件_华东师大版

思路分析: (1)本题的不等关系是:
生产A、B两种产品所需的甲种原料≤360 生产A、B两种产品所需的乙种原料≤290 (2) 列表看各量的关系
A一件 Ax件 B一件 Bx件 A、B共需 甲种 乙种 9 3 9x 3x 4 10 4(50-x) 10(50-x) 9x+ 4(50-x) 3x+10(50-x) 9x+4(50-X)≤360 3x+10(50-x)≤290
例2: 某工厂现有甲种原料360kg,乙种原料290kg,计划 利用这两种原料生产A,B两种产品共50件,已知生产一 件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需 要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产 品可获利1200元,那么采用哪种生产方案可使生产A、 B两种产品的总获利最大?最大利润是多少?
9.某汽车租赁公司要购买轿车和面包 车共10辆,其中轿车至少要购买3辆, 轿车每辆7万元,面包车每辆4万元, 公司可投入的购车款不超过55万元; (1)符合公司要求的购买方案有几 种?请说明理由; (2)如果每辆轿车的日租金为200元, 每辆面包车的日租金为110元,假设新 购买的这10辆车每日都可租出,要使 这10辆车的日租金不低于1500元,那 么应选择以上那种购买方案?
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即:
4x+19-6(x-1)>0
4x+19-6(x-1)<6
解得: 18.5<x<12.5
因为x是整数,所以x=10,11,12.
人教版初中数学(1-28章)目录大全

人教版初中数学(1-28章)目录大全人教版七年级上册数学目录•第一章有理数• 1.1 正数和负数• 1.2 有理数• 1.3 有理数的加减法• 1.4 有理数的乘除法• 1.5 有理数的乘方•第二章整式的加减• 2.1 整式• 2.2 整式的加减•第三章一元一次方程• 3.1 从算式到方程• 3.2 解一元一次方程(一)——合并同类项与移项• 3.3 解一元一次方程(二)——去括号与去分母• 3.4 实际问题与一元一次方程•第四章几何图形初步• 4.1 几何图形• 4.2 直线、射线、线段• 4.3 角• 4.4 课题学习设计制作长方体形状的包装纸盒人教版七年级下冊数学目录•第五章相交线与平行线• 5.1 相交线• 5.2 平行线及其判定• 5.3 平行线的性质• 5.4 平移•第六章实数• 6.1 平方根• 6.2 立方根• 6.3 实数•第七章平面直角坐标系•7.1 平面直角坐标系•7.2 坐标方法的简单应用•第八章二元一次方程组•8.1 二元一次方程组•8.2 消元——解二元一次方程组•8.3 实际问题与二元一次方程组•8.4 三元一次方程组的解法•第九章不等式与不等式组•9.1 不等式•9.2 一元一次不等式•9.3 一元一次不等式组•第十章数据的收集、整理与描述•10.1 统计调查•10.2 直方图•10.3 课题学习从数据谈节水人教版八年级上冊数学目录•第十一章三角形•11.1与三角形有关的线段•11.2 与三角形有关的角•11.3 多边形及其内角和•第十二章全等三角形•12.1 全等三角形•12.2 三角形全等的判定•12.3 角的平分线的性质•第十三章轴对称•13.1 轴对称•13.2 画轴对称图形•13.3 等腰三角形•13.4 课题学习最短路径问题•第十四章整式的乘法与因式分解•14.1 整式的乘法•14.2 乘法公式•14.3 因式分解•第十五章分式•15.1 分式•15.2 分式的运算•15.3 分式方程人教版八年级下册数学目录•第十六章二次根式•16.1 二次根式•16.2 二次根式的乘除•16.3 二次根式的加减•第十七章勾股定理•17.1 勾股定理•17.2 勾股定理的逆定理•第十八章平行四边形•18.1 平行四边形•18.2 特殊的平行四边形•第十九章一次函数•19.1 函数•19.2 一次函数•19.3 课题学习选择方案•第二十章数据的分析•20.1 数据的集中趋势•20.2 数据的波动程度•20.3 课题学习体质健康测试中的数据人教版九年级上册数学目录•第二十一章一元二次方程•21.1 一元二次方程•21.2 解一元二次方程•21.3 实际问题与一元二次方程•第二十二章二次函数•22.1 二次函数的图象和性质•22.2 二次函数与一元二次方程•22.3 实际问题与二次函数•第二十三章旋转•23.1 图形的旋转•23.2 中心对称•23.3 课题学习图案设计•第二十四章圆•24.1 圆的有关性质•24.2 点和圆、直线和圆的位置关系•24.3 正多边形和圆•24.4 弧长和扇形面积•第二十五章概率初步•25.1 随机事件与概率•25.2 用列举法求概率•25.3 用频率估计概率人教版九年级下册数学目录•第二十六章二次函数•26.1 二次函数及其图象•26.2 用函数观点看一元二次方程•26.3 实际问题与二次函数•第二十七章相似•27.1 图形的相似•27.2 相似三角形•27.3 位似•第二十八章锐角三角函数•28.1 锐角三角函数•28.2 解直角三角形•第二十九章投影与视图•29.1 投影•29.2 三视图•29.3 课题学习制作立体模型。
一元一次不等式组课件华东师大版七年级数学下册

x–1>0
x–1<0
x–1>0
x–1<0
(1)
;(2)
x+1>3
;(3) x+1<3
;(4) x+1<3
x+1>3 .
分析: 根据解不等式组的步骤,先分别求解,再在数轴上表示即可.
解:(1) x – 1 > 0 ① x+1>3 ②
由 ① 得:x > 1; 由 ② 得:x > 2;
数轴表示:
–1 0 1 2 3 4
大小小大中间找 1 < x < 2 (大于小的数,小于大的数)
大大小小解不了 无解 (大于大的数,小于小的数)
四、合作探究
归纳总结 2
(1)解不等式组的一般步骤: ① 分别解每一个不等式; ② 在同一数轴上表示每个不等式的解集; ③ 找出各不等式解集的公共部分.
(2)在数轴上表示不等式的解集时应注意: ① 大于向右画,小于向左画; ② 有等号的画实心圆点,无等号的画空心圆圈.
第八章 一元一次不等式 8.3 一元一次不等式组
学习导航
学习目标 新课导入 自主学习 合作探究 课堂总结
一、学习目标
1. 掌握一元一次不等式组、一元一次不等式组的解集的概念; 2. 会用数轴确定由两个一元一次不等式组成的不等式组的解集. (重点)
二、新课导入
同学们的零花钱平时都花在哪?
ቤተ መጻሕፍቲ ባይዱ
零食饮料?
(4x + 20) – 8 (x – 1) < 8
解得:5 < x < 7;
根据题意,x 的值应是整数,所以 x = 6;4x + 20 = 44人.
华师大版七年级下册数学练习课件-第8章-8.2 3 第3课时一元一次不等式的解法

基础过关
1.下列不等式中,属于一元一次不等式的是( D )
A.3x-2>y
B.2x2>0
C.x3-2<1x
D.x7<x
2.已知12(m+4)x|m|-3+6>0 是关于 x 的一元一次不等式,则 m 的值为( A )
A.4
B.±4
C.3
D.±3
4
▪ 3.【2019·四川凉山中考】不等式1-x≥x-1C的解集是( ) ▪ A.x≥1 B.x≥-1 ▪ C.x≤1 D.x≤-1
第8章 一元一次不等式
8.2 解一元一次不等式
3 解一元一次不等式
第三课时 一元一次不等式的解法
名师点睛
▪ 知识点1 一元一次不等式
▪ 只含有一个未知数,并且含未知数的式子都是整式,未知数 的次数都是1的不等式叫做一元一次不等式.
▪ 提示:一元一次不等式的两边都应满足以下条件:(1)都是整 式;(2)只含有一个未知数(若有其他字母,按常数对待);(3) 未知数的次数都是1.
15.若代数式x-3 5+1 的值不小于x+2 1-1 的值,则 x 的取值范围是____x≤_-__1___.
12
16.小明解不等式1+2 x-2x+3 1≤1 的过程如下图. 解:去分母,得 3(1-x)-2(2x+1)≤1.① 去括号,得 3+3x-4x+1≤1.② 移项,得 3x-4x≤1-3-1.③ 合并同类项,得-x≤-3.④ 两边都除以-1,得 x≤3.⑤
5
▪ 4.【2019·辽宁大连中考】不等式5x+1≥3x-1的解集在数 轴B 上表示正确的是( )
6
5.关于 x 的方程 3x-2m=1 的解为正数,则 m 的取值范围是( B )
A.m<-12
B.m>-12
初中数学《一元一次不等式和一元一次不等式组》单元教学设计以及思维导图

一元一次不等式和一元一次不等式组
主题单元学习目标
知识与技能:
1、经历将一些实际问题抽象成不等式的过程,体会不等式也是刻画现实世界中量与量之间关系的有效数学模型进一步发展符号感。
2、能够根据具体问题中的大小关系了解不等式的意义。
3、掌握不等式的基本性质。
4、理解不等式组的解及解集的含义,会解简单的一元一次不等式并能在数轴上表示一元一次不等式的解集,会解一元一次不等式组并会在数轴上确定其解集,初步体会数形结合的思想。
其他:纸、笔
学习活动设计
活动一、
如下图,正方形的边长和圆的直径都是acm。
1、如果要使正方形的周长不大于25cm,那么 a 应满足怎样的关系式?
2、如果要使圆的周长不小于100cm,那么a 应满足怎样的关系式?
3、当 a= 8 时,正方形和圆的周长哪个大?a = 12 呢?
4、你能得到什么猜想?改变a的取值再试一试。
观察由上述问题得到的关系式,它们有什么共同特点?
由4a 4a4a≤25, πa ≥100 ,3x+5>240得,这些关系式都是用不等号连接的式子.由此
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式
活动二、。
人教版七年级下册数学期末考复习专题05一元一次不等式及不等式组(知识点串讲)(解析版)
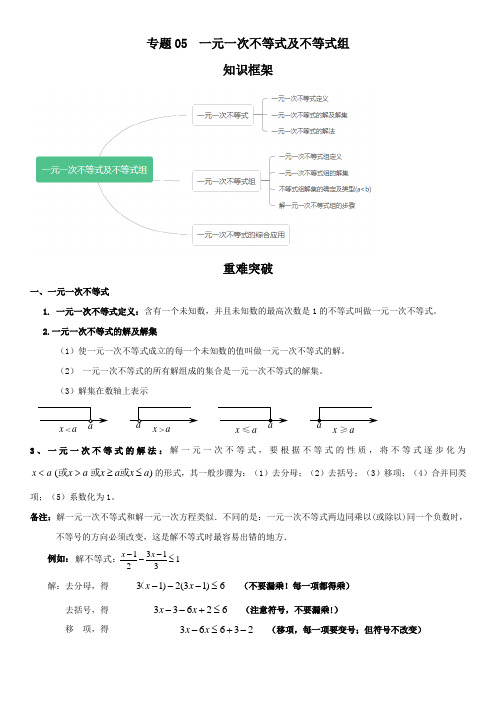
专题05 一元一次不等式及不等式组知识框架重难突破一、一元一次不等式1. 一元一次不等式定义:含有一个未知数,并且未知数的最高次数是1的不等式叫做一元一次不等式。
2.一元一次不等式的解及解集(1)使一元一次不等式成立的每一个未知数的值叫做一元一次不等式的解。
(2) 一元一次不等式的所有解组成的集合是一元一次不等式的解集。
(3)解集在数轴上表示3、一元一次不等式的解法:解一元一次不等式,要根据不等式的性质,将不等式逐步化为x a <(x a >或)x a x a ≥≤或或的形式,其一般步骤为:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1。
备注:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方.例如:131321≤---x x 解不等式: 解:去分母,得 6)13(2)13≤---x x ((不要漏乘!每一项都得乘) 去括号,得 62633≤+--x x (注意符号,不要漏乘!)移 项,得 23663-+≤-x x (移项,每一项要变号;但符号不改变)a a a a < > ≤ ≥合并同类项,得 73≤-x (计算要正确)系数化为1, 得 37-≥x (同除负,不等号方向要改变,分子分母别颠倒了) 例1.(2019·湖南广益实验中学初一期中)下列不等式中,是一元一次不等式的是( )A .1x >3B .x 2<1C .x +2y >0D .x <2x +1【答案】D【解析】解:A 、1x 是分式,因此1x>3不是一元一次不等式,故此选项不合题意; B 、x 2是2次,因此x 2<1不是一元一次不等式,故此选项不合题意;C 、x +2y >0含有2个未知数,因此不是一元一次不等式,故此选项不合题意;D 、x <2x +1是一元一次不等式,故此选项符合题意;故选:D .练习1.(2018·六安市裕安中学初一期中)下列不等式中,一元一次不等式有( )①2x 32x +> ②130x -> ③ x 32y -> ④x 15ππ-≥ ⑤ 3y 3>- A .1 个B .2 个C .3 个D .4 个 【答案】B【解析】详解:①不是,因为最高次数是2;②不是,因为是分式;③不是,因为有两个未知数;④是;⑤是.综上,只有2个是一元一次不等式.故选B .例2.(2019·洋县教育局初二期中)若437m x -+≤是关于x 的一元一次不等式,则m =__________.【答案】3【解析】解:∵437m x -+≤是关于x 的一元一次不等式,∴4-m =1,∴m=3,故答案为:3.练习1.(2019·山东省初二期中)已知12(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为()A.4 B.±4 C.3 D.±3【答案】A【解析】根据题意|m|﹣3=1且m+4≠0解得:|m|=4,m≠﹣4所以m=4.故选:A.例3.(2018·浙江省初二期中)一元一次不等式2(x﹣1)≥3x﹣3的解在数轴上表示为()A.B.C.D.【答案】B【解析】解: 2(x﹣1)≥3x﹣3去括号, 得2x-2≥3x-3,移项, 合并同类项, 得-x≥-1,得:x≤1故在数轴上表示为:故选B.练习1.(2020·万杰朝阳学校初一期中)如图,张小雨把不等式3x>2x-3的解集表示在数轴上,则阴影部分盖住的数字是____.【答案】-3【解析】由3x>2x-3,解得:x>-3,∴阴影部分盖住的数字是:-3.故答案是:-3.例4.(2020·监利县新沟新建中学初一期中)解不等式:14232-+->-x x . 【答案】x <−2【解析】解:去分母:2(x −1)−3(x +4)>−12,去括号:2x −2−3x −12>−12,合并同类项:−x >2,系数化1:x <−2. 练习1.(2018·福建省永春第二中学初一期中)解不等式3(21)x +<13(43)x --,并把解集在数轴上表示出来.【答案】x <2,数轴见解析【解析】去括号,得 6x +3<13-4+3x ,移项,得 6x -3x <13-4-3,即3x <6,两边同除以3,得x <2,在数轴上表示不等式的解集如下:例5.(2019·重庆市凤鸣山中学初一期中)关于x 的不等式22x a -+≥的解集如图所示,则a 的值是( )A .0B .2C .2-D .4- 【答案】A【解析】解:解不等式22x a -+≥,得22a x- ,∵由数轴得到解集为x ≤-1, ∴212a -=- ,解得:a =0. 故选:A .练习1.(2019·陕西省初二期中)不等式-4x -k ≤0的负整数解是-1,-2,那么k 的取值范围是( ) A .812k ≤<B .812k <≤C .23k ≤<D .23k <≤ 【答案】A【解析】解:∵-4x -k ≤0,∴x ≥-4k , ∵不等式的负整数解是-1,-2,∴-3<-4k ≤-2, 解得:8≤k <12,故选:A .二、一元一次不等式组1、一元一次不等式组定义: 含有同一个未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组。
8.3 一元一次不等式组 华东师大版数学七年级下册同步练习(含解析)

8.3 一元一次不等式组基础过关全练知识点1 一元一次不等式组及其解集1.(2020贵州毕节月考)下列是一元一次不等式组的是 ( )A.{2y −7<63x +3>1B.{x <1x >−2C.{x +2=63x +5>1D.{2a −7>13b +3=02.(2022广西梧州中考)不等式组{x >−1,x <2的解集在数轴上表示为( )A B C D3.(2022湖北十堰中考)关于x 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .4.【新独家原创】已知a 、b 在数轴上的对应位置如图所示,则(1)不等式组{x >a,x >b 的解集是 ;(2)不等式组{x >a,x <b的解集是 ;(3)不等式组{x <a,x >b 的解集是 ;(4)不等式组{x <a,x <b的解集是 .5.【新独家原创】【跨学科·生物】某中学生物兴趣小组利用课后服务的时间,在恒温箱中培养甲、乙两种菌种,通过观察发现,甲菌种适合的生长温度是32 ℃~36 ℃;乙菌种适合的生长温度是33 ℃~37 ℃,为了节约资源,兴趣小组决定将两种菌种放入同一恒温箱中,那么为了使两种菌种都生长良好,恒温箱的温度t (℃)应该设定的范围是 .知识点2 一元一次不等式组的解法 6.(2022山西中考)不等式组{2x +1≥3,4x −1<7的解集是( )A .x ≥1B .x <2C .1≤x <2D .x <127.(2022山东滨州中考)把不等式组{x −3<2x,x+13≥x−12中每个不等式的解集在同一条数轴上表示出来,正确的为( )A B C D8.【新独家原创】关于x 的不等式组{2x−13−5x+12≤1,x −1>a 的解集是x ≥-1,则a 的取值范围是( )A.a >-2B.a ≥-2C.a <-2D.a ≤-29.(2022四川宜宾中考)不等式组{3−2x ≥5,x+22>−1的解集为 .10.(1)(2022四川自贡中考)解不等式组:{3x <6,5x +4>3x +2,并在数轴上表示其解集;(2)(2022福建宁德古田期中)解不等式组:{3x −2<4,2(x −1)≤3x +1,并把它的解集在数轴上表示出来;(3)(2022福建三明尤溪期中)解不等式组:{x ≥3−2x,x−12−x−36<1,并把解集表示在数轴上;(4)(2022河南南阳新野期中)解不等式组:{x −4≤32(x −1),2x −3x+12<1,并把它的解集在数轴上表示出来.能力提升全练11.(2021湖南邵阳中考,7,)下列数值不是不等式组{5x −1>3x −4,−13x ≤23−x的整数解的是( )A.-2B.-1C.0D.1 12.(2022福建南平模拟,8,)如图,在数轴上A ,B ,C ,D 四个点所表示的数中是不等式组{x −1<2x,x 2≤0的解的是( )A.点A 表示的数B.点B 表示的数C.点C 表示的数D.点D 表示的数 13.(2022湖南邵阳中考,10,)关于x 的不等式组{−13x >23−x,12x −1<12(a −2)有且只有三个整数解,则a 的最大值是 ( )A.3B.4C.5D.6 14.(2022四川成都七中育才学校模拟,8,)若关于x 的一元一次不等式组{x +8<5x,x −1>m的解集为x >2,则m 的取值范围是( )A.m >1B.m ≤1C.m <1D.m ≥115.【易错题】(2022重庆北碚西南大学附中月考,10,)若关于x 的不等式组{x−23≤m,x −12>3−2x 无解,则m 的取值范围是( )A.m >1B.m ≥1C.m <1D.m ≤116.(2022黑龙江龙东地区中考,15,)若关于x 的一元一次不等式组{2x −1<3,x −a <0的解集为x <2,则a 的取值范围是 . 17.(2022四川成都青羊石室中学月考,12,)若关于x 的不等式组{2x −b ≥0,x +a ≤0的解集为3≤x ≤4,则a +b 的值为 . 18.(2022四川成都双流实验中学期中,16,)若关于x ,y 的二元一次方程组的解满足{2x +y =−m +5,x −y =4m −2,且x +y ≤0,求m 的取值范围.素养探究全练19.【运算能力】【新独家原创】若不等式组{x−52<3a,x−a3≥1无解,求a 的取值范围.20.【运算能力】(2022河南南阳南召期中)阅读下列材料:求不等式(2x -1)(x +1)>0的解集.解:根据“同号两数相乘,积为正”可得①{2x −1>0,x +1>0或 ②{2x −1<0,x +1<0.解不等式组①得x >12;解不等式组②得x <-1,∴不等式的解集为x >12或x <-1.请你仿照上述方法解决下列问题. (1)求不等式(2x -3)(x +3)<0的解集; (2)求不等式13x−1x+2≥0的解集.答案全解全析基础过关全练1.B 根据一元一次不等式组的定义知,{x <1,x >−2是一元一次不等式组.故选B.2.C 不等式组{x >−1,x <2的解集为-1<x <2,在数轴上表示为C.3. 答案 0≤x <1解析 由题图可知该不等式组的解集为0≤x <1. 4. 答案 (1)x >b (2)a <x <b (3)空集 (4)x <a解析 由数轴知,a <b ,所以{x >a,x >b 的解集是x >b ;不等式组{x >a,x <b 的解集是a <x <b ;不等式组{x <a,x >b 无解;不等式组{x <a,x <b的解集是x <a. 5. 答案 33≤t ≤36解析 甲菌种适合的生长温度是32 ℃~36 ℃,乙菌种适合的生长温度是33 ℃~37 ℃,则{32≤t ≤36,33≤t ≤37,∴33≤t ≤36.6.C 解不等式2x +1≥3,得x ≥1,解不等式4x -1<7,得x <2,则不等式组的解集为1≤x <2,故选C.7.C 解不等式x -3<2x ,得x >-3,解不等式x+13≥x−12,得x ≤5,故原不等式组的解集是-3<x ≤5,其解集在数轴上表示为C.8.C {2x−13−5x+12≤1①,x −1>a ②,解不等式①得x ≥-1,解不等式②得x >a +1,由题意得a +1<-1,解得a <-2.9. 答案 -4<x ≤-1解析 {3−2x ≥5①,x+22>−1②,解不等式①,得x ≤-1,解不等式②,得x >-4,故原不等式组的解集为-4<x ≤-1.10.解析 (1)由不等式3x <6,得x <2,由不等式5x +4>3x +2,得x >-1,∴不等式组的解集为-1<x <2. 解集在数轴上表示如下:(2)由3x -2<4,得x <2,由2(x -1)≤3x +1,得x ≥-3,则不等式组的解集为-3≤x <2.解集在数轴上表示如下:(3)由x ≥3-2x ,得x ≥1,由x−12−x−36<1,得x <3,∴不等式组的解集是1≤x <3.解集在数轴上表示如下:(4)由x -4≤32(x -1),得x ≥-5,由2x -3x+12<1,得x <3,则不等式组的解集为-5≤x <3.解集在数轴上表示如下:能力提升全练11.A {5x −1>3x −4①,−13x ≤23−x ②,解不等式①,得x >-32,解不等式②,得x ≤1, ∴不等式组的解集为-32<x ≤1,∴不等式组的整数解为-1,0,1,故选A.12.B 由x -1<2x ,得x >-1,由x2≤0,得x ≤0,则不等式组的解集为-1<x ≤0,符合此范围的为B 表示的数,故选B.13.C {−13x >23−x ①,12x −1<12(a −2)②,由①得x >1,由②得x <a ,∴1<x <a ,∵不等式组有且只有三个整数解,即2,3,4,∴4<a ≤5,∴a 的最大值是5,故选C. 14.B 由x +8<5x ,得x >2,由x -1>m ,得x >m +1,∵不等式组的解集为x >2,∴m +1≤2,解得m ≤1,故选B. 15.D 由x−23≤m ,得x ≤3m +2,由x -12>3-2x ,得x >5,∵不等式组无解,∴3m +2≤5,解得m ≤1,故选D.本题的易错之处是对端点值的取舍. 16. 答案 a ≥2解析 由2x -1<3,得x <2,由x -a <0,得x <a ,∵不等式组的解集为x <2, ∴a ≥2.故答案为a ≥2. 17. 答案 2解析 由2x -b ≥0,得x ≥b2,由x +a ≤0,得x ≤-a ,∴b2≤x ≤-a ,∵不等式组的解集为3≤x ≤4,∴b2=3,-a =4,解得a =-4,b =6,则a +b =-4+6=2.故答案为2.18.解析 解方程组得{x =m +1,y =−3m +3,∵x +y ≤0,∴m +1-3m +3≤0,解得m ≥2.素养探究全练19.解析{x−52<3a ①,x−a3≥1②,解不等式①得x <6a +5,解不等式②得x ≥a +3,因为不等式组无解,所以6a +5≤a +3,解得a ≤-25.20.解析 (1)根据“异号两数相乘,积为负”可得①{2x −3>0,x +3<0或②{2x −3<0,x +3>0.不等式组①无解,解不等式组②,得-3<x <32,∴原不等式的解集为-3<x <32.(2)根据“同号两数相除,商为正”可得①{13x −1≥0,x +2>0或②{13x −1≤0,x +2<0.解不等式组①,得x ≥3,解不等式组②,得x <-2,∴原不等式的解集为x ≥3或x <-2.。
2023七年级数学下册第8章一元一次不等式8

+7
≤3(x-1)+4,
2
去分母,得x+7≤6(x-1)+8.
去括号,得x+7≤6x-6+8.
移项、合并同类项,得-5x≤-5.
两边都除以-5,得x≥1.
这个不等式的解集在数轴上表示如下:
5. [2020河北中考]已知两个有理数:-9和5.
(1)计算:
(−9)+5
.
2
(2)若再添一个负整数m,且-9,5与m这三个数的平均数仍小于m,求m的值.
2+1
−1
≤2+
;
3
2
+7
≤3(x-1)+4.
2
(2)
答案
4.解:(1)1-
2+1
−1
≤2+
,
3
2
去分母,得6-2(2x+1)≤12+3(x-1).
去括号,得6-4x-2≤12+3x-3.
移项、合并同类项,得7x≥-5.
5
两边都除以7,得x≥-7.
这个不等式的解集在数轴上表示如下:
(2)
因为关于x的不等式x+2m≥0不是2x-3<x+m的“云不等式”,
所以-2m≥m+3,解得m≤-1.
故m的取值范围是m≤-1.
(3)解不等式x+3≥a,得x≥a-3,
解不等式ax-1<a-x,得(a+1)x<a+1.
①当a+1>0,即a>-1时,x<1.
依题意得a-3<1,即a<4,故-1<a<4.
合并同类项,得2x+2>0.
