2011年中考第一轮复习课件精品第1讲实数
合集下载
数学中考一轮复习专题01 实数(课件)
知识点梳理
6．实数的比较大小： （1）性质比较法：
①正数>0>负数； ②两个正数，绝对值大的较大；两个负数，绝对值大的反而 小 ； ③若一组数据中有正数，0，负数，求最大的数时在正数中找，求最小的数时在负数
中找． （2）数轴比较法：数轴上的两个点表示的数，右边的数总比左边的数 大 ．
（3）差值比较法：对于任意实数a，b：a-b>0⇔ a>b ；a-b=0⇔ a=b ；a-b<0⇔
的关键．
知识点1 ：实数的有关概念
典型例题
【例5】（3分）（2021•通辽1/26）| -2 |的倒数是（ ）
A．2
B．1
C．-2
D． 1
2
2
【考点】绝对值；倒数
1
【解答】解：| -2 |的倒数是 ．
2
故选：B．
【点评】主要考查倒数的定义，要求熟练掌握．需要注意的是倒数的性质：负数的
倒数还是负数，正数的倒数是正数，0没有倒数．倒数的定义：若两个数的乘积是1，
我们就称这两个数互为倒数．
知识点1 ：实数的有关概念
典型例题
【例6】（3分）（2021•天津6/25）估计 17 的值在（ ） A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间
【考点】估算无理数的大小 【分析】本题需先根据 17 的整数部分是多少，即可求出它的范围． 【解答】解：∵ 17 4.12 ， ∴ 17 的值在4和5之间． 故选：C． 【点评】本题主要考查了估算无理数的大小，在解题时确定无理数的整数部分即可 解决问题．
3 非负数
掌握非负数的性质，能求某 非负数性质的运用． 些特殊等式中字母的值． 常以选择题、填空题的形式命题．
中考命题说明
6．实数的比较大小： （1）性质比较法：
①正数>0>负数； ②两个正数，绝对值大的较大；两个负数，绝对值大的反而 小 ； ③若一组数据中有正数，0，负数，求最大的数时在正数中找，求最小的数时在负数
中找． （2）数轴比较法：数轴上的两个点表示的数，右边的数总比左边的数 大 ．
（3）差值比较法：对于任意实数a，b：a-b>0⇔ a>b ；a-b=0⇔ a=b ；a-b<0⇔
的关键．
知识点1 ：实数的有关概念
典型例题
【例5】（3分）（2021•通辽1/26）| -2 |的倒数是（ ）
A．2
B．1
C．-2
D． 1
2
2
【考点】绝对值；倒数
1
【解答】解：| -2 |的倒数是 ．
2
故选：B．
【点评】主要考查倒数的定义，要求熟练掌握．需要注意的是倒数的性质：负数的
倒数还是负数，正数的倒数是正数，0没有倒数．倒数的定义：若两个数的乘积是1，
我们就称这两个数互为倒数．
知识点1 ：实数的有关概念
典型例题
【例6】（3分）（2021•天津6/25）估计 17 的值在（ ） A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间
【考点】估算无理数的大小 【分析】本题需先根据 17 的整数部分是多少，即可求出它的范围． 【解答】解：∵ 17 4.12 ， ∴ 17 的值在4和5之间． 故选：C． 【点评】本题主要考查了估算无理数的大小，在解题时确定无理数的整数部分即可 解决问题．
3 非负数
掌握非负数的性质，能求某 非负数性质的运用． 些特殊等式中字母的值． 常以选择题、填空题的形式命题．
中考命题说明
人教板中考数学 第一轮复习 实数(共17张PPT)
有理数的运算律 ：
加法交换律： a+b=b+a 加法结合律： (a+b)+c=a+(b+c) 乘法交换律： a×b=b×a 乘法结合律 ： （a×b）×c=a×(b×c) 乘法分配律 ： a×(b+c)=a×b+a×c (a,b,c表示 任意有理数) 思想方法 ： 数形结合 ，分类讨论。
实数是初中数学教学的基础内容， 中考重点考查实数基本运算，中考此 部分知识的考查多以选择、填写为主， 题目简单，属于基础问题。另外出现 了趣味性考题考查有理数，估计无理 数大小等。
A. B. C. 0 D. -1.010101
填空题
1.-2009 的相反数__2_0_0_9__.
2.︱-1023︱=___1_0_2_3___.
3.一个正数的两个平方根分别是x+1和x-5，则 x=____2__
4.27的立方根是__3___. _
5.已知a，b满足（a-1）2+ b + 2=0,则a+b=__-1_____.
5. 科学记数法：把一个数写成a×10n的形式其中1≤a<10， n是整数。这种记数法叫做科学记数法。 6. 大小比较：正数大于0，负数小于0，两个负数，绝对 值大的反而小。
7. 数的乘方：求相同因数的积的运算叫乘方，乘方运算 的结果叫幂。
8.平方根：一般地，如果一个数x的平方等于a，即x2=a 那么这个数x叫做a的平方根也叫做二次方根。一个正数 有两个平方根，它们互为相反数；0只有一个平方根，它 是0本身；负数没有平方根。
7.下列各式中，正确的是 （ D ）
A. 9 =±3 B. (- 3)2=-3 C. 3 9 =3 D. 12 - 3 = 3
中考第一轮复习--第一章数与式
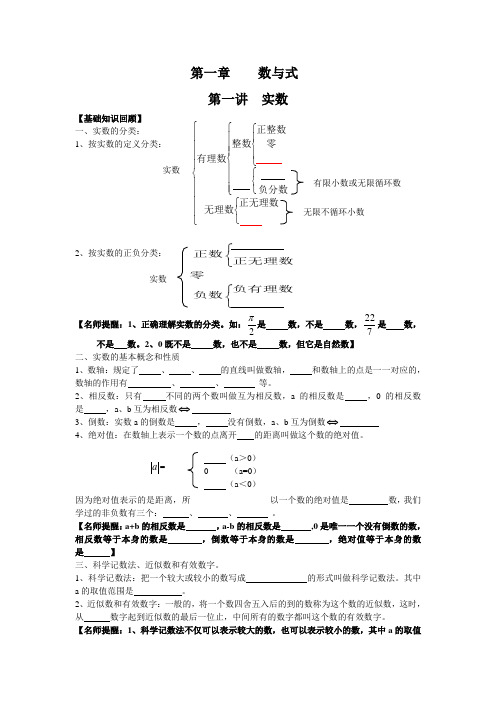
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类： 1、按实数的定义分类： 实数 有限小数或无限循环数2、按实数的正负分类：实数【名师提醒：1、正确理解实数的分类。
如：2π是 数，不是 数，722是 数，不是 数。
2、0既不是 数，也不是 数，但它是自然数】二、实数的基本概念和性质1、数轴：规定了 、 、 的直线叫做数轴， 和数轴上的点是一一对应的，数轴的作用有 、 、 等。
2、相反数：只有 不同的两个数叫做互为相反数，a 的相反数是 ，0的相反数是 ，a 、b 互为相反数⇔3、倒数：实数a 的倒数是 ， 没有倒数，a 、b 互为倒数⇔4、绝对值：在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离，所以一个数的绝对值是 数，我们学过的非负数有三个： 、 、 。
【名师提醒：a+b 的相反数是 ，a-b 的相反数是 ,0是唯一一个没有倒数的数，相反数等于本身的数是 ，倒数等于本身的数是 ，绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法：把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从 数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。
【名师提醒：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 （a ＞0） （a ＜0） 0 （a=0）范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。
最新人教版数学中考一轮复习第1讲实数的有关概念课件
ห้องสมุดไป่ตู้
第1讲┃实数的有关概念
解 析 第1行的第1列与第2列差个2，第2列与第3列差个3，第3
列与第4列差个4，…，第6列与第7列差个7；
第1讲┃实数的有关概念
(1)求一个数的相反数，直接在这个数的前面加上负 号，有时需要化简得出． (2)一个负数的绝对值等于它的相反数．反过来，一 个数的绝对值等于它的相反数，则这个数是非正数． (3)解绝对值和数轴的有关问题时常用到字母表示数 的思想、分类讨论思想和数形结合思想．
第1讲┃实数的有关概念
第1讲┃实数的有关概念
对无理数的判定，不能只被表面形式迷惑， 而应从最后结果去判断．一般来说，用根号表示 的数不一定就是无理数，如 3 27＝3 是有理数， 用三角函数符号表示的数也不一定就是无理数， 如sin30°、tan45°也不是无理数，一个数是不 是无理数关键在于不同形式表示的数的最终结果 是不是无限不循环小数．
第1讲┃实数的有关概念
考点2 实数的有关概念 正方向和__________ 原点 、________ 单位长度 1．数轴：规定了________
的直线。数轴上的点与实数一一对应。 符号 ， 2． 相反数： a 的相反数为________ 0 的相反数是 0。
乘积 是 1 的两个数互为倒数。0 没有 3．倒数：________
探究三 科学记数法
命题角度： 用科学记数法表示数． 例3 [2013²邵阳] 据邵阳市住房公积金管理会 议透露，今年我市新增住房公积金11.2亿元，其中 11.2亿元可用科学记数法表示为( B ) A．11.2³108元 B．1.12³109元 C．0.112³1010元 D．112³107元
解 析 1亿＝108，11.2亿＝1.12³109。
第1讲┃实数的有关概念
解 析 第1行的第1列与第2列差个2，第2列与第3列差个3，第3
列与第4列差个4，…，第6列与第7列差个7；
第1讲┃实数的有关概念
(1)求一个数的相反数，直接在这个数的前面加上负 号，有时需要化简得出． (2)一个负数的绝对值等于它的相反数．反过来，一 个数的绝对值等于它的相反数，则这个数是非正数． (3)解绝对值和数轴的有关问题时常用到字母表示数 的思想、分类讨论思想和数形结合思想．
第1讲┃实数的有关概念
第1讲┃实数的有关概念
对无理数的判定，不能只被表面形式迷惑， 而应从最后结果去判断．一般来说，用根号表示 的数不一定就是无理数，如 3 27＝3 是有理数， 用三角函数符号表示的数也不一定就是无理数， 如sin30°、tan45°也不是无理数，一个数是不 是无理数关键在于不同形式表示的数的最终结果 是不是无限不循环小数．
第1讲┃实数的有关概念
考点2 实数的有关概念 正方向和__________ 原点 、________ 单位长度 1．数轴：规定了________
的直线。数轴上的点与实数一一对应。 符号 ， 2． 相反数： a 的相反数为________ 0 的相反数是 0。
乘积 是 1 的两个数互为倒数。0 没有 3．倒数：________
探究三 科学记数法
命题角度： 用科学记数法表示数． 例3 [2013²邵阳] 据邵阳市住房公积金管理会 议透露，今年我市新增住房公积金11.2亿元，其中 11.2亿元可用科学记数法表示为( B ) A．11.2³108元 B．1.12³109元 C．0.112³1010元 D．112³107元
解 析 1亿＝108，11.2亿＝1.12³109。
中考数学总复习第1讲实数及其有关概念课件
实数的有关概念 1 C. 4 1 D．－ 4
1．(2016· 葫芦岛 1 题 3 分)4 的相反数是( B ) A ．4 B．－4
2．(2016· 丹东 1 题 3 分)－3 的倒数是( C ) A ．3 1 B. 3 1 C．－ 3 D．－3
3．(2015· 丹东 1 题 3 分)－2015 的绝对值是( B ) A．－2015 B．2015 1 1 C. D．－ 2015 2015
2 解：原式＝ 2－1＋2× －4－2 2 ＝2 2－7.
1.实数的运算
试题 (2016· 泸州)计算：( 2－1)0－ 12×sin60°＋(－2)2. 本题考查实数的运算，先分别计算出每一项的值，再根据实
审题视角
数混合运算的顺序进行计算，即先乘除，再加减，同级运算，按从左向 右进行计算． 规范答题
1.实数运算中的常见错误
试题 错解 1－ 3 计算：|1－ 2|＋2×cos45°－( ) 2＋ －8. 2 解：原式＝1－ 2＋2× 2 －(－4)＋2 2
＝1＋4＋2 ＝7. 剖析 (1)去绝对值符号时，要考虑是否变号，即要判断绝对值符号内数 据的正负；(2)负整数指数幂，指数是偶数则结果为正；(3)立方根的运算 中，正数的立方根为正数，负数的立方根为负数． 正解
4．实数的大小比较 (1)数轴比较法：数轴上的两个数，右边的数总大于左边的数； (2)代数比较法：正数＞0＞负数，两个负数比较大小，绝对值大的反而小； (3)差值比较法：①a－b＞0⇔a＞b；②a－b＝0⇔a＝b； ③a－b＜0⇔a＜b； a a a (4)求商比较法：若 b＞0，则① ＞1⇔a＞b；② ＝1⇔a＝b；③ ＜1⇔a＜ b b b b； 1 1 (5)倒数比较法：若 ＞ 且 a 与 b 同号时，a＜b； a b (6)平方比较法：对于任意正实数 a， b有 a2＞b⇔a＞ b.
中考数学一轮复习课件-第一讲实数
A.-1
B.0
C.0.5
D. 7
5. 1 的倒数是___2___.
2
6.比较大小:-1___<___2(填“>”或“<”). 7.梅州水资源丰富,水力资源的理论发电量为775 000千瓦,这个数据用科学记 数法可表示为___7_._7_5_×__1_0_5____千瓦.
高频考点·疑难突破
考点一 实数的有关概念
第一讲 实 数
一、有理数的有关概念
1.数轴:规定了原点、正方向、___单__位__长__度____的直线.
2.相反数:a的相反数是___-_a___.互为相反数的两个数的和是___0___.
1
3.倒数:乘积为___1___的两个数互为倒数,a(a≠0)的倒数是____a ___,___0___没
有倒数.
【示范题1】(1)(202X·玉林中考)2的倒数是
A. 1
B.- 1
C.2
2
2
(A) D.-2
(2)(202X·桂林中考)有理数2,1,-1,0中,最小的数是 ( C )
A.2
B.1
C.-1
D.0
【答题关键指点】 1.a,b互为相反数⇔a+b=0. 2.a,b互为倒数⇔ab=1. 3.倒数、相反数等于本身的数分别为±1和0. 4.若|a|=a,则a≥0,|a|=-a,则a≤0.
a（a＞0），
4.绝对值:(1)从“数”的角度看: a （0 a 0），
___a_（a＜0）.
(2)从“形”的角度看:一个数的绝对值就是表示这个数的点到___原__点____的距 离. 二、科学记数法 科学记数法的一般情势:把一个数写成___a_×__1_0_n__的情势(其中___1___≤ |a| < 10 ,n为整数).
中考数学第一轮复习精品课件第一章 第1讲实数
C．4.5×105
D．0.45×106
2．数轴上的点 A 到原点的距离是 3，则点 A 表示的数为 ( A ) A．3 或－3 C．－3
B．3
D．6 或－6
3．如果规定收入为正，支出为负．收入 500 元记作＋500 元，那么支出 237 元应记作( B ) A．－500 元 C．237 元 B．－237 元 D．500 元
第一章
数与式
第1讲 实数
1．了解无理数和实数的概念，理解实数的意义，能用数轴 上的点表示实数，会比较实数的大小．知道实数与数轴上的点 一一对应． 2．借助数轴理解相反数和绝对值的意义，会求实数的相反 数与绝对值(绝对值符号内不含字母)． 3．理解乘方的意义，会用科学记数法表示数，掌握实数的 加、减、乘、除、乘方及简单的混合运算(以三步为主)．
4．0 的特殊性．
0 (1)0 的相反数是__________ ．
0 (2)0 的绝对值是__________ ．
倒 (3)0 没有________ 数．
【学有奇招】 1．对于实数的概念，关键记住无理数的概念．在实数中只 有无限不循环小数是无理数，其他都是有理数．常见的无理数 有三种：①有规律但不循环的数，例如：0.101 001 000 100
π 001…；②π 及其衍生出来的数，例如：3π，2等；③含有根号 2 但开不尽方的数，例如： 2， 5， 2 等． 3
2．有理数的加法运算口诀：同号相加一边倒；异号相加 “大”减“小”，符号跟着大的跑；绝对值相等“零”正好． 注意：“大”减“小”是指绝对值的大小．
1．5 月的某一天，参观上海世博会的人数达到 450 000， 用科学记数法表示这个数为( C ) A．45×104 B. 4.5×106
实数中考总复习原创课件
解：
课后训练
1. －7的相反数是______；－7的倒数是______； 的绝对值是 ；绝对值是 的数是 _____ .
3.用科学记数法表示： 3 040 000＝ ___________； 0.00 507＝___________； －805 000＝___________； 25.6万＝___________.
【考点1】实数的有关概念
由已知，得a+b=0，cd=1.∴原式= =2x|＝0，求 的值
∵一个数的绝对值为非负数，∴x+2=0，y－2x=0.解得x=－2，y=－4.∴原式=
解：
【考点2】实数的运算
【例2】已知2x－1的平方根是±3，x－y－9的 立方根2，求|x2－y2|的值.
0
1
a
0
－a
a
－a
取相同的符号，并把 绝对值相加
取绝对值较大的符号，并把较大的绝对值减去较小的绝对值
相反数
（3）乘、除法：两数相乘或相除，同号得正， 异号得______， 并把它们的绝对值相乘或相除.（4）乘方：表示几个相同因数的________； a0＝________，a－n＝________(a≠0，n是正整数).（5）开方：如果x2＝a，那么x是a的________，记作 x＝________，a的算术平方根表示为________； 如果x3＝a，那么x是a的________，记作x＝________.
解：
原式=
=
= 1
解：
原式=
=
=
(4)
10．已知a满足： 求 a＋2 0192 的值．
由已知，得2 018－a≥0，解得a≤2 018，原等式化简为2 019－a－ =－a ，∴ =2 019，两边平方得 2 018－a=2 0192，∴ a+2 0192 =2 018.
课后训练
1. －7的相反数是______；－7的倒数是______； 的绝对值是 ；绝对值是 的数是 _____ .
3.用科学记数法表示： 3 040 000＝ ___________； 0.00 507＝___________； －805 000＝___________； 25.6万＝___________.
【考点1】实数的有关概念
由已知，得a+b=0，cd=1.∴原式= =2x|＝0，求 的值
∵一个数的绝对值为非负数，∴x+2=0，y－2x=0.解得x=－2，y=－4.∴原式=
解：
【考点2】实数的运算
【例2】已知2x－1的平方根是±3，x－y－9的 立方根2，求|x2－y2|的值.
0
1
a
0
－a
a
－a
取相同的符号，并把 绝对值相加
取绝对值较大的符号，并把较大的绝对值减去较小的绝对值
相反数
（3）乘、除法：两数相乘或相除，同号得正， 异号得______， 并把它们的绝对值相乘或相除.（4）乘方：表示几个相同因数的________； a0＝________，a－n＝________(a≠0，n是正整数).（5）开方：如果x2＝a，那么x是a的________，记作 x＝________，a的算术平方根表示为________； 如果x3＝a，那么x是a的________，记作x＝________.
解：
原式=
=
= 1
解：
原式=
=
=
(4)
10．已知a满足： 求 a＋2 0192 的值．
由已知，得2 018－a≥0，解得a≤2 018，原等式化简为2 019－a－ =－a ，∴ =2 019，两边平方得 2 018－a=2 0192，∴ a+2 0192 =2 018.