08-09第2学期高数A试卷A

合集下载

08-09-2高数试卷A(2)(A考试卷)共6页word资料

广东工业大学考试试卷 (A)
课程名称: 高等数学A(2) 试卷满分 100 分
考试时间: 2009年6月29日 (第20周星期一)
题号一二三四五六七八九十总分评卷得分评卷签名
复核得分复核签名一、填空题：（每小题4分，共20
分）
1．设，，令. 则向量的方向余弦为：。

2．曲面在点处的切平面方程为：。

3．设区域，则 = 。

4．设是由方程所确定的隐函数，其中具有
连续的偏导数，且，则。

5．设是周期为的周期函数，它在区间上的定义为
，则的傅里叶级数在处收敛于________．
二、选择题：（每小题4分，共20分）
1．平面的位置是（）.
A.平行于轴.
B.斜交于轴
C.垂直于轴.
D.通过轴.
2. 考虑二元函数的下面4条性质：
①在点处连续；②在点处的两个偏导数连续；
③在点处可微；④在点处的两个偏导数存在．
若用“”表示可由性质推出性质，则有（）
第 1 页
A ②③①；
B ③②①；
C ③④①；
D ③①④
学院：专业：学号：
姓名：
装订线
第 2 页
希望以上资料对你有所帮助，附励志名言3条：
1、生命对某些人来说是美丽的，这些人的一生都为某个目标而奋斗。

2、推销产品要针对顾客的心，不要针对顾客的头。

3、不同的信念，决定不同的命运。

第 6 页。

2008-2009年第二学期A2(基础要求层次)高数试卷答案答案

中国矿业大学徐海学院2008－2009学年第二学期《高等数学》试卷（A2）卷答案一、 AADAC 二、1.π 2.{(,)0,0}x y x x y >+> 3、24 4、3 5、（1，－2）三、1．（8分）计算二重积分22()Dx y dxdy +⎰⎰，其中2222:2,4D x y x x y x +≥+≤。

452π2．（6分）v u z ln 2=，x y u =，22y x v +=，求x z ∂∂,yz ∂∂。

解：⎥⎦⎤⎢⎣⎡+-+=)ln(22222232y x y x x x y z x ， ⎥⎦⎤⎢⎣⎡+++=)ln(2222222y x y x y xy z y 3、（8分）将13x+展开成x -2的幂级数. 解：2345234511111...........(1).......................(2)11111122[1()235(2)555515222()()()...........].. (555)(2)(1)5n n nn x x x x x x x x x x x x x x x x +-∞==-+-+-+<+--∴===-+-++-+----+-+-=-∑分（4分）或者2(137) (5)x x -<-<<即（2分）4、（8分）计算曲线积分dy y x x y dx x y xy L)3sin 21()cos 2(2223+-+-⎰，其中L 为在抛物线22y x ⋅=π 上由点（0，0）到)1,2(π的一段弧。

解：xQx y xy y P ∂∂=-=∂∂cos 262，积分与路径无关，故可以换路径为：AB OA →，其中)1,2(),0,2(ππB A在OA 上：x y ,0=从0变化到2π， 0)3sin 21()cos 2(2223=+-+-⎰dy y x x y dx x y xy OA；在AB 上：y x ,2π=从0变化到1，4)3sin 21()cos 2(22223π=+-+-⎰dy y x x y dx x y xy AB；所以：原式=42π。

浙江理工大学2008~2011各学年《高等数学A》期末试题合集[卷]

浙江理工大学2008~2009学年第二学期高等数学A 期终试题（A ）卷班级学号姓名题号一二三四五六七总分 1 2 3 1 2 得分阅卷教师一、选择题（每小题4分，满分28分）1、旋转抛物面2224z x y =+- 在点(1,1,1)--处的切平面方程为（）(A) 240x y z +-= (B) 244x y z --= (C) 244x y z +-= (D) 247x y z --= ２、二重积分2Dxydxdy ⎰⎰（其中2:0,01D y x x ≤≤≤≤）的值为（） (A)16 (B) 12 (C) 112(D) 14 3、微分方程23cos2x y y y ex -'''++=的特解应具有形式（） (A)(cos sin );xe a x b x -+ (B) sin cos ;xxe bx x aex --+(C) 233(cossin );22xea xb x -+ (D) 233(cos sin );22x xe a x b x -+ 4、设L 是从A (1,0)到B (1,2)-的直线段，则()222Lxxy y ds -+=⎰（）。

(A) 133-(B) 143(C) 22 (D) 0 5、设()11ln 1nn u n ⎛⎫=-+⎪⎝⎭，则下列说法正确的是（）。

(A)1nn u∞=∑与21nn u∞=∑都收敛 (B)1nn u∞=∑与21nn u∞=∑都发散(C)1nn u∞=∑收敛而21nn u∞=∑发散 (D)1nn u∞=∑发散而21nn u∞=∑收敛6、()110,yI dy f x y dx -=⎰⎰，则交换积分次序后得（）(A) ()2110,x I dx f x y dy +=⎰⎰（B ）()2110,x I dx f x y dy -=⎰⎰（C ）()110,yI dx f x y dy -=⎰⎰ （D ）()110,xI dx f x y dy -=⎰⎰7、设22u xy z =-，则u 在()1,1,1-处的方向导数的最大值为（）（A ）26 （B ）8 （C ）12 （D ）23二、填空题（每小题4分，满分20分）1、微分方程xxy y e '+=的通解是 2、设L 是圆周：226x y x +=-的正向，则=-+-⎰dy y x dx y x L)()(333、设幂级数()01nn a x ∞+∑的收敛域为()4,2-，则幂级数()03nn a x ∞-∑的收敛区间为4、微分方程22y y y '''++=的一般解是5、222y xdx edy -=⎰⎰三、把下列积分化为极坐标的形式，并计算积分值，()222200aa x I dx x y dya -=+>⎰⎰。

高等数学A(二)试卷及答案

高等数学A （二）考试试卷一、填空题（每小题5分，共25分）1. 设2u 1sin ,2xu e x y x y π-=∂∂∂则在（，）处的值为_________。

2. 改变二次积分10(,)x I dx f x y dy =⎰⎰的积分次序，则I=_______________。

3. 设平面曲线Γ为下半圆周y =22()x y ds Γ+⎰=___________。

4. 若级数1n n u∞=∑的前n 项部分和是：1122(21)n S n =-+，则n u =______________。

5. 设)2,5,3(-=a ，(2,1,4)b =，(1,1,1)c =，若c b a ⊥+μλ，则λ和μ满足。

二、计算题（每小题10分，共70分）1. 求由方程xyz =(,)z z x y =在点(1,0,1)-处的全微分。

(10分)2. 设21()x t f x e dx -=⎰，求10()f x dx ⎰。

（10分） 3. 计算xzdxdydz Ω⎰⎰⎰，其中Ω是由平面0,,1z z y y ===以及抛物柱面2y x =所围成的闭区域。

（10分）4. 计算dy xy ydx x L22+⎰，其中积分路径L 是xoy 平面上由点(2,0)A -顺次通过点(0,2)B 、(2,2)C 到点(2,4)D 的折线段。

（10分） 5. 把函数xx f 431)(+=展为1-x 的幂级数，并确定其收敛域。

6. 求点)3,2,1(-关于平面014=-++z y x 的对称点。

（10分）7. 要建造一个表面积为108平方米的长方形敞口水池，尺寸如何才能容积最大.。

（10分）三、证明题（5分）若0lim =∞→n n na ，且∑∞=+-+11])1[(n n n na a n 收敛于常数A ，试证明级数∑∞=1n n a 收敛。

答案课程名称：高等数学A(二) 试卷编号：5一、填空题。

（每小题5分，共25分）1.22e π，2.101(,)y dy f x y dx ⎰⎰，3.π，4.1(21)(21)n n -+， 5. 076=+μλ二、计算题。

暨南大学08-09高数II(A)参考答案word精品文档6页

暨南大学考试试卷1. 两平行平面23490x y z -++=与234150x y z -+-=的距离为（ C ）. (A)629 (B) 2429 (C) 2. 二元函数极限32lim2++∞→→y xyy x 的值为（ A ）. (A) 4 (B) ∞+ (C) 34(D) 0 3.下列说法正确的是( C ).(A) 若∑∞=1n n u ,∑∞=1n n v 都发散,则∑∞=+1)(n n n v u 发散;(B) 若∑∞=1n n u ,∑∞=1n n v 都发散, 则∑∞=1)(n n n v u 发散;(C) 若∑∞=1n n u 收敛, 则∑∞=11n n u 发散; (D) 若∑∞=1n n u 发散, 则∑∞=11n n u 收敛;4. 函数x e y y y x 2cos 52=+'-''的一个特解应具有形式：（ C ）(C) )2sin 2cos (x B x A xe x + (D) )2sin 2cos (2x B x A e x x + 5. 设曲线积分ydy x f ydx e x f cx cos )(sin ])([--⎰与路径无关，其中)(x f 具有一阶连续导数，且0)0(=f ，则)(x f 等于（ D ）(A))(21x x e e -- (B) )(21x x e e --(C) 1)(1---x x e e (D) )(211x x e e ---二、填空题（共5小题，每小题3分，共15分）1、曲面3=+-xy z e z 在点)0,1,2(处的切平面方程为240x y +-=。

2、曲线积分dx y x L⎰-)(22＝5615-，其中L 是抛物线2x y =上从点)0,0(到)4,2(的一段弧。

3、交换二次积分⎰⎰⎰⎰+121212212),(),(yydx y x f dy dx y x f dy 的积分顺序为211(,)xdx f x y dy⎰⎰。

2008-2009学年安徽大学《高等数学 C(二)》(A卷)考试试题及参考答案

安徽大学2008—2009学年第二学期院/系专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------《高等数学C （二）》考试试卷（A 卷）（闭卷时间120分钟）题号一二三四五总分得分阅卷人得分一、填空题（每小题2分，共10分）1．已知两个4维向量与21(1,,1,0)t α=2(2,1,3,2)t α=−正交，则＝ t . 2．幂级数221212n nn n x ∞−=−∑的收敛半径为 . 3．设，100220345A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠A ∗是A 的伴随矩阵，则1()A ∗−= .4．设平面区域：0,D 01x y y ≤≤≤≤(,)，f x y 在上连续，则利用极坐标变换可将二重积分D (,)Df x y d σ∫∫ 化为 .5．二次型22212312224243x x x x x x ++++x 的秩为 .得分二、单项选择题（每小题2分，共10分）6. 二元函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩在点处( ).(0,0)A. 连续，偏导数也存在 B. 连续，偏导数不存在C. 不连续，偏导数存在D. 不连续，偏导数也不存在7．若,A B 均为同阶可逆矩阵，则必有( ) . A. A 可经行初等变换变到B B. A B =C. 存在可逆矩阵，使得P 1P AP B −=D. A B +为可逆矩阵8．若阶矩阵n A 的一个特征值为2，则23A A E ++必有一个特征值为( ) .A. 0B. 1C. 11D. 不能确定9．若级数收敛，则( ) .1(n n n a b ∞=+∑)A. 、中至少有一个收敛 B. 1n n a ∞=∑1n n b ∞=∑1n n a ∞=∑、1n n b ∞=∑均收敛C. 1n n n a b ∞=+∑收敛 D. 1n n a ∞=∑、1n n b ∞=∑敛散性相同10. 差分方程的通解为 ( ) (其中为任意常数) .2132t t t y y y ++−+=02222C 1,C C A. B. C. 1C t C +12t C C +1(2)t C −+ D.12(1)t C C −+三、计算题得分(第11小题至第14小题每题8分，第15小题至第17小题每题10分，共62分)11. 已知sin y z x =，求(1) zx ∂∂、z y ∂∂； (2) ； (3) d z 2z x y ∂∂∂.12. 求二重积分cos Dxdxdy x∫∫，其中为直线D y x =与抛物线2y x =所围成的区域.院/系专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------13. 求微分方程32x y y y e −′′′−+=的通解.14. 将1()f x x=展开成的幂级数，并求该幂级数的收敛半径、收敛域. (3x −)⎟⎟15. 已知，. 若201030202A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠100010000B ⎛⎞⎜=−⎜⎜⎟⎝⎠X 满足22AX B BA X +=+，求X .16．求矩阵的特征值和特征向量；判断它是否可以对角化，并说明理由.110430102A −⎛⎞⎜⎟=−⎜⎜⎟⎝⎠⎟0,院/系专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------17．对于非齐次线性方程组1231231231,220.x x x x x x x x ax ++=⎧⎪++=⎨⎪−+=⎩(1) a 为何值时，方程组无解；(2) a 为何值时，方程组有解，并求其解.得分四、应用题（本题10分）18．在平面上求一点，使它到三条直线0x =、0y =、2160x y +−=距离的平方和最小.五、证明题（本题8分）得分19．设A 为矩阵，其秩为，m n ×AX b =r β是非齐次线性方程组的一个解，0AX =12,,,n r ααα−"是对应的齐次线性方程组的一个基础解系.证明：向量组12,,,,n r ααα−"β 线性无关.安徽大学2008－2009学年第二学期《高等数学 C（二）》考试试卷（A 卷）参考答案及评分细则一、填空题（每小题2分，共10分）1．1或； 3. 110A ； 4.csc 204(cos ,sin )d f r r r πθπθθ∫∫dr θ； 5. .2二、单项选择题（每小题2分，共10分）6. C；7. A；8. C；9. D； 10. B.三、计算题(第11小题至第14小题每题8分，第15小题至第17小题每题10分，共62分)11. 已知sin yz x =，求(1) z x ∂∂、z y ∂∂； (2) ； (3) d z 2z x y ∂∂∂.解：2cos z y y x x x ∂=−∂,1cos z y y x x∂=∂ 21cos cos y y ydz dx dy x x x x=−+22(cos )z y y x y y x ∂∂=−∂∂∂x 231cos sin y y y x x x x =−+ 12. 求二重积分cos Dxdxdy x∫∫，其中为直线D y x =与抛物线2y x =所围成的区域. 解：cos Dxdxdy x ∫∫210cos x x x dx dy x=∫∫120cos ()xx x dx x=−∫1(cos cos )x x x d =−∫x=1cos1−13. 求微分方程32x y y y e −′′′−+=的通解.解：方程对应的齐次微分方程为：32y y y 0′′′−+= 0 其特征方程为，解得232λλ−+=121, 2λλ==.故齐次方程的通解为：212x x C e C e +. 设非齐次方程的一个特解为x y Ae ∗−=代入原方程得到32x x x x Ae Ae Ae e −−−++=−，故16A =这样原方程的通解为：21216x x x C e C e e −++.14. 将1()f x x =展开成的幂级数，并求该幂级数的收敛半径、收敛域.解：(3x −)1111()33331()3f x x x x ===⋅−+−+ 而01(1)1n n n x x ∞==−+∑，，(1,1)x ∈− 故11331()3x ⋅−+013(1)()33n n n x ∞=−=−∑＝1(3)(1)3n n n n x ∞+=−−∑ 且313x −<，于是33x −<，收敛半径为3r =，收敛区域为.(0,6)15．已知，.若201030202A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠100010000B ⎛⎞⎜⎟⎟=−⎜⎜⎟⎝⎠X 满足22AX B BA X +=+，求X . 解：由 22AX B BA X +=+得到：(2)(2)A E X B A E −=−，从而1(2)(2)X A E B A E −=−−又，001(2)010200A E ⎛⎞⎜⎟−=⎜⎟⎜⎟⎝⎠11002(2)010100A E −⎛⎞⎜⎟⎜⎟−=⎜⎟⎜⎟⎜⎟⎝⎠这样，1200100001010010010100000200X ⎛⎞⎜⎟⎛⎞⎛⎞⎟⎟⎟⎠000010001⎛⎞⎜⎟=−⎜⎟⎜⎟⎝⎠⎜⎟⎜⎟⎜=−⎜⎟⎜⎟⎜⎜⎟⎜⎜⎟⎝⎠⎝⎜⎟⎝⎠⎟⎟16．求矩阵的特征值和特征向量；判断它是否可以对角化，并说明理由.110430102A −⎛⎞⎜=−⎜⎜⎟⎝⎠解：1104301022(1)(2λλE A λλλλ+−−=−−−)=−− 令0E A λ−=解得特征值为12λ=，231λλ== 对于12λ=，解方程组，得基础解系为：123(2)0x E A x x ⎛⎞⎜⎟−⎜⎟⎜⎟⎝⎠=1(0,0,1)T η=故属于12λ=的全部特征向量为1(0,0,1)T k 1(0k )≠ 对于231λλ==，解方程组，得基础解系为：123()x E A x x ⎛⎞⎜⎟−⎜⎟⎜⎟⎝⎠0=2(1,2,1)T η=−故属于231λλ==的全部特征向量为2(1,2,1)T k −2(0k )≠ 因A 只有两个线性无关的特征向量，故A 不能对角化.17．对于非齐次线性方程组1231231231,220.x x x x x x x x ax 0,++=⎧⎪++=⎨⎪−+=⎩(1) 为何值时，方程组无解；a (2) 为何值时，方程组有解，并求其解. a 解：方程组对应系数的增广矩阵为：11 1 112 2 011 0A a ⎛⎞⎜⎟=⎜⎟⎜⎟−⎝⎠111 1011 102 1 1 a ⎛⎞⎜⎟→−⎜⎟⎜⎟−−−⎝⎠11 1 1011 100 13 a ⎛⎞⎜⎟→−⎜⎟⎜⎟+−⎝⎠(1) 当时方程组无解；10a +=(2) 当即时，方程组有唯一解，其解为：10a +≠1a ≠− 123 23 113 1x x a x a ⎧⎪=⎪⎪=−⎨+⎪⎪=−⎪+⎩. 四、应用题（本题10分）18．在平面上求一点，使它到直线0x =，0y =及2160x y +−=的距离的平方和最小.解：设所求的点为(,)x y ，则它到0x =，0y =及2160x y +−=的距离分别为x ，y，于是由题意，距离的平方和为：221(216)5s x y x y =+++−2令22(216)0542(216)05s x x y x s y x y y∂⎧=++−=⎪∂⎪⎨∂⎪=++−=∂⎪⎩，解得唯一驻点816(,)55根据实际意义所求的点一点存在，即为816(,55.五、证明题（本题8分）设β是非齐次线性方程组AX b =的一个解，12,,,n r ααα−"是对应的齐次方程组的一个基础解系，证明：12,,,,n r ααα−"β线性无关.证明：设11220n r n r k k k k ααα−−++++="βr ，因为0,(1,2,,)i A i n α=="−，于是A 左乘上式两端得到0kA β=，而0A b β=≠，故0k =于是11220n r n rk k k ααα−−+++="，而12,,,n r ααα−"是0AX =的一个基础解系，从而线性无关，故，这样120n r k k k k −====="12,,,,n r ααα−"β线性无关.。

2008-2009学年第2学期期末考试 A卷试卷及解答

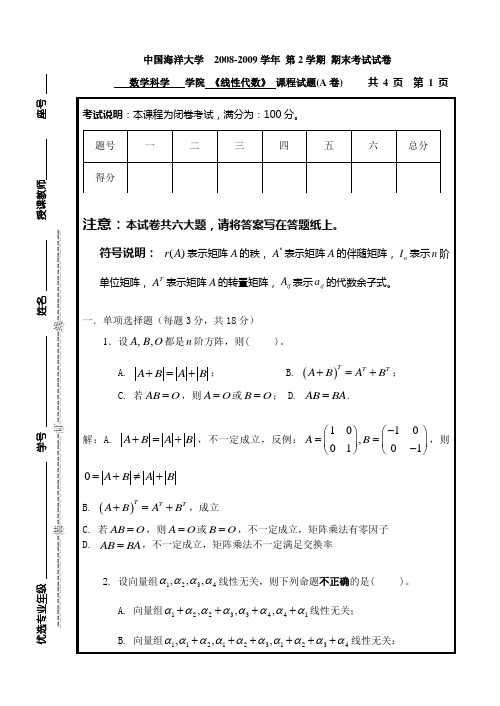
中国海洋大学2008-2009学年第2学期期末考试试卷数学科学学院《线性代数》课程试题(A卷) 共4 页第2 页中国海洋大学 2008-2009学年第2学期期末考试试卷数学科学学院《线性代数》课程试题(A 卷) 共 4 页第 3 页解： 1X A B -=，根据初等行变换求解可得 ()()213132132323102211022110221311133,201570015702,521891014510012110021010351,100121rr r r r r r r r r r r ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-------+---+-⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭--⎛⎫ ⎪-⨯-⨯-⎪ ⎪---⎝⎭uuuuuuuuuuuuu r uuuuu r uuuuuuuuuuuuu r uuuuu r 100210103500121--⎛⎫ ⎪--⎪ ⎪⎝⎭uuuuuuuuuuu因此213521X --⎛⎫ ⎪=-- ⎪ ⎪⎝⎭4. 已知3R 的两组基为()()()1231,0,0,1,1,0,1,1,1TTTααα==-=与()()()1231,2,1,2,3,3,3,7,1T T Tβββ===，求：（1）基{}123,,ααα到基{}123,,βββ的过渡矩阵；（2）向量()5,2,1Tα=在基{}123,,ααα下的坐标。

解：（1）设基{}123,,ααα到基{}123,,βββ的过渡矩阵为C ，则()()123123,,,,C βββααα=，即123111237011131001C ⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，因此1111123011237001131C -⎛⎫⎛⎫⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭，利用初等变换法求解得()2313122111123110012100118011237,010106,1010106001131001131001131r r r r r r r --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪----+⨯--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭uuuuuuuuuuu r uuuuuuuuuuuuur12,,,,n αααβL 线性无关；（2）若1β可由12,,,n αααL 表出，而2β不能由12,,,n αααL 表出，则1212,,,,n αααββ+L 线性无关。

08-09高数(下)(A)试卷及答案

08-09 高等数学(下) A 考试方式：闭卷完成时限： 120分钟一、填空（每小题3分，满分15分）：1. 与两平面34=-z x 和152=--z y x 的交线平行,且过点)5,2,3(-的直线方程_______________.2. 函数y xy ax x y x f 22),(22+++=在点)1,1(-处取得极值,则常数 =a _______________.3. 若积分区域D 为x y x 222≤+,则二重积分⎰⎰σDd y x f ),(化为极坐标下的二次积分为_____________.4. 设)ln(222z y x u ++=则=)(u grad _______________.5.若级数∑∞=0n n nx a在5-=x 处条件收敛,则该级数的收敛半径为._______. 二、单项选择（每小题3分，满分15分）：1. ()00,y x f x 和()00,y x f y 存在是函数()y x f ,在点()00,y x 连续的( )A. 必要非充分条件;B. 充分非必要条件;C. 充分且必要条件;D. 既非充分又非必要条件2. 已知 dy y x dx ay x )43()(+++为某一函数的全微分,则=a ( )A. 0 ;B. 1 ;C. 3 ;D. 4.3. 二次积分dx y x f dy y y⎰⎰22),(交换积分次序后为( )A. ⎰⎰⎰⎰+221210),(),(xxxdy y x f dx dy y x f dx;B.dy y x f dx x ⎰⎰22),( ;C.⎰⎰22),(xxdy y x f dx; D.⎰⎰⎰⎰+21221),(),(xxxdy y x f dx dy y x f dx .4. 22y x z +=在点(1,2)处沿着从点(1,2)到点)32,2(+的方向的方向导数为( )A. 32+ ;B. 321+ ;C. 342+;D. 34+ .5. 下列级数中条件收敛的是( )A.∑∞=-1)1(n nnB. ∑∞=-13)1(n nnC. ∑∞=--22)1(n n nn nD. ∑∞=-12)1(n nn 三、计算下列各题（每小题7分，满分49分）： 1. 求直线⎩⎨⎧=--+=++-0101z y x z y x 在平面0=++z y x 上的投影直线的方程.2. 设⎩⎨⎧=+=-10xv yu yv xu ，求y vx u ∂∂α∂ ,.3. 求曲线⎩⎨⎧=+-++=0253222z y x y x z 上点)9,2,1(-处的切线方程和法平面方程.4. 计算dy yye dx x y ⎰⎰-121 .5. 设Ω是由z y x 222=+和2=z 所围在的区域，求⎰⎰⎰Ω+dv y x z )(22. 6. 求幂级数nn n nx n ∑∞=-12)1(的收敛域.7. 设⎪⎩⎪⎨⎧=≠+=0 , 10 , arctan 1)(2x x x x x x f ,求)(x f 展开成x 的幂级数,并求级数∑+∞=--1241)1(n n n 的和. 四、应用题（每小题8分，满分16分）： 1.设长方体的三个面在坐标面上,其一顶点在平面1=++czb y a x 上,且.0,0,0>>>c b a 试问长方体的高z 取什么值时,其体积最大.2. 求球体2222R z y x ≤++与球体Rz z y x 2222≤++的公共部分的体积. 五、证明题（5分）设),2,1(,⋅⋅⋅=≤≤n b c a n n n ,并设级数∑∞=1n na和∑∞=1n nb均收敛,试证明∑∞=1n nc也收敛.08-09高数(下)A 参考答案一、填空题（每小题3分，共15分） 1153243-=-=+z y x ， 2 -5 3 ⎰⎰-θππρρθρθρθcos )sin ,cos (2022d f d4 )2,2,2(222222222zy x zz y x y z y x x ++++++ 5 5. 二、选择题（每小题3分，共15分） 1.D 2.C 3.A 4.B 5.A三、计算题（每小题7分，共49分）1.解: 现求过直线和平面垂直的平面方程有1=-z y (5)那么所求直线方程为⎩⎨⎧=++=-01z y x z y (7)2.解: 方程两边求微分，得⎩⎨⎧=+++=--+00vdx xdv udy ydu vdy ydv udx xdu …………………………………………………………(3) 22y x yvxu x u ++-=∂∂，……………………………………………………………………（5） 22yx yvxu y v ++-=∂∂……………………………………………………………………（7） 3. 解 ⎩⎨⎧='-'+'+='05342x x xx z y y y x z ，在点)9,2,1(-处，解得334,35='='xx z y ,…………..(3) 所以在点)9,2,1(-处的切向量为 {}34 ,5 ,3,……………………………………………..(5) 因此切线方程3495231-=-=+z y x ,.....................................................(6) 法平面方程 3133453=++z y x (7)4.解:交换积分次序,1d e d d 1e 1110==-=⎰⎰⎰y y x y yy I y yy (7)5.解: 采用柱面坐标，⎰⎰⎰=22320202d d d r z z r r I πθππ8d )44(2122043=-⋅=⎰r r r (7)6.解:收敛半径为 2121lim lim1=+==∞→+∞→n n a a R n n n n , (4)当21-=x 时,级数为∑∞=-11n n,发散； (5)当21=x 时,级数为∑∞=--11)1(n n n ,收敛， (6)所以收敛区间为 ]21,21(-； (7)7.解: 211x + ,)1(02∑∞=-=n n n x )1,1(-∈x ………………………………………….(1) x a r c t a n ∴ ⎰+=xx x 02d 11 ,12)1(012∑∞=++-=n n n x n ]1,1[-∈x ……………………(3) 于是)(x f ∑∞=+-+=1212)1(1n n n x n ∑∞=++-+02212)1(n n n xn ………………………………..…..(4) ∑∞=+-+=1212)1(1n n n x n ∑∞=---+12112)1(n nn x n (5)∑∞=⎥⎦⎤--+⎢⎣⎡-+=12121121)1(1n nn x n n ,41)1(21122∑∞=--+=n nn x n ]1,1[-∈x ……………………………………….(6) ∑∞=--∴1241)1(n nn]1)1([21-=f 214-=π (7)四、应用题（每小题8分，共16分）1.解: 1. 目标函数 xyz V =，约束条件1=++c zb y a x ，………………………….(2) 设拉格朗日函数 )1(-+++=czb y a x xyz L λ， (4)令 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++=+='=+='=+='1000cz b y a x c xy L b xz L a yz L z y x λλλ，解得唯一驻点 ⎪⎪⎪⎩⎪⎪⎪⎨⎧===333c z b y a x ， (7)由实际问题，当高3cz =时，其体积最大 (8)2.解: 可用三重积分⎰⎰⎰Ωdv ……计算, 也可用二重积分⎰⎰σ-Dd )(底顶…计算.⎰⎰⎰⎰⎰⎰⎰⎰⎰σ+σ==Ω)(2)(221z D RR z D R d dz d dzdv V (4)⎰⎰-π+-π=RR R dz z R dz z Rz 22222)()2( (6)=3125R π (8)五、证明题（每小题5分，共5分）证明：由条件知，n n n n a b a c -≤-≤0,),2,1( =n ,由题设∑∞=1n n a 和∑∞=1n n b 均收敛，故正项级数∑∞=-1)(n n n a b 收敛，由比较判别法知正项级数∑∞=-1)(n n na c也收敛，而n n n n a a c c +-=)(,),2,1( =n ，再由∑∞=1n n a 的收敛性，证明了∑∞=1n n c 收敛. (5分)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

海南师范大学
物理、信息科学技术学院各专业高等数学（A ） 2008 —2009 学年度第二学期期末考试（A ）卷
注意事项：1. 考前请将密封线内填写清楚 2. 所有答案请直接答在试卷上 3．考试形式：闭卷
4. 本试卷共四大题，满分100分，考试时间100分钟
一、单项选择题（本题共6小题，每小题 3分，共18 分）在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。

错选或未选均无分。

1. 设三个向量c
b a
,,满足关系式0
=++c b a ，则b
a ⨯=( )
A. b
c ⨯
B. c b ⨯
C. c a
⨯ D. a b ⨯
2. =
+→2
2
3
)
0,0(),(lim
y
x
x y x ( )
A. 2
B. 1
C. 0
D. ∞ 3．曲线x
z x y -==1,22
在点)2
1,
1,2
1(
处的切线一定垂直于（
）
A.
xoy
平面 B.
yoz
平面 C.平面0
=-+
z y x D. 平面0
=++
z y x
4．旋转抛物面2
12
2
y x
z
++
=在21≤≤z 那部分的曲面面积=S （）
A.
dxdy
y x
y x ⎰⎰≤+--22
2
2
2
1 B.
dxdy
y x
y x ⎰⎰
≤+++2
2
2
2
2
1
C.
d x d y y x
y x ⎰⎰
≤+--422
2
2
1
D.
dxdy
y x
y x ⎰⎰
≤+++4
2
2
2
2
1
5. 设级数)
cos
1()1(1
n
n n
α
--∑
∞
=，其中0>α，则下列说法正确的是（）
A ．该级数发散
B ．该级数条件收敛
C ．该级数绝对收敛
D ．收敛性与α有关
6.若级数∑
∞
=1
n n
a 与∑
∞
=1
n n
b 都发散，则（）
A.)(1n n n b a -∑
∞
=发散
B. )
(1n n n b a +∑
∞
=发散
C. n
n n b a ∑
∞
=1
发散 D. )
(1
n n n b a +∑
∞
=发散
二、填空题（每空 4分，共24分）
1、过点)1,2,1(-M 且与直线⎪⎩
⎪
⎨⎧-=-=+-=1331t z t y t x 垂直的平面方程是
2、曲面3=+-xy z e Z
在点（2，1，0）处的法线方程为
3、将二次积分dy
y x f dx
R
x
R x
R ⎰
⎰
----0
2
22
2
),(化为极坐标下的二次积分得
4、设x
z y x =ln
，则
=
∂∂z
x
5、若幂级数)0(1
2
>∑
∞
=a x a
n n
n
的收敛域为),(+∞-∞，则a
应满足
6、设幂级数∑
∞
=1
n n
n x
a 的收敛半径为3，则幂级数∑
∞
=-1
)
1(n n
n x a 的收敛区间为
三、计算题（本题共6小题，每小题 7分，共 42 分） 1、设)
,(2
xy x f x z
=，
f
具有二阶连续偏导数，求
y
x z
x z ∂∂∂∂∂2
,。

2、计算二重积分D
dxdy xy D
,2
⎰⎰
由2
,0=+=y x y
及2
x
y
=所围成。

3、计算三重积分⎰⎰⎰
Ω
zdv
，其中Ω是由曲面2
2
y
x
z
+=及2
2
2y
x
z
--=所围成的
闭区域。

4、计算曲面积分⎰⎰
∑
++zdxdy
ydzdx xdydz ，其中∑为球面2
2
2
2
)
1(R
z y
x =-++
的上半部分的上侧。

5、计算曲线积分⎰-+++-
L
dy
x y dx y x )635()42(，其中
L
为曲线
x
y --=11从对应于0=x 的点到2=x 的点。

6、判定级数∑
∞
=1
n s
n n
a )
0,0(>>s a 其中的敛散性。

四、应用题（每小题 8分，共 16 分）
1、设
,3,2==q p p 与q
的夹角3
πθ
=
，求以向量,2q p a -=q
p b
3+=为邻边的
平行四边形对角线的长。

2、在平面1=x
上求一点
P ，使它到三个平面0
1,0,0=++==z y z y
的
距离平方和为最小。