最新【考研数学】教材必做课后题资料
考研数学教材试题及答案

考研数学教材试题及答案试题:一、选择题(每题3分,共30分)1. 设函数 \( f(x) = x^2 - 4x + 3 \),则方程 \( f(x) = 0 \) 的根为:A. \( x = 0 \)B. \( x = 1 \)C. \( x = 3 \)D. \( x = 2 \)2. 极限 \( \lim_{x \to 0} \frac{\sin x}{x} \) 的值是:A. 0B. 1C. \( \frac{\pi}{2} \)D. \( \infty \)3. 若 \( \int_{0}^{1} x^2 dx \) 的值为 \( \frac{1}{3} \),则\( \int_{0}^{1} x dx \) 的值为:A. \( \frac{1}{2} \)B. \( \frac{1}{3} \)C. \( \frac{1}{4} \)D. \( \frac{1}{6} \)4. 设 \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \),\( B = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \),则\( AB \) 的值为:A. \( \begin{bmatrix} 2 & 1 \\ -1 & 0 \end{bmatrix} \)B. \( \begin{bmatrix} -3 & 4 \\ 0 & 1 \end{bmatrix} \)C. \( \begin{bmatrix} 1 & 0 \\ 2 & -1 \end{bmatrix} \)D. \( \begin{bmatrix} 4 & -3 \\ 1 & 0 \end{bmatrix} \)5. 设 \( \vec{a} = (2, 3) \),\( \vec{b} = (-1, 2) \),则\( \vec{a} \cdot \vec{b} \) 的值为:A. 4B. 5C. 6D. 76. 若 \( y = e^{2x} \),则 \( y' \) 的值为:A. \( 2e^{2x} \)B. \( e^{2x} \)C. \( 2e^x \)D. \( e^x \)7. 设 \( z = x^2 + y^2 \),其中 \( x = \cos t \),\( y = \sin t \),则 \( \frac{\partial z}{\partial t} \) 的值为:A. \( -2\cos t - 2\sin t \)B. \( -2\cos t + 2\sin t \)C. \( 2\cos t - 2\sin t \)D. \( 2\cos t + 2\sin t \)8. 若 \( \sum_{n=1}^{\infty} a_n \) 收敛,则级数\( \sum_{n=1}^{\infty} na_n \) 必定:A. 收敛B. 发散C. 条件收敛D. 绝对收敛9. 设 \( f(x) \) 在区间 \( I \) 上连续,则 \( \int_I f(x) dx \) 的值:A. 一定存在B. 可能不存在C. 一定为正D. 一定为负10. 若 \( \lim_{x \to \infty} \frac{f(x)}{g(x)} = L \),则\( \lim_{x \to \infty} f(x) \) 的值为:A. \( \infty \)B. \( -\infty \)C. 0D. L答案:一、选择题1. D2. B3. A4. B5. A6. A7. D8. B9. A10. D。
最新【考研数学】数一数二数三教材必做课后题
1.2.5.9.10.11.(数一:14.15.16.17.18.)
第十章第一节
10—1: 4(A).5(B).
第二节
二重积分换元法
10—2:1.2.4.5.6.9.10.11.12.13.14.15.
第三节
数二.数三不要求
10—3:4.5.6.7.9.10.11.
(2)物品的独一无二章节
调研结论:综上分析,我们认为在学院内开发“DIY手工艺品”商店这一创业项目是完全可行的。不要求掌握内容
上述所示的上海经济发展的数据说明:人们收入水平的增加,生活水平的提高,给上海的饰品业带来前所未有的发展空间,为造就了一个消费额巨大的饰品时尚市场提供了经济基础。使大学生对DIY手工艺品的时尚性消费,新潮性消费,体验性消费成为可能。要求做的习题
第五节
微分在近似计算中应用.
2—5:1.2.3(B).4(B).
总习题二
1.2.3.6.7.8.9.10.11.12.13.14.
第三章第一节
3—1:3.4.5.6.7.8.10.11.12.14.15.
第二节
3—2: 1(B).2.3.4.
第三节
3—3:1.2.3.4.5.6.7.
第四节
3—4: 3(B).4.5(A).6.9(B).11.12.13.14.15.
第三节
可化为齐次的方程
7—3: 1(A). 2(B). 3.
第四节
例2.伯努利方程(数一要)
7—4:1(B).2(A).3.4.6.7(1)(2).8(B).
第五节
例4.例6.数学三不要求
7—5:1(B).2(A).3.
第六节
例2.常数变易法
7—6: 3.
考研数学必做课后习题

第一轮复习:基础知识自我复习高等数学第一单元(课前或课后复习内容)计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版高等数学第一章函数与极限第1章第1节映射与函数(P1——P23)第1章第2节数列的极限(P23——P31)第1章第3节函数的极限(P31——P39)第1章第4节无穷小与无穷大(P39——P42)第1章第5节极限运算法则(P43——P50)本单元中我们应当学习——1.函数的概念及表示方法;2.函数的有界性、单调性、周期性和奇偶性;3.复合函数、分段函数、反函数及隐函数的概念;4.基本初等函数的性质及其图形;5.极限及左右极限的概念,极限存在与左右极限之间的关系;学习时间学习章节学习知识点习题章节必做题目巩固习题(选做)备注2.5h 第1章第1节映射与函数函数的概念函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数初等函数具体概念和形式,函数关系的建立习题1-14(3) (6) (8),5(3)★,9(2),15(4)★,17★4(4)(7),5(1),7(2),15(1)本节有两部分内容考研不要求,不必学习:1. “二、映射”;2. 本节最后——双曲函数和反双曲函数2h 第1章第2节数列的极限数列极限的定义数列极限的性质(唯一性、有界性、保号性)习题1-21(2) (5) (8)★3(1)1. 大家要理解数列极限的定义中各个符号的含义与数列极限的几何意义;2. 对于用数列极限的定义证明,看懂即可。
2h 第1章第3节函数的极限函数极限的概念函数的左极限、右极限与极限的存在性函数极限的基本性质(唯一性、局部有界性、局部保号性、不等式性质,函数极限与数列极限的关系等)习题1-32,4★3,1. 大家要理解函数极限的定义中各个符号的含义与函数极限的几何意义;2. 对于用函数极限的定义证明,看懂即可。
1h 第1章第4节无穷小与无穷大无穷小与无穷大的定义无穷小与无穷大之间的关系习题1-44,6★1,5 大家要搞清楚无穷大与无界的关系2h 第1章第5节极限运算法则极限的运算法则(6个定理以及一些推论)习题1-51(5)★(11)★(13)★, 3★,51(9)(10)(14),2(1),4有理分式函数当x 的极限要记住结论,以后直接使用。
考研数学(数学三)公认教材及参考书

考研数学(数学三)公认教材及参考书高等数学:同济五版线性代数:同济六版概率论与数理统计:浙大三版推荐资料:1、李永乐考研数学3--数学复习全书+习题全解(经济类)2、李永乐《经典400题》3、《李永乐考研数学历年试题解析(数学三)真题》考研数学规划:课本+复习指导书+习题集+模拟题+真题=KO复习资料来说:李永乐的不错,注重基础;陈文灯的要难一些。
经济类一般都用李永乐的(经济类数学重基础不重难度),基础好的话可以考虑下陈文灯的书。
李永乐的线性代数很不错陈文灯的高等数学很不错2009年全国硕士研究生入学统一考试数学(三)考试大纲考试科目:微积分、线性代数、概率论与数理统计考试形式和试卷结构:(一)试卷满分为150分考试时间为180分钟.(二)内容结构:高等教学约56%线性代数约22% 概率论与数理统计约22%(三)题型结构:单项选择:8小题,每小题4分,共32分填空题:6小题,每小题4分,共24解答题(包括证明题):9小题,共94分全国硕士研究生入学统一考试英语考试大纲完形填空:10分(20道选择题每题0.5分)[可以抛弃的题型]阅读:60分其中阅读A部分(阅读理解):40分(20道选择题每题2分)(这个是重中之重)阅读B部分(新题型):10分(5道题每题2分一共有四种题型)阅读C部分(翻译):10分(5道题每题2分)作文:30分(除了阅读A之外最重要的部分)小作文(书信作文):10分大作文(图画作文):20分2009年全国硕士研究生入学统一考试数学三考试大纲考点归纳(三)概率论与数理统计一随机事件和概率考试内容随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质古典型概率几何型概率条件概率概率的基本公式事件的独立性独立重复试验二随机变量及其分布考试内容随机变量随机变量分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布三多维随机变量的分布考试内容多维随机变量及其分布函数二维离散型随机变量的概率分布边缘分布和条件分布二维连续型随机变量的概率密度,边缘概率密度和条件密度随机变量的独立性和不相关性常见的二维随机变量的分布两个及两个以上随机变量的函数分布四随机变量的数字特征考试内容随机变量的数学期望(均值)方差标准差及其性质随机变量函数的数学期望切比雪夫不等式矩协方差相关系数及其性质五大数定律和中心极限定理考试内容切比雪夫大数定律伯努力大数定律辛钦大数定律棣莫弗-拉普拉斯定理列维-林德伯格定理六数理统计的基本概念考试内容总体个体简单的随机样本统计量经验分布函数样本均值样本方差和样本矩X2的分布t分布F分布分位数正态总体的常用抽样分布七参数估计考试内容点估计的概念估计量和估计值矩估计法最大似然估计法。
考研数学高频考点必刷题

考研数学高频考点必刷题
1.未定式极限的计算、无穷小比较以及极限的局部逆问题(客观题和解答题必考)
2.判断函数的连续性及间断点的分类(一般考客观题)
3.导数定义及几何意义相关题目(客观题和解答题都可能考)
4.各类函数(包括复合函数、幂指函数、隐函数、参数方程、变上限函数)的求导(客观题和解答题都可能考)
5.利用7个中值定理(零点定理、介值定理、罗尔定理、拉格朗日定理、柯西中值定理、泰勒定理、积分中值定理)证明等式或不等式(考证明题)
6.利用函数单调性和最值、中值定理证明函数或数值不等式(考证明题)
7.利用函数性态讨论方程的根的个数或曲线交点个数问题(考解答题)
8.判断函数的极值、拐点(客观题和解答题都可能考)
9.求曲线的渐近线或渐近线的条数(一般考客观题)
10.不定积分和原函数的概念的理解(一般考客观题)
11.不定积分的计算(一般考解答题)
12.定积分的计算和定积分性质的应用(客观题和解答题都可能考)
13.定积分的几何应用和物理应用的考查(一般考解答题,有时会和其他知识结合考综合题,物理应用仅数一、数二要求)
14.反常积分的计算和判断敛散性(一般考客观题)。
考研高等数学全面复习资料(电子版)

高等数学考研复习资料,最全篇,适合于一遍,二遍复习研究细节,祝你考研数学春风得意马,突破130分大关!目录一、函数与极限 (2)1、集合的概念 (2)2、常量与变量 (3)2、函数 (4)3、函数的简单性态 (4)4、反函数 (5)5、复合函数 (6)6、初等函数 (6)7、双曲函数及反双曲函数 (7)8、数列的极限 (8)9、函数的极限 (9)10、函数极限的运算规则 (11)一、函数与极限1、集合的概念一般地我们把研究对象统称为元素,把一些元素组成的总体叫集合(简称集)。
集合具有确定性(给定集合的元素必须是确定的)和互异性(给定集合中的元素是互不相同的)。
比如“身材较高的人”不能构成集合,因为它的元素不是确定的。
我们通常用大字拉丁字母A、B、C、……表示集合,用小写拉丁字母a、b、c……表示集合中的元素。
如果a是集合A中的元素,就说a属于A,记作:a∈A,否则就说a不属于A,记作:a∉A。
⑴、全体非负整数组成的集合叫做非负整数集(或自然数集)。
记作N⑵、所有正整数组成的集合叫做正整数集。
记作N+或N+。
⑶、全体整数组成的集合叫做整数集。
记作Z。
⑷、全体有理数组成的集合叫做有理数集。
记作Q。
⑸、全体实数组成的集合叫做实数集。
记作R。
集合的表示方法⑴、列举法:把集合的元素一一列举出来,并用“{}”括起来表示集合⑵、描述法:用集合所有元素的共同特征来表示集合。
集合间的基本关系⑴、子集:一般地,对于两个集合A、B,如果集合A中的任意一个元素都是集合B的元素,我们就说A、B有包含关系,称集合A为集合B的子集,记作A⊆B(或B⊇A)。
⑵相等:如何集合A是集合B的子集,且集合B是集合A的子集,此时集合A中的元素与集合B中的元素完全一样,因此集合A与集合B相等,记作A=B。
⑶、真子集:如何集合A是集合B的子集,但存在一个元素属于B但不属于A,我们称集合A是集合B的真子集。
⑷、空集:我们把不含任何元素的集合叫做空集。
云南省考研数学复习资料高等代数重点习题解析

云南省考研数学复习资料高等代数重点习题解析高等代数是数学专业考研的重要科目之一,对于考生来说,掌握高等代数的重点知识和解题方法是提升成绩的关键。
本文将针对云南省考研数学复习资料中的高等代数部分,对一些重点习题进行解析,帮助考生更好地复习备考。
一、矩阵与行列式1. 已知A为n阶方阵,且满足A^2=I,证明A的特征值只能是1或-1。
解析:首先根据矩阵的特征值与特征向量的定义,设λ为A的特征值,x为对应的特征向量。
由于A^2=I,我们有A^2x=Ix=x。
展开计算可以得到(A^2-λ^2I)x=0。
由于特征值不全为0,所以可以消去左边的矩阵,得到(A+λI)(A-λI)x=0。
根据矩阵的奇异性质,当(A+λI)x=0或(A-λI)x=0时,存在非零向量x使得方程成立。
因此,A+λI和A-λI是奇异矩阵,即它们的行列式为0。
解得λ^2=1,即λ=±1。
2. 证明:对任意n阶方阵A和B,有det(AB)=det(A)det(B)。
解析:根据行列式的定义,可以得到det(AB)=|AB|=|A||B|,其中|A|和|B|分别表示方阵A和B的行列式值。
因此,我们只需证明|A||B|=det(A)det(B)。
考虑到行列式的性质,|A||B|=|AB|,所以只需证明|AB|=det(A)det(B)。
展开|AB|的定义,可以得到行列式的乘积展开式,由于行列式展开式是通过对A的一行(或一列)进行展开,而对应乘积展开式也是通过对A的一行(或一列)展开,因此它们的结果是相同的。
所以,|AB|=det(A)det(B)。
二、向量空间1. 已知向量空间V是实数域上的n维列向量组成的集合,证明V是向量空间。
解析:要证明V是向量空间,需要满足向量空间的八条性质。
首先,V中的向量满足加法封闭性和数乘封闭性,即对于任意两个向量x和y∈V,有x+y和kx∈V。
其次,V中存在零向量0,使得对于任意向量x∈V,有x+0=x。
考研高等数学全面复习资料(电子版)

高等数学考研复习资料,最全篇,适合于一遍,二遍复习研究细节,祝你考研数学春风得意马,突破130分大关!目录一、函数与极限 (2)1、集合的概念 (2)2、常量与变量 (3)2、函数 (4)3、函数的简单性态 (4)4、反函数 (5)5、复合函数 (6)6、初等函数 (6)7、双曲函数及反双曲函数 (7)8、数列的极限 (8)9、函数的极限 (9)10、函数极限的运算规则 (11)一、函数与极限1、集合的概念一般地我们把研究对象统称为元素,把一些元素组成的总体叫集合(简称集)。
集合具有确定性(给定集合的元素必须是确定的)和互异性(给定集合中的元素是互不相同的)。
比如“身材较高的人”不能构成集合,因为它的元素不是确定的。
我们通常用大字拉丁字母A、B、C、……表示集合,用小写拉丁字母a、b、c……表示集合中的元素。
如果a是集合A中的元素,就说a属于A,记作:a∈A,否则就说a不属于A,记作:a∉A。
⑴、全体非负整数组成的集合叫做非负整数集(或自然数集)。
记作N⑵、所有正整数组成的集合叫做正整数集。
记作N+或N+。
⑶、全体整数组成的集合叫做整数集。
记作Z。
⑷、全体有理数组成的集合叫做有理数集。
记作Q。
⑸、全体实数组成的集合叫做实数集。
记作R。
集合的表示方法⑴、列举法:把集合的元素一一列举出来,并用“{}”括起来表示集合⑵、描述法:用集合所有元素的共同特征来表示集合。
集合间的基本关系⑴、子集:一般地,对于两个集合A、B,如果集合A中的任意一个元素都是集合B的元素,我们就说A、B有包含关系,称集合A为集合B的子集,记作A⊆B(或B⊇A)。
⑵相等:如何集合A是集合B的子集,且集合B是集合A的子集,此时集合A中的元素与集合B中的元素完全一样,因此集合A与集合B相等,记作A=B。
⑶、真子集:如何集合A是集合B的子集,但存在一个元素属于B但不属于A,我们称集合A是集合B的真子集。
⑷、空集:我们把不含任何元素的集合叫做空集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面点集
9—1: 4. 5(1)(2)(3)(4). 6.
第二节
9—2:1(B).4.5.6.7.8.
第三节
全微分在近似计算中应用
9—3:1.2.3.4.5.
第四节
9—4:2.3.5.9.10.11.12.
第五节
9—5:1.3.4.6.7.8.10.11.
第六节
本节数二.数三不要求;
向量值函数及导数
10—2:1.2.4.5.6.9.10.11.12.13.14.15.
第三节
数二.数三不要求
10—3:4.5.6.7.9.10.11.
第四节
数二.数三不要求
10—4:1.4.5.7(1).8.9.11.
总习题十
1.2(B).3.5.6.(数学一:8.9.10.)
第十一章第一节
(本章数二数三不要求)
11—1: 1. 3(B). 4. 5.
Beadwrks公司还组织各国的“芝自制饰品店”定期进行作品交流,体现东方女性聪慧的作品曾在其他国家大受欢迎;同样,自各国作品也曾无数次启发过中国姑娘们的灵感,这里更是创作的源泉。考研数学教材课后题精选
(二)上海的人口环境对饰品消费的影响高等数学(同济大学第六版)
(4)信息技术优势(2 (A)表示第2题的单数题;4(B)表示第4题的双数题)
一致连续性
1—10:1. 2. 3. 5.
总习题一
1. 2. 3. 4. 5.6.9.10.11.12.13.14.
第二章第一节
2—1:3. 6. 7.8.10至20.
第二节
2—2: 2(B).3. 4. 5. 6(B).7(B). 8(B). 9.
10. 11(B). 13.14.
第三节
2—3: 1(B).3. 4.9.10.11.12.
3—2: 1(B).2.3.4.
第三节
3—3:1.2.3.4.5.6.7.
第四节
3—4: 3(B).4.5(A).6.9(B).11.12.13.14.15.
第五节
3—5: 1(B).2.3.4.5.61. 4.
第七节
数学三不要求
3—7:1. 2.3.4.5.
总习题三
开了连锁店,最大的好处是让别人记住你。“漂亮女生”一律采用湖蓝底色的装修风格,简洁、时尚、醒目。“品牌效应”是商家梦寐以求的制胜法宝。我们熟练的掌握计算机应用,我们可以在网上搜索一些流行因素,还可以把自己小店里的商品拿到网上去卖,为我们小店提供了多种经营方式。
经常光顾□偶尔会去□不会去□1—2: 1.
第二节
11—2:3. 4. 5. 7.
第三节
11—3:1. 3.4(A).5.6(A).7.8(B).9
第三节
数学三不要求
6—3:4.5.6.7.10.11.12.
总习题六
3.4.5.6.7.
第七章第一节
7—1: 3. 5.
第二节
例4.
7—2: 1(B).2(B).4.6.7
第三节
可化为齐次的方程
7—3: 1(A). 2(B). 3.
第四节
例2.伯努利方程(数一要)
7—4:1(B).2(A).3.4.6.7(1)(2).8(B).
8—1:3.4.5.8.9.12.15.16.
第二节
8—2:1.3.7.9.10.
第三节
8—3:2.3.7.9(A).10(B).
第四节
8—4:3. 4. 5. 7.
第五节
8—5:1.2.3.5.6.8.9.
第六节
8—6:1.2.4.5.7.8.9.10(1).11.12.13.15.
总习题八
6.7.8..16.17.18.19.20.21.
章节
(3)个性体现不要求掌握内容
关于DIY手工艺制品的消费调查要求做的习题
第一章第一节
双曲函数
二、大学生DIY手工艺制品消费分析1—1: 4(B).5. 6 .12(B). 15. 16.
在上海,随着轨道交通的发展,地铁商铺应运而生,并且在重要商圈已经形成一定的气候,投资经营地铁商铺逐渐为一大热门。在人民广场地下的迪美购物中心,有一家DIY自制饰品店--“碧芝自制饰品店”第二节
第四节
相关变化率数三
2—4:1. 2. 3. 5 .7.8(B).(数一.二10.11.12)
第五节
微分在近似计算中应用.
2—5:1.2.3(B).4(B).
总习题二
1.2.3.6.7.8.9.10.11.12.13.14.
第三章第一节
3—1:3.4.5.6.7.8.10.11.12.14.15.
第二节
第三节
5—3: 1(B).2.3.4.5.6.7(B).
第四节
5—4: 1(A).2.
总习题五
1.2.3.4.5.6.7.8.9.10.11.12.13.14.
第六章第一节
第二节
弧长数学三不要求
6—2:1.2(B).3.4.6.8.9.10.11.12.15(B).16.
18. (数一.二:21.24.27.28)
第五节
例4.例6.数学三不要求
7—5:1(B).2(A).3.
第六节
例2.常数变易法
7—6: 3.
第七节
例4;例5.
7—7:1(A). 2.(B)
第八节
7—8:1. 2(B). 6.
第九节
数二.数三不要求
7—9:1. 2. 5.
总习题七
1.2.3(B).4(A).5.7.8.
第八章第一节
本章数二.数三不要求
1.2.3至20.
第四章第一节
4—1: 2(B) .4. 5. 6. 7.
第二节
4—2: 1(B). 2.(B)
第三节
4—3: 1.2.至24.
第四节
4—4: 1.2.至24.(单数)
总习题四
1.2.至40.(双数)
第五章第一节
5—1:3. 5. 7. 11. 12. 13(A).
第二节
5—2:1.2.3.4.5.6(A).9.10.11.12.13.14.
9—6:4.5.6.7.8.10.11.
第七节
数二.数三不要求
9—7:1.2.3.4.5.6.7.8.10.
第八节
9—8:1.2.5.6. 9.10.11.12.13.
总习题九
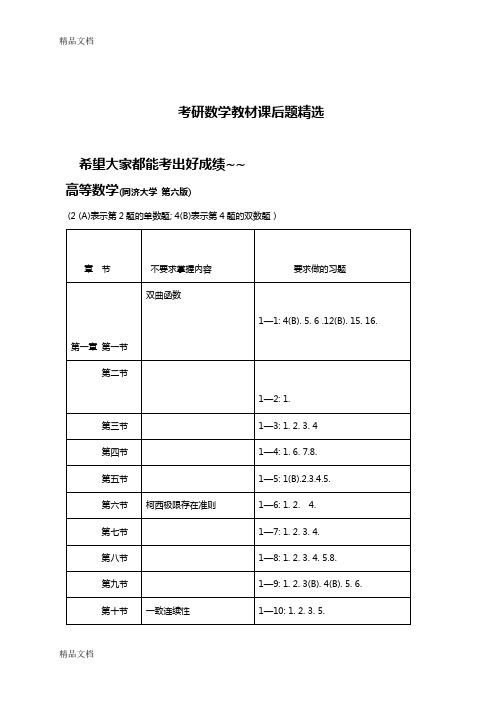
1.2.5.9.10.11.(数一:14.15.16.17.18.)
第十章第一节
10—1: 4(A).5(B).
第二节
二重积分的换元法
第三节
1—3:1. 2. 3. 4
第四节
1—4:1. 6. 7.8.
第五节
1—5: 1(B).2.3.4.5.
第六节
柯西极限存在准则
1—6:1. 2. 4.
第七节
1—7:1. 2. 3. 4.
第八节
1—8:1. 2. 3. 4. 5.8.
第九节
1—9:1. 2. 3(B). 4(B). 5. 6.
第十节
