基于CPLEX的原始—对偶嵌套分解算法
对偶与对偶算法教学课件

0 YˆT b AXˆ CT Xˆ YˆT AXˆ CT YˆT A Xˆ 0
所以 YˆT b AXˆ 0, Xˆ T ATYˆ C 0
例 原问题 max 2x1 4x2 x3 x4
1 3 0 1 8
s.t.
2 0
x1
1
1
x2
0
1
x3
0
YˆT b AXˆ 0, Xˆ T ATYˆ C 0
等价于
yˆi
bi
ai
Xˆ
0,i,
xˆ j PjTYˆ c j 0,j
含义:如果原(对偶)问题某不等式是松的(不等于0)
则其相应的对偶(原)变量必须是紧的(等于0)
证明充分性:
YˆT b AXˆ 0 bTYˆ YˆT AXˆ
Y 0
max bTY s.t. ATY C
Y 0
标准线性规划问题对偶问题的对偶问题
原问题
min
bT , bT
Y1
Y2
.t.
AT , AT
Y1 Y2
C
对偶问题
Y1 0, Y2 0
max CT X
A b
s.t.
A
X
b
X 0
max 2x1 x2 0x3 0x4 0x5
s.t. 0 1 1 5 0 0 3
1x1 0x2 1 15 x3 1 6 x4 0x5 3
0 0 2 15 1 6 1 1
x j 0, j 1,2,,5
将 x2, x1, x5 的表示式代入目标函数,原问题等价为
max
9
1 15
x3
1 3
x4
s.t. 0 1 1 5 0 0 3
1x1 0x2 1 15 x3 1 6 x4 0x5 3
cplex原理

cplex原理宝子!今天咱来唠唠Cplex这个超有趣的东西的原理呀。
Cplex呢,就像是一个超聪明的小管家,专门处理那些优化问题的。
你想啊,在生活里我们经常会碰到各种需要找到最佳方案的事儿,就像你要出门旅行,怎么安排行程能玩最多的景点还花最少的钱,这就是个优化问题,Cplex就擅长干这个。
它的原理呢,有点像在一个超级大的迷宫里找出口。
比如说,我们有好多的约束条件,这就好比迷宫里的墙壁啊、陷阱啥的。
这些约束条件规定了哪些路能走,哪些路不能走。
像在安排生产计划的时候,可能有机器的生产能力限制、原材料的数量限制这些约束,Cplex就得在这些限制里面去寻找那个最优解。
Cplex在这个大迷宫里开始探索的时候,它会运用一些超级厉害的算法。
这算法就像是它的小地图和指南针。
有一种算法就像是从一个点开始,然后慢慢向周围扩展,去看看哪个方向能让目标函数变得更好。
比如说目标是让利润最大化,那它就朝着利润可能增加的方向走。
这就好比你在找宝藏,你知道宝藏在一个方向能让你变得更富有,你就朝着那个方向走呗。
还有哦,Cplex在处理问题的时候,它会把那些复杂的数学模型转化成它能理解的形式。
这就像是把一篇超级难的文言文翻译成大白话一样。
那些数学公式、变量啥的,在它眼里就像是不同的小玩具,它要把这些小玩具按照规则摆弄好,找到那个最完美的组合。
比如说在物流配送问题里,货物的数量、车辆的载重、运输的距离这些变量,Cplex要把它们组合起来,让运输成本最低。
它还有一个很神奇的地方呢,就是它可以处理超级大规模的问题。
你想啊,要是有成千上万个变量和约束条件,这就像一个超级巨大的拼图,每个小块都得放在正确的位置。
Cplex就有这个本事,它不会被这么多的信息给搞晕,而是有条不紊地去分析、去计算。
这就像一个超级有耐心的小朋友在拼一个超级大的拼图,一块一块地试,直到拼出最完美的图案。
而且呀,Cplex在寻找最优解的过程中,它不是盲目地乱找。
它会根据之前的经验来调整自己的搜索策略。
3 LP问题的对偶理论
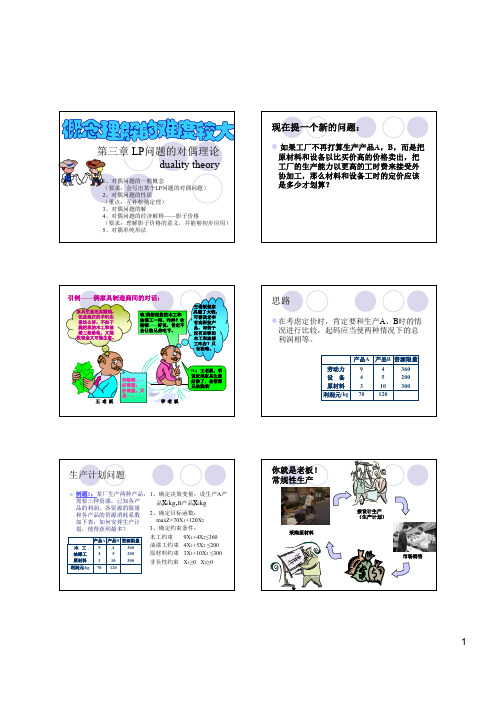
他/她——生产资料租用 者的投入: 租赁工厂的生产设备, 支付工时费和材料费, 考虑怎样的租赁价格可 以接受?
我——生产资料所有 者, 如何为每种资源定价?
产品A 产品B 资源限量 劳动力 设 备 原材料 利润元/kg 9 4 3 70 4 5 10 120 360 200 300
仅为理解“对偶规划”的意义 而设,现实生活中不存在“不劳 而获”的案例。如有发现“不劳 而获”存在,纯属巧合! 切勿认为“不劳而获”发生在 别人身上,也会发生在自己身上。
对偶问题(或原问题) 目标函数 MinW
对偶变量数:m个 第i个变量≥0 第i个变量≤0 第i个变量是自由变量 约束条件数:n 第i个约束条件类型为“≥” 第i个约束条件类型为“≤” 第i个约束条件类型为“=”
1、给每个原始约束条件定义一个非负对偶变量yi(i=1,2,…,n); 2、使原问题的目标函数系数cj变为其对偶问题约束条件的右端 常数; 3、使原问题约束条件的右端常数bi变为其对偶问题目标函数的 系数; 4、将原问题约束条件的系数矩阵转置,得到其对偶问题目标 函数的系数; 5、改变约束条件不等号的方向,即将“≤”改为“≥”; 6、原问题“max”型,对偶问题为“min”型
思路
在考虑定价时,肯定要和生产A、B时的情 况进行比较,起码应当使两种情况下的总 利润相等。
产品A 产品B 资源限量
价格嘛…… 好商量, 好商量。只 是…... 王 老 板 李 老 板
Hi:王老板,听 说近来家具生意 好惨了,也帮帮 兄弟我哦!
劳动力 设 备 原材料 利润元/kg
9 4 3 70
m aij yi cj j 1,2,, n s.t. i 1 i 1,2,, m yi符号不限,
第四章 线性规划的对偶问题

2 y1 2 y2 3 y3 4 y4 3000
因此得到的线性规划问题模型如下:
min w 600 y1 400 y2 300 y3 200 y4
3 y1 2 y2 y3 y4 2000 4 y y 3 y 2 y 4000 1 2 3 4 s.t. 2 y1 2 y2 3 y3 4 y4 3000 yi 0(i 1 ~ 4)
证明:
若(LP)有最优解,引进松弛变量y y1 ym 0,将
T
(LP)标准化得:
max cx 0T Y max cx x Ax Iy b,即 A, I b y x y 0 x, y 0
(LP)
(s.t.) u1 6u 2 28u3 5
2u1 3u 2 17 u3 6 u1 u 2 4u3 7 u 7u 2u 1 1 2 3 u1 , u 2 , u3 0
由于(LP) max cx 与(LD) min ub 形式上是等价的 Ax b uA c x 0 u 0 所以把它们称为一对对称的对偶规划。
表明(LP)极大化目标函数在可行域上有上界, 不可能无界。而一个有可行解的线性规划又不 可能为无界的情形,必然有最优解,从而 (LP)必有最优解。 同理:(LD)亦有最优解。
证明: 显然,有最优解的(LP)(LD),必有可行解。
推论2
如果x 、u 分别是( LP)(LD)的可行解,且 cx u b,则x 、u 分别是( LP)(LD)的最优解。
现在工厂考虑不进行生产而把全部可利用的资源都让给其它企 业单位,但又希望给这些资源订一个合理价格,既使别的单位愿意买, 又使工厂能得到生产这些产品时可以得到的最大效益. 这就需建立另一个线性规划模型,设y1 , y2 , y3 y4代表销售这四种资 源的价格,买方希望总售价尽可能低,即:
cplex 使用手册

线性规划及其对偶问题

10
3X1+2X2 60
X1+2X2 30
2X2 24
B C
可行域
0
10
2D0
30
X2 0
(2)、求最优解
X2
Z=40X1+50X2
30
0=40X1+50X2
(0,0), (10,-8) 20
C点: X1+2X2 =30
3X1+2X2 =60
A
10
可行解
Z=0
0
等值线
最优解:
令 XN 0
则
X
B 1b 0
定义 在约束方程组(2) 中,对于 一个选定的基B,令所有的非基变 量为零得到的解,称为相应于基B 的基本解。
定义 在基本解中,若该基本解满足非负约束,
即简称X 基B 可B行1解b ; 0对,应则的称基此B基称本为解可为行基基本。可行解,
基本解中最多有m个非零分量。
Min Z 0.1x1 0.3x2 0.9x3 0x4 1.1x5 0.2x6 0.8x7 1.4x8
2x1 x2 x3 x4 0x5 0x6 0x7 0x8 100
s.t.
0xx1102xx22xx3330xx4403xx5522xx6630xx7740xx88110000
bm
b1,b2,,bm 0
右端常数
(3) 线性规划模型矩阵形式
Max Z CX
s.t
AX b X 0
C c1 c2 cn
价值向量
x1
X
x2
xn
primal-dual method of multiplier -回复

primal-dual method of multiplier -回复这个问题要求我以“原始-对偶乘子法”为主题写一篇1500-2000字的文章,来逐步回答这个问题。
原始-对偶乘子法是一种优化算法,它在解决线性规划问题时特别有效。
我将为您逐步介绍原始-对偶乘子法的定义、基本原理、解决步骤以及它的应用领域和优点。
一、定义原始-对偶乘子法是一种优化算法,用于解决线性规划问题。
其基本思想是通过对问题的原始变量和对偶变量引入乘子,转化成求解一对互相关联的对偶问题,从而实现对原始问题的求解。
二、基本原理原始-对偶乘子法的基本原理是将原始问题和对偶问题联系起来,通过不断迭代求解原始问题和对偶问题,最终达到收敛的目标。
这种方法通过引入乘子,建立原始问题和对偶问题之间的关系,从而实现一种相互促进的求解过程。
三、解决步骤原始-对偶乘子法的解决步骤如下:1.建立原始问题和对偶问题的数学模型。
2.定义原始问题和对偶问题的目标函数及约束条件。
3.通过求解对偶问题的拉格朗日函数局部最小化问题,得到对偶问题的解,并更新乘子。
4.通过求解原始问题的凸优化问题,得到原始问题的解,并更新原始变量。
5.检查算法是否达到收敛条件,若达到则停止迭代,否则继续重复步骤3和步骤4。
四、应用领域原始-对偶乘子法在多个领域都有广泛的应用,包括但不限于:1.物流和供应链管理:用于优化货物运输和仓储的规划问题。
2.电力系统:用于电力市场调度和能源管理问题。
3.运输和交通问题:用于交通网络和路线规划优化。
4.生产计划和调度:用于生产资源分配和调度问题。
5.金融投资组合:用于优化资产配置和风险控制。
五、优点原始-对偶乘子法相比传统的优化算法具有以下优点:1.可以优化线性规划问题,并且对于某些特殊的问题类型有较好的效果。
2.能够获得原始问题的最优解和对偶问题的最优解。
3.具有较高的收敛速度和稳定性,能够在较短的时间内得到解决方案。
4.适用于大规模和复杂的问题,能够处理具有多个变量和约束的优化问题。
连续系统优化的嵌套分割算法实现

2004年1月系统工程理论与实践第1期 文章编号:100026788(2004)0120126204连续系统优化的嵌套分割算法实现路晓伟,蒋 馥(上海交通大学安泰管理学院,上海200052)摘要: 首先介绍了嵌套分割算法(N P 算法)用于离散系统优化的思想和方法,然后提出了连续系统优化的N P 算法实现的思路和方法,并通过将其用于一个经典问题的解决,说明了N P 算法应用于连续系统优化的可行性,同时展示了N P 算法在连续系统优化中优越的全局寻优能力Λ关键词: 嵌套分割算法;连续系统;优化;仿真中图分类号: N 945.15 文献标识码: A R ealizati on of N ested Partiti on s A lgo rithm A pp lyingto Con tinuou s System Op ti m izati onLU X iao 2w ei ,J I AN G Fu(A etna Schoo l of M anagem en t ,Shanghai J iao tong U n iversity ,Shanghai 200052,Ch ina )Abstract : F irst ,th is paper in troduces the idea and the m ethod of N ested Partiti on s A lgo rithm (N PA lgo rithm )app lying to discrete system op ti m izati on .T he p rinci p le of N P A lgo rithm app lying to con tin 2uou s system op ti m izati on is p ropo sed .F inally ,th is paper demon strates the feasib ility of N P A lgo rithmapp lying to con tinuou s system op ti m izati on and reveals its excellen t capab ility of global op ti m izati on byso lving a classical op ti m izati on p rob lem .Key words : nested partiti on s algo rithm ;con tinuou s system ;op ti m izati on ;si m u lati on收稿日期:2002212206资助项目:国家自然科学基金(70271038) 作者简介:路晓伟(1976-),男,汉族,山东人,上海交通大学管理学院博士生,主要从事仿真优化方法、管理信息系统等方面的研究1 引言在管理实践中,经常遇到一些复杂的系统优化问题,它们的输入和参数受到随机因素的影响,输出不确定,系统的目标函数也不能够用解析形式的表达式表示出来Λ近几年来,这种随机优化问题越来越受到人们的重视,并提出了许多能够有效解决这类问题的启发式仿真优化方法Λ如常用的遗传算法(GeneticA lgo rithm )、模拟退火算法(Si m u lated A nnealing )、蚂蚁算法(A n t algo rithm )等ΛSh i ,O ′lafsson 等于1997年提出了嵌套分割算法(N ested Partiti on s algo rithm ,简称N P 算法)[1,2],并从理论上对该算法的收敛性作了证明Λ这种优化方法将全局搜索与局部寻优结合在一起,具有开放性、并行性和全局性等突出的优点,能够解决许多复杂系统的确定型和随机型优化问题,并且具有很高的计算效率Λ它可以与其他优化方法进行有机的融合,兼收其他方法的优点Λ如Sh i ,O ′lafsson ,Chen (1999)等将嵌套分割算法与遗传算法结合起来,得到了比遗传算法更好的结果[3]Λ嵌套分割算法还具有显著的并行计算的特征,可以使用并行方法来进一步提高优化效率ΛSh i ,O ′lafsson ,Sun ,Chen ,Y ücesan (1999,2001)等将嵌套分割算法应用于T SP 问题、供应链管理、产品设计、机器分配等领域,取得了显著的效果[4-6]Λ虽然该方法具有非常广阔的应用前景,但国内目前还没有见到有关N P 算法研究和应用的文献Λ而且,现有的文献主要是侧重N P 算法在离散系统优化中的应用,文献[1]也只是提及N P 算法可以延伸到连续系统优化领域,没有对该算法在连续系统优化中的实现进行详细阐述,更没有这方面的应用案例Λ本文将在对离散系统优化的N P 算法进行简要介绍的基础上,提出完整的连续系统优化的N P 算法实现思路,然后通过将其应用于一个经典难题的解决说明了其实现过程,同时也展示了N P 算法在连续系统优化中的全局寻优能力Λ2 NP 算法的思想和方法对于复杂系统的优化问题,我们设系统参数的有限可行域为(,目标是优化系统的目标函数f :(→R ,即m in Η∈(f (Η)其中 ( <∞Ζ为便于分析,假设该问题有唯一的最优解Ηop t ∈(,满足对所有的Η∈( Ηop t ,有f (Ηop t )<f (Η)Ζ在实践中,f (Η)经常是复杂系统性能指标的测度,而且没有解析式用以表达系统性能指标与参数的解析关系Ζ这种情况下,需要用仿真的方法,用系统性能指标的仿真结果L t (Η)来估计f (Η)Ζ目标函数的形式既可以是确定型的,也可以是随机型的Ζ定义1 一个通过固定的分割策略得到的区域称为该策略下的可行域(V alid R egi on )Λ只含有一个单解的细分区域称为单解域(Singleton R egi on )Λ所有可行域的集合表示为2Ζ单解域具有特别的意义,我们把单解域的集合表示为20ΖN P 算法的实质是着眼于可行解的集合,而不是着眼于单个可行点,在这点上它是与其他启发式算法不同的ΖN P 算法是对可行域进行反复细分的过程Ζ从整个可行域(开始,将整个可行域逐渐细分,直到分为单解域或达到精度要求为止Ζ定义2 由原有限可行域开始进行分割,到达一个可行域的分割层数成为该可行域的深度(D ep th ),表示为d :2→N 0Ζ原可行域的深度为0,即d (()=0Ζ单解域具有最大深度,因此也被称为最大深度域Ζ定义3 如果一个可行域Ρ∈2是通过分割可行域Γ∈2得来的,则称Ρ为Γ的子域(Sub regi on ),Γ称为Ρ的母域(Sup erregi on )Ζ我们定义母域函数映射s :2→2,若Ρ∈2 (,则s (Ρ)=Γ∈2,当且仅当Ρ<ΓΖ为使定义完整起见,定义s (()=(Ζ设定效果函数I :2→R ,用来选择最有希望包含最优解的区域(最可能域),因此称之为品质索引数(P rom ising Index )ΛN P 算法具有开放性,可以根据需要设定品质索引数的形式,唯一的要求就是它要与单解域上的效果函数相一致Ζ假设经过第k 次重复分割,得到了最可能域Ρ(k )Α(Ζ然后把该可行域分割成M Ρ(k )个子域,并把Ρ(k )以外的整个区域看成一个区域Ζ在每一次重复分割的时候,我们都只是考虑M Ρ(k )+1个不相交的可行域的子集(初次分割除外)Ζ然后在得到的每个区域上利用随机抽样方法计算该区域的品质索引数,用以比较确定哪个区域是最可能域Ζ然后依此重复进行分割,直到得到不再变化的单解域为止Ζ如果Ρ(k )以外的整个区域被认为是最可能域,则要回溯到包含当前最可能域的较大区域,并将其作为下一步继续分割的最可能域Ζ由于所得到的分割区域是一层一层嵌套的,所以该优化方法称为嵌套分割法(N ested Partiti on s M ethod )ΛN P 算法包括四个基本算子:分割(Partiti on ),抽样(Sam p ling ),选区(Selecti on ),回溯(B ack 2track )Ζ其寻优过程也是反复使用这四个算子的重复过程Ζ在对得到的可行域进行抽样时,可以采取多种多样的随机抽样方法,只要满足区域中的每一个点被选择的概率大于0即可Ζ3 连续系统优化的NP 算法实现对于可行域是有限的连续空间的系统优化问题,不管是确定型的还是随机型的,仍然可以使用N P 算法来实现Λ在这种情况下,要把可行域无限分解为单解域理论上需要无穷次嵌套分割,因此几乎是不可能的Λ我们可以设定一个精度指标Ε,当得到的最优解在精度要求的范围之内,就可以认为得到了连续系统优化问题的最优解(满意解)Λ利用N P 算法实现连续系统优化,需要设计优化方案,包括分割区域的形状、每层的分割区域数目、嵌套分割深度、精度要求等Ζ设该连续系统优化问题具有n 个系统参数:x 1,x 2,…,x n ,其取值范围分别为721第1期连续系统优化的嵌套分割算法实现[x ib,x if](i=1,2,…,n)Ζ最优解的精度要求为ΕΖ考虑到分割策略一经确定,就应保持不变Ζ为方便起见,我们设定每个系统参数都是平均分割的,每次分割将参数x i平均分割为N i等份,分割区域的形状为凸多面体形Ζ当系统参数为二维时,分割区域为矩形;系统参数为三维时,分割区域为长方体Ζ有时为方便起见,可以将各个参数的分割数目设为相等,即N1=N2=…=N n=NΖ当达到精度要求时,应使经分割得到的最可能域的边长小于精度ΕΖ经过一次分割,将得到7n i=1N i个子域,得到的子域Ρ(k)大小缩减为原来的17n i=1N iΖ经过一次分割,每一个参数的范围都变为原来的1 N i,因此满足不等式m axi x if-x ibN D iΦΕ(1)的最小正整数D就是所需分割的最大深度Ζ图1 连续系统优化N P算法的实现流程图对当前最可行域的每个分区进行抽样时,确定每个分区的抽样点数目为m,并使得分区内的每一个点被抽样的概率大于0Ζ为适当增加第MΡ(k)+1个分区(即当前最可能域之外的整个区域)的抽样密度,保证N P算法对连续系统优化的全局寻优能力,可以适当增加该区域的抽样点数目,如我们可以设该数目为m ・d,其中d为当前分区的深度Ζ因此,每进行一次嵌套分割,所需的抽样点数目为m 7n i=1N i+m d,则D层深度的嵌套分割所需的最少抽样点数目为m D7n i=1Ni+D+12Ζ在仿真优化中,每进行一次抽样,就是调用一次仿真程序Ζ尤其是当仿真模型非常复杂时,仿真程序的执行时间占用了仿真优化的大部分时间Ζ因此,仿真优化的计算效率在很大程度上取决于调用仿真程序的次数Ζ在保证满足精确度要求和全局寻优能力的前提下,尽量减少调用仿真程序的次数,是提高N P算法计算效率的主要途径Ζ如果系统参数每次分割的数目N i减少,则所需的分割层数D就要相应增加Ζ而减少每个区域上的抽样数目m,又会使得N P算法的全局寻优能力降低Ζ因此,确定连续系统的N P算法优化方案,就是要合理平衡分割数目N i、分割深度D和每个区域上的抽样数目m,使得调用仿真程序的次数尽可能少Ζ连续系统优化的N P算法实现框图如图1所示Ζ将分割得到的最可能域是否满足精度要求作为判断优化是否结束的准则Ζ如果没有达到精度要求,则继续对当前最可能域进行分割,并对分割得到的各个子域及其之外的整个区域进行抽样,并通过比较,找到品质索引数最大的区域Ζ如果该区域是当前最可能域的子域,则将其作为最可能域Ζ如果该区域是当前最可能域之外的整个区域,则进行回溯,将深度减1,并将当前最可能域的母域作为下一步的最可能域Ζ依此重复进行,直到达到精度要求为止,此时取最终分区的几何中点作为连续系统优化问题的最优解(满意821系统工程理论与实践2004年1月解)Ζ4 NP 算法解决连续系统优化问题的算例我们考虑用N P 算法解决连续系统优化的“大海捞针”问题:m ax Z =30.05+(x 21+x 22)2+(x 21+x 22)2, x 1,x 2∈[-5.12,5.12]图2 连续系统算例的图象该问题具有唯一全局最优解,四个局部最优解,其图象如图2所示Ζ设定精确度要求Ε=0.001,两个系统参数的单次分割数目N 1=N 2=3,则经过一次分割,得到的子域为其母域大小的1 9Ζ根据式(1)可得:10.243DΦ0.001 取满足上式的最小正整数D ,得D =9Ζ因此,可以确定N P 算法的优化方案为:对最可能域每次将各个系统参数平均分割为3部分,最大分割深度为9,对每个区域随机抽样100个点,精度为0.001Ζ根据优化方案,编写C 语言程序,可以得到结果为:最优解(x 1,x 2)3=(0,0),最优值Z 3=0Ζ回溯次数为0,可见N P 算法用于解决该问题具有很强的收敛性Ζ5 结束语作为一种新的仿真优化方法,N P 算法从开始提出到付诸应用,主要都是针对离散系统的Λ而对于在管理实践中经常遇到的连续系统优化问题,N P 算法没有给出完整的规则和方法,也未见有该方面的应用实例Λ本文从N P 算法的理论基础出发,提出了将N P 算法用于解决连续系统优化的思路、方案和方法Λ通过将N P 算法用于一个经典难题的解决,我们可以看到,N P 算法经过适当的发展,完全可以应用于连续系统的优化问题,并且具有显著的全局寻优能力Λ参考文献:[1] Sh i L .N ested partiti on s m ethod fo r global op ti m izati on [J ].Operati on s R esearch ,2000,48(3):390-407.[2] O ′lafsson S ,Sh i L .A n in tegrated fram ew o rk fo r determ in istic and stochastic op ti m izati on [A ].P roceedings of the1997W in ter Si m u lati on Conference [C ].1997.358-365.[3] Sh i L ,O ′lafsson S ,Chen Q .A new hyb rid op ti m izati on algo rithm [J ].Compu ters &Indu strial Engineering ,1999,(36):409-426.[4] Sh i L ,O ′lafsson S ,Sun N .N ew parallel random ized algo rithm s fo r the traveling sales m an p rob lem [J ].Compu ters&Operati on s R esearch ,1999,(26):371-394.[5] Sh i L ,Chen C H ,Y ücesan E .Si m u ltaneou s si m u lati on experi m en ts and nested partiti on fo r discrete resou rce alloca 2ti on in supp ly chain m anagem en t [A ].P roceedings of the 1999W in ter Si m u lati on Conference [C ].1999.395-401.[6] Sh i L ,O ′lafsson S ,Chen Q .A n op ti m izati on fram ew o rk fo r p roduct design [J ].M anagem en t Science ,2001,47(12):1681-1692.921第1期连续系统优化的嵌套分割算法实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为 核 心 求 解 器 将 算 法 实 现 。原 始 — — 对 偶嵌 套 分 解 算 法 将 原 问 题 分 解 成 一 系 列 子 问 题 , 每个 子 问题 既 可 以 收 到 来 自前 一 阶 段 子 问题 的价 格 信 息 , 可 以收 到 来 自后 一 阶段 子 问 题 的 资 源 信 息 , 传 统 嵌 套 分 解 算 法 具 有 更 加 又 较 平 衡 的 信 息 传 递 方 式 和 良好 的 收敛 性 。 实验 数 据 表 明 , 算 法 在 求 解 较 大 规 模 、 疏 度 较 小 、 合 度 较 小 的 下 三 该 稀 耦 角 结 构 线 性 规 划 问题 时 , 比单 纯 形 法 , 时 间效 率 上 有 明 显 提 高 。 相 在
r to a d lw e iy a i n o d nst .
Ke or y w ds:i e rp o r mm ig; e t d d c mp sto t o p i ld a e o o i o CPL l a r g a n n n se e o o iin meh d; rma — u ld c mp st n; i EX ;i lx m eh d smp e t o
p o e it e i so u r b e s Ea h s b r blm a t rc n o ma in fo t e p e i u n sa d r — r blm n o a s re fs bp o lm . c u p o e h sboh p ie i fr t r m h r vo so e n e o
Ne t d Pr a _ a c mp st n Me h d Ba e n CPL se i l m Du l De o o io t o s d o i EX
L U J n h a AN B — in I u — u ,L o x o g
ቤተ መጻሕፍቲ ባይዱ
( colfE o o i n n g m n , s g u nvrt, ei 0 4 hn ) Sh o o cn m c a dMa a e et Ti h a U i sy B in 10 8 ,C ia s n ei jg 0
关 键 词 : 性 规 划 ; 套 分 解 算 法 ; 始 一对 偶 分 解 ; P E 单 纯 形 法 线 嵌 原 C L X; 中 图 分 类 号 :2 1 1 0 2 . 文章标识码 : A 文 章 编 号 :0 73 2 (0 8 0 —0 10 10 —2 1 2 0 )6 0 0 —5
0 引 言
由于管 理科 学 的 日趋 发展 和定 量 化 的研 究趋 势 , 有 庞大组 织体 系 的企业 单位 与行 政机 构不 断 涌现 , 具
实 际应用 中的线 性规 划 问题规 模通 常都 非 常巨 大 , 束 及变 量个 数 成 百 上千 , 至 更 多 。 同时 注意 到 , 约 甚 这 样 的大 规模 线性 规划 问题 通 常都有 自己的特 殊结 构 , 且 规 模越 大 , 种结 构 性 可能 越 明显 : 量或 约束 并 这 变
s u c n o m ain fo t e lte n s I a o e b l n e tu t r nd mo e rpi o v re c p e h n o r e i f r to r m h atr o e . th sa m r aa c d sr cu e a r a d c n e g n e s e d t a ta iina n se d c m p sto eh d . Co p t t n ltss ho t a h e td rma — u lde o p sto r d to l e t d e o o ii n m t o s m u a i a e t s w h tt e n se p i ld a c m o i n o i m eh d h sh g e i f ce c h n sm p e lo ih i o vn a g — c l i a r g a t o c u ln t o a i h rtme e i n y t a i lx a g rt m n s li g lr e s a elne rp o r ms wih l w o p i g i
对 偶嵌 套 分解 算 法
刘均华, 蓝伯雄
( 华 大学 经济 管理 学 院 , 京 10 8 ) 清 北 0 0 4
摘
要 : 文 介 绍 了 一 种求 解 大 规 模 下 三 角 结 构 线 性 规 划 问题 的原 始 一对 偶 嵌 套 分 解 算 法 , 以 C L X 9 0作 本 并 PE .
Abs r t Ths p p rito c sa n se rma — u ld c mp st n meh d frl r e s a elne rp o r mswi tac : i a e n r du e e t d p i ld a e o o ii t o o a g —c l i a r ga t a o h
第 l 7卷 第 6期
20 0 8年 1 2月
运 筹 与 管 理
OP ERATI ONS RES EARCH AND M ANAGEM ENT S ENCE CI
Vo . 7, . 1 1 No 6
De . 0 c 2 08
基 于 C L X 的原 始 PE
