管理科学与工程《高级运筹学》试题
管理运筹学试题及解题思路
习题答案或解题思路习题1x 1 、x 2吨，则问题是数学模型为： 1.2设一般时间、黄金时间、广播、报纸广告单元数分别为x 1、x 2、x 3、x 4，则线性规划模型为：1.3 设x 1为每周动物饲料量，x 2为每周谷物饮料量。
其数学模型为：1.4 设x 1、x 2、x 3分别为按各种下料所得的钢筋根数，y 1、y 2分别为满足90、60根后多余的根数，Z1.5用图解法得最优解为 X* ＝(10, 30)T ，Z*＝ 6800 1.6最优解为：X *＝ (15/4 , 3/4 , 0 , 0 )T ，Z * ＝ 33/41.7最优解为：X* = (0，10)T ，Z* = 20当 －20 ≤ △b 1 ≤ 60时，原最优解基不变，最优解为：X* ＝ (0，10+1/2△b 1，0，25+1/2△b 1，30-1/2△b 1，60+3/2△b 1)T ，Z* ＝ 20 +△b 1 1.8 (1) 最优解X * ＝ (2.5，25，0，0，0)T ，MaxZ = 57.5（2）最优解X * ＝ (5.5，19，3，0，0)T 1.9 甲395，乙45，丙01.10 A 1生产40万瓶，A 2生产100万瓶，最大利润62万元。
1.11 原问题的最优解如表1所示：1.12 设x j （j=1,…,8）分别表示八种产品的产量，则问题的数学模型如下：1.13 设 x j为第 j 种生产过程的日产量，j=1,2,3；y 为第 j 种生产过程是否可用，y j =0、1。
1.14 设购买远、中、短程客机分别为1.15（1）设定变量名称（各系列机床所安排的产销量）设i 为产品系列种类，i = 1~6；设j 为指标种类，j = 1~3；设x i 为第i 种产品系列的计划产销量，设A ij 为第i 种产品所实现的第j 种指标数值。
（2）编制目标函数（利润最大化）Max Z = (A 11-A 13) x 1 + (A 21-A 23) x 2+ (A 31-A 33) x 3+ (A 41-A 43) x 4 + (A 51-A 53) x 5+ (A 61-A 63) x 6（3）编制约束条件：CA系列生产9124台，小CAK系列生产1720台，普及型生产156台，则满足所有约束，并可得最大利润为6617.6万元。
管理运筹学试题二(含答案)
运筹学试题二
一、用单纯形法求解下述线性规划问题（20分）
⎧⎨⎪⎪⎩
⎪⎪0
,824424m ax 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z
二、设一线性规划问题为（25分）
234
700件，且在第二、三周能加班生产。
加班后，每周可增产200件产品，但成本每件增加5元。
产品如不能在本周交货，则每件每周存贮费是3元。
问如何安排生产计划，使总成本最小，要求建立运输问题数学模型求解。
（25分）
四、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知，每周星期一至星期五不能出席某一讲座的学生数如下表：（20分）
座的学生总数。
试题二答案
()0
1310232>=⎪⎪⎭⎫
⎝⎛-=r
6
*=Z
（3） 最优解不满足新增加的约束条件2231≥+-x x ∴最优解要发生改变 将约束条件改写为 22631-=+-x x x
加入最优表中继续迭代。
运筹学试卷与参考答案
运筹学 试卷B 及参考答案（本题20分）一、考虑下面的线性规划问题：Min z=6X 1+4X 2约束条件： 2X 1+X 2 ≥1 3X 1+4X 2≥3 X 1 , X 2 ≥ 0(1) 用图解法求解,并指出此线型规划问题是具有惟一最优解、无穷多最优解、无界解或无可行解；(2) 写出此线性规划问题的标准形式； (3) 求出此线性规划问题的两个剩余变量的值； (4) 写出此问题的对偶问题。
解：（1）阴影部分所示ABC 即为此线性规划问题的可行域。
其中，A （0，1），B （1，3/4），C （1/5，3/5）。
显然，C （1/5，3/5）为该线性规划问题的最优解。
因此，该线性规划问题有唯一最优解，最优解为：121/5,3/5,*18/5x x z ===。
——8分。
说明：画图正确3分；求解正确3分；指出解的情况并写出最优解2分。
（2）标准形式为：121231241234min 6421343,,,0z x x x x x x x x x x x x =++-=⎧⎪+-=⎨⎪≥⎩ X 1 X 2 AB——4分 （3）两个剩余变量的值为：340x x =⎧⎨=⎩——3分（4）直接写出对偶问题如下：12121212max '323644,0z y y y y y y y y =++≤⎧⎪+≤⎨⎪≥⎩——5分（本题10分）二、前进电器厂生产A 、B 、C 三种产品，有关资料下表所示：学模型，不求解）解：设生产A 、B 、C 三种产品的数量分别为x 1，x 2和x 3，则有：——1分123123123123123max 810122.0 1.5 5.030002.0 1.5 1.21000200250100,,0z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤⎪⎨≤⎪⎪≤⎪≥⎪⎩ ——14分，目标函数和每个约束条件2分（本题10分）三、某电子设备厂对一种元件的年需求为2000件，订货提前期为零，每次订货费为25元。
《管理运筹学》试题及答案
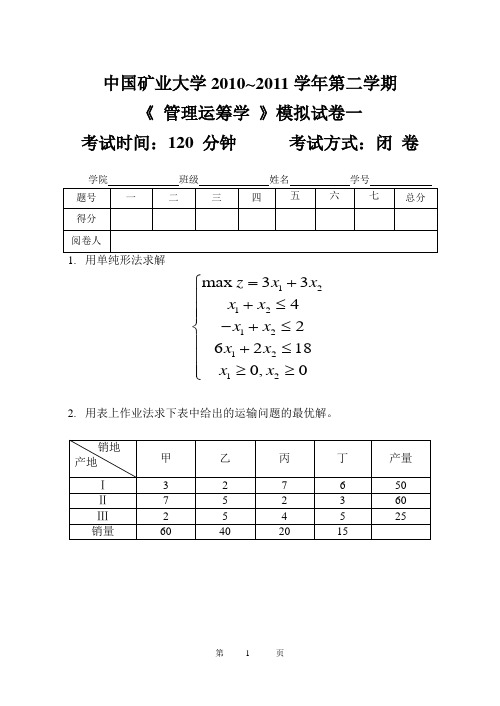
中国矿业大学2010～2011学年第二学期《 管理运筹学 》模拟试卷一考试时间：120 分钟 考试方式：闭 卷1212121212max 334262180,0z x x x x x x x x x x =+⎧⎪+≤⎪⎪-+≤⎨⎪+≤⎪≥≥⎪⎩2. 用表上作业法求下表中给出的运输问题的最优解。
答案： 1.解：加入人工变量，化问题为标准型式如下：1234512312412512345max 3300042.6218,,,,0z x x x x x x x x x x x s t x x x x x x x x =++++++=⎧⎪-++=⎪⎨++=⎪⎪≥⎩(3分)下面用单纯形表进行计算得终表为：所以原最优解为 *(3,0,1,5,0)T X =2、解： 因为销量：3+5+6+4+3=21；产量：9+4+8=21；为产销平衡的运输问题。
（1分）由最小元素法求初始解：（5分）用位势法检验得：（7分）所有非基变量的检验数都大于零，所以上述即为最优解且该问题有唯一最优解。
此时的总运费：min 45594103112011034150z =⨯+⨯+⨯+⨯+⨯+⨯+⨯=。
3、解：系数矩阵为：1279798966671712149151466104107109⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦（3分）从系数矩阵的每行元素减去该行的最小元素，得：50202 23000 010572 98004 06365⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦经变换之后最后得到矩阵：70202 43000 08350 118004 04143⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦相应的解矩阵：01000 00010 00001 00100 10000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦（13分）由解矩阵得最有指派方案：甲—B，乙—D,丙—E，丁—C，戊—A 或者甲—B,乙—C,丙—E，丁—D，戊—A （2分）所需总时间为：Minz=32 （2分）中国矿业大学2010～2011学年第二学期《管理运筹学》模拟试卷二考试时间：120 分钟考试方式：闭卷1.求解下面运输问题。
运筹学试卷A卷+答案
学年度第一学期期末考试《运筹学》（八）卷专业班级姓名学号一、单选题（每题的备选答案中只有一个最佳答案，每题2分，共30分）I、运筹学的主要内容包括：（）A.线性规划B.非线性规划C.存贮论D.以上都是2、下面是运筹学的实践案例的是：（）A.丁谓修守B.田忌赛马C.二战间，英国雷达站与防空系统的协调配合D.以上都是3、规划论的内容不包括：（）A.线性规划B.非线性规划C.动态规划D.网络分析4、关于运筹学的原意，卜冽说法不正确的是：Λ.作业研究B.运作管理C.作战研究D.操作研究5,运筹学模型：A.在任何条件下均有效B.只有符合模型的简化条件时才有效C.可以解答管理部门提出的任何问题D.是定性决策的主要工具6、最早运用运筹学理论的是：Λ.二次世界大战期间，英国军事部门将运筹学运用到军事战略部署B.美国最早将运筹学运用到农业和人口规划问逸上C.二次世界大战后，英国政府将运筹学运用到政府制定计划D.50年代,运筹学运用到研究人口，能源,粮食，第三世界经济发展等问题上7、下列哪些不是运筹学的研究范用：A.库存控制B.动态规划C.排队论D.系统设计8、对运筹学模型的下列说法，正确的是：A.在任何条件下均有效B.只有符合模型的简化条件时才有效C.可以解答管理部门提出的任何问题D.是定性决策的主要工具9、线性规划具有多重最优解是指（）A.目标函数系数与某约束系数对应成比例B.最优表中存在非基变量的检验数为零C.可行解集合无界D.基变量全部大丁•零10.图解法通常用于求解有（）个变量的线性规划问题。
A.1B.2C.4D.5Ik以下不属于运筹学求解目标的是：A.最优解B.次优解C.满意解D.劣解12、线性规划问返的最优解（）为可行解。
A.一定B.不一定C.一定不D.无法判断13、将线性规划问感转化为标准形式时,下列说法不正确的是:A.如为求Z的最小值，需转化为求-Z的垠大值B.如约束条件为W,则要增加一个松驰变量C.如约束条件为2,则要减去一个剩余变量D.如约束条件为=,则要增加一个人工变易14、关于图解法，下列结论最正确的是：A.线性规划的可行域为凸集。
运筹学试题及答案4套
《运筹学》试卷、（15分）用图解法求解下列线性规划问题max z = 3T:+4x2—两十2兀2 —8Xj + 2X2 < 12 + x2 <1S“ >0,x2 >0二、（20 分）下表为某求极大值线性规划问题的初始单纯形表及迭代后的表, 6为松弛变量，试求表中二至显的值及各变量下标怕至匸的值。
三、（15分）用图解法求解矩阵对策[2 5 -1 3 _A =其中[4 13 -2J四、（20分）（1）某项工程由8个工序组成，各工序之间的关系为试画出该工程的网络图。
（2）试计算下面工程网络图中各事项发生的最早、最迟时间及关键线路（箭线下的数字是完成该工序的所需时间，单位：天）五、（15分）已知线性规划问题maK z = 10工i + 24工？十20xj + 20^4+ 25x:］工1十工2十2X B十十5x s<19討彳2曲+ 4冏+3Xj 4- 2X4+ Xj < 57（勺“ Q=U3A5）其对偶问题最优解为-7' - ■■- :'- - ■，试根据对偶理论求原问题的最优解六、（15分）用动态规划法求解下面问题:MAX Z = x{+ x 3 =c匕i 八1,2"七、（30分）已知线性规划问题MAX 2 ■ 2毛一冷+叱心十呵十心三b ^t.i^ J 2 -P 2X 3<47i #x 2r x 3 王D用单纯形法求得最优单纯形表如下， 试分析在下列各种条件单独变化的情况下，最优解将如何变化。
（1） 目标函数变为山…--'---； （2） 约束条件右端项由」一变为一」； （3） 增加一个新的约束： "'八、（20分）某地区有A 、B 、C 三个化肥厂向甲、乙、丙、丁四个销地供应同一 种化肥，已知产地产量、销地需求量和各产地运往不同销地单位运价如下表，试 用最小元素法确定初始调运方案，并调整求最优运输方案《运筹学》试卷二、（20分）已知线性规划问题：min z - 2Z] +3龙立+2也兀]+ 2X2+3X3+ > 2sU - 2x x 4-J3一巧十？咒° 三-3gO（j 二12第）（a）写出其对偶问题；（b）用图解法求对偶问题的解；（c）利用（b）的结果及对偶性质求原问题的解。
2019级硕士研究生——《高级运筹学》(试卷A)(1)
x1 - x52 - 5x3 + 4x4
³
-10
) x1x2
-6
+
x2 + x42 x2 - 3x1
六、计算题：（10 分）
分数 评卷人
分别利用 ODE23 和 ODE45 函数求解下列常微分方程，并绘制各阶导数的函数曲线图，进 行比较分析。
共5页 第2页
3SIN(T)Y(5)+7COS(T)Y(4) +2Y'''-6Y''+7COS(T)Y=COS(T)-SIN(T)
分数 评卷人
分别用 FMINUNC 函数、FMINSEARCH 函数求解下列无约束非线性规划模型，并对解的 质量进行比对，从而说明两个函数所使用算法的优越性。提交 WORD 版纸质结果，并提 交.M 数据文件。（10 分）
min
f
( x)
=
eççèæ
x1
-
x2 x3
+ x4 x5
÷÷øö èæçç 3x12
复查人：
分数 评卷人
用 LINPROG 函数求解下列线性规划，并说明使用算法、迭代次数及优化结构体参数信息。 提交 WORD 版纸质结果，并提交.M 数据文件。（5 分）
max f (x) = 5x1 + 15x2 + 3x3 - 8x4 - 11x5 - 7x7 + 12x8
ì2x1 + 6x2 + 3x3
+
5 x25
-
3x3 x4 x1 +
-5 x5
+
lnççèæ 2
x2 x3 +
x5
- 1÷÷øö
2.1《管理运筹学》考试试卷(A)
2.1《管理运筹学》考试试卷（A）学号姓名成绩一、（ 20 分）下述线性规划问题Max z=-5x1+5x2+13x3ST-x1+x2+3x3 ≤ 20 ——①12x1+4x2+10x3 ≤ 90 ——②x1,x2,x3 ≥ 0先用单纯形法求出最优解，然后分析在下列条件下，最优解分别有什么变化？（ 1 ）约束条件①的右端常数由 20 变为 30 ；（ 2 ）约束条件②的右端常数由 90 变为 70 ；（ 3 ）目标函数中的 x3 的系数由 13 变为 8 ；（ 4 ）增加一个约束条件③ 2x1+3x2+5x3 ≤ 50（ 5 ）将原有约束条件②变为 10x1+5x2+10x3 ≤ 100二、（ 10 分）已知线性规划问题Max z= 2x1+x2+5x3+6x4 对偶变量2x1 +x3+x4 ≤ 8 y12x1+2x2+x3+2x4 ≤ 12 y2x1,x2,x3,x4 ≥ 0其对偶问题的最优解为 y1*=4 ， y2*=1 ，试用对偶问题的性质，求原问题的最优解。
三、（ 10 分）某地区有三个化肥厂，除供应外地区需要外，估计每年可供应本地区的数字为：化肥厂 A —— 7 万吨， B —— 8 万吨， C —— 3 万吨。
有四个产粮区需要该种化肥，需要量为：甲地区—— 6 万吨，乙地区—— 6 万吨，丙地区—— 3 万吨，丁地区—— 3 万吨。
已知从各化肥厂到各产粮区的每吨化肥的运价如下表所示（单位：元 / 吨）：根据上述资料指定一个使总的运费最小的化肥调拨方案。
四、（ 10 分）需要分配 5 人去做 5 项工作，每人做各项工作的能力评分见下表。
应如何分派，才能使总的得分最大？五、（ 10 分）用动态规划方法求解：Max F=4x 1 2 -x 2 2 +2x 3 2 +123x 1 +2x 2 +x 3 =9x1,x2,x3 ≥ 0六、（ 10 分）公司决定使用 1000 万元开发 A 、 B 、 C 三种产品，。