概率统计2006下B卷0701试题与答案
概率统计b复习题答案

概率统计b复习题答案1. 随机变量X服从标准正态分布,求P(X > 1.96)的值。
答案:根据标准正态分布表,P(X > 1.96) = 1 - P(X ≤ 1.96) = 1 - 0.975 = 0.025。
2. 设随机变量X服从二项分布B(n, p),其中n=10,p=0.3,求X的期望值和方差。
答案:期望值E(X) = np = 10 × 0.3 = 3,方差Var(X) = np(1-p) = 10 × 0.3 × 0.7 = 2.1。
3. 已知随机变量X服从泊松分布,其参数λ=5,求P(X ≥ 3)的值。
答案:P(X ≥ 3) = 1 - P(X ≤ 2) = 1 - (e^(-5) × (5^0/0! + 5^1/1! + 5^2/2!)) = 1 - (0.0067 + 0.0337 + 0.0842) = 0.8754。
4. 某工厂生产的零件寿命X服从指数分布,其概率密度函数为f(x) = 0.1e^(-0.1x),求零件寿命超过1000小时的概率。
答案:P(X > 1000) = ∫(1000, +∞) 0.1e^(-0.1x) dx = e^(-0.1 × 1000) = e^(-100)。
5. 已知随机变量X和Y的相关系数为0.8,求X和Y的协方差。
答案:由于相关系数ρ_{XY} = Cov(X, Y) / (σ_X × σ_Y),且已知ρ_{XY} = 0.8,但未给出X和Y的标准差,因此无法直接计算协方差Cov(X, Y)。
6. 设随机变量X服从正态分布N(μ, σ^2),其中μ=100,σ=10,求P(90 < X < 110)的值。
答案:首先将X标准化,得到Z = (X - μ) / σ = (X - 100) / 10。
然后求P(90 < X < 110) = P((90 - 100) / 10 < Z < (110 -100) / 10) = P(-1 < Z < 1)。
2006年全国各地高考数学试题12--第十二章概率与统计

第十二章概率与统计1.(2006年福建卷)一个均匀小正方体的6个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2。
将这个小正方体抛掷2次,则向上的数之积的数学期望是__49__。
2..(.2006年重庆卷)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg).,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是..(.C) (A)20..............................(B)30 (C)40.............................(D)503.(2006年全国卷II)一个社会调查机构就某地居民的月收入调查了10.000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10.000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)4.(2006年四川卷)()()1,2,3,4,1,2,3,4P k ak b k ξ==+=,又ξ的数学期望3E ξ=,则a b +=__10_____; 5.(2006年江苏卷)某人5次上班途中所花的时间(单位:分钟)分别为x ,y ,10,11, 9.已知这组数据的平均数为10,方差为2,则|x -y |的值为(A)1 (B)2 (C)3 (D)4解:.由平均数公式为10,得()11011910,5x y ++++⨯=则20x y +=;又由于方差为2,则()()()()()22222110101010111091025x y ⎡⎤-+-+-+-+-⨯=⎣⎦得22208 2=192x y xy +=,所以有4x y -===,故选(D)点评:本题主要考查平均数与方差的定义等统计方面的基础知识 6.(2006年江西卷)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出2个红球可获得奖金50元,现有甲,乙两位顾客,规定:甲摸一次,乙摸两次,令ξ表示甲,乙摸球后获得的奖金总额。
概率论与数理统计试题(含答案)

概率论与数理统计期末考试试卷参考解答及评分标准开/闭卷 闭卷A/B 卷A 课程编号2219002801-2219002811课程名称概率论与数理统计学分3命题人(签字) 审题人(签字) 年 月 日第一部分 基本题一、选择题(共6小题,每小题5分,满分30分。
在每小题给出的四个选项中,只有一个是符合题目要求的,把所选项前的字母填在题后的括号内)(每道选择题选对满分,选错0分) 1. 事件表达式A B 的意思是 ( ) (A) 事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 (C) 事件B 发生但事件A 不发生 (D) 事件A 与事件B 至少有一件发生 答:选D ,根据A B 的定义可知。
2. 假设事件A 与事件B 互为对立,则事件A B ( ) (A) 是不可能事件 (B) 是可能事件 (C) 发生的概率为1 (D) 是必然事件 答:选A ,这是因为对立事件的积事件是不可能事件。
3. 已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) (A) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 (C) 自由度为1的F 分布 (D) 自由度为2的F 分布答:选B ,因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的χ2分布。
4. 已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( ) (A) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3)答:选C ,因为相互独立的正态变量相加仍然服从正态分布,而E (X +Y )=E (X )+E (Y )=2-2=0, D (X +Y )=D (X )+D (Y )=4+1=5, 所以有X +Y ~N (0,5)。
5. 样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) (A) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计(C) 22X 是σ2的无偏估计(D) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计答:选B ,因为样本均值是总体期望的无偏估计,其它三项都不成立。
2)《概率统计》试题B卷答案

广州大学2008-2009学年第二学期考试卷概率论与数理统计(B 卷)参考解答与评分标准一、选择题(在各小题四个备选答案中选出一个正确答案,填在题末的括号中,本大题共5个小题,每小题3分,总计15分)1.对于任意两个事件A 与B ,若)()()(B P A P AB P =,则( A )。
A.)()()(B P A P B A P = B. )()()(B P A P AB P = C. ∅=AB D. )()|(B P B A P =2.下列哪种分布具有无记忆性( B )。
A. 均匀分布B. 指数分布C. 正态分布D. 泊松分布3.设)(x f ,)(x F 分别为某连续型随机变量的概率密度函数和分布函数, 则必有( A )。
A .)()(x f x F =' B. )(x f 连续 C.)()(x F x f =' D. 1)(lim =+∞→x f x4.若X 表示某个随机变量,)(),(X D X E 分别为期望和方差,则( B )A.0)(≥X E B. 0)(≥X D C. )()(X D X E ≤ D. 以上都不对5.设二维随机变量()的联合分布概率为则a 为( B )。
A. 1/3B. 5/12C. 1/6D. 2/3学院专业班 级 姓 名学号二、填空题(本大题共5小题,每小题3分,总计15分) (1) 掷三次硬币,三次都是正面的概率为_1/8____。
(2) 某人射击某一个目标的命中率为0.4,现不停的射击,直到命中为止,则第2次才命中目标的概率为_0.24__。
(3)设)6,1(~U X ,则=+)1(X E 4.5。
(4)设X 服从参数为2的指数分布,则)3(X D =36。
(5)若)(x Φ为标准正态的分布函数,且255.0)(=Φa ,则=-Φ)(a 0.745。
三、(本大题共2小题,每小题6分,总计12分)1. 在整数1至5中任取2个,这两个数的和大于等于4的概率是多少? 解:求大于等于4的对立事件,即小于等于3的概率。
2006级经管类集美大学概率试卷B卷
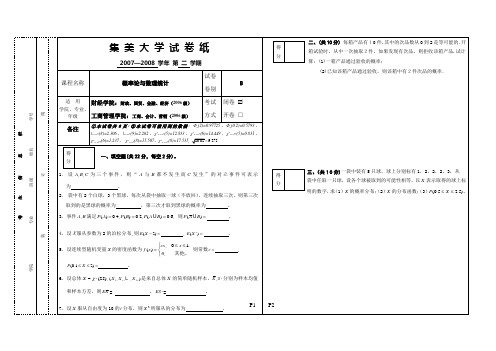
求(1) 的边缘密度函数 ;(2) ;(3) ;(4)判断 与 是否独立,是否相关.
六、(共8分)设一箱同型号的零件共有100个,已知各零件的重量都是随机变量,它们相互独立且服从相同的分布,其数学期望为100克,标准差为10克,求一箱零件的重量超过10200克的概率.
00258230600259226200255128330025614449097550831097561237005815507002581753586029275个黑球每次从袋中抽取一球不放回连续抽取三次则第三次取到的是黑球的概率为第三次才取到黑球的概率为设x服从参数为2的泊松分布则设连续型随机变量x的密度函数为是来自总体x的简单随机样本分别为样本均值和样本方差则e每箱产品有10件其中的次品数从0是等可能的
七、(共10分)设总体 服从参数为 的二项分布, 已知, 未知. 是来自总体 的一个简单随机样本,试求:
(1)参数 的矩估计量;(2)参数 的最大似然估计量.
八、(共8分)已知某单位职工每天的医疗费服从正态分布 现随机抽查了6天,其医疗费(单位:元)分别为:
221,191,202,205,256,236.
试以95%的可靠性对方差 进行区间估计.
九、(共10分)某工厂用自动生产线生产金属丝,假定金属丝的折断力 (单位: )服从正态分布,其合格标准为:平均值为580,方差不超过64.某日开工后,抽取9根作折断检测,测得样本均值 575.56,样本方差 86.02.试问:此日自动生产线是否工作正常?(显著性水平 0.05)
(2)已知该箱产品通过验收,则该箱中有2件次品的概率.
三、(共10分)一袋中装有5只球,球上分别标有1,2,2,2,3,从
概率统计练习题答案

概率统计练习题答案概率统计练习题答案概率统计是一门重要的数学学科,它研究的是随机事件的概率和统计规律。
在学习概率统计的过程中,练习题是非常重要的一部分,通过解答练习题可以巩固知识,提高解题能力。
下面我们来看一些常见的概率统计练习题及其答案。
1. 随机变量X服从正态分布N(2, 4),求P(X<3)。
答案:首先计算标准差,标准差为2,然后计算X的标准化值z=(3-2)/2=0.5。
查找标准正态分布表可得P(Z<0.5)=0.6915,所以P(X<3)=0.6915。
2. 一批产品中有10%的次品,从中随机抽取5个产品,求恰好有1个次品的概率。
答案:假设成功事件为抽到次品,失败事件为抽到正品。
根据二项分布的公式,概率P(X=k)=C(n,k)p^k(1-p)^(n-k),其中n为试验次数,k为成功次数,p为成功概率。
代入数据可得P(X=1)=C(5,1)0.1^1(1-0.1)^(5-1)=0.32805。
3. 某班级有60%的学生喜欢数学,40%的学生喜欢英语,20%的学生既喜欢数学又喜欢英语,求一个学生既不喜欢数学也不喜欢英语的概率。
答案:根据概率公式P(A∪B)=P(A)+P(B)-P(A∩B),其中A、B为事件。
代入数据可得P(数学∪英语)=P(数学)+P(英语)-P(数学∩英语)=0.6+0.4-0.2=0.8。
所以一个学生既不喜欢数学也不喜欢英语的概率为1-0.8=0.2。
4. 某地每天的天气有30%的可能是晴天,20%的可能是雨天,50%的可能是阴天。
如果今天是晴天,那么明天是雨天的概率是多少?答案:根据条件概率公式P(B|A)=P(A∩B)/P(A),其中A为今天是晴天的事件,B为明天是雨天的事件。
代入数据可得P(明天是雨天|今天是晴天)=P(今天是晴天∩明天是雨天)/P(今天是晴天)=0.3*0.2/0.3=0.2。
5. 一批产品中有10%的次品,从中随机抽取10个产品,求至少有1个次品的概率。
自考概率论与数理统计历年试题

⾃考概率论与数理统计历年试题概率论与数理统计(⼆)全国2006年7⽉⾼等教育⾃学考试试题课程代码:02197⼀、单项选择题(本⼤题共10⼩题,每⼩题2分,共20分)在每⼩题列出的四个备选项中只有⼀个是符合题⽬要求的,请将其代码填写在题后的括号。
错选、多选或未选均⽆分。
1.设事件A 与B 互不相容,且P(A)>0,P(B)>0,则有() A.P(A ?B)=P(A)+P(B) B.P(AB)=P(A)P(B) C.A=BD.P(A|B)=P(A)2.某⼈独⽴射击三次,其命中率为0.8,则三次中⾄多击中⼀次的概率为() A.0.002 B.0.008 C.0.08 D.0.1043.设事件{X=K}表⽰在n 次独⽴重复试验中恰好成功K 次,则称随机变量X 服从()A.两点分布B.⼆项分布C.泊松分布D.均匀分布4.设随机变量X 的概率密度为f(x)=<<-其它,02x 1),x 2x 4(K 2 则K=()A.165B.21C.43 D.54 5.则F(1,1) =() A.0.2 B.0.3 C.0.6D.0.76.设随机向量(X ,Y )的联合概率密度为f(x,y)=??<<<<--;,0,4y 2,2x 0),y x 6(81其它则P (X<1,Y<3)=()A.83B.84C.85 D.87 7.设随机变量X 与Y 相互独⽴,且它们分别在区间[-1,3]和[2,4]上服从均匀分布,则E (XY )=() A.1 B.2 C.3D.48.设X 1, X 2, …,X n ,…为独⽴同分布的随机变量序列,且都服从参数为21的指数分布,则当n 充分⼤时,随机变量Y n =∑=n1i iXn1的概率分布近似服从()A.N (2,4)B.N (2,n4) C.N (n41,21)D.N (2n,4n )9.设X 1,X 2,…,X n (n ≥2)为来⾃正态总体N (0,1)的简单随机样本,X 为样本均值,S 2为样本⽅差,则有() A.)1,0(N ~X n B.nS 2~χ2(n) C.)1n (t ~SX )1n (--D.)1n ,1(F ~XX )1n (n2i 2i21--∑=10.若θ)为未知参数θ的估计量,且满⾜E (θ))=θ,则称θ)是θ的()A.⽆偏估计量B.有偏估计量C.渐近⽆偏估计量D.⼀致估计量⼆、填空题(本⼤题共15⼩题,每⼩题2分,共30分)请在每⼩题的空格中填上正确答案。
2006级概率统计答案

评分标准一:填空题:(每小题3分)1. 0.7;2. 0.6;3. 22).exp{1/(2).[ln ]}0y y y σμ-->; 4. 4; 5. 53; 6. n/2; 7. (2)Φ二:计算题1. 解:记 A:取得正品硬币; B :投掷r 次,每次都得到国徽; 取{,}A A 作为样本空间的划分.(|)(|)()/[(|)()(|)()P A B P B A P A P B A P A P B A P A =+ 1.212.2rrr m m m n m n m n m n m n+==++++ 2. 解:某一次在窗口等待时间超过10分钟的概率记为P ,(/5)210(1/5)x P e dx e +∞--==⎰注意到顾客每月到银行五次也就是进行了五重的贝努利试验,每次试验得不到服务的概率为2e -. 所以2~(5,)Y B e -,即2255{}()(1)0,1,,5kk kP Y k C e e k ---==-=25{1}1{0}1(1)P Y P y e -≥=-==--3. 解:(1) ||22||21/(||)||()(,)0a x a x X a dy a x x a f x f x y dy a +∞--∞⎧=≤⎪==⎨⎪⎩⎰⎰其它 由对称性||22||21/(/||)||()(,)0a y a y Y a dx a y y a f y f x y dx a+∞--∞⎧=≤⎪==⎨⎪⎩⎰⎰其它 (2)当||y a <|||(,)(|)()0 X Y Y x a y f x y f x y f y ≤==⎩其它4. 解:记取出的四只电子管寿命分别为1234,,,X X X X ,所求概率为P ,则1234{min(,,,)180}P P X X X X =≥44{180}[1{180}] 1,2,3,4i i P X P X i =≥=-≤= 4[1(1)]0.00063=-Φ=5. 解:记圆盘面积为S ,圆盘直径为R ,则2(1/4)S R π=, 由随机变量函数的数学期望的计算方法有2()(1/4)(1/)ba E S rb a d r π=-⎰ 22(/12)()b ab a π=++三:解:(1) 矩法估计量()()| |x x x x xE X xf x dx edx xeedxe μμμθθθμμμμθμθμθμθ------+∞+∞+∞∞-∞--+∞===-+=-=+⎰⎰⎰2222222()()|2 2()()x x x x E X x f x dx edx x exedxμμμθθθμμμθμθμθμθθ------+∞+∞+∞∞-∞===-+=++=++⎰⎰⎰令 2222()()()()E X XE X A μθμθθ⎧=+=⎨=++=⎩ 解之得,μθ的矩法估计量:ˆX μ=ˆθ= (2) 极大似然估计1111(,)exp{()}min{,,}ni n ni L x n x x μθμμθθ==--<∑111ln ln ()min{,,}ni n i L n x n x x θμμθ==---<∑ln L nμθ∂=∂>0, 故ln L 是μ的递增函数,故1ˆmin{,}n x x μ= 由ln 0L θ∂=∂得 1ˆmin{,,}n x x x θ=- , 所以极大似然估计量为1ˆmin{,}n X X μ= ,1ˆmin{,,}nX X X θ=- 四:证明:由方差的计算公式有:2ˆ()E θ2ˆ[()]E θ==ˆ()D θ+2ˆ[()]E θ, 再由ˆθ是θ的无偏估计可得:2ˆ()E θ=2ˆ()D θθ+ 易见当ˆ()0D θ>时,2ˆθ2ˆ()θ=不是2θ的无偏估计. 五:构造检验统计量2122S F S =,当0H 为真时,211222~(1,1)S F F n n S =--,当0H 不真而1H 为真时,由2222111122222222/./S S F S S σσσσ==,即一个12(1,1)F n n --的统计量乘以一个小于1的数,2122S F S =有偏小的趋势. 所以当2122S F S =偏小时我们拒绝0H 而接受1H ,拒绝域的形式是:2122S F K S =<.由0H 为真时211222~(1,1)S F F n n S =--确定常数K ,得拒绝域为:2111222(1,1)S F F n n S α-=<--.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B、
1 n ∑ Xi n i =1
C、
min{ X i }
1≤ i ≤ n
D、
max{ X i }
1≤ i ≤ n
6、某厂有甲、乙、丙三个车间,生产同种产品,产量分别为全厂产量的 25%,35%,40%。各车间次品率分别 为 5%,4%,2%,检查员从全厂产品中任取一件恰好为次品,则它可能是甲车间生产的概率为 25/69。 7、设两个相互独立的随机变量 X 和 Y 的方差分别为 4 和 2,则随机变量 3 X 2Y 的方差是 44 。
武汉理工大学考试试题纸( B 卷)
课程名称 题号 题分 一 二 三 概率统计 四 五 六 七 专业班级 八 九 十 总分
备注:
学生不得在试题纸上答题(含填空题、选择题等客观题
一、单项选择与填空题(每题 3 分 10×3=30 分) 单项选择与填空题 选择与填空 1、事件 A,B 若满足 P(A)+P(B)>1,则 A,B 一定( A、独立 B、不独立 C、互斥 D ) D、不互斥
……………………… 8分
故拒绝 H 0 ,接受 H 1 。即今年居民用电量有所提高。 七、 F X ( x) = F ( x,+∞) = =
……………………… 10 分
x 1 π π π ( + )( + arctan ) 2 2 π 2 2 2
1 π x ( + arctan ) …………………………… 4 分 π 2 2 y 1 π π π FY ( y ) = F (+∞, y ) = 2 ( + )( + arctan ) 3 π 2 2 2 y 1 π = ( + arctan ) ………………………… 8分 π 2 3 1 π x π y F ( x, y ) = FX (x) FY ( y ) = 2 ( + arctan )( + arctan ) , π 2 2 2 3
三、(10 分)。设 X 为随机变量, C 为常数,证明: E ( X C ) 2 > D (X ) 四、(10 分) 在测量反应时间中,一位心理学家估计的标准差是 0.05 秒,为了以 α =0.5 的置信水平使平均反应 时 间 的 估 计 误 差 不 超 过 ( U α = 1.96 ; U
2 1
x ∈ [0,1] x ∈ [3,6] 其它
若 k 使得 P { x ≥ k } = 8/9
2 ,则 k 的取值范围是 [1,3] 3
。
解答题( 解答题 每题 10 分 7×10=70 分)
二、(10 分) 事件 A、B 相互独立, P ( AB ) =
1 , P ( A B ) = P ( AB ) ,求 P(A) 。 9
2σ n
U
1
,则
0.05 n
α
2
≤ 0.01
…………………… 8 分
n ≥ 96.04 ,取 n = 97
五、 Ai 表示第 i 门炮击中敌机, i = 1,2, L , n , B 表示敌机被击中
…………………… 10 分
P ( B ) = (∑ Ai ) = 1 ∏ P ( A i ) = 1 (1 0.2) n > 0.95
即 X , Y 独立。
+∞ +∞ +∞ x 2a e dx = e 2 a | = 1 , a 为任意实数 0 a
x2 x2
……………………… 10 分
八、 ∫
∞
f ( x)dx =
∫
0
……………… 4 分
当 x < 0 时, F (x) =0
x 2a 当 x ≥ 0 时, F (x) = ∫ e dx =1- e 2 a ∞ a
8、设随机变量 X ~ B(2,P), Y ~ B(3,P),若 P { x ≥ 1} =
5 ,则 P{Y ≥ 1} = 9
。
19/27
1 9、 X ~ U [1,2] , Y = 0 1
1 3 2 10、设随机变量 X ~ f ( x) = 9 0
X >0 X = 0 则 DY = X <0
二、 P ( A B ) = P ( AB ) → P ( A) = P ( B )
P ( AB ) = P ( A) P ( B ) = [1 P ( A)][1 P ( B )] = [1 P ( A)] 2 = P ( A) =
2 3 1 9
………………………… 4 分 …………………… 8 分 ……………………… 10 分
i =1 i =1
n
n
…………………… 6分
n>
ln 0.05 ≈ 14 ln 0.8
…………………… 10 分
六、 H 0 : = 32, H 1 : > 32
x = 34.25
n = 100
α = 0.05
…………………
3分
| U |=
| 34.25 32 | 10 / 100
= 2.25 > U 1α = 1.645
y 1 π x π ( + arctan )( + arctan ) ,问 2 2 2 3 π 2
x x e 2a 八、(10 分) 设 X ~ f ( x) = a 0
2
x > 0, a > 0 x≤0
Φ (1.64) = 0.95 ,
,求(1)a 的值; (2)分布函数 F(x) 。
附数据: Φ (1.28) = 0.90 ,
0.01
秒 , 求 测 量 的 样 本 容 量
n
最 小 应 取 多 大 ?
α
2
= 1.96 ; Uα = 1.645 U1α = 1.645 )
五、(10 分) 设在一次射击中,每门炮击中敌机的概率都是 0.2,问需几门炮一齐射击,才能使命中的概率达到 95%以上?(各炮独立) 六、(10 分) 设去年居民每月用电量服从 N (32,10 2 ) 分布。今年随机抽查了 100 户家庭,用电平均值为 34.25。 在 α = 0.05 置信水平下是否认为今年居民用电量有所提高? 七、(10 分) 设二维连续型随机变量(X,Y)的分布函数为 F ( x, y ) = X,Y 是否独立,为什么?
B、 (
A、
1 1 - 3 e e
1 1 1 )- 9 3e e
C、 e -
3
∫
9
x dx 9
D、F(
9 3 )-F( ) 9 9
5、 X 1 , X 2 , L X n 来自总体 X 的样本( n > 2 >2)中, EX = ,则下列统计量中关于 的最有效的估计量是 ( B ) A、
1 (X1 + X 2 ) ) 2
Φ (1.96) = 0.975 .
武汉理工大学教务处
试题标准答案及评分标准用纸
课程名称 概率统计
4、A
( B 卷)
5、B
一、单项选择与填空题(每题 3 分 3×10=30 分) 单项选择与填空题 选择与填空 1、D 2、 C 3、B
6、
25 69
7、 44
8、
19 27
9、
8 9
10、[1,3]
2、设随机变量 X 概率密度函数 P ( x) =
2 x 0
x ∈ [0, A] 其它
,则常数 A=(C )
A、
1 4
1 2
B、
1 2
1 4
C、 1
D、 2
3、X 服从 0~1 分布,P(X=1)=a,则 DX 的最大值是( B ) A、 B、 C、1 D、
1 8
4、X 服从参数 λ =
1 的指数分布,则 P {3 < x < 9} =( A ) 9
x x2
………………………… 8分
x2
x 1 e 2 a 即 F ( x) = 0
2
x≥0 x<0
………………………… 10 分
三、 E ( X C ) 2 = E ( X 2 ) 2CE ( X ) + C 2 = [C E ( X )] 2 + D( X ) > D( X ) 四、置信区间为 ( X 区间长为
………………………… 5分 ………………………… 10 分
σ
n
α
2
U
1
α
2
,X + U
σ
n
1
U
1
α
2
)
……………………… 4 分
