立体几何第二章复习
人教版A版必修二第二章立体几何复习题及答案

1一、选择题1. 如图,在体积为1的三棱锥A BCD -侧棱A BA C A D ,,上分别取点E F G ,,,使21AE EB AF FC AG GD ===∶∶∶∶,记O 为三平面BCG CDE DBF ,,的交点,则三棱锥O BCD -的体积等于( )A.19B.18C.17D.142.木星的体积约是地球体积的倍,则它的表面积是地球表面积的( ) A.60倍B.C.120倍D.3. 三棱锥P ABC -中,PA PB PC ,,互相两两垂直,且14PC PA x PB y x y ===+=,,,,则三棱锥P ABC -体积的最大值( )A.1 B.13C.23D.不存在4. 一条直线和直线外不在同一条直线上的三点所确定的过该直线的平面有( ) A.1个 B.2个 C.3个 D.至多3个5. 异面直线a b a b c ,,⊥,与a 成30角,则c 与b 成角范围是( )A.[6090],B.[3090],C.[60120],D.[30120],6. 在正方体1111ABCD A B C D -中,表面的对角线与1AD 成60的有( ) A.4条B.6条C.8条D.10条7. 如果两面角l αβ--的平面角是锐角,点P 到αβ,和棱l的距离分别为4和为( ) A.45或30B.15 或75C.30 或60D.15 或608. 下列四个命题,下确的结论个数有( )①若三条直线两两相交,则它们组成的图形为平面图形 ②一条直线和一个点确定一个平面 ③若四点不共面,则每三点一定不共线 ④三条平行线确定三个平面 A.1个 B.2个 C.3个 D.4个 9. 下列命题中正确的是( )A.两条直线可以确定一个平面 B.一组对边平行的四边形是平面图形 C.一个点与一条直线可以确定一个平面 D.两两相交的三条直线一定共面 10. 给出下列四个命题,其中正确的是( )①在空间若两条直线不相交,则它们一定平行 ②平行于同一条直线的两条直线 ③一条直线和两条平行直线的一条相交,那么它也和另一条相交④空间四条直线a ,b ,c ,d ,如果a b ∥,c d ∥,且a d ∥,那么b c ∥ A.①②③ B.②④ C.③④ D.②③ 11. 下列说法中错误..的个数是( ) ①过平面外一点有一条直线和该平面平行 ②过平面外一点只有一条直线和该平面平行 ③过平面一点外有且只有一条直线和该平面平行 A.0 B.1 C.2 D.3A EB FOCGD212. 已知直线a ∥直线b ,b ∥直线c ,c ∥平面α,则( ) A.a α∥ B.a α⊂ C.a 与α相交 D.a α∥或a α⊂ 13. 能保证直线a 与平面α平行的条件是( )A.a α⊄,b α⊂,a b ∥ B.b α⊂,a b ∥ C.b α⊂,c b ∥,a c ∥ D.b α⊂,A a ∈,B a ∈,C b ∈,D b ∈,且AC BD = 14. 下列四个命题中,不正确的命题是( )A.如果一条直线与两条平行直线中的一条垂直,那么也和另一条垂直B.已知直线a ,b ,c ,a b ∥,c 与a ,b 都不相交,若c 与a 所成的角为θ,则c 与b 所成的角也等于θ C.如果空间四个点不共面,则四个点中可能有三个点共线D.若直线a ∥平面α,点P α∈,则过点P 作a 的平行线一定在α内 15. 下列命题中,正确的是( )A.直线a ∥平面α,则a 平行于α内任何一条直线B.直线a 与平面α相交,则a 不平行于α内的任何一条直线 C.直线a 不平行于平面α,则a 不平行于α内任何一条直线D.直线a 不垂直于平面α内的某一条直线,则a 不垂直于α内任何一条直线二、填空题16. 已知m n ,是不同的直线,αβ,是不重合的平面,给出下列命题:① 若m n αβαβ⊂⊂,,∥,则m n ∥ ②若m n m n αββ⊂,,,∥∥,则αβ∥③若m n m n αβ⊥⊥,,∥,则αβ∥④m n ,是两条异面直线,若m m n n αβαβ,,,∥∥∥∥,则αβ∥ 上面命题中,真命题的序号是 (写出所有真命题的序号). 17. 若a b c a d b ∥,⊥,⊥,则c 与d 关系为 .18. 正方形ABCD 中,E F ,分别是AB CD ,中点,沿EF 将正方形折成60的二面角,则异面直线FB 与AE 所成的角的余弦值是 .19. 如图,1111ABCD A B C D -是正方体,E F , 分别是111AA A B ,的中点,则EF 与对角面11A C CA 所成角的度数是 .20. 如图,在空间四边形ABCD 中,2AD BC ==,E ,F 分别是AB ,CD的中点,若EF =AD ,BC 所成的角为.21. 有以下命题,正确命题的序号是 . ①直线与平面没有公共点,则直线与平面平行②直线与平面内的任何一条直线都不相交,则直线与平面平行; ③直线上有两点,它们到平面的距离相等,则直线与平面平行; ④直线与平面内的无数条直线不相交,则直线与平面平行.三、解答题22. 如图,在直三棱柱111ABC A B C -中,13454AC BC AB AA ====,,,,点D 是AB 的中点. (Ⅰ)求证1AC BC ⊥;(Ⅱ)求证1AC ∥平面1CDB ; (Ⅲ)求异面直线1AC 与1B C 所成角的余弦值.ABCED F 1A 1D 1C 1B F D AEB C1C 1B 1A CDAB323. 如图,在直四棱柱1111ABCD A B C D -中,2AB AD ==,DC =1AA =AD DC AC BC ⊥⊥,,垂足为E .(Ⅰ)求证11BD AC ⊥;(Ⅱ)求二面角11A BD C --的大小; (Ⅲ)求异面直线AD 与1BC 所成角的大小.24. 已知:四边形ABCD 中,AB CD AB BC DC AD ∥,,,,(或其延长线)分别与平α相交于E F G H ,,,四点.求证:E F G H ,,,四点共线.25. 在空间四边形ABCD 中,E F ,分别为AB BC ,的中点.求证:EF 和AD 为异面直线.26. 如图,在二面角l αβ--中,A B C D l α∈∈,,,,ABCD 为矩形,P β∈,PA α⊥,且PA AD =,M N ,依次是AB PC ,的中点.(1)求二面角l αβ--的大小;(2)求证:MN AB ⊥;(3)求异面直线PA 与MN 所成角的大小.DβαE CBM A QP Nl1AA 1DD1BE1C C427. 已知四边形ABCD 是空间四边形,E ,H 分别是线段AB ,AD 的中点,F ,G 分别是线段CB ,CD 上的点且23CF CG CB CD ==,求证:EF ,GH ,CA 交于一点.28. 如图所示,P 是ABC △所在平面外的一点,M ,N 分别是AB ,PC 的中点,已知PA BC m ==,PB AC =, (1)求证:MN 是AB 和PC 的公垂线;(2)当PA ,BC 成90角时,求AB 和PC 间的距离.29. 如图,正方体1111ABCD A B C D -中,AC BD O = ,11111AC B D O = .求证:1OO ⊥平面ABCD .30. 如图,在正方体1111ABCD A B C D -中,求1A B 与平面11A B CD 所成的角.CM BP NCO1O 1D 1A 1C 1B DC BA1A1D 1C1BOCBAD5一、选择题1. C.2. C.3. C4. D5. A 6. A 7. B8. A9. B10. B11. C12. D13. A14. C15. B二、填空题16. ③,④ 17. 平行、相交或异面.18.10. 19. 30 . 20. 6021. ①② 三、解答题22. (Ⅰ)∵直三棱柱111ABC A B C -底面三边长345AC BC AB ===,,,AC BC ⊥∴,且1BC 在平面ABC 内的射影为BC ,1AC BC ⊥∴.(Ⅱ)设1CB 与1C B 的交点为E ,连结DE .D ∵是AB 的中点,E 是1BC 的中点,1DE AC ∴∥. DE ⊂∵平面1CDB ,1AC ⊄平面1CDB ,1AC ∴∥平面1CDB .(Ⅲ)1DE AC ∵∥,CED ∠∴为1AC 与1B C 所成的角.在CED △中,11522ED AC ==,1522CD AB ==,112CE CB ==8cos 522CED ==∴ ∴异面直线1AC 与1B C23. (Ⅰ)在直四棱柱1111ABCD A B C D -中,1A A ⊥∵底面ABCD ,AC ∴是1AC 在平面ABCD 上的射影.BD AC ⊥∵,1BD AC ⊥∴. (Ⅱ)连结1111A E C E AC ,,.与(Ⅰ)同理可证1BD A E⊥,1BD C E ⊥, 11A EC ∠∴_为二面角11A BD C --的平面角.AD DC ⊥∵,11190A D C ADC ∠=∠= ∴.又112A D AD ==,11D C DC ==,1AA =AC BD ⊥,11413AC AE EC ===,,∴112A E C E ==,∴在11A EC △中,2221111AC A E C E =+61190A EC ∠= ∴,即二面角11A BD C --的大小为90 .(Ⅲ)过B 作BF AD ∥交AC 于F ,连结1FC ,则1C BF ∠就是AD 与1BC 所成的角.21AB AD BD AC AE ==⊥=,,∵,212BF EF FC BC DC ====,,,∴,11FC BC ==∴.在1BFC △中,1cos C BF ==1C BF ∠=∴ 即异面直线AD 与1BC所成的角的大小为 24. 证明:如图,AB CD ∥, AB CD ∴,确定一个平面β.BC AD ββ∴⊂⊂,.又E F G H ,,,分别在AB BC CD AD ,,,上,E F G H β∴∈,,,;又E F G H α∈,,,.E F G H ∴,,,必在平面αβ,的交线上E F G H ∴,,,四点共线.25. 证明:如图,假设EF 和AD 在同1平面α内, 则A D E F α∈,,,; 又A E AB AB B αα∈∴⊂∴∈,,,,同理C α∈ 故A B C D α∈,,,,这与ABCD 是空间四边形矛盾. EF ∴和AD 为异面直线.26. (1)解:连结PD ,PA α ⊥,AD l ⊥, PD l ∴⊥, PDA ∴∠是二面角l αβ--的平面角.由PA AD =,有45PAD ∠=,故二面角l αβ--的大小为45 .(2)证明:取CD 的中点为E ,连ME ,NE ,则EM AD ∥,EN PD ∥, CD ME ∴⊥,CD NE ⊥,CD ∴⊥平面MNE ,又AB CD ∥, AB ∴⊥平面MNE ,故AB MN ⊥,(3)解:取PD 中点为Q ,连QA ,QN ,则12QN CD∥,而12AM CD∥, QNMA ∴是平行四边形,AQ MN ∴∥,7PAQ ∴∠是异面直线PA 与MN 所成的角.PAD △为等腰直角三角形,AQ 为斜边上的中线, 45PAQ ∴∠= ,即PA 与MN 所成的角的大小为45 .27. 证明:如图,连结BD . EH ∵是ABD △的中位线,12EH BD ∴ ∥ 又23CF CG CB CD ==∵, 23FG BD ∴ ∥.EH FC ∴∥且EH FG <. ∴四边形EFGH 是一个梯形. 设EF 交GH 于P 点,EF ⊂∵平面ABC ,GH ⊂平面ACD , P ∴是平面ABC 与平面ACD 的公共点.∴点P 在两平面的交线AC 上,即EF ,GH ,CA 三线交于一点.28. (1)证明:连结AN 和BN ,在PAC △和CBP △中,PA BC =,AC PB =,PC PC =,PAC CBP ∴△≌△.N ∵是公共边PC 的中点,AN BN ∴=. M ∵是AB 的中点, NM AB ∴⊥.同理MN PC ⊥.故MN 是AB 和PC 的公垂线.(2)解:取PB 的中点D ,连结DM ,DN ,于是DM PA ∥,且1122DM PA m ==,同理DN BC ∥,且1122DN BC m ==,于是MDN ∠是异面直线PA ,BC 所成的角, 90MDC ∴∠=.从而MN =,即AB 和PC.29. 证明:1111ABCD A B C D -∵为正方体,1AA AB ∴⊥,1AA AD ⊥.AB AD A = ∵,1AA ∴⊥平面AC .11AA BB ∥∵,11BB CC ∥,11AA CC ∴ ∥.∴四边形11AA C C 为平行四边形. O ∵,1O 分别为AC ,11A C 的中点,11OO AA ∴∥,1OO ⊥平面AC .30. 解:连结1BC 交1B C 于O ,连结1AO ,在正方体1111ABCD A B C D -中各个面为正方形,设其棱长为a .11111111111111A B B C A B BCC B A B B B BC BCC B ⎫⎫⇒⎬⎪⎬⎭⎪⊂⎭平面平面⊥⊥⊥11111111A A B BC BC B CD BC B C ⇒⎫⇒⎬⎭平面⊥⊥ ⊥81AO ⇒为1A B 在平面11A B CD 内的射影 1B AO ⇒∠为1A B 与平面11A B CD 所成的角.111111111Rt 21sin 23030.BAO A B OB a OB BAO A B BAO BAO A B A B CD ⎫==⎪⎪⎪⎫⇒==⎪⎪⇒=⎬⎬⎪⎪∠⎭⎪⎪⇒⎪⎭在△中,, 为锐角与平面所成的角为。
必修2 立体几何第一二章复习
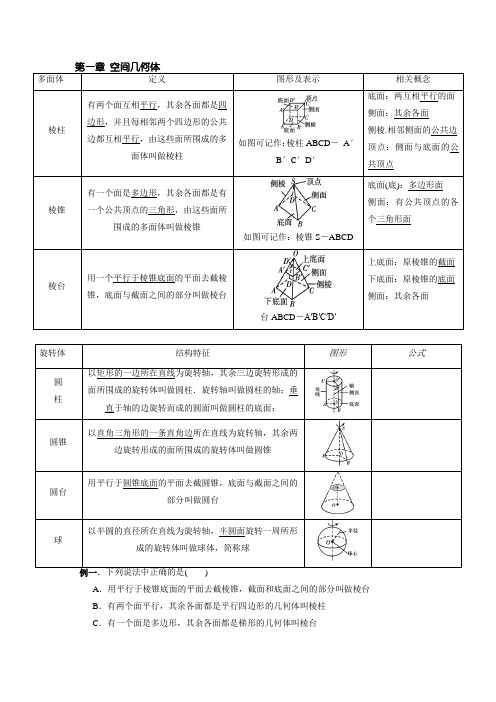
A.用平行于棱锥底面的平面去截棱锥,截面和底面之间的部分叫做棱台B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形,其余各面都是梯形的几何体叫棱台D .有一个面是多边形,其余各面都是三角形的几何体叫棱锥练习1.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括 A .一个圆台、两个圆锥 B .两个圆台、一个圆柱 C .两个圆台、一个圆锥 D .一个圆柱、两个圆锥2.把一个圆锥截成圆台,圆台的上、下底面半径之比1:4,母线长10,圆锥的母线长? 例二..梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图.若A 1D 1∥O ′y ′,A 1B 1∥C 1D 1,A 1B 1=23C 1D 1=2,A 1D 1=O′D 1=1. 试画出原四边形的形状,并求原图形的面积.例三.棱台的上、下底面面积分别为2,4,高为3,则棱台的体积是( )A .18+62B .6+2 2C .24D .18练习1.一个圆锥的轴截面为边长为A 的正三角形,则其表面积为________.例四(1) (2013·重庆高考)某几何体的三视图如图所示,则该几何体的表面积为________.(2)(2013·江西高考)一几何体的三视图如图所示,则该几何体的体积为________. (3)某几何体的三视图如图(3)所示,其中三角形的三边长与圆的直径均为2,则该几何体的体积为( ) A.4+33π B.32+833π C.32+33π D.4+333π练习1.在—个长方体中,过—个顶点的三条棱长的比是1∶2∶3,它的体对角线长是214,则这个长方体的体积是 ________.2.若圆锥的侧面展开图为一个半径为2的半圆,则圆锥的体积是________. 3.正四棱台的侧棱长为3,两底面边长分别为1和5,求该棱台的体积.例五 (1)一个正方体的所有顶点在一个球面上.球体积为9π2,则正方体的棱长为________.(2)已知球的两平行截面的面积为5 π和8 π,它们位于球心的同一侧,且相距为1,这个球的表面积________.练习.1用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为____.2.棱长为2的正方体的外接球的表面积是( )A.8πB.4πC.12πD.16π3.平面α截球O的球面所得圆的半径为1,球心O到平面α距离为2,则球的体积为_____第二章,空间点线面的位置关系1.空间两条直线的位置关系2.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.【练习】若∠AOB=45°,OA∥O′A′,OB∥O′B′,则∠A′O′B′等于() A.45°B.135°C.45°或135°D.以上都不对3.异面直线所成的角(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).(2)异面直线所成的角θ的取值范围:0°<θ≤90°.【练习】如图,在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,若EF=3,求异面直线AD、BC所成角的大小【练习】正方体ABCD-A1B1C1D1中,求:(1)异面直线AB与A1D1; AD1与DC1所成的角4.直线与平面的位置关系5.平面与平面的位置关系【练习】下列说法:①若直线a在平面α外,则a∥α;②若直线a∥b,直线b⊂α,则a∥α;③若直线a∥b,b⊂α,那么直线a就平行于平面α内的无数条直线.其中说法正确的个数为()A.0个B.1个C.2个D.3个【练习】已知a、b、c为三条不重合的直线,α、β为两个不重合的平面:①α∥β,a⊂α,b⊂β,则a∥b;②α∩β=b,a⊂α,则a与β一定相交;③a∥c,c∥α则a∥α;④a∥β,a∥α,则α∥β;其中正确的个数为()外一点,M,N分别是AB,PC的中点,求证:MN∥平面PAD.【练习】如图在正方体ABCD-A1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点。
立体几何第二章 (1)

立体几何第二章高三复习讲义(黄毅) 知识点归纳垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系 1 平行转化 线线平行⇔线面平行⇔面面平行2 垂直转化 线线垂直⇔线面垂直⇔面面垂直ααα////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄b a b a a ////⇒⎪⎭⎪⎬⎫=⊂βαβαβαβα//⇒⎭⎬⎫⊥⊥a a β β β β βα α α αα b a b a //////⇒⎭⎬⎫αα αα//////b a b a ⇒⎭⎬⎫ α αβααβ////,//,⇒⎪⎭⎪⎬⎫=⊂b a O b a b ab a b a //,//⎭⎬⎫==γβγαβαγ β α β α β α βγ β βαααββα////a a ⇒⎭⎬⎫⊂ αβαβ//'//,'//',',⇒⎪⎪⎭⎪⎪⎬⎫⊂=⊂b b a a b a O b a b aα βγβαγβγα//////⇒⎭⎬⎫b ac b c a //////⇒⎭⎬⎫βαβα⊥⇒⎭⎬⎫⊥a a // αα⊥⇒⎪⎭⎪⎬⎫⊥⊥=⊂a n a m a G n m n m ,,b a b a ⊥⇒⎭⎬⎫⊂⊥αα βαβαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=⊥a b a a b ,, αα α βααβ⊥⇒⎭⎬⎫⊂⊥a aγ ⎪⎩⎪⎨⎧⊥⊥⊥⇒⎪⎭⎪⎬⎫===⊥⊥⊥ac c b b a c b a αγγββααγγββα ,,, ⎪⎩⎪⎨⎧⊥⊥⊥⇒⎪⎭⎪⎬⎫⊥⊥⊥=αγγββαa c c b b a O c b a , POa OA a a A PO A PA ⊥⇔⊥⊂⊥.,,ααα于斜交于ααa b ba acn ab a a b a b b a baa b c a'b'a m ba caaa bbab aO POA o o O G 面面垂直线面垂直线线垂直面面平行线面平行线线平行直线与平面的平行和垂直关系的证明思路知识梳理1.空间两点间距离(1)若111(,,)A x y z ,222(,,)B x y z ,则()()()212212212z z y y x x AB -+-+-=特别地,A到原点的距离212121z y x AO ++=(2)夹角公式:112233222222123123cos ||||a b a b a b a ba b a b a a a b b b ++⋅⋅==⋅++++.2.求距离:求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离。
必修二 立体几何知识点总结第二章

高中数学必修2立体几何知识点复习 姓名第二章 空间点、直线、平面的位置关系 2015-12一、平面(1)平面① 平面的概念: A.描述性说明; B.平面是 的;② 平面的表示:通常用希腊字母α、β、γ表示,如平面α(通常写在一个锐角内);也可以用两个相对顶点的字母来表示,如平面BC 。
③ 点与平面的关系:点A 在平面α内,记作 ;点A 不在平面α内,记作A α∉点与直线的关系:点A 的直线l 上,记作: ; 点A 在直线l 外,记作A l ; 直线与平面的关系:直线l 在平面α内,记作 ;直线l 不在平面α内,记作l ⊄(2)公理1: 。
(即直线在平面内,或者平面经过直线)应用:检验桌面是否平; 判断直线是否在平面内用符号语言表示公理1:,,,A l B l A B l ααα∈∈∈∈⇒⊂(3)公理2: 。
推论:1一直线和直线外一点确定一平面;2两相交直线确定一平面;3两平行直线确定一平面。
公理2及其推论作用:①它是空间内确定平面的依据 ②它是证明平面重合的依据(4)公理3:符号:平面α和β相交,交线是a ,记作 。
符号语言:,P A B A B l P l ∈⇒=∈公理3的作用:①它是判定两个平面相交的方法。
②它说明两个平面的交线与两个平面公共点之间的关系:交线必过公共点。
③它可以判断点在直线上,即证若干个点共线的重要依据。
(5)公理4: 。
二、空间直线与直线之间的位置关系(一) 空间两条直线的位置关系有 、 、 。
(二)异面直线① 异面直线定义: 。
② 异面直线性质:既不平行,又不相交。
③异面直线判定:过平面外一点与平面内一点的直线与平面内不过该店的直线是异面直线。
④异面直线所成角:直线a、b是异面直线,经过空间任意一点O,分别引直线a’∥a,b’∥b,则把直线a’和b’所成的锐角(或直角)叫做异面直线a和b所成的角。
两条异面直线所成角的范围是(0°,90°],,我们就说这两条异面直线互相垂直。
高中数学立体几何知识点归纳总结

高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为矩形1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形;③过不相邻的两条侧棱的截面是平行四边形; ④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222c o s c o sc o s 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222co s co s co s 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形. 1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h 为棱柱的高)2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形.2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.2.4面积、体积公式:S =2rh π;S=222rh r ππ+,V=Sh=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(完整版)高中数学必修二立体几何知识点总结

第一章 立体几何初步特殊几何体表面积公式(c 为底面周长,h 为高,'h 为斜高,l 为母线)ch S =直棱柱侧面积'21ch S =正棱锥侧面积 ')(2121h c c S +=正棱台侧面积 rh S π2=圆柱侧 ()l r r S +=π2圆柱表rl S π=圆锥侧面积 ()l r r S +=π圆锥表 lR r S π)(+=圆台侧面积 ()22R Rl rl r S +++=π圆台表柱体、锥体、台体的体积公式 V Sh =柱13V Sh =锥'1()3V S S h =台 2V Sh r h π==圆柱h r V 231π=圆锥 '2211()()33V S S h r rR R h π=+=++圆台 (4)球体的表面积和体积公式:V 球=343R π ; S 球面=24R π第二章 直线与平面的位置关系2.11 2 三个公理:(1符号表示为A ∈LB ∈L => l α⊂ A ∈αB ∈α(2符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理(3公理 L A · α C · B · A · α2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系: 相交直线:同一平面内,有且只有一个公共点; 平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线a ∥bc ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为了简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, ); ③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
立体几何第二章复习

(6)如果一条直线与一个平面平行,则这 就日条直线上的所有的点到这个平面的距各 个离相等。
面面平行判定
(1)定义:如 行果 。两个平面没有公共点,则这两个平面平
(2)判定定理:
如果一个平面内的两条相交直线与另一个平面平 行,那么这两个平面平行。
M、N分别是AB、PC的中点.
(1) 求证:MN∥平面PAD;
(2)求证:MN⊥CD;
(3)若平面PCD与平面ABCD所成二面角为θ,问能
否确定θ的值,使得MN是异面直线AB与PC的公
垂线.
P
A M
B
N D
C
例 2 、 在 正 四 棱 柱 ABCD-A1B1C1D1 中 , 2 AA1= AB, 点 E、M 分 别 为 A1B、C1C 的 中 点 , 过 A1, B,M三点的平面交C1D1于点N。 (1)求证:EM∥平面A1ND1; (2)求二面角B-A1N-B1的正切值
(2)判定定理2——如果一条直线和一个 平面内的两条相交直线都垂直,则直线与 平面垂直。
(3)面面垂直的性质:如果两个平面垂直, 则在一个平面内垂直于它们的交线的直线 垂直于另一个平面
(4)面面垂直推论:如果两个相交平面都与另 一个平面垂直,则这两个平面的交线 l 垂直于 另一个平面
(5)面面平行性质:一直线垂直于两个平行 平面中的一个,则它也垂直于另一个平面
(5)线面垂直的性质: a⊥α bα
a⊥b
(6)利用线面垂直、 线面平行:
a⊥α b∥α
a⊥b
(7)利用三垂线定理: 在平面内的一条直线,
A
如果和这个平面的一条
斜线的射影垂直,则它
第二章空间向量与立体几何中线面角问题

第二章空间向量与立体几何中线面角问题一、解答题1.如图,在三棱锥A BCD -中,ABC 是等边三角形,90BAD BCD ∠=∠=︒,点P 是AC 的中点,连接,BP DP .(1)证明:平面ACD ⊥平面BDP ;(2)若6BD =,且二面角A BD C --为120︒,求直线AD 与平面BCD 所成角的正弦值.2.如图,直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求AM 与平面A 1MD 所成角的正弦值.3.如图所示,已知点P 在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.(1)求DP 与CC′所成角的大小.(2)求DP 与平面AA′D′D 所成角的大小.4.如图,四棱锥S ABCD -中,ABS 是正三角形,四边形ABCD 是菱形,点E 是BS 的中点.(I )求证:SD // 平面ACE ;(II )若平面ABS ⊥平面ABCD ,120ABC ∠=︒, 求直线AC 与平面ADS 所成角的正弦值.5.如图,直棱柱111ABC A B C -的底面△ABC 中,1CA CB == ,90ACB ∠=︒ ,棱12AA =,如图,以C 为原点,分别以1,,CA CB CC 为,,x y z 轴建立空间直角坐标系.(1)求平面11A B C 的法向量;(2)求直线AC 与平面11A B C 夹角的正弦值.6.如图,四棱锥P ABCD -中,PAB ∆为正三角形,ABCD 为正方形,平面PAB ⊥平面ABCD ,E 、F 分别为AC 、BP 中点.(1)证明://EF 平面PCD ;(2)求直线BP 与平面PAC 所成角的正弦值.7.在直三棱柱ABC ﹣A 1B 1C 1中,AB ⊥AC ,AB=AC=2,A 1A=4,点D 是BC 的中点;(I )求异面直线A 1B ,AC 1所成角的余弦值;(II )求直线AB 1与平面C 1AD 所成角的正弦值.8.如图1,45ACB ∠=,3BC =,过动点A 作AD BC ⊥,垂足D 在线段BC 上且异于点B ,连接AB ,沿AD 将△ABD 折起,使90BDC ∠=(如图2所示).(1)当BD 的长为多少时,三棱锥A BCD -的体积最大;(2)当三棱锥A BCD -的体积最大时,设点E ,M 分别为棱BC ,AC 的中点,试在棱CD 上确定一点N ,使得EN ⊥BM ,并求EN 与平面BMN 所成角的大小.9.已知长方体1111ABCD A B C D -中,2AD AB ==,11AA =,E 为11D C 的中点. (1)证明1//BD 平面1B EC ;(2)求直线1AD 与平面1B EC 所成角的正弦值.10.如图,在四棱锥E ABCD -中,底面ABCD 为菱形,BE ⊥平面ABCD ,G 为AC 与BD 的交点.(1)证明:平面AEC ⊥平面BED ;(2)若60BAD ∠=︒,AE EC ⊥,求直线EG 与平面EDC 所成角的正弦值.参考答案1.(1)见解析(2)22 【分析】 (1)由ABC 是等边三角形,90BAD BCD ∠=∠=︒,得AD CD =.再证明PD AC ⊥,PB AC ⊥,从而和证明AC ⊥平面PBD ,故平面ACD ⊥平面BDP 得证. (2)作CE BD ⊥,垂足为E 连接AE .由Rt Rt ABD CBD ⊆,证得,AE BD ⊥,AE CE =结合二面角A BD C --为120︒,可得2AB =,23AE =,6ED =.建立空间直角坐标系,求出点的坐标则60,,03D ⎛⎫ ⎪ ⎪⎝⎭,3,0,13A ⎛⎫- ⎪ ⎪⎝⎭,向量36,,133AD ⎛⎫=- ⎪ ⎪⎝⎭,即平面BCD 的一个法向量(0,0,1)m =,运用公式cos ,m AD m AD m AD ⋅〈〉=和sin cos ,m AD θ=〈〉,即可得出直线AD与平面BCD 所成角的正弦值.【详解】 解:(1)证明:因为ABC 是等边三角形,90BAD BCD ∠=∠=︒,所以Rt Rt ABD CBD ≅,可得AD CD =.因为点P 是AC 的中点,则PD AC ⊥,PB AC ⊥,因为PD PB P =,PD ⊂平面PBD ,PB ⊂平面PBD ,所以AC ⊥平面PBD ,因为AC ⊂平面ACD ,所以平面ACD ⊥平面BDP .(2)如图,作CE BD ⊥,垂足为E 连接AE .因为Rt Rt ABD CBD ⊆,所以,AE BD ⊥,AE CE =AEC ∠为二面角A-BD-C 的平面角.由已知二面角A BD C --为120︒,知120AEC ∠=︒.在等腰三角形AEC 中,由余弦定理可得AC =.因为ABC 是等边三角形,则AC AB =,所以AB =.在Rt △ABD 中,有1122AE BD AB AD ⋅=⋅,得BD =,因为BD =所以AD =. 又222BD AB AD =+,所以2AB =.则AE =,ED = 以E 为坐标原点,以向量,EC ED 的方向分别为x 轴,y 轴的正方向,以过点E 垂直于平面BCD 的直线为z 轴,建立空间直角坐标系E xyz -,则D ⎛⎫ ⎪ ⎪⎝⎭,A ⎛⎫ ⎪ ⎪⎝⎭,向量31AD ⎛⎫=- ⎪ ⎪⎝⎭,平面BCD 的一个法向量为(0,0,1)m =, 设直线AD 与平面BCD 所成的角为θ,则cos ,2m ADm AD m AD ⋅〈〉===,2sin |cos ,|2m AD θ=〈〉=所以直线AD 与平面BCD 所成角的正弦值为2. 【点睛】本题考查面面垂直的证明和线面所成角的大小,考查空间想象力和是数形结合的能力,属于基础题.2.(1)见解析(2 【分析】 要证线面平行,先证线线平行建系,利用法向量求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、如图,在底面是直角梯形的四棱锥S-ABCD 中,∠ABC=90°பைடு நூலகம்SA⊥面ABCD,SA=AB=BC=1, AD=1/2 , 则面SBA与面SCD所成的二面角的大小是 。
s
B C
A
D
4. 如图 , 四棱锥 P-ABCD 的底面是正方形 , PA⊥ 底面ABCD,AE⊥PD,EF∥CD,AM=EF (1)证明MF是异面直线AB与PC的公垂线; (2) 若PA= 3AB,求二面角 P E—AB—D平面角的正弦值. (3)若PA=3AB,求直线AC与 E 平面EAM所成角的正弦值. A
线面垂直性质
(1)定义——如果一条直线和一个平面垂直 则这条直线垂直于平面内的任意一条直线
(2)性质定理——如果两条直线同垂直于一 个平面,则这两条直线平行。
(3)一直线垂直于两个平行平面中的一个, 则它也垂直于另一个平面
(6)如果一个平面经过另一个平面的一条垂 线,则这两个平面互相垂直
(7)如果一个平面与另一个平面的垂线平行, 则这两个平面互相垂直
1. 在正方体ABCD—A1B1C1D1中,M为DD1的中 点,O为底面ABCD的中心,P为棱A1B1上任意一 点,则直线OP与直线AM所成的角是( )
A. 3
A1
D1
M
B. 4
C. 2
C1
D1
M E
D. 6
C1 B1 C B
P
B1
A1
D
O
C
D
O
A
B
A
2.已知∠AOB=90°,过O点引∠AOB所在平面的斜 线OC,与OA、OB分别成45°、60°,则以OC 为棱的二面角A—OC—B的大小为_________.
面面垂直判定
如果一个平面经过另一个平面的一 条垂线,则这两个平面互相垂直
推论:如果一个平面与另一个平面的垂 线平行,则这两个平面互相垂直
面面垂直性质
如果两个平面垂直,则在一个平面内垂直 于它们的交线的直线垂直于另一个平面 推论:如果两个相交平面都与另一个平面 垂直,则这两个平面的交线 l 垂直于另一 个平面
N
2.如图,直三棱柱ABC-A1B1C1的底面ABC为 等 腰 直 角 三 角 形 , ∠ ACB=900,AC=1,C 点 3 到AB1的距离为CE= ,D为AB的中点.
2
(1)求证:AB1⊥平面CED (2)求异面直线AB1与CD 之间的距离;
(3)求二面角B1—AC—B的
C1 A1 B1
平面角.
(3)推论:
如果一个平面内的两条相交直线与另一个平面的 两条相交直线分别平行,那么这两个平面平行。
(4)利用线面垂直:
如果两个平面分别垂直于同一条直线,那么这两 个平面平行。
(5)利用面面平行:
如果两个平面都平行于第三个平面,那么这两个 平面平行。
(6)利用距离:
如果一个平面上的所有点到另一个平面的距离相 等,那么这两个平面平行。
(5)如果一条直线与一个平面平行,事 实不则这条直线与平面所成的角为零度。
(6)如果一条直线与一个平面平行,则这 就日条直线上的所有的点到这个平面的距各 个离相等。
面面平行判定
如果两个平面没有公共点,则这两个平面平 (1)定义: 行。
(2)判定定理:
如果一个平面内的两条相交直线与另一个平面平 行,那么这两个平面平行。
(6)如果两个平面平行,则其中一个平面内的所有 点到另一个平面的距离相等。 (7)夹在两个平行平面间的平行线段相等。
平行与垂直
线线垂直 线线垂直判定
垂 直
线面垂直判定 线面垂直
线面垂直性质
面面垂直判定
面面垂直
面面垂直性质
线线垂直判定
(1)利用线线平行:一条直线垂直于两条 平行线中的一条,则垂直于另一条 (2)利用勾股定理逆定理
当二面角的棱已知时: (1)定义法 (2)垂面法
(3)三垂线定理法
当二面角的棱未知时:
寻找平行平面,将问题转化
利用射影面积公式S′=Scosθ
[例]在棱长为 a 的正方体 ABCD—A′B′C′D′ 中,E、F分别是BC、A′D′的中点.
(1)求证:四边形 B′EDF是菱形; ( 2 ) 求 直 线 A′C 与 DE 所 成的角; ( 3 ) 求 直 线 AD 与 平 面 B′EDF所成的角; (4)求面B′EDF与面 ABCD所成的角.
(3)利用等腰三角形性质
(4)利用平面图形性质
(5)线面垂直的性质: (6)利用线面垂直、 线面平行: (7)利用三垂线定理:
A B C a
a⊥ α
b α a⊥ α b∥α
a⊥ b
a⊥ b
α
在平面内的一条直线, 如果和这个平面的一条 斜线的射影垂直,则它 也和这条斜线垂直。 (反之也成立)
线面垂直判定
线面平行的性质
(1)性质定理:如果一条直线与一个平 面平行,过这条直线的平面与已知平面相 交,那么这条直线与交线平行。 (2)如果一条直线与一个平面平行,那么 这条直线与 这个平面没有公共点。 (3)如果一条直线与两个相交的平面都 平行,那么这条直线与交线平行。
(4)如果一条直线与一个平面平行,另 合乎一条直线与这个平面垂直,那么这两 天天条直线垂直。
M
F C
D
B
空间中的距离解法小结
求点到平面的距离: (1)直接法,即直接由点作垂线,求垂线段的长. (2)转移法,转化成求另一点到该平面的距离. (3)体积法
求异面直线的距离: (1)定义法,即求公垂线段的长. (2)转化成求直线与平面的距离或平面与平面的距离
1. 正方形ABCD边长为2,E、F分别是AB和CD的 中点,将正方形沿EF折成直二面角,M为矩形 AEFD内一点,如果∠MBE=∠MBC,MB和平面 BCF所成角的正切值为 0.5,那么点M到直线EF 的距离为 。
立体几何复习提要
1、线面关系中的平行与垂直 2、空间中的角与距离
3、典型题型分类解析
平行与垂直
线线平行 线线平行判定
平 行
线面平行判定 线面平行
线面平行性质
面面平行判定
面面平行
面面平行性质
线线平行判定
(1)定义:如果两条直线在同一平面内,且没有公共
点,则这两条直线平行。 (2)初中所学的判定方法(两条直线在同一平面内) (3)平行公理4
(8)利用所成角
如果两条直线与一个平面所成角相等且方向相 同,那么这两条直线平行。
线面平行判定
直线和平面没有公共点。 (1)定义:
(2)判定定理:平面外一条直线和平面 内一条直线平行,则这条直线和这个平面 平行。 (3)面面平行的性质:两个平面平行, 则其中一个平面内的直线必平行于另一 个平面。
(4)利用垂直 如果一条直线和一个平面分别与另一个平面垂 直,且直线不在这个平面内,则这条直线和这 个平面平行。 (5)利用平行 如果一条直线与两个平行平面中的一个 平行且不在另一个平面内,则这条直线 与另一个平面平行。 (6)利用距离 一条直线垂直于一个平面,同时垂直于另 一条直线,则另一条直线平行于这个平面。
面面平行的性质
(1)如果两个平面平行,那么这两个平面没有公共点。 (2)如果两个平面平行且都与第三个平面相交,则 交线平行。 (3)如果两个平面平行,则其中一个平面内的所有 直线与另一个平面平行。 (4)如果两个平面平行,且其中一个平面与一条直线 垂直,则另一个平面与这条直线也垂直。
(5)如果两个平面平行,那么这两个平面所成 的角为零度。
(4)线面平行的性质定理:
如果一条直线与一个平面平行,经过这条直线的 平面和这个平面相交,则这条直线与交线平行。
(5)面面平行的性质
如果两个平面和第三个平面相交,则交线平行。
(6)线面垂直性质
如果两条直线同时垂直于同一个平面,那么这两条 直线平行。
(7)利用距离
如果一条直线上的所有点到另一条直线的距 离相等,那么这两条直线平行。
A
M B C N D
例 2 、在正四棱柱 ABCD-A1B1C1D1 中, 2 AA1= AB,点 E、M 分别为 A1B、C1C 的中点,过 A1, B,M三点的平面交C1D1于点N。 (1)求证:EM∥平面A1ND1; (2)求二面角B-A1N-B1的正切值
D1 A1 A
E
N B1
C1
M C
B
E A D
C B
3. 如图,正三棱柱 A1B1C1-ABC 中,底面边长 和侧棱长都是 1, D、E分别是 C1C和 A1B1的中 点. (1)求点E到平面ABD的距离:
(2)求二面角A—BD—C的正切值
4、在直三棱柱ABC—A1B1C1中,底面是等腰直角三角 形,∠ ACB=90o,侧棱 AA1=2,D、E 分别是 CC1 与 A1B 的 中点,点E在平面ABD上的射影G是△ABD的重心。 (1)求A1B与平面ABD所成角的大小;
(2)求点A1到平面AED的距离。 A1
A1B与平面ABD所成的角是arcsin
C1
2 6 A1到平面AED的距离为 3
2 3
E G A
D
B1
C
B
(1)判定定理1——如果两条平行线中的 一条垂直于一个平面,则另一条也垂直于 这个平面。
(2)判定定理2——如果一条直线和一个 平面内的两条相交直线都垂直,则直线与 平面垂直。
(3)面面垂直的性质:如果两个平面垂直, 则在一个平面内垂直于它们的交线的直线 垂直于另一个平面
(4)面面垂直推论:如果两个相交平面都与另 一个平面垂直,则这两个平面的交线 l 垂直于 另一个平面 (5)面面平行性质:一直线垂直于两个平行 平面中的一个,则它也垂直于另一个平面
E
A
B C
D
立体几何专题复习 之二
