算法案例
k近邻算法经典案例
k近邻算法经典案例
1. 手写数字识别
手写数字识别是机器学习中的经典应用之一，k近邻算法也被广泛应用于其实现。
在这个案例中，我们将使用k近邻算法来训练一个模型，使其能够准确地识别手写数字。
2. 信用评估
信用评估是银行、信用卡公司等机构必须面对的问题。
这个案例中，我们将使用k近邻算法来构建一个模型，用于预测一个人是否有能力还款。
3. 疾病诊断
疾病诊断是医疗领域的一个重要应用，通过收集患者的症状和病史等信息，机器学习算法可以辅助医生进行诊断。
在这个案例中，我们将使用k近邻算法来构建一个模型，能够使用患者的症状和病史等信息进行疾病诊断。
4. 商品推荐
商品推荐是电商行业必须面对的问题。
在这个案例中，我们将使用k近邻算法来构建一个模型，来预测用户喜欢的商品，并推荐给用户。
5. 手写汉字识别
手写汉字识别与手写数字识别类似，但更具有挑战性。
在这个案例中，我们将使用k近邻算法来构建一个模型，使其能够准确地识别手写汉字。
四个经典的算法案例
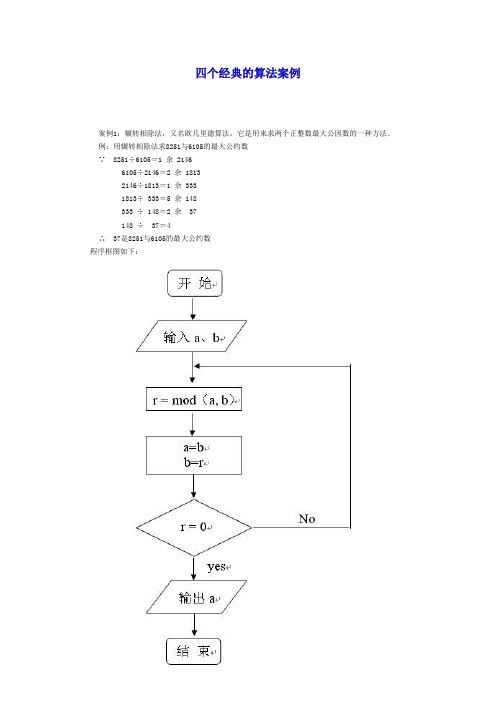
四个经典的算法案例案例1：辗转相除法，又名欧几里德算法，它是用来求两个正整数最大公因数的一种方法。
例：用辗转相除法求8251与6105的最大公约数∵ 8251÷6105＝1 余 21466105÷2146＝2 余 18132146÷1813＝1 余 3331813÷ 333＝5 余 148333 ÷ 148＝2 余 37148 ÷ 37＝4∴ 37是8251与6105的最大公约数程序框图如下：其中 r = mod（a, b） r表示a÷b的余数案例2：秦九韶算法，它是中国南宋时期数学家秦九韶提出的，用来解决多项式的求值问题，在西方被称作霍纳算法。
首先看一道例题：求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法：f(x)可表示为f(x)=（｛［（2x―5）x―4］x+3｝x―6）x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算，不需要乘方运算，它是多项式求值的简化算法。
下面看程序框图，其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3：排序：是一种基本并且常用的算法，排序的算法很多，可以参阅课本，这里不再叙述。
案例4：进位制例：画程序框图，表示把k进制数a（共有n位），转化为十进制数b的过程框图如下：其中：t = GET a│i│ t表示a右数第i位利用上面的算法，把2进制数110011化为十进制的数即：1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法，大家可以从中体会算法的基本思想和算法的基本结构，并尝试用算法的基本语句描述它。
算法解决问题的步骤经典案例
算法解决问题的步骤经典案例算法是解决问题的一种方法和步骤。
经典的案例中，算法一般包括以下步骤：问题定义、问题分析、算法设计、算法分析和算法实现。
下面，我们将介绍几个经典问题案例，并详细说明每个步骤的具体内容。
一、最小生成树问题问题定义：给定一个连通的无向图，每个边都有一个权重，需要找出一棵包含所有顶点但总权重最小的生成树。
问题分析：首先，需要理解连通图和生成树的概念。
然后，要明确最小生成树的定义和目标。
算法设计：可以使用Prim算法或Kruskal算法来解决最小生成树问题。
Prim算法从一个任意的顶点开始，逐步扩展生成树，选择与当前生成树相连的最小权重边。
Kruskal算法则是不断选择权重最小的边，直到生成树包含所有顶点为止。
算法分析：分别分析Prim算法和Kruskal算法的复杂度，比较两个算法的优劣。
算法实现：编写Prim算法和Kruskal算法的代码，并对其进行测试和调试。
二、背包问题问题定义：给定一系列物品和一个固定大小的背包，每个物品都有一个重量和一个价值。
需要确定一个最佳组合，使得背包能够装载最大价值的物品，同时不超过背包的重量限制。
问题分析：需要理解背包问题的定义和背包的限制条件。
可以将其分为01背包问题、完全背包问题和多重背包问题等。
算法设计：对于01背包问题，可以使用动态规划算法来解决。
从第一个物品开始，计算每个物品是否放入背包，使得总价值最大。
对于完全背包问题，也可以使用动态规划算法来解决，但需要考虑每个物品可以重复选择的情况。
对于多重背包问题，可以将其转化为01背包问题来解决。
算法分析：分析背包问题的复杂度，比较不同算法的效率和适用情况。
算法实现：编写动态规划算法来解决背包问题，并对其进行测试和调试。
三、图的最短路径问题问题定义：给定一个加权有向图，需要找到一个顶点到其他所有顶点的最短路径。
问题分析：需要理解最短路径的定义和目标。
可以使用Dijkstra 算法或Bellman-Ford算法来解决最短路径问题。
1.3.2算法案例2
要求多项式的值，应该先算最内层的一次多项式 的值，即 v 1 a n x an 1 然后，由内到外逐层计算一次多项式的值，即
v 2 v1 x an 2 v 3 v 2 x an 3
最后的一 项是什么？
vn vn1 x a0
这种将求一个n次多项式f（x）的值转化成求n个一 次多项式的值的方法，称为秦九韶算法.
所以，当x = 5时，0、a1、a2、a3、a4、a5 输入x0 n=0 v=a5 v= v· 0+a5-n x
n=n+1
n < 5? 否 输出v 结束
秦九韶算法检验
是
练习、已知多项式f(x)=x5+5x4+10x3+10x2+5x+1
f ( x) an x n an1 x n1 a1 x a0
对该多项式按下面的方式进行改写：
f ( x) an x n an1 x n1 a1 x a0
(an x n1 an1 x n2 a1 ) x a0
这是怎样的 一种改写方 式？最后的 结果是什么？
算法步骤：
第一步：输入多项式次数n、最高次项的系数an和x 的值. 第二步：将v的值初始化为an，将i的值初始化为n-1. 第三步：判断i是否大于或等于0，若是，则返回第
四步；否则，转第六步
第四步：输入i次项的系数ai 第五步：v=vx+ai, i=i-1 第六步：输出多项式的值v。
程序框图：
开始
v1 5 5 2 27 v2 27 5 3.5 138.5 v 3 138.5 5 2.6 689.9 v4 689.9 5 1.7 3451.2 v5 3451.2 5 0.8 17255.2
中国企业运用大数据+算法创新案例
我国企业运用大数据+算法创新案例一、案例背景在当前数字化时代，大数据和算法已成为企业创新的重要驱动力。
我国企业不断探索利用大数据和算法进行创新，以提高生产效率、改善用户体验和开拓新业务。
本文将以几个具体案例为例，探讨我国企业如何运用大数据和算法进行创新。
二、滴滴出行滴滴出行是我国领先的移动出行评台，致力于为用户提供安全、便捷的出行体验。
在大数据和算法技术的支持下，滴滴出行实现了智能派单、动态定价和乘客安全预警等功能，极大地提高了出行效率和用户满意度。
通过分析用户行为数据和交通状况，滴滴出行不仅能够预测用车高峰和热门路线，还可以精准计算价格和智能调度车辆，为用户提供更好的出行服务。
三、蚂蚁金服作为我国领先的金融科技企业，蚂蚁金服在金融领域广泛应用大数据和算法进行创新。
通过深度学习和机器学习等技术，蚂蚁金服可以快速、精准地识别用户的信用风险，实现智能风控和反欺诈。
蚂蚁金服还通过大数据分析用户行为和偏好，为用户提供个性化的金融服务和产品，提高了用户体验和满意度。
四、小米科技作为我国知名的科技企业，小米科技在智能硬件领域运用大数据和算法进行创新。
通过智能设备采集用户数据和行为信息，小米可以深入了解用户需求和使用习惯，从而不断优化产品设计和功能体验。
小米还利用大数据分析市场趋势和竞争对手动态，指导产品研发和营销策略，保持领先地位。
五、总结与展望通过以上案例的分析，我们可以看到我国企业在运用大数据和算法进行创新方面取得了显著成效。
未来，随着人工智能和大数据技术的不断发展，我国企业将会在更多领域深化应用，推动产业升级和创新发展。
我们也要关注数据隐私和信息安全等问题，不断完善相关法律法规和监管制度，确保大数据和算法创新能够更好地造福社会。
六、个人观点作为我的文章写手，我深切认识到大数据+算法在我国企业创新发展中的重要性。
这些案例充分展示了大数据和算法在提升企业效率、改善用户体验和促进产业升级方面的巨大潜力。
我对未来我国企业在大数据+算法领域的创新充满信心，也希望政府和企业能够共同努力，建立健全的数据治理和监管体系，更好地应用大数据和算法，推动经济社会发展。
五大经典算法以及案例
五大经典算法以及案例
1. 排序算法：使用冒泡排序算法对一个包含10个随机整数的数组进行排序。
案例：
给定数组：[4, 9, 2, 5, 1, 8, 3, 7, 6, 10]
排序后的数组：[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2. 查找算法：使用二分查找算法在一个有序整数数组中查找目标值。
案例：
给定有序数组：[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
目标值：11
查找结果：目标值在数组中的位置为5。
3. 图遍历算法：使用深度优先搜索算法遍历一个无向图。
案例：
给定无向图的邻接矩阵表示：
[0, 1, 1, 0, 0]
[1, 0, 0, 1, 1]
[1, 0, 0, 0, 1]
[0, 1, 0, 0, 0]
[0, 1, 1, 0, 0]
从节点1开始进行深度优先搜索的遍历结果：1 -> 2 -> 4 -> 3 -> 5
4. 动态规划算法：使用动态规划算法求解斐波那契数列的第n项。
案例：
求解斐波那契数列的第10项：
斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55
第10项为55。
5. 贪心算法：使用贪心算法解决背包问题。
案例：
给定背包容量为10，物品列表如下：
物品1：重量4，价值8
物品2：重量3，价值5
物品3：重量1，价值2
物品4：重量5，价值12
通过贪心算法选择物品装入背包的方案：
选择物品2，物品3，物品4装入背包，总重量为9，总价值为19。
高中数学_算法案例
算法案例知识图谱算法案例知识精讲一．更相减损术应用：求两个整数的最大公约数的算法更相减损术的步骤：1.任意给定两个正整数；判断它们是否都是偶数．若是，则用2约简；若不是则执行第二步．2.以两个数中较大的数减去较小的数，以差数和较小的数构成一对新的数，对这一对数再用大数减小数，以同样的操作一直做下去，直到产生一对相等的数为止，则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数．等值算法：用“更相减损术”设计出来的算法求最大公约数的算法称为“等值算法”，用等值算法可以求任意两个正整数的最大公约数．说明：《九章算法》是中国古代的数学专著，其中的“更相减损术”可以用来求两个数的最大公约数．以具体的例子来说明更相减损术求最大公约数的原理：以求117和182的最大公约数为例：，，，，，，，，(117182)(11765)(6552)(5213)(1339)(1326)(1313)→→→→→→每次操作后得到的两个数与前两个数的最大公约数相同，而且逐渐减少，故总能得到相等的两个数，即为所求的最大公约数．二．辗转相除法又称欧几里得算法，是由欧几里得在公元前300年左右首先提出来的求两个数的最大公约数的算法．辗转相除法的步骤：对于给定的两个数，以其中较大的数除以较小的数得到一个余数，将较小的数与余数看成一对新的数，重复上面的步骤，直到余数为零为止，此时上一步中较小的数即为所求的最大公约数．以求117和182的最大公约数为例：，，，，，,故13即为所求．→→→→(117182)(11765)(6552)(5213)(130)三．秦九韶算法—求多项式的值的算法应用：快速的求解对于任意一个n次的多项式在某点所取到的值.秦九韶算法：已知一个多项式函数，计算多项式在某点处的函数值的一种算法，是我国古代数学家秦九韶提出的，具体如下．对任意一个n 元多项式1110()n n n n f x a x a x a x a --=++++ ，改写成如下形式：12110()()n n n n f x a x a x a x a ---=++++ 231210(())n n n n a x a x a x a x a ---=+++++ = 1210((()))n n n a x a x a x a x a --=+++++ ，求多项式的值时，先计算最内层括号内的一次多项式的值，即11n n v a x a -=+，然后由内向外逐层计算一次多项式的值，即212n v v x a -=+，323n v v x a -=+， ，10n n v v x a -=+．这样，求一个n 次多项式的值，就转化为求n 个一次多项式的值．令1(1)(())k n n n k n k v a x a x a x a ----=++++ ，则递推公式为01n kk n k v a v v x a --=⎧⎨=+⎩，其中12k n = ，，，．到目前为止，此算法仍然是世界上多项式求值的最先进的算法．秦九韶算法与其它算法在计算量上面的比较：1110()n n n n f x a x a x a x a --=++++ ，1.直接求和法：先计算各个单项式的值，再把它们相加，乘法次数为(1)(1)212n n n n ++-+++= ，加法次数n ；2.逐项求和法：先计算x 的各项幂的值，再分别相乘，计算幂值需要乘法1n -次，将幂值与多项式系数k a 相乘需要乘法n 次，故共需要乘法21n -次，加法n 次．此方法对直接求和法有所改进，但仍然比秦九韶算法计算量大很多．3.秦九韶算法：计算量仅为乘法n 次，加法n 次．<备注>秦九韶算法是多项式求值的优秀算法，秦九韶算法的特点：（1）化高次多项式求值为一次多项式求值；（2）减少了运算次数，提高了效率；（3）步骤重复执行，容易用计算机实现．利用秦九韶算法计算多项式的值关键是能正确地将所给多项式改写，然后由内向外逐次计算，由于后项计算用到前项的结果，故应认真、细心，确保中间结果的准确性．若在多项式中有几项不存在时，可将这些项的系数看成0，即把这些项看做0·x n ．三点剖析一．注意事项1.辗转相除法与更相减损术联系（1）都是求最大公约数的方法，计算上，辗转相除法以除法为主，更相减损术以减法为主，计算次数上，辗转相除法计算次数相对较少，特别当两个数大小差距较大时，计算次数的区别比较明显；（2）从结果的体现形式来看，辗转相除法体现结果是以相除余数为零而得到，而更相减损术则是以减数与差相等而得到；（3）辗转相除法与更相减损术是统一的，因为做一次除法与做若干次减法的效果相同.二．方法点拨1.两个整数的最大公约数是两个整数的公约数中最大的数，与此类似，两个整数的最小公倍数是两个整数的公倍数中最小的数.2.穷举法是将集合中的元素进行一一列举，逐个条件进行验证，知道找出满足条件的元素为止，穷举法可以解决所有问题看，但是一般来说常常可以用来解决一些无规律可循的问题，例如求不定方程的解或者不定方程组的解，运用穷举法思想设计算法时，常常采用循环结构，将验证条件为循环结构的判断条件，将每一个元素作为循环体.求两个正整数的最大公约数例题1、8251与6105的最大公约数是____．例题2、用更相减损来求80和36的最大公约数？例题3、用更相减损术求294与84的最大公约数．随练1、两个数153和119的最大公约数是______________．随练2、用更相减损术求294与84的最大公约数．随练3、有甲、乙、丙三种溶液分别重147g、343g、133g，现要将它们分别全部装入小瓶中，每个小瓶装入液体的质量相同，问每瓶最多装多少？秦九韶算法例题1、用秦九韶算法求多项式f（x）=x4+2x3+x2-3x-1，当x=2时的值，则v3=______例题2、使用秦九韶算法计算x=2时f（x）=6x6+4x5-2x4+5x3-7x2-2x+5的值，所要进行的乘法和加法的次数分别为________随练1、用秦九韶算法求多项式f（x）=1+2x+x2-3x3+2x4在x=-1时的值，v2的结果是______随练2、用秦九韶算法计算多项式f（x）=5x5+4x4+3x3-2x2-x-1在x=-4时的值时，需要进行的乘法、加法的次数分别是_______拓展1、用更相减损术求78和36的最大公约数_________．2、三个数208，351，429的最大公约数是（）A.65B.91C.26D.133、用“辗转相除法”求得459和357的最大公约数是（）A.3B.9C.17D.514、用秦九韶算法求多项式f（x）=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4的值时，其中V1的值=_______5、用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时，需要做乘法和加法的次数分别是。
算法案例(秦九韶算法)
算法的步骤和流程
01
02
03
04
2. 将 $a_{i+1}$ 加到 $v$ 中。 3. 将 $v$ 存储在变量 $P$ 中。
步骤3：返回 $P$ 作为多项 式的值。
通过以上步骤，秦九韶算法可以 在 $O(n)$ 的时间内计算出一元 多项式的值，其中 $n$ 是多项式 的次数。与直接使用常规的求值 方法相比，秦九韶算法可以显著 减少乘法的次数，从而提高计算
缺点
对大系数多项式不适用
秦九韶算法适用于系数和次数都很大的多项式，但如果多项式的 系数非常大，可能会导致数值溢出或下溢，影响计算精度。
需要额外的存储空间
秦九韶算法需要存储中间结果，如果多项式的次数很大，需要额外 的存储空间。
对某些特殊多项式不适用
秦九韶算法不适用于某些特殊的多项式，如常数、一次多项式等。
秦九韶算法的应用场景
数值分析
秦九韶算法在数值分析中广泛应用于求解多项式方程的根，以及进行 数值积分和微分等计算。
科学计算
在科学计算领域，秦九韶算法被用于计算物理、化学、工程等领域中 的多项式函数值，以及进行数据拟合和插值等操作。
计算机图形学
在计算机图形学中，秦九韶算法被用于计算光线追踪和纹理映射等算 法中的多项式函数值，以提高渲染效率和精度。
05
秦九韶算法的优缺点
优点
高效性
秦九韶算法是一种快速算法，可以在多项式 时间内完成计算，比直接计算更高效。
易于编程实现
秦九韶算法的步骤明确，易于编程实现，可 以方便地应用于计算机程序中。
数值稳定性
秦九韶算法在计算过程中可以减少舍入误差， 提高数值稳定性。
适用范围广
秦九韶算法适用于多项式的系数和次数都很 大的情况，具有较广的适用范围。
算法案例(完整版)
例2 已知10b1（2）=a02（3）,求数字a， b的值.
10b1（2）=1×23+b×2+1=2b+9. a02（3）=a×32+2=9a+2. 所以2b+9=9a+2，即9a-2b=7.
故a=1，b=1.
小 结
1. k进制数使用0～（k-1）共k个数字， 但左侧第一个数位上的数字（首位数字） 不为0. 2.用 an an-1 a2 a1(k ) 表示k 进制数，其中k称为基数，十进制数不标 注基数. 3. 把k进制数化为十进制数的一般算式 是： an an-1 a2 a1(k )
第一步，输入a和n的值. 第二步，令b=0，i=1. i-1 b 第三步， = b + ai ´ 2 ， i=i+1. 第四步，判断i>n 是否成立.若是，则输 出b的值；否则，返回第三步.
同样地，把k进制数 a = an an-1 a2 a1(k )
化为十进制数b的算法和程序框图如何设 计？ 第一步，输入a，k和n的值. 第二步，令b=0，i=1.
“更相减损术”在中国古代数学专著《 九章算术》中记述为：
可半者半之，不可半者，副置分母、 子之数，以少减多，更相减损，求其等 也，以等数约之.
例1 分别用辗转相除法和更相减损 术求168与93的最大公约数. 辗转相除法：168=93×1+75，
93=75×1+18， 75=18×4+3， 18=3×6.
a=rnrn-1„r1r0(2)
知识探究(二):十进制化k进制的算法
思考1:根据上面的分析，将十进制数a化 为二进制数的算法步骤如何设计？ 第一步，输入十进制数a的值. 第二步，求出a除以2所得的商q，余数r. 第四步，若q≠0，则a=q，返回第二步； 否则，输出全部余数r排列得到 的二进制数.
古代数学中的算法案例
古代数学中的算法案例古代数学是人类发展历史中的重要组成部分，古代数学家们在没有现代计算设备的情况下，通过发展各种算法来解决实际问题。
以下是几个古代数学中的算法案例。
一、埃及乘法算法埃及乘法算法起源于古埃及时期，被用于解决大数字的乘法问题。
这个算法的基本思想是将一个数字分解为2的幂的和，然后将每个分解项相乘，最后将乘积相加得到结果。
例如，计算15乘以23，首先将15分解为2的幂的和，即15=1+2+4+8，然后将23与每个分解项相乘，得到23、46、92和184、最后将这些乘积相加，得到345，即15乘以23的结果。
二、中国割补算法中国割补算法是中国古代数学中的一种乘法算法，用于计算两个数的乘积。
这个算法的核心思想是通过不断削减和补充相乘数的位数，最终得到乘积。
以计算13乘以21为例，首先将13和21写成两列：```1321--23```然后将第一列的数字逐次除以2，直到最后为0，同时将第二列的数字逐次乘以2、每次除以2时，如果结果为奇数，则将第二列当前行的数字加到最后的乘积上，如果结果为偶数，则不加。
最后将所有加上的数字相加，得到乘积。
在这个例子中，结果为273三、印度乘法算法印度乘法算法是古印度数学中的一种乘法算法，用于计算两个数的乘积。
这个算法的基本思想是将一个数字分解为2的幂的和，然后将每个分解项与另一个数字相乘，最后将乘积相加得到结果。
以计算23乘以16为例，首先将23表示为2的幂的和，即23=1+2+4+16、然后将每个分解项与16相乘，得到16、32、64和256、最后将这些乘积相加，得到368，即23乘以16的结果。
四、巴比伦平方根算法巴比伦平方根算法是古巴比伦数学中的一种算法，用于求一个数字的平方根。
这个算法的基本思想是通过迭代逼近的方式，不断改进平方根的近似值。
例如，求解数字10的平方根。
首先假设一个初始近似值，例如2、然后通过将这个近似值与10除以这个近似值的平均值相加，得到新的近似值。
c语言十大算法案例
c语言十大算法案例C语言是一种广泛应用于编程的高级语言，具有简单、灵活、高效等特点。
在C语言中，有许多经典的算法案例，这些算法案例不仅有助于提高编程能力，还能帮助我们理解计算机科学的基本原理。
下面列举了十个C语言的经典算法案例。
1. 冒泡排序算法：冒泡排序是一种简单但效率较低的排序算法，它通过多次比较和交换相邻元素的方式将最大或最小的元素逐步移动到数组的一端。
2. 快速排序算法：快速排序是一种常用的排序算法，它通过选择一个基准元素，将数组分成两个子数组，然后对子数组进行递归排序。
3. 二分查找算法：二分查找是一种高效的查找算法，它通过将查找范围缩小一半来快速定位目标元素。
4. 链表反转算法：链表反转是一种常见的操作，它可以将链表中的节点顺序逆转。
5. 汉诺塔算法：汉诺塔是一种经典的递归问题，它通过将圆盘从一个柱子移动到另一个柱子来演示递归的思想。
6. 最大公约数算法：最大公约数是指能够同时被两个或多个整数整除的最大正整数，求最大公约数的算法有多种，如辗转相除法和欧几里德算法。
7. 斐波那契数列算法：斐波那契数列是一个数列，其中每个数字都是前两个数字之和，求斐波那契数列的算法有多种，如递归和循环。
8. 图的深度优先搜索算法：深度优先搜索是一种用于遍历图的算法，它通过递归的方式依次访问图中的每个节点。
9. 图的广度优先搜索算法：广度优先搜索也是一种用于遍历图的算法，它通过队列的方式依次访问图中的每个节点。
10. 最短路径算法：最短路径算法用于找到图中两个节点之间的最短路径，常用的最短路径算法有迪杰斯特拉算法和弗洛伊德算法。
这些算法案例涵盖了排序、查找、链表操作、递归、图算法等多个方面，是C语言学习中不可或缺的部分。
通过学习和理解这些经典算法案例，我们可以提高自己的编程能力，并在解决实际问题时能够选择合适的算法。
希望本文能够对读者有所帮助，激发他们对C 语言算法的兴趣，并在编程的道路上不断进步。
数据结构与算法的实际应用案例
数据结构与算法的实际应用案例如今，数据结构与算法在各个领域都扮演着重要的角色。
它们不仅可以提高程序的效率和性能，还能解决各种实际问题。
在本文中，我们将介绍几个有代表性的数据结构与算法实际应用案例，以展示它们的广泛应用和巨大潜力。
案例一：最短路径算法在导航系统中的应用导航系统已经成为我们日常生活中不可或缺的工具之一。
其中，最短路径算法被广泛应用于导航系统中的路线规划。
最著名的最短路径算法之一是Dijkstra算法，它能够找到两个地点之间的最短路径。
通过有向加权图的建模，Dijkstra算法根据各个路段的权重（比如道路长度或者交通拥堵程度），确定最优路径，从而为用户提供最佳的导航路线。
案例二：哈希表在数据库中的应用在数据库中，存储和检索数据是一项核心任务。
为了提高查找速度，哈希表经常被用于索引数据。
哈希表将数据存储在键-值对的形式下，并通过哈希函数将键映射到相应的位置。
这样一来，我们可以以常数时间复杂度进行数据的存取。
哈希表在大型数据库中的应用十分广泛，如索引管理、关系查询等。
案例三：图算法在社交网络分析中的应用随着社交网络的兴起，图算法也开始在社交网络分析中扮演重要角色。
以Facebook为例，它使用图算法来分析用户之间的关系和相似性，从而提供个性化的推荐和广告定向投放。
其中，深度学习算法和图嵌入技术常常与图算法相结合，使得社交网络分析更加精准和高效。
案例四：贪心算法在排课问题中的应用在学校的课程安排中，如何合理地排课是一项复杂而困难的任务。
贪心算法可以用来解决这个问题。
它从某个起点开始，逐步做出局部最优选择，最终得到全局最优解。
在排课问题中，贪心算法可以根据教室、教师和学生的时间限制，合理地安排课程表，使得时间冲突最小化，从而提高学校的教学效率和资源利用率。
结论综上所述，数据结构与算法在实际应用中发挥着巨大的作用。
从导航系统的路径规划到社交网络分析的个性化推荐，从数据库的快速检索到学校排课的优化安排，数据结构与算法的实际应用案例层出不穷。
贪心算法 思政案例
贪心算法思政案例贪心算法是一种常用的算法思想，它在很多问题的求解中具有良好的效果。
贪心算法的核心思想是每一步都采取当前状态下最优的选择，以期望从局部最优达到全局最优。
下面以思政教育案例来说明贪心算法的相关参考内容。
案例一：多次挑战班级积极分子某高中为了推动思政教育，特设立了"班级积极分子"这一称号。
根据规定，每个班级每学期只能评选一位同学为"班级积极分子"，并且这个称号不能重复评选。
现有10个班级，每个班级都有若干名同学希望获得这一称号。
请设计一个算法，使得每个班级都能评选出"班级积极分子"，且使得全体学生评选次数尽可能多。
解决思路：可以将每个班级内的积极分子候选人按照积极程度从高到低排序。
然后从第一个班级开始，选择当前班级的积极分子候选人列表中排名第一的同学，并将其加入获奖名单，同时将该同学从其他班级的候选人列表中删除。
接着切换到下一个班级，重复上述步骤，直到所有班级都评选出"班级积极分子"。
参考内容：1. 分析问题：通过理解问题需求和要求，设计合理的解决思路，考虑到全局最优的目标。
2. 形成排序：根据问题的特点，对候选人进行排序，以便能够在每个班级中选择最优的积极分子。
3. 进行选择：依次遍历每个班级，选择当前班级的最优积极分子，并将其加入获奖名单。
4. 更新候选人列表：在每次选择过程中，需要将已经选择的积极分子从其他班级的候选人列表中删除，避免重复评选。
5. 终止条件：在所有班级都评选出"班级积极分子"之后终止算法。
案例二：有效利用公共资源在学校的自习室中，有一块黑板用来为同学们提供公共资源，例如提醒事项和优秀学生的表彰。
由于黑板的空间有限，每天只能够展示有限数量的内容。
学校决定为黑板设计一个自动管理系统，能够在满足每天展示尽量多的内容的前提下，最大限度地利用黑板的空间。
解决思路：可以将输入的内容按照优先级从高到低进行排序，并从排在前面的内容开始逐个加入黑板展示。
1.3算法案例 课件-高一数学人教A版必修3
用秦九韶算法求这个多项式当x=5时的值。
解：根据秦九韶算法，把多项式改写成如下 形式：
f (x) ((((4x 2)x 3.5)x 2.6)x 1.7)x 0.8
按照从内到外的顺序，依次计算一次多项式当 x=5时的值：
WHILE d<>n
IF d>n THEN m=d
ELSE m=n
n=d
END IF d=m－n WEND d=2^k*d
PRINT d
END
问题2：怎样求多项式 f (x) x5 x4 x3 x2 x 1当x=5 的值呢？
方法1：把5代入多项式，计算各项的值，然后把它们加 起来。这时共做了1+2+3+4=10次乘法运算，5 次加法运算。
例1：用更相减损术求98与63的最大公约数。
解：由于63不是偶数，把98和63以大数减小数， 并辗转相减得，如图所示：
98－63=35 63－35=28 35－28=7 28－7=21 21－7=14 14－7=7
所以，98和63的最大公约数等于7。
思考：把更相减损术与辗转相除法比较，你有什么
发现？你能根据更相减损术设计程序，求两个正数的 最大公约数吗？
v1 an x an1
然后由内向外逐层计算一次多项式的值，即
v2 v1 x an2 ,
v3 v2 x an3 ,
vn vn1 x a0 ,
这样，求n次多项式f(x)的值就转化为求n个一次多项 式的值。
上述方法称为秦九韶算法。直到今天， 这种算法仍是 多项式求值比较先进的算法。
例2、已知一个5次多项式为
⑤十进制化k进制
数据挖掘十大算法案例
数据挖掘十大算法案例
以下是数据挖掘十大算法案例：
- C4.5：机器学习算法中的一个分类决策树算法，是决策树核心算法ID3的改进算法。
- The k-means algorithm：即K-Means算法。
- Support vector machines：支持向量机。
- The Apriori algorithm：Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。
- 最大期望(EM)算法。
- PageRank：网页排名算法。
- AdaBoost：一种迭代的学习算法。
- kNN：K最近邻（k-Nearest Neighbor，KNN）分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。
- Naive Bayes：朴素贝叶斯算法。
这些算法在数据挖掘和机器学习领域中得到了广泛的应用，并且每个算法都有其独特的特点和应用场景。
在实际应用中，需要根据具体的问题和数据特点选择合适的算法，以获得最佳的效果。
算法模型治理案例
算法模型治理案例
算法治理的案例有很多，以下是其中两个：
1. 某（中国）软件公司与安徽某科技公司不正当竞争纠纷案：此案系全国首例数据产品纠纷案，也是首例涉数据资源开发应用正当性及数据权属判定的新类型不正当竞争案件。
本案判决明确了网络运营者对于用户行为信息的安全保护责任，界定了数据收集、使用的合法性、正当性标准，首次通过司法判例初步厘清了各相关主体数据权益的权利边界，同时赋予数据产品开发者享有“竞争性财产权益”，确认其可以此为权利基础获得反不正当竞争法的保护，为相关立法的完善提供了可借鉴的司法例证。
2. 城市大脑数据治理理念：该理念强调利用数据资源优化城市公共资源，推动城市治理模式的提升。
例如，通过处理79个数据源的1000亿条结构化数据和非结构化数据，城市大脑可以实现城市运行的智能化和精细化。
这两个案例分别从企业与政府、企业的角度探讨了算法治理的实践应用，突出了算法治理在现代社会中的重要性和必要性。
算法学习中的实际应用案例分享
算法学习中的实际应用案例分享在当今信息时代，算法已经成为了人们生活中不可或缺的一部分。
无论是搜索引擎的排名算法，还是社交媒体的推荐算法，都离不开算法的支持。
算法学习不仅仅是一门学科，更是一种思维方式和解决问题的能力。
在本文中，将分享一些算法学习在实际应用中的案例，展示算法的强大威力。
一、图像识别算法在人脸识别中的应用图像识别算法是计算机视觉领域中的重要研究方向。
人脸识别作为其中的一个应用场景，一直备受关注。
通过图像识别算法，计算机可以识别和区分不同的人脸，实现自动化的人脸识别功能。
例如，我们常见的手机解锁功能，就是通过人脸识别算法来实现的。
人脸识别算法的实现过程包括图像采集、特征提取和匹配等步骤。
首先，通过摄像头采集到的图像会被算法处理，提取出人脸的特征。
然后，将提取到的特征与已有的人脸数据库进行匹配，找到最相似的人脸。
最后，根据匹配结果，判断是否为同一个人。
这种算法的应用不仅仅局限于手机解锁，还可以应用于安防领域、人脸支付等场景。
通过算法学习，不断优化算法的准确性和速度，可以提升人脸识别技术的应用性能。
二、推荐算法在电商平台中的应用推荐算法是电商平台中的核心技术之一。
通过分析用户的购买记录、浏览行为等数据，推荐算法可以为用户提供个性化的商品推荐，提高用户的购物体验和购买转化率。
推荐算法的实现过程主要包括数据收集、特征提取和推荐模型训练等步骤。
首先，电商平台会收集用户的购买历史、浏览记录等数据，构建用户行为模型。
然后，通过特征提取算法，将用户的行为数据转化为特征向量。
最后，通过训练推荐模型，根据用户的特征向量和商品的特征向量，计算出商品的推荐分数，从而为用户提供个性化的商品推荐。
推荐算法的应用不仅仅局限于电商平台，还可以应用于音乐、视频、新闻等领域。
通过算法学习，不断改进推荐算法的准确性和效果，可以提高用户的满意度和平台的盈利能力。
三、路径规划算法在物流配送中的应用路径规划算法是物流配送中的重要工具。
机器学习算法的应用案例及技巧
机器学习算法的应用案例及技巧随着科技的发展和数据的爆炸增长，机器学习算法在各个领域的应用越来越广泛。
机器学习算法通过对数据进行分析和学习，从而能够自动识别模式和进行预测。
在本文中，将介绍几个机器学习算法的应用案例，并提供一些相关的技巧。
一、垃圾邮件分类垃圾邮件过滤是机器学习中最常见的应用之一。
传统的垃圾邮件过滤器使用规则和规则引擎来分类邮件，但这种方法需要大量的人工劳动力和时间。
机器学习算法可以通过学习已有的标记邮件数据集，自动识别和分类垃圾邮件。
在垃圾邮件分类中，常用的算法包括决策树、朴素贝叶斯和支持向量机。
决策树算法通过构建一个树状的分类模型，根据邮件的特征（例如发件人、主题、内容等）进行分类。
朴素贝叶斯算法基于贝叶斯定理，利用特征之间的条件独立性进行分类。
支持向量机算法通过寻找一个最优的超平面来在特征空间中进行分类。
在实际应用中，为了提高垃圾邮件分类的准确性，可以采用集成学习的方法。
集成学习通过结合多个分类器的结果，来获得更为准确的分类结果。
常用的集成学习算法包括随机森林和梯度提升树。
二、图像识别图像识别是机器学习算法的另一个重要应用领域。
随着数字图像的普及和摄像头设备的大规模应用，图像识别技术在实际生活中被广泛使用。
图像识别可以用于人脸识别、物体检测、图像分类等任务。
常用的图像识别算法包括卷积神经网络（CNN）和深度学习。
卷积神经网络是一种特殊的神经网络结构，能够有效地处理图像和空间数据。
深度学习则是指使用深层的神经网络进行学习和训练。
在图像识别中，数据集的质量和大小对算法的性能有重要影响。
为了提高算法的准确性，可以使用数据增强和迁移学习技术。
数据增强可以通过对图像进行旋转、平移、缩放等操作来增加训练样本的多样性。
迁移学习则是利用已经训练好的模型来进行新任务的训练，可以减少对大规模数据集的依赖，提高训练速度和效果。
三、推荐系统推荐系统是在线电子商务平台中常用的功能，通过分析用户的历史行为和个人特征，向用户推荐个性化的商品或服务。
算法优化案例分析
算法优化案例分析随着人工智能和大数据时代的到来，算法优化已成为了提升企业竞争力的重要手段之一。
本文将介绍几个算法优化案例，并分析其优化效果。
1. 贪心算法优化案例某电商企业想提高广告推荐的效果，通过搜索历史、购买记录等数据建立了基于内容的推荐模型。
但是，该模型对于用户行为的反馈较慢，需要时间的积累才能够得到有效的结果。
为了解决这一问题，该企业采用了贪心算法优化推荐效果。
具体实现方法是，将用户历史记录按照时间顺序排序，针对每个用户优先推荐其最新的购买记录，然后根据购买记录的相关性向其推荐其他商品。
经过贪心算法的优化，该企业的推荐效果得到了显著提升，用户的点击率和转化率分别提高了20%和15%。
2. 遗传算法优化案例某物流公司想要优化货车的路径规划，以降低成本和提高效率。
该公司决定采用遗传算法来进行优化。
在遗传算法中，货车路径被看作是基因组。
该公司将所有可能的路径作为种群，并通过交叉、变异等操作产生新的种群。
在每一代种群中，通过计算每个路径的成本（例如行驶里程、耗时等），选择最优化的路径进行输出，作为下一代的基因组。
经过遗传算法的优化，该公司的货车路径规划得到了明显的改善。
货车行驶里程和时间降低了10%，配送效率提高了近15%。
3. 神经网络算法优化案例一家保险公司想要优化其车险投保模型。
该公司将用户的驾驶习惯、车辆品牌等数据输入到神经网络算法中，以判断该用户的风险系数。
为了提高模型的准确性，该公司采用了神经网络算法的正则化方法。
具体实现方式是，增加模型中的L1或L2项，使神经网络的权重限制在一个较小的范围内。
经过神经网络算法的优化，该公司的车险投保模型得到了显著提升。
误判率和漏判率分别降低了15%和8%，整体准确率提高了10%。
以上案例说明，算法优化在提升企业竞争力和效率方面具有重要作用。
不同的算法优化方法，可以针对不同的业务场景以达到最优化的效果。
算法特征的案例
算法特征的案例
以下是一些具有算法特征的案例：
1. 推荐算法：在线购物平台使用推荐算法根据用户的历史购买记录和浏览行为，为用户推荐相关的商品或服务。
2. 图像识别算法：社交媒体平台使用图像识别算法自动识别和标记上传的照片中的人物或物体。
3. 自然语言处理算法：智能助手应用使用自然语言处理算法，能够理解和解释用户的语言输入，并提供相关的回答或建议。
4. 聚类算法：零售公司使用聚类算法对顾客的购买行为进行分析，将顾客分成不同的群体，并为每个群体设计不同的销售策略。
5. 遗传算法：工程设计领域使用遗传算法进行优化，通过模拟生物进化的方式，寻找最优解决方案。
6. 最短路径算法：导航应用使用最短路径算法计算出从起点到终点的最短路径，并提供导航指引。
7. 随机森林算法：金融领域使用随机森林算法对借贷申请进行风险评估，预测申请人是否具有还款能力。
8. PageRank算法：搜索引擎使用PageRank算法对网页进行排名，根据页面的链接结构和权重来确定搜索结果的排序。
9. 支持向量机算法：医疗领域使用支持向量机算法进行癌症诊断，根据患者的病历数据判断患者是否患有癌症。
10. 强化学习算法：自动驾驶系统使用强化学习算法进行学习和决策，通过与环境的交互来提高驾驶性能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§1.3 算法案例（第一课时 辗转相除法与更相减损术）【课标定向】学习目标理解并应用求最大公约数的两种方法：辗转相除法与更相减损术． 提示与建议正确掌握两种算法的特点，加以联系与区别体会算法的实际应用．【互动探究】自主探究______的数（用变量m 表示）除以______的数（用变量n 表示），得到除式：______，反复执行这一步骤的次数由______决定． 2.更相减损术的步骤为：第一步：__________，第二步：____________．剖例探法★讲解点一 辗转相除法用辗转相除法求,m n 的最大公约数的方法是：计算出m n ÷的余数r ，若0r =，则n 就是,m n 的最大公约数；若0r ≠，则把前面的除数n 作为新的被除数，把余数r 作为新的除数，继续运算，直到余数为零，此时的除数即为自然数,m n 的最大约数．例题１求319，377，116的最大公约数． 【思维切入】求3个数的最大公约数，可以先求其中两个数的最大公约数，再求这个最大公约数与第三个数的最大公约数．【解析】3773191÷=（余58）， 319585÷=（余29）， 58292÷=（余0），∴377与319的最大公约数为29，再求29与116的最大公约数．∵116294÷=（余0），∴29与116的最大公约数为29．∴319，377，116的最大公约数为29．【规律技巧总结】利用辗转相除法求最大公约数，当余数为0时，除数就是所求的最大公约数．初学者不加以注意，往往会把这时候的商作为最大公约数．★讲解点二 更相减损术更相减损术是中国古代数学专著《九章算术》中的一个算法，课本对这段原文翻译有误，应如下解释：能用2约分的先用2约分，不能用2约分时，则将分子和分母上的数取出，用较大的数减去较小的数，再把得到的差与较小的数比较，并以大数减小数，反复相减，直到两数相等．例题2分别用辗转相除法和更相减损术求下列两数的最大公约数：⑴261，319；⑵1734，816．【思维切入】使用辗转相除法可依据m nq =，r +反复执行，直到0r =为止；用更相减损术就是根据m n r -=，反复执行，直到n r =为止．【解析】⑴辗转相除法： 3192161÷=（余58）， 261584÷=（余29）， 58292÷=（余0），∴377与319的最大公约数为29． 更相减损术： 31921658-=， 21658203-=， 20358145-=， 1455887-=， 875829-=， 582929-=，∴377与319的最大公约数为29． ⑵辗转相除法：17348161÷=（余102）， 8161028÷=（余0），∴1734与816的最大公约数为102．更相减损术：因为两数皆为偶数，首先除以2得到867，408，再求867与408的最大公约数．867408459-=， 45940851-=， 40851357-=， 35751306-=， 30651255-=， 25551204-=， 20451153-=， 15351102-=， 1025151-=，∴1734与816的最大公约数为102．【规律技巧总结】通过上例可以发现用辗转相除法和更相减损术求得的最大公约数是相同的，但用辗转相除法的步骤较少，而用更相减损术运算简易却步骤较多，在解题时应灵活运用． 精彩反思辗转相除法与更相减损术的统一性实际上，辗转相除法与更相减损术是统一的，我们举例说明这一点．如63183÷=（余9），而63181818--- 9=．这说明，做一次除法与做若干次减法的效果相同，商就是做减法的次数，余数就是最后的差．由此可知，二者是完全统一的，做除法运算的次数比做减法的次数一般要少．因此，辗转相除法能更快地得到结果，但减法运算比除法运算更容易，因此不能说哪种方法比另一种好，辗转相除法也未必比更相减损术效率高．【自我测评】1.用“辗转相除法”求得459与357的最大公约数是（ ）Ａ．3 Ｂ．9 Ｃ．17 Ｄ．512.两个整数490和910的最大公约数是（ ） Ａ．2 Ｂ．10 Ｃ．30 Ｄ．703.以下是利用更相减损术求78和36的最大公约数的操作步骤（78，36）→（42，36）→（6，30）→（6，24）→（6，18）→（6，12）→（6，6），那么78和36的最大公约数是 （ ） Ａ．1 Ｂ．12 Ｃ．6 Ｄ．364.用更相减损术求225和135的最大公约数为_____．5.下列程序的目的是（ ）．Ａ．求/a b 的余数 Ｂ．求,a b 的最小公倍数 Ｃ．求a 被b 除的商 Ｄ．求,a b 的最大公约数【拓展迁移】思维提升6.下面两个程序的作用是⑴______； ⑵______．视野拓展数学王子——高斯高斯（1777-1855）德国数学家、物理学家和天文学家．高斯在童年时代就表现出非凡的数学才华，年仅三岁，就学会了算术，八岁因发现等差数列求和公式而深得老师和同学的饮佩．大学二年级时得出正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件，解决了两千年来悬而未决的难题．1799年以代数基本定理的四个漂亮的证明获得博士学位．高斯的数学成就遍及各个领域，在数学许多方面的贡献都有着划时代的意义，并在天文学、大地测量学和磁学的研究中都有杰出的贡献．1801年发表的《算术研究》是数学史上为数不多的经典著作之一，它开辟了数论研究的全新时代．非欧几里得几何是高斯的又一重大发现，他的遗稿表明，他是非欧几何的创立者之一．§1.3 算法案例 （第二课时 辗秦九韶算法）【课标定向】学习目标多项式的秦九韶算法． 提示与建议理解秦九韶算法的算法思想，体会中国古代数学对世界数学发展的贡献，增强民族自豪感．【互动探究】自主探究1.秦九韶算法用于求______，算法中反复执行的一个递推公式为______．2.用秦九韶算法求函数432()23f x x x x =++x +1+在2x =处的值为（ ）．Ａ．46 Ｂ．47 Ｃ．48 Ｄ．49 剖例探法★讲解点一 秦九韶算法秦九韶算法是中国古代数学家秦九韶发明的一个算法，其作用是求一元n 次多项式的值．即使在现代，它仍是此类算法中最优秀的算法之一．设1110()n n n n f x a x a x a x a --=++++ ，要求()f x 当0x x =时的值，可有多种方法：⑴直接计算：即按顺序一项一项地计算然后相加，求得0()f x ，可知乘法的次数为(1)1232n n n +++++=，加法次数为n ． ⑵逐项求和法：在直接计算法的基础上作了改进，先把多项式写成11()n n n n f x a x a x --=⋅+⋅1010a x a x ++⋅+⋅ 的形式，这样多项式的每一项都是k a 与kx 的乘积（0,1,2,,k n = ）．在计算k k a x 项时把k x 的值保存在变量c 中，求项11k k a x ++时只须计算1k a x c +⋅⋅，同时把1k x c x+⋅=的值存入c 中，继续下一项的运算，这样以后每一项的求值只需做两次乘法，然后把这1n +项的值相加．容易看出逐项求和法所用乘法的次数为21n +，加法次数n ．⑶秦九韶算法：将()f x 改写成如下形式()f x =1210((()))n n n a a x a x a x a --+++++ ，其计算步骤为：先计算11n n v a x a -=+，再计算212n v v x a -=+，每次都是把上一次的结果乘以x 再与下一个系数相加，其计算量为乘法n 次，加法n次．当n ≥4时，(1)212n n n n +<+<，且随着n 的变大，三个数的差距越来越大．如100n =时，21201n +=，(1)50502n n +=．由此我们可以看到秦九韶算法比其它算法优越得多．秦九韶算法的主要优点是：⑴大大减少了乘法的次数，使计算量减少．在计算机上做一次乘法所需要的时间是做加法、减法的几倍到十几倍，减少做乘法的次数也就加快了计算的速度．⑵规律性强，便于利用循环语句来实现算法．⑶避免了对自变量x 单独做幂的计算，每次都是计算一个一次多项式的值，从而可提高计算的精度．例题用秦九韶算法求多项式54()38f x x x =+3235126x x x -++-当2x =时的值．【思维切入】秦九韶算法的关键在于把n 次多项式转化为求一次多项式的值，注意体会递推的实现过程．【解析】根据秦九韶算法，把多项式改写成如下形式：()((((38)3)5)12)6f x x x x x x =+-++-，按照从内到外的顺序，依次计算一次多项式当时2x =的值．03v =，102832814v v =⨯+=⨯+=， 2123142325v v =⨯-=⨯-=，3225252555v v =⨯+=⨯+=， 4321255212122v v =⨯+=⨯+=， 542612226238v v =⨯-=⨯-=．【规律技巧总结】直接代入求解，则计算机在执行时要进行15次乘法和5次加法运算，而利用秦九韶算法只需进行5次乘法、5次加法即可，要知道，让计算机进行一次乘法运算要比加法用的时间多很多，所以要减少运算中乘法的次数，这也就是秦九韶算法的优势所在了． 精彩反思用秦九韶算法计算多项式的值，关键是正确地将多项式改写，然后由内向外依次计算求得．【自我测评】1.用秦九韶算法计算多项式65432()3456781f x x x x x x x =++++++当0.4x =时的值，需要做乘法和加法次数分别为（ ）Ａ．6，6 Ｂ．5，6 Ｃ．5，5 Ｄ．6，52. 9876()102154f x x x x x =+++4332x x ++231x x +++，则(2)f =（ ）Ａ．11471 Ｂ．11472 Ｃ．11473 Ｄ．11474【拓展迁移】思维提升3.用秦九韶算法计算多项式65432()3456781f x x x x x x x =++++++当4x =-时，4v 的值是 （ ）Ａ．-57 Ｂ．220 Ｃ．-845 Ｄ．33924.用秦九韶算法计算多项式878710()f x a x a x a x a =+++当0x x =时的值，要做____次乘法运算，____次加法运算． 5.用秦九韶算法计算多项式432()320.687f x x x x x =++++当5x =时的值．视野拓展信仰“数即万物”的毕达哥拉斯毕达哥拉斯出生在爱琴海中的萨摩斯岛（今希腊东部小岛），自幼聪明好学，曾在名师门下学习几何学、自然科学和哲学．毕达哥拉斯学派很重视数学，企图用数学来解释一切．他们研究数学的目的并不在于实用，而是为了探索自然的奥秘．毕达哥拉斯本人以发现勾股定理著称，其实这个定理早为巴比伦人和中国人所知，不过最早的证明应归功毕达哥拉斯．毕达哥拉斯还是音乐理论的鼻祖，他阐明了单弦的乐音与弦长的关系．在天文方面．首创地圆说．毕达哥拉斯的思想和学说，对希腊文化有巨大的影响．§1.3 算法案例（第三课时进位制）【课标定向】学习目标进位制与数制转换． 提示与建议重点掌握十进制与其他进位制的相互转化．【互动探究】自主探究1.下列关于进位制说法错误的是（ ）．Ａ．进位制是人们为了计数和运算方便而约定的记数系统 Ｂ．二进制就是满二进一，十进制就是满十进一 Ｃ．满几进几，就是几进制，几进制的基数就是几Ｄ．为了区分不同的进位制，必须在数的右下角标注基数 2.四进制数(4)2231转化为十进制数是（ ）． Ａ．172 Ｂ．173 Ｃ．692 Ｄ．693 3.四进制数首位能用的数字有________．剖例探法★讲解点一 进位制及进位制的转化 1.进位制的基本原理十进制的原理是满十进一，一个十进制正整数N 可以写成11011010101010n n n n a a a a --⨯+⨯++⨯+⨯ 的形式，其中110,,,,n n a a a a - 都是0到9中的数字，且0n a ≠．例如23653106105=⨯+⨯+．一般地，k 进制数的原理是满k 进一，k 进制数一般在右下角处标注（k ）以示区别，例如270(8)表示270是一个8进制数，但十进制一般省略不写．在k 进制中，有：⑴有k 个不同的数字符号，即0,1,2,,1k - ；⑵“满k 进一”，即每位数计满k 后向高位进一．一个k 进位制的正整数就是各位数码与k 的方幂的乘积的和，其中幂指数等于相应数码所在位数（从右往左数）减1．例如543()230451230k k k k =⨯+⨯+⨯2451k k +⨯+⨯+．计算机中常用的数除十进制外，还有二进制，八进制和十六制． ⑴二进制：①只使用两个数字0和1； ②满二进一，即1+1=10． ⑵八进制：①使用0,1,2,3,4,5,6,7八个数字；②满八进一，如7+1=10．八进制的数转化为十进制的数由下面的算式给出：2(8)32738287=⨯+⨯+． ⑶十六进制：①使用0,1,2,3,4,5,6,7,8,9,,,,,,A B C D E F 十六个不同的数码，其中,,,,,A B C D E F 分别代表10,11,12,13,14,15；②满十六进一，如110F +=． 2.不同进位制之间的转换⑴把k 进位制的数转化为十进位制数 写成k 的方幂之和即可，即110n n a a a a -1110n n n n a k a k a k a --=⨯+⨯++⨯+ ．⑵十进位制数转化为其他进位制的数一般方法是除k 取余法，即先把十进制数a 除以k 商为1a ，余数为1r ，再把1a 除以k 商为2a 余数为2r ， ，反复进行这种除法，直到商n a 小于0为止，此时将所有余数按反向排列就得到所要的k 进制数121()n n k r r r r - ．例题1把十进制数25转化为二进制数．【思维切入】把一个十进制数转换为相应的二进制数，用2反复去除欲被转换的十进制数25，直到商为0为止，所得余数（从末位数读起）就是该十进制数25的二进制表示．【解析】(10)(2)2511001=．例题2把二进制数(2)10110101转化为十进制数．【思维切入】把二进制数转换为十进制数,就是将二进制数的最末位数乘以该位数的权02，倒数第二位乘以该位数的权12,, 依此类推，最后把各位相乘的结果相加即得该二进制数的十进制表示．【解析】765(2)10110101120212=⨯+⨯+⨯412+⨯321002120212+⨯+⨯+⨯+⨯(10)181=，即(2)(10)10110101181=．例题3把(6)154二进制数转化为七进制数．【思维切入】不同数制之间的转化（除十进制），我们可以把需要转化的数化成十进制数，然后再把十进制数化为要转化的数．【解析】210(6)(10)15416564670=⨯+⨯+⨯=， 把(10)70化为七进制数(10)(7)70130=所以(6)154化为七进制的数(7)130．精彩反思1.进位制的转化⑴进制数转化十进制数的方法是把k 进制数写成各位数字与k 的幂的乘积之和，从右起 第i 位数字对应的k 的幂指数是1i -；⑵十进制数转化为k 进制数用除k 取余法，短除法要除到商为0才停止； ⑶两非十进制的不同数制相互转化时，可以先把一数制转化为十进制，再把十进制转化为另一数制．2.不同进制数运算通常是先转化为十进制数再计算，计算的结果是十进制数，根据需要，可以把十进制数结果再转化为k 进制数．【自我测评】1.下列表示数的形式正确的有（ ） Ａ．(3)4212 Ｂ．(5)32413 Ｃ．(6)825 Ｄ．(4)12531542.以下给出的各数不可能是八进制数的是（ ） Ａ．312 Ｂ．10110 Ｃ．82 Ｄ．74573.把“二进制”数(2)1011011化为“五进制”数是 （ ） Ａ．(5)324 Ｂ．(5)234 Ｃ．(5)331 Ｄ．(5)4234.将二进制数1101化为十进制数为（ ） Ａ．10 Ｂ．11 Ｃ．12 Ｄ．135.下列二进制数中最大的数是（ ） Ａ．(2)111 Ｂ．(2)1001 Ｃ．(2)110 Ｄ．(2)1016.下列各数中最小的数是（ ） Ａ.(2)111111 Ｂ.(6)210 Ｃ.(4)1000 Ｄ.(8)81【拓展迁移】思维提升7.若k 进制数()123k 与十进制数38相等，则______k =． 8.(3)(4)(10)(10)2111310_____+-=．9.计算机中常用十六进制是逢16进1的计数制，采用数字0～9和字母A ～F 共16个计数符号，这些符号与十进制的数的对应关系如下表：例如，用十六进制表示：1E D B +=，则A B ⨯是（ ）Ａ．6E Ｂ．72 Ｃ．5F Ｄ．0B视野拓展江泽涵江泽涵于1902年10月6日出生于安徽省旌德县，1927年赴美国哈佛大学攻读博士学位．1931年回国，受聘在北京大学数学系任教授，1955年江泽涵被选为中国科学院学部委员，他还是中国国家科学技术委员会数学学科组成员．江泽涵在数学上的贡献主要在拓扑学方面， 江泽涵最先将拓扑学的临界点理论直接用到分析中去，得到了关于调函数的重要结果．江泽函在复迭空间和纤维丛方面进行了深入的研究，并证明了不可定向流形M 的任一可定向复迭必是M 可定向二叶复迭形M 的复迭形，且M 有一个周期为2的、无不动点的、反定向的自同胚．他计算了n 维球面的有线素流形的同调群，江泽涵也对不动点理论进行了长期的研究．。