与圆相关的最值问题
与圆有关的最值问题

O B
2
P
r 2 po r (1 2sin ) po 1 1 2( ) po 2 2 2 设po t (t 1) 则PAPB (t 1)(1 t ) t t 3 2 2 3
C O x
3 5. 易得 PM 的最小值为 10
二、利用所求式的几何意义转化为线 性规划问题求最值
例2:若实数x、y满足 x y 2x 4 y 0 求(1)x-2y的最大值.
2 2
y 1 ( 2) x 2
的取值范围。 2 2 ( x 2) ( y 1) 的取值范围。 ( 3) (4) x y 1 的取值范围。
2 2 ( x 2) ( y 1) (3)
表示为圆上任意一点P到点A(2,1)距离的平方
P
因为 所以
PA [CA 5, CA 5]
. C
A(2,1)
PA2 ( x 2)2 ( y 1)2 [50 10 2,50 10 2]
(4) 因为圆上任一点P(x,y)到直线 x y 1 0 的距离
E M A N G C F H O x
解(1)令圆心C到弦EF的距离为 EF+GH 2( 4 d12 4 d 2 2 )
d1,到弦GH的距离为 d2,则
又 d12 d22 CA2 1
4 d12 4 d22 4 d12 4 d22 2 2
(当且仅当 d1 d 2
2 取等号) 2 故EF+GH 2 8 1 14 2
与圆有关的最值问题

与圆有关的最值问题圆是自然界中优美的图形之一,也是数学中的重要研究对象.由于其图形的对称性和完美性,很多与圆有关的最值问题都可以运用圆的图形特点,利用数形结合来求解.当然,我们也会用到函数思想和基本不等式来处理与圆有关的最值问题.在处理与圆有关的最值问题时,应把握两个“思想”:几何思想和代数思想.所谓几何思想,即利用圆心,将最值问题转化为与圆心有关的问题.所谓代数思想,即利用圆的参数方程.【与圆有关的最值类型】①一定点与定圆上动点间距离的最大与最小值.处理方法:利用定点到圆心的距离加(减)圆的半径. ①定直线与定圆上动点间距离的最大与最小值. 处理方法:定点到圆心的距离加(减)圆的半径. ①分别在两定圆上的两动点间距离的最大与最小值. 处理方法:圆心距加(减)两圆的半径.例1.(1)圆x 2+y 2=1上点到直线l :3x +4y -25=0距离的最大和最小值分别是( ).A.6;3.B.6;4.C.5;3.D.5;4.(2)已知点P (a ,b )在圆x 2+y 2-2x +4y -20=0上,则a 2+b 2的最小值是_____. 解:(1)法1.圆心O 到直线的距离为d=25√32+42=5,而圆的半径为1,① 圆x 2+y 2=1上点到直线l :3x +4y -25=0距离的最大和最小值分别是5+1=6和5-1=4.故应选B.法2.设圆x 2+y 2=1上的点P(cos θ,sinθ),点P 到直线l :3x +4y -25=0距离d ′, 则 d ′=|3cosθ+4sinθ−25|5=|sin (θ+φ)−5|,① −1≤sin (θ+φ)≤1,① 圆x 2+y 2=1上点到直线l :3x +4y -25=0距离的最大和最小值分别是6和4.故应选B.(2)法1. ① 圆x 2+y 2-2x +4y -20=0的圆心和半径分别为(1,-2),r=5.而圆心到原点的距离d=√5,① 5−√5≤√a 2+b 2≤5+√5,⇒30−10√5≤a 2+b 2≤30+10√5. 因此,a 2+b 2的最小值是30-10 5.法2. ① 点P (a ,b )在圆x 2+y 2-2x +4y -20=0上,可设P(1+5cos θ,-2+5sin θ), ① a 2+b 2=(1+5cos θ)2+(-2+5sin θ)2=30+10√5sin (θ+φ),① −1≤sin (θ+φ)≤1, ① a 2+b 2的最小值是30-10 5.例2.在圆x 2+y 2=4上且与直线4x+3y -12=0距离最小的点的坐标是( ). A.(85,65). B.( 85,−65). C.( −85,65) D.( −85,−65). 解:法1.过原点且与直线4x+3y -12=0垂直的直线为3x -4y=0, 联立{x 2+y 2=4,3x −4y =0,⇒{x =85y =65或{x =−85y =−65.结合图4.7—1知选A. xyO 4x+3y -12=0CAE FGHxOM N y 图3.7—2法2.由圆的几何性质可知,所求点为与直线4x+3y -12=0平行且与圆x 2+y 2=4相切的切点.设切线方程为4x+3y+c=0,由|c|5=2,⇒c =∓10.结合图3.7—1 知,c=10.联立{4x +3y −10=0,x 2+y 2=4,⇒{x =85y =65, 故应选A. 法3.对于选择题,可结合图形知所求点应在第一象限内,再看选择支,极易确定选A.想一想①:1.圆x 2+y 2=1上与直线4x -3y -12=0距离最短的点坐标是 .2.已知A (0,1),B (2,3).Q 为圆C:(x -3)2+y 2=1上任一点,则S ΔOAB 的最小值为 .3.若实数x 、y 满足x 2+y 2+2x -4y=0,求x -2y 的最大值.例2.(1)已知a 、b 是单位向量且a ①b.若向量c 满足|c -a -b |=1,则|c |的取值范围是 .(2)已知点A(-1,1)和圆C :(x -5)2+(y -7)2=4.一束光线从A 点经过x 轴反射到圆周C 的最短路程是( ).A.10.B.2√6.C.4√6.D.8. 解:(1) ① a 、b 是单位向量且a ①b ,可设a=(1,0),b=(0,1),c=(x ,y),又① |c -a -b |=1,① (x -1)2+(y -1)2=1. ① 原点O 到圆心(1,1)的距离为√2.① |c | =√x 2+y 2∈[√2−1,√2+1].(2)由光学原理知,点A 关于x 轴的对称点A ′(-1,-1)在反射线上,① 光线从A 点经过x 轴反射到圆周C 的最短路程是过A ′且与圆相切的切线段长|A ′T|=√(−1−5)2+(−1−7)2−4= 4√6.应选C.例3.已知圆C :(x+2)2+y 2=4,过点A(-1,0)作两条互相垂直的直线l 1,l 2,l 1交圆C 与E 、F两点,l 2交圆C 与G 、H 两点.(1)EF+GH解:(1)令圆心C 到弦EF 的距离为d 1,到弦GH 则EF +GH =2(√4−d 12+√4−d 22),又d 12+d 22=CA 2=1由:√4−d 12+√4−d 222≤√8−(d 12+d 22)2=√8−12= √142,(当且仅当d 1=d 2= √22取等号).故EF +GH ≤√14. (2)① EF ⊥GH ,① S 四边形EFGH =12EF ×GH =2(√4−d 12√4−d 22 ≤2×8−(d 12+d 22)2=7.(当且仅当d 1=d 2= √22取等号).例4(1)如图3.7—3(1).点A 的坐标为(3,0),点B 为y 轴正半轴上的一点,点C 是第一象限内一点,且AC=2.设tan①BOC=m ,则m 的取值范围是_________.(2)如图3.7—3(2).在边长为1的等边①OAB 中,以边AB 为直径作①D , C 为半圆弧AB 上的一个动点(不与A 、B 两点重合).BC=a ,AC=b ,求a+b 的最大值.(3)如图3.7—3(3).线段AB=4,C 为线段AB 上的一个动点,以AC 、BC 为边作等边①ACD 和等边①BCE ,①O 外接于①CDE ,则①O 半径的最小值为( ). A.4. B. 2√33. C. √33. D.2._ B_y_ COED解:(1)由已知,点C 是第一象限内在圆(x -3)2+y 2=4点,结合图2.8—4(1)知,tan①AOC ∈(0,2√55],∵①AOC 与①BOC 互余,① m ≥√52. (2)① AC 2+BC 2=AB 2,即a 2+b 2=1 由柯西不等式得,(12+12)(a 2+b 2)≥(a+b)2, ① (a+b)≤√2,故 a +b 的最大值为√2.(3)设外接圆的半径为R ,由已知可得∠DOE =600.再由正弦定理知DE=2Rsin600,① R=√33DE .在∆DCE 内由余弦定理可得DE 2=DC 2+CE 2-DC ∙CE =(DC+CE)2-3DC ∙CE =16-3DC ∙CE ≥16-3(DC+CE 2)2=4,即DE ≥2. ① R=√33DE ≥2√33.应选B.想一想①:1.如图3.7—4.①M ,①N 的半径分别为2cm ,4cm ,圆心距MN=10cm .P 为①M 上的任意一点,Q 为①N 上的任意一点,直线PQ 与连心线所夹的锐角度数为α,当P 、Q 在两圆上任意运动时,tan α的最大值为( ).A.√612B.43.C.√33.D.34.2.如图3.7—5.①BAC=600,半径长为1的圆O 与①BAC 的两边相切, P 为圆O 上一动点,以P 为圆心,PA 长为半径的圆P 交射线AB 、AC 于D 、E 两点,连接DE ,则线段DE 长度的最大值为( ). A.3. B.6. C. .3√32.D. 3√3.例5.(1)过点M(−2,,0)的直线l 与曲线y=√4−x 2相交于A ,B 两点,当∆ABO (O 为坐标原点)的面积最大时,直线l 的斜率为 . (2)两个圆C 1:x 2+y 2+2ax+a 2-4=0(a ∈R )与圆C 2:x 2+y 2-2by+b 2-1=0(b ∈R )恰有三条公切线,则a+2b 的取值范围为 . 解:(1) ① 曲线y=√4−x 2的方程可变形为x 2+y 2=4(y ≥0),① 此曲线表示以原点为圆心,2为半径,在x 轴及其上方的半圆,如图3.7—6.① S ∆ABO =12OA ×OB ×sin∠AOB =2sin∠AOB , 当∆ABO 的面积最大时,∠AOB =900,此时∆ABO为等腰直角三角形,① 点O 到直线AB 的距离为√2. 设直线AB 的方程为 y=k(x+2√2),即kx -y+2√2k =0, ①2√2k √1+k 2=√2,解得k=±√33,又由已知k>0,① k= √33.(2) ① 圆C 1的圆心为C 1(-a ,0),半径为2;圆C 2的圆心为C 2(0,b),半径为1.l xy MABO 图3.7—6图3.7—4P QMNA D E BCP. . O图3.7—5由已知两圆外切,① | C 1 C 2|=2+1=3,即a 2+b 2=9.令a+2b=m ,则 √1+4≤3,解得 −3√5≤m ≤3√5,① a+2b 的取值范围为[−3√5,3√5].习题3.71.已知A 、B 两点的坐标分别为(-2,0)、(0,1),①C 的圆心坐标为(0,-1),半径为1,D 是①C 上的一个动点,射线AD 与y 轴交于点E ,则①ABE 面积的最大值是( ).A.3.B. 103. C.103. D.4. 2.圆x 2+y 2-2x -2y+1=0上的点到直线2x y -=距离的最大值是( ).A.2.B.1+√2.C.2+√22. D.1+2√2.3.由直线y=x +1上一点向圆C :(x -3)2+y 2=1引切线,则切线长的最小值为 .4.已知P 为直线y=x +1上一动点,过P 作圆C :(x -3)2+y 2=1的切线PA ,PB(A 、B 为切点),则四边形PACB 面积的最小值为 .5.求过直线2x+y+4=0和圆x 2+y 2+2x -4y+1=0的交点,且满足下列条件之一的圆的方程.①过原点;①有最小面积.6.求圆(x -2)2+(y+3)2=4上的点到直线x -y +2=0最远和最近的距离.7.已知圆M 过两点C(1,-1),D(-1,1),且圆心M 在x+y -2=0上. (1)求圆M 的方程. (2)设P 是直线3x+4y+8=0上的动点,PA ,PB 是圆M 的两条切线,A ,B 为切点.求四边形PAMB 面积的最小值.8.在平面直角坐标系中,M(3,4),P 是以M 为圆心,2为半径的①M 上一动点,A(-1,0)、B(1,0),连接PA 、PB ,求PA 2+PB 2最大值.9.过定点M 的直线l 1:ax+y -1=0与过定点N 的直线l 2:x - ay +2a -1=0交于点P.求|PM|∙|PN|的最大值.【参考答案】想一想①:1. (45,−35). 2.4+√2. 3.10.想一想①:1.D.考虑PQ 为两圆的内公切线时的情形.2.在△ADE 中,由正弦定理得|DE|=2Rsin600,其中R 为△ADE 的外接圆半径.如图2.8—4(3)知,AP 的最大值为|OP|+1=3,① |DE|max =3√3. 故应选D.习题3.71. A.2. B.3. √7.4. √7.5.(1)设圆的方程为x 2+y 2+2x -4y+1+λ(2x +y +4)=0,① 所求圆过原点,得λ=−14. ①x 2+y 2+32x+74y =0为所求.(2)设圆的方程为x 2+y 2+2x -4y+1+λ(2x +y +4)=0,① R 2=D 2+E 2−4F 4=5λ2−16λ+164,① 当 λ=85时R 2最小. ① x 2+y 2+265x −125y +375=0为所求6.7√2−42;7√2+42. 7.(1)设圆M 的方程为:(x -a)2+(y -b)2=r 2(r >0).根据题意得, {(1−a)2+(1+b)2=r 2,(−1−a)2+(1−b)2=r 2,a +b −2=0. 解得a=b=1,r=2.故所求圆M 的方程为(x -1)2+(y -1)2=4.(2)① 四边形PAMB 的面积S=S ①PAM +S ①PBM =|AM|·|PA|+|BM|·|PB|,又|AM|=|BM|=2,|PA|=|PB|,① S=2|PA|,而|PA|=√|PM|2−|AM|2=√|PM|2−4, 即S=2√|PM|2−4.因此要求S 的最小值,只需求|PM|的最小值即可, 即在直线3x+4y+8=0上找一点P,使得|PM|的值最小, ① |PM|min =√32+42=3.因此,四边形PAMB 面积的最小值为S=2√|PM|2−4=2√5.8.设P(3+2cos θ,4+2sin θ),则PA 2+PB 2=60+24cos θ+32sin θ=60+40sin(θ+φ)≤100. ① PA 2+PB 2最大值为100.9. 1. 由已知有,直线l 1过定点M(0,1),直线l 2过定点N(1,2),且|MN|=√2,l 1⊥l 2.由平面几何的知识知,点P 在以MN 为直径的圆上运动.设点P 到MN 的距离为PD ,则有|PM|∙|PN|=|MN||∙|PD| =√2∙|PD|,∴ 当|PD|取最大值√22 时,(|PM|∙|PN|)max =√2∙√22=1.。
与圆有关的最值问题,附详细答案

与圆有关的最值(取值范围)问题,附详细答案姓名1.在坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2.设tan∠BOC=m,则m的取值范围是____ _____.2.如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.(1)求证:AE=b+a;(2)求a+b的最大值;(3)若m是关于x的方程:x2+ax=b2+ab的一个根,求m的取值范围.3.如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,D.则线段DE长度的最大值为( ). A.3 B.6 C.24.如图,A点的坐标为(﹣2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值.5.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D是平面内的一个动点,且AD=2,M 为BD的中点,在D点运动过程中,线段CM长度的取值范围是 .6.如图是某种圆形装置的示意图,圆形装置中,⊙O的直径AB=5,AB的不同侧有定点C和动点P,tan∠CAB=.其运动过程是:点P在弧AB上滑动,过点C作CP的垂线,与PB的延长线交于点Q.(1)当PC= 时,CQ与⊙O相切;此时CQ= .(2)当点P运动到与点C关于AB对称时,求CQ的长;(3)当点P运动到弧AB的中点时,求CQ的长.(4)在点P的运动过程中,线段CQ长度的取值范围为。
7.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=D是线段BC上的一个动点,以AD 为直径作⊙O分别交AB,AC于E,F两点,连接EF,则线段EF长度的最小值为.8.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,则PM长度的最大值是.9.如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x <4),则当x= 时,PD•CD的值最大,且最大值是为 .10.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( ).D. 2211.在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P 在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B,线段AB长度的最小值是 .12.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB边上一点,过点D作CD的垂线交直线BC于点E,则线段CE长度的最小值是 .13.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是 .14.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为()A.B. C.3 D.215.(2015•济南)抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),交y轴于点C.(1)求抛物线的函数表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.16.如图,已知A、B是⊙O与x轴的两个交点,⊙O的半径为1,P是该圆上第一象限内的一个动点,直线PA、PB分别交直线x=2于C、D两点,E为线段CD的中点.(1)判断直线PE与⊙O的位置关系并说明理由;(2)求线段CD长的最小值;(3)若E点的纵坐标为m,则m的范围为.17.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( ).(A)4 (B)215(C)358(D)17418.如图,在Rt △ABC 中,∠C =90°,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CA 、CB 分别相交于点P 、Q ,则线段PQ 长度的最小值是( ).A .194 B .245 C .5 D .19.如图,在等腰Rt △ABC 中,∠C =90°,AC =BC =4,D 是AB 的中点,点E 在AB 边上运动(点E 不与点A 重合),过A 、D 、E 三点作⊙O ,⊙O 交AC 于另一点F ,在此运动变化的过程中,线段EF 长度的最小值为 .20.如图,等腰Rt △ABC 中,∠ACB =90°,AC =BC =4,⊙C 的半径为1,点P 在斜边AB 上,PQ 切⊙O 于点Q ,则切线长PQ 长度的最小值为( ). A. B.C. 321.在平面直角坐标系中,M (3,4),P 是以M 为圆心,2为半径的⊙M 上一动点,A (-1,0)、B (1,0),连接PA 、PB ,则PA 2+PB 2最大值是 .参考答案引例1.解:C在以A为圆心,以2为半径作圆周上,只有当OC与圆A相切(即到C点)时,∠BOC最小,AC=2,OA=3,由勾股定理得:OC=,∵∠BOA=∠ACO=90°,∴∠BOC+∠AOC=90°,∠CAO+∠AOC=90°,∴∠BOC=∠OAC,tan∠BOC=tan∠OAC==,随着C的移动,∠BOC越来越大,∵C在第一象限,∴C不到x轴点,即∠BOC<90°,∴tan∠BOC≥,故答案为:m≥.引例1图引例2图+≤引例2.a b原题:(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.(1)求证:AE=b+a;(2)求a+b的最大值;(3)若m是关于x的方程:x2+ax=b2+ab的一个根,求m的取值范围.【考点】圆的综合题.【分析】(1)首先连接BE,由△OAB为等边三角形,可得∠AOB=60°,又由圆周角定理,可求得∠E的度数,又由AB为⊙D的直径,可求得CE的长,继而求得AE=b+a;(2)首先过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,可得(a+b)2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,即可求得答案;(3)由x2+ax=b2+ab,可得(x﹣b)(x+b+a)=0,则可求得x的值,继而可求得m的取值范围.【解答】解:(1)连接BE,∵△OAB为等边三角形,∴∠AOB=60°,∴∠AEB=30°,∵AB为直径,∴∠ACB=∠BCE=90°,∵BC=a,∴BE=2a,CE=a,∵AC=b,∴AE=b+a;(2)过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,∴a2+b2=1,∵S△ABC=AC•BC=AB•CH,∴AC•BC=AB•CH,∴(a+b)2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,∴a+b≤,故a+b的最大值为,(3)∵x2+ax=b2+ab,∴x2﹣b2+ax﹣ab=0,∴(x+b)(x﹣b)+a(x﹣b)=0,∴(x﹣b)(x+b+a)=0,∴x=b或x=﹣(b+a),当m=b时,m=b=AC<AB=1,∴0<m<1,当m=﹣(b+a)时,由(1)知AE=﹣m,又∵AB<AE≤2AO=2,∴1<﹣m≤2,∴﹣2≤m<﹣1,∴m的取值范围为0<m<1或﹣2≤m<﹣1.【点评】此题考查了圆周角定理、等边三角形的性质、完全平方公式的应用以及一元二次方程的解法.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.引例3.解:连接EP,DP,过P点作PM垂直DE于点M,过O做OF⊥AC与F,连接AO,如图,∵∠BAC=60°,∴∠DPE=120°.∵PE=PD,PM⊥DE,∴∠EPM=60°,∴ED=2EM=2EP•sin60°=EP=P A.当P与A、O共线时,且在O点右侧时,⊙P直径最大.∵⊙O与∠BAC两边均相切,且∠BAC=60°,∴∠OAF=30°,OF=1,∴AO==2,AP=2+1=3,∴DE=PA=3.故答案为:D。
有关圆的最值问题几种类型及方法

圆的最值问题一圆心到定直线的距离的最值问题例1 设P 是直线043:=-y x l 上的动点,PA,PB 是圆012222=+--+y x y x 的两条切线,C 是圆心,那么四边形PACB 的最小值是_____________.变式:已知)(y x P ,是直线)0(04>=++k y kx 上一动点,PA,PB 是圆:0222=-+y y x 的两条切线,A,B 是切点,若四边形PACB 最小面积是2,则k=_____________。
二圆上动点到定直线的距离的最值问题例2 圆012222=+--+y x y x上的点到直线2=-y x 距离的最大值是_______________。
变式:已知P 是圆122=+y x上的一点,Q 是直线052:=-+y x l 上的一点,求PQ 最小值。
三圆的切线长最值问题例3 从点P(m,3)向圆C:()()12222=+++y x 引切线,则切线长的最小值为_____________。
变式:由直线2+=x y 上的点向圆()()12y 422=++-x 引切线,怎切线的最小值为____________。
四与圆的弦长有关的最值问题例4 在圆06222=--+y x y x 内,过点E(0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为_______________。
变式:已知圆O 的方程是01028y 22=+--+y x x,过点M(3,0)的最短弦所在的直线方程是_____。
五圆中“斜率”最值问题例3 在平面直角坐标系xOy 中,圆C 的方程为0158y 22=+-+x x 。
若直线2y -=kx 上至少存在一点,使得以改点为圆心,1为半径的圆与圆有公共点,则k 的最大值是_________________。
变式:如果实数x,y 满足等式(),1222=+-y x 那么13y -+x 的取值范围________________。
与圆有关的最值取值范围问题,附详细答案

与圆相关的最值(取值范围)问题,附详尽答案姓名1. 在座标系中,点 A 的坐标为 (3, 0),点 B 为 y 轴正半轴上的一点,点C 是第一象限内一点,且 AC=2.设 tan ∠ BOC=m ,则 m 的取值范围是 _________.2. 如图,在边长为 1 的等边 △ OAB 中,以边 AB 为直径作 ⊙ D ,以 O 为圆心 OA 长为半径作圆 O , C 为半圆 AB 上不与 A 、 B 重合的一动点,射线AC 交 ⊙ O 于点 E , BC=a , AC=b .( 1)求证: AE=b+ a ;( 2)求 a+b 的最大值;(3)若 m 是对于 x 的方程: x 2+ax=b 2+ab 的一个根,求 m 的取值范围.3. 如图,∠ BAC=60 °,半径长为 1 的圆 O 与∠ BAC 的两边相切,P 为圆 O 上一动点,以 P 为圆心, PA 长为半径的圆 P 交射线 AB 、AC 于 D 、 E 两点,连结DE ,则线段 DE 长度的最大值为 (). A .3 B . 63 3C .D .3 324.如图, A 点的坐标为(﹣ 2, 1),以 A 为圆心的⊙A 切 x 轴于点 B, P( m, n)为⊙A 上的一个动点,请研究 n+m 的最大值.5.如图,在Rt△ ABC中,∠ ACB=90 °, AC=4, BC=3,点 D 是平面内的一个动点,且 AD=2,M 为 BD 的中点,在 D 点运动过程中,线段CM 长度的取值范围是.6.如图是某种圆形装置的表示图,圆形装置中,⊙ O 的直径 AB=5,AB 的不一样侧有定点 C 和动点 P,tan ∠ CAB= .其运动过程是:点 P 在弧 AB 上滑动,过点 C 作 CP 的垂线,与PB的延伸线交于点Q.(1)当 PC=时,CQ与⊙O相切;此时CQ=.(2)当点 P 运动到与点 C 对于 AB 对称时,求 CQ的长;(3)当点 P 运动到弧 AB 的中点时,求 CQ 的长.(4)在点 P 的运动过程中,线段CQ 长度的取值范围为。
与圆有关的最值问题ppt课件
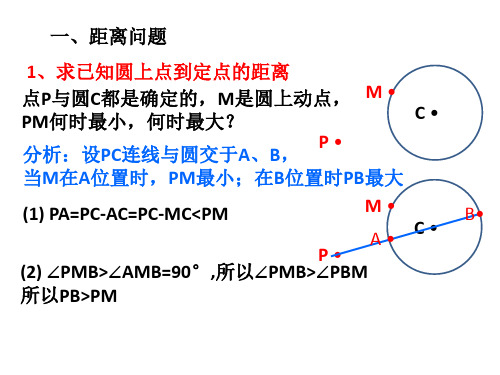
1、求已知圆上点到定点的距离
点P与圆C都是确定的,M是圆上动点, M •
PM何时最小,何时最大?
C•
分析:设PC连线与圆交于A、B, P •
当M在A位置时,PM最小;在B位• A• C•
B•
P•
(2) ∠PMB>∠AMB=90°,所以∠PMB>∠PBM
切线最短
-1 o C
x
所以PC⊥直线x=-1时,PC最短,从而切线最短, 此时m=0
3、其他举例
已知圆C内一定点P,过P的
P•
所有弦中,那一条最短
C•
上式中, r是定值, 所以d最大时,弦最短, 即P为弦的中点时
(3)求ΔCAB面积的最大值
所以PB>PM
y
o
x
2、圆上动点到定直线的距离
M是圆C上动点,什么时候M到L 距离最大或最小?
分析:过圆心作L的垂线交圆于A、B ,则M在A(B)位置时到L距离最小(大)
M到L的距离等于过M与L平行的 直线与L的距离
L
M• C•
L
M• A•
C• B•
y
o
x
y
因为r是定值。所以PC最小时, P•
圆的最值问题归纳-与圆有关的最值问题

圆的问题探究高中数学中,研究最多一种曲线是圆。
在研究圆相关问题时,最值问题又是研究的重点和热点,现把常见的与圆相关的最值问题,总结如下。
希望对读者有些启发。
类型一、“圆上一点到直线距离的最值”问题分析:求圆上一点到直线距离的最值问题,总是转化成求圆心到定直线的距离问题来解决。
1、求圆C: (x-2)2+(y+3)2=4上的点到直线l :x-y+2=0的最大、最小距离. 解析:作CH l ⊥交于H ,与圆C 交于A ,反向延长与圆交于点B 。
所以max min 2; 2.222CH BH AH d d d d d ===+==-2、求圆C: (x-1)2+(y+1)2=2上的点与直线l : x-y+4=0距离的最大值和最小值. 解析:方法同第一题, max min BH d d d ==== 3、圆222=+y x 上的点到直0254=+y 的距离的最小值为________________.解析:方法同第一题, min 5d =类型二、“圆上一点到定点距离的最值”问题分析:本质是两点间距离。
涉及与圆相关的两点的距离,总是转化为圆心与定点距离问题来解决。
1.已知点P (x,y )是圆C : x 2+y 2-2x-4y+4=0上一点,求P 到原点的最大最小距离.解析:连接OC 与圆交于A ,延长OC 交于B.max min 1;1.OC OC d d r d d r =+==-=2.已知圆C :04514422=+--+y x y x 及点()3,2-Q ,若M 是圆C 上任一点,求MQ 最大值和最小值. 解析:方法同第一题,max Q min Q C C d d r d d r =+===-==3 .已知x,y 满足条件 x 2+y 2-2x-4y+4=0,求22y x +范围.解析:方程看作是圆C ,表达式几何意义是圆C 上点(,)x y 与(0,0)距离范围,求max min ,d d 即可,与第一题答案相同.4.已知x,y 满足圆C : x 2+y 2-2x-4y+4=0,求22)2()2(+++y x 范围. 解析: 表达式几何意义是圆C 上点(,)x y 与P (-2,-2)距离的最值平方.max min 22maxmin5,6, 4.36,16.[16,36].CP d d dd=====所以范围是5.已知x,y 满足圆C : x 2+y 2-2x-4y+4=0,求z=x 2+y 2+2x+2y 范围.解析: 22(1)(1)2z x y =+++-表达式几何意义是圆C 上点(,)x y 与P (-1,-1)距离的最值的平方减去2.max min 22max min 2121)212[12CP d d z z ====-=+=-=--+所以范围是 6.已知圆()()143:22=-+-y x C ,点A (-1,0),B (1,0),点P 为圆上一动点,求22PB PA d +=的最大值和最小值及对应的P 点坐标. 解析:222222max min 2()2,.2(51)274;2(51)234.[34,74].d PA PB x y d d =+=++=++==-+=几何意义是点P 与原点O 距离的平方2倍加2|OC|=5,所以答案类型三、“过定点的弦长”问题1:已知直线:2830l mx y m ---=和圆22:612200C x y x y +-++=;(1)m R ∈时,证明l 与C 总相交。
圆中最值问题10种求法(供参考)

圆中最值的十种求法在圆中求最值是中考的常见题型,也是中考中的热点、难点问题,有的学生对求最值问题感到束手无策,主要原因就是对求最值的方法了解不多,思路不够灵活.现对在圆中求最值的方法,归纳如下:一、利用对称求最值1.如图:⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值.[分析]:延长AO交⊙O于D,连接CD交⊙O于P,即此时PA+PC最小,且PA+PC的最小值就等于弦CD的长.解:延长AO交⊙O于D,连接CD交OB于P连接PA,过O作OE⊥CD,垂足为E在△OCD中,因为∠AOC=60°所以∠D=∠C=30°在Rt△ODE中cos30°=即DE=2×cos30°= 所以CD=2DE=2即PA+PC的最小值为2.二、利用垂线段最短求最值2.如图:在直角坐标系中,点A的坐标为(-3, -2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则PQ长度的最小值为.[分析]:连接AQ、PA,可知AQ⊥PQ. 在Rt△PQA中,PQ=,求PQ的最小值转化为求PA的最小值,根据垂线段最短易求PA的最小值为2.解:连接PA、QA因为PQ切⊙A于点Q 所以PQ⊥AQ在Rt△APQ中,PQ2=PA2-AQ2即PQ=又因为A(-3,-2) ,根据垂线段最短。
所以PA的最小值为2所以PQ的最小值=三、利用两点之间线段最短求最值3.如图:圆锥的底面半径为2,母线PB的长为6,D为PB的中点,一只蚂蚁从点A 出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( )A.B.2C.3D.3[分析]:因为圆锥的侧面是曲面蚂蚁从A爬行到点D,不好求爬行的最小值,要把立体图形展开为平面图形,再利用两点之间线段最短来解决问题.解:圆锥的侧面展开图如图2,连接AB根据题意得:弧AC的长为2πr=2π·2=4π,PA=6因为4π= 所以n=120°即∠APB=60°又因为PA=PB所以△PAB是等边三角形因为D为PB中点所以AD⊥PB PD=DB=3在Rt△PAD中,AD=,故选C.四、利用直径是圆中最长的弦求最值4.如图:半径为2.5的⊙O中,直径AB的两侧有定点C和动点P,已知BC:CA=4:3,点P在劣弧AB上运动,过点C作CP的垂线,与PB的延长线交于点Q,(1)求∠P的正切值;(2)当CP⊥AB时,求CD和CQ的长;当点P运动到什么位置时,CQ取得最大值,并求出此时CQ的长.[分析]:易证明△ACB∽△PCQ,所以,即CQ=PC. 当PC最大时,CQ最大,而PC是⊙O 的动弦,当PC是⊙O的直径时最大.五、利用弧的中点到弦的距离最大求最值5.如图:已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点,(B、C两点除外),求△ABC面积的最大值.[分析]:设BC边上的高为h因为S△ABC=BC h=×2h=h当h最大时S△ABC最大,当点A在优弧的中点时h最大.解:当点A为优弧的中点时,作AD⊥BC于D连接BO 即BD=CD=在Rt△BDO中,OD2=OB2-BD2=22-()2=1所以OD=1 所以AD=2+1=3所以S△ABC=×BC·AD=×2×3=3即△ABC面积的最大值为3六、利用周长一定时,圆的面积最大求最值6.用48米长的篱笆材料,在空地上围成一个绿化场地,现有两种方案:一种是围成正方形的场地,另一种是围成圆形场地,试问选用哪一种方案,围成的场地面积较大?并说明理由.[分析]:周长一定的几何图形,圆的面积最大.解:围成圆形场地的面积较大设S1、S2分别表示围成的正方形场地、圆形场地的面积则S1=()2=144 S2=π·()2=因为π<4 所以>所以>=144 所以S2>S1 所以应选用围成圆形场地的方案面积较大七、利用判别式求最值7.如图:在半径为1的⊙O中,AB是弦,OM⊥AB,垂足为M,求OM+AB的最大值.[分析]:可设AM=x,把OM用x的代数式表示出来,构造关于x的一元二次方程,然后利用判别式来求最值.解:设AM=x,在Rt△OAM中OM=所以OM+AB=+2x=a整理得:5x2-4ax+(a2-1)=0因为△=(-4a)2-4×5×(a2-1)≥0即a2≤5 所以a≤所以OM+AB的最大值为八、利用一条弧所对的圆周角大于圆外角求最值8.如图:海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°,为避免触礁,轮船P与A、B的张角∠APB的最大值为.[分析]:连接AC,易知∠ACB=∠AOB=40°,又因为∠ACB≥∠P,所以∠P的最大值为40°.解:如图:连接AC,根据圆周角定理可知∠ACB=∠AOB=×80°=40°又因为∠ACB≥∠P 即∠APB≤40°所以∠APB的最大值为40°九、利用经过⊙O内一定点P的所有弦中,与OP垂直的弦最短来求最值9.如图:⊙O的半径为5cm,点P为⊙O内一点,且OP=3cm,则过点P的弦AB长度的最小值为cm.[分析]:过P作AB⊥OP,交⊙O于A、B,则AB的长最小.解:在Rt△OAP中,AP=所以AB=2AP=2×4=8所以AB的最小值为8十、利用经过圆外一点与圆心的直线与⊙O的两个交点与点P的距离最大或最小求最值10.如图:点P为⊙O外一点,PQ切⊙O于点Q,⊙O的半径为3cm,切线PQ的长为4cm,则点P与⊙O上各点的连线长度的最大值为,最小值为.[分析]:过P、O两点作直线交⊙O于A、B,则PA的长度最大,PB的长度最小.解:连接OQ 因为PQ切⊙O于Q所以OQ⊥PQ在Rt△PQO中PQ2+OQ2=OP2即42+32=OP2 所以OP=5所以PB=5-3=2 PA=6+2=8所以点P与⊙O上各点连线长度的最大为8cm,最小值为2cm.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与圆有关的最值(取值范围)问题引例1:在坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2.设tan∠BOC=m,则m的取值范围是_________.引例2:如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作⊙O,C为半圆弧 AB上的一个动点(不与A、B两点重合),射线AC交⊙O于点E,BC=a,AC=b,求a b的最大值.引例3:如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为( ).A.3 B.6 CD.一、题目分析:此题是一个圆中的动点问题,也是圆中的最值问题,主要考察了圆内的基础知识、基本技能和基本思维方法,注重了初、高中知识的衔接1.引例1:通过隐藏圆(高中轨迹的定义),寻找动点C与两个定点O、A构成夹角的变化规律,转化为特殊位置(相切)进行线段、角度有关计算,同时对三角函数值的变化(增减性)进行了延伸考查,其实质是高中“直线斜率”的直接运用;2.引例2:通过圆的基本性质,寻找动点C与两个定点A、B构成三角形的不变条件,结合不等式的性质进行转化,其实质是高中“柯西不等式”的直接运用;3.引例3:本例动点的个数由引例1、引例2中的一个动点,增加为三个动点,从性质运用、构图形式、动点关联上增加了题目的难度,解答中还是注意动点D、E与一个定点A 构成三角形的不变条件(∠DAE=60°),构造弦DE、直径所在的直角三角形,从而转化为弦DE与半径AP之间的数量关系,其实质是高中“正弦定理”的直接运用;综合比较、回顾这三个问题,知识本身的难度并不大,但其难点在于学生不知道转化的套路,只能凭直观感觉去寻找、猜想关键位置来求解,但对其真正的几何原理却无法通透.二、解题策略1.直观感觉,画出图形;2.特殊位置,比较结果;3.理性分析动点过程中所维系的不变条件,通过几何构建,寻找动量与定量(常量)之间的关系,建立等式,进行转化.三、中考展望与题型训练例一、斜率运用1.如图,A 点的坐标为(﹣2,1),以A 为圆心的⊙A 切x 轴于点B ,P (m ,n )为⊙A 上的一个动点,请探索n+m 的最大值.例二、圆外一点与圆的最近点、最远点1.如图,在Rt △ABC 中,∠ACB=90°,AC=4,BC=3,点D 是平面内的一个动点,且AD=2,M 为BD 的中点,在D 点运动过程中,线段CM 长度的取值范围是 .2.如图,⊙O 的直径为4,C 为⊙O 上一个定点,∠ABC=30°,动点P 从A 点出发沿半圆弧AB 向B 点运动(点P 与点C 在直径AB 的异侧),当P 点到达B 点时运动停止,在运动过程中,过点C 作CP 的垂线CD 交PB 的延长线于D 点.(1)在点P 的运动过程中,线段CD 长度的取值范围为 ;(2)在点P 的运动过程中,线段AD 长度的最大值为 .例三、正弦定理 1.如图,△ABC 中,∠BAC=60°,∠ABC=45°,AB=D 是线段BC 上的一个动点,以AD 为直径作⊙O 分别交AB ,AC 于E ,F 两点,连接EF ,则线段EF 长度的最小值为 .2. 如图,定长弦CD 在以AB 为直径的⊙O 上滑动(点C 、D 与点A 、B 不重合),M 是CD 的中点,过点C 作CP ⊥AB 于点P ,若CD=3,AB=8,则PM 长度的最大值是 .A例四、柯西不等式、配方法1.如图,已知半径为2的⊙O 与直线l 相切于点A ,点P 是直径AB 左侧半圆上的动点,过点P 作直线l 的垂线,垂足为C ,PC 与⊙O 交于点D ,连接PA 、PB ,设PC 的长为x (2<x <4),则当x= 时,PD•CD 的值最大,且最大值是为 .2.如图,线段AB=4,C 为线段AB 上的一个动点,以AC 、BC 为边作等边△ACD 和等边△BCE ,⊙O 外接于△CDE ,则⊙O半径的最小值为( ).D. 23.在平面直角坐标系中,以坐标原点O 为圆心,2为半径画⊙O ,P 是⊙O 上一动点,且P 在第一象限内,过点P 作⊙O 的切线与x 轴相交于点A ,与y 轴相交于点B ,线段AB 长度的最小值是 .例四、相切的应用(有公共点、最大或最小夹角)1.如图,在Rt △ABC 中,∠C=90°,AC=6,BC=8,D 为AB 边上一点,过点D 作CD 的垂线交直线BC 于点E ,则线段CE 长度的最小值是 .2.如图,Rt△ABC 中,∠C=90°,∠A=30°,AB=4,以AC 上的一点O 为圆心OA 为半径作⊙O ,若⊙O 与边BC 始终有交点(包括B 、C 两点),则线段AO 的取值范围是 .3.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为()A.B.C.3 D.2例五、其他知识的综合运用1.(2015•济南)抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C.(1)求抛物线的函数表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E 重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.2.(2013秋•相城区校级期末)如图,已知A、B是⊙O与x轴的两个交点,⊙O的半径为1,P是该圆上第一象限内的一个动点,直线PA、PB分别交直线x=2于C、D两点,E为线段CD的中点.(1)判断直线PE与⊙O的位置关系并说明理由;(2)求线段CD长的最小值;(3)若E点的纵坐标为m,则m的范围为.B【题型训练】1.如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C,若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径r的取值范围为 .2.已知:如图,RtΔABC中,∠B=90º,∠A=30º,BC=6cm,点O从A点出发,沿AB以每秒的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点,过E作EG⊥DE交射线BC于G.(1)若点G在线段BC上,则t的取值范围是;(2)若点G在线段BC的延长线上,则t的取值范围是 .3.如图,⊙M,⊙N的半径分别为2cm,4cm,圆心距MN=10cm.P为⊙M上的任意一点,Q 为⊙N上的任意一点,直线PQ与连心线l所夹的锐角度数为α,当P、Q在两圆上任意运动时,tanα∠的最大值为(B)43;; (D)344.如图,在矩形ABCD中,AB=3,BC=4,O 为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( ).(A)4 (B)215(C)358(D)174 5.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB 分别相交于点P、Q,则线段PQ长度的最小值是( ).A.194B.245C.5 D.6.如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E在AB边上运动(点E不与点A重合),过A、D、E三点作⊙O,⊙O交AC于另一点F,在此运动变化的过程中,线段EF长度的最小值为.7.如图,A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心的坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( ).A.2 B.1 C.2 D.28.如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ).A.3 B.113C.103D.49.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,⊙C的半径为1,点P在斜边AB上,PQ 切⊙O于点Q,则切线长PQ长度的最小值为( ).10.如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的范围为 .11.在直角坐标系中,点A的坐标为(3,0),点P(m n,)是第一象限内一点,且AB=2,则m n-的范围为 .12.在坐标系中,点A的坐标为(3,0),点P是y轴右侧一点,且AP=2,点B上直线y=x+1上一动点,且PB⊥AP于点P,则tan ABP m∠=,则m的取值范围是 .13.在平面直角坐标系中,M(3,4),P是以M为圆心,2为半径的⊙M上一动点,A(-1,0)、B(1,0),连接PA、PB,则PA2+PB2最大值是 .蔡老师点评:与圆有关的最值问题,看着无从下手,但只要仔细观察,分析图形,寻找动点与定点之间不变的维系条件,构建关系,将研究的问题转化为变量与常量之间的关系,就能找到解决问题的突破口!几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法;2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考试题中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法.参考答案:引例1.解:C在以A为圆心,以2为半径作圆周上,只有当OC与圆A相切(即到C点)时,∠BOC最小,AC=2,OA=3,由勾股定理得:OC=,∵∠BOA=∠ACO=90°,∴∠BOC+∠AOC=90°,∠CAO+∠AOC=90°,∴∠BOC=∠OAC,tan∠BOC=tan∠OAC==,随着C的移动,∠BOC越来越大,∵C在第一象限,∴C不到x轴点,即∠BOC<90°,∴tan∠BOC≥,故答案为:m≥.引例1图引例2图+≤引例2.a b原题:(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O 为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.(1)求证:AE=b+a;(2)求a+b的最大值;(3)若m是关于x的方程:x2+ax=b2+ab的一个根,求m的取值范围.【考点】圆的综合题.【分析】(1)首先连接BE,由△OAB为等边三角形,可得∠AOB=60°,又由圆周角定理,可求得∠E的度数,又由AB为⊙D的直径,可求得CE的长,继而求得AE=b+a;(2)首先过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,可得(a+b)2= a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,即可求得答案;(3)由x2+ax=b2+ab,可得(x﹣b)(x+b+a)=0,则可求得x的值,继而可求得m的取值范围.【解答】解:(1)连接BE,∵△OAB为等边三角形,∴∠AOB=60°,∴∠AEB=30°,∵AB为直径,∴∠ACB=∠BCE=90°,∵BC=a,∴BE=2a,CE=a,∵AC=b,∴AE=b+a;(2)过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,∴a2+b2=1,∵S△ABC=AC•BC=AB•CH,∴AC•BC=AB•CH,∴(a+b)2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,∴a+b≤,故a+b的最大值为,(3)∵x2+ax=b2+ab,∴x2﹣b2+ax﹣ab=0,∴(x+b)(x﹣b)+a(x﹣b)=0,∴(x﹣b)(x+b+a)=0,∴x=b或x=﹣(b+a),当m=b时,m=b=AC<AB=1,∴0<m<1,当m=﹣(b+a)时,由(1)知AE=﹣m,又∵AB<AE≤2AO=2,∴1<﹣m≤2,∴﹣2≤m<﹣1,∴m的取值范围为0<m<1或﹣2≤m<﹣1.【点评】此题考查了圆周角定理、等边三角形的性质、完全平方公式的应用以及一元二次方程的解法.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.引例3.解:连接EP,DP,过P点作PM垂直DE于点M,过O做OF⊥AC与F,连接AO,如图,∵∠BAC=60°,∴∠DPE=120°.∵PE=PD,PM⊥DE,∴∠EPM=60°,∴ED=2EM=2EP•sin60°=EP=PA.当P与A、O共线时,且在O点右侧时,⊙P直径最大.∵⊙O与∠BAC两边均相切,且∠BAC=60°,∴∠OAF=30°,OF=1,∴AO==2,AP=2+1=3,∴DE=PA=3.故答案为:D。
