2011—2017年新课标全国卷2文科数学试题分类汇编——15.几何证明选讲
2017年全国统一高考数学试卷(文科)(新课标ⅱ)及解析

2017年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A={1,2,3},B={2,3,4},则A∪B=()A.{1,2,3,4} B.{1,2,3}C.{2,3,4}D.{1,3,4}2.(5分)(1+i)(2+i)=()A.1﹣i B.1+3i C.3+i D.3+3i3.(5分)函数f(x)=sin(2x +)的最小正周期为()A.4πB.2πC.πD .4.(5分)设非零向量,满足|+|=|﹣|则()A .⊥B.||=|| C .∥D.||>||5.(5分)若a>1,则双曲线﹣y2=1的离心率的取值范围是()A.(,+∞)B.(,2)C.(1,)D.(1,2)6.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90π B.63π C.42π D.36π7.(5分)设x,y 满足约束条件,则z=2x+y的最小值是()A.﹣15 B.﹣9 C.1 D.98.(5分)函数f(x)=ln(x2﹣2x﹣8)的单调递增区间是()A.(﹣∞,﹣2) B.(﹣∞,﹣1) C.(1,+∞)D.(4,+∞)9.(5分)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则()A.乙可以知道四人的成绩 B.丁可能知道四人的成绩C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩第1页(共14页)10.(5分)执行如图的程序框图,如果输入的a=﹣1,则输出的S=()A.2 B.3 C.4 D.511.(5分)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()A .B .C .D .12.(5分)过抛物线C:y2=4x的焦点F ,且斜率为的直线交C于点M(M在x轴上方),l为C的准线,点N 在l上,且MN⊥l,则M到直线NF的距离为()A .B.2 C.2 D.3二、填空题,本题共4小题,每小题5分,共20分13.(5分)函数f(x)=2cosx+sinx的最大值为.14.(5分)已知函数f(x)是定义在R上的奇函数,当x∈(﹣∞,0)时,f(x)=2x3+x2,则f(2)= .15.(5分)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.16.(5分)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B= .三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤,第17至21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知等差数列{a n}的前n项和为S n,等比数列{b n}的前n项和为T n,a1=﹣1,b1=1,a2+b2=2.(1)若a3+b3=5,求{b n}的通项公式;(2)若T3=21,求S3.18.(12分)如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.(1)证明:直线BC∥平面PAD;(2)若△PCD面积为2,求四棱锥P﹣ABCD的体积.19.(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:第2页(共14页)第3页(共14页)(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较. 附:K 2=.20.(12分)设O 为坐标原点,动点M 在椭圆C :+y 2=1上,过M 作x 轴的垂线,垂足为N ,点P 满足=.(1)求点P 的轨迹方程; (2)设点Q 在直线x=﹣3上,且•=1.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .21.(12分)设函数f (x )=(1﹣x 2)e x. (1)讨论f (x )的单调性;(2)当x ≥0时,f (x )≤ax +1,求a 的取值范围.选考题:共10分。
2011—2017年新课标全国卷2文科数学试题分类汇编——解析几何

2011—2017年新课标全国卷2文科数学试题分类汇编——解析几何一、选择题(2017·5)若a >1,则双曲线2221-=x y a的离心率的取值范围是( )A. ∞)B. )C. (1D. 12(,)(2017·12)过抛物线C :y 2 = 4x 的焦点F ,C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN ⊥l,则M 到直线NF 的距离为A.B. C. D. (2016·5)设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( ) A .12B .1C .32D .2 (2016·6)圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =( )A .43-B .34-C D .2(2015·7)已知三点)0,1(A ,)3,0(B ,)3,2(C ,则ABC ∆外接圆的圆心到原点的距离为( )A.53B.C.D.43(2014·10)设F 为抛物线C :y 2 = 3x 的焦点,过F 且倾斜角为30°的直线交于C 于A 、B 两点,则|AB |=( )A B .6 C .12 D .(2014·12)设点M (x 0,1),若在圆O :x 2+y 2=1上存在点N ,使得∠OMN =45°,则x 0的取值范围是( )A .[1,1]-B .11[]22-,C .[D .[ (2013·5)设椭圆2222:1x y C a b+=(0)a b >>的左、右焦点分别为12,F F ,P 是C 上的点,212PF F F ⊥,1230PF F ∠=,则C 的离心率为( )AB .13C .12D (2013·10)设抛物线C : y 2=4x 的焦点为F ,直线l 过F 且与C 交于A ,B 两点. 若|AF |=3|BF |,则l 的方程为( )A .1y x =-或1y x =-+B .1)y x =-或1)y x =-C .1)y x =-或1)y x =-D .1)y x =-或1)y x =-(2012·4)设F 1、F 2是椭圆E :22221x y a b+=(a >b >0)的左、右焦点,P 为直线32a x =上一点,△F 1PF 2是底角为30°的等腰三角形,则E 的离心率为( )A .12B .23C .34D .45(2012·10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,||AB =则C 的实轴长为( )A B . C .4 D .8(2011·4)椭圆221168x y +=的离心率为( )A .13B .12 CD (2011·9)已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直. l 与C 交于A , B 两点,|AB |=12,P 为C 的准线上一点,则∆ABP 的面积为( ) A .18 B .24 C .36 D .48二、填空题(2015·15)已知双曲线过点,且渐近线方程为12y x =±,则该双曲线的标准方程为 .三、解答题(2017·20)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 作x 轴的垂线,垂足为N ,点P 满足NP uu u r r(1)求点P 的轨迹方程;(2)设点Q 在直线x =-3上,且1⋅=OP PQ u u u r u u u r.证明过点P 且垂直于OQ 的直线l 过C 的左焦点F.(2016·21)已知A 是椭圆E :22143x y +=的左顶点,斜率为k (k >0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA .(Ⅰ)当|AM|=|AN|时,求△AMN 的面积;(Ⅱ)当|AM|=|AN|2k <<.(2015·20)已知椭圆C :22221x y a b +=(a >b >0,点(2C 上.(Ⅰ)求C 的方程;(Ⅱ)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A 、B ,线段AB 的中点为M ,证明:直线OM 的斜率与直线l 的斜率的乘积为定值.(2014·20)设F 1 ,F 2分别是椭圆C :12222=+by a x (a >b >0)的左、右焦点,M 是C 上一点且MF 2与x 轴垂直,直线MF 1与C 的另一个交点为N .(Ⅰ)若直线MN 的斜率为43,求C 的离心率;(Ⅱ)若直线MN 在y 轴上的截距为2且|MN |=5|F 1N |,求a ,b .(2013·20)在平面直角坐标系xoy 中,已知圆P 在x 轴上截得线段长为在y 轴上截得线段长为(Ⅰ)求圆心P 的轨迹方程;(Ⅱ)若P 点到直线y x =P 的方程.(2012·20)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,F A为半径的圆F交l于B,D两点.(I)若∠BFD=90º,△ABD的面积为求p的值及圆F的方程;(Ⅱ)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.(2011·20)在平面直角坐标系xOy中,曲线261y x x=-+与坐标轴的交点都在圆C上.(Ⅰ)求圆C的方程;(Ⅱ)若圆C与直线0x y a-+=交与A,B两点,且OA OB⊥,求a的值.2011—2017年新课标全国卷2文科数学试题分类汇编——解析几何(解析版)一、选择题(2017·5)C 解析:由题意222222111+===+c a e a a a,因为a >1,所以21112<+<a ,则1<<e 选C.(2017·12)C 解析:由题意知1):=-MF y x ,与抛物线24=y x 联立得231030-+=x x ,解得12133,==x x ,所以M ,因为⊥MN l ,所以(1-N ,因为(1,0)F ,所以1):=-NF y x ,所以M 到NF(2016·5)D 解析:(1,0)F ,又因为曲线(0)ky k x=>与C 交于点P ,PF x ⊥轴,所以21k =,所以k =2,故选D.(2016·6)A 解析:圆心为(1,4),半径2r =1=,解得43a =-,故选A.(2015·7)B 解析:圆心在直线BC 垂直平分线上,即直线x =1上,设圆心D (1, b ),由DA =DB 得||3b b =⇒=,所以圆心到原点的距离3d ==(2014·10)C 解析:由题意,得3(,0).4F 又因为tan30k =︒=AB 的方程为3)4y x =-,与抛物线2=3y x 联立,得21616890x x -+=,设1122(,),(,)A x y B x y ,由抛物线定义得,12168312162AB x x p =++=+=,故选C .(2014·12)A 解析:由题意画出图形如图:∵点M (x 0,1),∴若在圆O :x 2+y 2=1上存在点N ,使得∠OMN =45°,∴圆上的点到MN 的距离的最大值为1,要使MN =1,才能使得∠OMN =45°,图中M ′显然不满足题意,当MN 垂直x 轴时,满足题意,∴x 0的取值范围是[-1,1].(2013·5)D 解析:因为21212,30PF F F PF F ⊥∠=,所以2122tan 30,PF c PF ===.又122PF PF a +==,所以c a ==,故选D.(2013·10)C 解析:抛物线y 2=4x 的焦点坐标为(1,0),准线方程为x =-1,设A (x 1,y 1),B (x 2,y 2),则因为|AF |=3|BF |,所以x 1+1=3(x 2+1),即x 1=3x 2+2,因为|y 1|=3|y 2|,x 1=9x 2,所以x 1=3,x 2=13,当x 1=3时,2112y =,所以此时1y ==±,若1y =则1(3,2(,3A B ,此时AB k 此时直线方程为1)y x =-. 若1y =-1(3,(A B -,此时AB k =此时直线方程为1)y x =-. 所以l 的方程是1)y x =-或1)y x =-,故选C.(2012·4)答案:C 解析:∵△F 2PF 1是底角为30º的等腰三角形,260PF A ∴∠=︒,212||||2PF F F c ==,∴2||AF =c ,322c a ∴=,34e ∴=,故选C.(2012·10)C 解析:由题设知抛物线的准线为:4x =,设等轴双曲线方程为:222x y a -=,将4x =代入等轴双曲线方程解得y =||AB =,∴=a =2, ∴C 的实轴长为4,故选C.(2011·4)D解析:c e a ===2228111162,b e e a =-=-=∴ D. (2011·9)C 解析:易知2P =12,即AB =12,三角形的高是P =6,所以面积为36,故选C.二、填空题(2015·15)2214x y -=解析:根据双曲线渐近线方程为12y x =±,可设双曲线的方程为224x y m -=,把代入得m =1.三、解答题(2017·20)设O 为坐标原点,动点M 在椭圆C :2212x y +=上,过M 作x 轴的垂线,垂足为N ,点P 满足NP uu u r r(1)求点P 的轨迹方程;(2)设点Q 在直线x =-3上,且1⋅=OP PQ u u u r u u u r.证明过点P 且垂直于OQ 的直线l 过C 的左焦点F.(2017·20)解析:(1)设(,)P x y ,(,)M x y '',(,0)N x ',NP uu u r r,(,))x x y y ''-=,即0x x x x y y '=⎧'-=⎧⎪⎪⇒⎨⎨'='=⎪⎩⎪⎩,代入椭圆方程2212x y ''+=,得到222x y +=,∴点P 的轨迹方程222x y +=.(2)由题意知,椭圆的左焦点为F (-1,0),设P (m ,n ),Q (-3,t ),则(,),OP m n =u u u r(3,)-,OQ t =u u u r (3),,PQ m t n =---u u u r (1),,PF m n =---u u u r 由1OP PQ ⋅=u u u r u u u r 得2231m m tn n --+-=,又由(1)知222m n +=,故3+30m tn -=.所以330OQ PF m tn ⋅=+-=u u u r u u u r ,即OQ PF ⊥u u u r u u u r . 又过点P存在唯一直线垂直于,所以过点P 且垂直于OQ 的直线l 过C 的左焦点F .(2016·21)已知A 是椭圆E :22143x y +=的左顶点,斜率为k (k >0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA .(Ⅰ)当|AM|=|AN|时,求△AMN 的面积; (Ⅱ)当|AM|=|AN|2k <<.(2016·21)解析:(Ⅰ)设11(,)M x y ,则由题意知10y >.由已知及椭圆的对称性知,直线AM 的倾斜角为4π,又(2,0)A -,因此直线AM 的方程为2y x =+.将2x y =-代入22143x y +=得27120y y -=,解得0y =或127y =,所以1127y =.因此AMN ∆的面积11212144227749AMN S ∆=⨯⨯⨯=. (Ⅱ)将直线AM 的方程(2)(0)y k x k =+>代入22143x y +=得2222(34)1616120k x k x k +++-=.由2121612(2)34k x k -⋅-=+得2122(34)34k x k -=+,故1||2|AM x +=由题设,直线AN 的方程为1(2)y x k =-+,故同理可得||AN =.由2||||AM AN =得2223443kk k=++,即3246380k k k -+-=. 设32()4638f t t t t =-+-,则k 是()f t 的零点,22'()121233(21)0f t t t t =-+=-≥,所以()f t 在(0,)+∞单调递增,又260,(2)60f f =<=>,因此()f t 在(0,)+∞有唯一的零点,且零点k在内,所2k <.(2015·20)已知椭圆C :22221x y a b +=(a >b >0,点(2C 上.(Ⅰ)求C 的方程;(Ⅱ)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A 、B ,线段AB 的中点为M ,证明:直线OM 的斜率与直线l 的斜率的乘积为定值.(2015·20)解析:(Ⅰ)由题意有22421a b=+=,解得228,4a b ==. 所以C 的方程为221.84x y += (Ⅱ)设直线1122:(0,0),(,),(,),(,).M M l y kx b k b A x y B x y M x y =+≠≠将y kx b =+代入22184x y +=得222(21)4280k x kbx b +++-=,故12222,22121M M M x x kb b x y kx b k k +-===+=++,于是直线OM 的斜率12M OM M y k x k ==-,即12OM k k ⋅=-,所以直线OM 的斜率与直线l 的斜率的乘积为定值.(2014·20)设F 1 ,F 2分别是椭圆C :12222=+by a x (a >b >0)的左、右焦点,M 是C 上一点且MF 2与x 轴垂直,直线MF 1与C 的另一个交点为N .(Ⅰ)若直线MN 的斜率为43,求C 的离心率;(Ⅱ)若直线MN 在y 轴上的截距为2且|MN |=5|F 1N |,求a ,b .(2014·20)解析:∵M 是C 上一点且MF 2与x 轴垂直,∴M 的横坐标为c ,当x=c 时,2b y a=,即2()b M c a ,,若直线MN 的斜率为34,则22123tan 224b a b MF Fc ac ∠===,即22232b ac a c ==-,亦即2231022c ac a --=,则22320e e --=,解得12e =,故椭圆C 的离心率为12.(Ⅱ)由题意,原点O 是F 1F 2的中点,则直线MF 1与y 轴的交点D (0,2)是线段MF 1的中点,故244b =,即b 2=4a ,由|MN |=5|F 1N |,解得|DF 1|=2|F 1N |,设N (x 1,y 1),由题意知y 1<0,则112()22c x cy --=⎧⎨-=⎩,即11321x c y ⎧=-⎪⎨⎪-⎩,代入椭圆方程得2229114c a b +=,将b 2=4a 代入得229(4)1144a a a a -+=,解得a =7,27b =.(2013·20)在平面直角坐标系xoy 中,已知圆P 在x 轴上截得线段长为22,在y 轴上截得线段长为23. (Ⅰ)求圆心P 的轨迹方程; (Ⅱ)若P 点到直线y x =的距离为2,求圆P 的方程.(2013·20)解析:(Ⅰ)设P (x ,y ),圆P 的半径为r . 由题设y 2+2=r 2,x 2+3=r 2. 从而y 2+2=x 2+3. 故P 点的轨迹方程为y 2-x 2=1. (Ⅱ)设P (x 0,y 0).由已知得0022=. 又P 点在双曲线y 2-x 2=1上,从而得002210||11x y y x -=⎧⎨-=⎩. 由00220011x y y x -=⎧⎨-=⎩,得0001x y =⎧⎨=-⎩. 此时,圆P 的半径3r =. 由00220011x y y x -=-⎧⎨-=⎩,得0001x y =⎧⎨=⎩. 此时,圆P 的半径3r =. 故圆P 的方程为x 2+(y -1)2=3或x 2+(y +1)2=3.(2012·20)设抛物线C :x 2=2py (p >0)的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,F A 为半径的圆F 交l 于B ,D 两点.(I)若∠BFD =90º,△ABD 的面积为42求p 的值及圆F 的方程;(Ⅱ)若A ,B ,F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值. (2012·20)解析:(Ⅰ)设准线l 于y 轴的焦点为E ,圆F 的半径为r ,则|FE |=p ,|F A |=|FB |=|FD |=r ,E 是BD 的中点,∵090BFD ∠=,∴||||=||2FA FB FD p=,|BD |=2p ,设A (0x ,0y ),根据抛物线定义得,|F A |=02py +,∵ABD ∆的面积为,∴ABD S ∆=01||()22p BD y +=122p ⨯=p =2,∴F (0,1), |F A|=F 的方程为:22(1)8x y +-=.(Ⅱ)【方法1】∵A ,B ,F 三点在同一条直线m 上, ∴AB 是圆F 的直径,090ADB ∠=,由抛物线定义知1||||||2AD FA AB ==,∴030ABD ∠=,∴m的斜率为或-,∴直线m的方程为:2p y x =+,∴原点到直线m 的距离1d=p ,设直线n的方程为:y x b =+,代入22x py =得,220x x pb ±-=,∵n 与C 只有一个公共点,∴∆=24803p pb +=,∴6p b =-,∴直线n的方程为:6p y x =-,∴原点到直线n 的距离2dp ,∴坐标原点到m ,n:3p p =.【方法2】由对称性设200(,)(0)2x A x x p>,则(0,)2p F ,点,A B 关于点F 对称得:22220000(,)3222x x p B x p p x p p p --⇒-=-⇔=得3,)2p A ,直线3:02p p p m y x x -=+⇔=,222233x x x py y y x p p p '=⇔=⇒==⇒=⇒切点)6pP ,直线:06p n y x x p -=⇔-=, 坐标原点到,m n3=.(2011·20)在平面直角坐标系xOy 中,曲线261y x x =-+与坐标轴的交点都在圆C 上.(Ⅰ)求圆C 的方程;(Ⅱ)若圆C 与直线0x y a -+=交与A ,B 两点,且OA OB ⊥,求a 的值.(2011·20)解析:(Ⅰ)曲线261y x x =-+与坐标轴的交点为(0,1))(0,223±,故可设圆的圆心坐标为(3,t )则有2222)22()1(3t t +=-+,解得t =1,则圆的半径为3)1(322=-+t ,所以圆的方程为9)1()3(22=-+-y x .(Ⅱ)设A (x 1, y 1),B (x 2, y 2)坐标满足方程组220(3)(1)9x y a x y -+=⎧⎨-+-=⎩,消去y 得到方程012)82(222=+-+-+a a x a x ,由已知可得判别式△=56-16a -4a 2>0,由韦达定理可得a x x -=+421,212221+-=a a x x ①,由OA ⊥OB ,可得12120x x y y +=,又1122y x ay x a =+=+,所以212122()0x x a x x a +++=②,由①②可得a =-1,满足△>0,故a =-1.。
几何证明选讲(全国卷文科)

几何证明选讲(2011-2015全国卷文科)(一)新课标卷1.(2011.全国新课标22)(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为ABC ∆的边AB ,AC 上的点,且不与ABC ∆的顶点重合.已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程2140x x mn -+=的两个根. (I )证明:C ,B ,D ,E 四点共圆;(II )若90A ∠=︒,且4,6,m n ==求C ,B ,D ,E 所在圆的半径.2.(2012.全国新课标22)(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交△ABC 的外接圆于F ,G 两点,若CF//AB ,证明: (Ⅰ)CD=BC ; (Ⅱ)△BCD ∽△GBDFGDE AB C(二)全国Ⅰ卷1.(2013.全国1卷22)(本小题满分10分)选修4—1:几何证明选讲如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D。
(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=3,延长CE交AB于点F,求△BCF外接圆的半径。
2.(2014.全国1卷22)(本小题满分10分)选修4-1,几何证明选讲如图,四边形ABCD是O的内接四边形,AB的延长线=.与DC的延长线交于点E,且CB CE∠=∠;(I)证明:D E=,(II)设AD不是O的直径,AD的中点为M,且MB MC ∆为等边三角形.证明:ABC3.(2015.全国1卷22)(本小题满分10分)选修4-1:几何证明选讲如图AB 是O 直径,AC 是O 切线,BC 交O 与点E . (I )若D 为AC 中点,证明:DE 是O 切线; (II )若3OACE = ,求ACB ∠的大小.(三)全国Ⅱ卷1.(2013.全国2卷22)(本小题满分10分)选修4—1:几何证明选讲如图,CD 为△ABC 外接圆的切线,AB 的延长线交直线CD 于点D ,E ,F 分别为弦AB 与弦AC 上的点,且BC·AE=DC·AF ,B ,E ,F ,C 四点共圆. (1)证明:CA 是△ABC 外接圆的直径.(2)若DB=BE=EA,求过B ,E ,F ,C 四点的圆的面积与△ABC 外接圆面积的比值2.(2014.全国2卷22)(本小题满分10分)选修4-1:几何证明选讲如图,P 是⊙O 外一点,PA 是切线,A 为切点,割线PBC 与⊙O 相交于点B ,C ,PC=2PA ,D 为PC 的中点,AD 的延长线交⊙O 于点E ,证明: (I )BE=EC ;(II )AD ·DE=2PB 2。
2017年(文科数学)(新课标Ⅱ)试卷真题+参考答案+详细解析
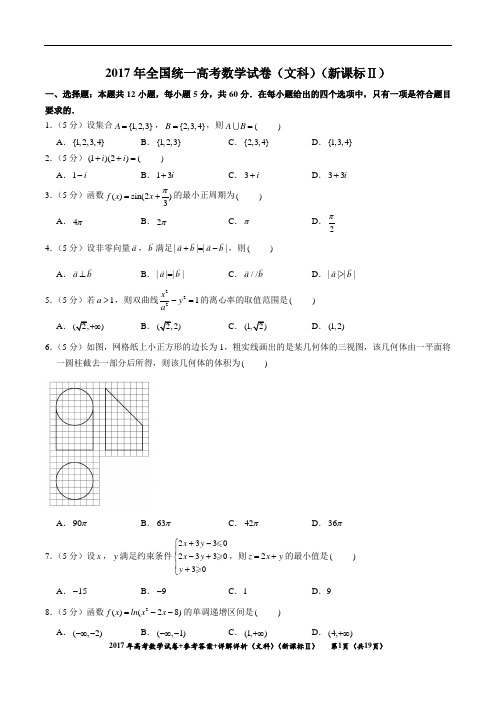
2017年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{1,2,3}A =,{2,3,4}B =,则(A B = )A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4}2.(5分)(1)(2)(i i ++= ) A .1i -B .13i +C .3i +D .33i +3.(5分)函数()sin(2)3f x x π=+的最小正周期为( )A .4πB .2πC .πD .2π 4.(5分)设非零向量a ,b 满足||||a b a b +=-,则( ) A .a b ⊥B .||||a b =C .//a bD .||||a b >5.(5分)若1a >,则双曲线2221x y a-=的离心率的取值范围是( )A.)+∞B.C.D .(1,2)6.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π7.(5分)设x ,y 满足约束条件2330233030x y x y y +-⎧⎪-+⎨⎪+⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .98.(5分)函数2()(28)f x ln x x =--的单调递增区间是( ) A .(,2)-∞-B .(,1)-∞-C .(1,)+∞D .(4,)+∞9.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( ) A .乙可以知道四人的成绩 B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩10.(5分)执行如图的程序框图,如果输入的1a =-,则输出的(S = )A .2B .3C .4D .511.(5分)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A .110B .15C .310D .2512.(5分)过抛物线2:4C y x =的焦点F ,3C 于点(M M 在x 轴上方),l 为C 的准线,点N 在l 上,且MN l ⊥,则M 到直线NF 的距离为( ) A 5B .22C .23D .33二、填空题,本题共4小题,每小题5分,共20分 13.(5分)函数()2cos sin f x x x =+的最大值为 .14.(5分)已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f = . 15.(5分)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 . 16.(5分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos cos b B a C c A =+,则B = .三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤,第17至21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,11a =-,11b =,222a b +=. (1)若335a b +=,求{}n b 的通项公式; (2)若321T =,求3S .18.(12分)如图,四棱锥P ABCD-中,侧面PAD为等边三角形且垂直于底面ABCD,12AB BC AD==,90BAD ABC∠=∠=︒.(1)证明:直线//BC平面PAD;(2)若PCD∆面积为27,求四棱锥P ABCD-的体积.19.(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg ),其频率分布直方图如下:(1)记A 表示事件“旧养殖法的箱产量低于50kg ”,估计A 的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量50kg <箱产量50kg旧养殖法 新养殖法(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较. 附:2()P K K0.050 0.010 0.001 K3.8416.63510.8282()()()()K a b c d a c b d =++++.20.(12分)设O为坐标原点,动点M在椭圆22:12xC y+=上,过M作x轴的垂线,垂足为N,点P满足2NP NM=.(1)求点P的轨迹方程;(2)设点Q在直线3x=-上,且1OP PQ=.证明:过点P且垂直于OQ的直线l过C的左焦点F.21.(12分)设函数2()(1)x f x x e =-. (1)讨论()f x 的单调性;(2)当0x 时,()1f x ax +,求实数a 的取值范围.(二)选考题:共10分。
2017年高考文科数学新课标2全国卷(word版含答案)

2017年普通高等学校招生全国统一考试新课标2文科数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{1,2,3},{2,3,4}A B ==,则A B =A .{}123,4,, B .{}123,, C .{}234,,D .{}134,, 2.(1i)(2i)++= A .1i -B .13i +C .3i +D .33i +3.函数π()sin(2)3f x x =+的最小正周期为 A .4π B .2πC .πD .π24.设非零向量a ,b 满足+=-a b a b ,则 A .a ⊥bB .=a bC .a ∥bD .>a b5.若1a >,则双曲线2221x y a-=的离心率的取值范围是A.)+∞ B. C.D .(1,2)6.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为 A .90π 符号B .63πC .42πD .36π7.设,x y 满足约束条件2+330,2330,30,x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩则2z x y =+的最小值是 A .15- B .9- C .1 D .98.函数2()ln(28)f x x x =--的单调递增区间是 A .(,2)-∞-B .(,1)-∞C .(1,)+∞D .(4,)+∞9.甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩,根据以上信息,则 A .乙可以知道四人的成绩 B .丁可以知道四人的成绩 C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩10.执行下面的程序框图,如果输入的1a =-,则输出的S =A .2B .3C .4D .511.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为 A .110B .15C .310D .2512.过抛物线2:4C y x =的焦点F ,C 于点M(M 在x 的轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为AB .C .D .二、填空题,本题共4小题,每小题5分,共20分. 13.函数()2cos sin f x x x =+的最大值为 .14.已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f = .15.长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 .16.ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B = . 三、解答题:共70分。
2011年高考全国卷2文科数学试卷(及答案)

绝密 ★ 启用前2011年普通高等学校招生全国统一考试文科数学(必修+选修Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至4页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目. 2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试..题.卷上作答无效....... 3.第Ⅰ卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.一 选择题(1)设集合U={ 1,2,3,4 },M={ 1,2,3 },N={ 2,3,4 }, 则()Cu M N = ( )(A ){1,2} (B ){2,3} (C ){2,4} (D) {1,4}(2)函数(0)y x =≥的反函数是( )(A )2()4x y x R =∈ (B )2(0)4x y x =≥ (C )24()y x x R =∈ (D )24(0)y x x =≥(3)设向量,a b 满足||||1a b ==,12a b ∙=-,则|2|a b +=( ) (A(B(C(D) (4)若变量,x y 满足约束条件6321x y x y x +≤⎧⎪-≤-⎨⎪≥⎩,则23z x y =+的最小值为( )(A )17 (B )14 (C )5 ( D ) 3(5)下列四个条件中,使a b >成立的充分不必要的条件是( )(A )1a b >+ (B )1a b >- (C )22a b > (D) 3a b >(6)设n S 为等差数列的前n 项和,若11a =,公差2,d =,224,k k S S +-=则k=( )(A )8 (B )7 (C )6 (D)5(7)设函数()cos (0),f x wx w =>将()y f x =的图像向右平移3π个单位长度后的图像与原图像重合,则w 的最小值等于( )(A )13(B )3 (C )6 (D) 9 (8)已知二面角,l αβ--点,,A AC l C α∈⊥为垂足,点,,B BD l D β∈⊥为垂足,若AB=2,AC=BD=1,则CD=( )(A )2 (B (C (D) 1(9)4位同学每人从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法有多少种( )(A )12 (B )24 (C )30 (D) 36(10)设()f x 是周期为2的奇函数,当01x ≤≤时,()2(1)f x x x =-则5()2f -=( ) (A )12-(B )14- (C )12 (D) 14 (11)设两圆12C C 都和两坐标轴相切,且都过(4,1)则两个圆心的距离12||C C =( )(A )4 (B ) (C )8 (D) (12)已知平面α截一球面得圆M ,过圆心M 且α与成60二面角的平面β截该球面得圆N ,若该球面的半径为4,圆M 的面积为4π,则圆N 的面积为( )(A )4π (B )9π (C )11π (D) 13π绝密 ★ 启用前2011年普通高等学校招生全国统一考试文科数学(必修+选修Ⅱ)第Ⅱ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域 内作答,在试题卷上作答无效.......... 3.第Ⅱ卷共10小题,共90分.二、填空题(13)10(1)x -的二项展开式中,x 的系数与9x 的系数之差为____________(14)已知:3(,),tan 2,2παπα∈=则cos α=____________ (15)已知:正方体1111ABCD A BC D -中,E 是11C D 的中点,则异面直线AE 与BC 所成角的余弦值为____________(16)已知:12,F F 分别是双曲线C :221927x y -=的左右焦点,点A C ∈,点M 的坐标为(2,0),AM 为-12F AF ∠的平分线,则2||AF ____________三、解答题.(17)(本小题满分10分)设等比数列{}n a 的前n 项和为n S ,已知26a =,13630a a +=,求n a 和n S(18)(本小题满分12分)ABC ∆的内角,,A B C 的对边分别为,,a b c ,sin sin sin sin a A c C C b B +=(1)求B ; (2) 若75A ︒=,2b =,求,a c .(19)(本小题满分12分)根据以往统计资料,某地车主购买甲种保险的概率是0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.(1)求该地一位车主至少购买甲乙两种保险中的1中的概率.(2)求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率.(20)(本小题满分12分)如图,四棱锥S-ABCD 中,AB //CD ,BC ⊥CD ,侧面SAB 为等边三角形,AB=BC=2,CD=SD=1(1) 证明:SD ⊥平面SAB(2) 求AB 与平面SBC 所成角的大小.(21)(本小题满分12分)已知函数:32()3(36)124f x x ax a x a =++-+-(a R ∈)(1)证明:曲线()y f x =在0x =出的切线过点(2,2) (2)若()f x 在0x x =处取得极小值,0(1,3)x ∈,求a 的求值范围(22)(本小题满分12分)已知O 为坐标原点,F 为椭圆C :2212y x +=在y 轴正半轴上的焦点,过F 且斜率为l 与C 交与A ,B 两点,点P 满足0OA OB OP ++=(1) 证明:点P 在C 上设点P 关于O 的对称点为Q(2) ,证明:A 、P 、B 、Q 四点在同一个圆上.。
2011—2017年新课标全国卷2文科数学试题分类汇编——15.几何证明选讲

ABCD E FG15.几何证明选讲一、解答题(2016·22)【选修4-1:几何证明选讲】如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE =DG ,过D 点作DF ⊥CE ,垂足为F . (Ⅰ)证明:B ,C ,G ,F 四点共圆;(Ⅱ)若AB =1,E 为DA 的中点,求四边形BCGF 的面积.(2015·22)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M 、N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点. (Ⅰ)证明:EF ∥BC ;(Ⅱ)若AG 等于⊙O 的半径,且AE=MN=23,求四边形EBCF 的面积.(2014·22)如图,P 是⊙O 外一点,P A 是切线,A 为切点,割线PBC 与⊙O 相交于点B 、C ,PC =2P A ,D 为PC 的中点,AD 的延长线交⊙O 于点E . 证明:(Ⅰ)BE = EC ;(Ⅱ)AD ·DE = 2PB 2.(2013·22)如图,CD 为ABC △外接圆的切线,AB 的延长线交直线CD 于点D ,E ,F 分别为弦AB 与弦AC 上的点,且BC AE DC AF ⋅=⋅,B 、E 、F 、C 四点共圆.(Ⅰ)证明:CA 是ABC △外接圆的直径;(Ⅱ)若DB BE EA ==,求过B 、E 、F 、C 四点的圆的面积与ABC △外接圆面积的比值.(2012·22)如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交于△ABC 的外接圆于F ,G 两点,若CF // AB ,证明: (Ⅰ)CD = BC ; (Ⅱ)△BCD ∽△GBD .(2011·22)如图,D ,E 分别为△ABC 的边AB ,AC 上的点,且不与△ABC 的顶点重合. 已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根. (Ⅰ)证明:C 、B 、D 、E 四点共圆;(Ⅱ)若∠A =90º,且m =4,n =6,求C 、B 、D 、E 所在圆的半径.F GDE ABCAB CD E FG15.几何证明选讲(逐题解析版)(2016·22)【选修4-1:几何证明选讲】如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE =DG ,过D 点作DF ⊥CE ,垂足为F .(Ⅰ)证明:B ,C ,G ,F 四点共圆;(Ⅱ)若AB =1,E 为DA 的中点,求四边形BCGF 的面积.22. 证明:(Ⅰ)∵DF CE ⊥,∴Rt Rt DEF CED △∽△,∴GDF DEF BCF ∠=∠=∠,DF CF DG BC =,∵DE DG =,CD BC =,∴DF CFDG BC =,∴GDF BCF △∽△,∴CFB DFG ∠=∠,∴GFB GFC CFB ∠=∠+∠90GFC DFG DFC =∠+∠=∠=︒, ∴180GFB GCB ∠+∠=︒.∴B ,C ,G ,F 四点共圆.(Ⅱ)∵E 为AD 中点,1AB =,∴12DG CG DE ===,∴在Rt GFC △中,GF GC =,连接GB ,Rt Rt BCG BFG △≌△,∴1112=21=222BCG BCGF S S =⨯⨯⨯△四边形.(2015·22)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M 、N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点. (Ⅰ)证明:EF ∥BC ;(Ⅱ)若AG 等于⊙O 的半径,且AE=MN=23,求四边形EBCF 的面积.(2015·22)解析:(Ⅰ)由于ABC ∆是等腰三角形,AD BC ⊥,所以AD 是CAB∠的平分线,又因为⊙O 分别与AB ,AC 相切于点E ,F ,所以AE AF =,故AD EF ⊥,从而//EF BC . (Ⅱ)由(Ⅰ)知,AE AF =,AD EF ⊥,故AD 是EF 的垂直平分线.又EF 为⊙O 的弦,所以O 在AD 上. 连结,OE OM ,则OE AE ⊥,由AG 等于⊙O 的半径得2AO OE =,所以30OAE ∠=o,因此ABC ∆和AEF ∆都是等边三角形.因为23AE =,所以4,2AO OE ==. 因为12,32OM OE DM MN ====,所以1OD =. 于是5,AD =1033AB =. 所以四边形EBCF 的面积为221103313163()(23)22⨯⨯-⨯⨯=.(2014·22)如图,P 是⊙O 外一点,P A 是切线,A 为切点,割线PBC 与⊙O 相交于点B 、C ,PC =2P A ,D 为PC 的中点,AD 的延长线交⊙O 于点E . 证明:(Ⅰ)BE = EC ;(Ⅱ)AD ·DE = 2PB 2.(2014·22)解析:(Ⅰ)∵PC =2P A ,PD =DC ,∴P A =PD ,△P AD 为等腰三角形. 连接AB ,则∠P AB = ∠DEB =β,∠BCE =∠BAE =α,∵∠P AB +∠BCE =∠P AB +∠BAD =∠P AD =∠PDA =∠DEB +∠DBE ,∴β+α=β+∠DBE ,即α=∠DBE ,亦即∠BCE =∠DBE ,所以BE =EC .(Ⅱ)∵AD ·DE =BD ·DC ,P A 2=PB ·PC ,PD =DC =P A , ∴BD ·DC =(P A -PB ) ·P A =PB ·PC -PB ·P A =PB ·(PC -P A ), ∴PB ·P A =PB ·2PB =2PB 2.(2013·22)如图,CD 为ABC △外接圆的切线,AB 的延长线交直线CD 于点D ,E ,F 分别为弦AB 与弦AC 上的点,且BC AE DC AF ⋅=⋅,B 、E 、F 、C 四点共圆.(Ⅰ)证明:CA 是ABC △外接圆的直径;(Ⅱ)若DB BE EA ==,求过B 、E 、F 、C 四点的圆的面积与ABC △外接圆面积的比值.(2013·22)解析:(Ⅰ)因为CD 为△ABC 外接圆的切线,所以∠DCB =∠A ,由题设知BC DCFA EA=,故△CDB ∽△AEF ,所以∠DBC =∠EF A .因为B ,E ,F ,C 四点共圆,所以∠CFE =∠DBC ,故∠EF A =∠CFE =90°.所以∠CBA =90°,因此CA 是△ABC 外接圆的直径.(Ⅱ)连结CE ,因为∠CBE =90°,所以过B ,E ,F ,C 四点的圆的直径为CE ,由DB =BE ,有CE =DC ,又BC 2=DB ·BA =2DB 2,所以CA 2=4DB 2+BC 2=6DB 2. 而DC 2=DB ·DA =3DB 2,故过B ,E ,F ,C 四点的圆的面积与△ABC 外接圆面积的比值为12.(2012·22)如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交于△ABC 的外接圆于F ,G 两点,若CF // AB ,证明: (Ⅰ)CD = BC ; (Ⅱ)△BCD ∽△GBD .(2012·22)解析:(Ⅰ) ∵D ,E 分别为△ABC 边AB ,AC 的中点,∴DE //BC . ∵CF //AB ,DF //BC ,∴CF //BD 且CF =BD ,∵又D 为AB 的中点,∴CF //AD 且CF =AD ,∴CD =AF . ∵CF //AB ,∴BC =AF ,∴CD =BC .(Ⅱ)由(Ⅰ)知,BC //GF ,∴GB =CF =BD ,∠BGD =∠BDG =∠DBC =∠BDC ,∴△BCD ∽△GBD .(2011·22)如图,D ,E 分别为△ABC 的边AB ,AC 上的点,且不与△ABC 的顶点重合. 已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根.(Ⅰ)证明:C 、B 、D 、E 四点共圆;FGDE ABCDE AB C(Ⅱ)若∠A =90º,且m =4,n =6,求C 、B 、D 、E 所在圆的半径.(2011·22)解析:(Ⅰ)连结DE ,根据题意在△ADE 和△ACB 中,AD ×AB =mn =AE ×AC ,即ABAEAC AD,又∠DAE =∠CAB ,从而△ADE ∽△ACB ,因此∠ADE =∠ACB ,所以C 、B 、D 、E 四点共圆.(Ⅱ)m =4,n =6,方程x 2-14x +mn =0的两根为2,12. 即AD =2,AB =12,取CE 的中点G ,DB 的中点F ,分别过G 、F 作AC 、AB 的垂线,两垂线交于点H ,连结D 、H ,因为C 、B 、D 、E 四点共圆,所以圆心为H ,半径为DH . 由于∠A =90º,故GH ∥AB ,HF ∥AC . 从而HF =AG =5,DF =5,故半径为52.。
2011年高考试题解析数学(文科)分项版之专题16 选修系列:几何证明选讲

2011年高考试题解析数学(文科)分项版16 选修系列:几何证明选讲一、填空题:1. (2011年高考天津卷文科13)如图,已知圆中两条弦AB 与CD 相交于点F,E 是AB 延长线上一点,且,AF:FB:BE=4:2:1.若CE 与圆相切,则线段CE 的长为 .【解析】设AF=4x,BF==2x,BE=x,则由相交弦定理得:2DF AF FB =⋅,即282x =,即214x =,由切割线定理得:2CE EB EA =⋅=2774x =,所以CE =.2.(2011年高考广东卷文科15)(几何证明选讲选做题)如图4,在梯形ABCD 中,AB ∥CD ,AB =4,CD =2,E 、F 分别为AD 、BC 上点,且EF =3,EF ∥AB ,则梯形ABFE 与梯形EFCD 的面积比为.【答案】.75【解析】由题得EF 是梯形的中位线,75)43(21)32(21=∙+∙+=∴h hS S EFCDABFE 梯形梯形 3.(2011年高考陕西卷文科15) B.(几何证明选做题)如图,,,B D AE BC ∠=∠⊥090,ACD ∠=且6AB =,4AC =,12,AD =则AE =_______. 【答案】2【解析】:Rt ABE Rt ADC ≅ 所以AB AEAD AC=, 即64212AB AC AE AD ⨯⨯===二、解答题:4.(2011年高考江苏卷21)选修4-1:几何证明选讲(本小题满分10分) 如图,圆1O 与圆2O 内切于点A ,其半径分别为1r 与212()r r r >,21-A 第图圆1O 的弦AB 交圆2O 于点C (1O 不在AB 上), 求证::AB AC 为定值。
解析:考察圆的切线的性质、三角形相似的判定及其性质,容易题。
证明:由弦切角定理可得11212,O B r AB AO C AO B AC O C r∴== 5. (2011年高考全国新课标卷文科22)(本小题满分10分)选修4-1几何证明选讲 如图,D ,E 分别是AB,AC 边上的点,且不与顶点重合,已知AB AD n AC m AE ,,,==为方程0142=+-mn x x 的两根, (1) 证明 C,B,D,E 四点共圆;(2) 若6,4,90==︒=∠n m A ,求C,B,D,E 四点所在圆的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
C
D E F
G
15.几何证明选讲
一、解答题
(2016·22)【选修4-1:几何证明选讲】
如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE =DG ,过D 点作DF ⊥CE ,垂足为F . (Ⅰ)证明:B ,C ,G ,F 四点共圆;
(Ⅱ)若AB =1,E 为DA 的中点,求四边形BCGF 的面积.
(2015·22)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M 、N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点. (Ⅰ)证明:EF ∥BC ;
(Ⅱ)若AG 等于⊙O 的半径,且
AE=MN=EBCF 的面积.
(2014·22)如图,P 是⊙O 外一点,P A 是切线,A 为切点,割线PBC 与⊙O 相交
于点B 、C ,PC =2P A ,D 为PC 的中点,AD 的延长线交⊙O 于点E . 证明:(Ⅰ)BE = EC ;
(Ⅱ)AD ·DE = 2PB 2.
(2013·22)如图,CD 为ABC △外接圆的切线,AB 的延长线交直线CD 于点D ,
E ,
F 分别为弦AB 与弦AC 上的点,且BC AE DC AF ⋅=⋅,B 、E 、F 、C 四
点共圆.
(Ⅰ)证明:CA 是ABC △外接圆的直径;
(Ⅱ)若DB BE EA ==,求过B 、E 、F 、C 四点的圆的面积与ABC △外接圆面积的比值.
(2012·22)如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交于△ABC 的外接圆于F ,G 两点,若CF // AB ,证明: (Ⅰ)CD = BC ; (Ⅱ)△BCD ∽△GBD .
(2011·22)如图,D ,E 分别为△ABC 的边AB ,AC 上的点,且不与△ABC 的顶点重合. 已知AE 的长为
m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根. (Ⅰ)证明:C 、B 、D 、E 四点共圆;
(Ⅱ)若∠A =90º,且m =4,n =6,求C 、B 、D 、E 所在圆的半径.
A
B C
D E F
G
15.几何证明选讲(逐题解析版)
(2016·22)【选修4-1:几何证明选讲】
如图,在正方形ABCD 中,E ,G 分别在边DA ,DC 上(不与端点重合),且DE =DG ,过D 点作DF ⊥CE ,垂足为F .
(Ⅰ)证明:B ,C ,G ,F 四点共圆;
(Ⅱ)若AB =1,E 为DA 的中点,求四边形BCGF 的面积.
22. 证明:(Ⅰ)∵DF CE ⊥,∴Rt Rt DEF CED △∽△,∴GDF DEF BCF ∠=∠=∠,
DF CF DG BC =,∵DE DG =,CD BC =,∴DF CF
DG BC =,∴GDF BCF △∽△,
∴CFB DFG ∠=∠,∴GFB GFC CFB ∠=∠+∠90GFC DFG DFC =∠+∠=∠=︒, ∴180GFB GCB ∠+∠=︒.∴B ,C ,G ,F 四点共圆.
(Ⅱ)∵E 为AD 中点,1AB =,∴1
2DG CG DE ===,∴在Rt GFC △中,GF GC =,连接GB ,
Rt Rt BCG BFG △≌△,∴111
2=21=222BCG BCGF S S =⨯⨯⨯△四边形.
(2015·22)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M 、N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点. (Ⅰ)证明:EF ∥BC ;
(Ⅱ)若AG 等于⊙O 的半径,且
AE=MN=EBCF 的面积.
(2015·22)解析:(Ⅰ)由于ABC ∆是等腰三角形,AD BC ⊥,所以AD 是CAB
∠的平分线,又因为⊙O 分别与AB ,AC 相切于点E ,F ,所以AE AF =,故A D E F ⊥,从而//EF BC . (Ⅱ)由(Ⅰ)知,AE AF =,AD EF ⊥,故AD 是EF 的垂直平分线.又EF 为⊙O 的弦,所以O 在AD 上. 连结,OE OM ,则OE AE ⊥,由AG 等于⊙O 的半径得
2AO OE =,所以30OAE ∠=,因此ABC ∆和AEF ∆都是等边三角形.
因
为
AE =,所以4,2AO OE ==. 因
为
1
2,32
O M O E
D M N ====所以1OD =. 于是5,AD
=3
AB =
. 所以四边形EBCF
的面积为22112
2⨯⨯=
(2014·22)如图,P 是⊙O 外一点,P A 是切线,A 为切点,割线PBC 与⊙O 相交
于点B 、C ,PC =2P A ,D 为PC 的中点,AD 的延长线交⊙O 于点E . 证明:(Ⅰ)BE = EC ;
(Ⅱ)AD ·DE = 2PB 2.
(2014·22)解析:(Ⅰ)∵PC =2P A ,PD =DC ,∴P A =PD ,△P AD 为等腰三角形. 连接AB ,则∠P AB = ∠DEB =β,∠BCE =∠BAE =α,∵∠P AB +∠BCE =∠P AB +∠BAD =∠P AD =∠PDA =∠DEB +∠DBE ,∴β+α=β+∠DBE ,即α=∠DBE ,亦即∠BCE =∠DBE ,所以BE =EC .
(Ⅱ)∵AD ·DE =BD ·DC ,P A 2=PB ·PC ,PD =DC =P A , ∴BD ·DC =(P A -PB ) ·P A =PB ·PC -PB ·P A =PB ·(PC -P A ), ∴PB ·P A =PB ·2PB =2PB 2.
(2013·22)如图,CD 为ABC △外接圆的切线,AB 的延长线交直线CD 于点D ,
E ,
F 分别为弦AB 与弦AC 上的点,且BC AE DC AF ⋅=⋅,B 、E 、F 、C 四
点共圆.
(Ⅰ)证明:CA 是ABC △外接圆的直径;
(Ⅱ)若DB BE EA ==,求过B 、E 、F 、C 四点的圆的面积与ABC △外接圆面积的比值.
(2013·22)解析:(Ⅰ)因为CD 为△ABC 外接圆的切线,所以∠DCB =∠A ,由题设知
BC DC
FA EA
=
,故△CDB ∽△AEF ,所以∠DBC =∠EF A .因为B ,E ,F ,C 四点共圆,所以∠CFE =∠DBC ,故∠EF A =∠CFE =90°.所以∠CBA =90°,因此CA 是△ABC 外接圆的直径.
(Ⅱ)连结CE ,因为∠CBE =90°,所以过B ,E ,F ,C 四点的圆的直径为CE ,由DB =BE ,有CE =DC ,又BC 2=DB ·BA =2DB 2,所以CA 2=4DB 2+BC 2=6DB 2. 而DC 2=DB ·DA =3DB 2,故过B ,E ,F ,C 四点的圆的面积与△ABC 外接圆面积的比值为12
.
(2012·22)如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交于△ABC 的外接圆于F ,G 两点,若CF // AB ,证明: (Ⅰ)CD = BC ; (Ⅱ)△BCD ∽△GBD .
(2012·22)解析:(Ⅰ) ∵D ,E 分别为△ABC 边AB ,AC 的中点,∴DE //BC . ∵CF //AB ,DF //BC ,∴CF //BD 且CF =BD ,∵又D 为AB 的中点,∴CF //AD 且CF =AD ,∴CD =AF . ∵CF //AB ,∴BC =AF ,∴CD =BC .
(Ⅱ)由(Ⅰ)知,BC //GF ,∴GB =CF =BD ,∠BGD =∠BDG =∠DBC =∠BDC ,∴△BCD ∽△GBD .
(2011·22)如图,D ,E 分别为△ABC 的边AB ,AC 上的点,且不与△ABC 的顶点重合. 已知AE 的长为
m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根. (Ⅰ)证明:C 、B 、D 、E 四点共圆;
(Ⅱ)若∠A =90º,且m =4,n =6,求C 、B 、D 、E 所在圆的半径.
G
(2011·22)解析:(Ⅰ)连结DE ,根据题意在△ADE 和△ACB 中,AD ×AB =mn =AE ×AC ,即
AB
AE
AC AD
,又∠DAE =∠CAB ,从而△ADE ∽△ACB ,因此∠ADE =∠ACB ,所以C 、B 、D 、E 四点共圆.
(Ⅱ)m =4,n =6,方程x 2-14x +mn =0的两根为2,12. 即AD =2,AB =12,取CE 的中点G ,DB 的中点F ,分别过G 、F 作AC 、AB 的垂线,两垂线交于点H ,连结D 、H ,因为C 、B 、D 、E 四点共圆,所
以圆心为H ,半径为DH . 由于∠A =90º,故GH ∥AB ,HF ∥AC . 从而HF =AG =5,DF =5,故半径为。
