华东师大3013版八年级上册数学定理公式
华东师大版数学初一到初三所有公式定理

初一到初三,华东师大版数学的所有公式与定理1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角作者:李云熙2005-12-4 20:00 回复此发言--------------------------------------------------------------------------------2 几何公式和定理61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
(完整版)最新华东师大版八年级数学上册知识点总结
角形,等腰大于等边)
②等边三角形的三条边相等
判定:①定义:三条边都相
等的三角形是等边三角形
③等边三角形的三个角相等,都为 60º。
③有一个角等于 60º的等腰
三角形是等边三角形
3
② 三 个 角都 相 等的 三角 形
是等边三角形
第十四章:勾股定理
知识点
内容
备注
等边三角形
①等腰三角形的两腰相等
②等腰三角形的两底角相等
③等腰三角形“三线合一”(顶角的平分线,
底边上的中线,底边上的高重合)
④等腰三角形是轴对称图形,只有一条对称轴
⑤等腰三角形的两底角的平分线相等(两条腰
上的中线相等,两条腰上的高相等)
考点:
①若∆, = ,则说明
∆是等腰三角形
②等腰三角形“三线合一”
A
①定义法:在同一三角形中,有两条边相等的
三角形是等腰三角形。
②判定定理:在同一三角形中,有两个角相等
的三角形是等腰三角形(简称:等角对等边)。 B
性质定理:线段垂直平分线上的点到线段两端
点的距离相等
已知:若 EF⊥ ,垂足为点 C,AC=BC,点 D 是直
线 EF 上任意一点
()=
()=
备注
+
逆用:
= ×
例:+ = ×
逆用: = ( ) = ( )
例: = ( ) = ( )
逆用: = ()
例(
( ×
)
)
×(
的一个因式
多项式除于单项式
多项式除于单项式,先用这个
【华东师大版】数学八年级上册数学:勾股定理
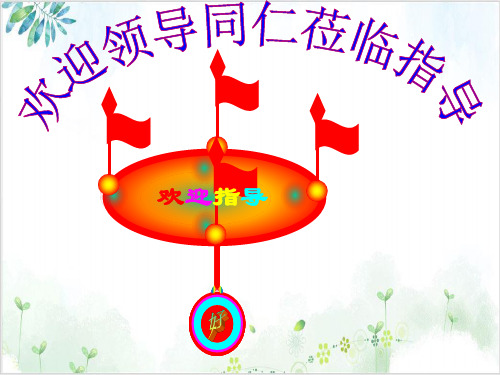
❖ AC2+BC2=AB2 → ∠ACB为直角
❖ AC2+BC2>AB2 → ∠ACB为锐角
C
A
C
A
BC
A B
B
归纳应用方法:
用勾股定理的逆定理判断直角三角形的步骤:
△ABC中
①、确定最大边(最大边c所对的角是最大角)
②、验证:c2与a2+b2是否相等 若 c2 == a2 ++ b2则△ABC是以∠C=90°的直角三角形
BC = 4 , CD = 12 , AD = 13, 求 四
边形ABCD的面积?
S C
四边形ABCD=36
B D
A
华东师大版八年级上册数学:勾股定 理-精品 课件pp t(实用 版)
华东师大版八年级上册数学:勾股定 理-精品 课件pp t(实用 版)
2. 已知a,b,c为△ABC的三边,且 满足
练一练
1、 三 角 形 三 边 长 a、 b、 c满 足 条 件 a:b:c= = 9:12:15,则 此 三 角 形 是 ( B )
A、锐角三角形 C、钝角三角形
B、直角三角形 D、等边三角形
2. 满足下列条件△ABC,不是直角三角形的是( D )
A.b2=a2-c2
B. a:b:c=3:4:5
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等边三角形
华东师大版八年级上册数学:勾股定 理-精品 课件pp t(实用 版)
思 维 激 活
华东师大版八年级上册数学:勾股定 理-精品 课件pp t(实用 版)
1、△ABC三边a,b,c为边向外作 正方形,(以三边为直径作半 圆,)若S1+S2=S3成立, 则△ABC 是直角三角形吗?
华东师大3013版八年级上册数学定理公式

华东师大3013版八年级上册数学定理公式一、整式运算法则1)幂的运算同底数幂的乘法:同底数幂相乘,底数不变,指数相加。
a m·a n=a m+n(m、n为正整数) 幂的乘方:幂的乘方,底数不变,指数相乘。
(a m)n=a mn (m、n为正整数)积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。
(ab)n=a n b n(n为正整数)同底数幂的除法:同底数幂相除,底数不变,指数相减。
a m÷a n=a m-n2)整式的乘法单项式与单项式相乘:只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,连同它的指数一起作为积的一个因式。
多项式与多项式相乘:先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
(m+n)(a+b)=ma+mb+na+nb3)整式的除法单项式除以单项式:单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式。
多项式除以单项式:先用这个多项式的每一项除以这个单项式,再把所得的商相加。
4)乘法公式平方差公式:(a+b)(a-b)=a2- b2完全平方公式:(a+b)2=a2 +2ab+ b2(a-b)2=a2 - 2ab+ b25)因式分解一提(提公因式):ma+mb+mc=m(a+b+c)二套(公式法):a2 +2ab+ b2 = (a+b) 2 a2 - 2ab+ b2= (a-b)2 a2- b2 = (a+b)(a-b)三分组乘法与因式分解:a3+b3=(a+b)(a2 - ab+ b2) a3- b3=(a-b)(a2 +ab+ b2)二、数据的处理频数:表示每个对象出现的次数。
频率:每个对象出现的次数与总次数的比值(或者百分比)。
频数和频率都能够反映每个对象出现的频繁程度。
三、定理两点确定一条直线两点之间,线段最短过一点有且只有一条直线与已知直线垂直过直线外一点有且只有一条直线与这条直线平行两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行全等三角形的判定条件边角边(SAS) 两边及其夹角分别相等的两个三角形全等角边角(ASA) 两角及其夹边分别相等的两个三角形全等角角边(AAS) 两角分别相等且其中一组等角的对边相等的两个三角形全等边边边(SSS) 三边分别相等的两个三角形全等斜边直角边(HL) 斜边和一条直角边分别相等的两个直角三角形全等等腰三角形的性质等腰三角形的两底角相等(等边对等角)等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)三条边都相等的三角形是等边三角形等边三角形的各个角都相等,并且每一个角都等于60°等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)三个角都相等的三角形是等边三角形有一个角等于60°的等腰三角形是等边三角形线段垂直平分线性质定理:线段垂直平分线上的点到线段两端的距离相等逆定理:到线段两端距离相等的点在线段的垂直平分线上线段的垂直平分线可看作到线段两端点距离相等的所有点的集合外心:三角形三边垂直平分线的交点,到三角形每个顶点的距离相等角平分线性质定理:角平分线上的点到角两边的距离相等逆定理:角的内部到角两边距离相等的点在角的平分线上角的平分线是到角的两边距离相等的所有点的集合内心:三角形三内角平分线交点,到三角形三边的距离相等勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
华东师大版八年级上册数学知识总结

八年级上第11 章数的开方1.平方根( 1)假如一个数的平方等于a,那么这个数就叫做 a 的平方根。
即:假如 x2 a ,那么 x 叫做 a 的平方根( 2)一个正数有两个平方根,它们互为相反数。
此中:正数 a 的正的平方根,叫做 a 的算术平方根,记作a,读作“根号a”,另一个平方根是它的相反数,即 a 。
所以,正数 a 的平方根能够记作 a 。
a称为被开方数。
0 的平方根只有一个,就是0,记作00 。
负数没有平方根。
a 0(a0 )( 3)求一个非负数的平方根的运算,叫做开平方。
2.立方根( 1)假如一个数的立方等于a,那么这个数叫做 a 的立方根。
即:假如x3a,那么x叫做a 的立方根数 a 的立方根,记作3a,读作“三次根号a”,此中 a 称为被开方数, 3 称为根指数。
(2)求一个数的立方根的运算,叫做开立方。
(3)任何数(正数、负数、 0)都有立方根,而且只有一个。
正数有一个正的立方根。
负数有一个负的立方根。
0的立方根是 0。
3.无理数无穷不循环小数叫做无理数。
实数有理数和无理数统称为实数。
实数与数轴上的点一一对应。
第 12 章整式的乘除1.幂的运算( 1)同底数幂相乘,底数不变,指数相加。
a m a n a m n(m、n为正整数)(2)幂的乘方幂的乘方,底数不变,指数相乘。
a mnamn( m、n 为正整数)(3)积的乘方积的乘方,等于把积中每一个因式分别乘方,再把所得的幂相乘。
ab n a n b n(n为正整数)(4)同底数幂的除法同底数幂相除,底数不变,指数相减。
(m、 n 为正整数, m>n, a0 )2.整式的乘法( 1)单项式与单项式相乘将它们的系数、同样字母的幂分别相乘,关于只在一个单项式中出现的字母,则连同它的指数一同作为积的一个因式。
( 2)单项式与多项式相乘将单项式分别乘以多项式的每一项,再将所得的积相加。
(3)多项式与多项式相乘先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
华师大版-数学-八年级上册-华师八上第十四章 勾股定理知识归纳

【同步教育信息】一. 本周教学内容: 勾股定理[教学目标]1. 了解勾股定理的证明,掌握勾股定理的内容,初步会用它进行有关的计算和证明。
2. 通过勾股定理的应用,培养方程的思想和逻辑推理能力。
3. 了解勾股定理的证明,培养学生的爱国情怀。
二. 重点、难点: 勾股定理的应用。
三. 教学过程设计: (一)勾股定理的证明 发现勾股定理的是毕达哥拉斯(约公元前580~公元前500年),他是一个哲学家,也是一个著名的数学家。
我国西周开国时期的商高(公元前1120年)就发现了这个定理。
因而,西方的发现比我国要迟好几百年。
由于古书中记有“勾广三,股修四,径隅五”,因此我国把这个定理简称为勾股定理。
我国古代数学家利用割补、拼接图形计算面积的思路提供了很多种证明方法。
(二)勾股定理:如果直角三角形的两直角边长分别为a 、b ,斜边长为c ,那么a b c 222+=。
勾股定理的应用方法:(1)在Rt △ABC 中,∵∠C =90°,∴AB AC BC 222=+又∵AB >0,∴AB AC BC =+22(2)在Rt △ABC 中,∵∠C =90°,∴AC AB BC 222=- 又∵AC >0,∴AC AB BC =-22【典型例题】例1. (1)在Rt △ABC 中,∠C =90°,a =6,b =8,求c 。
(2)在Rt △ABC 中,∠C =90°,a =40,c =41,求b 。
解:(1)在Rt △ABC 中,∵∠C =90°,∴c a b 222=+ 又∵c >0,∴c a b =+=+=22226810 (2)在Rt △ABC 中,∵∠C =90°,∴b c a 222=- 又∵b >0,∴b c a =-=-=222241409例2. 已知直角三角形的两边长AB cm BC cm ==68,,求第三边的长。
解:(1)若AB 、BC 均为直角边AC AB BC =+=+=22226810(2)若BC 为斜边AC BC AB =-=-=-==22228664362827例3. (1)在等腰Rt △ABC 中,∠C =90°,AC :BC :AB =___________; (2)如图所示,∠ACB =90°,∠A =30°,则BC :AC :AB =___________;若AB =8,则AC =___________;又若CD ⊥AB ,则CD =___________。
华师大版八年级数学上册 14.1勾股定理

C
a
B 则a2+b2=C2
回
青
N
M C
Fa B
b C
P A
欧
D
E
M C
Fa
b
B
A
C
D
E
M C
Fa
b
B
A
C
D
E
N
M C
Fa B
b C
P A
D
E
N
M C
Fa B
b C
P A
D
E
N
M C
Fa B
b C
P A
D
E
N
M C
Fa B
b C
P A
D
EGຫໍສະໝຸດ NM CFa B
b C
P A
D
E
G
N
M C
Fa B
b C
P A
D
E
G
N
M C
Fa B
b C
P A
ou
D
E
G
N
M C
Fa B
b C
P A
ou
D
E
G
刘徽的“青朱出入图”
I
E F
D
C
A
BH
G
收获:
一个定理——勾股定理 一个思想——以形证数 一次探索——从特殊到一般 一份自豪——中国人的骄傲
华师版八年级(上)第十四章
勾股定理
勾股定理: 直角三角形两直角边的平方和等 于斜边的平方。
cD
勾股定理:
直角三角形两直角边的平方和等
于斜边的平方。
C a
b
在Rt△ABC中, 若∠A=900
华师版数学八年级上册 公式法

例4 把下列各式分解因式:
(1)3ax2 + 6axy + 3ay2;(2)(a+b)2 - 12(a + b) + 36.
分析:(1)中有公因式 3a,应先提出公因式,再进一 步分解因式;(2)中将 a + b 看成一个整体,设 a + b = m,则原式化为 m2 - 12m + 36. 解:(1)原式 = 3a(x2 + 2xy + y2) = 3a(x + y)2.
解:(1)原式 = ( x2 )2 - ( y2 )2
= ( x2 + y2 )( x2 - y2 ) = ( x2 + y2 )( x - y )( x - y ).
分解因式的 一般步骤
(2) 原式 = ab(a2 -1) ………… 一提(公因式) = ab(a +1)(a -1). …… 二套(公式)
(2)原式 = (a + b)2 - 2·(a + b)·6 + 62 = (a + b - 6)2.
例5 利用两数和(或差)平方公式简便计算:
(1) 1002 - 2×100×99 + 99²;
(2) 342 + 34×32 + 162.
本题利用两数和(或
解:(1) 原式 = (100 - 99)²
= (4m + n)(3n - 2m) = -(4m + n)(2m - 3n). 当 4m + n = 40,2m - 3n = 5 时,
原式 = -40×5 = -200.
公式法 因式分
解
公式
平方差公式:a2-b2 = (a + b)(a - b)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东师大3013版八年级上册数学定理公式
一、整式运算法则
1)幂的运算
同底数幂的乘法:同底数幂相乘,底数不变,指数相加。
a m·a n=a m+n(m、n为正整数) 幂的乘方:幂的乘方,底数不变,指数相乘。
(a m)n=a mn (m、n为正整数)
积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。
(ab)n=a n b n(n为正整数)
同底数幂的除法:同底数幂相除,底数不变,指数相减。
a m÷a n=a m-n
2)整式的乘法
单项式与单项式相乘:只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,连同它的指数一起作为积的一个因式。
多项式与多项式相乘:先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
(m+n)(a+b)=ma+mb+na+nb
3)整式的除法
单项式除以单项式:单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式。
多项式除以单项式:先用这个多项式的每一项除以这个单项式,再把所得的商相加。
4)乘法公式
平方差公式:(a+b)(a-b)=a2- b2
完全平方公式:(a+b)2=a2 +2ab+ b2(a-b)2=a2 - 2ab+ b2
5)因式分解
一提(提公因式):ma+mb+mc=m(a+b+c)
二套(公式法):a2 +2ab+ b2 = (a+b) 2 a2 - 2ab+ b2= (a-b)2 a2- b2 = (a+b)(a-b)
三分组
乘法与因式分解:a3+b3=(a+b)(a2 - ab+ b2) a3- b3=(a-b)(a2 +ab+ b2)
二、数据的处理
频数:表示每个对象出现的次数。
频率:每个对象出现的次数与总次数的比值(或者百分比)。
频数和频率都能够反映每个对象出现的频繁程度。
三、定理
两点确定一条直线
两点之间,线段最短
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与这条直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
全等三角形的判定条件
边角边(SAS) 两边及其夹角分别相等的两个三角形全等
角边角(ASA) 两角及其夹边分别相等的两个三角形全等
角角边(AAS) 两角分别相等且其中一组等角的对边相等的两个三角形全等
边边边(SSS) 三边分别相等的两个三角形全等
斜边直角边(HL) 斜边和一条直角边分别相等的两个直角三角形全等
等腰三角形的性质
等腰三角形的两底角相等(等边对等角)
等腰三角形底边上的高、中线及顶角的平分线互相重合(三线合一)
三条边都相等的三角形是等边三角形
等边三角形的各个角都相等,并且每一个角都等于60°
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
三个角都相等的三角形是等边三角形
有一个角等于60°的等腰三角形是等边三角形
线段垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等
逆定理:到线段两端距离相等的点在线段的垂直平分线上
线段的垂直平分线可看作到线段两端点距离相等的所有点的集合
外心:三角形三边垂直平分线的交点,到三角形每个顶点的距离相等
角平分线
性质定理:角平分线上的点到角两边的距离相等
逆定理:角的内部到角两边距离相等的点在角的平分线上
角的平分线是到角的两边距离相等的所有点的集合
内心:三角形三内角平分线交点,到三角形三边的距离相等
勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即a2+b2=c2(a、b表示直角边,c表示斜边)
勾股定理的逆定理:如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角。
四、补充
在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半直角三角形斜边上的中线等于斜边上的一半
多边形内角和定理:n边形的内角的和等于(n-2)×180°
任意多边的外角和等于360°。
