2016春苏科版数学九下6.7《用相似三角形解决问题》word导学案3
【最新苏科版精选】苏科初中数学九下《6.7用相似三角形解决问题》word教案 (1).doc

6.7用相似三角形解决问题教学目标:1.了解平行投影的意义.2.知道在平行光线照射下,不同物体的物高与影长成比例,会利用平行投影画出图形并能利用其原理测量物体的高度.3.经历“探索—发现—猜想”,通过实际问题的研究,提高分析问题、解决问题的能力,建立“相似三角形”的模型.4.综合运用判定相似三角形的条件和三角形相似的性质解决问题,增强用数学的意识.教学重点:理解平行光线照射下,不同物体的物高与影长的关系,并能进行运用.教学难点:利用平行投影的原理求物体的高度.学习过程:一、创设情景,感悟新知1.判定三角形相似有哪些方法?相似三角形有哪些性质?2.当人们在阳光下行走时,会出现怎样的现象?二、合作探究:1.课本数学实验室.在平行光线照射下,物体所产生的影称为平行投影.在平行光线照射下,不同物体的物高与影长成比例.2.课本尝试1、2.三、练习巩固:1.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?2.如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5m,窗户的高度AF为2.5m,求窗户外遮阳蓬外端一点D 到窗户上掾的距离AD.(结果精确到0.1m)3.如图,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米长木杆的影长为2米,则电线杆的高度为多少米?4.利用镜面反射可以计算旗杆的高度,如图,一名同学(用AB表示),站在阳光下,通过镜子C恰好看到旗杆ED的顶端,已知这名同学的身高是1.60米,他到镜子的距离是2米,镜子到旗杆的距离是8米,求旗杆的高.2题图 3题图 4题图四、当堂检测:1.小明在操场上练习双杠,在练习的过程中他发现双杠的两横杆的影子在地面上是()A.相交B.平行C.垂直D.无法确定2.如图,小华拿一个矩形的木框在阳光下玩,矩形的木框在地面上形成的投影不可能是()3.冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射,此时竖一根a米长的竹竿,其影长为b米,某单位计划想建m米高的南北两栋宿舍楼,如图所示.试问两栋楼相距至少有多少米时,后楼的采光一年四季不受影响(用m、a、b表示)?4.如图,要测量河两岸相对的两点A、B间的距离,先从B处出发沿与AB成90°角的方向,向前走40m到C处,在C处立一标杆,然后方向不变继续向前走8m到D处,在D处作DE⊥BD,沿DE方向走12m到E处,恰好使A、C、E在一条直线上,求A、B两点间距离.五、小结思考:六、教学反思:。
新苏科版九年级数学下册《6章图形的相似6.7用相似三角形解决问题》教案_25

6.7用相似三角形解决问题(1)-----平行投影教学目标:1、知道在平行光线的照射下,物体所产生的影称为平行投影.如物体在阳光下的影称为平行投影.2、了解平行投影的性质,会用其解决问题.教学重点:用平行投影的性质解决问题教学过程:一、导入新课平行投影的概念二、新知探索例1、亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M 、颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置 C 、D .然后测出两人之间的距离 C D =1.25 m ,颖颖与楼之间的距离 D N =30 m (C 、D 、N在同一条直线上),颖颖的身高 B D =1.6 m ,亮亮蹲地观测时眼睛到地面的距离 A C = 0.8 m .你能根据以上测量的数据帮助他们求出住宅楼的高度吗?例2、如图,小明从路灯下向前走了 5 米,发现自己在地面上的影子长DE 是 2 米,如果小明的身高为 1.6 米,那么路灯离地面的高度AB 是米.例3、小亮同学想利用影长测量学校旗杆AB 的高度,如图,他在某一时刻立 1 米长的标杆测得其影长为 1.2 米,同时旗杆的投影一部分在地面上BD 处,另一部分在某一建筑的墙上CD 处,分别测得其长度为9.6 米和 2 米,求旗杆AB 的高度.例4、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为 1 米的竹竿的影长为0.5米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2 米,一级台阶高为0.3 米,如图所示,若此时落在地面上的影长为 4.4 米,则树高为多少?三、课堂小结。
新苏科版九年级数学下册《6章 图形的相似 6.7 用相似三角形解决问题》教案_1

6.7 用相似三角形解决问题(1)本节课要达到的目标:1.通过用相似三角形有关知识解决实际问题的过程,提高学生分析、解决实际问题的能力;2.学会建构“用相似三角形解决问题”的基本数学模型;本节课的难点:将实际问题抽象、建模以辅助解题。
操作1:如图6-42中,甲木杆AB在阳光下的影长为BC.试在图中画出同一时刻乙、丙两根木杆在阳光下的影长.观察与思考:1、在阳光下,同一时刻,物体高度与物体的影长存在的关系是:物体的高度越高,物体的影长就________.2、如何用相似三角形的知识说明在平行光线的照射下,不同物体的物高与影长成比例?说说你的想法。
要想测量一个物体的高度,我们需要测量哪些量就可以用数学方法来计算即可?说一说你的想法。
巩固练习1.如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=30m,在DC的延长线上找一点A,使AC=5m,过A作AB∥DE交EC的延长线于点B,测得AB=6.5m,求池塘的宽DE.2.在阳光下,身高为1.68m的小强在地面上的影长为2m.在同一时刻,测得旗杆在地面上的影长为18m.求旗杆的高度(精确到0.1m).3.在阳光下,高为6m的旗杆在地面上的影长为4m.在同一时刻,测得附近一座建筑物的影长为36m.求这座建筑物的高度背景故事:古埃及国王为了知道金字塔的高度,请一位学者来解决这个问题.在某一时刻,当这位学者确认在阳光下他的影长等于他的身高时,要求他的助手测出金字塔的影长,这样他就十分准确地知道了金字塔的高度.转化成数学问题:如图6-43,AC是金字塔的高,如果此时测得金字塔的影DB 的长为32 m,金字塔底部正方形的边长为230 m,你能计算这座金字塔的高度吗?挑战一下:小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.。
新苏科版九年级数学下册《6章 图形的相似 6.7 用相似三角形解决问题》教案_14

6.7用相似三角形解决问题(1)学习目标:1.通过探索在平行光的照射下,不同物体的物高与影长之间的关系的过程,了解平行射影的概念.2.经历测量物高与影长的过程,会用相似三角形的性质解决有关平行射影的实际问题. 情境创设在平行光线的照射下,物体所产生的影称为平行投影.探究交流在操场上,分别竖立长度不同的甲、乙、丙3根木杆,在同一时刻分别测量这3根木杆在阳光下的影长,并将有关数据填入下表:木杆木杆长度杆影长度杆影长度木杆长度甲10 6 0.6乙7 4.2 0.6丙 5 3 0.6点拨矫正点拨矫正例1.某一时刻甲木杆的影子如下图所示,你能画出乙木杆的影子吗?(用线段表示)例2. 在太阳光下,身高为1.6m的小芳在地面上的影长为2m,在同一时刻,测得旗杆在地面上的影长为18m,求旗杆的高度.才艺展示通过观察、测量,你发现了什么?请与同学交流.结论:①在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长②在平行光线的照射下,.人生在勤,不索何获. 2018-9-21 1.身高为1.5m的小华在打高尔夫球,她在阳光下的影长为2.1m,此时她身后一棵水杉树的影长为10.5m,则这棵水杉树高为A.7.5m B.8m C.14.7m D.15.75m2.在阳光下,身高为1.68米的小强在地上的影长为2米.在同一时刻,测得旗杆在地面上的影长为18米,求旗杆的高度(精确到0.1米)3. 小军想出了一个测量建筑物高度的方法:在地面上C处平放一面镜子,并在镜子上做一个标记,然后向后退去,直至看到建筑物的顶端A在镜子中的象与镜子上的标记重合.如果小军的眼睛距地面1.65m,BC、CD的长分别为60m、3m,求这座建筑物的高度.4. 小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.5.小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=2m,BC=10m,CD与地面成45°,求电线杆的高度.6.7用相似三角形解决问题(1)2主备人:张启慧审核人:王媛媛九年级()班学号()姓名 .【基础练习】一、选择题1.小明在操场上练习的过程中他发现双杠的两横杠的影子在地上是A.相交的B.平行的C.垂直的D.重合的2.小兵身高1.4m,他的影长是2.1m,若此时学校旗杆的影长是18m,那么旗杆的高度是A.9m B.11 m C.12 m D.27m3.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶A.0.5m B.0.55m C.0.6m D.2.2m4.如图,小李打网球时,球恰好打过网,且落在离网4m的位置上,则球拍击球的高度h为A.0.6m B.1.2m C.1.3m D.1.4m二、填空题5.如图所示,某班上体育课,甲、乙两名同学分别站在 C、D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙同学相距米.6.一天,小青想利用影子测量校园内一根旗杆的高度,在同一时刻内,小青的影长为2米,旗杆的影长为20米,若小青的身高为1.60米,则旗杆的高度为米.7.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC= 米.三、解答题8.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.(1)请你在图中画出此时DE在阳光下的投影;(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.9.为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离树(AB)8.1m的点E处,然后观测考沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,(第5题图)(第7题图)(第4题图)(第6题图)人生在勤,不索何获. 2018-9-21 再用皮尺量得DE=2.7m,观测者目高CD=1.6m,求树高AB.10.如图所示,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2米和1米,求塔高AB.【拓展提高】11.如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面,影长为 2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?4。
6.7用相似三角形解决问题(课件)九年级数学下册(苏科版)

木杆
木杆长度 杆影长度
甲
80cm
16cm
5
乙
120cm
2cm
5
丙
160cm
32cm
5
结论:在平行光的照射下,在同一时刻,不同物体的
物高与影长成比例
02 知识精讲
Q2:在阳光下,不同时刻,同一物体的影长相等吗? 结论:在平行光的照射下,在不同时刻,同一物体的 影长不相等
02 知识精讲
在平行光的照射下: (1)在同一时刻,不同物体的物高与影长成比例 (2)在不同时刻,同一物体的影长不相等
苏科版九年级下册第6章图形的相似
用相似三角形解决问题
Solve problems with similar triangles
教学目标
01 了解平行投影与中心投影的意义,会利用平行投影与中心 投影画图
02 理解在平行光与点光源的照射下,物体的物高与影长的关 系,并能利用其中的原理进行相关测量与计算
6m 2m
8m
24m
【中心知投识影精】讲
例3、学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑 AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH, 两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处 ,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三 点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
夜晚,当人在路灯下行走时,会看到一个有趣的现象:在灯光照射范围 内,离开路灯越远,影子就越长(如图)
通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的
新苏科版九年级数学下册《6章图形的相似6.7用相似三角形解决问题》教案_20

6.7 用相似三角形解决问题(1) 主备人:教学目标1.通过用相似三角形有关知识解决实际问题的过程,提高学生分析、解决实际问题的能力;2.学会建构“用相似三角形解决问题”的基本数学模型;3.通过知识拓展,激发学生学数学的兴趣,使学生积极参与探索活动,体验成功的喜悦,培养科学的数学观.教学重点根据实际问题,依据相似三角形的有关知识,构建数学模型,解决实际问题.教学难点将实际问题抽象、建模以辅助解题.教学过程二次备课情景引入1.当人们在阳光下行走时,会出现一个怎样的现象?生:影子.2.你能举出生活中的例子吗?生:……活动探究活动一实验探究1.阅读“平行投影”的概念,了解平行投影;2.现有A、B、C三根长度不同的木杆,在同一时刻分别测得这三根木杆在阳光下的影长,现将数据整理如下:木杆木杆长度杆影长度A 0.8 1B 1.2 1.5C 1.6 2结论:在阳光下,在同一时刻,物体高度与物体的影长存在的关系是:物体的高度越高,物体的影长就越长.即:在平行光线照射下,不同物体的物高与影长成比例.思考操作如图,木杆AB在阳光下的影长为BC.试在图中画出同一时刻A1B1、A2B2两根木杆在阳光下的影长.(此处填写二次备课)思考:如何用相似三角形的知识说明在平行光线的照射下,不同物体的物高与影长成比例?根据“太阳光可以看成平行光线”的表述,画出与图中虚线平行的线段.若MN=2.4,NC=1.6,BN=2,则AB=_____.例如:一根 1.5米长的标杆直立在水平地面上,它在阳光下的影长为 2.1米;此时一棵水杉树的影长为10.5米,求这棵水杉树的高度。
【练一练】(1)在同一时刻,高度为 1.6米的小树在阳光下的影长为0.8米,一棵大树的的影长为4.8米,则大树的高度为______米.(2)在阳光下,高为6m的旗杆在地面上的影长为4m.在同一时刻,测得附近一座建筑物的影长为36m.这座建筑物的高度为_______米.活动二应用举例(一)古埃及国王为了知道金字塔的高度,请一位学者来解决这个问题.在某一时刻,当这位学者确认在阳光下他的影长等于他的身高时,要求他的助手测出金字塔的影长,这样他就十分准确地知道了金字塔的高度.问题:AC是金字塔的高,如果此时测得金字塔的影DB的长为32 m,金字塔底部正方形的边长为230 m,你能计算这座金字塔的高度吗?为了知道目前这座金字塔的高度,用同样的方法现测得金字塔的影DB的长为22m,金字塔底部正方形的边长为230m,你能计算现在这座金字塔的高度吗?你能用这种方法测量出学校附近某一物体的高度吗?(二)当楼房顶部、标杆顶端与皮皮的眼睛在一条直线上时,他请别人测出AB=4米,BC=20米,已知皮皮眼睛离地面 1.6米,标杆长5米,你能帮他算出楼房的高度吗?【练一练】如图,树立在点B处的标杆AB高2.5米,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上。
新苏科版九年级数学下册《6章图形的相似6.7用相似三角形解决问题》教案_19

距胶片 20 cm,那么光源 S 距屏幕 ________m 时,放映的图像刚好布满整个屏幕.
7.顺次连接三角形三边上的中点所构成的三角形的高与原三角形对应高的比为
_______.
8.如图,点 M 是△ ABC 内一点.过点 M 分别作直线平行于△ ABC 的各边,所形成的三个小三 角形 (图中阴影部分 )的面积分别是 4、 9 和 49,则△ ABC 的面积是 ________.
参考答案
1.B 2.解:设长臂端点升高 x 米,则 3.解:如图,根据常识桌面与地面平行,所以,△
,∴ x=8. C ADE ∽△ ABC ,
∴ = ,即 = ,解得 BC=1.8 ,
所以,地面上阴影部分的面积 =π?( ) 2=0.81 π平方米, B
4.设剪的是第 x 张,则
,x=6,故选 C.
BC AD BC AD
__ __ ____.____
A B = ____,
相似三角形对应高的比等于 ___________ .
三角形中的特殊线段还有哪些?它们是否也具有类似的性质呢?你有何猜想?
合作探究:
问题一:
△ ABC ∽△ A ′B ′C′,AD 和 A′D ′分别是△ ABC 和△ A′B′C′的中线,设相似比为 k ,那么 AD ? A'D '
DE 2
11. (1) AD=8 (2)
DF 3 8x
12.(1) 种方案更好一些. 设方案 (1)中 DE=x.根据题意, 得
2x
8 .解得 x
12
24 ,2x
7
48
,
7
面积为 1152 ;设方案 (2) 中 DE =2y.根据题意,得 8 2 y
2016春苏科版数学九下6.7《用相似三角形解决问题》word导学案1
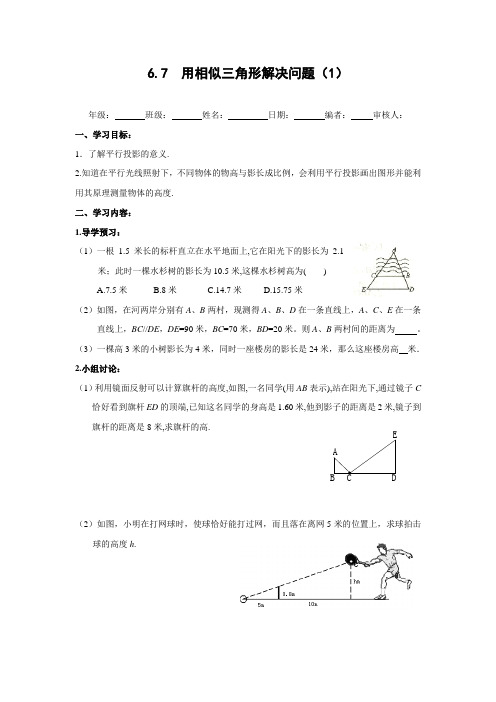
6.7 用相似三角形解决问题(1)年级: 班级: 姓名: 日期: 编者: 审核人: 一、学习目标: 1.了解平行投影的意义.2.知道在平行光线照射下,不同物体的物高与影长成比例,会利用平行投影画出图形并能利用其原理测量物体的高度. 二、学习内容: 1.导学预习:(1)一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为( ) A.7.5米 B.8米 C.14.7米 D.15.75米(2)如图,在河两岸分别有A 、B 两村,现测得A 、B 、D 在一条直线上,A 、C 、E 在一条直线上,BC //DE ,DE =90米,BC =70米,BD =20米。
则A 、B 两村间的距离为 。
(3)一棵高3米的小树影长为4米,同时一座楼房的影长是24米,那么这座楼房高 米. 2.小组讨论:(1)利用镜面反射可以计算旗杆的高度,如图,一名同学(用AB 表示),站在阳光下,通过镜子C恰好看到旗杆ED 的顶端,已知这名同学的身高是1.60米,他到影子的距离是2米,镜子到旗杆的距离是8米,求旗杆的高.(2)如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h .3.展示提升:(1)某人身高1.7米,某一时刻影长2.04米,同时一棵树影长为10.2米,则此树高 米。
(2)小刚身高1.7m ,测得他站立在阳光下的影子长为0.85m ,紧接着他把手臂竖直举起,测得影子长为1.1m ,那么小刚举起的手臂超出头顶( ) A .0.5mB .0.55mC .0.6mD .2.2m(3)一位同学想利用树影测量树高(AB ),他在某一时刻测得长为1m 的竹竿影长为0.9m ,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD ),他先测得留在墙上的影高(CD )为1.2m ,又测得地面部分的影长(BC )为2. 7m ,他求得树高应为多少?4.质疑拓展:已知,如图,AB 和DE 是直立在地面上的两根立柱.AB =5m ,某一时刻AB 在阳光下的投影BC =3m .(1)请你在图中画出此时DE 在阳光下的投影; (2)在测量AB 的投影时,同时测量出DE 在阳光 下的投影长为6m ,请你计算DE 的长.BC DEA5.学习小结: 6.达标检测:(1)如图,高低杠AB =2.5m ,EC =2m ,已知四边形ABCD 和四边形ECGF 都是矩形,若AB 在地面上的影长为3m ,则E ′D ′= . (2)某旅游风景区中某两个景点之间的距离为75米,在一张比例尺为1:2000的导游图上,它们之间的距离大约相当于 ( ) A .一根火柴的长度 B .一支钢笔的长度 C .一支铅笔的长度D .一根筷子的长度(3)阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m 长的影子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B
O 1 O 6.7 用相似三角形解决问题(3)
年级: 班级: 姓名: 日期: 编者: 审核人:
一、学习目标:
1.了解盲区等概念,并应用盲区进行测量.
2.深刻感受测量是现实生活中经常遇到的问题,能结合实际选择合适的测量方法和工具.
二、学习内容:
1.导学预习:
(1)如图是一盏圆锥形灯罩AOB ,两母线的夹角90AOB ∠=︒,
若灯炮O 离地面的高OO 1是2米时,则光束照射到地面的
面积是 米
(2)一条河的两岸有一段是平行的,在河的南岸边每隔5米有一
棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸
边15米的点P 处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
(3)一个钢筋三角架三 长分别为20cm ,50cm ,60cm ,现要再做一个与其相似的钢筋三角架,
而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )
A .一种
B .两种
C .三种
D .四种
2.小组讨论:
如图所示,一段街道的两边缘所在直线分别为AB 、PQ ,并且AB ∥PQ ,建筑物的一端DE 所在的直线MN ⊥AB 于点M ,交PQ 于点N ,小亮从胜利街的A 处,•沿着AB 方向前进,小明一直站在点P 的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在的位置(•用点C 标出);
(2)已知:MN =20m ,MD =8m ,PN=24m .求(1)中的点C 到胜利街口的距离CM .
3.展示提升:
(1)一个钢筋三脚架三边长分别为20 cm . 50 cm .60 cm ,现在要做一个与其相似的钢筋三
脚架,而只有长为30 cm 和50 cm 的两根钢筋,要求以其中一根为一边,从另一根上截下两段(准许有余料)作为两边,则有多少种不同的截法?并分别求出?
(2)画图并填空:
如图,在正方形网格中,△OAB 的顶点分别为O (0,0),A
(1,2),B (2,-1).
①以点O (0,0)为位似中心,按比例尺3:1在位似中心的同
侧将△OAB 放大为△OA’B’,放大后点A 、B 的对应点分别为
A’、B’ .画出△OA’B’,并写出点A’、B’的坐标:A’( ),
B’( ).
②在(1)中,若()C a b ,为线段AB 上任一点,写出变化后点C 的对应点C 的坐标 ( ).
(3)如图,梯形ABCD 中,AD ∥BC ,AD =3,CD =5,BC =10,梯形的高为4,动点M 从B
点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动,动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向中点D 运动,设运动时间为t 秒。
①当MN ∥AB 时,求t 的值;
②试探究:当t 为何值时,△CMN 是等腰三角形.
4.质疑拓展:
(1)如图,在平面直角坐标系中,四边形OABC 是等腰梯形,BC ∥OA ,OA =7,AB =4,∠COA =60°,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合,连结CP ,过点P 作PD 交AB 于D 点.
①求点B 的坐标;
②当点P 运动到什么位置时,△OCP 为等腰三角形?求这时点P 的坐标;
③当点P 运动到什么位置时,使得∠CPD =∠OAB ,且=?求这时点P 的坐标.
5.学习小结:
6.达标检测:
(2011广东汕头)如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与DE 重合,AB =EF =9,∠BAC =∠DEF =90°,固定△ABC ,将△EFD 绕点A 顺时针旋转,当DF 边与AB 边重合时,旋转中止.不考虑旋转开始和结束时重合
的情况,设DE 、DF (或它们的延长线)分别
交BC (或它的延长线)于G 、H 点,如图(2).
①问:始终与△AGC 相似的三角形有
及 ;
②设CG =x ,BH =y ,求y 关于x 的函数关系
式(只要求根据2的情况说明理由);
③问:当x 为何值时,△AGH 是等腰三角形?
7.学习反思:
G。
