2019北京市西城区高二(下)期末数学
北京市西城区2018_2019学年高二数学下学期期末考试试题(含解析)
f (x) g(x) 2x 1 2x2 1 2(x
2 )(x 2
2) 2
xx
x
因为 x 0,
2 2
,
f
(x)
g
(
x)
0;
x
2 2
,
,
f
(
x)
g(
x)
0;
6
精品文档，欢迎下载！
x
2 , f (x) g(x) 0 ，所以 x
2
2 时， f (x) g(x) 有最小值 1 ln 2 1 0
D. sin x 【答案】D 【解析】 【分析】
1
精品文档，欢迎下载！
根据余弦函数的求导公式即可.
【详解】 cos x sin x ，故选 D.
【点睛】本题考查常见函数的求导，属于基础题.
3.用 0，1，2，3，4，5 这 6 个数字，可以组成没有重复数字的四位数的个数是( ) A. 360 B. 300
C. 240
D. 180
【答案】B 【解析】 【分析】 分为有 0 和没 0 两类求解. 【详解】当四个数字中没有 0 时，没有重复数字的四位数有： A54 120 种；
当四个数字中有 0 时，没有重复数字的四位数有： A31 A53 180 种,
两类相加一共有 300 种，故选 B. 【点睛】本题考查排列组合与分类加法计数原理，考查分类讨论思想，属于基础题.
B. 1 i C. 1 i D. 1 i 【答案】B
【解析】
【分析】
先化简，再求共轭复数.
2 【详解】 1 i
21 i 1 i1 i
1
i
2
，所以复数
1i
的共轭复数是1
北京市西城区2019—2020学年度第二学期期末试卷高二数学答案
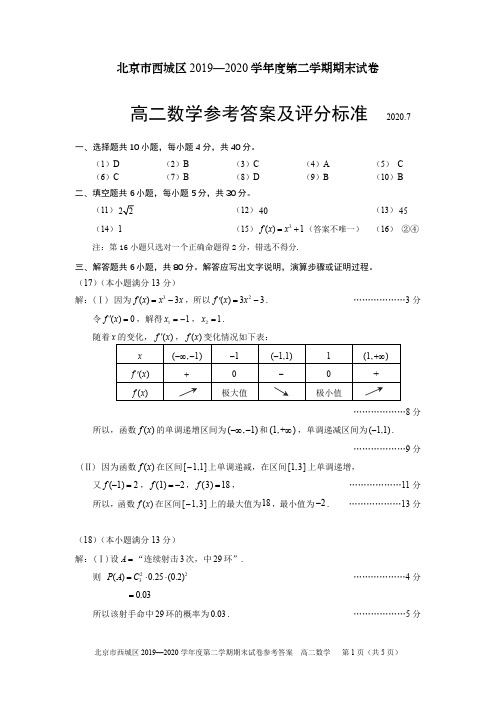
北京市西城区2019—2020学年度第二学期期末试卷高二数学参考答案及评分标准 2020.7一、选择题共10小题，每小题4分，共40分。
（1）D （2）B （3）C （4）A （5） C（6）C（7）B（8）D（9）B（10）B二、填空题共6小题，每小题5分，共30分。
（11）（12）40（13）45（14）1（15）3()1f x x =+（答案不唯一） （16） ②④注：第16小题只选对一个正确命题得2分，错选不得分.三、解答题共6小题，共80分。
解答应写出文字说明，演算步骤或证明过程。
（17）（本小题满分13分）解：(Ⅰ) 因为3()3f x x x =-，所以2()33f x x '=-. ………………3分令()0f x '=，解得11x =-，21x =.随着x 的变化，()f x '，()f x 变化情况如下表：x(,1)-∞- 1- (1,1)- 1 (1,)+∞()f x ' +-+()f x极大值 极小值………………8分所以，函数()f x 的单调递增区间为(,1)-∞-和(1,+)∞，单调递减区间为(1,1)-.………………9分(Ⅱ) 因为函数()f x 在区间[1,1]-上单调递减，在区间[1,3]上单调递增，又(1)2f -=，(1)2f =-，(3)18f =， ………………11分 所以，函数()f x 在区间[1,3]-上的最大值为18，最小值为2-. ………………13分（18）（本小题满分13分）解：(Ⅰ)设A =“连续射击3次，中29环”.则 223()0.25(0.2)P A C =⋅⋅ ………………4分0.03=所以该射手命中29环的概率为0.03. ………………5分(Ⅱ)设B =“连续射击3次，命中不少于28环”,依题意，命中30环的概率为3(0.2)0.008=； ………………7分 命中28环的概率为2222330.15(0.2)(0.25)0.2C C ⋅⋅+⋅⋅ ………………11分0.0180.03750.0555=+=； ………………12分由（1）知，命中29环的概率为0.03；所以 ()0.0080.05550.030.0935P B =++=, ………………13分 所以该射手连续射击3次，命中不少于28环的概率为0.0935.（19）（本小题满分13分）解：（Ⅰ）当1a =时，()ln f x x x =-，所以11()1x f x x x-'=-=. ………………3分 所以(1)0f '=，又因为(1)1f =，所以曲线()y f x =在点(1,(1))f 处的切线方程为1y =. …………5分 （Ⅱ）由已知，()1a x af x x x-'=-=，(0,)x ∈+∞.① 当0a <时，()0f x '>，函数()f x 在定义域内是增函数，不存在极值. ………………7分 ② 当0a >时，令()0f x '=，解得x a =. 随着x 的变化，()f x '，()f x 变化情况如下表：x(0,)aa (,)a +∞()f x ' -0 +()f x极小值………………9分所以，函数()f x 在区间(0,)a 上单调递减，在区间(,)a +∞上单调递增，…………10分 所以，函数()f x 的极小值点为x a =，极小值为()ln f a a a a =-， …………12分 函数()f x 不存在极大值. ………………13分综上，当0a <时，函数()f x 没有极值；当0a >时，()f x 有极小值ln a a a -，极小值点为x a =，无极大值. （20）（本小题满分14分）解：(Ⅰ)设A =“从样本中随机选1人，该学生选择了化学”，则 17121074501(),1001002P A ++++===所以，从样本中随机选1人，该学生选择了化学的概率为12. ………………4分(Ⅱ) 第8、9、10组共有11人，其中选择政治的有6人.所以X 的所有可能取值为0,1,2. ………………5分252112(0)11C P X C ===， ………………6分11562116(1)11C C P X C ===， ………………7分262113(2)11C P X C ===. ………………8分………………9分故X 的期望26312()0+1211111111E X =⨯⨯+⨯=. ………………11分 (Ⅲ) 选择地理的总人数为： 20141210975279+++++++=.所以P （“同时选择生物”）14+12+9+237==7979； P （“同时选择化学”）12+10+729==7979； P （“同时选择政治”）20222==7979+；P （“同时选择物理”）109524==7979++；P （“同时选择历史”）=20147546==7979+++. ………………13分因为4679最大，所以一个学生选择了地理，同时选择历史的可能性最大. …………14分 （21）（本小题满分13分）解：(Ⅰ)当0a =时，()e 1x f x x =--，所以()e 1x f x '=-. ………………1分解()0f x '>，得0x >；解()0f x '<，得0x <.所以()f x 在区间(,0)-∞上单调递减，在区间(0,)+∞上单调递增， ………………3分 所以()f x 的最小值为(0)0f =，所以()0f x ≥. ………………5分(Ⅱ) 因为2()e 12xa f x x x =---，所以()e 1x f x ax '=--.设()e 1x g x ax =--，则曲线()y f x =的切线斜率不存在最小值等价于()g x 不存在最小值. ……………7分()e x g x a '=-.① 当0a ≤时，()0g x '>恒成立，所以()g x 在区间(,)-∞+∞上单调递增，不存在最小值，所以0a ≤符合题意. ………………9分 ② 当0a >时,解()0g x '>，得ln x a >；解()0g x '<，得ln x a <.所以()g x 在区间(,ln )a -∞上单调递减，在区间(ln ,)a +∞上单调递增，……………10分 所以()g x 在ln x a =处取得最小值，所以0a >不符合题意. ………………12分 综上, a 的取值范围为{0}a a ≤. ………………13分（22）（本小题满分14分）解：(Ⅰ)函数()f x 定义域为{|0}x x >，11()ax f x a x x+'=+=. ① 当0a ≥时,()0f x '>恒成立，函数()f x 的单调递增区间为(0,)+∞. ……………2分 ② 当0a <时,解()0f x '>，得10x a <<-；解()0f x '<，得1x a>-.所以()f x 的单调递增区间为1(0,a -，单调递减区间为1(,)a-+∞. ………………4分综上，当0a ≥时，()f x 单调递增区间为(0,)+∞；当0a <时，()f x 的单调递增区间为1(0,a -，单调递减区间为1(,)a-+∞.(Ⅱ)证法1：由已知1()e ln x g x x ax a -=--+，0x >.因为(1)1g =，所以只需证明()g x 存在最小值，但1x =不是最小值点，即min ()(1)1g x g <=. ……6分因为e ()ln e x g x x ax a =--+，所以11()e x g x a x-'=--.因为函数1e x y -=，1y x=-在区间(0,)+∞上是增函数，所以()g x '在区间(0,)+∞上是增函数， ………………8分因为1a >，所以(1)0g a '=-<，11(1ln(1))1101ln(1)1ln(1)g a a a a a '++=+--=->++++.所以方程()0g x '=在区间(0,)+∞上存在唯一解， ………………10分 不妨设为0x ，则01x >，随着x 的变化，()g x '，()g x 变化情况如下表：x0(0,)x 0x 0(,)x +∞()g x ' -+()g x极小值所以()g x 有最小值，最小值为0()(1)1g x g <=. ………………13分 所以函数1()e ()x g x f x -=-存在最小值，且最小值小于1. ………………14分 证法2: 由已知1e ()eln ln exx g x x ax a x ax a -=--+=--+，0x >.所以11()e x g x a x-'=--， 因为1e x y -=，1y x=-在区间(0,)+∞上是增函数， 所以()g x '在(0,)+∞上是增函数， ………………6分因为1a >，所以(1)0g a '=-<，1(1ln(1))101ln(1)g a a a a '++=+-->++.所以方程()0g x '=存在唯一解， ………………8分 不妨设为0x ，则01x >，随着x 的变化，()g x '，()g x 变化情况如下表：x0(0,)x 0x 0(,)x +∞()g x ' -+()g x极小值 所以01min000()()e ln x g x g x x ax a -==--+，且0101e x a x --=. ………………10分所以0011min 0001()2e ln e 1x x g x x x x --=--+-，01x >. 设111()2e ln e 1x x h x x x x--=--+-， 11122111()=e e (1)(e )x x x h x x x x x x---'--+=-+， 当1x >时，()0h x '<，所以()h x 在区间(1,)+∞上单调递减. ………………12分 所以当1x >时，()(1)1h x h <=，即()g x 的最小值小于1， ………………13分 所以函数()g x 存在最小值，且最小值小于1. ………………14分。
最新北京市西城区2019-2019学年下学期高二年级期末试卷
北京市西城区2019-2019学年下学期高二年级期末试卷化学试卷2011.7试卷满分：120分考试时间：100分钟A卷[选修模块5] 满分100分可能用到的相对原子质量：H 1 C 12 O 16 Na 23第一部分（选择题共50分）每小题只有一个选项．．．．．．符合题意（1～25小题，每小题2分）1. 下列有机物的命名中，正确的是A. 2，2-二甲基丁烷B. 3，3-二甲基丁烷C. 2-乙基丁烷D. 2，3，3-三甲基丁烷2. 键线式可以简明地表示有机物的结构，表示的物质是A. 丁烷B. 丙烷C. 丙烯D. 1-丁烯3. 下列有机物中，属于芳香烃的是A. B.C. D.4. 分子式为C4H9Cl的有机物有A. 2种B. 3种C. 4种D. 8种5. 下列有关油脂的叙述中，不正确．．．的是A. 植物油能使溴水褪色B. 油脂的氢化又称为油脂的硬化C. 植物油、牛油、甘油、汽油统称为油脂D. 油脂在碱性溶液中的水解反应又称为皂化反应6. 下列反应中，属于消去反应的是A.B.C.D.7. 下列各组物质中，不属于．．．同分异构体的是A. 和B. 和C. 和D. 和8. 下列有机物分子中，所有原子一定不在同一平面内的是A. B.C. D.9. 只用一种试剂鉴别正己烷、1-己烯、乙醇、苯酚水溶液4种无色液体，应选用A. 酸性KMnO4溶液B. 饱和溴水C. NaOH溶液D. AgNO3溶液10. 下列物质中，沸点最高的是A. 乙烷B. 丙烷C. 乙醇D. 乙二醇11. 某有机物X催化氧化的产物是(CH3)2CHCHO，有机物X是A. 乙醇的同系物B. 乙醛的同系物C. 丙醇的同分异构体D. 丙醛的同分异构体12. 下列玻璃仪器的洗涤方法不正确．．．的是A. 附着油脂的试管，用热碱溶液洗涤B. 残留在试管内壁上的碘，用酒精洗涤C. 做过银镜反应实验后的试管，用氨水洗涤D. 残留有苯酚的试管，用酒精洗涤13. 下列实验装置一般不用于．．．分离物质的是14. 下列有关蛋白质的说法中，正确的是A. 蛋白质只要变性，就不能发生水解反应B. 向蛋白质溶液中加入饱和硫酸钠溶液可产生沉淀C. 蛋白质是仅由C、H、O、N 4种元素组成的高分子化合物D. 蛋白质在酸、碱或酶的作用下，最终水解成较小的肽类化合物15. 欲除去下列各物质中的少量杂质，括号内试剂选择正确的是A. 溴苯中的溴（KI溶液）B. 溴乙烷中的乙醇（NaOH溶液）C. 苯中的甲苯（溴水）D. 乙酸乙酯中的乙酸（饱和Na2CO3溶液）16. 下列物质中，既能发生消去反应生成烯烃，又能发生氧化反应生成醛的是A. CH3OHB.C. D.17. 咖啡酸具有止血、镇咳、祛痰等疗效，其结构简式为，下列有关咖啡酸的说法中，正确的是A. 咖啡酸分子中的所有碳原子不可能共平面B. 咖啡酸可以发生加成、酯化、加聚等反应C. 1 mol咖啡酸与足量Na反应，最多产生3 mol H2D.1 mol咖啡酸与饱和溴水反应，最多消耗2.5 mol Br218. 下列各组有机物，以任意比混合，只要总物质的量一定，则完全燃烧时消耗的氧气的量恒定不变的是A. C3H6和C3H8B. C4H6和C3H8C. C6H10和C6H6D. C3H6和C3H8O19. A、B、C 3种醇同足量的金属钠完全反应，在相同条件下产生相同体积的氢气，消耗这3种醇的物质的量之比为2：6：3，则A、B、C 3种醇分子中含羟基数目之比是A. 3:2:1B. 3:1:2C. 2:1:3D. 2:6:321. “诺龙”属于国际奥委会明确规定的违禁药品类固醇，其结构简式如下图所示.下列关于“诺龙”的说法中，不正确．．．的是A. 分子式是C18H26O2B. 既能发生加成反应，也能发生酯化反应C. 能在NaOH醇溶液中发生消去反应D. 既能发生氧化反应，也能发生还原反应22. 下列叙述中，正确的是A. 用溴水除去苯中的苯酚B. 用核磁共振氢谱鉴别1-丙醇和2-丙醇C. 不慎将苯酚溶液沾到皮肤上，立即用稀NaOH溶液清洗D. 苯与酸性KMnO4溶液混合振荡、静置分层，下层液体为无色23. 下列叙述中，正确的是A. 1 mol乙醇分子中含有共价键的数目为7N AB. 1 mol甲基（—CH3）中含有电子的数目为10N AC. 14g乙烯和丙烯的混合物中含有碳原子的数目为N AD. 28 g C16O与28 g C18O中含有质子的数目均为14N A24. 对羟基扁桃酸是合成香料的重要中间体，它可由如下反应制得：下列说法中，不正确．．．的是A. 上述反应的原子利用率是100%B. 对羟基扁桃酸的核磁共振氢谱有6个吸收峰C. 对羟基扁桃酸可以发生加成反应、取代反应和缩聚反应D. 1 mol对羟基扁桃酸与足量NaOH溶液反应，消耗3 mol NaOH25. 已知：乙醇可被强氧化剂氧化为乙酸.可经三步反应制取，其中第二步的反应类型是A. 加成反应B. 水解反应C. 氧化反应D. 消去反应第二部分（非选择题共50分）26. （8分）I. 在实验室利用下列装置，可制备某些气体并验证其化学性质.完成下列表格：II. 工业上用乙烯和氯气为原料，经下列各步合成聚氯乙烯（PVC ）：甲的结构简式是__________________________________________________； 反应（3）的化学方程式是_________________________________________.27. （12分）羟基是重要的官能团.某化学小组以下列4种物质的溶液作为研究对象，比较不同物质的羟基中氢原子的活泼性.①碳酸 ②乙醇 ⑧苯酚 ④乙酸II. 乙同学在研究了甲同学的实验方案后，提出如下改进方案，能一次比较乙酸、碳酸和苯酚的羟基中氢原子的活泼性，实验仪器如下图所示.（1）利用上述仪器组装实验装置，其中A管插入（填字母，下同）_______中，B管插入__________中，C管插入_________中.（2）丙同学查资料发现乙酸有挥发性，于是在试管F之前增加了一个盛有________溶液的洗气装置，使乙同学的实验设计更加完善.28. （10分）肉桂醛（C9H8O）是一种常用香精，在食品、医药化工等方面都有应用.肉桂醛与其他有机物具有如下转化关系，其中A为一氯代烃.（1）肉桂醛是苯的一取代物，与H2加成的产物中没有支链，肉桂醛结构简式是_______.（2）反应A→B的化学方程式是_____________________________________________.（3）Z不能．．发生的反应类型是（填字母）___________.a. 取代反应b. 加聚反应c. 加成反应d. 消去反应（4）Y与乙醇在一定条件下反应的化学方程式是___________________________________________________________________.（5）写出符合下列条件的Y的一种同分异构体的结构简式：___________________________________________________________________.①属于酯类②苯环上只有一个取代基③能发生银镜反应.29. （10分）合成高分子材料用途广泛、性能优异，其功能与分子结构有密切的关系.下面是几种高分子材料的结构简式：（1）A是天然橡胶的主要成分，易老化，A中含有的官能团的名称是____________.（2）B的单体是苯酚和___________，这两种单体在碱催化下，可得到网状高分子化合物，俗称电木，是（填“热塑性”或“热固性”）_________塑料.（3）C与NaOH溶液在一定条件下反应，生成高吸水性树脂，该树脂的结构简式是___________________________________.（4）D是合成纤维中目前产量第一的聚酯纤维——涤纶，可由两种单体在一定条件下合成，该合成反应的化学方程式是_________________________________________.30. （10分）有机物A常用于食品行业.已知9.0 g A在足量O2中充分燃烧，混合气体依次通过足量的浓硫酸和碱石灰，分别增重5.4 g和13.2 g，经检验剩余气体为O2.（1）A分子的质谱图如下图所示，从图中可知其相对分子质量是90，则A的分子式是______________________.（2）A能与NaHCO3溶液发生反应，A一定含有的官能团名称是__________________.（3）A分子的核磁共振氢谱有4个峰，峰面积之比是1：1：1：3，则A的结构简式是_________________________________.（4）0.1 mol A与足量Na反应，在标准状况下产生H2的体积是__________L.（5）A在一定条件下可聚合得到一种聚酯，用于制造手术缝合线，其反应的化学方程式是___________________________________________________________________.B卷[选修模块5] 满分20分1. （10分）葡萄糖不仅是重要的营养物质，而且是重要的工业原料.某厂按如下转化关系生产葡萄糖及其相关产品.（1）山梨醇的分子式是_____________.（2）反应③生成六元环状葡萄糖酸内酯，它在（填“阴”或“阳”）________极生成.（3）反应④的化学方程式是_______________________________________________；可以用来确定葡萄糖酸中官能团的仪器分析方法是_________________________.（4）反应⑤得到葡萄糖酸钙溶液，从该溶液中分离出葡萄糖酸钙晶体的实验操作是加热浓缩、_________、过滤、洗涤、干燥.2. （10分）石油被称为“工业血液”.A是从石油中得到的链状烃，相对分子质量为42.I. 以A为原料，利用下述反应合成甘油，在方框内填上中间体的结构简式.II. 从A出发存在如下转化（某些产物已略去）：已知：回答下列问题：（1）B为无色晶体，其溶液可与饱和溴水反应生成白色沉淀，B的结构简式是______.（2）G含有支链，其分子中含有羧基和碳碳双键，则G的结构简式是_________.（3）已知由G和F通过酯化反应生成K，K加聚后可制得长效阿司匹林，长效阿司匹林的结构简式是_______________________________.（4）G的同分异构体中可以使溴的四氯化碳溶液褪色的酯（含顺反异构体）有_______种.【试题答案】A卷[选修模块5] 满分100分每小题只有一个选项符合题意（1~25小题，每小题2分）26. （8分）I. （1）B→D→E（答全，得1分）（2分）（2）（2分）Ⅱ. CH2ClCH2Cl（1分）（2分）27. （12分，每空2分）I. 产生白色浑浊④①③②II. （1）D（或E），E（或D），F（答全，得2分）（2）饱和NaHCO3 28. （10分，每空2分）（1）（2）（3） b（4）（5）29. （10分，每空2分）（1）碳碳双键（2）HCHO（或甲醛）热固性（3）（4）30. （10分，每空2分）（1）C3H6O3（2）羧基（3）（4）2.24（5）B卷[选修模块5] 满分20分1. （10分，每空2分）（1）C6H14O6（2）阳（3）红外光谱（4）冷却结晶2. （10分，每空2分）I. （各1分，共2分）II. （1）（2）（3）（4）611 / 11。
2019-2020学年北京市西城区数学高二下期末考试试题含解析
2019-2020学年北京市西城区数学高二(下)期末考试试题一、单选题（本题包括12个小题，每小题35，共60分．每小题只有一个选项符合题意） 1．若2223340a b c +-=，则直线0ax by c ++=被圆221x y +=所截得的弦长为（ ） A ．23B ．1C ．12D ．342．四大名著是中国文学史上的经典作品，是世界宝贵的文化遗产.在某学校举行的“文学名著阅读月”活动中，甲、乙、丙、丁、戊五名同学相约去学校图书室借阅四大名著《红楼梦》、《三国演义》、《水浒传》、《西游记》（每种名著至少有5本），若每人只借阅一本名著，则不同的借阅方案种数为（ ） A ．54B ．45C ．·45CD ．45A3．已知函数()1n(3)x f x e x =-+,则下面对函数()f x 的描述正确的是（ ） A ．1(3,),()3x f x ∀∈-+∞≥B ．1(3,),()2x f x ∀∈-+∞>- C ．00(3,),()1x f x ∃∈-+∞=-D ．min ()(0,1)f x ∈4．已知a ＝253()5，b ＝352()5，c ＝252()5，则( )A ．a<b<cB ．c<b<aC ．c<a<bD ．b<c<a5．从5名男同学，3名女同学中任选4名参加体能测试，则选到的4名同学中既有男同学又有女同学的概率为( ) A ．2829B ．2729C ．1114D ．13146．设()f x 是定义在R 上的偶函数，且当0x ≥时，()21,0122,1xx x f x x ⎧-+≤<=⎨-≥⎩，若对任意的[],1x m m ∈+，不等式()()1f x f x m -≤+恒成立，则实数m 的最大值是（ ） A ．1- B ．13-C ．12-D ．137．设函数'()f x 是奇函数()f x （x ∈R ）的导函数，(1)0f -=，当0x >时，'()()0xf x f x -<，则使得()0f x >成立的x 的取值范围是（ ） A ．(,1)(0,1)-∞-U B ．(1,0)(1,)-?? C ．(,1)(1,0)-∞--UD ．(0,1)(1,)⋃+∞8．已知f(x)是定义在R 上的以3为周期的偶函数，若f(1)<1，f(5)＝231a a -+，则实数a 的取值范围为( ) A ．(－1,4)B ．(－2,0)C ．(－1,0)D ．(－1,2)9．已知函数()22x f x x e =-（e 为自然对数的底数），()()1,R g x mx m =+∈，若对于任意的[]11,1x ∈-，总存在[]01,1x ∈-，使得()()01g x f x = 成立，则实数m 的取值范围为（ ）A ．][()22,11,e e -∞-⋃-+∞ B ．221,1e e ⎡⎤--⎣⎦ C ．][()22,11,e e ---∞-⋃-+∞ D ．221,1e e --⎡⎤--⎣⎦10．函数()ln f x x x =的大致图象是（ ）A ．B ．C ．D ．11．已知函数()21xf x a =⋅-与函数()()321g x x ax a R =++∈，下列选项中不可能是函数()f x 与()g x 图象的是( )A ．B ．C ．D ．12．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是 A ．球B ．三棱锥C ．正方体D ．圆柱二、填空题（本题包括4个小题，每小题5分，共20分）13．求曲线3231y x x =-+在点()1,1-处的切线方程是________.14．已知关于x 的不等式13ax x -≤+的解集为{}2x x ≥-，则实数a =______.15．已知正项数列{a n }满足22116n n n n a a a a ++-=，若a 1＝2，则数列{a n }的前n 项和为________．16．对于任意的实数b ，总存在[]0,1x ∈，使得21x ax b ++≥成立，则实数a 的取值范围为_____.三、解答题（本题包括6个小题，共70分）17．命题:p 方程()2221mx m y +-=表示双曲线；命题:q 不等式()()21120m x m x -+-+>的解集是R . p q ∧为假， p q ∨为真，求m 的取值范围.18．已知定圆M ：22(1)16x y -+=，动圆N 过点F (1,0)-且与圆M 相切，记圆心N 的轨迹为E ． (1)求曲线E 的方程；(2)已知直线:l 1y x =-交圆M 于,A B 两点.,C D 是曲线E 上两点，若四边形ACBD 的对角线AB CD ⊥，求四边形ACBD 面积的最大值.19．（6分）在同一直角坐标系中，经过伸缩变换12x xy y ⎧'='=⎪⎨⎪⎩后，曲线C 的方程变为221x y ''+=.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线/的极坐标方程为33sinπρθ=（-）.（1）求曲线C 和直线l 的直角坐标方程；（2）过点(1,0)P 作l 的垂线l 0交C 于A ，B 两点，点A 在x 轴上方，求11||||PA PB -的值. 20．（6分）如图，直三棱柱111ABC A B C -中，AB AC =且AB AC ⊥，D ，E 分别为1AA ，1B C 的中点.（1）证明：DE ⊥平面1BCC ；（2）若直线1B C 与平面BCD 所成的角的大小为30°，求锐二面角A BD C --的正切值. 21．（6分）已知03x π=是函数()sin cos f x m x x ωω=-（0>ω）的一条对称轴，且()f x 的最小正周期为π.（1）求m 值和()f x 的单调递增区间；（2）设角,,A B C 为ABC ∆的三个内角，对应边分别为,,a b c ，若()2f B =， 3b =，求2ca -的取值范围.22．（8分）央视传媒为了解央视举办的“朗读者”节目的收视时间情况，随机抽取了某市名30观众进行调查，其中有12名男观众和18名女观众，将这30名观众收视时间编成如图所示的茎叶图（单位：分钟），收视时间在35分钟以上（包括35分钟）的称为“朗读爱好者”，收视时间在35分钟以下（不包括35分钟）的称为“非朗读爱好者”.（1）若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取5名，再从这5名观众中任选2名，求至少选到1名“朗读爱好者”的概率；（2）若从收视时间在40分钟以上（包括40分钟）的所有观众中选出男、女观众各1名，求选出的这两名观众时间相差5分钟以上的概率.参考答案一、单选题（本题包括12个小题，每小题35，共60分．每小题只有一个选项符合题意） 1．B 【解析】因为22243a b c +=，所以圆心(0,0)O 到直线0ax by c ++=的距离2232c d a b==+，所以2212212l r d =-=⨯=，应选答案B 。
2019-2020学年北京市西城区高二下学期期末数学试卷
2019-2020学年北京市西城区高二下学期期末数学试卷一、单选题（本大题共10小题，共40.0分） 1.设i 是虚数单位，则复数i1+i 在复平面内所对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.已知函数y =f(x)的图象如图，则f′(x A )与f′(x B )的大小关系是( )．A. f′(x A )>f′(x B )B. f′(x A )<f′(x B )C. f′(x A )=f′(x B )D. 不能确定3.盒中装有6个大小相同的小球，其中4个黄色的，2个红色的，从中任取3个，若至少有一个是红色的不同取法种数是m ，则二项式(m +x 2)6的展开式中x 8的系数为( )A. 3600B. 3840C. 5400D. 60004.若函数y =f(x)的图象在点P(1,f(1))处的切线方程为2x +y −1=0，那么f(1)+f′(1)=( )．A. 0B. −3C. 3D. −25.设随机变量x ～B(n,p)，若Ex =2.4，Dx =1.44则( )A. n =4，p =0.6B. n =6，p =0.4C. n =8，p =0.3D. n =24，p =0.16.随机变量ξ的分布列为P(ξ=k)=ck(1+k)，k =1，2，3，其中c 为常数，则P(ξ≥2)等于( )A. 89B. 23C. 13D. 297.设函数f(x)在R 上可导，且f(x −1)=x 2−2x ，则f′(3)=( )A. 0B. 4C. 6D. 88.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数，若函数y =f(x)−g(x)在[a,b]上有两个不同的零点，则称f(x)与g(x)在[a,b]上是“关联函数”，区间[a,b]称为f(x)与g(x)的“关联区间”.若f(x)=13x 3−x 2−x 与g(x)=2x +b 的“关联区间”是[−3,0]，则b 的取值范围是( )A. [−9,0]B. [0,53]C. [0,53)D. [−9,53)9.某届足球赛的计分规则是：胜一场得3分，平一场得1分，负一场得0分．某球队参赛15场，积33分．若不考虑比赛顺序，则该队胜、平、负的情形有( )种．A. 15B. 11C. 9D. 3x2+bln(x+2)在(−1,+∞)上单调递减，则b的取值范围是()10.f(x)=−12A. (−∞,−1)B. (−1,+∞)C. (−∞,−1]D. [−1,+∞)二、单空题（本大题共6小题，共30.0分）11.复数z=2+4i，则|z|=______ ．1+i)12的二项展开式中的常数项为m，则m=______ ．12.若(x+2x213.某科技小组有女同学2名、男同学x名，现从中选出3名去参加展览．若恰有1名女生入选时的不同选法有20种，则该科技小组中男生的人数为______ ．14.设随机变量ξ的分布列为：则m=______ ；随机变量ξ的数学期望Eξ=______ ．+sinx，则关于a的不等式f(a−2)+f(a2−4)<0的解集是______．15. 已知函数f(x)=ln1+x1−x16. 事件“对任意实数x与y，都有x2+y2≥2xy成立”的否定形式为______．三、解答题（本大题共6小题，共80.0分），其中k∈R．17. 已知函数f(x)=x+2k+1x(1)当k≥0时，证明f(x)在[√2k+1,+∞)上单调递增；(2)若对任意k∈[1,7]，不等式f(x)≥m在x∈[2,3]上恒成立，求实数m的取值范围；(3)若关于x的方程f(|2x−−1|)−3k−2=0有三个不同的实数解，求实数k的取值范围．18. 一部车床生产某种零件的不合格品率为2%，若从这部车床生产的一组5个零件的随机样本中发现有2个或2个以上的不合格品，则停机维修，试求停机维修的概率．ax+b．19. 已知函数f(x)=lnx，g(x)=12(1)若f(x)与g(x)在x=1处相切，试求g(x)的表达式；(2)若φ(x)=m(x−1)−f(x)在[1,+∞)上是减函数，求实数m的取值范围；x+1(3)证明不等式：2n n+1<1ln2+1ln3+1ln4+⋯+1ln(n+1)．20. 设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作．若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元．(Ⅰ)设X 表示一周5天内机器发生故障的天数，求X 的分布列； (Ⅱ)以Y 表示一周内所获利润，则一周内利润的期望是多少？21. 已知函数f(x)=ax ，g(x)=lnx ，其中a ∈R ． (Ⅰ)若函数F(x)=f(x)−g(x)有极值点1，求a 的值；(Ⅱ)若函数G(x)=f[sin(1−x)]+g(x)在区间(0,1)上为增函数，求a 的取值范围； (Ⅲ)证明：∑sin n k=11(k+1)2<ln2．．22. 已知函数f(x)=mx −alnx −m ，g(x)=xe x−1，其中m ，a 均为实数． (Ⅰ)求函数g(x)的极值；(Ⅱ)设m =1，a <0，若对任意的x 1、x 2∈[3,4](x 1≠x 2)，|f(x 2)−f(x 1)|<|1g(x 2)−1g(x 1)|恒成立，求实数a 的最小值．【答案与解析】1.答案：A解析：利用复数代数形式的乘除运算化简，求出复数i1+i在复平面内所对应的点的坐标得答案．本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础的计算题．解：由i1+i =i(1−i)(1+i)(1−i)=12+12i，可得复数i1+i 在复平面内所对应的点的坐标为(12,12)，位于第一象限．故选：A．2.答案：B解析：分别作出A、B两点的切线，由图可知k B>k A，即f′(x B)>f′(x A).3.答案：B解析：先求出至少有一个是红色的不同取法种数m的值，再二项展开式的通项公式求出r的值，即可求出答案．本题考查了排列与组合的应用问题，也考查了二项式定理的应用问题，是计算题目．解：∵至少有一个是红色的不同取法种数是m=C21×C42+C22×C41=2×6+1×4=16；∴二项式(m+x2)6=(16+x2)6展开式的通项是：T r+1=C6r⋅166−r⋅x2r，令2r=8，则r=4；∴C64×162=15×256=3840，即展开式中x8的系数为3840．故选：B．4.答案：B解析：本题主要考查导数的几何意义，根据条件求出切线斜率是解决本题的关键．根据导数的几何意义进行求解即可．解：∵函数y =f(x)的图象在点P(1,f(1))处的切线方程为2x +y −1=0， ∴切线方程为y =−2x +1，则切线斜率k =f′(1)=−2，且f(1)=−2+1=−1， 则f(1)+f′(1)=−1−2=−3， 故选：B ．5.答案：B解析：解：∵随机变量x ～B(n,p)，Ex =2.4，Dx =1.44，∴{np =2.4np(1−p)=1.44∴n =6，p =0.4 故选B ．根据x ～B(n,p)，Ex =2.4，Dx =1.44，建立方程组，即可求得n ，p 的值． 本题考查二项分布，考查学生的计算能力，属于基础题．6.答案：C解析：解：根据分布列中所有的概率和为1，得c1×2+c2×3+c3×4=1， 解得c =43∴P(ξ=k)=431k(1+k) ∴P(ξ≥2)=P(ξ=2)+P(ξ=3)=43(12×3+13×4)=13故选C ．先根据分布列中所有的概率和为1求出参数c ，再判断出满足条件的ξ≥2的值，代入分布列求出值． 解决随机变量的分布列问题，一定要注意分布列的特点，各个概率值在[0,1]之间；概率和为1；常与求随机变量的期望、方差一起出题，常出现在高考题中的解答题中．7.答案：C解析：解：∵f(x −1)=x 2−2x =(x −1)2−1， ∴f(x)=x 2−1， ∴f′(x)=2x ， ∴f′(3)=6， 故选：C ．先计算f(x)，再求导，再代入值计算即可． 本题考查导数的运算，求出f(x)是计算的关键．8.答案：C解析：解：∵f(x)=13x 3−x 2−x 与g(x)=2x +b ，∴设y =m(x)=f(x)−g(x)=13x 3−x 2−x −2x −b =13x 3−x 2−3x −b ， 则m′(x)=x 2−2x −3，由m′(x)=x 2−2x −3=0，解得m =−1或m =3， ∵f(x)与g(x)在[−3,0]上是“关联函数”，∴当x =−1是函数m(x)在[−3,0]上的极大值，同时也是最大值， 要使m(x)=f(x)−g(x)在[−3,0]上有两个不同的零点， 则{m(0)≤0m(−1)>0m(−3)≤0.即{−b ≤053−b >0−9−b ≤0，则{b ≥0b <53b ≥−9，解得0≤b <53，故b 的取值范围是[0,53)， 故选：C求出函数y =f(x)−g(x)的表达式，利用导数求出函数的极值和单调性，根据关联函数的定义建立不等式关系即可得到结论．本题考查函数“关联函数”的定义，导数的应用以及二次函数的性质，体现了转化的数学思想，综合性较强，设计的知识点较多．9.答案：D解析：解：设该球队的胜、平、负的场次分别为x 、y 、z ，则{x +y +z =153x +y =33. 解得x =11−y3，所以{x =11y =0z =4，{x =10y =3z =2，{x =9y =6z =0.共3种情形．故选：D ．本题设出该球队的胜、平、负的场次分别为x 、y 、z ，以积分作为等量关系列出方程，即可得出结论． 本题考查积分问题，考查学生的计算能力，设出不同的情况，然后根据题目所给的条件限制求出解是解题的关键．10.答案：C解析：本题考查了函数的单调性与导数之间的关系，是中档题．函数f(x)=−12x2+bln(x+2)的定义域为(−2,+∞)，f′(x)=−x2+2x−bx+2，令g(x)=x2+2x−b，则g(x)≥0在(−1,+∞)上恒成立，即b⩽x2+2x在(−1,+∞)上恒成立，求出y=x2+2x在(−1,+∞)上的取值范围即可．解：由x+2>0，得x>−2，所以函数f(x)=−12x2+bln(x+2)的定义域为(−2,+∞)，再由f(x)=−12x2+bln(x+2)，得：f′(x)=−x+bx+2=−x2+2x−bx+2，要使函数f(x)在(−1,+∞)内是单调减函数，则f′(x)在(−1,+∞)上恒小于等于0，因为x+2>0，令g(x)=x2+2x−b，则g(x)≥0在(−1,+∞)上恒成立，即b⩽x2+2x在(−1,+∞)上恒成立．又x2+2x=(x+1)2−1>−1，故b≤−1．故选C．11.答案：√10解析：解：复数z=2+4i1+i ，则|z|=|2+4i1+i|=|2+4i||1+i|=√20√2=√10．故答案为：√10；直接利用复数的模的求法运算法则求解即可．本题考查复数的基本运算，模的求法，考查计算能力．12.答案：7920解析：解：(x+2x2)12的展开式的通项公式为T r+1=C12r⋅x12−r⋅(2x2)r=2r⋅C12r⋅x12−3r，令12−3r=0，解得r=4；∴常数项m=24⋅C124=16×12×11×10×94×3×2×1=7920．故答案为：7920．根据二项式展开式的通项公式，求出展开式为常数时r的值，再计算常数项m即可．本题考查了二项式定理的应用问题，也考查了组合公式的应用问题，是基础题目．13.答案：5解析：本题考查排列、组合的应用，涉及组合数公式的计算，关键是列出关于x 的方程．由分步计数原理分析可得恰有1名女生入选时的不同选法为C x 2C 21，结合题意可得C x 2C 21=20，解可得x 的值，即可得答案．解：根据题意，从男女学生中选出3名去参加展览．若恰有1名女生入选时的不同选法有C x 2C 21种， 则有C x 2C 21=20，即C x2=10， 即x(x−1)2=10，解可得x =5或−4(舍去) 故答案为：5．14.答案：16 23解析：解：由离散型随机变量的分布列的性质可得：12+13+m =1， 解得m =16，则E(ξ)=0×12+1×13+2×16=23， 故答案为：16；23．根据分布列的性质即可求出m 的值，由此即可求出期望．本题考查了离散型随机变量的分布列的性质以及期望，考查了学生的运算能力，属于基础题．15.答案：(√3,2)解析：解：由1+x1−x >0，求得−1<x <1，故函数的定义域为(−1,1)．再根据函数满足f(−x)=ln(1−x1+x )+sin(−x)=−ln 1+x1−x −sinx =−f(x)，可得函数为奇函数， 故关于a 的不等式f(a −2)+f(a 2−4)<0，即f(a −2)<−f(a 2−4)=f(4−a 2)，再由函数1+x1−x 、sin x 在的定义域(−1,1)上单调递增，可得函数f(x)在其定义域上单调递增，可得 {−1<a −2<1−1<a 2−4<1a −2<4−a 2，解得√3<a <2， 故答案为(√3,2)． 分析：由1+x1−x >0，求得函数的定义域为(−1,1).再根据函数为奇函数，不等式即 f(a −2)<−f(a 2−4)=f(4−a 2).函数f(x)在其定义域上单调递增， 可得{−1<a −2<1−1<a 2−4<1a −2<4−a 2，从而求得不等式的解集．本题主要考查求函数的定义域、函数的单调性和奇偶性的应用，属于中档题．16.答案：存在实数x 与y ，x 2+y 2<2xy 成立解析：解：命题为全称命题，则命题的否定为：存在实数x 与y ，x 2+y 2<2xy 成立． 故答案为：存在实数x 与y ，x 2+y 2<2xy 成立． 根据含有量词的命题的否定即可得到结论． 本题主要考查含有量词的命题的否定，比较基础．17.答案：(1)证明：由f(x)=x +2k+1x，得f′(x)=1−2k+1x 2=x 2−(2k+1)x 2，当k ≥0时，若x ∈[√2k +1,+∞)，则x 2−(2k +1)≥0， ∴f(x)在[√2k +1,+∞)上单调递增； (2)解：由k ∈[1,7]，得2k +1∈[3,15]， 函数f(x)=x +2k+1x在(0,√2k +1]上为减函数，在[√2k +1,+∞)上为增函数，当√2k +1<2，即2k +1∈[3,4)时，f(x)min =f(2)=k +52≥72； 当√2k +1>3，即2k +1∈(9,15]时，f(x)min =f(3)=103+2k 3>6；当2≤√2k +1≤3，即2k +1∈[4,9]时，f(x)min =f(√2k +1)=2√2k +1≥4． ∴对任意k ∈[1,7]，不等式f(x)≥m 在x ∈[2,3]上恒成立，则实数m 的取值范围是m ≤72； (3)设2x −1=t ，则t >−1，且t ≠0， 方程f(|2x −1|)−3k −2=0，即|t|+2k+1|t|=3k +2，当t >0时，方程可化为：t 2−(3k +2)t +(2k +1)=0，由题意得{(3k +2)2−4(2k +1)>03k +2>02k +1>0，解得：−12<k −49或k >0 ①，当−1<t <0时，方程可化为：t 2+(3k +2)t +(2k +1)=0， 设f(t)=t 2+(3k +2)t +(2k +1)， 只需对称轴x =−3k+22<−1，f(−1)<0，f(0)>0即可，∴{−3k+22<−11−(3k+2)+(2k+1)<02k+1>0，解得：k>0②，①，②取交集得：k>0，∴实数k的取值范围是(0,+∞)．解析：(1)求出原函数的导函数，利用导函数在[√2k+1,+∞)上大于0说明f(x)在[√2k+1,+∞)上单调递增；(2)对k分类求出函数在x∈[2,3]上的最小值得答案；(3)设2x−1=t，将问题转化为求方程t2−(3k+2)t+(2k+1)=0在(0,+∞)有2个交点，方程t2+ (3k+2)t+(2k+1)=0在(−1,0)有1个交点求解．本题考查函数单调性的性质，考查了函数的最值及其几何意义，训练了根的存在性及根的个数的判定方法，体现了分类讨论的数学思想方法，是中档题．18.答案：解：一部车床生产某种零件的不合格品率为2%，从这部车床生产的一组5个零件的随机样本中发现有2个或2个以上的不合格品，则停机维修，停机维修的概率为：P=1−C50×0.985−C51⋅0.984⋅0.02=0.0038144．解析：利用对立事件概率计算公式和n次独立重复试验中事件A恰好发生k次的概率计算公式直接求解．本题考查概率的求法，考查对立事件概率计算公式和n次独立重复试验中事件A恰好发生k次的概率计算公式等基础知识，考查运算求解能力，是基础题．19.答案：解：(1)∵f(x)=lnx，∴f′(x)=1x ，∴f′(1)=1=12a，得：a=2．又∵g(1)=0=12a+b，∴b=−1，∴g(x)=x−1；(2)φ(x)=m(x−1)x+1−f(x)=m(x−1)x+1−lnx在[1,+∞)上是减函数，∴ϕ′(x)=−x2+(2m−2)x−1x(x+1)2≤0在[1,+∞)上恒成立．即x2−(2m−2)x+1≥0在[1,+∞)上恒成立，由2m−2≤x+1x，x∈[1,+∞)，∵x+1x∈[2,+∞),∴2m−2≤2得m≤2；证明：(3)由(1)可得：当x≥2时：lnx<x−1≤x2(x−1)，∴lnx<12x(x−1)得：2x(x−1)<1lnx，∴2(1x−1−1x)<1lnx．当x=2时：2(11−12)<1ln2，当x=3时：2(12−13)<1ln3，当x=4时：2(13−14)<1ln4，…当x=n+1时：2(1n−1n+1)<1ln(n+1)，n∈N+，n≥2，上述不等式相加得：2(1−1n+1)<1ln2+1ln3+1ln4+⋯+1ln(n+1)，即：2nn+1<1ln2+1ln3+1ln4+⋯+1ln(n+1)．解析：(1)求导数，利用f(x)与g(x)在x=1处相切，可求g(x)的表达式；(2)φ(x)=m(x−1)x+1−f(x)在[1,+∞)上是减函数，可得导函数小于等于0，在[1,+∞)上恒成立，分离参数，利用基本不等式，可求实数m的取值范围；(3)当x≥2时，证明2(1x−1−1x)<1lnx，当x=2时，当x=3时，当x=4时，…，当x=n+1时，利用叠加法，即可得到结论．本题考查利用导数研究曲线上某点的切线方程，考查利用导数研究函数的单调性，考查基本不等式的运用，考查叠加法，考查学生分析解决问题的能力，是中档题．20.答案：解：(Ⅰ)以X表示一周5天内机器发生故障的天数，则X−B(5,0.2)，P(X=k)=C5k0．2k0．85−k，k=0，1，2，3，4，5，∴X的分布列为：(Ⅱ)以Y表示一周内所获利润，则y=g(X)={10,X=0 5,X=1 0,X=2−2,X≥3，P(Y=10)=P(X=0)=0.32768，P(Y =5)=P(X =1)=0.4096， P(Y =0)=P(X =2)=0.2048，P(Y =−2)=P(X ≥3)=0.0512+0.0064+0.00032=0.05792， ∴一周内利润的期望为：EY =10×0.32768+5×0.4096+(−2)×0.05792=5.20896(万元)．解析：(Ⅰ)以X 表示一周5天内机器发生故障的天数，则X −B(5,0.2)，由此能求出X 的分布列． (Ⅱ)以Y 表示一周内所获利润，则y =g(X)={10,X =05,X =10,X =2−2,X ≥3，一周内利润的期望值．本题考查离散型随机变量的分布列和数学期望的求法，是中档题，在历年高考中都是必考题型．21.答案：解：(Ⅰ)∵函数f(x)=ax ，g(x)=lnx ，其中a ∈R ．∴F(x)=ax −lnx ，则F′(x)=a −1x ， ∵函数F(x)=f(x)−g(x)有极值点1， ∴F′(1)=0，∴a −1=0，解得a =1；(Ⅱ)∵函数G(x)=f[sin(1−x)]+g(x)=asin(1−x)+lnx ， ∴G′(x)=acos(1−x)×(−1)+1x ，只要G′(x)在区间(0,1)上大于等于0， ∴G′(x)=acos(1−x)×(−1)+1x ≥0， ∴a ≤1xcos(1−x)，求1xcos(1−x)的最小值即可，求ℎ(x)=xcos(1−x)的最大值即可，0<1−x <1， ∵ℎ′(x)=cos(1−x)+xsin(1−x)>0， ∴ℎ(x)在(0,1)增函数， ℎ(x)<ℎ(1)=1， ∴1xcos(1−x)的最小值为1， ∴a ≤1；(Ⅲ)∵0<1(k+1)2<1，∵sinx <x 在x ∈(0,1)上恒成立，∴∑sin n k=11(k+1)2=sin 122+sin132+⋯+sin1(n+1)2≤122+132+⋯+1(n+1)2<14+19+116+14×5+15×6+⋯+1n(n+1)=97144−1n+1<97144<ln2，∴∑sin n k=11(k+1)2<ln2；解析：(Ⅰ)根据已知条件函数F(x)=f(x)−g(x)有极值点1，可得F′(1)=0，得出等式，求出a 值； (Ⅱ)因为函数G(x)=f[sin(1−x)]+g(x)在区间(0,1)上为增函数，可以对其进行转化，可以转化为G′(x)>0在(0,1)上恒成立，利用常数分离法进行求解；(Ⅲ)这个证明题可以利用一个恒等式，sinx <x ，然后对∑sin n k=11(k+1)2从第三项开始进行放缩，然后进行证明；第一问利用导数可以很容易解决，第二问利用了常数分离法进行证明，第三问需要进行放缩证明，主要利用sinx <x 进行证明，此题难度比较大，计算量比较大；22.答案：解：(Ⅰ)g′(x)=1−xe x−1，令g′(x)=0，得x =1，列表如下：∴当x =1时，g(x)取得极大值g(1)=1，无极小值；(Ⅱ)当m =1时，a <0时，f(x)=x −alnx −1，x ∈(0,+∞)， ∵f′(x)=x−a x >0在[3,4]恒成立，∴f(x)在[3,4]上为增函数，设ℎ(x)=1g(x)=e x−1x，∵ℎ′(x)=e x−1(x−1)x 2>0在[3,4]上恒成立，∴ℎ(x)在[3,4]上为增函数，不妨设x 2>x 1，则|f(x 2)−f(x 1)|<|1g(x 2)−1g(x 1)|等价于：f(x 2)−f(x 1)<ℎ(x 2)−ℎ(x 1)，即f(x 2)−ℎ(x 2)<f(x 1)−ℎ(x 1)，设u(x)=f(x)−ℎ(x)=x −alnx −1−e x−1x，则u(x)在[3,4]上为减函数，∴u′(x)=1−ax −e x−1(x−1)x 2≤0在[3,4]上恒成立，∴a ≥x −ex−1+e x−1x恒成立，∴a ≥(x −e x−1+e x−1x)max ，x ∈[3,4]，设v(x)=x −e x−1+e x−1x，∵v′(x)=1−e x−1+e x−1(x−1)x 2=1−e x−1[(1x −12)2+34]，x ∈[3,4]，∴e x−1[(1x −12)2+34]>34e2>1，∴v′(x)<0，v(x)为减函数，∴v(x)在[3,4]上的最大值v(3)=3−23e2，∴a≥3−23e2，∴a的最小值为3−23e2；解析：(Ⅰ)对函数g(x)求导，得到g′(x)=0，得到极值点，求出极值．(Ⅱ)不妨设x2>x1，则|f(x2)−f(x1)|<|1g(x2)−1g(x1)|等价于：f(x2)−f(x1)<ℎ(x2)−ℎ(x1)，即f(x2)−ℎ(x2)<f(x1)−ℎ(x1)，分离参数，利用导数求最值求出参数范围即可．本题主要考查了利用导数求函数极值和利用导数求参数范围，属于中档题型，在高考中经常涉及．。
北京市西城区2019-2020学年数学高二下期末考试试题含解析
北京市西城区2019-2020学年数学高二下期末考试试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知复数z 满足()12z i i +=,则复数z 在复平面内对应点所在的象限是( ) A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】A 【解析】 【分析】把已知变形等式，再由复数代数形式的乘除运算化简得答案. 【详解】 由()12z i i +=，得()122=1255i i ii z i -+==+， ∴复数z 在复平面内对应的点的坐标为2155⎛⎫⎪⎝⎭，，在第一象限． 故选：A ． 【点睛】本题考查复数的代数表示法及其几何意义，属于基础题.2．已知12,F F 是椭圆和双曲线的公共焦点，P 是它们的一个公共点，且124F PF π∠=，则椭圆和双曲线的离心率乘积的最小值为（ ） A ．12B．2C ．1 D【答案】B 【解析】设椭圆的长半轴长为1a ，双曲线的实半轴常为2a 1211222{2PF PF a PF PF a +=⇒-= 1PF ⇒=12,a a +212PF a a =-222121212124()()2()()cos4c a a a a a a a a π⇒=++--+-⇒2221111124(2(24c a a =+-⇒=≥=⇒122e e ≥,故选B. 3．用反证法证明命题：“三角形的内角中至少有一个不大于60°”时，反设正确．．的是( )A．假设三内角都不大于60°B．假设三内角都大于60°C．假设三内角至多有一个大于60°D．假设三内角至多有两个大于60°【答案】B【解析】【分析】“至少有一个”的否定变换为“一个都没有”，即可求出结论.【详解】“三角形的内角中至少有一个不大于60°”时，反设是假设三内角都大于60 .故选：B.【点睛】本题考查反证法的概念，注意逻辑用语的否定，属于基础题.4．已知，则函数的单调递减区间为( )．A．B．C．D．【答案】B【解析】【分析】求出函数的定义域，并对该函数求导，解不等式，将解集与定义域取交集得出函数的单调递减区间。
北京市西城区2019-2020学年高二下学期数学期末考试试题 Word版含解析
北京市西城区2019—2020学年度第二学期期未试卷高二数学一､选择题1. 在复平面内，复数1i +的共轭复数所对应的点位于（ ） A. 第一象限 B. 第二象限C. 第三象限D. 第四象限 【答案】D 【解析】 【分析】求出复数的共轭复数，即可得出对应点所在象限. 【详解】复数1i +的共轭复数为1i -，∴其对应的点()1,1-位于第四象限.故选：D.【点睛】本题考查复数的几何意义，属于基础题.2. 函数y =1x =处的瞬时变化率为（ ）A. 2B.12C. 12-D. 1【答案】B 【解析】 【分析】函数在某点处的瞬时变化率即为函数在改点的导数值，求导得解 【详解】,y x y '=∴=112x y =∴='所以函数y =1x =处的瞬时变化率为12故选：B【点睛】本题考查函数在某点处的导数值，属于基础题. 3. 4(1)x +的展开式中2x 的系数是（ ） A. 8B. 7C. 6D. 4【答案】C 【解析】 【分析】根据二项式定理展开式的通项公式，令2r 即可得出答案．【详解】4(1)x +的展开式中，14,(0,1,2,3,4)r r r r T x +==，令2r，2x ∴的系数为246C =．故选：C ．【点睛】本题考查二项式定理的应用，考查推理能力与计算能力，属于基础题． 4. 曲线2y x=在点()1,2Q 处的切线方程为（ ） A. 240x y +-= B. 240x y ++= C. 10x y -+= D. 10x y +-=【答案】A 【解析】 【分析】求出函数在1x =处的导数值，即切线斜率，即可求出切线方程. 【详解】2y x =，22y x'∴=-， 当1x =时，2y '=-，故切线斜率为2-，∴切线方程为()221y x -=--，即240x y +-=.故选：A.【点睛】本题考查利用导数求切线方程，属于基础题.5. 某批数量很大的产品的次品率为p ，从中任意取出4件，则其中恰好含有3件次品的概率是（ ） A. 3p B. 3(1)p p -C. 334(1)C p p -D. 334C p【答案】C 【解析】 【分析】根据独立重复试验的概率计算公式，由题中条件，可直接得出结果. 【详解】由题意，从这批产品中任取4件，所得次品数记作X ， 则X 服从二项分布，即()4,XB p ，所以从中任意取出4件，则其中恰好含有3件次品的概率是()3343(1)P X C p p ==-. 故选：C.【点睛】本题主要考查求独立重复试验对应的概率，属于基础题型.6. 已知某一随机变量ξ的概率分布列如图所示，且E(ξ)＝6.3，则a 的值为( )A. 5B. 6C. 7D. 8【答案】C 【解析】分析：先根据分布列概率和为1得到b 的值，再根据E(X)=6.3得到a 的值. 详解：根据分布列的性质得0.5+0.1+b=1,所以b=0.4.因为E(X)=6.3，所以4×0.5+0.1×a+9×0.4=6.3， 所以a=7. 故答案为C.点睛：（1）本题主要考查分布列的性质和随机变量的期望的计算，意在考查学生对这些知识的掌握水平.(2) 分布列的两个性质：①0i P ≥，1,2,3,,,i n =；②121n P P P ++++=.7. 已知函数()cos sin f x x x x =-，则2f π⎛⎫'⎪⎝⎭的值为（ ） A.2π B. 2π-C. 1-D. π-【答案】B 【解析】 【分析】根据基本初等函数的导数公式及导数的运算法求出函数的导数，再代入计算即可； 【详解】因为()cos sin f x x x x =-所以()()cos cos cos cos sin cos sin f x x x x x x x x x x x x '''=+-=--=- 所以sin 2222f ππππ⎛⎫'=-=-⎪⎝⎭故选：B【点睛】本题考查基本初等函数的导数计算，属于基础题.8. 已知函数()f x 和()g x 的导函数()f x '､()g x '图象分别如图所示，则关于函数()()=-y g x f x 的判断正确的是（ ）A. 有3个极大值点B. 有3个极小值点C. 有1个极大值点和2个极小值点D. 有2个极大值点和1个极小值点【答案】D 【解析】 【分析】根据题中图像可知，()f x '､()g x '的图像有三个不同交点，其交点横坐标按从小到大的顺序，依次记为1x ､2x ，3x ，其中20x =；结合题中函数图像，判定函数()()=-y g x f x 的单调性，进而可得极值点.【详解】由题中图像可知，()f x '､()g x '的图像有三个不同交点，其交点横坐标按从小到大的顺序，依次记为1x ､2x ，3x ，其中20x =，由图像可得，当1x x <时，()()x g x f '>'，即()()0y g x f x '''=->，则函数()()=-y g x f x 单调递增；当10x x <<时，()()x g x f '<'，即()()0y g x f x '''=-<，则函数()()=-y g x f x 单调递减；当30x x <<时，()()x g x f '>'，即()()0y g x f x '''=->，则函数()()=-y g x f x 单调递增；当3x x >时，()()x g x f '<'，即()()0y g x f x '''=-<，则函数()()=-y g x f x 单调递减； 所以()()=-y g x f x 有两个极大值点1x 和3x ；有一个极小值点0. 故选：D.【点睛】本题主要考查导函数图像与原函数之间的关系，考查极值点个数的判定，属于基础题型.9. 万历十二年，中国明代音乐理论家和数学家朱载堉在其著作《律学新说》中，首次用珠算开方的办法计算出了十二个半音音阶的半音比例，这十二个半音音阶称为十二平均律十二平均律包括六个阳律（黄钟、太簇、姑洗、蕤宾、夷则、无射）和六个阴律（大吕、夹钟、中吕、林钟、南吕、应钟）.现从这十二平均律中取出2个阳律和2个阴律，排成一个序列，组成一种旋律，要求序列中的两个阳律相邻，两个阴律不相邻，则可组成不同的旋律（ ） A. 450种 B. 900种 C. 1350种 D. 1800种【答案】B 【解析】 【分析】分为两步，第一步，取出2个阳律和2个阴律，第二步，两个阳律相邻，两个阴律不相邻，利用分步计数原理可得.【详解】第一步，取出2个阳律和2个阴律，有2266225C C =种，第二步，两个阳律相邻，两个阴律不相邻，有22224A A =种，根据分步计数原理可得，共有2254900⨯=种. 故选：B.【点睛】本题考查排列组合与计数原理的问题，属于基础题.10. 设函数()f x 定义域为D ，若函数()f x 满足：对任意c D ∈，存在,a b D ∈，使得()()()f a f b f c a b-'=-成立，则称函数()f x 满足性质Γ.下列函数不满足性质Γ的是（ ） A. 2()f x x = B. 3()f x x = C. ()xf x e =D.()ln f x x =【答案】B 【解析】 【分析】构造函数()()()g x f x f c x '=-，可得()()g x f x ''''=，则()f x ''在定义域内正负号不变时满足性质Γ，若()f x ''有唯一变号零点0x 时不满足性质Γ，则通过计算()f x ''即可判断. 【详解】()()()f a f b f c a b-'=-可化为()()()()f a f c a f b f c b ''-=-，令()()()g x f x f c x '=-，则()()()g x f x f c '''=-，()()g x f x ''''=，∴若()f x ''在定义域内正负号不变，那么x c =是()g x '的变号零点，则()g x 在x c =的两侧的单调性不一致，因此满足性质Γ；若()f x ''有唯一变号零点0x ，那么取0c x =，则()g x '在定义域内的正负号不变，进而函数()g x 在定义域内单调，因此不满足性质Γ.对于A ，()2f x x '=，则()20f x ''=>，所以满足性质Γ；对于B ，()23f x x '=，则()6f x x ''=有唯一变号零点0，所以不满足性质Γ；对于C ，()x f x e '=，则()0xf x e ''=>，所以满足性质Γ； 对于D ，()1f x x '=，则()210f x x''=-<，所以满足性质Γ. 故选：B.【点睛】本题考查利用导数解决新定义问题，属于较难题.二､填空题11. 若复数41z i=-，则||z =___________.【答案】【解析】 【分析】先利用复数除法运算求出z ，再求出模即可. 【详解】()()()4142+2111i z i i i i +===--+，||z ∴==故答案为：【点睛】本题考查复数的除法运算和模的求解，属于基础题.12. 在5232x x ⎛⎫+ ⎪⎝⎭的展开式中，常数项为___________.(用数字作答)【答案】40 【解析】 【分析】先求出展开式的通项105152r r rr T C x-+=，令1050r -=即得解. 【详解】设展开式的通项为2510515532()()2r rr r r r r T C x C x x--+==， 令1050,2r r -=∴=，所以常数项为225240C =.故答案为：40【点睛】本题主要考查二项式定理的应用，意在考查学生对这些知识的理解掌握水平. 13. 从3名男医生和5名女医生中，选派3人组成医疗小分队，要求男､女医生都有，则不同的选取方法种数为__________(用数字作答). 【答案】45 【解析】 【分析】根据题意分为两类：2男1女和1男2女，结合分类计数原理和组合数的计算公式，即可求解.【详解】由题意，从3名男医生和5名女医生中，选派3人组成医疗小分队，要求男､女医生都有，可分为两类：第一类，若2男1女，共有213515C C =种不同的选取方法； 第二类，若1男2女，共有123530C C =种不同的选取方法，由分类计数原理，可得不同的选取方法种数为153045+=种. 故答案为：45.【点睛】本题主要考查了分类计数原理的应用，以及组合数的计算，其中解答中根据题设条件，合理分类，结合分类计数原理求解是解答的关键，着重考查分析问题和解答问题的能力. 14. 中国福利彩票3D 游戏(以下简称3D )，是以一个3位自然数(如：0记作000)为投注号码的彩票.投注者从000~999这些3位自然数中选择一个进行投注，每注2元，如果与官方公布的三位数相同，则视为中奖，获得奖金1000元，反之则获得奖金0元.某人随机投了一注，他的奖金的期望是______元. 【答案】1 【解析】 【分析】求出此人中奖和不中奖的概率，利用期望的公式，即可求得数学期望，得到答案.【详解】由题意，此人中奖的概率为11000，不中奖的概率为9991000，所以此人随机投注一次，他的奖金的期望为：199910000110001000⨯+⨯=元. 故答案为：1.【点睛】本题主要考查了离散型随机变量的数学期望的求法，其中解答中正确理解题意，求得此人中奖和不中奖的概率，结合期望的计算公式求解是解答的关键，属于基础题. 15. 能说明“若()f x '为偶函数，则()f x 为奇函数”为假命题的一个函数是__________.【答案】3()1f x x =+(答案不唯一)【解析】 【分析】根据题中条件，只需任意写出满足题意的函数即可.【详解】若3()1f x x =+，则()23f x x '=是偶函数，但3()1()f x x f x -=-+≠-，所以()f x 不是奇函数；能满足“若()f x '为偶函数，则()f x为奇函数”为假命题.故答案为：3()1f x x =+.【点睛】本题主要考查命题真假的判定，涉及导数的计算，以及函数奇偶性的判定，属于基础题型.16. 辛普森悖论(Simpson’sParadox)有人译为辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”.辛普森悖论为英国统计学家E .H .辛普森(E.H.Simpson)于1951年提出的，辛普森悖论的内容大意是“在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论：关于某高校法学院和商学院新学期已完成的招生情况，现有如下数据： 某高校申请人数性别 录取率 法学院200人男50%女 70% 商学院300人男60% 女90% 对于此次招生，给出下列四个结论： ①法学院的录取率小于商学院的录取率； ②这两个学院所有男生的录取率小于这两个学院所有女生的录取率；③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率； ④法学院的录取率不一定小于这两个学院所有学生的录取率. 其中，所有正确结论的序号是___________. 【答案】②④ 【解析】 【分析】根据题意，结合古典概型的概率计算公式，逐项进行判定，即可求解. 【详解】设申请法学院的男生人数为x ，女生人数为y ，则200x y +=， 法学院的录取率为0.50.70.50.7(200)0.70.001200200x y x x x ++⨯-==-，设申请商学院的男生人数为m ，女生人数为n ，则300m n +=， 商学院的录取率为0.60.90.60.9(300)0.90.001200200m n m m m ++⨯-==-，由()()0.90.0010.70.0010.20.001()0.001(200)m x m x m x ---=--=-+， 该值的正负不确定，所以①错误，④正确； 这两个学院所有男生的录取率为0.50.6x mx m++，这两个学院所有女生的录取率为0.70.9y ny n++，因为0.50.60.70.90.20.40.10.30()()x m y n xy xn my nmx m y n x m y n +++++-=<++++，所以②正确；③错误. 故答案为：②④.【点睛】本题主要考查了古典概型的概率公式的应用，其中解答中正确理解题意，结合古典概型的概率计算公式求得相应的概率是解答的关键，着重考查数学阅读能力，属于基础题.三､解答题17. 已知函数3()3f x x x =-. （1）求函数()f x 的单调区间；（2）求函数()f x 在区间[]1,3-上的最大值和最小值.【答案】（1）函数()f x 的单调递增区间为(,1)-∞-和(1,)+∞，单调递减区间为()1,1-；（2）最大值为18，最小值为2-. 【解析】 【分析】（1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可； （2）根据函数的单调性求出函数的极值点，从而求出函数的最值即可． 【详解】（1）因为3()3f x x x =-，所以2()33f x x '=-. 令()0f x '=，解得11x =-，21x =.随着x 的变化，()f x '，()f x 变化情况如下表：所以，函数()f x 的单调递增区间为(,1)-∞-和(1,)+∞，单调递减区间为()1,1-. （2）因为函数()f x 在区间[]1,1-上单调递减，在区间[]1,3上单调递增， 又(1)2f -=，(1)2f =-，(3)18f =，所以，函数()f x 在区间[]1,3-上的最大值为18，最小值为2-.【点睛】本题考查了函数的单调性，极值，最值问题，考查导数的应用，属于基础题 18. 某射手打靶命中8环､9环､10环的概率分别为0.15.0.25.0.2.如果他连续打靶三次，且每次打靶的命中结果互不影响. （1）求该射手命中29环的概率； （2）求该射手命中不少于28环的概率. 【答案】（1）0.03；（2）0.0935. 【解析】 【分析】（1）根据题中条件，由独立事件的概率计算公式，即可得出结果；（2）根据题中条件，分别计算出命中30环，命中28环，命中29环对应的概率，再求和，即可得出结果.【详解】（1）设A =“连续射击3次，中29环”.则223()0.25(0.2)P A C =⋅⋅0.03=所以该射手命中29环的概率为0.03.（2）设B =“连续射击3次，命中不少于28环”， 依题意，命中30环的概率为3(0.2)0.008=；命中28环的概率为2222330.15(0.2)(0.25)0.2C C ⋅⋅+⋅⋅0.0180.03750.0555=+=；由（1）知，命中29环的概率为0.03；所以()0.0080.05550.030.0935P B =++=，所以该射手连续射击3次，命中不少于28环的概率为0.0935.【点睛】本题主要考查独立事件的概率，考查求互斥事件发生的概率，属于常考题型. 19. 已知函数()ln (0)f x x a x a =-≠.（1）当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； （2）求函数()f x 的极值点和极值. 【答案】（1）1y =；（2）答案见解析. 【解析】 【分析】（1）当1a =时，求得11()1x f x x x'-=-=，得到()01f '=，()11f =，即可求得曲线()y f x =在点(1,(1))f 处的切线方程；（2）求得0(,())1,a x x x af x x-∈'-=+∞=，分0a <和0a >两种情况讨论，分别求得函数的单调性，进而求得函数的极值，得到答案.【详解】（1）当1a =时，函数()ln f x x x =-，可得11()1x f x x x'-=-=，则()01f '=， 又因为()11f =，所以曲线()y f x =在点(1,(1))f 处的切线方程为1y =. （2）由函数()ln f x x a x =-，可得0(,())1,a x x x af x x-∈'-=+∞=， ①当0a <时，()0f x '>，函数()f x 在(0,)+∞上单调递增，不存在极值；②当0a >时，令()0f x '=，解得x a =.随着x 的变化，()f x '，()f x 变化情况如下表：x()0,aa(),a +∞()f x '-+所以函数()f x 在区间()0,a 上单调递减，在区间(,)a +∞上单调递增，所以，函数()f x 的极小值点为x a =，极小值为()ln f a a a a =-，无极大值， 综上可得，当0a <时，函数()f x 没有极值；当0a >时，()f x 有极小值ln a a a -，极小值点为x a =，无极大值.【点睛】本题主要考查了利用导数的几何意义求曲线在某点处的切线方程，以及利用导数研究函数的单调性与极值，其中解答中熟记导数与原函数的关系，正确运算是解答的关键，着重考查推理与运算能力.20. 高中必修课程结束之后，学生需要从物理､化学､生物､历史､地理､政治六科中选择三科，继续学习选择性必修课程.某地记者为了了解本地区高一学生的选择意向，随机采访了100名学生作为样本进行情况调研，得到下表：（1）从样本中随机选1名学生，求该学生选择了化学的概率；（2）从第8组､第9组､第10组中，随机选2名学生，记其中选择政治的人数为X ，求X 的分布列和期望；（3）如果这个地区一名高一学生选择了地理，则在其它五科中，他同时选择哪一科的可能性最大？并说明理由. 【答案】（1）12；（2）分布列答案见解析，数学期望：1211；（3）选择历史的可能性最大，理由见解析. 【解析】 【分析】（1）先找出选择了化学的学生数，再利用古典概型求解即可；（2）X 的所有可能取值为0，1，2，再利用超几何分布求概率的方式逐一求出每个X 的取值所对应的概率即可得分布列，进而求得数学期望；（3）由表可知，选择地理的总人数为79，然后依次求出同时选择生物、化学、政治、物理或历史的概率，取最大者即可．【详解】解：（1）设A =“从样本中随机选1人，该学生选择了化学”， 则17121074501()1001002P A ++++===，所以，从样本中随机选1人，该学生选择了化学的概率为12. （2）第8､9､10组共有11人，其中选择政治的有6人. 所以X 的所有可能取值为0，1，2.252112(0)11C P X C ===，11562116(1)11C C P X C ===，262113(2)11C P X C ===.所以X 的分布列为故X 的期望()01211111111E X =⨯+⨯+⨯=. （2）选择地理的总人数为：20141210975279+++++++=.所以P (“同时选择生物”)141292377979+++==；P (“同时选择化学”)12107297979++==；P (“同时选择政治”)202227979+==；P (“同时选择物理”)1095247979++==； P (“同时选择历史”)201475467979+++==.因为4679最大，所以一个学生选择了地理，同时选择历史的可能性最大.【点睛】本题考查古典概型、离散型随机变量的分布列和数学期望，考查学生对数据的分析与处理能力，属于中档题． 21. 已知函数2()12xa f x e x x =---. （1）若0a =，证明：()0f x ≥；（2）若曲线()y f x =的切线斜率不存在最小值，求a 的取值范围. 【答案】（1）证明见解析；（2）{}0a a ≤. 【解析】 【分析】（1）当0a =时，求得()1x f x e =-'，根据()'f x 的符号，求得函数的单调性与最小值，即可求解；（2）求得函数导数()1xf x e ax '=--，设()1xg x e ax =--，把曲线()y f x =的切线斜率不存在最小值，即函数()g x 不存在最小值，利用导数，分类讨论求得函数()g x 单调性与最值，即可求解.【详解】（1）当0a =时，函数()1xf x e x =--，可得()1xf x e =-'， 令()0f x '>，即10x e ->，解得0x >；令()0f x '<，即10x e -<，解得0x <，所以()f x 在区间(,0)-∞上单调递减，在区间(0,)+∞上单调递增， 所以()f x 的最小值为()00f =，所以()0f x ≥.（2）由函数2()12xa f x e x x =---，可得()1x f x e ax '=--， 设()1xg x e ax =--，可得()xg x e a '=-由曲线()y f x =的切线斜率不存在最小值，即函数()g x 不存在最小值，①当0a ≤时，()0g x '>恒成立，所以()g x 在区间(,)-∞+∞上单调递增，不存在最小值， 所以0a ≤符合题意. ②当0a >时，令()0g x '>，即0x e a ->，解得ln x a >； 令()0g x '<，即0-<x e a ，解得ln x a <，所以()g x 在区间(,ln )a -∞上单调递减，在区间(ln ,)a +∞上单调递增， 所以()g x 在ln x a =处取得最小值，最小值()ln ln ln 11ln a g a e a a a a a =--=--,所以0a >不符合题意（舍去）.综上可得，实数a 的取值范围为{}0a a ≤.【点睛】本题主要考查导数在函数中的综合应用，其中解答中熟练应用导数求得函数的单调性与极值（最值），以及把曲线()y f x =的切线斜率不存在最小值，转化为函数()g x 不存在最小值是解答的关键，着重考查转化思想，以及推理与运算能力. 22. 已知函数()ln f x x ax a =+-. （1）求函数()f x 的单调区间；（2）求证：当1a >时，函数1()()x g x e f x -=-存在最小值，且最小值小于1.【答案】（1）答案见解析；（2）证明见解析. 【解析】 【分析】（1）求出()f x 的导数，讨论0a ≥和0a <时导数情况，即可求出单调区间；（2）由题可得所以只需证明()g x 存在最小值，但1x =不是最小值点，求出()g x 的导数，讨论其单调性，即可进行判断.【详解】解：（1）函数()f x 定义域为()0,∞+，11()ax f x a x x'+=+=. ①当0a ≥时，()0f x '>恒成立，函数()f x 的单调递增区间为(0,)+∞. ②当0a <时，由()0f x '>，得10x a<<-；由()0f x '<，得1x a >-.所以()f x 的单调递增区间为10,a ⎛⎫-⎪⎝⎭，单调递减区间为1,a ⎛⎫-+∞ ⎪⎝⎭.综上，当0a ≥时，()f x 单调递增区间为(0,)+∞； 当0a <时，()f x 的单调递增区间为10,a ⎛⎫-⎪⎝⎭，单调递减区间为1,a ⎛⎫-+∞ ⎪⎝⎭.（2）由已知1()ln x g x e x ax a -=--+，0x >.因为()11g =，所以只需证明()g x 存在最小值，但1x =不是最小值点， 即min ()(1)1g x g <=.因为()ln x e g x x ax a e=--+，所以11()x g x e a x -'=--.因为函数1x y e-=，1y x=-在区间(0,)+∞上是增函数， 所以()g x '在区间(0,)+∞上是增函数， 因为1a >，所以(1)0g a '=-<，11(1ln(1))1101ln(1)1ln(1)g a a a a a '++=+--=->++++.所以方程()0g x '=在区间(0,)+∞上存在唯一解， 不妨设为0x ，则01x >，随着x 的变化，()g x '，()g x 变化情况如下表：所以()g x 有最小值，最小值为()()011g x g <=. 所以函数1()()x g x ef x -=-存在最小值，且最小值小于1.【点睛】本题考查利用导数讨论函数的单调性，考查利用导数求函数最值，属于较难题.。
北京市西城区2019-2020学年数学高二第二学期期末考试试题含解析
北京市西城区2019-2020学年数学高二第二学期期末考试试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．9的展开式中有理项的项数为（ ） A ．1 B ．2C ．3D ．4【答案】B 【解析】 【分析】求得二项式展开式的通项公式，由此判断出有理项的项数. 【详解】192(x 的展开式通项为2751962199()C (1)(1)C x r r r r r rr T x x --+=⋅-=⋅⋅⋅⋅-，当3r =或9r =时，为有理项，所以有理项共有2项. 故选：B 【点睛】本小题主要考查二项式展开式的通项公式，属于基础题.2．下列关于曲线24:14x y Γ+=的结论正确的是（ ）A ．曲线Γ是椭圆B ．关于直线y x =成轴对称C ．关于原点成中心对称D ．曲线Γ所围成的封闭图形面积小于4【答案】C 【解析】 【分析】A 根据椭圆的方程判断曲线24:14x y Γ+=不是椭圆；B 把曲线Γ中的(x ，y )同时换成(y ，x )，判断曲线Γ是否关于直线y x =对称； C 把曲线Γ中的(x ，y )同时换成(x -，y -)，判断曲线Γ是否关于原点对称； D 根据||2x ，||1y ，判断曲线24:14xy Γ+=所围成的封闭面积是否小于1．【详解】曲线24:14x C y +=，不是椭圆方程，∴曲线Γ不是椭圆，A ∴错误；把曲线Γ中的(x ，y )同时换成(y ，x )，方程变为2414yx +=，∴曲线Γ不关于直线y x =对称，B 错误；把曲线Γ中的(x ，y )同时换成(x -，y -)，方程不变，∴曲线Γ关于原点对称，C 正确；||2x ，||1y ，∴曲线24:14x C y +=所围成的封闭面积小于428⨯=，令x y =∴=所以曲线Γ上的四点,,（,（围成的矩形面积为4>， 所以选项D 错误. 故选：C ． 【点睛】本题主要考查了方程所表示的曲线以及曲线的对称性问题，解题时应结合圆锥曲线的定义域性质进行解答，是基础题．3．利用数学归纳法证明不等式*n 1111...(n)(n 2,)2321f n N ++++<≥∈-的过程，由n k =到+1n k =时，左边增加了（ ） A ．1项 B ．k 项C ．12k -项D ．2k 项【答案】D 【解析】 【分析】分别计算n k =和+1n k =时不等式左边的项数，相减得到答案. 【详解】n k =时，不等式左边：1111 (2)321k++++-共有21k - +1n k =时，：1111111 (2321221)k k k ++++++++--共有121k +- 增加了1(21)(21)2k k k +---=故答案选D 【点睛】本题考查了数学归纳法的项数问题，属于基础题型.4．已知定义在R 上的奇函数f （x ）满足()32f x f x ⎛⎫-= ⎪⎝⎭，f （－2）＝－3，数列{a n }是等差数列，若a 2＝3，a 7＝13，则f （a 1）＋f （a 2）＋f （a 3）＋…＋f （a 2018）＝（ ） A ．－2B ．－3C ．2D ．3【答案】B 【解析】 【分析】 【详解】分析：利用函数的奇偶性和对称性推出周期，求出前三项的值，利用周期化简式子即可． 详解：定义在R 上的奇函数()f x 满足()32f x f x ⎛⎫-=⎪⎝⎭，故周期T 3=,()()()()()()213,300,523f f f f f f -==-==== 数列{}n a 是等差数列，若23a =，713a =,故21n a n =-，所以：()()()()()()1231350f f f f a f a f a ++=++=，()()()()()()1232018133f a f a f a f a f f +++⋯+=+=-点睛：函数的周期性，对称性，奇偶性知二推一，已知()y f x =奇函数，关于轴x a =对称，则()()()()f x f x 1f 2a x f x 2-=-+=-，，令x x 2a =-代入2式，得出()()f x f x 2a =--，由奇偶性()()()()()f 2a x f x f x f x 2a f x 2a ⎡⎤+=-=-=---=-⎣⎦，故周期T 4a =. 5．如图所示，在一个边长为2.的正方形AOBC 内，曲2y x =和曲线y x =围成一个叶形图(阴影部分)，向正方形AOBC 内随机投一点(该点落在正方形AOBC 内任何一点是等可能的)，则所投的点落在叶形图内部的概率是（ ）A ．12B ．14C ．13D ．16【答案】C 【解析】 【分析】欲求所投的点落在叶形图内部的概率，须结合定积分计算叶形图（阴影部分）平面区域的面积，再根据几何概型概率计算公式求解． 【详解】联立2y x y x⎧=⎪⎨=⎪⎩得(1,1)C . 由图可知基本事件空间所对应的几何度量1OBCA S=正方形， 满足所投的点落在叶形图内部所对应的几何度量：S （A ）3123120021()()|33x x dx x x =-=-⎰13=． 所以P （A ）1()1313OBCAS A S ===正方形． 故选：C ． 【点睛】本题综合考查了几何概型及定积分在求面积中的应用，考查定积分的计算，意在考查学生对这些知识的理解掌握水平.6．在圆C 中，弦AB 的长为4，则AB AC ⋅=（ ） A ．8 B ．-8C ．4D ．-4【答案】A 【解析】分析：根据平面向量的数量积的定义，老鹰圆的垂径定理，即可求得答案. 详解：如图所示，在圆C 中，过点C 作CD AB ⊥于D ，则D 为AB 的中点，在Rt ACD ∆中，122AD AB ==，可得2cos AD A AC AC ==， 所以2cos 48AB AC AB AC A AC AC⋅=⋅=⨯⨯=，故选A.点睛：本题主要考查了平面向量的数量积的运算，其中解答中涉及到圆的性质，直角三角形中三角函数的定义和向量的数量积的公式等知识点的综合运用，着重考查了分析问题和解答问题的能力. 7．如果函数在区间上存在，满足，，则称函数是区间上的“双中值函数”.已知函数是区间上的“双中值函数”，则实数的取值范围是（ ）A ．（，）B ．（，3）C ．（，1）D ．（，1） 【答案】C 【解析】 试题分析：，，所以函数是区间上的“双中值函数”等价于在区间有两个不同的实数解，即方程在区间有两个不同的实数解，令，则问题可转化为在区间上函数有两个不同的零点，所以，解之得，故选C.考点：1.新定义问题；2.函数与方程；3.导数的运算法则.【名师点睛】本题考查新定义问题、函数与方程、导数的运算法则以及学生接受鷴知识的能力与运用新知识的能力，难题.新定义问题是命题的新视角，在解题时首先是把新定义问题中的新的、不了解的知识通过转翻译成了解的、熟悉的知识，然后再去求解、运算.8．在一项调查中有两个变量x 和y ，下图是由这两个变量近8年来的取值数据得到的散点图，那么适宜作为y 关于x 的回归方程的函数类型是( )A ．y a bx =+B ．y c x =+C ．2y m nx =+D ．x y p qc =+（0q >）【答案】B 【解析】 【分析】根据散点图的趋势，选定正确的选项. 【详解】散点图呈曲线，排除A 选项，且增长速度变慢，排除选项C 、D ，故选B ． 【点睛】本小题主要考查散点图，考查回归直线方程等知识，属于基础题.9．从集合{0，1，2，3，4，5，6}中任取两个互不相等的数a ，b 组成复数a bi +，其中虚数有（ ） A ．30个 B ．42个C ．36个D ．35个【答案】C 【解析】 【分析】 【详解】解：∵a ，b 互不相等且为虚数，∴所有b 只能从{1，2，3，4，5，6}中选一个有6种， a 从剩余的6个选一个有6种，∴根据分步计数原理知虚数有6×6=36（个）． 故选C10．已知某企业上半年前5个月产品广告投入与利润额统计如下：由此所得回归方程为7.5ˆyx a =+，若6月份广告投入10（万元）估计所获利润为（ ） A ．97万元 B ．96.5万元C ．95.25万元D ．97.25万元【答案】C 【解析】 【分析】首先求出x y ，的平均数，将样本中心点代入回归方程中求出a 的值，然后写出回归方程，然后将10x =代入求解即可 【详解】()19.59.39.18.99.79.35x =⨯++++=()19289898793905y =⨯++++=代入到回归方程为7.5ˆy x a =+，解得20.25a = 7.25ˆ50.2yx ∴=+ 将10x =代入7.50.5ˆ22yx =+，解得ˆ95.25y = 故选C【点睛】本题是一道关于线性回归方程的题目，解答本题的关键是求出线性回归方程，属于基础题。
2019-2020学年北京市西城区数学高二(下)期末考试试题含解析
2019-2020学年北京市西城区数学高二(下)期末考试试题一、单选题（本题包括12个小题，每小题35，共60分．每小题只有一个选项符合题意） 1．定积分)10x dx =⎰（ ）A ．142π+B ．12π+ C ．14π+ D ．122π+【答案】A 【解析】 【分析】先根据定积分的几何意义计算定积分，即求被积函数y 0x =，1x =所围成的图形的面积，在求出1xdx ⎰，可得答案.【详解】解：由定积分的几何意义可知⎰是由曲线y =0x =，1x =所围成的图形的面积，也就是单位圆的14，故4π=⎰，12101122xdx x ==⎰，故)11142x dx xdx π=+=+⎰⎰⎰， 故选：A. 【点睛】本题主要考查定积分的有关计算，属于基础题，注意运算准确.2．两个半径都是()1r r ＞的球1O 和球2O 相切，且均与直二面角l αβ--的两个半平面都相切，另有一个半径为1的小球O 与这二面角的两个半平面也都相切，同时与球1O 和球2O 都外切，则r 的值为（ ） A1 B3C．12D．32【答案】D 【解析】 【分析】取三个球心点所在的平面，过点1O 、2O 分别作1O M l ⊥、2O N l ⊥，垂足分别为点,M N ，过点O 分别作OA l ⊥，12OB O O ⊥，分别得出OA 、OB 以及AB ，然后列出有关r 的方程，即可求出r 的值． 【详解】因为三个球都与直二面角l αβ--的两个半平面相切， 所以l 与1O 、2O 、O 共面，如下图所示，过点1O 、2O 分别作1O M l ⊥、2O N l ⊥， 垂足分别为点,M N ，过点O 分别作OA l ⊥，12OB O O ⊥，则122O M O N r ==，2OA 12O B O B r ==，121OO OO r ==+，2211||21OB OO O B r =-=+2212AB OA OB r r =++=2122r r +=等式两边平方得221242r r r +=-+， 化简得22610r r -+=，由于1r >，解得732r =，故选D ． 【点睛】本题主要考查球体的性质，以及球与平面相切的性质、二面角的性质，考查了转化思想与空间想象能力，属于难题．转化是数学解题的灵魂，合理的转化不仅仅使问题得到了解决，还可以使解决问题的难度大大降低，本题将空间问题转化为平面问题是解题的关键.3．用反证法证明命题“三角形的内角中至少有一个大于060，反证假设正确的是( ) A ．假设三内角都大于060 B ．假设三内角都不大于060 C ．假设三内角至多有一个大于060 D ．假设三内角至多有两个大于060【答案】B 【解析】 【分析】反证法的第一步是假设命题的结论不成立，根据这个原则，选出正确的答案. 【详解】假设命题的结论不成立，即假设三角形的内角中至少有一个大于060不成立，即假设三内角都不大于060，故本题选B. 【点睛】本题考查了反证法的第一步的假设过程，理解至少有一个大于的否定是都不大于是解题的关键. 4．设{}n a 是等差数列.下列结论中正确的是（ ）A ．若120a a +>，则230a a +>B ．若130a a +<，则120a a +<C ．若120a a <<，则2a >D ．若10a <，则()()21230a a a a -->【答案】C 【解析】 【分析】 【详解】先分析四个答案，A 举一反例1232,1,4a a a ==-=-，120a a +>而230a a +<，A 错误，B 举同样反例1232,1,4a a a ==-=-，130a a +<，而120a a +>，B 错误，D 选项，2132,,a a d a a d -=-=-22132()()0,a a a a d ∴--=-≤故D 错，下面针对C 进行研究，{}n a 是等差数列，若120a a <<，则10,a >设公差为d ，则0d >，数列各项均为正，由于22213111()(2)a a a a d a a d -=+-+22221111220a a d d a a d d =++--=>，则2113a a a >1a ⇒>故选C.考点：本题考点为等差数列及作差比较法，以等差数列为载体，考查不等关系问题，重 点是对知识本质的考查.5．用反证法证明“,20x x ∀∈>R ”时，应假设（ ） A ．00,20x x ∃∈≤RB ．00,20x x ∃∈<R C ．,20x x ∀∈≤R D ．00,20x x ∃∈>R【答案】A 【解析】 【分析】根据反证法的步骤，假设是对原命题结论的否定，即可得出正确选项． 【详解】根据反证法的步骤，假设是对原命题的否定，P （x 0）成立的否定是使得P （x 0）不成立，即用反证法证明“∀x ∈R ，2x ＞0”，应假设为∃x 0∈R ，02x ≤0 故选：A ． 【点睛】本题考查反证法的概念，全称命题的否定，注意 “ 改量词否结论”6．已知一个等比数列{}n a ，这个数列21n a a -=且所有项的积为243，则该数列的项数为（ ）A ．9B ．10C ．11D ．12【答案】B 【解析】 【分析】根据等比数列性质列式求解 【详解】3322121221((39)3)n n n n n n a a a a a a --⋅⋅==⋅=Q L224335,10.2n nn ∴===，选B. 【点睛】本题考查利用等比数列性质求值，考查基本分析求解能力，属基础题. 7．命题“320,0x x x ∀>+>”的否定是（） A ．320000,0x x x ∃>+≤ B ．320000,0x x x ∃≤+≤ C ．320,0x x x ∃>+≤ D ．320,0x x x ∃≤+≤【答案】A 【解析】 【分析】根据全称命题的否定形式书写. 【详解】根据全称命题的否定形式可知“320,0x x x ∀>+>”的否定是“3200,0x x x ∃>+≤”.故选A. 【点睛】本题考查全称命题的否定形式，属于简单题型.8．一个三棱锥的正视图和侧视图如图所示(均为真角三角形),则该三棱锥的体积为（ ）A ．4B ．8C ．16D ．24【答案】B【解析】【分析】根据三视图知，三棱锥的一条长为6的侧棱与底面垂直，底面是直角边为2、4的直角三角形，利用棱锥的体积公式计算即可.【详解】由三视图知三棱锥的侧棱AO与底OCB垂直，其直观图如图，可得其俯视图是直角三角形，直角边长为2，4，6OA∴=，∴棱锥的体积11246832V=⨯⨯⨯⨯=，故选B.【点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于中档题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.9．把67化为二进制数为A．1100001(2)B．1000011(2)C．110000(2)D．1000111(2)【答案】B【解析】如图：所以把67化为二进制数为1 000 011(2)．故选B.考点：二进制法.10．定义在（0，+∞）上的函数f （x ）的导数'()f x 满足x 2'()f x ＜1，则下列不等式中一定成立的是（ ）A ．f （14）+1＜f （13）＜f （12）﹣1 B ．f （12）+1＜f （13）＜f （14）﹣1 C ．f （14）﹣1＜f （13）＜f （12）+1D ．f （12）﹣1＜f （13）＜f （14）+1【答案】D 【解析】 【分析】构造函数g （x ）＝f （x ）1x+，利用导数可知函数在（0，+∞）上是减函数，则答案可求． 【详解】由x 2f ′（x ）＜1，得f ′（x ）21x＜，即得f ′（x ）21x -＜0， 令g （x ）＝f （x ）1x +，则g ′（x ）＝f ′（x ）21x -＜0，∴g （x ）＝f （x ）1x+在（0，+∞）上为单调减函数，∴f （12）+2＜f （13）+3＜f （14）+4，则f （12）＜f （13）+1，即f （12）﹣1＜f （13）；f （13）＜f （14）+1．综上，f （12）﹣1＜f （13）＜f （14）+1．故选：D ． 【点睛】本题考查利用导数研究函数的单调性，正确构造函数是解题的关键，是中档题． 11．函数()cos xf x e x =⋅在()()0,0f 处切线斜率为（ ）A ．0B ．1-C ．1D ．2【答案】C 【解析】分析：首先求得函数()f x 的导函数，然后结合导函数研究函数的切线即可. 详解：由函数的解析式可得：()()()'cos sin cos sin xxxf x e x e x ex x =+⨯-=-，则()()()0'0cos0sin01101f e =-=⨯-=，即函数()xf x e cosx =⋅在()()0,0f 处切线斜率为1.本题选择C 选项.点睛：本题主要考查导函数与原函数切线之间的关系，意在考查学生的转化能力和计算求解能力. 12．某校实行选科走班制度，张毅同学的选择是物理、生物、政治这三科，且物理在A层班级，生物在B 层班级，该校周一上午课程安排如下表所示，张毅选择三个科目的课各上一节，另外一节上自习，则他不同的选课方法有A．8种B．10种C．12种D．14种【答案】B【解析】【分析】根据表格进行逻辑推理即可得到结果.【详解】张毅不同的选课方法如下：（1）生物B层1班，政治1班，物理A层2班；（2）生物B层1班，政治1班，物理A层4班；（3）生物B层1班，政治2班，物理A层1班；（4）生物B层1班，政治2班，物理A层4班；（5）生物B层1班，政治3班，物理A层1班；（6）生物B层1班，政治3班，物理A层2班；（7）生物B层2班，政治1班，物理A层3班；（8）生物B层2班，政治1班，物理A层4班；（9）生物B层2班，政治3班，物理A层1班；（10）生物B层2班，政治3班，物理A层3班；共10种，故选B.【点睛】本题以实际生活为背景，考查了逻辑推理能力与分类讨论思想，属于中档题.二、填空题（本题包括4个小题，每小题5分，共20分）13．设0x >，0y >，24x y +=，则(1)(21)x y xy++的最小值为__________.【答案】92. 【解析】 【分析】把分子展开化为(1)(21)2212552x y xy x y xy xy xy xy xy++++++===+，再利用基本不等式求最值．【详解】由24x y +=，得24x y +=≥，得2xy ≤(1)(21)221255592222x y xy x y xy xy xy xy xy ++++++===+≥+=，等号当且仅当2x y =，即2,1x y ==时成立．故所求的最小值为92． 【点睛】使用基本不等式求最值时一定要验证等号是否能够成立．14． “直线l 与平面α内无数条直线垂直”是“l α⊥”的______条件.（填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”） 【答案】必要不充分. 【解析】 【分析】根据平面α内与斜线l 在平面α内的射影垂直的直线必定与l 垂直，可知充分性不成立；根据线面垂直的定义，可得必要性成立．由此得到正确答案 【详解】解：（1）充分性：当直线l 与平面α斜交，且l 在平面α内的射影为l '，若α内的直线m 与l '垂直时m 与l 垂直，并且满足条件的直线m 有无数条．这样平面α内有无数条直线l 垂直，但l 与α不垂直，因此充分性不成立；（2）必要性：当“l α⊥”成立时，α内的任意一条直线都与l 垂直，因此“直线l 与平面α内无数条直线垂直”成立，所以必要性成立. 故答案为:必要不充分. 【点睛】本题考查了判断两命题间的充分、必要条件，考查了直线与平面的位置关系.对于两个命题p ，q ，判断他们的关系时，常常分为两步，以p 为条件，判断q 是否成立；以q 为条件，判断p 是否成立. 15．已知直线l 在矩阵1201A -⎡⎤=⎢⎥⎣⎦对应的变换作用下变为直线'l ：10x y --=，则直线l 的方程为__________． 【答案】310x y --= 【解析】分析：用相关点法求解，设直线l 上的点为()x,y 直线'l 上的点为()a,b ，所以，12201x a a x yy b b y -=-⎡⎤⎡⎤⎡⎤⎧=⇒⎨⎢⎥⎢⎥⎢⎥=⎣⎦⎣⎦⎣⎦⎩，代入直线'l 的方程 详解：设直线l 上的点为()x,y 直线'l 上的点为()a,b ，直线l 在矩阵1201A -⎡⎤=⎢⎥⎣⎦对应的变换作用下所以：12201x a a x yy b b y -=-⎡⎤⎡⎤⎡⎤⎧=⇒⎨⎢⎥⎢⎥⎢⎥=⎣⎦⎣⎦⎣⎦⎩，代入直线'l 的方程整理可得直线l 的方程为 310x y --=。
高二下学期期末考试数学试题(图片版)
，则 .………………………………………10分
故函数在 和 上单调递增…………………………………………11分
在 上单调递减.………………………………………………………………12分
17．（本小题满分12分）
解：（Ⅰ）由A∩B＝{3,7}得 2＋4 ＋2＝7，解得 ＝1或 ＝－5.………………4分
所以 ， 在 上单调递减，……………………………………10分
.………………………………………………………………………11分
所以 最小值为 .…………………………………………………………………12分
所以至少一种产品研发成功的概率为 .………………………………………5分
(2)依题意, ,……………………6分
由独立试验同时发生的பைடு நூலகம்率计算公式可得:
;………………………………………………7分
;…………………………………………………8分
;……………………………………………………9分
;…………………………………………………………10分
所以 的分布列如下:
………………………………………………………………………………………11分
则数学期望 .
…………………………………………………………………………………………12分
20．（本小题满分12分）
解：（Ⅰ）函数 …………………………………………………1分
所以 ………………………………………………………………3分
当 ＝1时，集合B＝{0,7,3,1}；……………………………………………………5分
当 ＝－5时，因为2- =7，集合B中元素重复．…………………………………6分
北京市西城区2019-2020学年数学高二下期末考试试题含解析
北京市西城区2019-2020学年数学高二下期末考试试题一、单选题（本题包括12个小题，每小题35，共60分．每小题只有一个选项符合题意） 1．曲线cos y x =在3x π=处的切线斜率是( )A ．12-B ．12C ．3-D ．3 2．在空间中，设α，β表示平面，m ，n 表示直线.则下列命题正确的是（ ） A ．若m∥n，n⊥α，则m⊥α B ．若m 上有无数个点不在α内，则m∥α C ．若,m αβα⊥⊂，则m β⊥D ．若m∥α，那么m 与α内的任何直线平行3．若关于x 的不等式2ln 0ax x x --≥恒成立，则实数a 的取值范围（ ） A ．(1,)+∞B ．[)1,+∞C ．(,)e +∞D ．[),e +∞4．已知关于x 的方程2e 0x x t a +-=，[]11x ∈-，，若对任意的[]13t ∈，，该方程总存在唯一的实数解，则实数a 的取值范围是（ ） A ．12,e 1e⎛⎤++ ⎥⎝⎦B ．13,e 1e ⎛⎤++⎥⎝⎦C ．11,e e ⎡⎤+⎢⎥⎣⎦D ．(]1,e5．某程序框图如图所示，若运行该程序后输出S =（ ）A ．53B ．74C ．95D ．1166．若1sin 63a π⎛⎫-= ⎪⎝⎭，则2cos 23a π⎛⎫+= ⎪⎝⎭（） A ．79-B ．13-C ．13D ．797．《九章算术》中，将底面是直角三角形的直三梭柱称之为“堑堵”.已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为( )A ．16213+ B．32413+ C ．52813+ D ．26413+8．记者要为5名志愿者和他们帮助的2位老人拍照，要求排成一排，2位老人相邻但不排在两端，不同的排法共有（ ） A ．1440种B ．960种C ．720种D ．480种9．下列命题不正确的是（ ）A ．研究两个变量相关关系时，相关系数r 为负数，说明两个变量线性负相关B ．研究两个变量相关关系时，相关指数R 2越大，说明回归方程拟合效果越好．C ．命题“∀x ∈R ，cosx≤1”的否定命题为“∃x 0∈R ，cosx 0＞1”D ．实数a ，b ，a ＞b 成立的一个充分不必要条件是a 3＞b 3 10．已知i 为虚数单位，若复数11tiz i-=+在复平面内对应的点在第四象限，则t 的取值范围为（ ） A ．[1,1]- B ．(1,1)- C ．(,1)-∞-D ．(1,)+∞ 11．已知函数在上可导，且，则（ ） A ．B ．C ．D ．12．已知函数()xe f x ax x=-，(0,)x ∈+∞，当21x x >时，不等式()()1221f x f x x x <恒成立，则实数a 的取值范围为（ ） A ．(,]e -∞B ．(,)e -∞C ．,2e ⎛⎫-∞ ⎪⎝⎭D ．,2e ⎛⎤-∞ ⎥⎝⎦二、填空题（本题包括4个小题，每小题5分，共20分）13． “杨辉三角”是我国数学史上的一个伟大成就，是二项式系数在三角形中的一种几何排列.如图所示，去除所有为1的项，依此构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前46项和为_____.14．已知函数f （x ）＝x 3﹣3x+1，则函数y ＝f （x ）的单调递减区间是_____15．i 是虚数单位，则复数67i12i++的虚部为______． 16．若1x =是函数()()25xx a e f x x =+-的极值点，则()f x 在[]22-,上的最小值为______. 三、解答题（本题包括6个小题，共70分）17．旅游业作为一个第三产业，时间性和季节性非常强，每年11月份来临，全国各地就相继进入旅游淡季，很多旅游景区就变得门庭冷落.为改变这种局面，某旅游公司借助一自媒体平台做宣传推广，销售特惠旅游产品.该公司统计了活动刚推出一周内产品的销售数量，用x 表示活动推出的天数，用y 表示产品的销售数量（单位：百件），统计数据如下表所示.根据以上数据，绘制了如图所示的散点图，根据已有的函数知识，发现样本点分布在某一条指数型函数ˆˆbx ay e +=的周围.为求出该回归方程，相关人员确定的研究方案是：先用其中5个数据建立y 关于x 的回归方程，再用剩下的2组数据进行检验.试回答下列问题： （1）现令ln t y =，若选取的是1,2,3,4,5x =这5组数据，已知518ln 26ln 3ii t==+∑，5126ln 222ln 3i ii x t==+∑，请求出t 关于x 的线性回归方程（结果保留一位有效数字）；（2）若由回归方程得到的估计数据与选出的检验数据的误差均不超过10，则认为得到的回归方程是可靠的，试问（1）中所得的回归方程是否可靠？参考公式及数据：对于一组数据1122()()()n n x y x y x y ，，，，，，，其回归直线ˆˆˆy bx a =+的斜率和截距的最小二乘法估计分别为1211221()()ˆ()n iii nni ii ni i i i x y n x x y y bx x x yx nx====----==-∑∑∑∑， ˆˆay bx =-；ln 20.69,ln 3 1.10≈≈；4554, 1.22e e ≈≈．18．已知函数()ln()af x x x=--有两个零点1x ，2x . （Ⅰ）求a 的取值范围； （Ⅱ）证明：122x x e+<-. 19．（6分）如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱长为3, 1AE A B ⊥,垂足为F ,AE 交1B B 于点E .(1)求证: 1D B ⊥平面AEC ;(2)记直线AE 与平面1ACD 所成的角θ,求sin θ的值.20．（6分）已知空间向量与的夹角为，且，，令，．求，为邻边的平行四边形的面积S ； 求的夹角．21．（6分）在平面直角坐标系xOy 中，曲线1C 的参数方程为5sin x y αα⎧=⎪⎨=⎪⎩（α为参数）.以坐标原点O为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为cos 83πρθ⎛⎫+= ⎪⎝⎭.（1）写出1C 的普通方程和2C 的直角坐标方程；（2）设点M 在1C 上，点N 在2C 上，求MN 的最小值及此时M 的直角坐标.22．（8分）2021年，广东省将实施新高考，2018年暑期入学的高一学生是新高考首批考生，新高考不再分文理科，采用312++模式，其中“3”是指语文、数学、外语；“1”是指在物理和历史中必选一科（且只能选一科）；“2”是指在化学，生物，政治，地理四科中任选两科.为积极推进新高考，某中学将选科分为两个环节，第一环节：学生在物理和历史两科中选择一科；第二环节：学生在化学，生物，政治，地理四科中任选两科.若一个学生两个环节的选科都确定，则称该学生的选考方案确定；否则，称该学生选考方案待确定.该学校为了解高一年级1000名学生选考科目的意向，随机选取50名学生进行了一次调查，这50人第一环节的选考科目都确定，有32人选物理，18人选历史；第二环节的选考科目已确定的有30人，待确定的有20人，具体调查结果如下表：（1）估计该学校高一年级选考方案确定的学生中选考政治的学生有多少人？ （2）从选考方案确定的12名历史选考生中随机选出2名学生，设随机变量0,1.X ⎧=⎨⎩两名学生选考方案不同两名学生选考方案相同，求X 的分布列及数学期望()E X .（3）在选考方案确定的18名物理选考生中，有11名学生选考方案为物理、化学、生物，试问剩余7人中选考方案为物理、政治、地理的人数.（只需写出结果）参考答案一、单选题（本题包括12个小题，每小题35，共60分．每小题只有一个选项符合题意） 1．C 【解析】 【分析】根据已知对cos y x =求导，将3x π=代入导函数即可.【详解】∵y′=(cosx)′=-sinx ， ∴当3x π=时，=3y sinπ'=-故选C.本题考查利用导数求切线斜率问题，已知切点求切线斜率问题，先求导再代入切点横坐标即可，属于基础题. 2．A 【解析】 【分析】根据线面位置关系的判定定理与性质定理，逐一判定，即可求解，得到答案. 【详解】对于A 中，若//,m n n α⊥，则m α⊥，根据线面垂直的判定定理，可知是正确的； 对于B 中，若直线与平面相交，则除了交点以外的无数个点都不在平面内，所以不正确； 对于C 中，若,m αβα⊥⊂，则m β⊥或//m β或m 与β相交，所以不正确； 对于D 中，若//m α，则m 与平面α内的直线平行或异面，所以不正确， 故选A. 【点睛】本题主要考查了线面位置关系的判定与证明，其中解答中熟记线面位置关系的判定定理和性质定理是解答的关键，着重考查了推理与运算能力，属于基础题. 3．B 【解析】 【分析】2ln 0ax x x --≥恒成立等价于()2ln 0x x a x x +>≥恒成立，令()2ln x xf x x +=， 则问题转化为()max a f x ≥，对函数()f x 求导，利用导函数求其最大值，进而得到答案 。
2019北京市西城区高二(下)期末数学
2019北京市西城区高二（下）期末数学 2019.7 本试卷共5页，共150分。
考试时长120分钟。
考生务必将答案写在答题纸上，在试卷上作答无效。
一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.10. 算筹是在珠算发明以前我国独创并且有效的计算工具，为我国古代数学的发展做出了很大贡献.在算筹计数法中，以“纵式”和“横式”两种方式来表示数字，如下图：表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推，遇零则置空，如下图：67286708如果把5根算筹以适当的方式全部放入右面的表格中，那么可以表示的三位数的个数为（）（A）46（B）44（C）42（D）40二、填空题：本大题共6小题，每小题5分，共30分. 11. 已知函数e xy x=，则=')1(f _______.12. 二项式261(2)x x -的展开式中的常数项是_______.（用数字作答）13. 若复数z 满足i 12i z ⋅=+，则||z =_________.14. 能说明“若(0)=0f '，则0x =是函数()y f x =极值点”为假命题的一个函数是______________．15. 北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌，如图所示.设某人到达银行的时间是随机的，记其到达银行时服务窗口的个数为X ，则()E X =______________．16. 容器中有,,A B C 3种粒子，若相同种类的两颗粒子发生碰撞，则变成一颗B 粒子；不同种类的两颗粒子发生碰撞，会变成另外一种粒子. 例如，一颗A 粒子和一颗B 粒子发生碰撞则变成一颗C 粒子.现有A 粒子10颗，B 粒子8颗，C 粒子9颗，如果经过各种两两碰撞后，只剩1颗粒子. 给出下列结论： ① 最后一颗粒子可能是A 粒子 ② 最后一颗粒子一定是C 粒子③ 最后一颗粒子一定不是B 粒子 ④ 以上都不正确其中正确结论的序号是________.（写出所有正确结论的序号）三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分13分）已知函数321()3f x x x bx =-+，且(2)3f '=-. （Ⅰ）求b ；（Ⅱ）求()f x 的单调区间.某工厂生产一种汽车的元件，该元件是经过A、B、C三道工序加工而成的，A、B、C三道工序加工的元件合格率分别为12、23、34．已知每道工序的加工都相互独立，三道工序加工都合格的元件为一等品；恰有两道工序加工合格的元件为二等品；其它的为废品，不进入市场．（Ⅰ）生产一个元件，求该元件为二等品的概率；（Ⅱ）若从该工厂生产的这种元件中任意取出3个元件进行检测，求至少有2个元件是一等品的概率.19．（本小题满分13分）已知函数()()e xf x x a=+.（Ⅰ）求()f x的单调区间；（Ⅱ）求()f x在区间[0,4]上的最小值.20．（本小题满分13分）某校在学年期末举行“我最喜欢的文化课”评选活动，投票规则是一人一票，高一（1）班44名学生和高一（7）班45名学生的投票结果如下表（无废票）：该校把上表的数据作为样本，把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.（Ⅰ）如果数学学科的“好感指数”比高一年级其他文化课都高，求a的所有取值；（Ⅱ）从高一（1）班投票给政治、历史、地理的学生中任意选取3位同学，设随机变量X为投票给地理学科的人数，求X的分布列和期望；（Ⅲ）当a为何值时，高一年级的语文、数学、外语三科的“好感指数”的方差最小?（结论不要求证明）已知函数()e ln x f x a x x =--.（Ⅰ）当1a =-时，求曲线()y f x =在点(1,(1))f 处的切线方程； （Ⅱ）若()f x 在区间(0,1)上存在极值点，求a 的取值范围.22．（本小题满分14分）已知函数ln ()(1)xf x a x x=+-. （Ⅰ）若0a =，求()f x 的极值；（Ⅱ）若在区间()∞+，1上()0f x <恒成立，求a 的取值范围； （Ⅲ）判断函数()f x 的零点个数.（直接写出结论）2019北京市西城区高二（下）期末数学参考答案一、选择题：本大题共10小题，每小题4分，共40分.1. B2. D3. B4. D5. A6. A7. C8. B9. D 10. B 二、填空题：本大题共6小题，每小题5分，共30分. 11. 0 12. 6014. 3()f x x = 或()1f x =等，答案不唯一 15. 3.5625 16. ①③注：16题选对一个正确结论得3分，错选不得分. 三、解答题：本大题共6小题，共80分. 17. （本小题满分13分）解：（Ⅰ）由已知2()2f x x x b '=-+， ……………………3分所以 (2)443f b '=-+=-，所以 3b =-. ……………………5分 （Ⅱ）由（Ⅰ）知2()23f x x x '=--，解()0f x '>，得1x <-或3x >，解()0f x '<，得13x -<<. ……………………9分 所以函数()f x 的单调递增区间为(,1)-∞-，(3,)+∞，单调递减区间为(1,3)-.……………………13分18. （本小题满分13分）解：（Ⅰ）不妨设元件经,,A B C 三道工序加工合格的事件分别为,,A B C .所以1()2P A =,2()3P B =,3()4P C =.1()2P A =,1()3P B =,1()4P C =. …………2分设事件D 为“生产一个元件，该元件为二等品”. 由已知,,A B C 是相互独立事件.根据事件的独立性、互斥事件的概率运算公式，()()P D P ABC ABC ABC =++()()()P ABC P ABC P ABC =++ ………………6分123123123(1)(1)(1)234234234=-⨯⨯+⨯-⨯+⨯⨯-11.24=所以生产一个元件，该元件为二等品的概率为1124. ……………………8分 （Ⅱ）生产一个元件，该元件为一等品的概率为12312344p =⨯⨯=. ……………………9分设事件E 为“任意取出3个元件进行检测，至少有2个元件是一等品”，则2233131()()()444P E C =⨯+ ……………………12分1056432==. 所以至少有2个元件是一等品的概率为532. ……………………13分 19.（本小题满分13分）解：（Ⅰ）()e ()e (1)e x x x f x x a x a '=++=++. ……………………2分由()0f x '>，解得1x a >--； 由()0f x '<，解得1x a <--.所以函数()f x 的单调减区间为(,1)a -∞--，单调增区间为(1,)a --+∞. ………4分 （Ⅱ）① 当14a --≥，即5a ≤-时，()f x 在[0,4]上单调递减，所以4min ()(4)(4)e .f x f a ==+ ……………………7分 ② 当10a --≤，即1a ≥-时， ()f x 在[0,4]上单调递增，所以min ()(0).f x f a == ……………………10分③ 当51a -<<-时，所以1min 1()(1)e .e a a f x f a --+=--=-=-……………………13分综上，当5a ≤-时，4min ()(4)e f x a =+；当1a ≥-时，min ()f x a =；当51a -<<-时，min 11().e a f x +=-20.（本小题满分13分）解：（Ⅰ）由已知14a b += ，所以14b a =-. ……………………1分依题意， 966,967,a b +>+⎧⎨+>+⎩ ……………………3分即 966,967(14),a a +>+⎧⎨+>+-⎩解得 69a <<，又a ∈N ，所以 7a =，8a =. ……………………4分 （Ⅱ）由已知，随机变量X 是高一（1）班同学中投票给地理学科的人数，所以0,1,2X =. ……………………5分36385(0)14C P X C ===， ……………………6分21623815(1)28C C P X C ===， ……………………7分 1262383(2)28C C P X C ===. ……………………8分 9分51533()0121428284E X =⨯+⨯+⨯=. ……………………10分（Ⅲ）7a =或8a =. ……………………13分 21.（本小题满分14分）解：（Ⅰ） 当1a =-时，()e ln x f x x x =+-，0x >.所以1()e 1x f x x'=+-， ……………………2分 所以 (1)e 1f =-，(1)e f '=，曲线()y f x =在点(1,(1))f 处的切线方程为(e 1)e(1)y x --=-，整理得 e 10.x y --= ……………………4分 （Ⅱ）因为()e ln x f x a x x =--，0x >.所以e ()e 1x xa x x af x x x--'=--=， ……………………6分依题意，()f x '在区间(0,1)上存在变号零点. ……………………7分 因为0x >，设()e x g x x x a =--，所以()g x 在区间(0,1)上存在变号零点. ……8分 因为()e (1)1x g x x '=+-， ……………………9分 所以，当(0,1)x ∈时，e 1x >，11x +>，所以e (1)1x x +>，即()0g x '>，所以()g x 在区间(0,1)上为单调递增函数， ……………………12分 依题意， (0)0,(1)0,g g <⎧⎨>⎩ 即0,e 10.a a -<⎧⎨-->⎩……………………13分解得 0e 1a <<-. ……………………14分 所以，若()f x 在区间(0,1)上存在极值点，a 的取值范围是(0,e 1)-. 22.（本小题满分14分）解：（Ⅰ）当0a =时，定义域为{|0}x x >.因为ln ()x f x x =，所以21ln ()xf x x -'=. ……………………1分 令()0f x '=，解得e x =，所以()f x 在区间(0,e)上单调递增，在区间(e,+)∞上单调递减. ……………3分 所以()f x 有极大值，极大值为1(e)ef =；没有极小值. ……………………4分 （Ⅱ）因为0x >，所以在(1,)+∞上()0f x <恒成立，即2ln 0x ax ax +-<在(1,)+∞恒成立. ……………………5分设2()ln .g x x ax ax =+-①当0a ≥时，(2)ln 220g a =+>，不符合题意. ……………………7分 ②当0a <时，2121()2ax ax g x ax a x x-+'=+-=. ……………………8分 令()0g x '=,即2210ax ax -+=，因为方程2210ax ax -+=的判别式280a a ∆=->，两根之积102a<. 所以()0g x '=有两个异号根. 设两根为12,x x ，且120x x <<， ……………………9分i ）当21x >时，所以()g x 在区间2(1,)x 上单调递增，在区间2(,+)x ∞上单调递减，所以2()(1)0g x g >=，不符合题意； ……………………10分 ii ）当21x ≤时，(1)0g '≤，即1a ≤-时，()g x 在(1,)+∞单调递减，所以当(1,)x ∈+∞时，()(1)0g x g <=，符合题意.综上，1a ≤-. ……………………11分（Ⅲ）当0a ≥或1a =-时，()f x 有1个零点；当0a <且1a ≠-时，函数()f x 有2个零点.……………………14分16题提示：1、最后剩下的可能是A粒子10颗A粒子两两碰撞，形成5颗B粒子；9颗C粒子中的8个两两碰撞，形成4颗B粒子；所有的17颗B粒子两两碰撞，剩下一颗B粒子；这个B粒子与剩下的一颗C粒子碰撞形成A粒子。
北京市西城区2019-2020学年高二下学期数学期末试题
北京市西城区2019-2020学年高二下学期数学期末试题一、单选题1．在复平面内，复数1i +的共轭复数所对应的点位于（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限2．函数y =1x =处的瞬时变化率为（ ）A ．2B ．12C ．12-D ．13．4(1)x +的展开式中2x 的系数是（ ） A ．8 B ．7C ．6D ．44．曲线2y x=在点()1,2Q 处的切线方程为（ ） A ．240x y +-= B ．240x y ++= C ．10x y -+=D ．10x y +-=5．某批数量很大的产品的次品率为p ，从中任意取出4件，则其中恰好含有3件次品的概率是（ ） A ．3pB ．3(1)p p -C ．334(1)C p p -D ．334C p6．已知某一随机变量ξ的概率分布列如图所示，且E(ξ)＝6.3，则a 的值为( )A ．5B ．6C ．7D ．87．已知函数()cos sin f x x x x =-，则2f π⎛⎫' ⎪⎝⎭的值为（ ） A ．2πB ．2π-C ．1-D ．π-8．已知函数()f x 和()g x 的导函数()f x '､()g x '图象分别如图所示，则关于函数()()=-y g x f x 的判断正确的是（ ）A ．有3个极大值点B ．有3个极小值点C ．有1个极大值点和2个极小值点D ．有2个极大值点和1个极小值点9．万历十二年，中国明代音乐理论家和数学家朱载堉在其著作《律学新说》中，首次用珠算开方的办法计算出了十二个半音音阶的半音比例，这十二个半音音阶称为十二平均律十二平均律包括六个阳律（黄钟、太簇、姑洗、蕤宾、夷则、无射）和六个阴律（大吕、夹钟、中吕、林钟、南吕、应钟）.现从这十二平均律中取出2个阳律和2个阴律，排成一个序列，组成一种旋律，要求序列中的两个阳律相邻，两个阴律不相邻，则可组成不同的旋律（ ） A ．450种B ．900种C ．1350种D ．1800种10．设函数()f x 定义域为D ，若函数()f x 满足：对任意c D ∈，存在,a b D ∈，使得()()()f a f b f c a b-'=-成立，则称函数()f x 满足性质Γ.下列函数不满足性质Γ的是（ ）A ．2()f x x =B ．3()f x x =C ．()x f x e =D ．()ln f x x =二、填空题 11．若复数41z i=-，则||z =___________. 12．在5232x x ⎛⎫+ ⎪⎝⎭的展开式中，常数项为___________.(用数字作答) 13．从3名男医生和5名女医生中，选派3人组成医疗小分队，要求男､女医生都有，则不同的选取方法种数为__________(用数字作答).14．中国福利彩票3D 游戏(以下简称3D )，是以一个3位自然数(如：0记作000)为投注号码的彩票.投注者从000~999这些3位自然数中选择一个进行投注，每注2元，如果与官方公布的三位数相同，则视为中奖，获得奖金1000元，反之则获得奖金0元.某人随机投了一注，他的奖金的期望是______元.15．能说明“若()f x '为偶函数，则()f x 为奇函数”为假命题的一个函数是__________. 16．辛普森悖论(Simpson’sParado x)有人译为辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”.辛普森悖论为英国统计学家E .H .辛普森(E.H.Simpson)于1951年提出的，辛普森悖论的内容大意是“在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论：关于某高校法学院和商学院新学期已完成的招生情况，现有如下数据：对于此次招生，给出下列四个结论： ①法学院的录取率小于商学院的录取率；②这两个学院所有男生的录取率小于这两个学院所有女生的录取率； ③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率； ④法学院的录取率不一定小于这两个学院所有学生的录取率. 其中，所有正确结论的序号是___________.三、解答题17．已知函数3()3f x x x =-. （1）求函数()f x 的单调区间；（2）求函数()f x 在区间[]1,3-上的最大值和最小值.18．某射手打靶命中8环､9环､10环的概率分别为0.15.0.25.0.2.如果他连续打靶三次，且每次打靶的命中结果互不影响. （1）求该射手命中29环的概率； （2）求该射手命中不少于28环的概率. 19．已知函数()ln (0)f x x a x a =-≠.（1）当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； （2）求函数()f x 的极值点和极值.20．高中必修课程结束之后，学生需要从物理､化学､生物､历史､地理､政治六科中选择三科，继续学习选择性必修课程.某地记者为了了解本地区高一学生的选择意向，随机采访了100名学生作为样本进行情况调研，得到下表：（1）从样本中随机选1名学生，求该学生选择了化学的概率；（2）从第8组､第9组､第10组中，随机选2名学生，记其中选择政治的人数为X ，求X 的分布列和期望；（3）如果这个地区一名高一学生选择了地理，则在其它五科中，他同时选择哪一科的可能性最大？并说明理由. 21．已知函数2()12xa f x e x x =---. （1）若0a =，证明：()0f x ≥；（2）若曲线()y f x =的切线斜率不存在最小值，求a 的取值范围. 22．已知函数()ln f x x ax a =+-. （1）求函数()f x 的单调区间；（2）求证：当1a >时，函数1()()x g x e f x -=-存在最小值，且最小值小于1.。
3.西城高二期末·
北京市西城区2018－2019学年上学期高二年级期末考试数学试卷（满分150分，考试时间120分钟） 2019.1.17一、选择题共10小题，每小题4分，共40分.1.椭圆22143x y +=的离心率为 （ ）A.14B.12C.34解析：12c e a ==，选B.2.命题“对任意的x R ∈，210x ->”的否定是 （ ） A.不存在x R ∈，210x -> B.存在x R ∈，210x -< C.存在x R ∈，210x -≤ D.对任意的x R ∈，210x -≤ 解析：改2处，选C.3.数列{}n a 的前n 项和为n S ，且13a =12()n n a a n N *+=∈，则5S 等于 （ ） A.32 B.48 C.62 D.93 解析：首项3，公比2的等比数列，553(12)9312S ⨯-==-.当然这个题用递推公式傻算也成，53612244893S =++++=.选D.4.已知点(2,0,1)A ，(4,2,3)B ，P 是AB 的中点，则小强数学点P 的坐标为 （ ） A.(3,1,2) B.(3,1,4) C.(0,2,1)-- D.(6,4,5) 解析：送分题，相加除2，选A.5.平面α经过三点(0,0,0)O ，(2,2,0)A ，(0,0,2)B ，则平面α的法向量可以是（ ） A.(1,0,1) B.(1,0,1)- C.(0,1,1) D.(1,1,0)- 解析：(2,2,0)OA =,(0,0,2)OB =,法向量与这两个向量都垂直，选D.6.如果0a b <<，那么小强数学下列不等式中正确的是 （ ） A.2b ab > B.2ab a > C.22a b > D.a b < 解析：代特值排除筛选，2a =-，1b =-，选C.7.已知双曲线2222:1(0,0)x y C a b a b-=>>的一条渐近线方程为y =，一个焦点坐标为(2,0)，则小强数学双曲线C 的方程为（ ）A.22126x y -=B.22162x y -=C.2213y x -= D.2213x y -=解析:由题baa x =，b =，22c x ==，故1a =，b C.8.设数列{}n a 是等比数列，则“21a a >”是“{}n a 为递增数列”的 （ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 解析：本题为2017年海淀二模试题. 前推后，举反例，1,2,4,8,--⋅⋅⋅，不充分，选B.9.某采摘园的樱桃前n 年的总产量n S 与n 之间的关系如图所示，从图中记录的结果看，前x 年的平均产量最高，第y 年的年产量小强数学最高，则x 和y 的值分别为 （ ）A.7和4B.7和8C.10和4D.10和10 解析：平均产量最高，即n S n 最大，即00n S n --最大，也就是各个点与原点连线斜率的最大值，前7年的平均产量最高；产量最高，即1n n S S --最大，第4年最大，选A.10.已知0x y >>，将四个数x ，x y -，x y +个数列，则（ ）A.当0x >时，存在满足已知条件的x ，y ，四个数构成等比数列B.当0x >时，存在满足已知条件的x ，y ，四个数构成等差数列C.当0x <时，存在满足已知条件的x ，y ，四个数构成等比数列D.当0x <时，存在满足已知条件的x ，y ，四个数构成等差数列解析：当0x >时，x y x x y +>>-，若四个数构成等差数列，则2()()x y x x y -=++，即222x y x y -=+，显然不可能成立，A 错； 若四个数构成等比数列，则2()()x y x x y -=⋅+，解得3y x =，显然不可能成立，B 错；当0x <x y x x y >+>>-，若四个数构成等比数列，则2()()x x y x y =+⋅-，即20y =，不合题意，D 错；若四个数构成等差数列，则2()(),2()x x y x y x y x =++-⎧⎪⎨+=⎪⎩，即45y x =-，存在，选C.二、填空题（每小题5分，共30分） 11抛物线24y x =-的焦点坐标为_______.解析：焦点在x 轴上，开口向左，焦点坐标(1,0)-.12.在数列0，14，13，38，⋅⋅⋅，12n n -，⋅⋅⋅中，37是它的第_______项.解析：1327n n -=，解得7n =. 13.不等式111x >-的解集为_______. 解析：这个题谁错了谁请我吃饭哈.1101x ->-，即201x x -+>-，(2)(1)0x x --<，解得12x <<，即解集为{}|12x x <<.14.在正方体1111ABCD A B C D -中，E 为1CC 中点，则1CD 与平面11ADD A 所成角的大小为_______；CD 与AE 所成角小强数学的余弦值为_______. 解析:不建系干啥呢？想用几何法的自己算去. 设棱长为2建系就行，D 点为坐标原点.111sin cos ,2DC CD DC CD DC CD θ⋅====⨯⋅，故线面夹角4π； 42cos cos ,233DC AE DC AE DC AEϕ⋅====⨯⋅，故CD 与AE 所成角的余弦值为23. 15.设函数()(0)af x x a x=+>.①当1a =时，()f x 在区间(0,)+∞上的最小值为_______；②若()fx 在区间(2,)+∞上存在最小值，则满足条件的一个a 的值为_______.解析：①小对勾函数，最小值为2；②函数()f x 在上递减，在)+∞2，即4a >.16.已知椭圆1C ，抛物线2C 的焦点均在x 轴上，1C 的中心和2C 的顶点均为坐标原点. 下表给出坐标的5个点中，有两个点在C 上，小强数学另有两个点在C 上.112解析：(2,0)-肯定不过2C ，且2C 开口向右，若过2C ，不合题意，若(3,-过2C ，(4,4)-也过2C ，符合题意，即22:4C y x =；经判断，(2,0)-，在椭圆上，即221:14x C y +=， 1C 的左焦点为(，2C 准线为1x =-1.三、解答题（共6小题，80分）17.（本题13分）已知等差数列{}n a 的公差为2，且1a ，3a ，4a 成等比数列. （I ）求{}n a 的通项公式；（II ）设{}n a 的前n 项和为n S ，求20S 的值. 注意：给的是2d =，不是12a =，审题！解析:（I ）2314a a a =⋅，即2111(4)(6)a a a +=⋅+，解得18a =-，故1(1)82(1)210()n a a n d n n n N *=+-=-+-=-∈；（II ）1202020()10(822010)10222202a a S +==⨯-+⨯-=⨯=.18.（本题13分）已知函数2()2f x x ax =-，a R ∈. （I ）当1a =时，求满足()0f x <的x 的取值范围； （II ）解关于x 的不等式2()3f x a <.（III ）若对于任意的(2,)x ∈+∞，()0f x >均成立，求a 的取值范围.19.（本小题13分）已知椭圆2222:1(0)x y C a b a b+=>>(1,0)F .（I ）求椭圆C 的标准方程；（II ）直线:(2)l y k x =+交椭圆C 与A ，B 两点，若线段AB 中点小强数学的横坐标为23-，求直线l 的方程及FBA ∆的面积.20.（本小题14分）如图，四棱锥S ABCD -的底面是直角梯形，//AB CD ，90BAD ADC ∠=∠=︒，SD ⊥平面ABCD ，M 是SA 的中点，22AD SD CD AB ====.（I ）证明：DM ⊥平面SAB ；（II ）求二面角A SB C --的大小；（III ）线段SC 上是否存在一点E ，使得直线//SA 平面BDE .若存在，确定E 点的位置；若不存在，说明理由.21.（本小题14分）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12，左顶点B 与右焦点2F 之间的距离为3.（I ）求椭圆C 的标准方程；（II ）设直线()x t t a =>交x 轴于点S ，过2F 且斜率不为0的小强数学直线l 与椭圆C 相交于两点M ，N ，连接BM ，BN ，并延长分别与直线x t =交于两点P ，Q ，若22PF S F QS ∠=∠，求点S 的坐标.22.（本小题13分）已知a 为实数，数列{}n a 满足1a a =，13,3,()4,3,n n n n n a a a n N a a *+->⎧=∈⎨-+≤⎩.（I ）当0.2a =和7a =时，分别写出数列{}n a 的前5项； （II ）证明：当3a >时，存在正整数m ，使得02m a <≤；（III ）当01a ≤≤时，是否存在实数a 及正整数n ，使得小强数学数列的前{}n a 项和2019n S =？若存在，求出实数a 及正整数n 的值；若不存在，说明理由.。
2019年北京市西城区第二学期期末高二数学试卷(解析版)
北京市西城区2018—2019学年度第二学期期末试卷高二数学2019.7一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1.复数21i-的共轭复数是（ ） A. 1i + B. 1i - C. 1i -+ D. 1i -- 【答案】B 【解析】 【分析】先化简，再求共轭复数. 【详解】()()()2121111i i i i i +==+--+，所以复数21i-的共轭复数是1i -，故选B. 【点睛】本题考查复数的运算与共轭复数，属于基础题.2.已知()cos f x x =，则()f x '=（ ） A. cos x B. cos x - C. sin x D. sin x - 【答案】D 【解析】 【分析】根据余弦函数的求导公式即可. 【详解】()cos sin x x '=-，故选D.【点睛】本题考查常见函数的求导，属于基础题.3.用0，1，2，3，4，5这6个数字，可以组成没有重复数字的四位数的个数是( ) A. 360 B. 300 C. 240 D. 180 【答案】B 【解析】 【分析】分为有0和没0两类求解.【详解】当四个数字中没有0时，没有重复数字的四位数有：45120A =种；当四个数字中有0时，没有重复数字的四位数有：1335180A A =种,两类相加一共有300种，故选B.【点睛】本题考查排列组合与分类加法计数原理，考查分类讨论思想，属于基础题.4.曲线3y x x =+在点(0,0)处的切线方程为（ ） A. 2y x =- B. y x =- C. 2y x = D. y x = 【答案】D 【解析】 【分析】先求导求斜率，再求切线.【详解】231y x '=+，切线的斜率01x k y ='==，所以切线方程为y x =，故选D.【点睛】本题考查曲线的切线方程和导数的几何意义.b5.已知函数()f x 在R 上有导函数，()f x 图象如图所示，则下列不等式正确的是（ ）A. ()()()f a f b f c <''<'B. ()()()f b f c f a <''<'C. ()()()f a f c f b <''<'D. ()()()f c f a f b <''<' 【答案】A 【解析】 【分析】作出三点处的切线，比较斜率即可. 【详解】如图，分别作曲线,,x a x b x c ===三处的切线123,,l l l ， 设切线的斜率分别为123,,k k k ，易知123k k k <<，又123(),(),()f a k f b k f c k '''===，所以()()()f a f b f c '''<<. 故选A.【点睛】本题考查导数的几何意义，考查直线斜率的关系，属于基础题.6. 某班级要从4名男士、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为A．14 B．24 C．28 D．48【答案】A.【解析】法一：4人中至少有1名女生包括1女3男及2女2男两种情况，故不同的选派方案种数为．故选A.法二：从4男2女中选4人共有种选法，4名都是男生的选法有种，故至少有1名女生的选派方案种数为-=15-1=14．故选A7.甲、乙、丙、丁4个人进行网球比赛，首先甲、乙一组，丙、丁一组进行比赛，两组的胜者进入决赛，决赛的胜者为冠军、败者为亚军．4个人相互比赛的胜率如右表所示，表中的数字表示所在行选手击败其所在列选手的概率．那么甲得冠军且丙得亚军的概率是( )A. 0.15B. 0.105C. 0.045D. 0.21【答案】C【解析】【分析】若甲得冠军且丙得亚军，则甲、乙比赛甲获胜，丙、丁比赛丙获胜，决赛甲获胜.【详解】甲、乙比赛甲获胜的概率是0.3，丙、丁比赛丙获胜的概率是0.5， 甲、丙决赛甲获胜的概率是0.3，根据独立事件的概率等于概率之积，所以， 甲得冠军且丙得亚军的概率：0.30.50.30.045⨯⨯=. 故选C.【点睛】本题考查独立事件的概率，考查分析问题解决问题的能力.8.设01p <<，随机变量ξ的分布列为那么，当p 在(0,1)内增大时,()D ξ的变化是（ ） A. 减小 B. 增大 C. 先减小后增大 D. 先增大后减小 【答案】B 【解析】 【分析】先求期望，再求方差，根据函数单调性求解. 【详解】32()0121333p p p E ξ-=⨯+⨯+⨯= ()()()222322()0111213333p p p p D ξ-=-⨯+-⨯+-⨯=则()D ξ是在R 上的递增函数， 所以()D ξ是在(0,1)上的递增，故选B.【点睛】本题主要考查随机变量及其分布列，考查计算能力，属于基础题.9.已知函数2()1f x x =-，()ln g x x =，下列说法中正确的是（ ）A. (),()f x g x 在点(1,0)处有相同的切线B. 对于任意0x >，()()f x g x ≥恒成立C. (),()f x g x 的图象有且只有一个交点D. (),()f x g x 的图象有且只有两个交点 【答案】D 【解析】 【分析】根据导数与切线，函数的关系求解.【详解】因为()2f x x '=，(1)2f '=，1()g x x'=，(1)1g '=， 所以(),()f x g x 在点(1,0)处的切线不同。
北京市西城区2018-2019学年高二下学期期末考试文数试题Word版含解析
北京市西城区2018-2019学年下学期期末考试高二文数试题第Ⅰ卷（共60分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则( )A. B. C. D.【答案】B【解析】分析：由题意，求得，利用集合的交集的运算，即可得到答案.详解：由题意可得，，所以，故选B.点睛：本题主要考查了集合的运算，其中正确求解集合和准确把握集合的交集运算是解答的关键，着重考查了推理与运算能力.2.下列函数中，定义域为的单调递减函数是( )A. B. C. D.【答案】C【解析】分析：根据基本初等函数的性质，逐一判定即可得到答案.详解：由题意，函数在上不是单调函数，所以A不正确；函数在是单调递减函数，在上不是单调函数，所以B不正确；函数在上是单调递减函数，所以C正确；函数的定义域为，所以D不正确，综合可知，只有函数在上是单调递减函数，故选C.点睛：本题主要考查了函数的单调性的判定，其中熟记基本初等函数的性质是解答的关键，着重考查了推理与论证能力，属于基础题.3.在复平面内，复数对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】C【解析】分析：利用复数的运算法则，求解，再根据复数的表示，即可得到答案.详解：由题意，复数，所以在复平面内对应点的坐标为，所以复数对应的点位于第三象限，故选C.点睛：本题主要考查了复数的运算与复数的表示，其中熟记复数的四则运算法则和复数的表示是解答的关键，着重考查了推理与运算能力.4.如果，那么下列不等式一定成立的是( )A. B. C. D.【答案】B【解析】分析：根据幂函数的单调性，即可判定得到答案.详解：当时，此时，但，且，所以A、C不正确；由函数为单调递增函数，当时，，所以D不正确，由函数是上的单调递增函数，所以当时，成立，所以B是正确的，故选B.点睛：本题主要考查了不等式的比较大小问题，其中熟记幂函数的单调及其应用是解答的关键，着重考查了推理与论证能力.5.执行如图所示的程序框图，若输入的，则输出的属于( )..A. B. C. D.【答案】D【解析】分析：根据题意，执行循环结构的程序框图，根据二次函数的性质，求解函数的值域，即可得到结果.详解：由题意，根据给定的程序框图可知：输入，不满足判断条件，计算，满足条件，计算的值域，输出，故选D.点睛：识别算法框图和完善算法框图是近年高考的重点和热点．解决这类问题：首先，要明确算法框图中的顺序结构、条件结构和循环结构；第二，要识别运行算法框图，理解框图解决的问题；第三，按照框图的要求一步一步进行循环，直到跳出循环体输出结果，完成解答．近年框图问题考查很活，常把框图的考查与函数和数列等知识考查相结合．6.已知函数的定义域为，则“为奇函数”是“”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】试题分析：因函数的定义域是,故,是充分条件；反之,若,则函数不一定是奇函数,不是必要条件,如函数,应选A.考点：充分必要条件.7.若，则( )A. B. C. D.【答案】C【解析】分析：根据对数及其对数的运算的性质，利用作差比较法，即可得到的大小关系.详解：由题意，，则，所以，又由，所以，所以，故选C.点睛：本题主要考查了对数式的比较大小问题，其中熟记对数的运算及对数函数的图象与性质，合理采用作差比较法是解答的关键，着重考查了推理与运算能力，以及转化思想方法的应用.8.某电影院共有个座位.某天，这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生，三所学校的观影人数分别是985人， 1010人，2019人(同一所学校的学生有的看上午场，也有的看下午场，但每人只能看一-场).已知无论如何排座位，这天观影时总存在这样的一个座位，上、下午在这个座位上坐的是同一所学校的学生，那么的可能取值有( )A. 12个B. 11个C. 10个D. 前三个答案都不对【答案】A【解析】分析：由题意要保证三所学校的学生都看一场电影，则，依次验证即可得到答案.详解：由题意要保证三所学校的学生都看一场电影，则，当时，则丙中学的学生2019人中分上、下场至少有12人在同一座位上；当时，则丙中学的学生2019人中分上、下场至少有11人在同一座位上；当时，则丙中学的学生2019人中分上、下场至少有1人在同一座位上；当时，则甲乙丙中学的学生可以没有人在同一座位上；所以当有取法，即有12个取值，故选A.点睛：本题主要考查了适应应用问题，其中解答中正确理解题意，合理选择方法是解答的关键，着重考查了分析问题和解答问题的能力，以及推理与论证能力，试题属于中档试题.第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9.已知命题，则__________.【答案】.【解析】分析：根据全称命题和存在性命题的关系，即可作出命题的否定.详解：由题意，根据全称命题与存在性命题的关系可知：命题：“”的否定：“”.点睛：本题主要考查了命题的否定，其中熟记全称命题存在性命题的关系是正确作出改写的关键，着重考查了推理与论证能力.10.曲线在处切线的斜率为__________.【答案】.【解析】因为，且，即函数在处的切线的斜率为.11.当时，函数的最小值为__________.【答案】3.【解析】分析：由题意，函数化为，利用基本不等式的求解，即可得到答案.详解：由题意，函数，当且仅当，即取得等号，所以函数的最小值为.点睛：本题主要考查了利用基本不等式求最小值，其中解答中熟记基本不等式的使用条件和合理对函数作出化简，构成基本不等式的使用条件是解答的关键，利用着重考查了转化思想方法，以及推理与运算能力.12.已知实数满足，则__________.【答案】4.【解析】分析：由题意得出，再利用对数的运算公式化简，即可得到结果.详解：由题意满足，则，则.点睛：本题主要考查了实数指数幂的运算和对数的运算的综合应用，其中熟记实数指数幂的运算公式和对数的运算公式的合理运用是解答的关键，着重考查了推理与运算能力.13.若函数则__________；使得方程有且仅有两解的实数的取值范围为__________．【答案】 (1). 0. (2). .【解析】分析：要使得方程有且仅有两解，则只需使得和的图象有两个不同的交点，作出函数的图象，结合图象，即可求解.详解：由题意，函数，则，要使得方程有且仅有两解，则只需使得和的图象有两个不同的交点，作出函数的图象，如图所示，结合图象可知，要使的方程有且仅有两解，只需，即实数的取值范围是.点睛：本题考查了分段的求值和分段函数的图象的应用，其中解答中把使得方程有且仅有两解，则只需使得和的图象有两个不同的交点，作出函数的图象，是解答的关键，着重考查了数形结合思想和转化思想方法的应用.14.某个产品有若千零部件构成，加工时需要经过6道工序，分别记为.其中，有些工序因为是制造不同的零部件，所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理，所以存在加工顺序关系.若加工工序必须要在工序完成后才能开工，则称为的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下：现有两台性能相同的生产机器同时加工该产品，则完成该产品的最短加工时间是__________小时.（假定每道工序只能安排在一台机器上，且不能间断）.【答案】8.【解析】分析：由题意，根据题意两台性能相同的生产机器同时加工该产品，确定好加工顺序，即可得到答案.详解：由题意，可确定如图所示的加工顺序，如图所示，可得用两台性能相同的生产机器同时加工该产品，要完成该产品的最短加工时间为8小时.点睛：本题主要考查了实际应用问题，其中解答中正确理解题意，分析工艺的流程，确定好加工的顺序，得出加工顺序的图形是解答的关键，着重考查了分析问题和解答问题的能力，以及推理与论证能力.三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15.已知函数，且.(Ⅰ)求的值.(Ⅱ)写出能够说明“任给，”是假命题的一组的值.【答案】(1)-1.(2) 答案不唯一，如.【解析】分析：（Ⅰ）解：由题意，解得，确定函数的解析式，即可求解；(Ⅱ)根据对数函数的图象与性质和一次函数的图象与性质，即可得出其中一组解.详解：（Ⅰ）解：由题意，所以，即.则.(Ⅱ)解：答案不唯一，如.点睛：本题主要考查了对数函数的图象与性质以及对数的基本运算，其中熟记对数的运算公式和对数函数的图象与性质是解答的关键，着重考查了推理与运算能力.16.已知函数，其中.(Ⅰ)若，解不等式；(Ⅱ)记不等式的解集为，若，求的取值范围.【答案】(1) ，或.(2) .【解析】分析：（Ⅰ）解：由题意，当时，得不等式，根据一元二次不等式的解法，即可求得不等式的解集；(Ⅱ) 由不等式的解集为，且，得，即，分类讨论，即可求解实数的取值范围.详解：（Ⅰ）解：由题意，得不等式，解得，或.所以不等式的解集为，或.(Ⅱ)解：因为不等式的解集为，且，所以，即当时，不等式不成立；当时，不等式等价于，解得.综上，的取值范围是.点睛：本题主要考查了一元二次不等式的解法以及一元二次函数的应用，其中熟记一元二次不等式的解法和一元二次函数的图像与性质是解答的关键，着重考查了推理与运算能力和转化思想方法的应用.17.设，函数在区间上单调递增，在区间上单调递减.（Ⅰ）求满足的关系；（Ⅱ）求证:.【答案】(1) .(2)证明见解析.【解析】分析：(Ⅰ)求导，得，由题意可得，即可得到答案；(Ⅱ)解：由(Ⅰ)，可得函数，求得，分类讨论得出函数的单调性，即可证得结论.详解：(Ⅰ)解：求导，得.因为函数在区间上单调递增，在区间上单调递减，所以.即(Ⅱ)解：由(Ⅰ)，得，即.所以，.当时，得当时，，此时，函数在上单调递增，这与题意不符.当时，随着的变化，与的变化情况如下表：所以函数在，上单调递增，在上单调递减.因为函数在区间上点掉递增，在区间上单调递减，所以时符合题意.综上，.点睛：本题主要考查了导数在函数中的应用，以及不等式的证明，着重考查了转化与化归思想、逻辑推理能力与计算能力，其中熟记导函数与原函数的关系，准确运算是解答此类问题的关键，同时注意转化思想方法和数形结合思想的应用.18.现行的个税法修正案规定：个税免征额由原来的2000元提高到3500元，并给出了新的个人所得税税率表：例如某人的月工资收入为5000元，那么他应纳个人所得税为：（元）.（Ⅰ）若甲的月工资收入为6000元，求甲应纳的个人收的税；（Ⅱ）设乙的月工资收入为元，应纳个人所得税为元，求关于的函数；（Ⅲ）若丙某月应纳的个人所得税为1000元，给出丙的月工资收入.（结论不要求证明）【答案】(1) （元）.(2) .(3) 丙的月工资收入为11275元.【解析】分析：(Ⅰ)根据题意，利用表格中的要求，即可计算甲的月工资收入为6000元，其应纳的个人所得税；(Ⅱ)根据题意，借助表格总的要求，分别计算收入在不同的范围内的应用的函数解析式，最后利用分段函数表示应纳个人所得税与的函数关系式；（Ⅲ）由（2）中的函数的解析式，即可得到丙的月工资收入.详解：(Ⅰ)解：甲的月工资收入为6000元，其应纳的个人所得税为（元）.(Ⅱ)解：当时，乙应纳个人所得税元.当时，乙应纳个人所得税元.当时，乙应纳个人所得税元.当时，乙应纳个人所得税元.所以（Ⅲ）丙的月工资收入为11275元.点睛：本题主要考查了函数的实际应用问题，其中解答中认真审题，正确理解题意，根据题设的要求，找出合适的等量关系，建立函数解析式是解答的挂念，着重考查了分析问题和解答问题的能力.19.设函数，其中.（Ⅰ）当时，求函数的极值；（Ⅱ）当时，证明：函数不可能存在两个零点.【答案】(1) 存在极小值，不存在极大值.(2)证明见解析.【解析】分析：(Ⅰ)由题意得，因为，所以，进而得出函数的单调性，求解函数的极值；(Ⅱ)由方程，得，由，得，得出函数的单调性与极值，即可判定函数至多在区间存在一个零点，得出结论.详解：(Ⅰ)解：求导，得，因为，所以，所以当时，，函数为减函数；当时，，函数为增函数.故当时，存在极小值，不存在极大值.(Ⅱ)证明：解方程，得.由，得.随着的变化，与的变化情况如下表：所以函数在，上单调递增，在上单调递减.又因为，所以函数至多在区间存在一个零点；所以，当时函数不可能存在两个零点.点睛：本题主要考查导数在函数中的应用，以及不等式的证明，着重考查了转化与化归思想、逻辑推理能力与计算能力，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，求解曲线在某点处的切线方程；(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数；(3)利用导数求函数的最值(极值)，解决函数的恒成立与有解问题，同时注意数形结合思想的应用.20.已知函数.（Ⅰ）求曲线在点处的切线方程；（Ⅱ）若函数在区间上单调递增，求实数的取值范围；（Ⅲ）设函数，其中.证明：的图象在图象的下方.【答案】(1) .(2) .(3)证明见解析.【解析】分析：（Ⅰ）求出函数的导数，计算和的值，点斜式求出切线方程即可.（Ⅱ）设，并求导.将问题转化为在区间上，恒成立，或者恒成立，通过特殊值，且，确定恒成立，通过参数分离，求得实数的取值范围；(Ⅲ）设，将问题转化为证明，利用函数的导数确定函数最小值在区间，并证明. 即的图象在图象的下方.详解：解：（Ⅰ）求导，得，又因为所以曲线在点处的切线方程为（Ⅱ）设函数，求导，得，因为函数在区间上为单调函数，所以在区间上，恒成立，或者恒成立，又因为，且，所以在区间，只能是恒成立，即恒成立.又因为函数在在区间上单调递减，，所以.(Ⅲ）证明：设.求导，得.设，则（其中）.所以当时，（即）为增函数.又因为，所以，存在唯一的，使得且与在区间上的情况如下：所以，函数在上单调递减，在上单调递增，所以.又因为，，所以，所以，即的图象在图象的下方.点睛：本题考查了利用导数研究曲线在某点处的切线方程，函数的单调性与导数的关系，考查了恒成立问题的参数分离方法. 将的图象在图象的下方，通过构造新函数，转化恒成立是解题关键.。
2019-2020学年北京市西城区数学高二下期末考试试题含解析
2019-2020学年北京市西城区数学高二下期末考试试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知扇形的圆心角为150︒，弧长为()5rad π，则扇形的半径为（ ） A ．7 B ．6C ．5D ．4【答案】B 【解析】 【分析】求得圆心角的弧度数，用lr α=求得扇形半径.【详解】依题意150为5π6，所以5656lr ππα===．故选B. 【点睛】本小题主要考查角度制和弧度制转化，考查扇形的弧长公式的运用，属于基础题. 2．复数(1)(2)z i i =--（i 为虚数单位），则z 的共轭复数z 的虚部是（ ） A ．3i B ．3i -C ．3D ．3-【答案】C 【解析】分析：求出复数z ，得到z ，即可得到答案. 详解：()()1213,13,z i i i z i =--=-∴=+ 故z 的共轭复数z 的虚部是3. 故选C.点睛：本题考查复数的乘法运算，复数的共轭复数等，属基础题. 3．复数2ii+的虚部为（ ） A ．2- B ．1-C ．1D ．2【答案】A 【解析】 【分析】由复数除法化复数为代数形式，根据复数概念可得． 【详解】 因为()()()2i i 2i 12i i i i +⋅-+==-⋅-，所以复数2ii+的虚部为2-，故选：A. 【点睛】本题考查复数的除法运算，考查复数的概念．属于简单题． 4． “0x ∀>，2sin x x >”的否定是( ) A ．0x ∀>，2sin x x < B ．0x ∀>，2sin x x ≤ C ．00x ∃≤，002sin x x ≤ D ．00x ∃>，002sin x x ≤【答案】D 【解析】 【分析】通过命题的否定的形式进行判断． 【详解】因为全称命题的否定是特称命题，故“0x ∀>， 2sin x x >”的否定是“00x ∃>， 002sin x x ≤”. 故选D. 【点睛】本题考查全称命题的否定，属基础题. 5．给出下列四个说法：①命题“0,x 都有12x x +≥”的否定是“00,x ∃≤使得012x x +<”；②已知0a b 、＞>a b >”的逆命题是真命题；③1x >是21x >的必要不充分条件;④若0x x =为函数2()2ln xf x x x x e -=++-的零点，则002ln 0x x +=，其中正确的个数为（ ）A ．0B ．1C ．2D ．3【答案】C 【解析】 【分析】对于①②③④分别依次判断真假可得答案. 【详解】 对于①，命题“0,x 都有12x x+≥”的否定是“00,x ∃>使得0012x x +<”，故①错误；对于②，>a b >”的逆命题为“若a b >>1x >则21x >，若21x >则1x >或1x <-，因此1x >是21x >的充分不必要条件，故③错误；对于④，若0x x =为函数2()2ln x f x x x x e -=++-，则020002ln =0x x x x e -++-，即()020000=2ln 0x x x e x x --+>，可令000()2ln h x x x =+，则002'()10h x x =+>，故0()h x 为增函数，令()02000=()0x g x e x x -->，显然0()g x 为减函数，所以方程00()=()h x g x 至多一解，又因为002ln 0x x +=时022000ln 0x x x e x ---∴==，所以002ln 0x x +=，则④正确，故选C. 【点睛】本题主要考查真假命题的判断，难度中等.6．在平面直角坐标系中，设点(),P x y ，定义[]OP x y =+，其中O 为坐标原点，对于下列结论：()1符合[]2OP =的点P 的轨迹围成的图形面积为8； ()2设点P220y +-=上任意一点，则[]1min OP =；()3设点P 是直线：()1y kx k R =+∈上任意一点，则使得“[]OP 最小的点有无数个”的充要条件是1k =；()4设点P 是椭圆2219x y +=上任意一点，则[]max OP =．其中正确的结论序号为( ) A ．()()()123 B ．()()()134C ．()()()234D ．()()()124【答案】D 【解析】 【分析】()1根据新定义由[]1OP x y =+=，讨论x 、y 的取值，画出分段函数的图象，求出面积即可；()2运用绝对值的含义和一次函数的单调性，可得[]OP 的最小值；()3根据k 等于1或1-都能推出[]OP 最小的点P 有无数个可判断其错误；()4把P 的坐标用参数表示，然后利用辅助角公式求得[]OP x y =+的最大值说明命题正确． 【详解】()1由[]2OP =，根据新定义得：2x y +=，由方程表示的图形关于,x y 轴对称和原点对称，且()202,02x y x y +=≤≤≤≤，画出图象如图所示：四边形ABCD 为边长是228，故()1正确；()()2,P x y 为直线3220x y +-=上任一点，可得312y x =-， 可得31x y x +=+， 当0x ≤时，[]3111OP x ⎛=-+≥ ⎝⎭；当03x <<时，[]3113OP x ⎛⎛=+∈ ⎝⎝⎭； 当3x ≥时，可得[]31123OP x ⎛⎫=-++≥ ⎪ ⎪⎝⎭[]OP 的最小值为1，故()2正确； ()()311x y x y k x +≥+=++，当1k =-时，11x y +≥=，满足题意；而()11x y x y k x +≥-=--，当1k =时，11x y +≥-=，满足题意，即1k =±都能 “使[]OP 最小的点P 有无数个”，()3不正确；()4点P 是椭圆2219x y +=上任意一点，因为求最大值，所以可设3cos x θ=，sin y θ=，0,2πθ⎡⎤∈⎢⎥⎣⎦，[]()3cos sin 10sin OP x y θθθϕ=+=+=+，0,2πθ⎡⎤∈⎢⎥⎣⎦，[]10max OP ∴=()4正确．则正确的结论有：()1、()2、()4，故选D ． 【点睛】此题考查学生理解及运用新定义的能力，考查了数形结合的数学思想，是中档题．新定义题型的特点是：通过给出一个新概念，或约定一种新运算，或给出几个新模型来创设全新的问题情景，要求考生在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，实现信息的迁移，达到灵活解题的目的.遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，“照章办事”，逐条分析、验证、运算，使问题得以解决.7．已知,,a b c 为正数，则“222a b c +>”是“a b c +>”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】A 【解析】 【分析】根据不等式的关系，结合充分条件和必要条件的定义进行判断即可． 【详解】①当2,2,3a b c ===时，满足a b c +>， 但222a b c +>不成立，即必要性不成立， ②若222a b c +>，则22()2a b ab c +->， 即222()2a b c ab c +>+>，故a b c +>，成立，即充分性成立，综上所述，“a b c +>”是“222a b c +>”的充分不必要条件． 故选：A ． 【点睛】本题主要考查了判断必要不充分条件，解题关键是掌握判断充分条件和必要条件的方法，考查了分析能力和计算能力，属于基础题.8．已知一袋中有标有号码1、2、3的卡片各一张，每次从中取出一张，记下号码后放回，当三种号码的卡片全部取出时即停止，则恰好取5次卡片时停止的概率为（ ） A ．585B ．1481C ．2281D ．2581【答案】B 【解析】分析：由题意结合排列组合知识和古典概型计算公式整理计算即可求得最终结果. 详解：根据题意可知，取5次卡片可能出现的情况有53种； 由于第5次停止抽取，所以前四次抽卡片中有且只有两种编号， 所以总的可能有()24322C -种； 所以恰好第5次停止取卡片的概率为()24352214381C p -==.本题选择B 选项.点睛：有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数．(1)基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举．(2)注意区分排列与组合，以及计数原理的正确使用.9．设函数()f x 满足()()()222,2,8x e e x f x xf x f x +=='则0x >时，()f x ( )A ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值又有极小值D ．既无极大值也无极小值【答案】D 【解析】 【分析】 【详解】函数()f x 满足2'()2()xex f x xf x x+=，()2'x e x f x x⎡⎤∴=⎣⎦，令()()2F x x f x =， 则()()()2',24?22x e e F x F f x ===，由()()2'2x e x f x xf x x +=，得()()32'x e F x f x x-=，令()()2xx e F x ϕ=-， 则()()()2'2',x xe x x e F x xϕ-=-=()x ϕ∴在()0,2上单调递减，在()2,+∞上单调递增， ()x ϕ∴的最小值为()()()22220,0e F x ϕϕ=-=∴≥.又()()0,'0,x f x f x >∴≥∴在()0,∞+单调递增，()f x ∴既无极大值也无极小值，故选D.考点：1、利用导数研究函数的单调性；2、利用导数研究函数的极值及函数的求导法则. 【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则，属于难题.求解这类问题一定要耐心读题、读懂题，通过对问题的条件和结论进行类比、联想、抽象、概括，准确构造出符合题意的函数是解题的关键；解这类不等式的关键点也是难点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数.本题通过观察导函数的“形状”，联想到函数()()2F x x f x =，再结合条件判断出其单调性，进而得出正确结论.10．已知定义在R 上的连续奇函数()f x 的导函数为()f x '，当0x >时，()()0f x f x x'+>，则使得()()()2213310xf x x f x +-->成立的x 的取值范围是（ ）A ．()1,+∞B ．()11,1,5⎛⎫-+∞ ⎪⎝⎭C ．1,15⎛⎫⎪⎝⎭D ．(),1-∞【答案】C 【解析】 【分析】根据0x >时()()0f x f x x'+>可得：()()0xf x f x '+>；令()()g x xf x =可得函数在()0,∞+上单调递增；利用奇偶性的定义可证得()g x 为偶函数，则()g x 在(),0-∞上单调递减；将已知不等式变为()()231g x g x >-，根据单调性可得自变量的大小关系，解不等式求得结果.【详解】当0x >时，()()0f x f x x'+> ()()0xf x f x '∴+>令()()g x xf x =，则()g x 在()0,∞+上单调递增()f x 为奇函数 ()()()()g x xf x xf x g x ∴-=--== ()g x ∴为偶函数则()g x 在(),0-∞上单调递减()()()2213310xf x x f x ∴+-->等价于()()231g x g x >-可得：231x x >-，解得：115x << 本题正确选项：C 【点睛】本题考查函数奇偶性和单调性的综合应用问题，关键是能够构造函数，根据导函数的符号确定所构造函数的单调性，并且根据奇偶性的定义得到所构造函数的奇偶性，从而将函数值的大小关系转变为自变量之间的比较.11．已知函数3()3(,)f x ax bx a b =++∈R .若(2)5f =，则(2)f -=（ ） A ．4 B ．3 C ．2 D ．1【答案】D 【解析】 【分析】令()3g x ax bx =+，则()g x 是R 上的奇函数，利用函数的奇偶性可以推得(2)f -的值．【详解】令3()g x ax bx =+ ，则()g x 是R 上的奇函数，又(2)3f =，所以(2)35g +=， 所以(2)2g =，()22g -=-，所以(2)(2)3231f g -=-+=-+=，故选D. 【点睛】本题主要考查函数的奇偶性的应用，属于中档题．12．已知变量x ，y 之间具有线性相关关系，其回归方程为()ˆ1yax a =--，若615ii x==∑，618i i y ==∑，则a 的值为( ) A ．1411B ．32C ．711D ．1【答案】A 【解析】 【分析】 根据题意615i i x ==∑，618i i y ==∑可知，56x =，43y =，代入即可求这组样本数据的回归直线方程，即可求解出答案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019北京市西城区高二（下）期末数学 2019.7 本试卷共5页，共150分。
考试时长120分钟。
考生务必将答案写在答题纸上，在试卷上作答无效。
一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.10. 算筹是在珠算发明以前我国独创并且有效的计算工具，为我国古代数学的发展做出了很大贡献.在算筹计数法中，以“纵式”和“横式”两种方式来表示数字，如下图：表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推，遇零则置空，如下图：67286708如果把5根算筹以适当的方式全部放入右面的表格中，那么可以表示的三位数的个数为（）（A）46（B）44（C）42（D）40二、填空题：本大题共6小题，每小题5分，共30分. 11. 已知函数e xy x=，则=')1(f _______.12. 二项式261(2)x x -的展开式中的常数项是_______.（用数字作答）13. 若复数z 满足i 12i z ⋅=+，则||z =_________.14. 能说明“若(0)=0f '，则0x =是函数()y f x =极值点”为假命题的一个函数是______________．15. 北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌，如图所示.设某人到达银行的时间是随机的，记其到达银行时服务窗口的个数为X ，则()E X =______________．16. 容器中有,,A B C 3种粒子，若相同种类的两颗粒子发生碰撞，则变成一颗B 粒子；不同种类的两颗粒子发生碰撞，会变成另外一种粒子. 例如，一颗A 粒子和一颗B 粒子发生碰撞则变成一颗C 粒子.现有A 粒子10颗，B 粒子8颗，C 粒子9颗，如果经过各种两两碰撞后，只剩1颗粒子. 给出下列结论： ① 最后一颗粒子可能是A 粒子 ② 最后一颗粒子一定是C 粒子③ 最后一颗粒子一定不是B 粒子 ④ 以上都不正确其中正确结论的序号是________.（写出所有正确结论的序号）三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分13分）已知函数321()3f x x x bx =-+，且(2)3f '=-. （Ⅰ）求b ；（Ⅱ）求()f x 的单调区间.某工厂生产一种汽车的元件，该元件是经过A、B、C三道工序加工而成的，A、B、C三道工序加工的元件合格率分别为12、23、34．已知每道工序的加工都相互独立，三道工序加工都合格的元件为一等品；恰有两道工序加工合格的元件为二等品；其它的为废品，不进入市场．（Ⅰ）生产一个元件，求该元件为二等品的概率；（Ⅱ）若从该工厂生产的这种元件中任意取出3个元件进行检测，求至少有2个元件是一等品的概率.19．（本小题满分13分）已知函数()()e xf x x a=+.（Ⅰ）求()f x的单调区间；（Ⅱ）求()f x在区间[0,4]上的最小值.20．（本小题满分13分）某校在学年期末举行“我最喜欢的文化课”评选活动，投票规则是一人一票，高一（1）班44名学生和高一（7）班45名学生的投票结果如下表（无废票）：该校把上表的数据作为样本，把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.（Ⅰ）如果数学学科的“好感指数”比高一年级其他文化课都高，求a的所有取值；（Ⅱ）从高一（1）班投票给政治、历史、地理的学生中任意选取3位同学，设随机变量X为投票给地理学科的人数，求X的分布列和期望；（Ⅲ）当a为何值时，高一年级的语文、数学、外语三科的“好感指数”的方差最小?（结论不要求证明）已知函数()e ln x f x a x x =--.（Ⅰ）当1a =-时，求曲线()y f x =在点(1,(1))f 处的切线方程； （Ⅱ）若()f x 在区间(0,1)上存在极值点，求a 的取值范围.22．（本小题满分14分）已知函数ln ()(1)xf x a x x=+-. （Ⅰ）若0a =，求()f x 的极值；（Ⅱ）若在区间()∞+，1上()0f x <恒成立，求a 的取值范围； （Ⅲ）判断函数()f x 的零点个数.（直接写出结论）2019北京市西城区高二（下）期末数学参考答案一、选择题：本大题共10小题，每小题4分，共40分.1. B2. D3. B4. D5. A6. A7. C8. B9. D 10. B 二、填空题：本大题共6小题，每小题5分，共30分. 11. 0 12. 6014. 3()f x x = 或()1f x =等，答案不唯一 15. 3.5625 16. ①③注：16题选对一个正确结论得3分，错选不得分. 三、解答题：本大题共6小题，共80分. 17. （本小题满分13分）解：（Ⅰ）由已知2()2f x x x b '=-+， ……………………3分所以 (2)443f b '=-+=-，所以 3b =-. ……………………5分 （Ⅱ）由（Ⅰ）知2()23f x x x '=--，解()0f x '>，得1x <-或3x >，解()0f x '<，得13x -<<. ……………………9分 所以函数()f x 的单调递增区间为(,1)-∞-，(3,)+∞，单调递减区间为(1,3)-.……………………13分18. （本小题满分13分）解：（Ⅰ）不妨设元件经,,A B C 三道工序加工合格的事件分别为,,A B C .所以1()2P A =,2()3P B =,3()4P C =.1()2P A =,1()3P B =,1()4P C =. …………2分设事件D 为“生产一个元件，该元件为二等品”. 由已知,,A B C 是相互独立事件.根据事件的独立性、互斥事件的概率运算公式，()()P D P ABC ABC ABC =++()()()P ABC P ABC P ABC =++ ………………6分123123123(1)(1)(1)234234234=-⨯⨯+⨯-⨯+⨯⨯-11.24=所以生产一个元件，该元件为二等品的概率为1124. ……………………8分 （Ⅱ）生产一个元件，该元件为一等品的概率为12312344p =⨯⨯=. ……………………9分设事件E 为“任意取出3个元件进行检测，至少有2个元件是一等品”，则2233131()()()444P E C =⨯+ ……………………12分1056432==. 所以至少有2个元件是一等品的概率为532. ……………………13分 19.（本小题满分13分）解：（Ⅰ）()e ()e (1)e x x x f x x a x a '=++=++. ……………………2分由()0f x '>，解得1x a >--； 由()0f x '<，解得1x a <--.所以函数()f x 的单调减区间为(,1)a -∞--，单调增区间为(1,)a --+∞. ………4分 （Ⅱ）① 当14a --≥，即5a ≤-时，()f x 在[0,4]上单调递减，所以4min ()(4)(4)e .f x f a ==+ ……………………7分 ② 当10a --≤，即1a ≥-时， ()f x 在[0,4]上单调递增，所以min ()(0).f x f a == ……………………10分③ 当51a -<<-时，所以1min 1()(1)e .e a a f x f a --+=--=-=-……………………13分综上，当5a ≤-时，4min ()(4)e f x a =+；当1a ≥-时，min ()f x a =；当51a -<<-时，min 11().e a f x +=-20.（本小题满分13分）解：（Ⅰ）由已知14a b += ，所以14b a =-. ……………………1分依题意， 966,967,a b +>+⎧⎨+>+⎩ ……………………3分即 966,967(14),a a +>+⎧⎨+>+-⎩解得 69a <<，又a ∈N ，所以 7a =，8a =. ……………………4分 （Ⅱ）由已知，随机变量X 是高一（1）班同学中投票给地理学科的人数，所以0,1,2X =. ……………………5分36385(0)14C P X C ===， ……………………6分21623815(1)28C C P X C ===， ……………………7分 1262383(2)28C C P X C ===. ……………………8分 9分51533()0121428284E X =⨯+⨯+⨯=. ……………………10分（Ⅲ）7a =或8a =. ……………………13分 21.（本小题满分14分）解：（Ⅰ） 当1a =-时，()e ln x f x x x =+-，0x >.所以1()e 1x f x x'=+-， ……………………2分 所以 (1)e 1f =-，(1)e f '=，曲线()y f x =在点(1,(1))f 处的切线方程为(e 1)e(1)y x --=-，整理得 e 10.x y --= ……………………4分 （Ⅱ）因为()e ln x f x a x x =--，0x >.所以e ()e 1x xa x x af x x x--'=--=， ……………………6分依题意，()f x '在区间(0,1)上存在变号零点. ……………………7分 因为0x >，设()e x g x x x a =--，所以()g x 在区间(0,1)上存在变号零点. ……8分 因为()e (1)1x g x x '=+-， ……………………9分 所以，当(0,1)x ∈时，e 1x >，11x +>，所以e (1)1x x +>，即()0g x '>，所以()g x 在区间(0,1)上为单调递增函数， ……………………12分 依题意， (0)0,(1)0,g g <⎧⎨>⎩ 即0,e 10.a a -<⎧⎨-->⎩……………………13分解得 0e 1a <<-. ……………………14分 所以，若()f x 在区间(0,1)上存在极值点，a 的取值范围是(0,e 1)-. 22.（本小题满分14分）解：（Ⅰ）当0a =时，定义域为{|0}x x >.因为ln ()x f x x =，所以21ln ()xf x x -'=. ……………………1分 令()0f x '=，解得e x =，所以()f x 在区间(0,e)上单调递增，在区间(e,+)∞上单调递减. ……………3分 所以()f x 有极大值，极大值为1(e)ef =；没有极小值. ……………………4分 （Ⅱ）因为0x >，所以在(1,)+∞上()0f x <恒成立，即2ln 0x ax ax +-<在(1,)+∞恒成立. ……………………5分设2()ln .g x x ax ax =+-①当0a ≥时，(2)ln 220g a =+>，不符合题意. ……………………7分 ②当0a <时，2121()2ax ax g x ax a x x-+'=+-=. ……………………8分 令()0g x '=,即2210ax ax -+=，因为方程2210ax ax -+=的判别式280a a ∆=->，两根之积102a<. 所以()0g x '=有两个异号根. 设两根为12,x x ，且120x x <<， ……………………9分i ）当21x >时，所以()g x 在区间2(1,)x 上单调递增，在区间2(,+)x ∞上单调递减，所以2()(1)0g x g >=，不符合题意； ……………………10分 ii ）当21x ≤时，(1)0g '≤，即1a ≤-时，()g x 在(1,)+∞单调递减，所以当(1,)x ∈+∞时，()(1)0g x g <=，符合题意.综上，1a ≤-. ……………………11分（Ⅲ）当0a ≥或1a =-时，()f x 有1个零点；当0a <且1a ≠-时，函数()f x 有2个零点.……………………14分16题提示：1、最后剩下的可能是A粒子10颗A粒子两两碰撞，形成5颗B粒子；9颗C粒子中的8个两两碰撞，形成4颗B粒子；所有的17颗B粒子两两碰撞，剩下一颗B粒子；这个B粒子与剩下的一颗C粒子碰撞形成A粒子。