第2章 能级与辐射b汇总
《原子物理学》(褚圣麟)第二章 原子的能级和辐射要点
第2章 原子的能级和辐射
一、 黑体辐射 普朗克能量子
第2章 原子的能级和辐射 二、光电效应 爱因斯坦光量子 （1）光电效应的实验规律
早在1887年,德国物理学家赫兹第一个观察到用紫光照射的尖端放电特别容 易发生，这实际上是光电效应导致的。由于当时还没有电子的概念，所以对其机 制不是很清楚。直到1897年汤姆逊发现了电子。人们才注意到一定频率的光照 射在金属表面上时，有大量电子从表面逸出，称之为光电效应。
第2章 原子的能级和辐射
经过近二个月的努力，普朗克在同年12月14日的一次德国物理学会议上提出： 对一定频率的电磁波，物体只能以 h为单位吸收或发射它，即吸收或发射电磁 波只能以“量子”方式进行，每一份能量 叫一能量子。
电子辐射的能量
E nhv (n 1,2,3)
这一概念严重偏离了经典物理；因此，这一假设提出后的5年时间内，没有 引起人的注意，并且在这以后的十多年时间里，普朗克很后悔当时的提法，在 很多场合他还极力的掩饰这种不连续性是“假设量子论”。
难点 • 量子理论的建立
• 空间量子化
第2章 原子的能级和辐射
2.1 玻尔理论的实验基础
1. 黑体辐射 普朗克能量子 2. 光电效应 爱因斯坦光量子 3. 氢原子光谱
第2章 原子的能级和辐射
卢瑟福模型把原子看成由带正电的原子核和围绕核运动的一些电子组成， 这个模型成功地解释了α粒子散射实验中粒子的大角度散射现象，可是当我们 准备进入原子内部作进一步的考察时，却发现已经建立的物理规律无法解释原 子的稳定性，同一性和再生性。
原子能级和辐射知识点总结
原子能级和辐射知识点总结一、原子能级1. 原子结构原子是由原子核和绕核运动的电子组成的，原子核由质子和中子组成，质子带正电荷，中子不带电。
电子是带负电的，围绕原子核轨道运动。
2. 能级原子的电子围绕原子核运动时，由于受到电子自旋磁矩和轨道磁矩的相互作用，会产生能级分裂，形成多个能级。
电子在这些能级上运动时，会处于不同的状态。
3. 能级跃迁当电子从一个能级跃迁到另一个能级时，会吸收或发射光子，这种光子的能量正好等于两个能级之间的能差。
这是光子的辐射。
4. 能级的确定能级取决于原子核的质量和电子的位置，不同的原子核和电子分布形式会导致不同的能级结构。
每个原子都有特定的能级，这些能级是由原子的物理特性所决定的。
5. 能级的作用原子的能级决定了原子的光谱特性，不同原子的能级结构不同，因此存在着不同的光谱线。
通过研究原子的能级结构，可以揭示原子内部的物理特性，从而为原子物理学和量子力学的研究提供重要的信息。
6. 能级分布原子的能级是离散的，即只能取一些特定的数值。
在研究光谱时，我们经常需要计算原子的能级分布，以便理解光谱线的产生机制。
二、辐射1. 辐射的概念辐射是指从一个物体发射出的能量或粒子，并向外传播的过程。
辐射可以是电磁波、光子、中子等形式，通常是由原子、分子或亚原子粒子发射出来的。
2. 辐射的分类辐射可以分为电磁辐射和粒子辐射两大类。
电磁辐射包括可见光、紫外线、X射线和γ射线等，而粒子辐射包括α射线、β射线和中子辐射等。
3. 电磁辐射电磁辐射是由电磁场振荡产生的，具有电磁波的性质。
根据频率不同，电磁辐射可以分为不同的波段，包括无线电波、微波、红外线、可见光、紫外线、X射线和γ射线等。
不同波长的电磁辐射具有不同的能量和穿透能力。
4. 粒子辐射粒子辐射是由高速粒子产生的，包括α粒子、β粒子和中子。
这些粒子具有质量和电荷，与物质相互作用时会产生不同的效应。
5. 吸收和发射物质对辐射的吸收和发射是辐射研究的重要课题。
原子物理学课件：第二章：原子的能级和辐射
2020/9/30
21
实验装置示意图
单色光照射到作为正极的 金属板表面，引起光电子 的逸出。
在另一端加上负电压（减速势）V，它的大小是电子能量的直接
量度。如果从正极发射出来的电子的最大动能为
eV
eV0
1 2
m
vm2
1 2
m
vm2
，那么当
时，就没有一个电子能够到达负极，于是电流i为零。V0被称为遏
止电压。 2020/9/30
1 n2
),n
4,5, 6,
（4）布喇开系(红外):
1 RH ( 42
1 n2
),n
5, 6, 7,
（5）普丰特系（红外）:
RH
(
1 52
1 ),n n2
6, 7,8,
2020/9/30
38
3、里德伯公式 （1889年）
1 RH ( m2
1 n2
)
m=1,2,3……； 对每个m, n=m+1,m+2,m+3……构成谱线系
2020/9/30
5பைடு நூலகம்
从理论上分析，黑体腔壁可认为是由大量作谐振动的 谐振子(作谐振动的电偶极矩)组成
振动的固有频率可从(0-∞)连续分布，谐振子通过发 射与吸收电磁波，与腔中辐射场不断交换能量。
(2) 基尔霍夫定律 1859年
黑体辐射达平衡时，辐射能量密度E(v,T)随v的变化曲线 只与黑体的T有关，而与空腔的形状及组成材料无关。
2020/9/30
8
维恩 (Wilhelm Wien 德国人 1864-1928)
2020/9/30
热辐射定律的发现 1911年 诺贝尔物理学奖获得者 斯特藩—玻耳兹曼定律和维恩位移 律是测量高温、遥感和红外追踪等 技术的物理基础。
第2章 能级与辐射
,
v2 e2 me = r 4πε 0 r 2 m vr = nh 量子化条件, e
e
n = 1, 2,3L
ε 0h2 rn = n 2 2 π me e
,
n = 1, 2,3L
表明轨道是不连续的，电子只能在分立的轨道上运动。 表明轨道是不连续的，电子只能在分立的轨道上运动。 R是关于n的映射
hν =| Ei − E f | ，
量子化条件: 3) 量子化条件:
mevr = nh, n = 1, 2, 3⋅⋅⋅
2πr·mv（位移*动量） =2π·mvr（角移*角动量）=nh
h h= 2π
2. 玻尔的基本假设
1913年 1913年，玻尔提出了原子模型 1）定态假设：电子在一些特定的、分立轨道上运动不辐射电 定态假设：电子在一些特定的、 磁波，这时原子处于稳定状态（简称定态） 磁波，这时原子处于稳定状态（简称定态）。 频率法则：电子从一个轨道跃迁到另一个轨道 轨道跃迁到另一个轨道时 2) 频率法则：电子从一个轨道跃迁到另一个轨道时，原子会发 射或吸收光子，频率ν满足跃迁公式： 射或吸收光子，频率ν满足跃迁公式：
me e 4 RH = 2 3 = 1.0973731× 107 m −1 8ε 0 h c
实验值： 实验值：
RH = 1.0967758 ×107 m −1
里德伯常数
理论与实验测值符合很好。 理论与实验测值符合很好。
4.类氢离子光谱 4.类氢离子光谱
1) 类氢离子
He + Li ++ Be +++ Z =2 Z =3 Z =4
ε 0h 2 & a1 = r1 = = 0.53 × 10−10 m=0.53 A π mee 2
第二章原子的能级和辐射
2
Z 13.59 2 n
2
n 1,2,.....
能量的数值是分立的，能量量子化
基态（ground state）
n 1 E1 13.6 eV r1 a0
激发态（excited state）
n2
En E1 n2
自 氢原子能级图 由 态 n E / eV 0 0.85 激 n4 1.51 发 n3 态 3.4 n2
电子离原子核很远时， 势能为零，原子体系能量为：
1 2 E m 0 2
非量子化的轨 道
量子化轨 道
（正值） 1 2 Ze2 -e 接近核的能量 E m 2 4 0 r （任何值）
（当这电子向原子核接近时，路经一个双曲线的一支）电子从
非量子化的轨道跃迁到一个量子化轨道时，原子发射光子。
1 2 m V 俘获前： 2 e
俘获后：电子处于氢原子某一能量状态， Rhc En 2 n 减少的能量以光子的形式辐射， 1 Rhc 由于速度连续变化，则 2 h meV -（- 2 ） 频率连续分布，产生连 2 n
续谱。
2.4 类氢离子及其光谱
1．类氢离子光谱
类氢 离子
原子核外只有一个 电子的离子，但 原子核带有Z >1的正电荷，Z不同 代表不同的类氢体系。
线光谱
带光谱 按光谱机制分类
分子发光
发射光谱
样品光源 分光器 纪录仪
I
I
吸收光谱
连续光源 样品
分光器 纪录仪
光谱由物质内部运动决定，包含内部结构信息
2.2氢原子的光谱实验规律
一．氢原子光谱的线系 1.巴尔末系 光谱的研究从1853年发现 条谱线 开始。 1885年，已观察到14
第二章原子的能级和辐射
里德伯公式准确地表述了氢原子 光谱线系，而且其规律简单而明显， 这就说明它深刻地反映了氢原子内在 的规律性。最明显的一点是，氢原子 发射的任何一条谱线的波数都可以表 示成两项之差，即：
~
RH m2
RH n2
其中，每一项都是正整数的函数，并且两项的形式一样。 若我们用T来表示这些项值，则有
T (m)
B
n2 n2
4
n3 ,4,5 B36 .54n 6m
氢原子光谱（可见区）的计算值和观测值
n 谱线 计算值（nm）
观测值(nm)
差数（nm）
3
H
4
H
5
H
6
H
656.208 468.080 434.000 410.130
656.210 468.074 434.010 410.120
+0.002 -0.006 +0.010 -0.010
（二）频率条件
hmn EnEm En Em
h h~ c h m 2 H c R hn 2 H c R hc (m )T hc (n )T
Emhmc2HRhc(T m)
能量 En 只与n 有关，只能取一定的分立值；
在某一状态 n 上，无论电子有无加速度，其 能量都是一定的： 定态
原子的线状光谱来源于电子由高能级到低能级 的跃迁。
现在的问题是：
哪些状态是定态？ 哪些轨道是定态轨道？
第三个假设：角动量量子化条件！
能量量子化 轨道半径 r 是量子化的
分立的值 rn 角动量 L = m v r 是量子化的。
(三)．角有通过实验检验。
m2 Ze2
r 40r2
r
rn
442m 0h2e2
第二章 原子的能级和辐射
（1）爱因斯坦光子假说
(a)一束光是一粒一粒以光速 c 运动的粒子流。这些粒子称为光量子，也称光子。
(b)光与物质的作用是光子与微观粒子的作用,频率为ν 光子的能量为ε =hν ，不可 分割,只能整个被吸收或辐射,频率不同，光子的能量则不同.
(c)单色光的能流密度(光强):单位时间垂直通过单位面积的光能与频率ν 、光子 数N的关系为: S=N hν .
•说明： (1)黑体是个理想化的模型。
(2)对于黑体，在相同温度下的辐射规律是相同的。
背景介绍
3 经典物理的困难
维恩公式 －从热力学出发
实验
M c1v3ec2v /T
M (T )
瑞利-金斯
在短波范围与实验符合较好,在长波处与 实验相差很大！
瑞利－金斯公式 －从电动与统计物理出发
M
8
c3
k Tv2
在低频部分与实验曲线相符合，在高频 则完全不能适用。在高频（短波）部分， 趋于“无限大”——“紫外灾难”。
维恩
Mλ (T)：从热力学温度为T 的黑体 的单位面积上、单位时间内、在单 位波长范围内所辐射的电普朗克假说 普朗克黑体辐射公式
(1) 普朗克假说
应是连续的光谱。
2.3 玻尔的氢原子理论 1序
卢瑟福氢原子(1H)模型
e
-
+ e
经典理论解释
- e
e +
实验结果：
(1)原子相当稳定。 (2)实验测得原子光谱是不连续的谱线。
经典理论无法解释实验结果!
卢瑟福有核原子模型无法解释原子的稳定性，无法解释氢原子光谱 的规律。
1序
2.3 玻尔的氢原子理论
H
656.2 红
原子的能级和辐射
2、光电效应的实验规律
①光照与产生电流几乎同时（△t<1ns）； ②逸出的电子数正比于光的强度； ③光电子的最大能量与光强I无关； ④光电子的最大能量与光的频率v有关。
实验发现，对于一 定的阴极材料，遏止电 压 V0 与入射光的强度无 关而与光的频率ν成正比 。 当 ν 减 小 时 V0 线 性 地减小，当ν小到某一数 值 ν0 时， V0=0 ，这时即 使不加负电压也不会有 光电子发射了。 ν0 称为 光电效应的遏止频率或 相应的波长 λ0=c/ν0 称为 光电效应的红限。
光子的能量 hv 减去电子在金属中的结 合能(脱出功)Φ等于电子的最大动能。 当hv<Φ时，电子不能脱出金属表面， 因而没有光电子产生。光的频率决定了光 子的能量，也就决定了电子的能量。光的 强度只决定光子的数目；光子多，产生的 光电子也多，但能不能产生光电子则决定 于光的频率。
1922 年爱因斯坦因光电效应（而不是相对论）获得诺贝尔物理奖。
二、量子假说根据之二：光电效应
1、光电效应的发现
1887 年，赫兹发现电磁波时，发现光电效 应的征兆； 1888 年，霍尔瓦希斯进一步研究，发现锌 板在紫外光照射下获得正电荷，而带负电的板 在光照射下失掉其负电荷； 1900 年，林纳证明金属在紫外光照射下发 射电子； 1905 年，爱因斯坦提出光量子假说，解释 光电效应； 1916 年，密立根测量了光的频率和逸出电 子能量之间的关系，验证爱因斯坦的光电效应 量子公式，并精确测定普朗克常量。
遏止电压与频率的关系
3、光电效应的经典解释
经典物理认为，光是一种波动。当光照 在电子上时，电子就得到能量，集聚到一定 能量时，电子就能脱离原子的束缚而逸出。 但这个时间要很长： 107s 。这与实验事实不 符。 按照经典理论，决定电子能量的是光强， 而不是光的频率。但实验事实却是：光电子 能量与光强无关，而与频率有关。
第二章 原子的能级和辐射
第二章 原子的能级和辐射一、学习要点：1.氢原子光谱：线状谱、五个线系（记住名称、顺序）、广义巴尔末公式)11(~22nm R -=ν、 光谱项()2nR n T =、并合原则：)()(~n T m T -=ν 2.玻尔氢原子理论：(1)玻尔三条基本假设的实验基础和内容（记熟） (2)圆轨道理论（会推导）：氢原子中假设原子核静止，电子绕核作匀速率圆周运动02200202220A 529,04,Z Z 4≈===em a n a n e m r e e n πεπε;13714,Z Z 40202≈===c e n c n e c e n πεααπευ；()n hcT nhc R ne m E e n --=-=∞2222422Z 2Z )41(πε，n ＝１.2.3……(3)实验验证：（a ）氢原子五个线系的形成)11(Z ~,)4(222232042nm R c h e m R e -==∞∞νπεπ (会推导）非量子化轨道跃迁)(212n E E mv h -+=∞ν（b ）夫－赫实验：装置、.结果及分析；原子的电离电势、激发电势 3.类氢离子（+++Li,He ,正电子偶素.-μ原子等）(1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等 (2)理论处理（会推导）：计及原子核的运动，电子和原子核绕共同质心作匀速率圆周运动ee m M m M +⋅=μ, 正负电荷中心之距Ze n rn22204μπε =.能量224222Z )41(n e E n μπε-=，里德伯常数变化Mm R R eA +=∞11重氢（氘）的发现 4.椭圆轨道理论索末菲量子化条件q qnh n pdq ,⎰=为整数an n b n em a ne m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,222022422，n n n ,,3,2,1;,3,2,1 ==ϕn 一定，n E 一定，长半轴一定，有n 个短半轴，有n 个椭圆轨道（状态），即n E 为n 度简并。
原子物理学 课件-第二章 原子的能级和辐射
pdq nh ?
原子物理学
证明:
P dq n h 既包含了玻尔圆周运动量子化条件, 又有普朗克的量子论推论.它确实是量子化通则.
i i i
原子物理学
§2.7
索末菲对玻尔理论的推广
玻尔理论的发展： 推广 修正 索末菲理论 量子力学
玻尔理论的建立： 引子 内容 验证 光谱之谜 玻尔假设 夫一赫实验
n 1,2,3,, n 同一 n nr n 1, n 2, n 3,,0 n n, nr 0, b a n n, nr 0,
椭圆轨道 圆轨道
n , nr n对
一个圆轨道 ， n-1个椭圆轨道
有n个不同的b值，n个形状不同的轨道
例如：
a1 n 1, n 1, a b 圆 z a1 a1 n 1, a 4 , b 2 z z n2 a1 n 2, a b 4 圆 z
电离态 8
（1）量子化轨道图 赖曼系 巴尔末系 赖曼系 巴尔末系
4 3
激 发 态
n =2
n =1 基态
原子物理学
轨道能级图的特点：
1）邻近轨道间隔随n增加而增加，n越大，相邻轨道越远离.
2）邻近能级间隔随n增加而减小，n越大，相邻能ห้องสมุดไป่ตู้越密集.
3）轨道与能级一一对应。 基态 第一激发态
原子物理学
§2.2 氢原子光谱的实验规律 一、氢原子光谱线系
1885年，光谱学家发现氢光谱（14条，可见区4条）。
原子物理学
氢原子光谱的五个线系： 紫外区：赖曼系： 可见区：巴尔未系： 近红外区：帕邢系： 近红外，布喇开系： 远红外，普丰特系：
原子的能级和辐射培训课件.ppt
赖曼系
R（H 112
1） n2
，
巴耳末系
R（H
1 22
1） n2
n 2 ，3，4 n 3，4 ，5
精品
从能级图上看跃迁产生的谱线情况可知，谱线系间有一个整 体差距，差别较大，形成了紫外、可见光、红外、近红外、远 红外区的线系。
同一线系内也是同样的道理，能级间隔大的，产生高频（短 波）谱线，能级间隔小的，产生低频（长波）谱线，随n的增加 相邻能级的间距减小，向比它们低的同一能级跃迁时产生的辐 射频率（波长）间距减小，谱线密集。
精品
四、氢原子的能级和电子轨道半径
1、电子轨道半径
由
ze2
4 0 r 2
2
m r
2 r m nh ， n 1，2 ，3
可得
r
4 0 h2 4 2me2
n2 z
， n 1，2 ，3
可见，r 由n决定，n称为主量子数
令 a1
4 0 h2 4 2me2
=0.529166×10-10 米
精品
三、光谱仪的工作原理
L2
L3
L1
I
每一条确定的谱线都对应于一个确定波长的光，可用已知波长 的光的光谱与之比较，就可知道各谱线的波长。从浓度可以定 出强弱
精品
四、光谱的类别
从谱线的形状来分，光谱可分三类:线状、带状、连续
1、线状光谱：谱线是一条一条的，彼此分明的细线。因为每
一条谱线代表一个波长成分，谱线是一条一条的，彼此分明的，
P
mr
n h
2
h
2
1.05461034 焦耳·秒
原子的能级和辐射-近代物理学教学课件
玻尔的氢原子理论 一般可用能级图来形象地表示原子量子化的能 量值． 在能级图上用一条横续表示原子可能有的一个能 量值，称为一个能级。其高度是按能量大小成比例画 出来的。 能量随n增加而迅速升高，其绝对值反比于n2。
9, 氢原子可以具有的能量分别为 E1 , E1 / 4, E1 / ，
第二章 原子的能级和辐射
玻尔的氢原子理论 由上式可知，电子绕核运动的半径期将逐渐缩小， 电子最终将因不断损失能量而落到原子核上，整个原 子塌缩成只有原子核那样大小。 显然．这是与实际观察的事实不符，事实表明原 子的大小是稳定的，其大小约为10-10m的数量级。
经典理论认为原子所发射光的频率应等于原子 中电子运动的频率
玻尔将他得知这一公式比作“七 巧板中的最后一块”
第二章 原子的能级和辐射
玻尔的氢原子理论 α粒子散射实验证明了原子的核式结构，但其中 并未考虑电子的情况，在此基础上，玻尔结合已有光 谱资料在1913年发展了氢原子的理论。
1、电子的运动及经典理论的困难
卢瑟福模型与太阳系有极大的相似之处：
它们都受1／r2力支配；体系总质量的99．9％都 集中在中心(原子核或太阳)．
通常用一条水平线表示 一个能量状态。 原子的辐射和吸收过程 可以用右图表示。
能量最低的状态称为 基态。 通过这条假设，玻尔将 原子的状态和原子光谱联系 起来。 第二章 原子的能级和辐射
玻尔的氢原子理论 （3）角动量量子化 玻尔假设原子中电子的轨道角动量是量子化的， 它的值只能是 的整数倍。一般也叫普朗克 h / 2 常数。 所以电子绕原子核作圆周运动的角动量的值为：
光谱——研究原子结构的重要途径之一 光谱的类别： 太阳光、白炽灯等光源 （1）连续光谱（多为固体发光）： 发出的光具有各种波长，光强随频率的变化是连续的， 当这种光通过分光元件形成的光谱就是连续光谱。 （2）带状光谱（分子发光）： 有些光源发的光形成的光 谱是由许多片连续的光谱带组成的。 （3）线光谱（原子发光）： 由一条条细线组成，这表明 这种光源发出的光只含有某一些频率（波长）成份， 其中每一条谱线代表一种波长，谱线间的间距代表波 长差。 第二章 原子的能级和辐射
原子物理学褚圣麟第二章习题解答（ＰＤＦ）
第二章 原子的能级和辐射2.1 试计算氢原子的第一玻尔轨道上电子绕核转动的频率、线速度和加速度。
解：电子在第一玻尔轨道上即n=1。
根据量子化条件，πφ2hnmvrp == 1010.52910r a m −==×可得：频率 21211222ma hma nh a v πππν===1516.5610s −=×速度：m/s 61110188.2/2×===ma h a v νπ加速度：221/8.9810w v a ==×2m /s 22.2 试由氢原子的里德伯常数计算基态氢原子的电离电势和第一激发电势。
解：电离能为，把氢原子的能级公式代入，得：1E E E i −=∞2/n Rhc E n −=Rhc hc R E H i =∞−=111(2=13.60eV。
电离电势：60.13==eE V ii V 第一激发能为将电子从n=1的能级激发到n=2的能级上所需要的能量：20.1060.134343)2111(22=×==−=Rhc hc R E H i eV 第一激发电势：20.1011==eE V V 2.3 用能量为12.5电子伏特的电子去激发基态氢原子，问受激发的氢原子向低能基跃迁时，会出现那些波长的光谱线？解：由氢原子能级公式：2/H E hcR n =−得：113.6E eV =−2 3.4E e =−3 1.51E e ，，V V −40.85E eV ，==−可见，具有12.5电子伏特能量的电子只能激发H 原子至3≤n 的能级。
跃迁时可能发出的光谱线的波长为：1221111(5/36656323H H R R A ολλ=−=⇒=222232231113()12151241118()1025.7139H H H H R R R R οAAολλλλ=−=⇒==−=⇒=2.4 试估算一次电离的氦离子、二次电离的锂离子的第一玻尔轨道半径、电离电势、第一激发电势和赖曼系第一条谱线波长分别与氢原子的上述物理量之比值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一个m就对应一个谱线系。
氢原子光谱特点的实验总结
~
RH
1 m2
1 n2
1）光谱是线状的，波长可以用一个公式表达出来。
2）每一谱线的波数都可以表达为二光谱项之差：
~ T (m) T (n)
T (n)
RH n2
称为光谱项。
直到1913年，虽有一大批精确的光谱数据，但还 没有满意的理论解释
§2.2玻尔的氢原子理论
实验值： RH 1.0967758107 m1
理论与实验测值符合很好。
Bohr因其提出的原子结构的量子理论（1913）及其后对 量子力学发展所作的贡献，于1922年获Nobel奖
Bohr理论开创了原子光谱和分子光谱的理论研究和实验 研究的新时代，是研究原子和分子结构的有力工具，极大地 推动了原子和分子结构理论的发展。
称为氢原子第一波尔轨道半径。
第n级轨道半径 rn n 2r1 (n 1,2,3 )
电子轨道半径可能值为
, , , , a1 4a1 9a1 16a1 L n2a1
2)电子速率
vn
e2
4 0 nh
v1
e2
4 0 h
c
,
1
137
为精细结构常数
3)氢原子能量
原子能量
En
1 2
m
evn2
e2
4 0rn
1.模型：
e2
4 0 r 2
me
v2 r
原子氢能量（核静止）
E
1 2
mev2
e2
40r
1
40
e2 2r
电子轨道运动频率
ve
1
f
2 r 2
4 0 me r 3
这能否解释理论？
遭遇的困难！
e
（1）稳定性问题
加速带电粒子辐射电磁波，电子能量不 断减小，最后落入原子核中。
e +
（2）辐射频率解释困难。 轨道连续变化，辐射电磁波频率也应是连续的
解： 基态 n = 1
L1
n
h
2
6.6 10 34
2
1.055 10 34 J s
v1
L1 m er1
9.11
1.055 10 34 10 31 0.529
10
10
2.19 10 6 m/s
例2：用 12.6eV 的电子轰击基态氢原子，这些氢原子所能达到最 高态。
解：设电子能达到第n激发态，则有
En
E1
E1 n2
E1
12.6
eV
n
E1 13.6 eV
13.6 n 3
4). 氢原子光谱公式
电子从n跃迁到m轨道：
h En Em
由
En
1 n2
me 4
802h
2
和 % 1 c
得
%
ห้องสมุดไป่ตู้mee4
802h3c
(
1 m2
1 n2
)
RH
1 m2
1 n2
RH
mee4
8 02 h3c
1.0973731107 m1
由
vn
e2
2 0 nh
和
rn
n
2
0h 2 m ee2
可求得：
En
1 n2
me4
8 02 h2
(n 1, 2, 3L )
氢原子能量只能取一些分立值，这种现象称之为能量量子化。
n=1，称为基态
E1 13.6eV
n>1，称为激发态
n=2，第一激发态 n=3，第二激发态
E2 13.6eV / 4 E3 13.6eV / 9
4.类氢离子光谱
1) 类氢离子
一次电离的氦离子 二次电离的锂离子 三次电离的铍离子
He Li Be
Z 2 Z 3 Z 4
me
v2 r
Ze2
40r 2
mevr nh
,
e2 Ze2
课堂练习：计算类氢离子下述各量
a)轨道半径
一般情形，有：
En
E1 n2
(n 1,2,3 )
问题 :
a) 电子逃逸的能量是多少？电子电离的能量是多少？
b) 电子由第一激发态跃迁到第三激发态需能量多少？
E2
E1 22
3.4eV
E3
E1 32
1.51eV
E4
E1 42
0.85eV
n n 4 n 3
n 2
E 0
0.85eV
布拉开系
1.51eV
h h
2
3. 理论 1) 电子的轨道半径
氢原子中电子绕核作圆周运动
v2
e2
me
r
40r 2
mevr nh
,
n 1, 2,3L e
rn
n2
0h2 mee2
n 1, 2,3L
表明轨道是不连续的，电子只能在分立的轨道上运动。
a1
r1
0h2 mee2
0.531010 m=0.53A&
第二章
原子的能级 和辐射
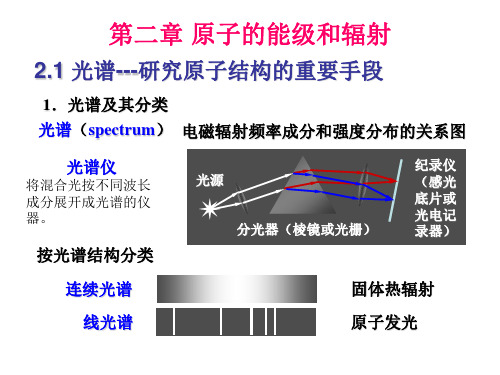
§2.1 光谱
光谱是电磁辐射波长成分的分布情况
可见光波长范围：390nm~760nm
光谱可分为三类： 线状光谱：一般与原子运动有关 带状光谱：一般与分子运动有关 连续光谱：一般固体运动有关
通过认识光谱就可以研究原子的内部运动。以下重点讨 论线状谱，先从最简单的氢原子我们的开始研究。
§2.2 氢原子光谱
1. 巴尔末光谱线系
1885年，瑞典一位中学数学教师发现一部分氢光谱可以用经 验公式表示
巴尔末公式
%
RH
1 22
1 n2
,
n 3, 4, 5
波数：
% 1
里德伯常数 RH 1.097373107 m1
n=3，4，5，6, 分别对应四条可见光谱线H、H、H、H
氢原子巴尔末线系
H
H H H H
n 3 4
5
656 .3 486 .3
364 .56 nm
氢原子光谱的其它谱线也先后被发现，一个
在紫外区，由莱曼发现，还有三个在红外区，分 别由帕邢、布喇开、普丰特发现。
2. 莱曼线系
莱曼线系
3. 其它线系
%
RH
1 12
1 n2
,
n 2, 3, 4
帕邢系
%
RH
1 32
1 n2
帕邢系
巴尔末系
3.40eV
n 1
赖曼系
13 .6 eV
电离能：把电子从氢原子第一玻尔轨道移到无穷远所需能量。
E E E1 13 .6eV
例1：计算氢原子基态电子的轨道角动量、线速度。
例2：用 12.6eV 的电子轰击基态氢原子，讨论这些氢原 子所能达到最高态。
例1：计算氢原子基态电子的轨道角动量、线速度。
,
n 4, 5, 6
布喇开系
%
RH
1 42
1 n2
,
n 5, 6, 7
普丰特系
%
RH
1 52
1 n2
,
n 6, 7, 8
帕邢系 普丰特系
莱曼系
巴尔末系 布拉开系
1889年里德伯发现氢原子光谱可用一个普遍经验公式表示：
里德伯公式
~
RH
1 m2
1 n2
m 1, 2, 3L , n m 1, m 2, m 3,L
结论与实验完全不符！
实验表明（1）原子相当稳定 （2）原子光谱是线状谱
2. 玻尔的基本假设
1913年，玻尔提出:
1）定态假设：电子在特定轨道上运动不辐射电磁波。
2) 频率法则：电子从一个轨道跃迁到另一个轨道时，原子会发
射或吸收光子，频率满足跃迁公式：
3) 量子化条件:
h | Ei E f |
mevr nh, n 1, 2, 3