“单循环赛”模型的建立及在几何中的应用
单循环赛中选手胜负序列求解问题v-数据结构与算法课程设计报告

合肥学院计算机科学与技术系课程设计报告2009~2010学年第二学期课程数据结构与算法课程设计名称单循环赛中选手胜负序列求解问题学生姓名管明璐学号0804012038专业班级08计科(2)班指导教师王昆仑、张贯虹2010年6月一、问题分析和任务定义单循环赛,是所有参加比赛的队均能遭遇一次,两队之间非胜即负,最后按各队在全部比赛中的积分、得失分率排列名次。
如果参赛球队不多,而且时间和场地都有保证,通常都采用这种竞赛方法。
本题可以从两个方面进行思考,一是按比赛过程中的积分排名产生胜负序列,二是根据比赛过程中各选手之间的胜负关系产生胜负序列。
针对第一种情况,比赛规定各选手之间只能遭遇一次,获胜的选手得一分,失败的一方不得分,比赛结束时按照各选手之间的积分排名决定他们的胜负序列,在设计过程中要用到排序的算法。
针对第二种情况,按照比赛过程中的胜负关系产生胜负序列,不过这种方法产生的胜负序列可能不是唯一的,但是实际情况是比赛结束时一定会产生一种胜负序列。
为此需要用合适的数据结构进行存储,来确定如何产生胜负序列,选取哪位选手作为第一名,假如该选手已经在序列中,在后面的筛选过程中,如何将该选手排除等一系列问题。
二、概要设计和数据结构选择(1)针对第一种情况,所采用的数据结构是类。
将选手的编号、积分以及胜负过程中的积分处理等封装在类中。
其中,以编号和积分作为私有成员,而设置编号、获胜处理、失败处理、获取积分、获取编号等作为公有成员。
此时将该问题转化为对选手积分进行排序的问题。
在实际操作时,我想分别输入选手的姓名,根据姓名来判断积分的高低,但是当姓名也作为私有成员时,由于权限问题,不能在主调函数中直接输入,所以使用了另外一个数据结构:结构体,将姓名放入结构体中,在排序时让姓名与积分一一对应。
(2)针对第二种情况,采用的数据结构是有向图,将每个选手作为有向图的一个顶点,选手间的胜负关系作为有向弧,从箭头出发的一方作为获胜者,所以该问题转化为了有向图的深度遍历问题,即求解一条包含所有顶点的简单路径。
数学模型课件图论方法建模

§9.2 循环比赛的排名问题问题:n 支球队参加循环比赛,两两交锋,一场决胜,不容平局,“0、1”打分。
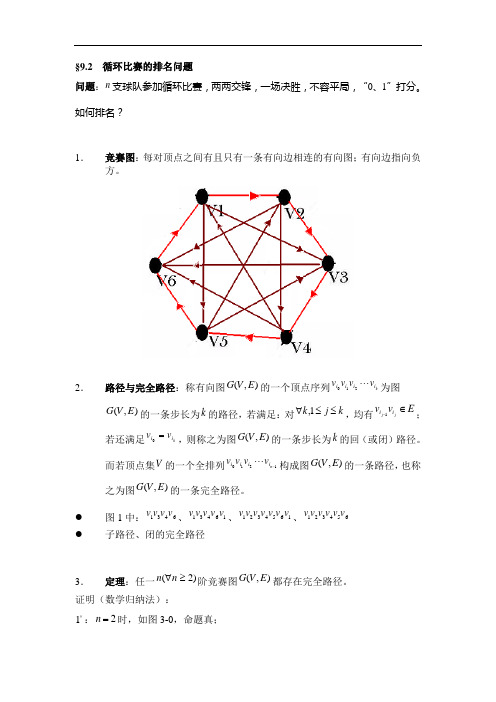
如何排名?1.竞赛图:每对顶点之间有且只有一条有向边相连的有向图;有向边指向负方。
2.路径与完全路径:称有向图),(E V G 的一个顶点序列k i i i i v v v v 210为图),(E V G 的一条步长为k 的路径,若满足:对k j k ≤≤∀1,,均有E v v j j i i ∈-1;若还满足k i i v v =0,则称之为图),(E V G 的一条步长为k 的回(或闭)路径。
而若顶点集V 的一个全排列1210-n i i i i v v v v 构成图),(E V G 的一条路径,也称之为图),(E V G 的一条完全路径。
● 图1中:6431v v v v 、16431v v v v v 、1654321v v v v v v v 、654321v v v v v v ● 子路径、闭的完全路径3.定理:任一)2(≥∀n n 阶竞赛图),(E V G 都存在完全路径。
证明(数学归纳法):1:2=n 时,如图3-0,命题真;2:设k n =时命题真;3:当1+=k n 时,设{}121,,,+=k k v v v v V 为顶点集,记{}k v v v V ,,21~=,~G 为图),(E V G 关于{}k v v v V ,,21~=的生成子图;由归纳假设2,在~G 中存在完全路径,不失一般性,设k k v v v v 121...-为~G 中的一条完全路径,考虑顶点1+k v 与{}k v v v V ,,21~=的邻接关系,有如下三种情形:图3-1:k k k v v v v v 1211...-+为G 中的一条完全路径;图3-2:1121...+-k k k v v v v v 为G 中的一条完全路径图3-3:k k i k i v v v v v v v 11121......-+-为G 中的一条完全路径。
赛程安排

赛 程 安 排陈启表 刘荣涛 张善邦 指导教师:陈晓江 黄春棋 九江职业技术学院(332007)摘 要本模型是赛程安排及编制过程的具体问题。
1.对问题1)采用单循环法来安排赛程,根据这种方法容易找出n =5时每两队之间比赛至少间隔一场的赛程安排。
2.模型在n =8,9时,赛程编制过程中分别采用表格和程序的方法,并得到所有队每两场比赛中间相隔的场次数上限的一个结论,即当队数为双数时,其上限M(n)=2n-2,当队数为单数时,其上限M(n)= 21 n -2。
3.对问题3),当n =8时也采用单循环法找到一种每两队中间比赛至少间隔两场休息的赛程;当n =9时将单循环法改用C 语言编程实现32种赛程安排,这时候每两队中间比赛至少间隔三场休息。
4.除了每两场比赛间隔次数这一指标来衡量一个赛程的优劣外,我们还考虑每个队赛场次数安排的离散程度作为衡量赛程公平性的另一个指标。
一、问题的简述本题为球赛单循环赛程安排的实际问题,实践性强。
当有n 支球队比赛时,在考虑公平性的情况下,编制赛程表,并求“上限”值以及评价赛程的优劣。
其中对问题2)中的“上限”应理解为各队每两场比赛中间相隔的场次数尽量均等(即赛程安排公平)时的至少相隔场次的最大数。
二、模型假设1.设n 支球队进行单循环比赛,球队的编码依此为A 、B 、C ……。
2.每一场比赛都在同一场地上进行,且场地不空场。
3.各队每两场比赛中间相隔的场次数尽量均等。
4.n 个队的所有比赛中,各队每两场比赛中间所有能相隔的场次数的最大值称为上限,记为M (n )。
5.不考虑其他因素,比赛始终能正常进行。
三、模型的建立及求解有n 支球队1、2、3、……n ,在赛程安排时要考虑赛程的公平性,而公平性主要看各队每两场比赛中间得到的休整时间的均等程度。
在赛程安排时各队每两场比赛中间相隔的场次数达到上限时才能保证对各球队的公平。
1.问题1)求解:对于5支球队,我们把这5支球队看成是五边形的顶点,把它转化成平面网络图来分析。
数学模型课件图论方法建模2
§9.2 循环比赛的排名问题问题:n 支球队参加循环比赛,两两交锋,一场决胜,不容平局,“0、1”打分。
如何排名?1.竞赛图:每对顶点之间有且只有一条有向边相连的有向图;有向边指向负方。
2.路径与完全路径:称有向图),(E V G 的一个顶点序列ki i i i v v v v 210为图),(E V G 的一条步长为k 的路径,若满足:对k j k ≤≤∀1,,均有E v v j j i i ∈-1;若还满足ki i v v =0,则称之为图),(E V G 的一条步长为k 的回(或闭)路径。
而若顶点集V 的一个全排列1210-n i i i i v v v v 构成图),(E V G 的一条路径,也称之为图),(E V G 的一条完全路径。
● 图1中:6431v v v v 、16431v v v v v 、1654321v v v v v v v 、654321v v v v v v ●子路径、闭的完全路径3.定理:任一)2(≥∀n n 阶竞赛图),(E V G 都存在完全路径。
证明(数学归纳法):1:2=n 时,如图3-0,命题真;2:设k n =时命题真;3:当1+=k n 时,设{}121,,,+=k k v v v v V 为顶点集,记{}k v v v V ,,21~=,~G 为图),(E V G 关于{}k v v v V ,,21~=的生成子图;由归纳假设2,在~G 中存在完全路径,不失一般性,设k k v v v v 121...-为~G 中的一条完全路径,考虑顶点1+k v 与{}k v v v V ,,21~=的邻接关系,有如下三种情形:图3-1:k k k v v v v v 1211...-+为G 中的一条完全路径;图3-2:1121...+-k k k v v v v v 为G 中的一条完全路径图3-3:k k i k i v v v v v v v 11121......-+-为G 中的一条完全路径。
数学单循环双循环问题

数学单循环双循环问题
数学单循环和双循环问题是数学中常见的问题类型。
单循环问题是指在一个循环中进行一次迭代,而双循环问题是指在两个嵌套的循环中进行迭代。
在单循环问题中,常见的例子是计算一个数列的和。
我们可以使用一个循环来依次将数列中的数相加,并最终得到总和。
单循环问题通常涉及到一些简单的迭代计算。
这类问题可以通过循环的技巧和数学公式来解决。
双循环问题则更加复杂一些。
一个常见的例子是计算一个矩阵的和。
在这种情况下,我们需要使用一个外层循环来迭代每一行,同时在内层循环中迭代每一列,并将相应的元素相加。
双循环问题通常需要考虑到数组的索引和迭代的顺序。
需要特别注意的是,双循环问题往往会涉及到更多的计算和时间复杂度。
因此,在解决这类问题时,我们需要仔细考虑算法的效率和优化策略,以避免不必要的计算和提高代码的执行效率。
总之,数学单循环和双循环问题是数学中常见的问题类型。
我们可以通过循环和数学公式,灵活运用不同的算法和优化策略,解决这些问题并得到正确的结果。
单循环问题公式

单循环问题公式
单循环问题公式是一种广泛应用的数学方法,它有许多不同的应用。
其中最经典的用法是用来解决单循环问题,即从一个可行解中找出最优解,使后续步骤执行得最完美对应。
单循环问题公式分为两个部分:约束条件和目标函数。
约束条件是解决单循环问题时所必须满足的条件,必须满足的条件包括:约束变量的取值范围是有限的;约束函数的表达式形式;相关变量的约束关系等等。
而目标函数,就是在给定约束条件的情况下,寻求使得目标函数的值最优的解。
在求解单循环问题时,首先要从原始数据出发,根据数据规律确定求解问题的类型,最后再结合实际应用情况,根据单循环问题公式,建立模型,求解最优解。
在现实应用中,单循环问题公式已经广泛应用于网络规划、行车调度、复杂运筹规划、空间分配、时间管理、资源配置等环境下。
比如,在网络规划中,单循环问题公式可以帮助求解网络的最优流方向,以及网络的最优结构,以使其尽可能高效地实现它的目标。
在行车调度中,单循环问题公式可以通过最小化其所耗费的总时间与距离来求解出最优的行车调度方案。
此外,单循环问题公式还可以应用于人工智能领域,如自动驾驶、机器学习等问题中。
在自动驾驶中,单循环问题公式可以用来解决车辆路径规划问题,可以通过模型优化,将路径规划时间最小化,以达到最优的驾驶策略。
机器学习中也有单循环方法,可以通过提高模型
准确性,提升机器学习的性能。
总之,单循环问题公式是一种高效有效的数学模型,它具有优良的求解效果,被广泛应用于工程、科学和社会等各个领域,可以为各类问题提供有效的解决方案。
赛程安排——精选推荐

赛 程 安 排陈启表 刘荣涛 张善邦 指导教师:陈晓江 黄春棋 九江职业技术学院(332007)摘 要本模型是赛程安排及编制过程的具体问题。
1.对问题1)采用单循环法来安排赛程,根据这种方法容易找出n =5时每两队之间比赛至少间隔一场的赛程安排。
2.模型在n =8,9时,赛程编制过程中分别采用表格和程序的方法,并得到所有队每两场比赛中间相隔的场次数上限的一个结论,即当队数为双数时,其上限M(n)=2n-2,当队数为单数时,其上限M(n)= 21 n -2。
3.对问题3),当n =8时也采用单循环法找到一种每两队中间比赛至少间隔两场休息的赛程;当n =9时将单循环法改用C 语言编程实现32种赛程安排,这时候每两队中间比赛至少间隔三场休息。
4.除了每两场比赛间隔次数这一指标来衡量一个赛程的优劣外,我们还考虑每个队赛场次数安排的离散程度作为衡量赛程公平性的另一个指标。
一、问题的简述本题为球赛单循环赛程安排的实际问题,实践性强。
当有n 支球队比赛时,在考虑公平性的情况下,编制赛程表,并求“上限”值以及评价赛程的优劣。
其中对问题2)中的“上限”应理解为各队每两场比赛中间相隔的场次数尽量均等(即赛程安排公平)时的至少相隔场次的最大数。
二、模型假设1.设n 支球队进行单循环比赛,球队的编码依此为A 、B 、C ……。
2.每一场比赛都在同一场地上进行,且场地不空场。
3.各队每两场比赛中间相隔的场次数尽量均等。
4.n 个队的所有比赛中,各队每两场比赛中间所有能相隔的场次数的最大值称为上限,记为M (n )。
5.不考虑其他因素,比赛始终能正常进行。
三、模型的建立及求解有n 支球队1、2、3、……n ,在赛程安排时要考虑赛程的公平性,而公平性主要看各队每两场比赛中间得到的休整时间的均等程度。
在赛程安排时各队每两场比赛中间相隔的场次数达到上限时才能保证对各球队的公平。
1.问题1)求解:对于5支球队,我们把这5支球队看成是五边形的顶点,把它转化成平面网络图来分析。
单循环双循环数学问题

单循环双循环数学问题
单循环和双循环是编程中常见的控制结构,用来处理循环执行的问题。
数学中也常常涉及到使用循环来解决问题,下面是一些常见的数学问题,可以使用单循环或双循环来解决。
1. 计算1到n的累加和:使用单循环结构可以遍历从1到n的数字,并将它们依次相加得到结果。
2. 判断一个数是否为质数:对于给定的数字n,使用双循环遍历2到n-1之间的所有数字,判断是否能被其中任何一个数整除,若能,则不是质数。
3. 找出一个数的所有因子:对于给定的数字n,使用双循环遍历1到n之间的所有数字,判断每一个数字是否是n的因子,并将其打印或存储起来。
4. 找出两个数的最大公约数:对于给定的两个数字a和b,使用单循环递减的方式,从较小的数开始,判断两个数能否被该数整除,若能,则找到最大公约数。
5. 找出连续数列中的最大值:对于给定的连续数列,使用单循环遍历每一个数字,比较当前数字与之前的最大值,更新最大值。
这些都是常见的数学问题,可以使用单循环或双循环来解决。
具体使用哪种循环取决于问题的要求和实际情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解法 2 转化 为“ 单循 环赛 ” 模型. 据“ 根 两点确 定
一
个角 ; 2条射线 , 画 图中共有
—
—
个角 ; 画3条射线 ,
条直线 ” 可知 , 过平面内的任意两点可 以画一条直线 ,
图 中共有
个角, 画 n n为大 于 1的整 数 ) 求 ( 条射 线
相 当于每两点作用一次 , 以本题可转化 为“ 所 单循环赛 ”
何表 示?( 人教版九年级上册 习题 2 . 第 7 ) 21 题 若换成
“
n家公司参加商品交易会 , 每两家公 司之间签 订一份合
同” 签订合 同总份数如何表示?( 教版九年级上册习 , 人
题 2. 2 2第 7 ) 题 问题 2 这些问题有何共性?
的生活 经验 出发 , 建立数 学模型 , 其他相关 问题转 化 把
例 1 根据题 意 , 完成下列填空 : 平面 内两点确定一 条直线 , 如果在 这个平 面 内再 画第三 个点 , 么这三个 那 点最多可确定 条直线 ; 如果在这个平 面 内再 画
— —
看各组一共击掌几次?然后总结规律。 每个 同学 经历 让
观察 、 实验 、 猜想 、 归纳 、 总结等过程 , 学生对 问题 的理解 更加 透彻 , 更容易探究出解决 问题 的方法. 分析 设应邀请 n个 队参赛 , 每个 队要与其他 ( n一
单循环赛是学生喜闻乐见 的体育活动形式 , 参与程 度高 , 有一定 经验基础. 问题 架起 了数 学与生 活的桥 此
梁, 学生感到亲切、 熟悉而有兴趣. 建模 建立数 学模 型的过 程是把实际 问题 简化 、 抽
象为合理的数学结构 的过程.
与之类似的生活问题 , 而且可 以作为有 效模型解答几何 中类似的确定几何 图形个数 的问题.
+3 +… + 一1 条直线. )
问的比赛重复计算一次, 故而全部 比赛共计÷n n 1 (一 )
二
场.
讨 论
问题 1 若将“7 队参赛 , /个 , 每两 队之 间 比赛 一场 ”
换成 “ n个人 聚会 , 每两人 之间握手一 次” 握手总 次数如
・ 教材教法 ・
十・般’ (l年 3 初中 ) 7 7 2o 第 期・ 版 o
1 0
中。擞 ・ ( o g 期・ 中 ) 7 ? 2  ̄ 初 版 m 3
・ 教材教法 ・
军循 赛" 型 的建 立及在 几何 中的应 用
80 1 新疆 乌鲁木 齐 市第五 十八 中学 309 陈 欢
数学模 型是为 了某个 特定 目的对现 实 中的原型 作 出一些必要 的简化和假设 , 运用适 当的数 学工具得 到一 个数学结构. 把现实模型抽象 、 简化 为某 种数学结 构 , 是 数学模 型的基本 特征. 平时 的学 习 中, 在 要善 于从 已有
2 1 确定 直线的条数 .
笔者首 先组织学生进行探索 活动 : 请三名 同学现 邀 场演示 , 击掌 一次表示 比赛一场 , 每两人都要击 掌一次 , 观察其击 共掌几 次。 然后 再把全班 同学分成若 干组 , 四
人一组、 五人 一组 、 人一 组、 六 七人 一组 ……再 做 实验 ,
1 “ 单循环赛” 数学模型的建立
y=
有n 个对象 , 每两个对象作用 一次 , 共作用 y次 , 则
1 (1 ?
- .
1. )
问题
某地要组织一次排球邀请赛 , 参赛 的每两个 数学模 型是数 学抽 象、 概括 的产 物. 带领 学生经 历
建立数学 模 型的过 程 , 有助 于 培 养学 生 透过 现 象看 本
1
分析
与例 3 比较 , 相 此题 仅是有 公共端点 的射线
+ 一 = ( 一1 , n 1 ÷nn )这就是计算连续 自然数的和的方
二
由 n条转变为( 2 条 , 然可转 化为“ n+ ) 故依 单循环赛 ” 模
第 四个点 , 么这 四个点最 多可确 定 那
条直线.
— —
由此可以猜想 : 同一平面 内, 在 6个点最多可确定
一
条直线. ( n大于 1的整数 ) n为 个点 最多可确 定 条直线. 分析
—
—
1 个队各赛 1 , 计 ( ) 次 共 n~1 次, 由于 甲队对 乙队 ) 但 的比赛和 乙队对 甲队的比赛 是同一场 比赛 , 即每两 队之
为模型 , 从而 以简驭 繁 、 化难 为易 、 特殊 为一般 , 问 化 使 题的解决更加 简洁. 本文 对人教 版九年级 上册 “ 单循 环
通过讨论 帮助学生抓住单循 环赛 问题 的实质 , 将问 题 简化、 象为“ 抽 单循环赛” 模型 :
赛” 数学模型 的题进行探究 , 以供 同行参考.
队之间都 要 比赛一 场 , 根据 场地和 时间等条件 , 赛程计 划安排 7 , 天 每天安排 4场 比赛 , 比赛组织者应邀请 多少
个队参赛 ?
质, 并对其进 行抽象 和概括 , 帮助学 生体会 数学 的应 用 价值 , 培养 数学 的应 用意识 和数学 创造力. 提高分析 问
题和解决问题的能力. 2 “ 单循环 赛” 数学模型的应用 “ 单循环赛” 型 为我们提 供 的结 论不仅 可 以解答 模
1
所得的角的个 数.
这一模型. 故而在同一平面内 , 聘个点最多 可确定 ( 1
二
一ห้องสมุดไป่ตู้
1 条直线 , 由一般到特殊 , 出 n= , , ) 再 求 3 4 6时对 应 的
兰 三 三
图3
直线条数 , 显然解法 2起到了事半功倍 的效果.
由解法 1 和解法 2又可得到一个 等式 1+ 3+… 2+
1
解法 1 ( 由特殊到一般 的归纳猜想法 ) 两 ,
点确定一条直线 , 再画一个点最 多可分别 与前 两个点各 确定一条直线 , 出 2条直 线 , 时确定 的直 线最 多为 多 这 ( 2 条. 画出第 4个点 , 1+ ) 再 最多 可分别 与前三个 点各 确定 一条直 线 , 出三条直 线 , 时确定 的直线最 多为 多 这 ( + 3 条. 1 2+ ) 由此可 以猜想 : 点最 多可确定 ( 2 n个 1+
