电工电子学_03交流电路
2019年电工学-第3章-交流电路习题及答案.ppt

3.2.2 已知 A = 8 + j6 , B 8 45 。求(1)A+B ;(2) B A A-B;(3)A B ;(4) ;(5)j A+B ;(6) 。 A j B
返回主页 下一页
第 3 章
交 流 电 路
3.3.1 在图3.6(教材图3.01)所示 电路中,已知R 100 , L 31.8 mH,C 318 F, 求电源的频率和电压分别为50 Hz、100 V 和1 000 Hz,100 V两种情况下,开关S 合向 a、b、c 位置时电流表的读数,并 计算各元件中的有功功率和无功功率。 3.4.1 在图3.7(教材图3.02)所示电路中,三个照明相同 , R XC X L ,试问接于交流电源上时,照明灯的亮度有什么不 同?若该接到电压相同的直流电源上,稳定后,与接交流电 源时相比,各照明灯的亮度有什么变化? 3.4.2 求串联交流电路中下列三种情况下电路中的 R 和 X 各为多少?指出电路的性质和电压对电流的相位差
图3.15
j10 , Z 2 (40 j 30) , I
I 2 和U 。 。求:I 1 、 5 30 A
图3.17
返 回 上一页 下一页
第 3 章
交 流 电 路
Байду номын сангаас
3.5.5
在图3.18(教材图3.09)所
示电路中,已知 R X C , U 220V 总电压U 与总电流 I 相位相同。
1 1 若T 10 m s,则 f Hz 100Hz 3 T 10 10
I 7.07 180 A 7.07 180 A 7.07 A
电工电子学第三章

负半周
3
设正弦交流电流: 设正弦交流电流:
Im
Ψ
i
O π T 2π π
ωt
i = I m sin (ω t + ψ )
初相角:决定正弦量起始位置 初相角: 角频率:决定正弦量变化快慢 角频率: 幅值:决定正弦量的大小 幅值:
幅值、角频率、初相角成为正弦量的三要素。 幅值、角频率、初相角成为正弦量的三要素。
5
3.1.2 幅值与有效值 幅值: 幅值:Im、Um、Em
幅值必须大写, 幅值必须大写, 下标加 m。
有效值: 有效值:与交流热效应相等的直流定义为交流电的 有效值。 有效值。
∫0
T
2 i 2R dt = I RT
交流
直流
则有
I =
1 T
∫
T
0
i 2dt
Im 1 T 2 2 有效值必 = ∫0 Imsin ωt dt = 2 须大写 T U Em 同理: 同理: U = m E= 2 2
12
3. 正弦量的相量表示
实质:用复数表示正弦量 实质: 复数表示形式 为复数: 设A为复数 为复数 (1) 代数式 A =a + jb 式中: a = r cos ψ 式中
+j
b
A
r ψ
0
2 2
a
+1
b = r sin ψ
(2) 三角式 由欧拉公式: 由欧拉公式
r = a + b 复数的模 b ψ = arctan 复数的辐角 a
16
⑥“j”的数学意义和物理意义 因子: 旋转 90o因子:e± j90o
± j90o
e
= cos 90° ± jsin90° = ±j
电工电子学-交流电路

求:i i1 i2 。
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A (16.5 - j3.18)A 16.8 10.9 A
解: (1) 相量式
+j
U 2
U 1
+1
220 20V U 1 110 45 V U 2
(2) 相量图
落后于U U 2 1
2018/7/19 2018/7/19 电工电子学B
45 20
U 2
超前 落后 U 1 ?
例2: 已知 i1 12 .7 2 sin (314 t 30 )A i2 11 2 sin(314t 60 )A
+j
b
0
2
A
2
r
a
+1
式中: a r cos ψ
b r sin ψ
(2) 三角式 由欧拉公式:
r a b 复数的模 b ψ arctan 复数的辐角 a
A r cos ψ j r sin ψ r (cos ψ j sin ψ )
cos ψ e
jψ
e 2
j ψ
e j ψ e j ψ , sin ψ 2j
2018/7/19 2018/7/19
电工电子学B
可得:
(3) (4)
cos ψ j sin ψ 指数式 A r e j ψ 极坐标式 A r ψ e
jψ
A a jb r cos j r sin re r ψ
电工学第三章三相交流电ppt课件
6
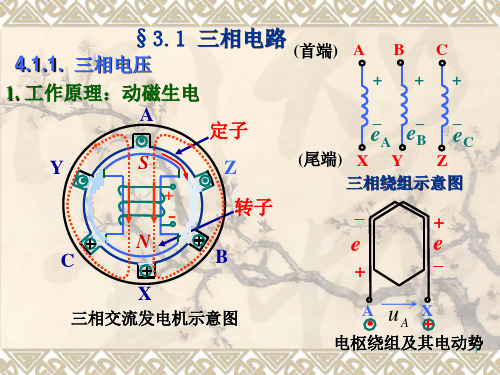
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载:需三相电源同时供电
负载
三相电动机等
单相负载:只需一相电源供电
照明负载、家用电器
对称三相负载:ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下,B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压(220V) ,这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流: 线电流:
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路,如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
电工电子学第三章习题答案 (2)

第三章交流电路3-1 试写出表示u A =)120314sin(2220,314sin 22200-==t u tV u B A 和V t u C )120314sin(22200+=的,并画出相量图。
解:V U V U V U C B A 0.00120220,120220,0220∠=-∠=∠=•••3-2 如图所示的是时间t=0时电压和电流的相量图,并已知U=220V ,I 1=10A ,I 2=52A ,试分别用三角函数式和复数式表示各正弦量。
3-3已知正弦电流i 1=22sin(100πt+60°)A, i 2=32sin(100πt+30°)A,试用相量法求i=i 1+i 2。
解A tg j j j j I I I 010000210.4284.4)598.3232.3(3914.23232.3598.3)213232(23321230sin 330cos 360sin 260cos 2∠=∠=+=⨯+⨯+⨯+⨯=+++=+=-•••i= 4.842 sin (100πt+42.00) A3-4在图示电路中,已知R=100Ω,L=31.8mH ,C=318uF 。
求电源的频率和电压分别为50Hz 、100V 和1000Hz 、100V 的两种情况下,开关S 合向a 、b 、c 位置时电流表的读数,并计算各元件中的有功功率和 无功功率.解:当F=50HZ 、U=100V 时,S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(1099.9100108.312501003A LV ==⨯⨯⨯=-πω 无功功率为:Q=UIb=1000Var S 接到c ,)(10100103182506A C V Ic =⨯⨯⨯⨯==-πω。
无功功率为:q=UIc=-1000Var当F=1000HZ 、U=100V 时S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(5.08.199100108.31210001003A L V ==⨯⨯⨯=-πω 无功功率为:Qb=UIb=50Var S 接到c ,)(8.19910010318210006A C V Ic=⨯⨯⨯⨯==-πω。
电工学-第3章交流电路

j ( ω t u )
]
+j
Um=√2 U
Um
U
2 Im[U e
= √2 Im[U = √2 Im[U]
j u
]
O
ψ ] u
+1
第 3 章 交 流 电 路
设正弦量 u U msin( ω t ψ ) 电压的有效值相量 用相量表示: 相量的模=正弦量的有效值 jψ
O
ψ
ωt1
ωt
正弦交流电可以用 一个固定矢量表示 最大值相量 Im 有效值相量 I
O
ωt2 +j I +1 Im ψ
大连理工大学电气工程系
11
第 3 章 交 流 电 路
一、复数的基础知识 1. 复数的表示方法
+j
几何法
b
ψ
p 模 a +1 辐角
O
Op = a + j b
= c (cosψ + j sinψ ) = c e jψ
瞬时值最大值
i Im
角频 初相位 率
ψ
O
ωt
最大值 角频率 初相位
正弦交流电的三要素
3
第 3 章 交 流 电 路
正弦交流电的波形:
i ψ = 0° i 0<ψ<180°
O
ωt
O ψ
ωt
i
-180°<ψ < 0°
i
ψ = ±180°
O ψ
ωt
O
ωt
4
第 3 章 交 流 电 路
一、交流电的周期、频率、角频率
u
2 I R sin (ω1t i )
U I 。 R
(1) 频率相同。 (2)大小关系:对电阻而言,电压有效值 与电阻有效值之间符合欧姆定律。 相位差 : (3)相位关系 :
第三章交流电路优秀课件

•
U
220
45V?
42si(nωt30)A ?
2
有效值
j45
U m22e405V ?
瞬时值
4.已知:
U 10 015V
2.已知: I1060A U10V 0?负号
? i1s0i(n ω t60 )A ? 最大值
U 100ej15V
例1: 将 u1、u2 用相量表示
u 1 2 2 02sin(ω t 2 0 )V
A a j b r co jr si n r e jψ rψ
相量: 表示正弦量的复数称相量
设正弦量: uU m si(ω ntψ )
相量表示:
U Ujψ eUψ相量的模=正弦量的有效值
相量辐角=正弦量的初相角
电压的有效值相量
或:U mU m ejψU mψ相相量量辐的角模==正正弦弦量量的的初最相大角值
iIm sin(ω tψ 2)
(t 1 ) (t 2 )
ψ1 ψ2
ui u i
若 ψ1ψ20
O
电压超前电流
ωt
ψ1ψ20
电流超前电压
ui i
u
O
ωt
电压与ψ 电1 流ψ 同2相0
ui u
i
O
ωt
ψ 1ψ 290
电流超前电压90
ui u i
O
ωt
90°
ψ1ψ2180
电压与电流反相
ui u i
O
ωt
3.2 正弦量的相量表示法
1.正弦量的表示方法
u
波形图
O
ωt
瞬时值表达式 uU m si n t ()
相量 U Uψ
必须 小写
2020年电工学第3章 交流电路
量的进程。
t=0时的相位角称为初相位角或初相位
若所取计时时刻不同,则正弦量的初相位不同
相位差
ui u
i
0
2
1
i
i1
i2
0
i3
u= Umsin( t+1) 第3章 3 1
i = Imsin( t+2)
两个同频率正弦量的相位角 之差或是初相角之差,称为
相位差,用表示。
t u和i的相位差
求 i1 + i2
解:(1)用相量图法求解 (2)用复数式求解
j
•
Im2
i2 i1
0
•
Im
•
Im1
1
正弦电量 (时间函数)
变换
相量 (复数)
正弦量运算
相量运算 (复数运算)
所求正弦量 反变换 相量结果
•
Im =
•
Im1
+
•
Im2
i= I msin( t+)
交流电的瞬时值表达式: i= Imsin( t+)
P=0 Q=UI=356.4 Var 额定电压 311V
(三) 纯电感电路
第3章 3 3
i
1.电压电流关系
+
设 i = Imsin t
u
L
由
u=
L
di dt
有
–
u= L Imcos t= Umsin( t+90)
Um= Im L = Im XL
感抗 XL= L
XL
电感线圈对高频电流的阻碍作
•
I
U•
t 0
+1
电压与电流同频率、同相位
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幅值、角频率、初相位反映了正弦量的大小、变化的快慢和初始值等 正弦特征,因而幅值、角频率、初相位称为正弦量的三要素。 下面讨论三要素以及相关量。 1. 瞬时值、幅值和有效值 正弦量在任一瞬间的数值称为瞬时值,用小写字母 u、i 来表示,其 中最大的瞬时值称为幅值或最大值,用带下标m的大写字母 U m 、、I m 来表示。
图3.1.3 初相不等的正弦量
6
上图两正弦量的相位差为: (t u ) (t i ) u i (3.1.9) 上式表明,两个同频率正弦量之间的相位之差并不随时间改变,它等 于两者的初相位之差。当计时起点改变时,正弦量的相位和初相位跟 着改变,但两者之间的相位差保持不变。
L
12
应当注意,感抗只是电感电压与电流的幅值或有效值之比,而不是瞬 时值之比,这与电阻电路不同。若用相量表示电感电压与电流的关系, . U Ue j 90 ; I Ie 则有
.
j 0
U I
. .
Ue j 90 Ie j 0
U j 90 e jL jX L I
U m I m sint cost
1 U m I m sin 2t 2
(3.2.10)
UI sin 2t
13
3.2.3 纯电容交流电路
图 3.2.4 电容元件的交流电路 图3.2.4(a)所示为一电容元件的交流电路。在图示的关联参考方 向下: du
iC dt
14
7
正弦量由幅值、角频率、初相位三要素来确定。而平面坐标内的一个 旋转矢量可以表示出正弦量的三要素,因此旋转矢量可以表示正弦量。 3. 2 纯电阻、纯电感、纯电容单相正弦交流电路 交流电路的分析主要有两个方面,一是确定电路中电压与电流 的关系。二是电路中能量的转换和功率的问题。 3.2.1 纯电阻交流电路
第三章
交流电路
电工电子学
1
3.1 正弦交流电的基本概念
图3.1.2 正弦交流电的波形
2
3.1 正弦交流电的基本概念
正弦电压和电流是随时间按照正弦规律变化的,称之为正弦交流电, 其波形如图3.1.2所示,正弦电压和电流等物理量都称为正弦量,其 表达式为: u U m sin(t u ) (3.1.1) (3.1.2) i I m sin(t i )
LI m sin(t 90 ) U m sin(t 90 )
(3.2.6)
可见,电压和电流是同频率的正弦量,其波形如图3.2.2(b)所示。 它们之间的关系为 相位关系 电压超前电流 大小关系 U m LI m Um U 或 (3.2.7) L
Im I
当电感电压一定时, 愈大,流过电感的电流愈小。可见 L 具有阻碍 交流电流的性质。因而称之为感抗,单位为 (欧姆),用 X 表示。 即 X L L 2fL (3.2.8)
Im I
若用相量表示,则有 U Ue j 0
.
I Ie j 0
.
U I
. .
Ue j 0 Ie j 0
.
U j 0 e R I
.
即 U RI . . 同理有 U m RIm
(3.2.3)
9
交流电路的电压和电流是随时间变化的,故电阻所消耗的功率也随时 间变化。在任一瞬间,电压瞬时值与电流瞬时值的乘积称为瞬时功率。 用小写字母 p表示。即 (3.2.4) p ui U m sint I m sint
串联交流电路如图3.3.1(a)所示,选取电流为参考正弦 量。即 i I m sint
17
同频率的正弦量相加,仍是同频率的正弦量,由KVL可得 (3.3.1) u uR uL uC U msin(t )
U U R U LU C
. . . .
T
5
3. 相位、初相位和相位差
在正弦量的表达式u U m sin(t u ) ,i I m sin(t i ) 中, (t u ) 和 (t i ) 都是随时间变化的电角度,称为正弦量的相位或相位角,它 反映了正弦量的变化进程。相位的单位是弧度,也可用度。 t 0 时的相位叫做正弦量的初相位或初相位角。初相位确定了正弦 量在 t 0 时刻的值,即初始值。初相位与计时起点的选择有关,计 时起点选的不同,正弦量的初相位就不同,正弦量的初始值也就不同。 在同一个交流电路中,电压 u和电流i 的频率是相同的,但初相 位不一定相同。两个同频率正弦量的相位之差称为相位差。用 表示。 如图3.1.3所示。
T
0
m
i
1 T1 2 I m [1 cos 2(t i )]dt T 0 2 Im 2
Um 2
同理,正弦电压和正弦电动势的有效值:
U
E
Em 2
(3.1.5) (3.1.6)
4
可见,交流电的有效值等于它的瞬时值的平方在一个周期内积分的平 均值再取平方根。所以有效值也称为方均根值。有效值用大写字母表 示。虽然与表示直流的字母相同,但物理含义不同。 2. 周期、频率和角频率 正弦量重复变化一次所需要的时间称为周期, 用T表示,单位为s (秒)。每秒内重复变化的次数称为频率,用 f表示,单位为 (赫 兹)。 周期与频率互为倒数关系,即: f 1 T (3.1.7) 我国电厂生产的交流电频率为 ,这一频率称为工业标准频率,简称 工频。 正弦量每重复变化一次,相当于变化了 弧度。为了避免与机械角度 混淆,这里称为电角度。正弦量每秒变化 次,则每秒变化的电角度 为 弧度。即每秒变化的弧度数称为正弦量的角频率或电角速度,单 位为 (弧度/秒)。 (3.1.8) 2π 2 πf
Im I
C
当电压一定时, 愈大,电流愈小。可见 具有阻碍交流电流的性 质。因而称之为容抗,单位为 (欧姆),用 X 表示,即
C
1 C
1 C
XC
1 1 C 2fC
15
若用相量表示电容电压与电流的关系,则有
U Ue
U I
. .
.
j 0
I Ie j 90
U j 90 e jX C I
.
.
Ue j 0 Ie
.
j 90
即
I I U jX C I j C jC
.
.
(3.2.16)
同理, U m jX C I m 上两式是电容电压与电流关系的相量形式。它反映了电容电压与电流 的大小及相位关系。电压和电流的相量图如图3.2.4(c)所示。 电理
U jL I jX L I
.
.
(3.2.9)
U m jL I m
.
.
上两式是电感电压和电流关系的相量形式,它反映了电感电压与电流 的大小及相位关系。电压和电流的相量图如图3.2.2(c)所示。 电感电路吸收的瞬时功率为
p ui U msin(t 90 ) I msint
2UIsin 2 t 1 U m I m (1 cos2t ) 2 UI (1 cos2t )
由瞬时功率 的表达式和波形图可知,除了过零点外,其余时间均为 正值。即 p≥0,这说明电阻元件从电源取用电能,并将电能转换为 热能,这是一种不可逆的能量转换过程。所以电阻元件是耗能元件。 瞬时功率只能说明功率的变化情况,实用意义不大。通常所说电路的 功率是指瞬时功率在一个周期内的平均值,称为平均功率,用大写字 母 P表示。即 1 1 (3.2.5) P pdt UI (1 cos 2t )dt
p ui U msint I msin(t 90 )
.
.
U m I m sint cost 1 U m I m sin 2t 2
UI sin 2t
(3.2.17)
16
3.3 简单单相正弦交流电路的计算 3.3.1 R、L、C串联交流电路
图3.3.1 、 串联交流电路
k 1
n
(3.3.12) (3.3.13)
图3.3.5 复阻抗串联 由此可见,n个复阻抗串联,其总复阻抗等于各个串联复阻抗之和。
19
图3.3.6为n个复阻抗并联的电路。由基尔霍夫电流定律得到
U U U I I 1 I 2 In Z1 Z 2 Zn . 1 .1 1 1 U( ) U Z1 Z 2 Zn Z
3
通常用有效值来表示正弦量的大小。 有效值是从电流热效应的角度规定的。设一个交流电流 和某个直流 电流 分别通过阻值相同的电阻 ,并且在相同的时间内(如一个周期 ) 产生的热量相等,则这个直流电流 的数值叫做交流电流 的有效值, T 2 2 按此定义,有: 0 Ri dt RI T 即 1 T 2 I i dt T 0 (3.1.3) 对于正弦电流 的有效值为 1 T (3.1.4) I [ I sin(t )]2 dt
图3.2.1 电阻元件的交流电路
8
设电流为参考正弦量。即 i I m sint 则有 u Ri RI m sint U m sint (3.2.1) 可见,电阻上的电流 与它两端的电压 是同频率同相位的正弦量。如图 3.2.1(b)所示,它们间的大小关系为 U m RI m 或 U m U R (3.2.2)
