浅谈分离式热管换热器在电解铜行业的应用
铜冶炼行业板式换热器的应用
减少了饱和水分的含量;烟气再进一步进行电除雾,除去夹带来的酸雾,经干燥后进入转化器,将 SO2 转化成 SO3,根据实际成品酸的要求,用 93% 或 98%的浓硫酸在吸收塔内吸收 SO3,塔底成品酸经成品酸板式换热器降温后,送入成品酸储槽。
含 SO2 的烟气,先除尘洗涤,再用经板式换热器冷却后的稀酸进行吸收, 这既吸收了其中冶炼过程中产生的少量 SO3,也降低了气体测温度,
洗 涤 塔 烟气
冷 却 塔
电 除 雾
成品酸冷却器
成品酸 40℃
稀酸冷却器
稀酸 52℃ 烟 气 铜精矿等 水 43℃
循环冷却水塔
成品酸储槽 稀酸槽
烟 气 电解液,65℃ 饱和蒸汽 133℃ 凝结水 133℃
熔炼 吹炼 精炼 铸锭 阳极铜板 电解 阴极铜
电解液,58℃
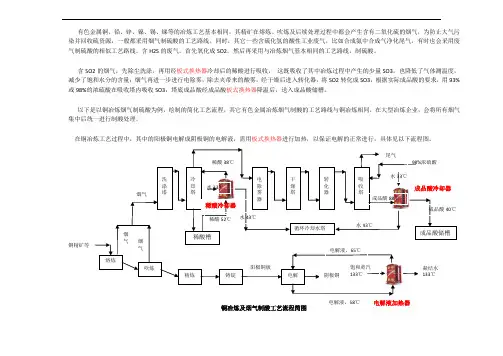
以下是以铜冶炼烟气制硫酸为例,绘制的简化工艺流程,其它有色金属冶炼烟气制酸的工艺路线与铜冶炼相同,在大型冶炼企业,会将所有烟气 集中后统一进行制酸处理。
在铜冶炼工艺过程中,其中的阳极铜电解成阴极铜的电解液,需用板式换热器进行加热,以保证电解的正常进行,具体见以下流程图。
稀酸 38℃ 水 33℃ 尾气 水 33℃ 成品酸 88℃ 98%浓硫酸
有色金属铜、铅、锌、镍、锡、锑等的冶炼工艺基本相同,其精矿在熔炼、吹炼及后续处理过程中都会产生含有二氧化硫的烟气,为防止大气污 气制硫酸的相似工艺路线。含 H2S 的废气,首先氧化成 SO2,然后再采用与冶炼烟气基本相同的工艺路线,制硫酸。 染并回收硫资源,一般都采用烟气制硫酸的工艺路线。同时,其它一些含硫化氢的酸性工业废气,比如合成氨中合成气净化尾气,有时也会采用废
电解液加热器
铜冶炼及烟气制酸工艺流程简图
浅谈热管及热管气-气换热器的应用

浅谈热管及热管气-气换热器的应用热管是一种利用液体和蒸汽相变以传热的设备,具有高效、节能、灵活、可靠等特点,被广泛应用于工业生产、航天航空、军事设备等领域。
热管气-气换热器也是一种热管的应用形式,它能够实现气体之间的换热,广泛应用于空调、采暖、化工等领域。
热管的原理是利用液体在吸热后蒸发,将热量带到高温端,然后在高温端再凝结成液体,将热量释放出来。
经过这样的循环,热量就能够从低温端传递到高温端。
热管具有高效率、传热均匀、无需外部能源等优点,因此在许多领域得到了广泛的应用。
热管的应用领域非常广泛。
在工业生产中,热管被用于散热、温度控制、传热等方面。
一些工业设备需要保持稳定的温度,可以使用热管来实现。
在航天航空领域,热管被用于热控系统、空调系统、温控系统等方面,能够帮助控制设备的温度,提高设备的工作效率。
在军事设备领域,热管也被广泛应用于火箭发动机、导弹引导系统等方面。
热管气-气换热器是一种热管的应用形式,它将热管的原理应用到了气体之间的换热过程中。
热管气-气换热器具有传热效率高、体积小、重量轻、结构简单等优点,因此在空调、采暖、化工等领域得到了广泛的应用。
热管气-气换热器在空调领域的应用非常广泛。
在空调系统中,冷却剂需要和空气进行换热,以实现室内温度的调节。
热管气-气换热器能够高效地实现冷却剂和空气之间的换热,提高空调系统的效率。
热管气-气换热器还可以用于采暖系统中,实现热水和空气之间的换热,提高采暖系统的能效。
在化工领域,热管气-气换热器也有着重要的应用。
在化工生产过程中,许多反应需要控制温度,热管气-气换热器能够有效地实现热量的传递,帮助控制反应过程的温度,提高生产效率。
热管及热管气-气换热器具有着广泛的应用前景,能够在许多领域发挥重要的作用。
随着技术的不断进步,热管及其应用形式将会得到进一步的发展,为人类的生产生活带来更多便利。
试析热管换热器在煤化工企业中的应用及节能对策

传热 系数在是衡量 工业用换 热器 是否先进和 高效的一个重要的 参考指数 。传热 系数值较高 ,则换热器体积 就比较 小,材料和 动力
热管出现 于上个世纪六十年 代中期,它的特点是构造简单 ,传
的消耗就会 降低 。 相反 , 传热系数值较低,则换热器 体积就 比较大 , 材 料和动 力的消耗就会增多,也影响传热的效果。 2 . 2适用温度范 围广 热管工作 液和内外换热 条件 决定着热管的工作 温度,工作液的
3 . 1 工 业 用炉 ’
【 关键词 】 热管换热器 ;煤化工企业 ;应用 ;节能
1热管换 热器 的结构特征和材料要求
热管是一种真空密封容 器, 内部填 充了一 定量 的工作介质 , 具有 高效的传热功能 。热管的种类主要有吸液芯 、重力式 、旋转式 、分
离型热管等。 吸液 芯热管是蒸发一 冷凝 与毛细吸力作 用相结合 的一种新型传
气在热管换热器 的蒸 发端冷却,放 出热量将冷凝 端的高炉煤 气和助
燃空气 同时预热 。
用热管换 热器 回收甲基 萘管 式加热炉烟气 余热,于回收烟气热 量 的过程 中,降低 了烟气 的排 空温 度, 将烟气的热量 传递给助燃空
气和高炉煤气 ,使助燃空气 和高炉 煤气 的温度得 打了提高,因此, 煤气 的使用量 降低 ,减少 了成本的投入 ,节约的资源,企业的经济
热性 能好, 温度适 中,无 需运动部件,工作稳定可靠等,受到人们
的高度 重视 ,并且在 短期内得到了快速 的发展。 日前作为一项专 门 技术 ,广泛地应用 于电子行业、航天部 门、化工企业等部 门。热管 换热器在 回收热能方面效果 明显。 国内外对此都进行 了大量的研究 , 国内在 化工 行业中成功应 用于锅炉、加热炉等排气余热回收 。国外 还将 热管应 用于工艺热能利用。利用热管换热器可 以提高效率 ,节 省原料 ,降低生产成本,减少资金投入 。使企业的生产走上一条资 源节 约型和环境友好型的道路,确保企业的长远和可持续发展 。当 前,随着技 术的发展,热管挽热器也应该不断进行创新 ,不断优化 设计 ,提高各项功能,使热管换热器在化工业的生产 中发挥更大 的
浅议热管技术及其在热能工程中的应用.doc

浅议热管技术及其在热能工程中的应用热管技术现在运用的越来越频繁,本文对热管的基本组成,热管的工作原理,以及热管的分类和热管在应用的过程中,所要解决的技术关键做了详细的分析,并且对热管技术在热能工程的应用进行了分析和研究,给以后的热管研究提供了参考。
随着科学技术的发展越来越快,热能工程的发展也是与日俱进,热管技术也投入到了应用。
热管的导热系数非常高,是铝、银等金属的上千倍。
如果使用热管技术,热管的截面非常的小,并且不需要加入任何的动力就可以让巨大的热能,进行传输。
因此,热管在热能工程的应用越来越广泛。
热管的组成和原理1.1.热管的组成典型的热管由管壳、吸液芯和端盖组成,将管内抽成1.3×(10负1---10负4)Pa的负压后充以适量的工作液体,使紧贴管内壁的吸液芯毛细多孔材料中充满液体后加以密封。
管的一端为蒸发段(加热段),另一端为冷凝段(冷却段),根据应用需要在两段中间可布置绝热段。
当热管的一端受热时毛纫芯中的液体蒸发汽化,蒸汽在微小的压差下流向另一端放出热量凝结成液体,液体再沿多孔材料靠毛细力的作用流回蒸发段。
如此循环不己,热量由热管的一端传至另—端。
热管在实现这一热量转移的过程中,包含了以下六个相互关联的主要过程:1.1.1.热量从热源通过热管管壁和充满工作液体的吸液芯传递到(液---汽)分界面;1.1.2.液体在蒸发段内的(液--汽)分界面上蒸发;1.1.3.蒸汽腔内的蒸汽从蒸发段流到冷凝段;1.1.4.蒸汽在冷凝段内的汽.液分界面上凝结:1.1.5.热量从(汽--液)分界面通过吸液芯、液体和管壁传给冷源:1.1.6.在吸液芯内由于毛细作用使冷凝后的工作液体回流到蒸发段。
1.2.热管的原理在加热热管的蒸发段,管芯内的工作液体受热蒸发,并带走热量,该热量为工作液体的蒸发潜热,蒸汽从中心通道流向热管的冷凝段,凝结成液体,同时放出潜热,在毛细力的作用下,液体回流到蒸发段。
这样,就完成了一个闭合循环,从而将大量的热量从加热段传到散热段。
分离式液-气热管换热器的设计与应用

分离式液-气热管换热器的设计与应用摘要:文中介绍一种利用工艺中液体冷却放出热量来加热气体的分离式热管换热器。
对液———气换热进行了热力分析与强度、结构的设计计算,以及系统的水动力循环分析。
同时给出了实际应用实例,充分说明这种联合换热形式的换热器是合理、可靠的。
1 前言分离式热管换热器以其传热效率高、远程传热、现场布置灵活而具特色。
其最大的特点是加热段与冷凝段可以相互独立。
以往大部分的分离式热管换热器都是采用一种热流体同时加热两种或两种以上的冷流体,冷、热流体间多为气———气换热形式,然而,将二种或两种以上的热流体(液体) 来加热冷流体(气体) ,目前还不多见。
在结构上加热段完全采用普通管板式列管换热器,热流体走壳程;冷凝段为带有翅片管束的换热器,其翅片管外流经被加热气体,管内通过上升管、下降管与列管换热器管程构成回路,将其抽成真空状态,充装工质。
这样壳程内热流体通过对流换热将热量传输给管程内的液态工质,工质吸收热量在真空状态下蒸发,蒸汽沿上升管流至冷段凝结放出汽化潜热将流经翅片管外的气体加热。
2 结构形式与设计计算方法根据热管加热段的换热,结构上采用普通管板式列管换热器,热流体流经壳程管程为热管工质,换热器管程由若干根换热管组成一个单元,每个单元相互独立,热管的冷凝段则为翅片管换热器,管外流经需要被加热的空气,管内通过若干根上升管、下降管与列管换热器每个单元管程内构成回路,将其抽成真空状态,充装工质。
其结构如图1。
首先进行热力计算,热流体在壳程被冷却,放出热量Q ,为强化传热壳程布置了一定数量的折流板,其壳程流体的换热系统可根据公式:Nu = 0.36 Re0155 Pr1/ 3 (μf μw) 0114 (1)求出。
管程流体的换热系数可通过传热因子jh 导出:jh = Nu·Pr - 1/ 3·(μf μw) - 0114 (2)式中μf ———流体粘度;μw ———流体在壁温下的粘度;因此,热管热段列管式换热器的总传热系数可以求出,传热面积也可求得,换热管根数可以确定。
热管换热器的特点及应用范围

热管换热器的特点及应用范围
热管换热器的特点及应用范围
热管换热器,也有的称其为热交换器,在石油化工、钢铁冶炼、汽车制造、食品烘干及其他许多领域有着广泛的应用。
热管换热器在工业领域作为一种余热回收设备,对高温废气和新风进行热量的交换,利用废气中含有的高温热量对新风进行预热的处理,提高进炉空气温度,这部分回收的热量也可以进行烘干作业,达到热回收的节能效果。
热管换热器具有较高的热交换率,设备内部没有运动部件,使用寿命长,重要的是热传导率高。
热管换热器在设计时,冷热流通道密闭性好,新风与排风不会发生串风,确保新风的干净度;根据使用环境不同,热管换热器的外壳所使用的或喷涂的材料也不同,确保设备具备一定的防腐、防锈等特点。
应用范围:
热管换热器广泛应用于竹板、蔬菜、种子、干果、海鲜、食品等烘干工艺,在高岭土喷雾干燥热风炉中的余热回收,玻璃窑炉中的余热回收,水泥窑炉中的余热回收,各种陶瓷倒燃炉及隧道窑中的余热回收等等。
热管换热器的工业用途[工程类精品文档]
热管换热器的工业用途[工程类精品文档]本文内容极具参考价值,如若有用,请打赏支持,谢谢!化学工业1、硫酸系统热管换热器回收焚烧炉出口高温SOx气体的余热、在转化工段回收高温气体的余热,产生热水或蒸汽供系统使用。
2、医药、日化工业热管换热器可用于回收药气或废气的余热,生产清洁热风,干燥物料。
3、利用可变热导热管可对反应床层进行恒温控制的同时,取出或输入反应热。
4、大型化肥厂合成对流段盘管;中、小型氮肥厂造气工程、变换工段,利用热管式蒸发器回收工艺气余热产生蒸汽供合成氨系统使用,变换工段一、二水加热器。
5、甲醇转化炉对流段盘管。
6、苯酐装置热容器。
电力工业利用热管换热器可作为各种锅炉的尾部受热面。
如热管式空气预热器可替代传统的回转式空气预热器和列管式空气预热器,提高受热面壁温,避免露点腐蚀,提高炉膛进风温度和炉膛含氧量,减少漏风,延长锅炉运行周期。
1、工业锅炉尾部的热管空气预热器。
热管式省煤器或翅片管省煤器。
2、电站锅炉尾部的热管空气预热器可分下列几种用途:(1)在原低温段空气预热器的空气入口前设置一热管式空气预热器,进一步降低锅炉排烟温度,减少排烟热损,提高锅炉效率;(2)整个低温段空气预热器均为热管式结构;(3)用锅炉排放的热烟气加热脱硫后的冷烟气,即电站脱硫的GGH.3、燃气锅炉对流段后部。
4、电力输送线路的保护,在高海拔及寒冷地区的电力输送塔、变电站等都需要热管来保护其地基不会因季节变化而过度膨胀或者融沉。
石油化工1、炼油厂的常压炉、减压炉、常减压二合一炉、加氢炉。
减粘炉、重整炉等,利用热管式空气预热器回收出炉烟气的余热加热空气,以提高加热炉的送风温度。
2、炼油厂催化装置再生烟气和各种内、外取热器的余热回收,可产生中压蒸汽并用于动力系统。
3、乙烯裂解炉对流段盘管、炼油厂加热炉对流段盘管。
冶金工业1、炼铁厂用高炉烟气来预热空气、煤气的单预热或双预热整体式或分离式热管换热器,回收热风炉烟气余热,节约煤气,提高热风炉的升温速度、炉顶温度和送风温度降低炼铁焦比,节约焦炭。
浅谈热管技术在热能工程中的应用
§4.3 三角函数的图象与性质最新考纲 1.能画出y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性.2.借助图象理解正弦函数、余弦函数在[0,2π],正切函数在⎝ ⎛⎭⎪⎫-π2,π2上的性质(如单调性、最大值和最小值、图象与x 轴交点等). 1.用五点法作正弦函数和余弦函数的简图(1)在正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫3π2,-1,(2π,0).(2)在余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )函数y =sin x y =cos x y =tan x图象定义域 R R 错误! x ≠k π+错误!}值域 [-1,1] [-1,1] R 周期性 2π 2π π 奇偶性 奇函数偶函数 奇函数递增区间⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2[2k π-π,2k π]⎝⎛⎭⎪⎫k π-π2,k π+π2递减区间⎣⎢⎡⎦⎥⎤2k π+π2,2k π+3π2 [2k π,2k π+π]无对称中心 (k π,0)⎝ ⎛⎭⎪⎫k π+π2,0⎝ ⎛⎭⎪⎫k π2,0对称轴方程 x =k π+π2x =k π无概念方法微思考1.正(余)弦曲线相邻两条对称轴之间的距离是多少?相邻两个对称中心的距离呢?提示 正(余)弦曲线相邻两条对称轴之间的距离是半个周期;相邻两个对称中心的距离也为半个周期.2.思考函数f (x )=A sin(ωx +φ)(A ≠0,ω≠0)是奇函数,偶函数的充要条件? 提示 (1)f (x )为偶函数的充要条件是φ=π2+k π(k ∈Z );(2)f (x )为奇函数的充要条件是φ=k π(k ∈Z ). 题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)y =sin x 在第一、第四象限是增函数.( × )(2)由sin ⎝ ⎛⎭⎪⎫π6+2π3=sin π6知,2π3是正弦函数y =sin x (x ∈R )的一个周期.( × )(3)正切函数y =tan x 在定义域内是增函数.( × ) (4)已知y =k sin x +1,x ∈R ,则y 的最大值为k +1.( × ) (5)y =sin|x |是偶函数.( √ ) 题组二 教材改编2.函数f (x )=cos ⎝ ⎛⎭⎪⎫2x +π4的最小正周期是.答案 π3.y =3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域是.答案 ⎣⎢⎡⎦⎥⎤-32,3解析 当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1,故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即y =3sin ⎝ ⎛⎭⎪⎫2x -π6的值域为⎣⎢⎡⎦⎥⎤-32,3.4.函数y =-tan ⎝⎛⎭⎪⎫2x -3π4的单调递减区间为.答案 ⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z )解析 由-π2+k π<2x -3π4<π2+k π(k ∈Z ),得π8+k π2<x <5π8+k π2(k ∈Z ),所以y =-tan ⎝⎛⎭⎪⎫2x -3π4的单调递减区间为 ⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z ).题组三 易错自纠5.下列函数中最小正周期为π且图象关于直线x =π3对称的是( )A .y =2sin ⎝⎛⎭⎪⎫2x +π3 B .y =2sin ⎝ ⎛⎭⎪⎫2x -π6C .y =2sin ⎝ ⎛⎭⎪⎫x 2+π3D .y =2sin ⎝⎛⎭⎪⎫2x -π3 答案 B解析 函数y =2sin ⎝⎛⎭⎪⎫2x -π6的最小正周期T =2π2=π, 又sin ⎝⎛⎭⎪⎫2×π3-π6=1,∴函数y =2sin ⎝ ⎛⎭⎪⎫2x -π6的图象关于直线x =π3对称.6.函数f (x )=4sin ⎝⎛⎭⎪⎫π3-2x 的单调递减区间是.答案 ⎣⎢⎡⎦⎥⎤k π-π12,k π+512π(k ∈Z ) 解析 f (x )=4sin ⎝ ⎛⎭⎪⎫π3-2x=-4sin ⎝⎛⎭⎪⎫2x -π3. 所以要求f (x )的单调递减区间,只需求y =4sin ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间.由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z ),得-π12+k π≤x ≤512π+k π(k ∈Z ). 所以函数f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤-π12+k π,512π+k π(k ∈Z ). 7.cos23°,s in68°,cos97°的大小关系是. 答案 sin68°>cos23°>cos97° 解析 sin68°=cos22°,又y =cos x 在[0°,180°]上是减函数,∴sin68°>cos23°>cos97°. 题型一 三角函数的定义域1.函数f (x )=-2tan ⎝⎛⎭⎪⎫2x +π6的定义域是( ) A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π6 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠-π12 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠k π+π6(k ∈Z )D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠k π2+π6(k ∈Z )答案 D解析 由正切函数的定义域,得2x +π6≠k π+π2,k ∈Z ,即x ≠k π2+π6(k ∈Z ),故选D.2.函数y =sin x -cos x 的定义域为. 答案 ⎣⎢⎡⎦⎥⎤2k π+π4,2k π+5π4(k ∈Z )解析 方法一 要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]内,满足sin x =cos x 的x 为π4,5π4,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z. 方法二 利用三角函数线,画出满足条件的终边范围(如图中阴影部分所示).所以定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z. 3.函数y =lg(sin x )+cos x -12的定义域为.答案 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π<x ≤2k π+π3,k ∈Z解析 要使函数有意义,则⎩⎪⎨⎪⎧sin x >0,cos x -12≥0,即⎩⎪⎨⎪⎧sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k π,k ∈Z ,-π3+2k π≤x ≤π3+2k π,k ∈Z ,所以2k π<x ≤π3+2k π(k ∈Z ),所以函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π<x ≤2k π+π3,k ∈Z. 思维升华三角函数定义域的求法求三角函数的定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.题型二 三角函数的值域(最值)例1 (1)函数y =2sin ⎝⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( )A .2-3B .0C .-1D .-1- 3 答案 A解析 因为0≤x ≤9,所以-π3≤πx 6-π3≤7π6,所以-32≤sin ⎝ ⎛⎭⎪⎫πx 6-π3≤1,则-3≤y ≤2. 所以y max +y min =2- 3.(2)函数y =cos2x +2cos x 的值域是( ) A .[-1,3]B.⎣⎢⎡⎦⎥⎤-32,3C.⎣⎢⎡⎦⎥⎤-32,-1 D.⎣⎢⎡⎦⎥⎤32,3 答案 B解析 y =cos2x +2cos x =2cos 2x +2cos x -1=2⎝⎛⎭⎪⎫cos x +122-32,因为cos x ∈[-1,1],所以原式的值域为⎣⎢⎡⎦⎥⎤-32,3.思维升华求解三角函数的值域(最值)常见到以下几种类型:(1)形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+c 的形式,再求值域(最值);(2)形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);(3)形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).(4)一些复杂的三角函数,可考虑利用导数确定函数的单调性,然后求最值.跟踪训练1(1)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π3,a ,若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,则实数a 的取值范围是.答案 ⎣⎢⎡⎦⎥⎤π3,π解析 ∵x ∈⎣⎢⎡⎦⎥⎤-π3,a ,∴x +π6∈⎣⎢⎡⎦⎥⎤-π6,a +π6,∵当x +π6∈⎣⎢⎡⎦⎥⎤-π6,π2时,f (x )的值域为⎣⎢⎡⎦⎥⎤-12,1,∴由函数的图象(图略)知,π2≤a +π6≤7π6, ∴π3≤a ≤π. (2)(2018·长沙质检)函数y =sin x -cos x +sin x cos x 的值域为.答案 ⎣⎢⎡⎦⎥⎤-12-2,1解析 设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x ·cos x ,sin x cos x =1-t 22,且-2≤t ≤ 2.∴y =-t 22+t +12=-12(t -1)2+1,t ∈[-2,2].当t =1时,y max =1;当t =-2时,y min =-12- 2.∴函数的值域为⎣⎢⎡⎦⎥⎤-12-2,1. 题型三 三角函数的周期性与对称性例 2 (1)若函数f (x )=2tan ⎝ ⎛⎭⎪⎫kx +π3的最小正周期T 满足1<T <2,则自然数k 的值为________. 答案 2或3解析 由题意得1<πk<2,k ∈N ,∴π2<k <π,k ∈N , ∴k =2或3.(2)(2018·武汉模拟)若函数y =cos ⎝ ⎛⎭⎪⎫ωx +π6(ω∈N *)图象的一个对称中心是⎝ ⎛⎭⎪⎫π6,0,则ω的最小值为___________.答案 2 解析 由题意知ωπ6+π6=k π+π2(k ∈Z ), ∴ω=6k +2(k ∈Z ),又ω∈N *,∴ωmin =2.思维升华 (1)对于函数y =A sin(ωx +φ)(A ≠0,ω≠0),其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点. (2)求三角函数周期的方法 ①利用周期函数的定义.②利用公式:y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π|ω|,y =tan(ωx +φ)的最小正周期为π|ω|. 跟踪训练2 (1)函数y =2sin ⎝ ⎛⎭⎪⎫2x +π3的图象( ) A .关于原点对称B .关于点⎝ ⎛⎭⎪⎫-π6,0对称C .关于y 轴对称D .关于直线x =π6对称答案 B解析 ∵当x =-π6时,函数y =2sin ⎝ ⎛⎭⎪⎫-π6×2+π3=0,∴函数图象关于点⎝ ⎛⎭⎪⎫-π6,0对称.(2)若直线x =54π和x =94π是函数y =cos(ωx +φ)(ω>0)图象的两条相邻对称轴,则φ的一个可能取值为( ) A.34πB.π2C.π3D.π4 答案 A解析 由题意,函数的周期T =2×⎝ ⎛⎭⎪⎫94π-54π=2π,∴ω=2πT =1,∴y =cos(x +φ),当x =54π时,函数取得最大值或最小值,即cos ⎝ ⎛⎭⎪⎫54π+φ=±1,可得54π+φ=k π,k ∈Z ,∴φ=k π-54π,k ∈Z .当k =2时,可得φ=34π.题型四 三角函数的单调性 命题点1 求三角函数的单调区间例3(1)函数f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为.答案 ⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z )解析 f (x )=sin ⎝ ⎛⎭⎪⎫-2x +π3=sin ⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫2x -π3=-sin ⎝⎛⎭⎪⎫2x -π3,由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故所求函数的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12(k ∈Z ).(2)函数f (x )=tan ⎝⎛⎭⎪⎫2x +π3的单调递增区间是.答案 ⎝ ⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z )解析 由k π-π2<2x +π3<k π+π2(k ∈Z ),得k π2-5π12<x <k π2+π12(k ∈Z ),所以函数f (x )=tan ⎝⎛⎭⎪⎫2x +π3的单调递增区间为 ⎝⎛⎭⎪⎫k π2-5π12,k π2+π12(k ∈Z ).(3)函数y =12sin x +32cos x ⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0,π2的单调递增区间是.答案 ⎣⎢⎡⎦⎥⎤0,π6解析 ∵y =12sin x +32cos x =sin ⎝ ⎛⎭⎪⎫x +π3,由2k π-π2≤x +π3≤2k π+π2(k ∈Z ),解得2k π-5π6≤x ≤2k π+π6(k ∈Z ).∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤2k π-5π6,2k π+π6(k ∈Z ), 又x ∈⎣⎢⎡⎦⎥⎤0,π2,∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤0,π6.命题点2 根据单调性求参数例4已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π上单调递减,则ω的取值范围是.答案 ⎣⎢⎡⎦⎥⎤12,54解析 由π2<x <π,ω>0,得ωπ2+π4<ωx +π4<ωπ+π4, 又y =sin x 的单调递减区间为⎣⎢⎡⎦⎥⎤2k π+π2,2k π+3π2,k ∈Z ,所以⎩⎪⎨⎪⎧ωπ2+π4≥π2+2k π,ωπ+π4≤3π2+2k π,k ∈Z ,解得4k +12≤ω≤2k +54,k ∈Z .又由4k +12-⎝ ⎛⎭⎪⎫2k +54≤0,k ∈Z 且2k +54>0,k ∈Z ,得k =0,所以ω∈⎣⎢⎡⎦⎥⎤12,54.引申探究本例中,若已知ω>0,函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π上单调递增,则ω的取值范围是.答案 ⎣⎢⎡⎦⎥⎤32,74解析 函数y =cos x 的单调递增区间为[-π+2k π,2k π],k ∈Z ,则⎩⎪⎨⎪⎧ωπ2+π4≥-π+2k π,ωπ+π4≤2k π,k ∈Z ,解得4k -52≤ω≤2k -14,k ∈Z ,又由4k -52-⎝ ⎛⎭⎪⎫2k -14≤0,k ∈Z 且2k -14>0,k ∈Z ,得k =1,所以ω∈⎣⎢⎡⎦⎥⎤32,74.思维升华 (1)已知三角函数解析式求单调区间求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,可借助诱导公式将ω化为正数,防止把单调性弄错.(2)已知三角函数的单调区间求参数.先求出函数的单调区间,然后利用集合间的关系求解.跟踪训练3 (1)已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫π4-2x ,则函数f (x )的单调递减区间为( )A.⎣⎢⎡⎦⎥⎤3π8+2k π,7π8+2k π(k ∈Z )B.⎣⎢⎡⎦⎥⎤-π8+2k π,3π8+2k π(k ∈Z )C.⎣⎢⎡⎦⎥⎤3π8+k π,7π8+k π(k ∈Z )D.⎣⎢⎡⎦⎥⎤-π8+k π,3π8+k π(k ∈Z ) 答案 D解析 函数的解析式可化为f (x )=-2sin ⎝⎛⎭⎪⎫2x -π4.由2k π-π2≤2x -π4≤2k π+π2(k ∈Z ),得-π8+k π≤x ≤3π8+k π(k ∈Z ),即函数f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤-π8+k π,3π8+k π(k ∈Z ).(2)(2018·武汉联考)若函数g (x )=sin ⎝ ⎛⎭⎪⎫2x +π6在区间⎣⎢⎡⎦⎥⎤0,a 3和⎣⎢⎡⎦⎥⎤4a ,7π6上均单调递增,则实数a 的取值范围是.答案 ⎣⎢⎡⎭⎪⎫π6,7π24解析 由2k π-π2≤2x +π6≤2k π+π2(k ∈Z ),可得k π-π3≤x ≤k π+π6(k ∈Z ),∴g (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ).又∵函数g (x )在区间⎣⎢⎡⎦⎥⎤0,a 3和⎣⎢⎡⎦⎥⎤4a ,7π6上均单调递增,∴⎩⎪⎨⎪⎧a 3≤π6,4a ≥2π3,4a <7π6,解得π6≤a <7π24.三角函数的图象与性质纵观近年高考中三角函数的试题,其有关性质几乎每年必考,题目较为简单,综合性的知识多数为三角函数本章内的知识,通过有效地复习完全可以对此类题型及解法有效攻破,并在高考中拿全分.例(1)在函数①y =cos|2x |;②y =|cos x |;③y =cos ⎝ ⎛⎭⎪⎫2x +π6;④y =tan ⎝ ⎛⎭⎪⎫2x -π4中,最小正周期为π的所有函数为( ) A .①②③ B .①③④ C .②④ D .①③答案 A解析 ①y =cos|2x |=cos2x ,最小正周期为π; ②由图象知y =|cos x |的最小正周期为π; ③y =cos ⎝ ⎛⎭⎪⎫2x +π6的最小正周期T =2π2=π;④y =tan ⎝⎛⎭⎪⎫2x -π4的最小正周期T =π2,故选A. (2)(2017·全国Ⅲ)设函数f (x )=cos ⎝⎛⎭⎪⎫x +π3,则下列结论错误的是( )A .f (x )的一个周期为-2πB .y =f (x )的图象关于直线x =8π3对称C .f (x +π)的一个零点为x =π6D .f (x )在⎝ ⎛⎭⎪⎫π2,π上单调递减 答案 D解析 A 项,因为f (x )=cos ⎝⎛⎭⎪⎫x +π3的周期为2k π(k ∈Z ),所以f (x )的一个周期为-2π,A项正确;B 项,因为f (x )=cos ⎝⎛⎭⎪⎫x +π3的图象的对称轴为直线x =k π-π3(k ∈Z ),所以y =f (x )的图象关于直线x =8π3对称,B 项正确;C 项,f (x +π)=cos ⎝ ⎛⎭⎪⎫x +4π3.令x +4π3=k π+π2(k ∈Z ),得x =k π-5π6(k ∈Z ),当k=1时,x =π6,所以f (x +π)的一个零点为x =π6,C 项正确;D 项,因为f (x )=cos ⎝ ⎛⎭⎪⎫x +π3的单调递减区间为⎣⎢⎡⎦⎥⎤2k π-π3,2k π+2π3(k ∈Z ),单调递增区间为⎣⎢⎡⎦⎥⎤2k π+2π3,2k π+5π3(k ∈Z ), 所以⎝ ⎛⎭⎪⎫π2,2π3是f (x )的单调递减区间,⎣⎢⎡⎭⎪⎫2π3,π是f (x )的单调递增区间,D 项错误.故选D.(3)函数f (x )=cos(ωx +φ)(ω>0)的部分图象如图所示,则f (x )的单调递减区间为. 答案 ⎝⎛⎭⎪⎫2k -14,2k +34,k ∈Z 解析 由图象知,周期T =2×⎝ ⎛⎭⎪⎫54-14=2,∴2πω=2,∴ω=π.由π×14+φ=π2+2k π,k ∈Z ,不妨取φ=π4,∴f (x )=cos ⎝⎛⎭⎪⎫πx +π4.由2k π<πx +π4<2k π+π,k ∈Z ,得2k -14<x <2k +34,k ∈Z ,∴f (x )的单调递减区间为⎝⎛⎭⎪⎫2k -14,2k +34,k ∈Z .(4)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎢⎡⎦⎥⎤π6,π2上具有单调性,且f ⎝ ⎛⎭⎪⎫π2=f ⎝ ⎛⎭⎪⎫2π3=-f ⎝ ⎛⎭⎪⎫π6,则f (x )的最小正周期为. 答案 π解析 记f (x )的最小正周期为T .由题意知T 2≥π2-π6=π3,又f ⎝ ⎛⎭⎪⎫π2=f ⎝ ⎛⎭⎪⎫2π3=-f ⎝ ⎛⎭⎪⎫π6,且2π3-π2=π6, 可作出示意图如图所示(一种情况): ∴x 1=⎝⎛⎭⎪⎫π2+π6×12=π3,x 2=⎝ ⎛⎭⎪⎫π2+2π3×12=7π12, ∴T 4=x 2-x 1=7π12-π3=π4,∴T =π. 1.(2018·广州质检)下列函数中,是周期函数的为( )A .y =sin|x |B .y =cos|x |C .y =tan|x |D .y =(x -1)0答案 B解析 ∵cos|x |=cos x , ∴y =cos|x |是周期函数.2.函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4在区间⎣⎢⎡⎦⎥⎤0,π2上的最小值为( ) A .-1 B .-22 C.22D .0答案 B解析 由已知x ∈⎣⎢⎡⎦⎥⎤0,π2,得2x -π4∈⎣⎢⎡⎦⎥⎤-π4,3π4,所以sin ⎝ ⎛⎭⎪⎫2x -π4∈⎣⎢⎡⎦⎥⎤-22,1, 故函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4在区间⎣⎢⎡⎦⎥⎤0,π2上的最小值为-22.故选B.3.函数y =sin x 2的图象是( ) 答案 D解析 函数y =sin x 2为偶函数,排除A ,C ; 又当x =π2时函数取得最大值,排除B ,故选D. 4.函数y =cos 2x -2sin x 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2答案 D解析 y =cos 2x -2sin x =1-sin 2x -2sin x =-sin 2x -2sin x +1, 令t =sin x ,则t ∈[-1,1],y =-t 2-2t +1=-(t +1)2+2, 所以y max =2,y min =-2.5.已知函数f (x )=2sin(2x +φ)⎝ ⎛⎭⎪⎫|φ|<π2的图象过点(0,3),则f (x )图象的一个对称中心是( )A.⎝ ⎛⎭⎪⎫-π3,0B.⎝ ⎛⎭⎪⎫-π6,0C.⎝⎛⎭⎪⎫π6,0D.⎝ ⎛⎭⎪⎫π12,0 答案 B解析 函数f (x )=2sin(2x +φ)⎝ ⎛⎭⎪⎫|φ|<π2的图象过点(0,3),则f (0)=2sin φ=3,∴sin φ=32,又|φ|<π2,∴φ=π3, 则f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3,令2x +π3=k π(k ∈Z ),则x =k π2-π6(k ∈Z ),当k =0时,x =-π6, ∴⎝ ⎛⎭⎪⎫-π6,0是函数f (x )的图象的一个对称中心. 6.已知函数f (x )=sin(2x +φ),其中φ为实数,若f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π4对任意x ∈R 恒成立,且f ⎝ ⎛⎭⎪⎫π6>0,则f (x )的单调递减区间是( ) A.⎣⎢⎡⎦⎥⎤k π,k π+π4(k ∈Z ) B.⎣⎢⎡⎦⎥⎤k π-π4,k π+π4(k ∈Z ) C.⎣⎢⎡⎦⎥⎤k π+π4,k π+3π4(k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ) 答案 C解析 由题意可得函数f (x )=sin(2x +φ)的图象关于直线x =π4对称,故有2×π4+φ=k π+π2,k ∈Z ,即φ=k π,k ∈Z .又f ⎝ ⎛⎭⎪⎫π6=sin ⎝⎛⎭⎪⎫π3+φ>0,所以φ=2n π,n ∈Z ,所以f (x )=sin(2x +2n π)=sin2x .令2k π+π2≤2x ≤2k π+3π2,k ∈Z ,求得k π+π4≤x ≤k π+3π4,k ∈Z ,故函数f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π+π4,k π+3π4,k ∈Z . 7.函数y =1tan ⎝⎛⎭⎪⎫x -π4的定义域为.答案 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠k π2+π4,k ∈Z解析 要使函数有意义必须有tan ⎝⎛⎭⎪⎫x -π4≠0,则⎩⎪⎨⎪⎧x -π4≠π2+k π,k ∈Z ,x -π4≠k π,k ∈Z .所以x -π4≠k π2,k ∈Z ,所以x ≠k π2+π4,k ∈Z ,所以原函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠k π2+π4,k ∈Z. 8.(2018·珠海模拟)设函数f (x )=3sin ⎝ ⎛⎭⎪⎫π2x +π4,若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为. 答案 2解析 |x 1-x 2|的最小值为函数f (x )的半个周期, 又T =4,∴|x 1-x 2|的最小值为2.9.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,其中ω为常数,且ω∈(1,2),则函数f (x )的最小正周期为. 答案6π5解析 由函数f (x )=2sin ⎝ ⎛⎭⎪⎫ωx -π6+1(x ∈R )的图象的一条对称轴为x =π,可得ωπ-π6=k π+π2,k ∈Z ,∴ω=k +23,又ω∈(1,2),∴ω=53,∴得函数f (x )的最小正周期为2π53=6π5.10.已知函数f (x )=⎪⎪⎪⎪⎪⎪tan ⎝ ⎛⎭⎪⎫12x -π6,则下列说法正确的是.(填序号)①f (x )的周期是π2;②f (x )的值域是{y |y ∈R ,且y ≠0};③直线x =5π3是函数f (x )图象的一条对称轴;④f (x )的单调递减区间是⎝ ⎛⎦⎥⎤2k π-2π3,2k π+π3,k ∈Z . 答案 ④解析 函数f (x )的周期为2π,①错;f (x )的值域为[0,+∞),②错;当x =5π3时,12x -π6=2π3≠k π2,k ∈Z ,∴x =5π3不是f (x )的对称轴,③错;令k π-π2<12x -π6≤k π,k ∈Z ,可得2k π-2π3<x ≤2k π+π3,k ∈Z ,∴f (x )的单调递减区间是⎝⎛⎦⎥⎤2k π-2π3,2k π+π3,k ∈Z ,④正确.11.(2017·北京)已知函数f (x )=3cos ⎝ ⎛⎭⎪⎫2x -π3-2sin x cos x .(1)求f (x )的最小正周期;(2)求证:当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )≥-12. (1)解 f (x )=32cos2x +32sin2x -sin2x =12sin2x +32cos2x =sin ⎝⎛⎭⎪⎫2x +π3.所以f (x )的最小正周期T =2π2=π. (2)证明 因为-π4≤x ≤π4,所以-π6≤2x +π3≤5π6.所以sin ⎝ ⎛⎭⎪⎫2x +π3≥sin ⎝ ⎛⎭⎪⎫-π6=-12.所以当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )≥-12. 12.(2018·天津河西区模拟)已知函数f (x )=2cos 2x -cos ⎝ ⎛⎭⎪⎫2x +π3-1.(1)求函数f (x )的最小正周期和对称轴方程;(2)讨论函数f (x )在⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解 (1)f (x )=2cos 2x -cos ⎝ ⎛⎭⎪⎫2x +π3-1=cos2x -12cos2x +32sin2x =sin ⎝ ⎛⎭⎪⎫2x +π6,因为ω=2,所以最小正周期T =2πω=π,令2x +π6=π2+k π,k ∈Z ,所以对称轴方程为x =π6+k π2,k ∈Z .(2)令-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,得-π3+k π≤x ≤π6+k π,k ∈Z ,设A =⎣⎢⎡⎦⎥⎤-π4,π4, B =⎩⎪⎨⎪⎧⎦⎥⎤x ⎪⎪⎪-π3+k π≤x ≤π6+k π,k ∈Z, 易知A ∩B =⎣⎢⎡⎦⎥⎤-π4,π6, 所以,当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π6上单调递增;在区间⎣⎢⎡⎦⎥⎤π6,π4上单调递减.13.(2018·湖南衡阳八中月考)定义运算:a *b =⎩⎪⎨⎪⎧a ,a ≤b ,b ,a >b .例如1*2,则函数f (x )=sin x *cos x 的值域为( )A.⎣⎢⎡⎦⎥⎤-22,22 B .[-1,1] C.⎣⎢⎡⎦⎥⎤22,1 D.⎣⎢⎡⎦⎥⎤-1,22 答案 D解析 根据三角函数的周期性,我们只看两函数在一个最小正周期内的情况即可,设x ∈[0,2π],当π4≤x ≤5π4时,sin x ≥cos x ,此时f (x )=cos x ,f (x )∈⎣⎢⎡⎦⎥⎤-1,22,当0≤x <π4或5π4<x ≤2π时,cos x >sin x ,此时f (x )=sin x ,f (x )∈⎣⎢⎡⎭⎪⎫0,22∪[-1,0].综上知f (x )的值域为⎣⎢⎡⎦⎥⎤-1,22. 14.已知函数f (x )=2cos(ωx +φ)+1⎝ ⎛⎭⎪⎫ω>0,|φ|<π2,其图象与直线y =3相邻两个交点的距离为2π3,若f (x )>1对任意x ∈⎝ ⎛⎭⎪⎫-π12,π6恒成立,则φ的取值范围是( )A.⎣⎢⎡⎦⎥⎤-π6,π6B.⎣⎢⎡⎦⎥⎤-π4,0C.⎝ ⎛⎦⎥⎤-π3,-π12D.⎣⎢⎡⎦⎥⎤0,π4答案 B解析 由题意可得函数f (x )=2cos(ωx +φ)+1的最大值为3.∵f (x )的图象与直线y =3相邻两个交点的距离为2π3,∴f (x )的周期T =2π3,∴2πω=2π3,解得ω=3,∴f (x )=2cos(3x +φ)+1.∵f (x )>1对任意x ∈⎝ ⎛⎭⎪⎫-π12,π6恒成立,∴2cos(3x +φ)+1>1,即cos(3x+φ)>0对任意x ∈⎝ ⎛⎭⎪⎫-π12,π6恒成立,∴-π4+φ≥2k π-π2且π2+φ≤2k π+π2,k ∈Z ,解得φ≥2k π-π4且φ≤2k π,k ∈Z ,即2k π-π4≤φ≤2k π,k ∈Z .结合|φ|<π2可得,当k =0时,φ的取值范围为⎣⎢⎡⎦⎥⎤-π4,0.15.已知函数f (x )=cos(2x +θ)⎝ ⎛⎭⎪⎫0≤θ≤π2在⎣⎢⎡⎦⎥⎤-3π8,-π6上单调递增,若f ⎝ ⎛⎭⎪⎫π4≤m 恒成立,则实数m 的取值范围为. 答案 [0,+∞)解析 f (x )=cos(2x +θ)⎝⎛⎭⎪⎫0≤θ≤π2,当x ∈⎣⎢⎡⎦⎥⎤-3π8,-π6时,-3π4+θ≤2x +θ≤-π3+θ,由函数f (x )在⎣⎢⎡⎦⎥⎤-3π8,-π6上是增函数得⎩⎪⎨⎪⎧-π+2k π≤-3π4+θ,-π3+θ≤2k π,k ∈Z ,则2k π-π4≤θ≤2k π+π3(k ∈Z ).又0≤θ≤π2,∴0≤θ≤π3,∵f ⎝ ⎛⎭⎪⎫π4=cos ⎝ ⎛⎭⎪⎫π2+θ,又π2≤θ+π2≤5π6, ∴f ⎝ ⎛⎭⎪⎫π4max =0,∴m ≥0.16.设函数f (x )=2sin ⎝ ⎛⎭⎪⎫2ωx -π6+m 的图象关于直线x =π对称,其中0<ω<12. (1)求函数f (x )的最小正周期.(2)若函数y =f (x )的图象过点(π,0),求函数f (x )在⎣⎢⎡⎦⎥⎤0,3π2上的值域.解 (1)由直线x =π是y =f (x )图象的一条对称轴, 可得sin ⎝ ⎛⎭⎪⎫2ωπ-π6=±1,∴2ωπ-π6=k π+π2(k ∈Z ),即ω=k 2+13(k ∈Z ).又0<ω<12,∴ω=13,∴函数f (x )的最小正周期为3π.(2)由(1)知f (x )=2sin ⎝ ⎛⎭⎪⎫23x -π6+m ,∵f (π)=0, ∴2sin ⎝⎛⎭⎪⎫2π3-π6+m =0,∴m =-2,∴f (x )=2sin ⎝ ⎛⎭⎪⎫23x -π6-2,当0≤x ≤3π2时,-π6≤23x -π6≤5π6,-12≤sin ⎝ ⎛⎭⎪⎫23x -π6≤1.∴-3≤f (x )≤0,故函数f (x )在⎣⎢⎡⎦⎥⎤0,3π2上的值域为[]-3,0.。
热管换热器在节能减排中的应用
热管换热器在节能减排中的应用1.热管换热器可以提高能源利用效率,有利于节能减排。
Heat pipe heat exchanger can improve energy utilization efficiency, which is beneficial for energy saving andemission reduction.2.通过热管换热器,可以实现热能的有效传递,减少能源的浪费。
Through heat pipe heat exchanger, the effective transferof heat energy can be achieved, reducing energy waste.3.热管换热器可以大大降低工业生产过程中的能源消耗。
Heat pipe heat exchanger can significantly reduce energy consumption in industrial production processes.4.在建筑空调系统中使用热管换热器可以提高空调系统的效率,减少能源消耗。
The use of heat pipe heat exchanger in building air conditioning systems can improve the efficiency of the air conditioning system and reduce energy consumption.5.热管换热器可以用于废气余热回收,减少工厂的二氧化碳排放。
Heat pipe heat exchanger can be used for waste gas waste heat recovery, reducing CO2 emissions from factories.6.利用热管换热器进行余热利用可以减少工业生产过程中的能源消耗。
Utilizing heat pipe heat exchanger for waste heatutilization can reduce energy consumption in industrial production processes.7.热管换热器可以降低工业锅炉燃料的使用量,节约能源成本。
浅谈热管及热管气-气换热器的应用
浅谈热管及热管气-气换热器的应用热管是一种通过液体或气体在内部循环流动来传递热量的装置。
它由内管、外管、工作介质和蒸发器、冷凝器等组成。
工作介质在蒸发器内受热后蒸发成为气体,通过热管内部的循环流动进入冷凝器,之后被冷凝成液体,再通过毛细结构返回蒸发器,形成闭合循环。
热管的传热效率高、传热能力强,被广泛应用在工业领域。
热管的应用非常广泛,特别是在电子、航天、军事等领域。
热管可以用于电子产品的散热。
现代电子设备的集成度越来越高,功率密度也越来越大,产生的热量也越来越多。
为了保证电子设备的正常工作,热管可以将散热效果大大提高,将热量快速传递到散热器中,保持设备的温度在可控范围内。
热管还可以应用在航天领域。
航天器在进入大气层时,会受到高温的热辐射,而且在返回大气层时,会产生大量的热量。
为了保护航天器,热管可以将其余热迅速传递到航天器的表面,通过辐射散热的方式降低温度,起到保护航天器的作用。
热管还可以用于军事领域。
军事装备在战斗过程中,会产生大量的热量,如果不能及时有效地散热,会影响装备的正常工作。
热管可以快速地将热量传输到散热器中,并利用大面积散热器将热量排出,保证装备的正常运行。
除了以上应用,热管气-气换热器也是热管的重要应用之一。
热管气-气换热器是利用热管的高传热效率和换热容量来实现气体之间的换热的装置。
该技术在工业生产中具有重要的应用价值。
热管气-气换热器可以应用于各种气体的换热过程中,例如氢气、氧气、空气等。
它广泛应用于化工、电力、石油、冶金等工业领域。
热管气-气换热器的工作原理是:一个热管作为蒸发器,在蒸发过程中吸热,另一个热管作为冷凝器,在冷凝过程中释放热量。
当气体通过蒸发器和冷凝器时,与热管内的工作介质进行热交换,实现热量的传递和平衡。
热管气-气换热器具有许多优点。
它具有高热交换效率和传热能力,能够快速地将热量传递给另一个气体。
热管具有自动调节热量传递的能力,可以根据需要自动调整热量的传递速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浅谈分离式热管换热器在电解铜行业的应用
引言
电解铜行业中原本利用板式换热器进行散热,但由于板式换热器密封不严,换热过程中溶液里的强酸蒸发溶于到冷凝水中,使得该冷凝水无法用于生产、生活再利用,只能排放到大气中,从而导致能源浪费。
而分离式热管换热器全程密封,换热效率高,可以实现冷热流体之间零泄漏,冷凝水无污染且温度适中,可以用于回收再利用。
一、分离式热管的工作原理
分离式热管的蒸发段和冷凝段是分开的,通过蒸汽上升管和液体下降管连通起来,形成一个自然循环回路[1]。
工作时,在热管内加入一定量的工质,这些工质汇集在蒸发段,蒸发段受热后,工质蒸发,其内部蒸汽压力升高,产生的蒸汽通过蒸汽上升管到达冷凝段释放出潜热而凝结成液体,在重力作用下,经液体下降管回到蒸发段,如此循环往复运行。
分离式热管的冷凝段必须高于蒸发段,液体下降管与蒸汽上升管之间会形成一定的密度差,这个密度差所能提供的压头与冷凝段和蒸发段的高度差密切相关,用以平衡蒸汽流动和液体流动的压力损失,维系着系统的正常運行,而不再需要外加动力。
二、电解铜行业中常用换热器的应用缺陷
电解铜行业中常用的换热器为板式换热器。
板式换热器是由一系列具有波纹形的传热板片与橡胶垫片按一定的间隔组成的可拆卸的换热装备。
板式换热器在电解铜行业中存在多种问题:
1)单位长度的压力损失大。
由于传热面之间的间隙较小,传热面上有凹凸,因此比传统的光滑管的压力损失大。
2)易堵塞。
由于板片间通道很窄,一般只有2~5mm,当换热介质含有较大颗粒或纤维物质时,容易堵塞板间通道。
3)溶液有可能泄露。
板式换热器主要由框架和板片两大部分组成,板片的周边及角孔处用橡胶垫片加以密封,由于硫酸铜溶液中含有强酸,容易腐蚀橡胶垫,造成溶液泄露。
三、分离式热管换热器在电解铜行业中的应用
在电解铜行业中,由于生产电解铜箔对其电解溶液(硫酸铜溶液)的洁净度和温度要求非常严格,所以我们要利用蒸汽通过换热装置对电解液进行加温,且必须保证没有任何介质会溶于硫酸铜溶液中对其造成污染,否则会对铜箔外观及内在质量产生很大的影响。
分离式热管换热器能实现冷、热两流体远程换热,且冷、热流体可以完全隔离,相较板式换热器,除了满足其所有优点之外,分离式热管换热器还具有以下优势[2]:
(1)电解溶液中含有强酸,会严重腐蚀金属管道和橡胶垫,而热管材质多式多样,可供选择余地大,我们可以根据冷、热流体的性能及工艺要求选择不同的结构参数和材质来增强抗腐蚀性和抗氧化性,例如钛热管即可满足要求。
(2)热管传热效率高,结构简单,投资小。
热管是一种传热极高的换热元件,其内部是靠工质相变和连续工质循环实现热量传递,它的当量热导率可达金属的103~104倍。
(3)能够有效的避免冷、热流体的串流。
每根热管都是相对独立的密闭单元,冷、热流体都在管外流动。
并且可根据现场条件灵活的安置壳体,将冷、热流体隔开。
(4)热管的换热元件是由多根热管组成。
各根之间相互独立,当一根甚至几根热管失效时,两种换热流体也不可能互混,不影响整个系统的安全运行,这就使高效率的现代化连续大生产获得了可靠的保证;板式换热器是间壁换热,冷热流体分别在器壁的两侧流过,如管壁或器壁有泄漏,则将造成停产损失,由热管组成的换热设备,则是二次间壁换热,即热流要通过热管的蒸发段管壁和冷凝段管壁才能传到冷流体,热管一般不可能在蒸发段和冷凝段同时破坏,大大增强了设备运行的可靠性。
四、分离式热管换热器在电解铜行业中的选型要求
(1)工作液体的选择:
热管是依靠工作液体的相变来传递热量的,因此工作液体的各种物理性质对于热管的工作特性也就具有重要的影响,一般应考虑一下一些原则:1)工作液体应适应热管的工作温度区,并有适当的饱和蒸汽压。
良好的热管工作时,工作液体必然处于气液两相状态,因此所选择的工作液体的熔点应低于热管的工作温度,热管才有可能正常工作;
2)工作液体与壳体、吸液芯应相容,且具有良好的热稳定性。
工作液体与壳体、吸收芯材料的相容性是最重要的考虑因素,工作液体的不相容及热稳定性都会到时产生不凝性气体使热管性能降低,甚至不能工作。
3)工作液体应具有良好的热物理性质
(2)管壳材料的选择
壳体材料首先应满足于工作液体的相容性要求,除此之外,壳体材料还应满足在工作温度下的强度和刚度要求及对环境介质的抗蚀性要求,由于硫酸铜溶液余热利用下,热源温度低,因此在此温度下工作的管壳材料的强度要求均可满足,但一般的管材如铜管,钢管对硫酸铜的抗腐蚀性较差,因此选用钛热管。
金属钛的密度为4.51g/立方厘米,高于铝而低于钢、铜、镍,但比强度位于金属之首。
金属钛的导热系数虽然比碳钢和铜低,但由于钛优异的耐腐蚀性能与密度小比强度高的优点,所以壁厚可以大大减薄,而且表面与硫酸铜溶液的换热方式为对流换热,减少了热组,钛表面不结垢也可减少热阻,使钛的换热性能显著提高。
因此选用钛热管作为热管换热器的管材。
(3)工作要求
热管正常工作是依靠工质的循环,因此毛细压头即工作循环的压力,须克服气态工质从蒸发器流向冷凝器的压力降,液态工质从冷凝器回流到蒸发器的压力降及重力对液体流动的引起的压力降,即△Pc≥△Pl+△Pv+△Pg。
其中△Pc表示毛细作用压头,△Pl表示气态工质沿管路的压力损失,△Pv表示液态工质沿管路的压力损失,△Pg表示重力作用造成的压力损失。
同时我也应该考虑到分离式热管换热器的体积,相较板式换热器来说,它的体积要大得多,这需要铜箔生产厂家预留出足够的空地用来安放相关设备。
五、结论
分离式热管换热器可使冷、热源分开,远距离传输能量且不需外加动力,热管传热效率高,结构简单,投资小,既可以降低能耗,同时也可减少设备腐蚀和环境污染,使用热管换热器的蒸汽置换出的冷凝水不含强酸等杂质,可以用于生产、生活再利用,不仅减少了设备腐蚀和环境污染,同时实现了节能效益和经济效益。
所以分离式热管技术在电解铜行业中替代板式换热器是可行的,并且具有很大的节能潜力。
参考文献:
[1]庄骏,张红.热管技术及其工程应用.北京:化学工业出版社,2000.
[2]杨昭,吴志光.熟管热回收装置在空调系统中的应用研究.能源研究与利用,热管技术与应用,2004.。
