小学数学四年级《几何图形剪拼》练习题
小学数学《图形的剪拼(一)》练习题(含答案)

小学数学《图形的剪拼(一)》练习题(含答案)例1 如右图所示是由三个正方形组成的图形,请把它分成大小、形状都相同的四个图形?分析如果我们不考虑分成的四个图形的形状,只考虑它的面积,就要求把原来三个正方形分成四个面积相等的部分.每部分面积应是正方形面积的图形,于是我们就有了如图(2)的分法.仿照例1的分法我们把如右图这样由五个正方形组成的图形,分成四块正方形,则可把每个正方形分成四个面积相等的小正方形,每块图形应有五个这样的小正方形,如右图所示.例2 把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成一半,得到如下左图所示的图形.分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右图所示的符合条件的图形.例3长方形的长和宽各是9厘米和4厘米,要把它剪成大小、形状都相同的两块,并使它们拼成一个正方形.分析已知长方形面积9×4=36(平方厘米),所以正方形的边长应为6厘米,因此可以把长方形上半部剪下6厘米,下半部剪下3厘米,分成相等的两块,合起来正好拼成一个边长为6厘米的正方形,如下右图.例4把一个正方形分成8块,再把它们拼成一个正方形和一个长方形,使这个正方形和长方形的面积相等.分析连接正方形的对角线,把正方形分成了4个相等的等腰直角三角形,再连接各腰中点,又把它们分成4个小等腰直角三角形和4个等腰梯形.(如下页图(1)所示)出于分成正方形、长方形面积相等的要求考虑:分别取出两个小等腰直角三角形和两个梯形,就能一一拼出所要求的正方形和长方形了(如图(2)、(3)所示).除这种方法外,还有多种拼接方法.例5 在下左图中画5条线,把小圆圈分开,并使每块大小、形状都相等.分析因为图中有8个小圆圈,画5条线把图形应分成8块,根据小圆圈的分布特点,分法如下图(右)所示.例6 把下图中两个图形中的某一个分成三块,最后都拼在一起,使它们成为一个正方形.分析不管分其中的哪一块,最后拼得正方形的面积与图中两块面积和相等,甲面积=10×5=50平方厘米;乙面积=10×7-(7-2)×4=70-20=50平方厘米.所以甲面积+乙面积=50+50=100平方厘米,也就是最后拼得正方形的边长为10厘米.甲、乙两图形各有一边是10厘米,可视为正方形的一条边,然后把乙剪成三块(如下图所示)拼成的正方形,即可.当然,除这种拼凑的方法之外,还有其他多种方法,同学们可自行构思、设计.例7 如下左图将其切成3块,使之拼成一个正方形.分析原图形面积是32,所以拼成正方形的面积也应是32,即正方形边长,如下右图所示,切成甲、乙、丙3块,甲拼到甲′位置,乙拼到乙′位置,这样甲′、乙′、丙便构成一个正方形.例8 如下左图所示,这是一张十字形纸片,它是由五个全等正方形组成,试沿一直线将它剪成两片,然后再沿另一直线将其中一片剪成两片,使得最后得到的三片拼成两个并列的正方形.分析实际拼成两个并列的正方形就是一个长方形,其长是宽的2倍,设所求长方形的长可视为一直角三角形直角边分别是3和1的斜边.它恰是两个对角顶点的连线.剪拼方法如下图右所示,甲拼在甲′位置,乙拼在乙′位置,就可得符合题意的图形.本题小结:假若沿第二条线把另一片也剪成两片,那么共剪成的4片是4个全等多边形,这时两条直线都经过十字形的中心,并且互相垂直.剪开的这4个图形其中一个绕中心旋转90°也和另一个重合.由此我们便得到一个示.例9 把如下图(1)所示的图形切成两块,然后拼成一个正方形.分析原图形面积为16(平方单位),所以拼成的正方形面积也应为16(平方单位),边长为4(长度单位).切开后,须将右片向左平移2个单位,然后再向上平移1个单位.(如下图(2)所示)恰拼成一个正方形.例10 如右图两个正方形的边长分别是a和b(a>b),将边长为a的正方形切成四块大小、形状都相同的图形,与另一个正方形拼在一起组成一个正方形.分析拼成大正方形的面积应是a2+a2设边长c,则有等式c2=a2+b2,又因为将边长为a的正方形切成四个全等形,那么分割线一定经过正方形中心,假设切割线MN为大正方形边长,如下图(1),一定有MN2=a2+b2,而MH=a,将MN绕中心O旋转90°到EF位置,即可把正方形切成符合要求的4块.如下图(2)及下图(3).这种分法同时确保图(3)的中间部分就是边长为b的小正方形.这是因为:①中心四边形的角即边长为a的正方形的四个角,∠A,∠B,∠C,∠D,又因为各边长度相等.因此中心四边形是正方形.=a-(a-b)=b.因此,中间部分是边长为b的正方形.习题九1.如右图,将一个底角为60°,上底和腰相等的等腰梯形切割成4块大小、形状都相同的图形.2.如右图,方框外面边长为5,里面边长为3,把方框锯成4块,拼成一个正方形,问怎样拼法?3.如右图,分别将两图形,分成8个大小、形状相同,面积相等的图形.4.如右图,把它锯成3块再拼成一个正方形.5.把一个正方形分成20个大小形状完全一样的三角形.6.长方形长24厘米,宽15厘米.把它剪成两块,使它们拼成一个长20厘米,宽18厘米的长方形.7.将下列各图均切成三块,每三块拼成一个正方形.习题九解答1.2.面积为16(平方单位).3.4.5.6.长方形面积=24×15=360平方厘米,拼成的长方形面积=20×18=360平方厘米,面积相等,只是长、宽不等,但它们都可以分成30个4×3的小长方形,拼成的长方形的一半应有15个4×3的小长方形,即5+4+3+2+l=15.所以才有如下的剪切方法:7.。
小学数学 图形剪拼练习题

1)小朋友,你能把一个等边三角形分成大小、形状相等的3个、6个和9个三角形吗?试试看吧。
2)将一个底角为60度,上底和腰相等的等腰梯形切割成4块大小、形状都相同的图形。
3)将图形分成8个大小、形状相同的图形。
4)如下图,把一块地分给4个小组种植,性状大小要相同(每一块有相同的点数),怎么分?
5)找一找,下面的两个图形分别是由那几块组成的?
6)分别用3个、4个和5个下图中的等腰梯形拼成一个更大的等腰梯形。
7)下面是一副拼板,小朋友,你们能用它们拼成一个正方
8)小朋友,你能用七巧板拼出风车和小船吗?除此之外,还能另外再拼出两种你喜欢的小动物吗?
1)将方框(方框外边长为5,内边长为3)锯成4块,再拼成一个正方形。
2)将图分成3块,再拼成一个正方形。
3)将下列各图均切成3块,再各自拼成一个正方形。
4)将图划分成形状、大小完全相同的4块,而且每块中都含有一个字母。
小学奥数思维训练-几何图形剪拼通用版

8.(1)
(2)
【解析】
试题分析:(1)将大正方形方的边长平均分成3等份,则可将大正方形分割为9个相等的小正方形,其中4个相邻的组成1个,其余5个小的各成1个.
(2)将大正方形方的边长平均分成4等份,分成3个2×2,4个1×1即可.
(1)如果分别剪开这两个正方形,再拼接成一个大正方形,应该怎么办?
(2)如果只允许剪开一个正方形,再拼接成一个大正方形,应该怎么办?
10.如图是由若干个小正方形组成的图形,你能将其剪成两块,然后拼成一个正方形吗?
11.请在图中标出分割线,把下图沿格线分成形状、大小都相同的四个部分,(如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的)
试题分析:因为共有24个三角形,沿格线分割成形状、大小都相同的四个部分,每部分包括6个三角形,由此进行划分即可.
解:
点评:此题考查了图形的拆拼,明确每部分包括6个三角形,是解答此题的关键.
13.
【解析】
试题分析:将图分割成形状、大小完全相同的四块,即每个图形的面积占整个图形面积的 ,结合图形,进行分割即可.
3.如图,在一块正方形纸片中有一个正方形的空洞.现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两部分,应该怎么办?
4.请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形.
5.请把图沿格线分成形状、大小都相同的三部分,使得每部分都恰好含有一个“○”.
6.如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来.
11.作图如下
【解析】
试题分析:因为共有16个方格,分成形状、大小都相同的四个部分,那么每个部分就有4个方格,根据原图形状,可分成4个“L”形的图形,解决问题.
四年级几何图形剪拼学生版

知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形(不要求大小相等)将一个正方形分割成若干个正方形(不要求大小相等)n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何(本讲)一、 三角形面积公式:三角形面积=底⨯高2÷,即S 三角形2a h =⨯÷。
二、 平行四边形面积公式:平行四边形面积=底⨯高,即S 平行四边形a h =⨯。
三、 梯形面积公式:梯形面积=(上底+下底)⨯高2÷,即S 梯形()2a b h =+⨯÷。
四、 菱形面积公式:菱形面积=两条对角线乘积的一半,即S 菱形2m n =⨯÷ 五、n 边形的内角和公式:n 边形的内角和(2)180n =-⨯o 。
图形面积【例 1】如图所示,已知三角形的一条边为a,这条边上的高为h。
请用图形剪拼的方法,求出这个三角形的面积S三角形。
hahaha【例 2】如图所示,已知平行四边形的一条边为a,这条边上的高位h。
请用图形剪拼的方法,求出这个平行四边形的面积S平行四边形。
ha【例 3】如图所示,已知梯形的两条平行的边分别为a、b,梯形的高为h。
请用图形剪拼的方法,求出这个梯形的面积S梯形。
hab【例 4】如图所示,已知菱形的两条对角线分别为m、n。
请用图形剪拼的方法,求出这个平行四边形的面积S菱形。
(提示:菱形的两条对角线相互垂直)mn图形分割【例 5】 (2005年12月第六届“中环杯”小学生思维能力训练活动四年级复赛第二(5)题)将一个长方形分成形状完全一样的四块,至少画出8种分法,请用图表示。
(形状一样,排列方向不一样,只能看作一种分法)【例 6】 如图所示为一个34⨯的长方形方格纸,请用5种不同的方法将它分割成完全相同的两部分(保持每个小方格的完整)。
【例 7】 如图所示,请将44⨯的正方形分成形状相同、大小相等的四个图形,并且使其中每个图形都含有“上海世博”这四个字。
第11讲 几何图形剪拼
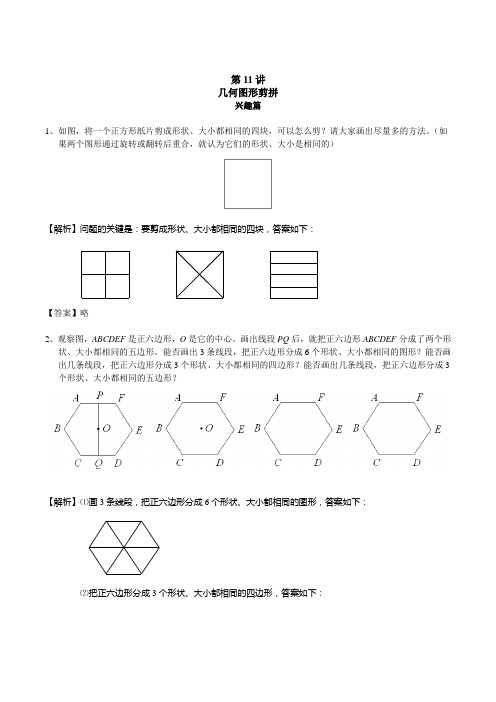
第11讲几何图形剪拼兴趣篇1、如图,将一个正方形纸片剪成形状、大小都相同的四块,可以怎么剪?请大家画出尽量多的方法。
(如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的)【解析】问题的关键是:要剪成形状、大小都相同的四块,答案如下:【答案】略2、观察图,ABCDEF是正六边形,O是它的中心。
画出线段PQ后,就把正六边形ABCDEF分成了两个形状、大小都相同的五边形。
能否画出3条线段,把正六边形分成6个形状、大小都相同的图形?能否画出几条线段,把正六边形分成3个形状、大小都相同的四边形?能否画出几条线段,把正六边形分成3 个形状、大小都相同的五边形?【解析】⑴画3条线段,把正六边形分成6个形状、大小都相同的图形,答案如下:⑵把正六边形分成3个形状、大小都相同的四边形,答案如下:⑶把正六边形分成3个形状、大小都相同的五边形,答案如下:【答案】3、如图,在一块正方形纸片中有一个正方形的空洞。
现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两部分,应该怎么分?【解析】过中心点的直线分面积相等,只要作出正方形空洞的中心,连结此中心与大正方形即可。
如下图:【答案】4、请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形。
【解析】⑴图中共有12个方格,要分成四个形状、大小都相同的图形,则每个图形有:12÷4=3(个)方格。
分法如图:⑵图中共有12个小三解形,分成的4个形状、大小都相同的图形,每个图形有12÷4=3(个)小三解形。
分法如下图:【答案】5、请把图沿格线分成形状、大小都相同的三部分,使得每部分都恰好含有一个“○”。
【解析】图中共有12个小正方形,分成形状、大小都相同的三部分,每部分:12÷3=4(个)小正方形。
分法如下:【答案】6、如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来。
【解析】采用分割法知共需12个三解形,分法如下图:【答案】12个,7、如图,左图是由五个相同大小的小正方形拼成的,右图是由一个正方形和一个等腰直角三角形拼成的。
四年级几何图形剪拼教师版

知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形(不要求大小相等)将一个正方形分割成若干个正方形(不要求大小相等)n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何(本讲)一、 三角形面积公式:三角形面积=底⨯高2÷,即S 三角形2a h =⨯÷。
二、 平行四边形面积公式:平行四边形面积=底⨯高,即S 平行四边形a h =⨯。
三、 梯形面积公式:梯形面积=(上底+下底)⨯高2÷,即S 梯形()2a b h =+⨯÷。
四、 菱形面积公式:菱形面积=两条对角线乘积的一半,即S 菱形2m n =⨯÷ 五、n 边形的内角和公式:n 边形的内角和(2)180n =-⨯o 。
图形面积【例 1】 如图所示,已知三角形的一条边为a ,这条边上的高为h 。
请用图形剪拼的方法,求出这个三角形的面积S 三角形。
hahaha【分析】当三角形的高在三角形的边上;用两个一摸一样的直角三角形拼在一起,斜边重合,拼成一个长方形。
长方形的长和宽分别是a 和h ,面积S 长方形=a h ⨯;所以直角三角形的面积是长方形的面积的一半,即S 三角形2a h =⨯÷。
当三角形的高在三角形的内部,用两个一摸一样的三角形拼在一起,其中一个沿高剪开,拼成一个长方形。
长方形的长和宽分别是a 和h ,面积S 长方形=a h ⨯;所以三角形的面积是长方形的面积的一半,即S 三角形2a h =⨯÷。
当三角形的高在三角形的外部,三角形的面积等于大直角三角形的面积减去小直角三角形的面积, 即S 三角形(')2'22a a h a h a h =+⨯÷-⨯÷=⨯÷。
所以三角形的面积三角形2a h =⨯÷。
ahaha'ha【例 2】 如图所示,已知平行四边形的一条边为a ,这条边上的高位h 。
第4讲 几何图形剪拼-完整版

第4讲几何圆形剪拼内容概述与图形的剪切、拼接有关的问题。
学会利用对称性和面积计算对剪拼问题进行分析;了解某些特殊的剪拼办法。
典型问题兴趣篇1.如图4-1,将一个正方形纸片剪成大小、形状都相同的4块,可以怎么剪?请大家出尽量多的图形.(如果两个图形通过旋转或翻转后重合,就认为它们的大小、形状是相同的)答案:解析:要把一个图形平均分成4部分,可以先把图形平均分成2份,再把平均分成的2份再一分为二即可,如答案第一、第二行的5种分法.再观察答案第三行前2个图发现,它们都是利用穿过正方形中心的两条直线把正方形分成了4块,考虑到正方形的对称性,知道正方形是一个旋转对称图形,利用这个特性旋转上面两条直线,发现过的两条互相垂直的直线.都可把正方形分成大小、形状都相同的4决.更一般地,从中心出发向边界连出一条曲线,再把它依次旋转90。
,同样可以把正方形分成形状、大小都相同的4块,如答案第三行的第3种分法,从上面的分析可以看出,满足要求的方法实际上有无穷多种.2.如图4-2,在一块正嘉纛凳墓中有一个正方形的空洞.现在要求用一条经过大正形中心点的线段,把纸片分成面积相等的两部分,应该怎么分?答案:解析:先考虑纸片无洞的情形.由正方形的对称性可知,经过大正方形中心点的任意一条直线,都可以把纸片分成面积相等的两部分,再考虑有空洞的隋形.如果空洞刚好处于合适的位置,如图1所示,这时就可以利用对称性来分.当空洞处于一般位置的时候,不再具备对称性.因为题目中并没有要求分成的两部分形状相同,所以只需要考虑面积的因素.如图2所示,如果分割线不通过空洞.正方形纸片被分成本身的面积是相等的两部分,但是其中一部分中有一个正方形空洞,所以这种剪法不行.如图3所示,如果分割线通过空洞,但空洞没有被平分,因为大正方形分成的两部分面积仍然相同,所以各自挖去空洞的一部分后剩下的面积还是不同,这种剪法仍然不行.从上面这2种剪法可以看出:要使分成的两部分面积相等,这条直线必须把空洞也分成面积相等的两部分,因为空洞的形状也是正方形,同样由对称性,过空洞中心的任意一条直线也可以把空洞分成面积相等的两部分,因此网时经过空洞正方形的中心与大正方形的中心的直线就可以把以上图形划分为面积相等的两部分,即过这2个中心点的直线.3.如图4-3,三角形和六角星的每条边长都相等.那么用多少个三角形可以拼成六角星?请在图中表示出来.答案:12个解析;因为六角星的每条边和正三角形的边相等,所以它突出来的6个角都可以用1个三角形填满,如图所示:剩下的中间部分是一个正六边形,也不难用三角形填满,如答案所示,共可数出12个三角形可拼成六角星.4.如图4-4,在正方形边上的40个点中,选出6个点,连出3条线段,将正方形分成6个部分,使得每个部分都恰好有1个三角形、2个小正方形。
小学数学 图形的剪拼 课件+作业(带答案)

先把每一个正方形分割成四个小 正方形。
20÷4=5(个) 5个小正方形组成的图形,可以选择
一种剪法如右图所示:
答案不唯一。
总结:对于不好直接剪切的图形,我们可以先画网格线,再进行剪切。
练习2:下图是由18个小正方形组成的图形,请将它沿格线分割成 6 个完全相同的图形。
春夏 夏 秋冬春 春冬秋夏 秋冬夏春冬秋
总结:要先求出分割出来的图形所占的方格数量,最后剪切时要注意限制条件。
练习6:请将下图沿格线分割成形状相同、大小相等的四个图形,并使每个图形中都有“学习思考”这
四个字。 16÷4=4(个)
4个小正方形可以拼成的形状有:
一种剪法如右图所示:
知识点三:复杂分割
8、下图是由五个相同的正方形组成的图形,要把它分成形状相同、大小相等的四个图形,应该怎样分?
先把每一个正方形分割成四个小 正方形。
20÷4=5(个) 5个小正方形组成的图形,可以选择
一种剪法如右图所示:
9、把下图沿哪条格线剪开后,可以拼成一个正方形? 如下图所示 拼成
10、请将下图沿格线分割成大小相等、形状相同的四块,并拼成一个正方形。
经过尝试,一种剪法 如右图所示:
知识点三:复杂分割
例题6:请将下面的图形沿格线分割成形状相同、大小相等的四块,并使每一块中都有“春夏秋冬”四
个字。
分析:
16÷4=4(个)
先计算出,分割成的四块, 每块中有几个小正方形。
4个小正方形可以拼成的形状有:
注意限制条件,每一块中都 有“春夏秋冬”四个字。
一种剪法如右图所示:
长方形纸条的面积:5×3=15(平方厘米) 大正方形的面积:11×11=121(平方厘米) 121÷15=8(个)……1(平方厘米) 理论上,最多能裁出8个长5厘米,宽3厘米的 长方形纸条。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学四年级《几何图形剪拼》练习题
【例1】将一张矩形纸对折再折(如下图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是()。
A. 矩形B. 三角形
C. 梯形D. 菱形
分析:本题需充分发挥想象力.因为所得四边形的两条对角线互相垂直平分,所以①展开后得到的平面图形是一个菱形。
答案:D。
【例2】四块如图①所示的瓷砖拼成一个正方形图案,使拼成的图案成一轴对称图形(如图②).请你分别在图③、图④中各画一种与图②不同的拼法,要求两种拼法各不相同,且至少有一个图形既是中心对称图形,又是轴对称图形。
分析:这道图形的组拼问题要求我们用轴对称、中心对称的性质解决问题,主要考查的是类比能力,知识迁移能力,动手能力。
答案:如下图:(答案不惟一)
【例3】现有一张长和宽之比为2∶1的长方形纸片,将它折两次(第一次折后也可以打开铺平再折第二次),使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作),如图a(虚线表示折痕).除图a外,请你再给出三种不同的操作,分别将折痕画在图c至图e 中(规定:一个操作得到的四个图形和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作,如图a和图b表示相同的操作)。
分析:要完成此题主要是动手操作,还要有一定的空间想象能力。
答案:如图所示:
【例4】直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形,方法如下图所示:
请你用上面图示的方法,解答下列问题:
对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形,如下图:
分析:见例5。
【例5】对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形,如下图:
分析:例4中根据已知条件中直角三角形剪切后拼成矩形的方法考虑一般三角形.
直角三角形中剪切的部分与待补的部分是全等的,一般三角形也如此。
(C)
E
E
D
C
B
A
C
B A
答案:例4如下图:
【例6】已知⊿ABC 为等腰三角形,AB=AC ,现沿着
过其一腰AC 的中点D 且垂直于底边的直线(裁剪线)将此 三角形剪成两部分,再在平面上把这两部分拼成一个直角梯 形。
试模仿上述做法,在图中的等腰⊿ABC 中再找出其他的裁 剪线,把它剪成两部分,再拼成一个平行四边形或矩形。
作出图形(直接画在图上,若有直角请标出); 指出裁剪线:沿( )剪开。
答案:中位线DE ,或底边上的高AD 。
【例7】一张正方形纸片经过两次对折,并在如图位置上剪去一个小正方形,打开后是( )
答案:B 。
D
E
D C(A)
B A D D C(A)
B A(B)A
(B)
D C(D)
B
A
【例8】如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞展开铺平,得到的图形是( )。
答案:D 。
【例9】请将一个正六边形分割成3个完全相同的五边形。
答案:
【例10】请将一个正八边形用两种不同方法分割成4个五边形,其中一种要求4个完全相同,另一种要求4个互不相同。
答案:
【例11】分别将一个正方形分割成7、8个正方形。
附加1
附加2
附加3
【作1】请将一个10边形分割成9个互不相同的五边形。
答案:
【作2】请将一个正三角形分割成9个相同的正三角形。
答案:
【作3】请将一个正三角形分割成12个相同的等腰三角形。
答案:
【作4】请将一个正三角形分割成54个相同的直角三角形。
答案:
【作5】请将一个正三角形分割成11个正三角形。
答案:。
