砌体第3章无筋砌体受压构件计算
《砌体结构》第3章 无筋砌体构件承载力计算

• 3.3.3 受剪构件计算 • 沿通缝或齿缝受剪构件的承载力,应按下式计
算。
• 3.3.4 计算示例
• 2)在确定影响系数 时,考虑到不同种类砌体 在受力性能上的差异,应先对构件高厚比分别 乘以下列系数:
• ①粘土砖、空心砖、空斗墙砌体和混凝土中型 空心砌块砌体1.0;
• ②混凝土小型空心砌块砌体1.1;
• ③粉煤灰中型实心砌块、硅ห้องสมุดไป่ตู้盐硅、细料石和 半细料石砌体1.2;
• ④粗料石和毛石砌体1.5。
• 图3.7 局部均匀受压
• 根据试验研究,砌体局部受压可能出现以下三 种破坏形式。
• (1)因纵向裂缝的发展而破坏
• [图3.9(a)] • (2)劈裂破坏 • [图3.9(b)]
• 图3.9 砌体局部均匀受压破坏 • (3)局压面积下砌体的压碎破坏
• 3.2.2 砌体局部均匀受压 • (1)局部抗压强度提高系数 • 砌体的抗压强度为f,局部抗压强度可取为γf,
• (3)梁端支承处砌体局部受压承载力计算
• 根据局部受压承载力计算的原理,梁端砌体局 部受压的强度条件为
• 由梁端支座反力N1在局部受压面上引起的平均 应力为σ= ,于是,(3.28)式可表达为:
• 因此可得梁端支承处砌体的局部受压承载力计 算公式为:
• (4)梁端下设有垫块时砌体的局部受压承载力计 算
• ②当0.7y<e≤0.95y时,除按式(3.16)验算受 压构件的承载力外,为了防止受拉区水平裂缝 的过早出现及开展较大,尚应按下式进行正常 使用极限状态验算。
• ③当e>0.95y时,直接采用砌体强度设计 值计算偏心受拉构件的承载力:
• 3.1.6 计算示例 • 3.2 局部受压 • 3.2.1 概述
无筋砌体受压构件承载力计算公式中

无筋砌体受压构件承载力计算公式中
无筋砌体受压构件是一种常见的建筑材料。
在进行承载力计算时,需要使用相应的公式。
下面将介绍无筋砌体受压构件承载力计算公式及其相关解释。
首先,无筋砌体受压构件的承载力可以用以下公式表示:
N = 0.45f_m * A
其中,N表示无筋砌体受压构件的承载力,f_m表示砌体的抗压强度,A表示砌体截面的有效面积。
需要注意的是,砌体的抗压强度是指砌体在受压状态下能承受的最大应力,通常使用试验数据进行评估。
砌体截面的有效面积是指砌体截面中,不考虑中空部分的实际有效面积。
此外,根据公式可以发现,无筋砌体受压构件的承载力与砌体抗压强度和砌体截面的有效面积有关。
因此,在进行承载力计算时,需要准确测量砌体的抗压强度和截面的有效面积。
最后,需要注意的是,该公式适用于无筋砌体受压构件在受压状态下的承载力计算。
对于其他类型的构件如受弯构件,其承载力的计算需要使用相应的公式。
总之,无筋砌体受压构件承载力计算公式是一个重要的结构工程计算公式,建筑工程师需要熟练掌握,以确保建筑结构的安全性和稳定性。
砌体结构3章
1.5 0.5 A0
Al
砌体结构
3 梁端砌体局部受压计算 《规范》规定梁端砌体局部受压承载力采用如下
公式计算:
N0 Nl hfAl
1.5 0.5 A0 Al
N0 0 Al
Al a0b
a0 10
hc f
砌体结构
上部荷载的折减系数,当A0/Al大于等于3时, 应取 等于0;
ei i
1 1
0
纵向弯曲系数
0
1
1 hb
2
h1
ei
12
1
0
矩形截面
当砂浆强度等级≥M5时,h0.0015
当砂浆强度等级为M2.5时,h0.002 当砂浆强度为零时,h=0.009
h——与砂浆强度等级有关的系数
e
1 1 12( e
ei h
)2
规范中考虑纵向弯曲 和偏心距影响的系数:
1
12
e h
1.25
A0 (a h)h
砌体结构
3.2.2 梁端支承处砌体的局部受压
1.梁端有效支承长度 a0
梁端底面没有离开砌体的长度称为有效支承度 a0
令
Nl h l a0b
h 梁端底面压应力图形完整系数;
l 边缘最大局压应力。
按弹性地基梁理论有:l kymax k 为垫层系数; ymax 为墙体边缘最大变形; 代入上式得:
1、修改构件截面尺寸和形状 (如;增加梁高或增加墙垛)
2、设置具有中心装 置的垫块或缺口垫块
3.2 砌体局部受压承载力计算
砌体局部受压是砌体结构中常见的受力形式,由于局部受 压面积小,而上部传下来的荷载往往很大,当设计或施工不当 时,均可酿成极其严重的工程事故。
第3章受压构件精品文档
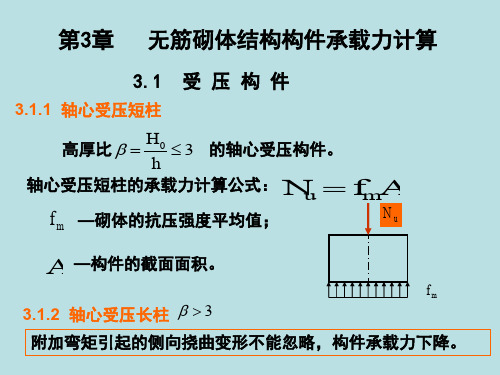
e M 3 0 0 .2 m 2 0 0 m m 0 .6 y 2 9 7 m m N 1 5 0
满足规范要求。
(2)承载力验算
MU10烧结粘土砖与M5混合砂浆砌筑,查表得
=1.0;
HO hT
1.0 5 7.07 0.707
1
1 e
ei
2
i
考虑纵向弯曲和 的偏 影心 响距 系
ei 附加偏心距。
e0,0ei i
1 1
0
1ei
1
1
0
12
/ i2
i
h 12
代入
对矩形截 面 1
2
112e h
11210 1
1.2 5 9.68 0.62
及
e12m5m
查表得
0.4 6 5
查表得,MU10蒸压灰砂砖与M5水泥砂浆砌筑的砖砌体 抗压强度设计值f=1.5MPa。
柱底截面承载力为:
a fA
=0.465×1.0×1.5×490×620×10-3=211.9kN>150kN。
(2)弯矩作用平面外承载力验算 对较小边长方向,按轴心受压构件验算,此时
没有考虑砌体的弹塑性性能和破坏时边缘 应力的提高,计算值均小于实验值。
e
1 1(e/
i)2
e
1
1
ey i2
《砌体规范》进行修正:
e
Nu
Nu A
1
e2 i2
fm
fm
fm
e
1 1(e/
砌体无筋砌体受压构件计算
计算得到
e
e
查表(三个参数: 、 或 h、砂浆hT 强度等级)
—f—砌体抗压强度设计值; (注意调整系数 的适用a 条件)
—A—截面面积,对各类砌体均可按毛面积计算。
二、注意问题
砌体结构
• 对矩形截面构件,当轴向力偏心方向的截面边长大于
另一方向的边长时(即弯矩偏向于长边时),除按偏
心受压计算外,还应对较小边长方向按轴心受压进行
f 1.30MPa
砌体结构
A 0.37 0.49 0.181 m2 0.3 m2
a 0.7 A 0.7 0.181 0.881
H0 h
1.0 3.6 0.37
9.73 3
砌体结构
2. 柱底截面所承受的轴力最大,因此验算此截面。
砖柱自重设计值:
1.35180.1813.6=15.83 kN
减小,截面刚度相应削弱,构件承载力显著
e
降低。因此,在 很y大时,从经济性和合理性 角度看,都不宜采用无筋砌体构件。为设计
合理并保证使用安全,对无筋砌体偏心受压
构件,《规范》规定轴向力的偏心距不应超
过
0。.6 y
砌体结构
❖ 当 e 0.时6y,应采用配筋砌体或采取一定的构造措施减 小偏心距。
如:在梁或屋架端部设置垫块以调整力的作用位置,或 改变截面尺寸以减小偏心距。
—y—受压边缘到截面形心轴的距离
当偏心距不大,全截面受压或者受拉边缘没有开裂的情况下,
当受压边缘的应力达到砌体的抗压强度 时,fm短柱所能承受的
压力为:
砌体结构
Nu
1
1
ey i2
Afm
a ' Afm
a' 1
1
《砌体结构》课后习题答案(本)

第三章 无筋砌体构件承载力的计算3.1柱截面面积A=0.37×0.49=0.1813m 2<0.3 m 2砌体强度设计值应乘以调整系数γa γa =0.7+0.1813=0.8813查表2-8得砌体抗压强度设计值1.83Mpa ,f =0.8813×1.83=1.613Mpa7.1037.06.31.10=⨯==h H βγβ 查表3.1得:ϕ= 0.8525 kN N kN N fA 1403.249103.249101813.0613.18525.036=>=⨯=⨯⨯⨯=ϕ满足要求。
3.2(1)沿截面长边方向按偏心受压验算 偏心距mm y mm N M e 1863106.06.03210350102.1136=⨯=<=⨯⨯== 0516.062032==h e 548.1362070002.10=⨯==h H βγβ 查表3.1得:ϕ= 0.6681 柱截面面积A=0.49×0.62=0.3038m 2>0.3 m 2 γa =1.0查表2-9得砌体抗压强度设计值为2.07Mpa , f =1.0×2.07=2.07 MpakN N kN N fA 35015.4201015.420103038.007.26681.036=>=⨯=⨯⨯⨯=ϕ满足要求。
(2)沿截面短边方向按轴心受压验算14.1749070002.10=⨯==h H βγβ 查表3-1得:φ0= 0.6915因为φ0>φ,故轴心受压满足要求。
3.3(1)截面几何特征值计算截面面积A=2×0.24+0.49×0. 5=0.725m 2>0.3m 2,取γa =1.0 截面重心位置m y 245.0725.025.024.05.049.012.024.021=⎪⎭⎫ ⎝⎛+⨯⨯+⨯⨯= y 2=0.74-0.245=0.495m截面惯性矩()()232325.0495.05.049.0125.049.012.0245.024.021224.02-⨯⨯+⨯+-⨯⨯+⨯=I =0.02961m 4截面回转半径 m A I i 202.0725.002961.0=== T 形截面折算厚度h T =3.5i=3.5×0.202=0.707m(2)承载力m y m N M e 147.0245.06.06.01159.0630731=⨯=<=== 164.0707.01159.0==T h e 22.12707.02.72.10=⨯==T h H βγβ 查表3-1得:ϕ= 0.4832 查表2-7得砌体抗压强度设计值f =2.07Mpa则承载力为 kN kN N fA 63016.7251016.72510725.007.24832.036>=⨯=⨯⨯⨯=ϕ3.4(1)查表2-8得砌体抗压强度设计值f =1.83 Mpa砌体的局部受压面积A l =0.2×0.24=0.048m 2影响砌体抗压强度的计算面积A 0=(0.2+2×0.24)×0.24=0.1632m 2(2)砌体局部抗压强度提高系数 5.1542.11048.01632.035.01135.010>=-+=-+=l A A γ 取5.1=γ (3)砌体局部受压承载力kNN kN N fA l 13576.1311076.13110048.083.15.136=≈=⨯=⨯⨯⨯=γ%5%46.2%10076.13176.131135<=⨯- 承载力基本满足要求。
无筋砌体构件局部受压计算书
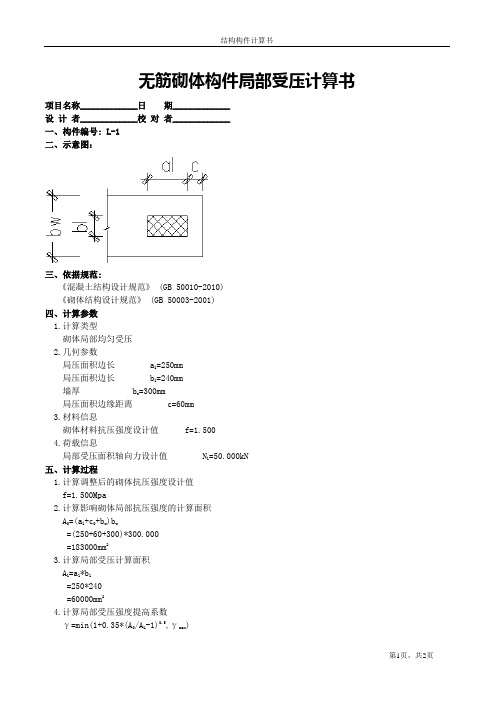
无筋砌体构件局部受压计算书项目名称_____________日期_____________
设计者_____________校对者_____________
一、构件编号: L-1
二、示意图:
三、依据规范:
《混凝土结构设计规范》 (GB 50010-2010)
《砌体结构设计规范》 (GB 50003-2001)
四、计算参数
1.计算类型
砌体局部均匀受压
2.几何参数
局压面积边长a l=250mm
局压面积边长b l=240mm
墙厚b w=300mm
局压面积边缘距离c=60mm
3.材料信息
砌体材料抗压强度设计值f=1.500
4.荷载信息
局部受压面积轴向力设计值N l=50.000kN
五、计算过程
1.计算调整后的砌体抗压强度设计值
f=1.500Mpa
2.计算影响砌体局部抗压强度的计算面积
A0=(a l+c0+b w)b w
=(250+60+300)*300.000
=183000mm2
3.计算局部受压计算面积
A l=a l*b l
=250*240
=60000mm2
4.计算局部受压强度提高系数
γ=min(1+0.35*(A0/A L-1)0.5,γmax)
=min(1+0.35*(183000/60000-1)0.5,2.500)
=min(1.501,2.500)
=1.501
5.计算局部受压承载力
N=γ*f*A l
=1.501*1.500*60000
=135.101kN
6.验算结果
N l=50.000kN≤N=135.101kN,局部受压承载力满足要求。
第三章无筋砌体受压构件计算

在截面尺寸和材料强度等级一定的条件下,以 及在施工质量得到保证的前提下,影响无筋砌
体受压承载力的主要因素是构件的高厚比
和相对偏心距。
《砌体规范》用承载力影响系数Ψ考虑以上两种 因素的影响。
(2) 在设计无筋砌体偏心受压构件时,偏心距 过大,容易在截面受拉边产生水平裂缝,致使 受力截面减小,构件刚度降低,纵向弯曲影响 增大,构件的承载力明显降低,结构既不安全 又不经济,所以《砌体规范》限制偏心距不应 超过0.6y(y为截面重心到轴向力所在偏心方 向截面边缘的距离)。
h 12 0
三、受压构件承载力计算
砌体材料类别 烧结普通砖、烧结多孔砖 混凝土及轻骨料混凝土砌块 蒸压灰砂砖、蒸压粉煤灰砖、细料石、半细料石
粗料石、毛石
1.0 1.1 1.2 1.5
本章小结
(1) 无筋砌体受压构件按照高厚比的不同以及 荷载作用偏心距的有无,可分为轴心受压短柱、 轴心受压长柱、偏心受压短柱和偏心受压长柱。
I
2、受剪承载力计算公式 VS
Ib
M ftmW
V fvbz
z I S
三、受剪构件(P41)
V ( fv 0 ) A
当永久荷载分项系数γG=1.2时
0.26 0.082 0
f
当永久荷载分项系数γG=1.35时
0.23 0.065 0
f
【例1】截面490×620mm的砖柱,采用 MUl0烧结普通砖及M2.5水泥砂浆砌筑, 计算高度H0=5.6m,柱顶承受轴心压 力标准值Nk=189.6kN(其中永久荷载 135 kN,可变荷载54.6 kN)。试验算 核柱柱底截面承载力(柱体容重为 18kN/m2)。
N A
My I
N A
(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
受拉,则矩形截面受压区的高度为:
h' 3(he)h(1.53e)
2
h
则此时短柱能承受的压力为:
N u 1 2 b h 'fm 1 2 b h ( 1 .5 3 h e )fm ( 0 .7 5 1 .5 h e )A fm
砌体结构
此时:
a' 0.751.5 e h
讨论:轴心受压时,e=0,a’=1;当偏心受压时,a’<1;
砌体结构
第3章 无筋砌体受压构件承载力计算
学习要点 • 了解无筋砌体受压构件的破坏形态和影响受压承
载力的主要因素。 • 熟练掌握无筋砌体受压构件的承载力计算方法。 • 了解无筋砌体受弯、受剪及受拉构件的破坏特征
及承载力的计算方法。
砌体结构
砌体结构
砌体结构
对T形截面:
H0 hT
砌体结构
式中: hT——T形截面的折算厚度,近似取 hT 3.5 i
hT
—i—截面回转半径
i I A
截面惯性矩 截面面积
二、承载力分析
砌体结构
受压短柱承受轴向压力N时,如果把砌体当成匀质弹性 体,按照材料力学的方法,N AN IeyN A(1ei2 y)
式中:
A、I、—i—分别为砌体的截面面积、惯性矩和回转半径
e——轴向压力的偏心距
承载力的影响系数
当 e时0,
0
1 1 (ei
)2
i
则, (ei )2 1 1
i
0
砌体结构
解得:ei i
1 1
0
对矩形截面:i
,h
12
ei
h 12
1 1
0
代入可推出:
112he
1
1(1
12 0
2 1)
• 从上式可以看出:
砌体结构
当 e ,0
h
当 e ,0
h
0时,1.0为轴压短柱 —— 0时,1.0为轴压长柱 ——
f2
2.5Mpa ,
0.002
f2 0Mpa , 0.009
3.1.3 偏心受压长柱的承载力分析
砌体结构
如果取长柱的偏心距为荷载作用偏心距 e和
纵向挠曲引起的附加偏心距 之e和i ,则受压构件
的影响系数 为:
N
1
1 (e ei )2
i
式中:——高厚比 和 轴向力的
e ei
偏心距 对受压e构件
砌体结构
砌体结构
无筋砌体在轴向压力作用下,认为截面应力分布是均匀 的,破坏时构件被若干条竖向裂缝分割为小柱体,并出现 明显侧向鼓胀,截面应力达到砌体的轴心抗压强度 (上页
图a)。
当轴向力具有较小偏心时,截面应力不再均匀分布,由于 砌体的弹塑性性能,应力图形呈曲线形,一侧压应力较大, 另一侧压应力较小(图b)或出现较小的拉应力(图c)。构 件首先在压应力较大区域出现竖向裂缝,然后逐渐扩展;破 坏时,压应力较大的一侧可能出现块体压碎现象。构件边缘
—y —受压边缘到截面形心轴的距离
当偏心距不大,全截面受压或者受拉边缘没有开裂的情况下,
当受压边缘的应力达到砌体的抗压强度 时,f m短柱所能承受的
压力为:
砌体结构
Nu
1
1
ey i2
Afm
a'
Afm
a' 1
1
ey i2
对于矩形截面柱,若h为沿轴向力偏心方向的边长,则有:
a
'
1
1 6e
h
对于偏心距较大,受拉边缘已经开裂的情况,不考虑砌体
根据大量的试验资料,规定砌体受压时的偏心影响系数按
下列公式计算:
1
1
1 e i
2
i—截面回转半径; e—偏心距
对于矩形截面(b×h):
1
1
1
1
2
e h
2
砌体结构
对于“T”形和“+”字形截面折算:厚度
1
1
1 12
e hT
2
hT 12i 3.5i
砌体结构
3.1.2 轴心受压长柱的承载力分析
a’称为按材料力学计算的砌体偏心距影响系数。
砌体结构
大量的砌体构件受压试验表明,按材料力学公式计算的 承载力远低于试验结果。
1、轴心受压时,截面中应力均匀分布; 2、偏心距逐渐增加时,截面中应力成曲线分布; 3、当受拉边缘的应力大于砌体抗拉强度时,产生水平裂缝。 随着裂缝的发展,荷载对实际受压面积的偏心距在逐渐变小, 裂缝不至无限发展导致构件破坏,而是在剩余面积和减小的 偏心距作用下达到新的平衡。
砌体结构
根据第一章知识,取 E460fm fm(1fm)
代入公式,则相应的临界应力为:
cri 4602fm fm(1fc m ri)(H i)2
则轴心受压时的稳定系数为:
0fc m ri 4602 fm(1fc m ri)(H i0)2
令 1 4602 fm(Hi0)2 ,当为矩形截面时 i
最大压应变和最大压应力略大于轴心受压构件(即 1 )f。
砌体结构
当轴向力偏心距较大时,构件截面的拉应力较大,当 拉应力超过砌体的抗拉强度时,在受拉边出现水平裂缝, 实际的受压截面不断减小,纵向力对实际受压截面的偏心 距随之减小(由e 3 降为 e)4 ,剩余截面的应力合力与偏心 压力保持新的平衡,仍可继续承受荷载,最后受压区出现 竖向裂缝,块体被压碎而破坏(图d)。受压较大边的极
h 12
取 H0 h
可得
1 3702
1
fm 2
砌体结构
则轴心受压时的稳定系数可表示为:
0
1
111
1
1 1
370 fm
2
1
12
稳定系数表示长柱与短柱轴心受压之比, 0 1
规范给出了计算轴心受压柱的稳定系数:
0
1
1
2
式中: ——与砂浆强度有关的系数
f2 5Mpa , 0.0015
限压应变和压应力随偏心矩的增大而增大。
砌体结构
可以看出,受压构件随着偏心距的增大,尽管 321f ,局部受压强度有所提高,但截面应力分布越来越不均匀,甚 至部分截面因开裂退出工作,使受压构件的承载力随偏心距的
增大而明显降低,即: N u1N u2N u3N u4
因此,在材料力学偏心距影响系数公式形式的基础上,
长柱受压 → 侧向变形 → 纵向弯曲 → 严重者破坏 → N长< N短
轴心受压长柱承载力计算中一般是采用稳定系数 0
考虑纵向弯曲的影响。根据欧拉公式,长柱发生纵向
弯式曲中破:坏的临界应力为:criA 2EH02I2EHi0
2
E——弹性模量
H0——柱的计算高度
砌体的弹性模量是随应力的增加而降低,当应力达到 临界应力时,弹性模量已经有较大程度的降低,此时的 弹性模量可取临界应力时处的切线模量。
(稳定系数)
1.0
0
当 e ,0
h
当 e ,0
h
0时,1.0为偏压短柱 ——
e
(偏心影响系数)
0时,1.0为偏压长柱 ——
(综合影响系数)
➢
对于T形截面构件,用折算厚度
