圆环体表面积计算公式
球的表面积和体积的计算

球的表面积和体积的计算在我们的日常生活和学习中,球是一种常见的几何图形。
从足球、篮球到地球,球的形状无处不在。
而了解球的表面积和体积的计算方法,不仅在数学学习中至关重要,在实际生活和科学研究中也有着广泛的应用。
要计算球的表面积和体积,首先我们得明确球的定义。
球是空间中到一定点的距离等于定长的所有点组成的图形,这个定点称为球心,定长称为球的半径。
我们先来探讨球的表面积的计算。
球的表面积公式为:S =4πr²,其中S 表示球的表面积,r 表示球的半径,π是一个常数,约等于314。
为了更直观地理解这个公式,我们可以想象将一个球沿着经线和纬线切成很多小块,然后把这些小块展开铺平。
你会发现,这些小块近似于一个个小的矩形,而矩形的长就是球的周长2πr,宽就是球面上很小的一段弧长 dr。
对这些小矩形的面积进行积分,就可以得到球的表面积。
假设我们把球分成无数个很薄的圆环,每个圆环的宽度为 dr。
那么每个圆环的周长就是2πr,面积就是2πr × dr。
对所有圆环的面积从 0到 r 进行积分,就得到了球的表面积:∫(0 到r) 2πr × dr =2π ∫(0 到 r) r dr =2π × r²/2 (0 到 r) =4πr²接下来,我们看看球的体积的计算。
球的体积公式是:V =(4/3)πr³ 。
理解球体积的计算,可以通过一种叫做“祖暅原理”的方法。
想象一个半球装满了水,然后将它倒置在一个与半球等底等高的圆柱形容器中。
此时,半球内的水刚好充满圆柱形容器和一个与圆柱等底等高的圆锥之间的空间。
因为我们知道圆柱的体积是底面积乘以高,即πr²h (这里 h 就是球的半径 r),圆锥的体积是(1/3)πr²h ,所以半球的体积就是圆柱体积减去圆锥体积,即:πr³ (1/3)πr³ =(2/3)πr³ ,那么整个球的体积就是(4/3)πr³ 。
面积的单位换算、公式及计算

面积的单位换算、公式及计算计算长方形:{长方形面积=长×宽}[1]正方形:{正方形面积=边长×边长}平行四边形:{平行四边形面积=底×高}三角形:{三角形面积=底×高÷2}梯形:{梯形面积=(上底+下底)×高÷2}圆形(正圆):{圆形(正圆)面积=圆周率×半径×半径}圆环:{圆形(外环)面积={圆周率×(外环半径^2-内环半径^2)}扇形:{圆形(扇形)面积=圆周率×半径×半径×扇形角度/360}长方体表面积:{长方体表面积=(长×宽+长×高+宽×高)×2}正方体表面积:{正方体表面积=棱长×棱长×6}球体(正球)表面积:{球体(正球)表面积=圆周率×半径×半径×4}椭圆(其中π(圆周率,a,b分别是椭圆的长半轴,短半轴的长).半圆:(半圆形的面积公式=圆周率×半径的平方÷2)面积单位换算常用的面积单位有公顷、亩、平方公里、平方米、平方厘米等。
这里所说的换算,常指面积之间单位的互换计算。
如:1亩=0.0666666公顷=666.6666平方米等。
目录1常用公式2台湾公式3国外公式1常用公式常用土地面积换算公式 1亩=60平方丈=6000平方尺,1亩=666.6平方米其实在民间还有一个更实用的口决来计算:平方米换为亩,计算口诀为“加半左移三”。
1平方米=0.0015亩,如128平方米等于多少亩?计算方法是先用128加128的一半:128+64=192,再把小数点左移3位,即得出亩数为0.192。
亩换平方米,计算口诀为“除以三加倍右移三”。
如要计算24.6亩等于多少平方米,24.6÷3=8.2,8.2加倍后为16.4,然后再将小数点右移3位,即得出平方米数为16400。
高中数学的几何体表面积和体积公式是哪些

高中数学的几何体表面积和体积公式是哪些高中数学的几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)数学基础差的学生如何提高数学成绩基础薄弱的同学提高数学成绩的方法数学基础打牢,是个非常重要的事,很多及格成绩不到的同学,基本是连计算和公式都不是很过关。
对于这一类学生有以下几点建议。
圆环的底面积公式

圆环的底面积公式
圆环的底面积公式为:$S=\pi(R^2-r^2)$,其中$R$为圆环的外半径,$r$为圆环的内半径,$S$为圆环的底面积。
除了圆环的底面积,圆环还有其他几个重要的性质和公式,例如:
1.圆环的周长公式为$C=2\pi(R+r)$,其中$C$为圆环的周长。
2.圆环的面积公式可以通过将圆环截成若干个扇形,并计算出每
个扇形的面积来计算。
一个扇形的面积为$S_{\text{扇
形}}=\frac{1}{2}r^2\theta$,其中$r$为圆环的半径,$\theta$为扇
形的圆心角度数,然后将所有扇形的面积相加即可得到圆环的面积公式。
3.圆环的体积公式为$V=\pi h(R^2-r^2)$,其中$h$为圆环的高度。
4.圆环的内外表面积公式为$S_{\text{内表面积}}=\pi r h$和
$S_{\text{外表面积}}=\pi R h$,分别表示圆环内表面和外表面的面积。
综上所述,圆环是一个重要的几何形体,在不同的应用中,需要使用不同的圆环公式。
圆外表面积公式

圆外表面积公式圆的面积公式和表面积公式,我们在计算圆的面积公式推导方法其实有很多种,计算圆的面积是小学的相关知识,我已经为大家搜集和整理好了圆的面积公式和表面积公式的相关信息,一起来了解一下吧。
圆的面积公式和表面积公式1S=πr(r—半径,d—直径,π—圆周率)。
把圆平均分成若干份,可以拼成一个近似的长方形。
长方形的宽就等于圆的半径(r),长方形的长就是圆周长(C)的一半。
长方形的面积是ab,那圆的面积就是:圆的半径(r)的平方乘以π。
即圆的面积=半径×半径×圆周率。
圆的性质1、圆是轴对称图形,其对称轴是任意一条通过圆心的直线。
圆也是中心对称图形,其对称中心是圆心。
2、在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的`其余各组量都分别相等。
3、如果两圆相交,那么连接两圆圆心的线段(直线也可)垂直平分公共弦。
圆环面积求法:1、圆环面积S=外圆面积-内圆面积=圆周率×(大半径平方-小半径平方)=π(R×R-r×r)=π(R-r)。
2、圆环面积S=π[(R-r)×(R+r)]。
R=大圆半径,r=圆环宽度=大圆半径-小圆半径。
圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
生活中的例子有空心钢管,甜甜圈,指环等,截取圆环一部分的叫扇环。
圆的面积公式和表面积公式2π---园周率S---面积L---周长r---圆半径d----圆直径圆的面积计算公式:S = π×r2 =3.1416×r2圆周长计算公式:L = 2×π×r(圆的面积说白了一点就是:半径乘于半径乘于3.14)已知圆的面积求直径:直径:2√(面积÷园周率)求面积例:一个单根直径为80毫米的电缆线,求其截面积3.14×(40×40)或3.14×402= 3.14×1600 = 5024(平方毫米)求球的体积计算公式:4.18879×半径×半径×半径。
多面体的体积和表面积计算公式大全
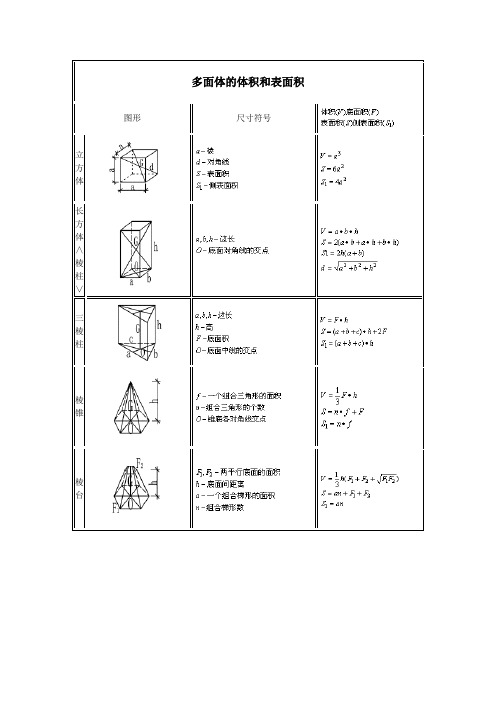
多面体的体积和表面积图形尺寸符号
立
方
体
长
方
体
∧
棱
柱
∨
三
棱
柱
棱
锥
棱
台
圆柱和空心圆柱∧管∨
斜线直圆柱
直圆锥
圆台
球
球扇形∧球楔∨
球缺
圆环体∧胎∨
球
带
体
桶
形
椭
球
体
a,b,c-半轴
交
叉
圆
柱
体
梯
形
体
常用图形求面积公式
图形尺寸符号面积(F)表面积
(S)
正方形
长方形
三角形
平行四边
形
任意四边
形
正多边形菱形梯形圆形
椭圆形a·b-主轴F= (π/4) a·b
扇形
弓形
圆环
部分圆环
新月形
L d/102d/10 3d/10 4d/105d/10 6d/10 7d/10
P 0.400.79 1.18 1.56 1.91 2.25 2.55
抛物线形
等多边形
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
球体体积和表面积计算公式

球体体积和表面积计算公式球体是一个非常常见的几何形状,它具有一些特殊的性质。
在本文中,我们将讨论球体的体积和表面积的计算公式,并对其进行解释和推导。
让我们来看看球体的体积计算公式。
球体的体积是指球体所占据的空间。
为了计算球体的体积,我们需要知道球体的半径。
球体的半径是指从球心到球体表面上的任意一点的距离。
球体的体积计算公式如下:V = (4/3)πr³其中,V表示球体的体积,π是一个常数,近似取值为3.14159,r 表示球体的半径。
接下来,让我们来看看球体的表面积计算公式。
球体的表面积是指球体表面的总面积。
为了计算球体的表面积,同样需要知道球体的半径。
球体的表面积计算公式如下:A = 4πr²其中,A表示球体的表面积,π是一个常数,近似取值为3.14159,r表示球体的半径。
下面,我们将对这两个公式进行推导和解释。
首先,让我们从球体的体积公式开始推导。
球体可以看作是无限多个无穷小的圆柱叠加而成。
每个圆柱的体积可以表示为:Vc = πr²h,其中,r是圆柱的底面半径,h是圆柱的高度。
当我们将无限多个无穷小的圆柱叠加在一起时,高度h将趋近于0,而底面半径r将趋近于球体的半径r。
因此,我们可以得到球体的体积公式:V = lim(ΔVc) = lim(πr²h) = πr²lim(h) = πr²(0) = 0但是,我们知道球体是有体积的,因此上述推导是不正确的。
事实上,球体的体积公式应该是使用积分来表示。
通过对圆柱体积的连续求和,我们可以得到球体的体积公式:V = ∫(0 to R)πr²dh = π∫(0 to R)r²dh = πr²h∣∣∣(0 to R) = πr²R其中,R是球体的半径。
这个公式是通过使用积分来考虑球体的无穷小高度h,从而得到球体的体积。
接下来,让我们来看看球体的表面积公式的推导。
圆的体积和面积

圆的体积和面积一、引言圆是我们生活中常见的几何图形之一,它具有独特的性质和特点。
其中,圆的面积和体积是我们最为关注的两个问题。
本文将从理论、公式和实际应用等方面详细介绍圆的面积和体积。
二、圆的面积1. 定义圆的面积是指一个圆形所围成区域的大小,通常用单位平方(如平方厘米)表示。
2. 公式计算圆的面积需要使用圆周率π,其值为3.1415926...。
根据定义可知,一个半径为r的圆形所围成区域的面积为πr²。
3. 实例分析例如,一个半径为5厘米的圆形所围成区域的面积为25π平方厘米(约78.54平方厘米)。
4. 圆环面积当我们需要计算两个同心圆之间环形区域(即圆环)的面积时,可以使用以下公式:(π(R²-r²))。
其中R表示外层圆半径,r表示内层圆半径。
三、圆的体积1. 定义一个立体图形所包含空间大小称为其体积。
对于一个球体来说,其体积被称为球的体积。
2. 公式计算一个半径为r的球体的体积可以使用以下公式:(4/3)πr³。
3. 实例分析例如,一个半径为10厘米的球体的体积为(4/3)π1000立方厘米(约4188.79立方厘米)。
4. 圆柱体积当我们需要计算一个圆柱的体积时,可以使用以下公式:πr²h。
其中r 表示圆柱底面半径,h表示圆柱高度。
5. 圆锥体积当我们需要计算一个圆锥的体积时,可以使用以下公式:(1/3)πr²h。
其中r表示圆锥底面半径,h表示圆锥高度。
四、应用案例1. 地球表面积和体积地球是一个近似于球形的天体。
根据测量数据可知,地球赤道半径约为6378.1公里,极半径约为6356.8公里。
因此,地球表面积约为510,072,000平方公里(约196,935,000平方英里),地球总体积约为1.08 × 10¹²立方公里(约259,875,159立方英里)。
2. 建筑物空间设计在建筑物设计中,需要考虑建筑物内部空间的大小和形状。
